Prediction of Electrical Resistance with Conductive Sewing Patterns by Combining Artificial Neural Networks and Multiple Linear Regressions
Abstract
:1. Introduction
2. Materials and Experiments
2.1. Materials
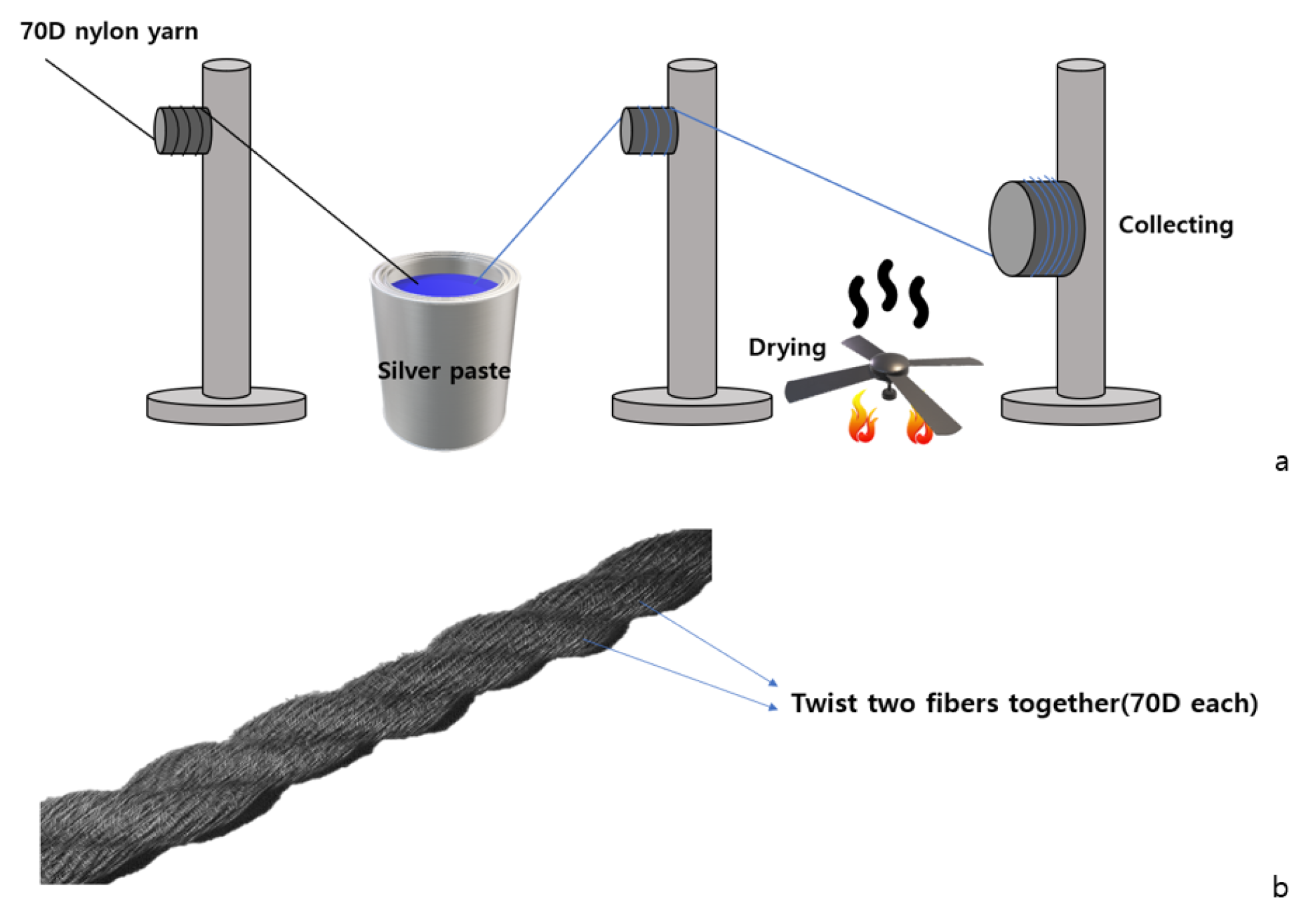
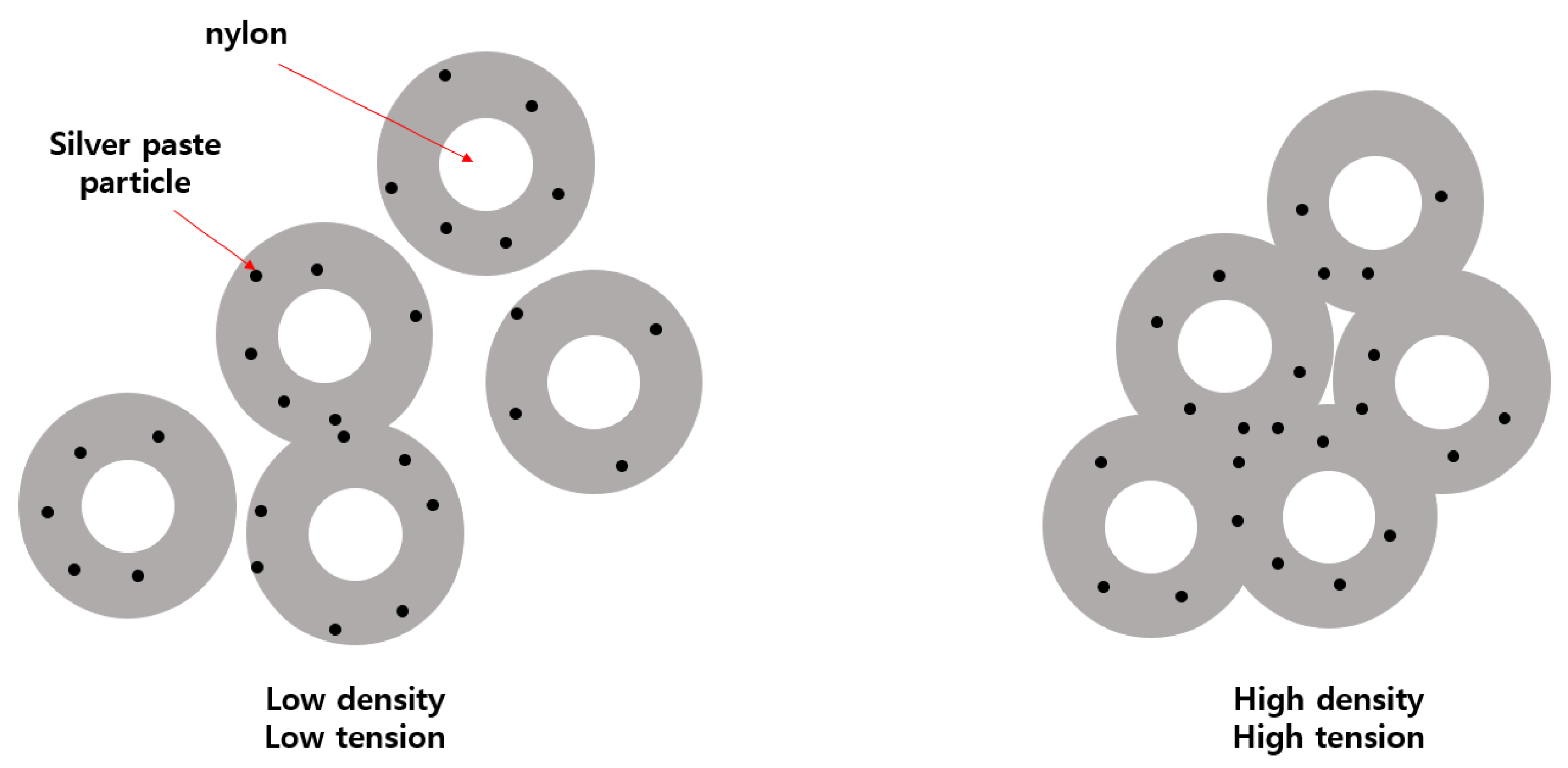
2.2. Experiments
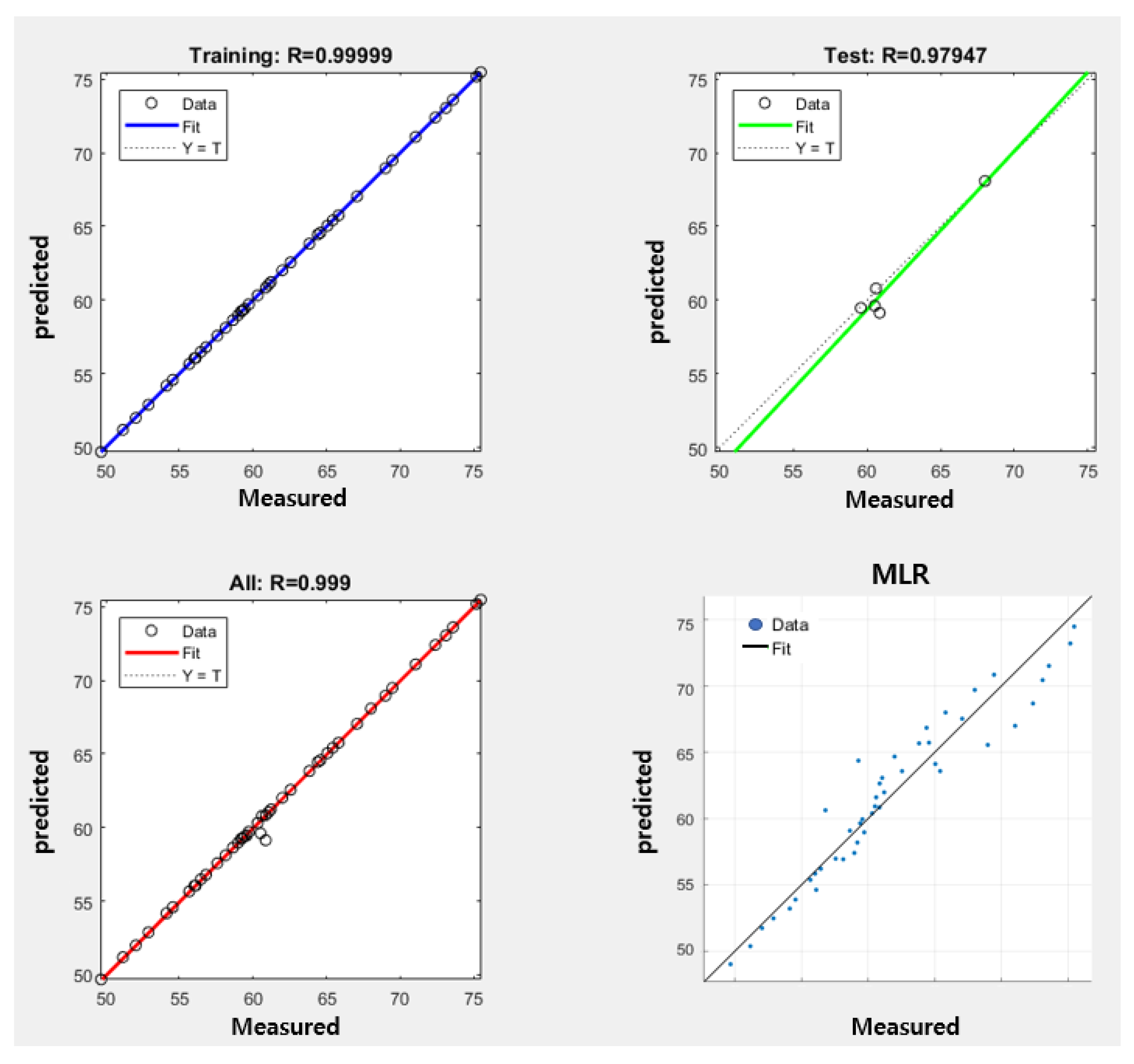
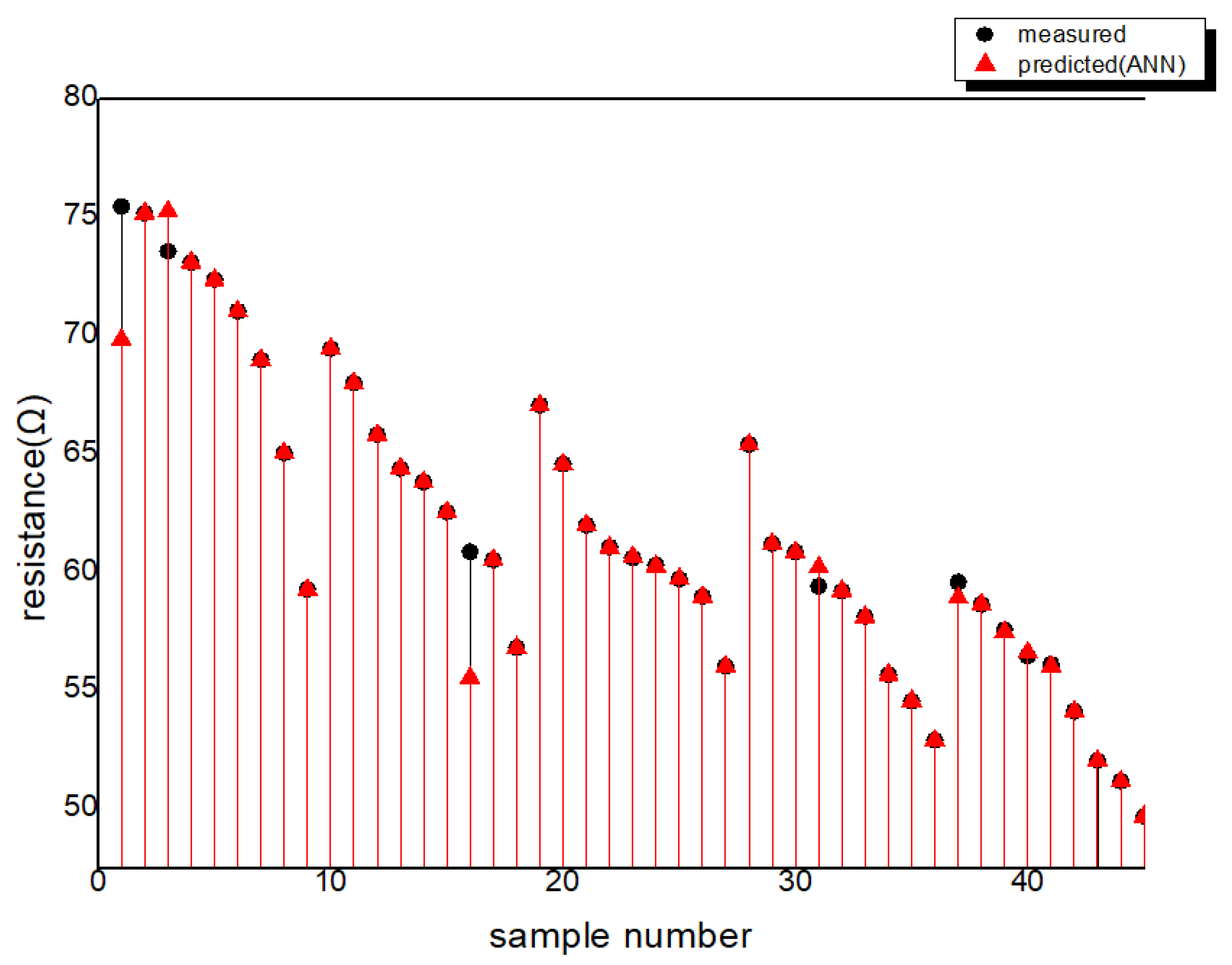
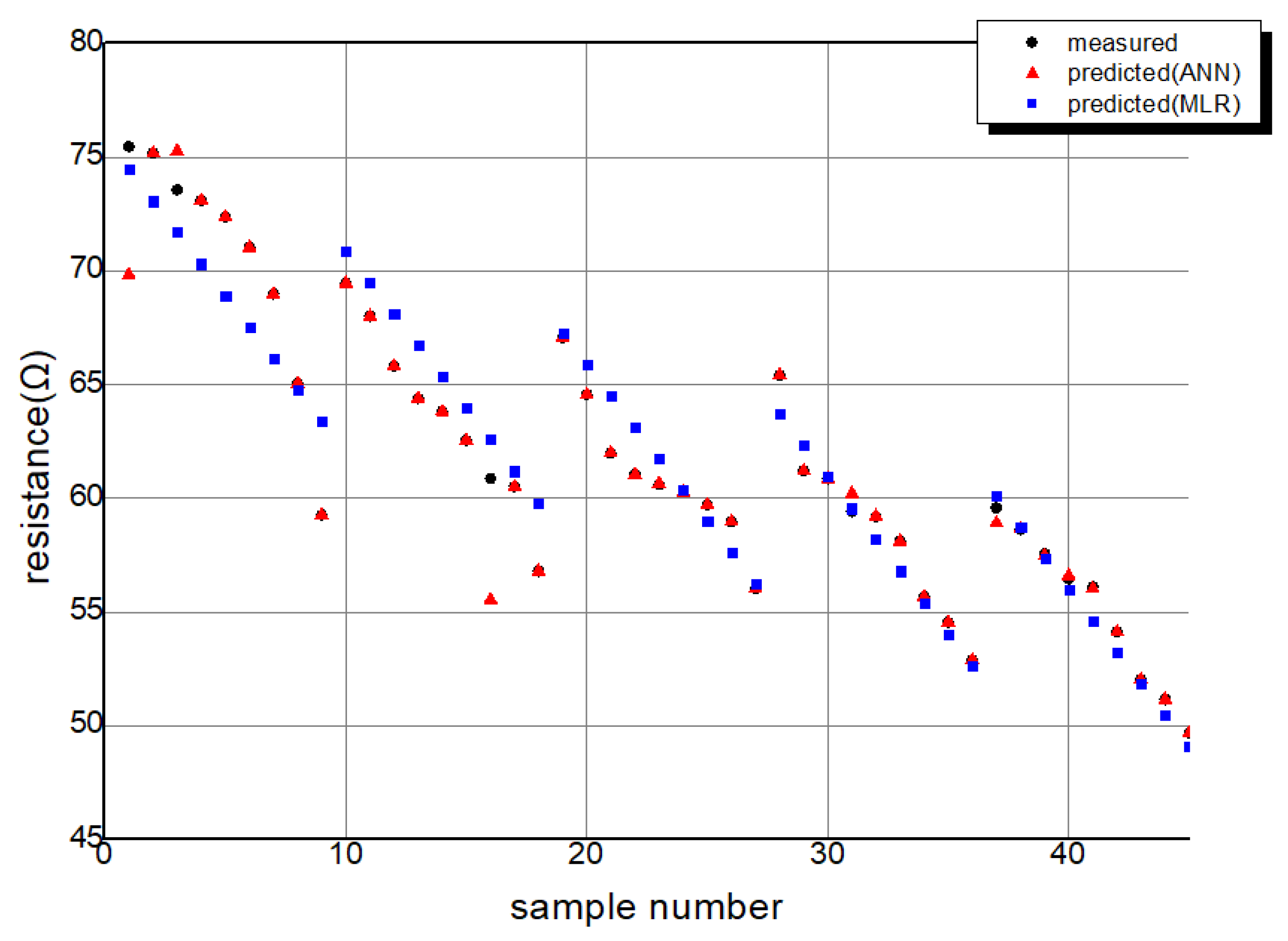
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hu, H.; Huang, Y.; Zhu, M.; Meng, W.; Liu, C.; Pei, Z.; Hao, C.; Wang, Z.; Zhi, C. From Industrially Weavable and Knittable Highly Conductive Yarns to Large Wearable Energy Storage Textiles. ACS Nano 2015, 9, 4766–4775. [Google Scholar]
- Ismar, E.; Bahadir, S.K.; Kalaoglu, F.; Koncar, V. Futuristic Clothes: Electronic Textiles and Wearable Technologies. Glob. Chall. 2020, 4, 1900092. [Google Scholar] [CrossRef]
- Heo, J.S.; Eom, J.; Kim, Y.-H.; Park, S.K. Recent progress of textile-based wearable electronics: A comprehensive review of materials, devices, and applications. Small 2018, 14, 1703034. [Google Scholar] [CrossRef] [PubMed]
- Lund, A.; Tian, Y.; Darabi, S.; Müller, C. A polymer-based textile thermoelectric generator for wearable energy harvesting. J. Power Sources 2020, 480, 228836. [Google Scholar] [CrossRef]
- Jeong, M.J.; Yun, T.-I.; Baek, J.J.; Kim, Y.T. Wireless power transmission using a resonant coil consisting of conductive yarn for wearable devices. Text. Res. J. 2015, 86, 1543–1548. [Google Scholar] [CrossRef]
- Sun, X.; He, J.; Qiang, R.; Nan, N.; You, X.; Zhou, Y.; Shao, W.; Liu, F.; Liu, R. Electrospun Conductive Nanofiber Yarn for a Wearable Yarn Supercapacitor with High Volumetric Energy Density. Materials 2019, 12, 273. [Google Scholar] [CrossRef]
- Yoo, H.-J. Your Heart on Your Sleeve: Advances in Textile-Based Electronics Are Weaving Computers Right into the Clothes We Wear. IEEE Solid-State Circuits Mag. 2013, 5, 59–70. [Google Scholar] [CrossRef]
- Chen, L.; Wang, T.; Shen, Y.; Wang, F.; Chen, C. Stretchable Woven Fabric-Based Triboelectric Nanogenerator for Energy Harvesting and Self-Powered Sensing. Nanomaterials 2023, 13, 863. [Google Scholar] [CrossRef]
- Kim, J.-S.; Truong, T.; Kim, J. Development of Sewing-Type Sensor Capable of Detecting Respiration Using the Capacitive Method. Polymers 2023, 15, 503. [Google Scholar] [CrossRef]
- Veske, P.; Bossuyt, F.; Thielemans, F.; Vanfleteren, J. Measuring the Flex Life of Conductive Yarns in Narrow Fabric. Micromachines 2023, 14, 781. [Google Scholar] [CrossRef]
- Stoppa, M.; Chiolerio, A. Wearable Electronics and Smart Textiles: A Critical Review. Sensors 2014, 14, 11957–11992. [Google Scholar] [CrossRef] [PubMed]
- Fernández-Caramés, T.M.; Fraga-Lamas, P. Towards the Internet of Smart Clothing: A Review on IoT Wearables and Garments for Creating Intelligent Connected E-Textiles. Electronics 2018, 7, 405. [Google Scholar] [CrossRef]
- Gonçalves, C.; da Silva, A.F.; Gomes, J.; Simoes, R. Wearable E-Textile Technologies: A Review on Sensors, Actuators and Control Elements. Inventions 2018, 3, 14. [Google Scholar] [CrossRef]
- Chatterjee, K.; Tabor, J.; Ghosh, T.K. Electrically Conductive Coatings for Fiber-Based E-Textiles. Fibers 2019, 7, 51. [Google Scholar] [CrossRef]
- Weder, M.; Hegemann, D.; Amberg, M.; Hess, M.; Boesel, L.F.; Abächerli, R.; Meyer, V.R.; Rossi, R.M. Embroidered Electrode with Silver/Titanium Coating for Long-Term ECG Monitoring. Sensors 2015, 15, 1750–1759. [Google Scholar] [CrossRef]
- Ryu, J.-W.; Kim, H.-J.; Jee, Y.-J.; Kwon, S.-Y.; Yoon, N.-S. Effect of Strain Change of Electrically Conductive Yarn on Electric Resistance and Its Theoretical Analysis. Sen’i Gakkaishi 2010, 66, 209–214. [Google Scholar] [CrossRef]
- Pleşa, I.; Noţingher, P.V.; Stancu, C.; Wiesbrock, F.; Schlögl, S. Polyethylene Nanocomposites for Power Cable Insulations. Polymers 2019, 11, 24. [Google Scholar] [CrossRef]
- Sun, K.; Liu, S.; Long, H. Structural Parameters Affecting Electrothermal Properties of Woolen Knitted Fabrics Integrated with Silver-Coated Yarns. Polymers 2019, 11, 1709. [Google Scholar] [CrossRef]
- Li, X.; Li, X.; Wang, M.; Zheng, R.; Jin, Y.; Gu, Z. Flexible and strain conductive cotton yarn enabled by low-temperature sintering of silver paste with multifunctional sensing capability in human motion detection and wearable applications. Chem. Eng. J. 2023, 471, 144843. [Google Scholar] [CrossRef]
- Ding, X.; Zhong, W.; Jiang, H.; Li, M.; Chen, Y.; Lu, Y.; Ma, J.; Yadav, A.; Yang, L.; Wang, D. Highly Accurate Wearable Piezoresistive Sensors without Tension Disturbance Based on Weaved Conductive Yarn. ACS Appl. Mater. Interfaces 2020, 12, 35638–35646. [Google Scholar] [CrossRef]
- Kim, S.; Truong, T.; Jang, J.; Kim, J. The Programmable Design of Large-Area Piezoresistive Textile Sensors Using Manufacturing by Jacquard Processing. Polymers 2022, 15, 78. [Google Scholar] [CrossRef] [PubMed]
- Truong, T.; Kim, J.-S.; Kim, J. Design and optimization of embroidered antennas on textile using silver conductive thread for wearable applications. Fibers Polym. 2021, 22, 2900–2909. [Google Scholar] [CrossRef]
- Nejatdarabi, S.; Mohebbi, M. Predicting the rehydration process of mushroom powder by multiple linear regression (MLR) and artificial neural network (ANN) in different rehydration medium. J. Food Meas. Charact. 2023, 17, 1962–1973. [Google Scholar] [CrossRef]
- El Hajjaji, S.; Kherraf, S.; Bakkouche, C.; Barhmi, S.; Mabrouki, J.; Elfatni, O.; Dhiba, D.; Maissine, K. Forecasting of Permeate Conductivity using MLR and ANN Methods of Boujdour Seawater Reverse Osmosis Desalination Plant. Curr. Anal. Chem. 2023, 19, 348–355. [Google Scholar]
- Zanwar, D.R.; Zanwar, H.D.; Shukla, H.M.; Deshpande, A.A. Prediction of Anthropometric Dimensions Using Multiple Linear Regression and Artificial Neural Network Models. J. Inst. Eng. India Ser. C 2023, 104, 307–314. [Google Scholar] [CrossRef]
- Ahmad, S.A.; Abdulrahman, A.S.; Ramezanianpour, A.M.; Rafiq, S.K.; Mahmood, K.O.F.; Jafer, F.S. Modeling the mechanical properties of sustainable mortar modified with waste glass granular (particles) using ANN and multi-scale approaches. Preprint 2023. [Google Scholar] [CrossRef]
- Faloye, O.T.; Ajayi, A.E.; Babalola, T.; Omotehinse, A.O.; Adeyeri, O.E.; Adabembe, B.A.; Ogunrinde, A.T.; Okunola, A.; Fashina, A. Modelling Crop Evapotranspiration and Water Use Efficiency of Maize Using Artificial Neural Network and Linear Regression Models in Biochar and Inorganic Fertilizer-Amended Soil under Varying Water Applications. Water 2023, 15, 2294. [Google Scholar] [CrossRef]
- Xi, H.; Kong, D.R.; Peng, Y.Q.; Zhang, S.M.; Shi, Q.; Le, G.G. Prediction of Spatial Peak Overpressure Profile of Air Blast Shocks Using Multiple Linear Regression and Artificial Neural Network. J. Phys. Conf. Ser. 2023, 2478, 072036. [Google Scholar] [CrossRef]
- Kim, B.-J.; Yune, C.-Y. Prediction Model of Ground Temperature Near a Heat Exchanger Using an Artificial Neural Network (Ann) and Multiple Regressions Approach. SSRN 2023. [Google Scholar] [CrossRef]
- Ghamali, M.; Chtita, S.; Ousaa, A.; Elidrissi, B.; Bouachrine, M.; Lakhlifi, T. QSAR analysis of the toxicity of phenols and thiophenols using MLR and ANN. J. Taibah Univ. Sci. 2017, 11, 1–10. [Google Scholar] [CrossRef]
- Chakraborty, A.; Goswami, D. Prediction of slope stability using multiple linear regression (MLR) and artificial neural network (ANN). Arab. J. Geosci. 2017, 10, 385. [Google Scholar] [CrossRef]
- Roh, M.-H.; Nishikawa, H.; Tsutsumi, S.; Nishiwaki, N.; Ito, K.; Ishikawa, K.; Katsuya, A.; Kamada, N.; Saito, M. Pressureless Bonding by Micro-Sized Silver Particle Paste for High-Temperature Electronic Packaging. Mater. Trans. 2016, 57, 1209–1214. [Google Scholar] [CrossRef]
- Liu, S.; Yang, C.; Zhao, Y.; Tao, X.M.; Tong, J.; Li, L. The impact of float stitches on the resistance of conductive knitted structures. Text. Res. J. 2016, 86, 1455–1473. [Google Scholar] [CrossRef]
- Giacomino, A.; Abollino, O.; Malandrino, M.; Mentasti, E. The role of chemometrics in single and sequential extraction assays: A Review. Part II. Cluster analysis, multiple linear regression, mixture resolution, experimental design and other techniques. Anal. Chim. Acta 2011, 688, 122–139. [Google Scholar] [CrossRef]
- Tiryaki, S.; Özşahin, Ş.; Yıldırım, İ. Comparison of artificial neural network and multiple linear regression models to predict optimum bonding strength of heat treated woods. Int. J. Adhes. Adhes. 2014, 55, 29–36. [Google Scholar] [CrossRef]
- Ceylan, I. Determination of Drying Characteristics of Timber by Using Artificial Neural Networks and Mathematical Models. Dry. Technol. 2008, 26, 1469–1476. [Google Scholar] [CrossRef]
- Esteban, L.G.; Fernández, F.G.; de Palacios, P. MOE prediction in Abies pinsapo Boiss. timber: Application of an artificial neural network using non-destructive testing. Comput. Struct. 2009, 87, 1360–1365. [Google Scholar] [CrossRef]
- Ali, N.; Rehan, A.M.; Ahmed, Z.; Memon, H.; Hussain, A. Effect of different types of seam, stitch class and stitch density on seam performance. J. Appl. Emerg. Sci. 2016, 5, 32–43. [Google Scholar]
- Akter, M.; Khan, M.R. The effect of stitch types and sewing thread types on seam strength for cotton apparel. Int. J. Sci. Eng. Res. 2015, 6, 198–205. [Google Scholar]
- Kakde, M.; Rajput, B.; Gulhane, S.; Mohite, S.; Pp, R. Effect of Sewing Parameters on Seam Strength and Seam Efficiency. Trends Text. Eng. Fash. Technol. 2018, 4, 1–5. [Google Scholar] [CrossRef]







| Length of single sewing stitch | 1 mm | 2 mm | 3 mm | 4 mm | 5 mm |
| Width of single sewing stitch | 0.144 mm | 0.135 mm | 0.132 mm | 0.128 mm | 0.121 mm |
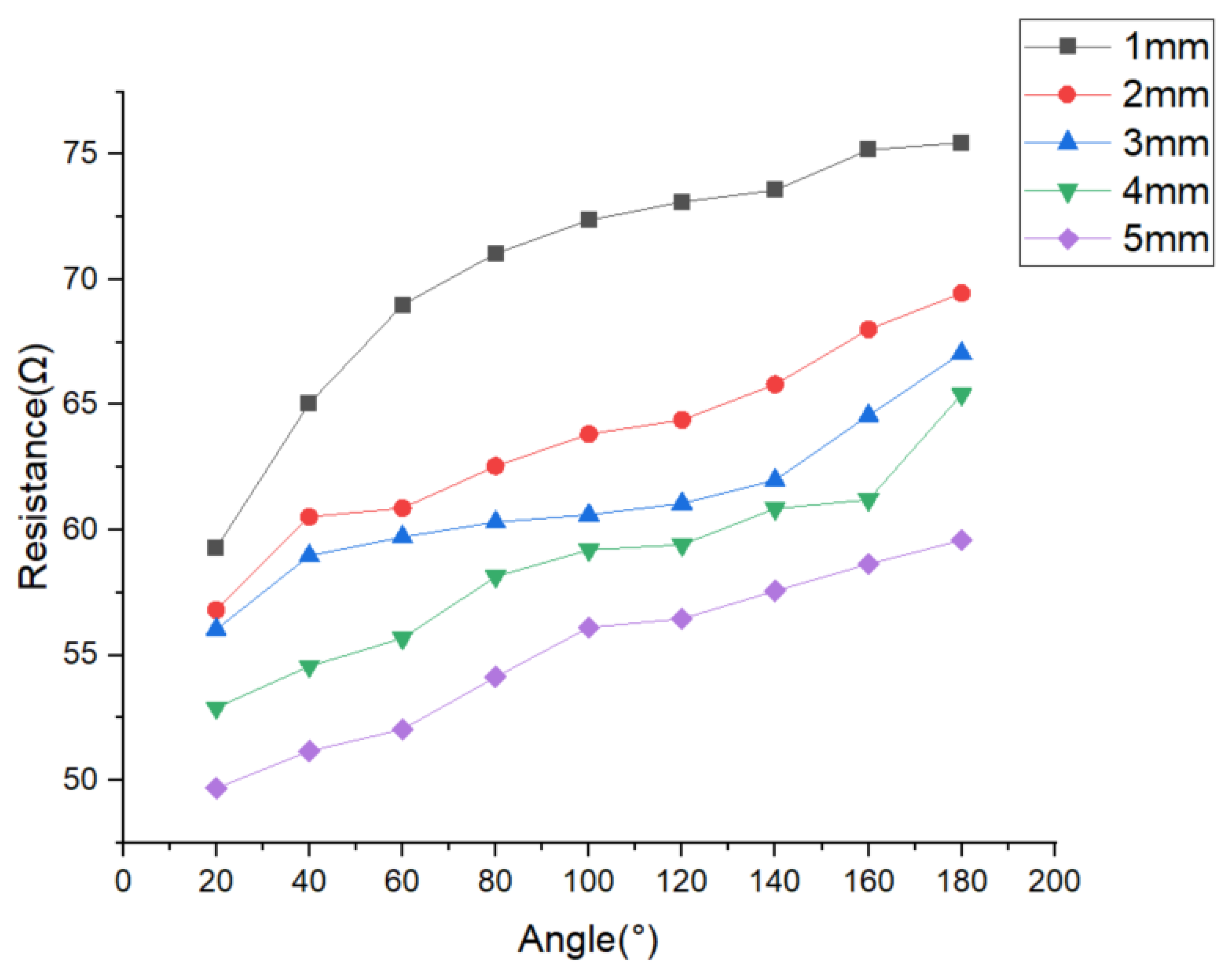
| Stitch Angle (°) | Stitch Length (mm) | Resistance (Ω) |
|---|---|---|
| 180 | 1 | 75.46562 |
| 160 | 1 | 75.17814 |
| 140 | 1 | 73.57052 |
| 120 | 1 | 73.09852 |
| 100 | 1 | 72.37586 |
| 80 | 1 | 71.03588 |
| 60 | 1 | 68.98456 |
| 40 | 1 | 65.05209 |
| 20 | 1 | 59.27464 |
| 180 | 2 | 69.45544 |
| 160 | 2 | 68.00751 |
| 140 | 2 | 65.81475 |
| 120 | 2 | 64.39168 |
| 100 | 2 | 63.82584 |
| 80 | 2 | 62.55164 |
| 60 | 2 | 60.86941 |
| 40 | 2 | 60.51869 |
| 20 | 2 | 56.80353 |
| 180 | 3 | 67.06255 |
| 160 | 3 | 64.57084 |
| 140 | 3 | 61.98866 |
| 120 | 3 | 61.06079 |
| 100 | 3 | 60.60671 |
| 80 | 3 | 60.30651 |
| 60 | 3 | 59.71375 |
| 40 | 3 | 58.97164 |
| 20 | 3 | 56.02832 |
| 180 | 4 | 65.41049 |
| 160 | 4 | 61.21312 |
| 140 | 4 | 60.85553 |
| 120 | 4 | 59.41257 |
| 100 | 4 | 59.19793 |
| 80 | 4 | 58.13526 |
| 60 | 4 | 55.67235 |
| 40 | 4 | 54.55707 |
| 20 | 4 | 52.90243 |
| 180 | 5 | 59.58104 |
| 160 | 5 | 58.63749 |
| 140 | 5 | 57.56939 |
| 120 | 5 | 56.45359 |
| 100 | 5 | 56.1087 |
| 80 | 5 | 54.12524 |
| 60 | 5 | 52.04365 |
| 40 | 5 | 51.16842 |
| 20 | 5 | 49.68008 |
| Model | Performance Criteria | |
|---|---|---|
| MSE | ||
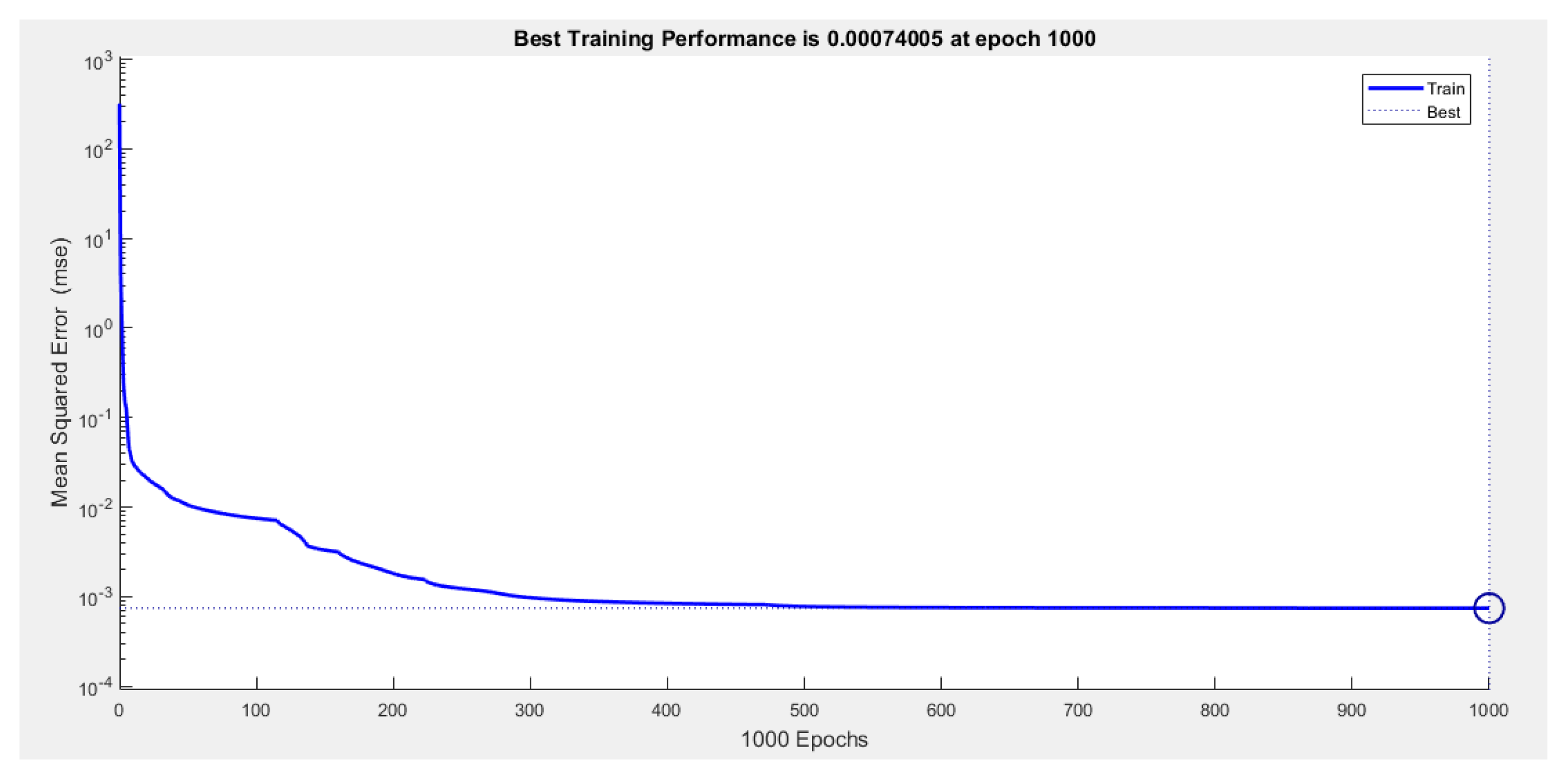
| MLR | 3.0503 | 0.933 |
| ANN | 0.0007 | 0.979 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jang, J.; Kim, J. Prediction of Electrical Resistance with Conductive Sewing Patterns by Combining Artificial Neural Networks and Multiple Linear Regressions. Polymers 2023, 15, 4138. https://doi.org/10.3390/polym15204138
Jang J, Kim J. Prediction of Electrical Resistance with Conductive Sewing Patterns by Combining Artificial Neural Networks and Multiple Linear Regressions. Polymers. 2023; 15(20):4138. https://doi.org/10.3390/polym15204138
Chicago/Turabian StyleJang, JunHyeok, and JooYong Kim. 2023. "Prediction of Electrical Resistance with Conductive Sewing Patterns by Combining Artificial Neural Networks and Multiple Linear Regressions" Polymers 15, no. 20: 4138. https://doi.org/10.3390/polym15204138
APA StyleJang, J., & Kim, J. (2023). Prediction of Electrical Resistance with Conductive Sewing Patterns by Combining Artificial Neural Networks and Multiple Linear Regressions. Polymers, 15(20), 4138. https://doi.org/10.3390/polym15204138








