Polymer-Embedding Germanium Nanostrip Waveguide of High Polarization Extinction
Abstract
:1. Introduction
2. Material and Methods
2.1. Waveguide Design
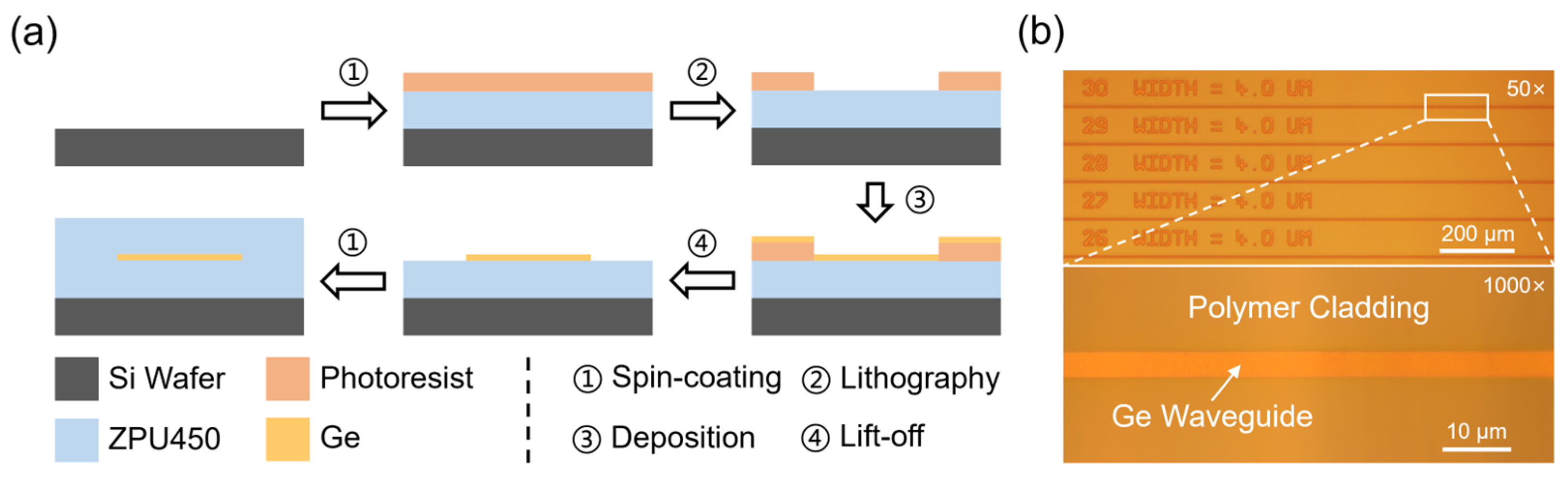
2.2. Fabrication Workflow
2.3. Experimental Setup
3. Results
3.1. Waveguide Measurement
3.2. n-κ Model Correction
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Pillarisetty, R. Academic and industry research progress in germanium nanodevices. Nature 2011, 479, 324–328. [Google Scholar] [CrossRef] [PubMed]
- Chander, S.; Sinha, S.K.; Chaudhary, R.; Singh, A. Ge-Source Based L-Shaped Tunnel Field Effect Transistor for Low Power Switching Application. Silicon 2022, 14, 7435–7448. [Google Scholar] [CrossRef]
- Kim, S.H.; Agarwal, S.; Jacobson, Z.A.; Matheu, P.; Hu, C.; Liu, T.J.K. Tunnel Field Effect Transistor with Raised Germanium Source. IEEE Electron Device Lett. 2010, 31, 1107–1109. [Google Scholar] [CrossRef]
- Bardeen, J.; Brattain, W.H. The Transistor, A Semi-Conductor Triode. Phys. Rev. 1948, 74, 230–231. [Google Scholar] [CrossRef]
- Liu, J.; Camacho-Aguilera, R.; Bessette, J.T.; Sun, X.; Wang, X.; Cai, Y.; Kimerling, L.C.; Michel, J. Ge-on-Si optoelectronics. Thin Solid Films 2012, 520, 3354–3360. [Google Scholar] [CrossRef]
- Chen, G.; Yu, Y.; Shi, Y.; Li, N.; Luo, W.; Cao, L.; Danner, A.J.; Liu, A.Q.; Zhang, X. High-Speed Photodetectors on Silicon Photonics Platform for Optical Interconnect. Laser Photonics Rev. 2022, 16, 2200117. [Google Scholar] [CrossRef]
- Wang, B.; Jifang, M. High-speed Si-Ge avalanche photodiodes. PhotoniX 2022, 3, 8. [Google Scholar] [CrossRef]
- Srinivasan, S.A.; Pantouvaki, M.; Gupta, S.; Chen, H.T.; Verheyen, P.; Lepage, G.; Roelkens, G.; Saraswat, K.; Van Thourhout, D.; Absil, P.; et al. 56 Gb/s Germanium Waveguide Electro-Absorption Modulator. J. Light. Technol. 2016, 34, 419–424. [Google Scholar] [CrossRef]
- Vivien, L.; Polzer, A.; Marris-Morini, D.; Osmond, J.; Hartmann, J.M.; Crozat, P.; Cassan, E.; Kopp, C.; Zimmermann, H.; Fédéli, J.M. Zero-bias 40Gbit/s germanium waveguide photodetector on silicon. Opt. Express 2012, 20, 1096–1101. [Google Scholar] [CrossRef]
- Zhao, R.; Qiu, J.; Sun, S.; Sui, Z.; Yang, F.; Zhang, H.; Zhao, X. The nonlinear optical property of germanium saturable absorber and its application in normal dispersion Er-doped fibre laser. Infrared Phys. Technol. 2022, 127, 104445. [Google Scholar] [CrossRef]
- Mu, H.; Liu, Y.; Bongu, S.R.; Bao, X.; Li, L.; Xiao, S.; Zhuang, J.; Liu, C.; Huang, Y.; Dong, Y.; et al. Germanium Nanosheets with Dirac Characteristics as a Saturable Absorber for Ultrafast Pulse Generation. Adv. Mater. 2021, 33, 2101042. [Google Scholar] [CrossRef] [PubMed]
- Yang, C.C.; Cheng, C.H.; Chen, T.H.; Lin, Y.H.; Tseng, W.H.; Chang, P.H.; Wu, C.I.; Lin, G.R. Ultrathin amorphous Ge film enabling stabilized femtosecond fibre laser pulsation. Opt. Laser Technol. 2021, 136, 106761. [Google Scholar] [CrossRef]
- Zhao, Z.; Lim, C.-M.; Ho, C.; Sumita, K.; Miyatake, Y.; Toprasertpong, K.; Takagi, S.; Takenaka, M. Low-loss Ge waveguide at the 2-µm band on an n-type Ge-on-insulator wafer. Opt. Mater. Express 2021, 11, 4097–4106. [Google Scholar] [CrossRef]
- Fujigaki, T.; Takagi, S.; Takenaka, M. High-efficiency Ge thermo-optic phase shifter on Ge-on-insulator platform. Opt. Express 2019, 27, 6451–6458. [Google Scholar] [CrossRef] [PubMed]
- Gallacher, K.; Millar, R.; Griškevičiūte, U.; Baldassarre, L.; Sorel, M.; Ortolani, M.; Paul, D. Low loss Ge-on-Si waveguides operating in the 8–14 µm atmospheric transmission window. Opt. Express 2018, 26, 25667–25675. [Google Scholar] [CrossRef] [PubMed]
- Osman, A.; Nedeljkovic, M.; Soler Penades, J.; Wu, Y.; Qu, Z.; Khokhar, A.Z.; Debnath, K.; Mashanovich, G.Z. Suspended low-loss germanium waveguides for the longwave infrared. Opt. Lett. 2018, 43, 5997–6000. [Google Scholar] [CrossRef] [PubMed]
- Nedeljkovic, M.; Penades, J.S.; Mittal, V.; Murugan, G.S.; Khokhar, A.Z.; Littlejohns, C.; Carpenter, L.G.; Gawith, C.B.; Wilkinson, J.S.; Mashanovich, G.Z. Germanium-on-silicon waveguides operating at mid-infrared wavelengths up to 8.5 μm. Opt. Express 2017, 25, 27431–27441. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Anantha, P.; Bao, S.; Lee, K.H.; Guo, X.; Hu, T.; Zhang, L.; Wang, H.; Soref, R.; Tan, C.S. Germanium-on-silicon nitride waveguides for mid-infrared integrated photonics. Appl. Phys. Lett. 2016, 109, 241101. [Google Scholar] [CrossRef]
- Kang, J.; Takenaka, M.; Takagi, S. Novel Ge waveguide platform on Ge-on-insulator wafer for mid-infrared photonic integrated circuits. Opt. Express 2016, 24, 11855–11864. [Google Scholar] [CrossRef]
- Marris-Morini, D.; Vakarin, V.; Ramirez, J.M.; Liu, Q.; Ballabio, A.; Frigerio, J.; Montesinos, M.; Alonso-Ramos, C.; Le Roux, X.; Serna, S.; et al. Germanium-based integrated photonics from near- to mid-infrared applications. Nanophotonics 2018, 7, 1781–1793. [Google Scholar] [CrossRef]
- Xie, Y.; Chen, L.; Li, H.; Yi, Y. Polymer and Hybrid Optical Devices Manipulated by the Thermo-Optic Effect. Polymers 2023, 15, 3721. [Google Scholar] [CrossRef]
- Oh, M.C.; Chu, W.S.; Shin, J.S.; Kim, J.W.; Kim, K.J.; Seo, J.K.; Lee, H.K.; Noh, Y.O.; Lee, H.J. Polymeric optical waveguide devices exploiting special properties of polymer materials. Opt. Commun. 2016, 362, 3–12. [Google Scholar] [CrossRef]
- Oh, M.C.; Kim, K.J.; Chu, W.S.; Kim, J.W.; Seo, J.K.; Noh, Y.O.; Lee, H.J. Integrated Photonic Devices Incorporating Low-Loss Fluorinated Polymer Materials. Polymers 2011, 3, 975–997. [Google Scholar] [CrossRef]
- Wang, C.; Zhang, D.; Yue, J.; Lin, H.; Zhang, X.; Zhang, T.; Chen, C.; Fei, T. On-chip optical sources of 3D photonic integration based on active fluorescent polymer waveguide microdisks for light display application. PhotoniX 2023, 4, 13. [Google Scholar] [CrossRef]
- Ullah, F.; Deng, N.; Qiu, F. Recent progress in electro-optic polymer for ultra-fast communication. PhotoniX 2021, 2, 13. [Google Scholar] [CrossRef]
- Kleinert, M.; de Felipe, D.; Zawadzki, C.; Brinker, W.; Choi, J.H.; Reinke, P.; Happach, M.; Nellen, S.; Möhrle, M.; Bach, H.-G.; et al. Photonic integrated devices and functions on hybrid polymer platform. Phys. Simul. Optoelectron. Devices XXV 2017, 10098, 100981A. [Google Scholar]
- Zhang, Z.; Felipe, D.; Katopodis, V.; Groumas, P.; Kouloumentas, C.; Avramopoulos, H.; Dupuy, J.Y.; Konczykowska, A.; Dede, A.; Beretta, A.; et al. Hybrid Photonic Integration on a Polymer Platform. Photonics 2015, 2, 1005–1026. [Google Scholar] [CrossRef]
- De Felipe, D.; Zhang, Z.; Brinker, W.; Kleinert, M.; Novo, A.M.; Zawadzki, C.; Moehrle, M.; Keil, N. Polymer-Based External Cavity Lasers: Tuning Efficiency, Reliability, and Polarization Diversity. IEEE Photonics Technol. Lett. 2014, 26, 1391–1394. [Google Scholar] [CrossRef]
- Lee, E.S.; Chun, K.W.; Jin, J.; Oh, M.C. Frequency Response of Thermo-Optic Phase Modulators Based on Fluorinated Polyimide Polymer Waveguide. Polymers 2022, 14, 2186. [Google Scholar] [CrossRef]
- Xie, Y.; Han, J.; Qin, T.; Ge, X.; Wu, X.; Liu, L.; Wu, X.; Yi, Y. Low Power Consumption Hybrid-Integrated Thermo-Optic Switch with Polymer Cladding and Silica Waveguide Core. Polymers 2022, 14, 5234. [Google Scholar] [CrossRef]
- Chen, T.; Dang, Z.; Ding, Z.; Zhang, Z. Programmable Parallel Optical Logic Gates on a Multimode Waveguide Engine. Photonics 2022, 9, 736. [Google Scholar] [CrossRef]
- Wang, C.; Liu, J.; Zhang, Z. Transmission characteristics of femtosecond laser pulses in a polymer waveguide. Opt. Express 2022, 30, 31396–31406. [Google Scholar] [CrossRef]
- Lin, B.; Lian, T.; Sun, S.; Zhu, M.; Che, Y.; Sun, X.; Wang, X.; Zhang, D. Ultra-Broadband and Compact TM-Pass Polarizer Based on Graphene-Buried Polymer Waveguide. Polymers 2022, 14, 1481. [Google Scholar] [CrossRef] [PubMed]
- Chu, Y.; Liu, Z.; Ding, Z.; Zhang, Z. Birefringent and Complex Optical Properties of Monolayer Graphene Investigated by Ellipsometry and Waveguide Integration. J. Phys. Chem. C 2021, 125, 2124–2131. [Google Scholar] [CrossRef]
- Wang, X.; Feng, H.; Wu, Y.; Jiao, L. Controlled Synthesis of Highly Crystalline MoS2 Flakes by Chemical Vapor Deposition. J. Am. Chem. Soc. 2013, 135, 5304–5307. [Google Scholar] [CrossRef]
- Yoo, S.J.; Park, Q.H. Spectroscopic ellipsometry for low-dimensional materials and heterostructures. Nanophotonics 2022, 11, 2811–2825. [Google Scholar] [CrossRef]
- Chu, Y.; Zhang, Z. Birefringent and Complex Dielectric Functions of Monolayer WSe2 Derived by Spectroscopic Ellipsometer. J. Phys. Chem. C 2020, 124, 12665–12671. [Google Scholar] [CrossRef]
- Roeloffzen, C.G.H.; Hoekman, M.; Klein, E.J.; Wevers, L.S.; Timens, R.B.; Marchenko, D.; Geskus, D.; Dekker, R.; Alippi, A.; Grootjans, R.; et al. Low-Loss Si3N4 Triplex Optical Waveguides: Technology and Applications Overview. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 4400321. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, D.; De Felipe, D.; Liu, A.; Keil, N.; Grote, N. Polymer embedded silicon nitride thermally tuneable Bragg grating filters. Appl. Phys. Lett. 2013, 102, 181105. [Google Scholar] [CrossRef]
- Ciesielski, A.; Skowronski, L.; Pacuski, W.; Szoplik, T. Permittivity of Ge, Te and Se thin films in the 200–1500 nm spectral range. Predicting the segregation effects in slver. Mater. Sci. Semicond. Process. 2018, 81, 64–67. [Google Scholar] [CrossRef]
- Tompkins, H.; Hilfiker, J. Representing Optical Functions. In Spectroscopic Ellipsometer: Practical Application to Thin Film Characterization; Momentum Press: New York, NY, USA, 2015; pp. 71–87. [Google Scholar]
- Ophir Laser Beam Profilers. Available online: https://www.ophiropt.com/laser--measurement/beam-profilers (accessed on 16 September 2023).
- THORLABS CMOS Camera Beam Profiler. Available online: https://www.thorlabs.com/newgrouppage9.cfm?objectgroup_ID=3483 (accessed on 16 September 2023).
- Tauc, J.; Grigorovici, R.; Vancu, A. Optical Properties and Electronic Structure of Amorphous Germanium. Phys. Status Solidi 1966, 15, 627–637. [Google Scholar] [CrossRef]
- Liu, P.; Longo, P.; Zaslavsky, A.; Pacifici, D. Optical bandgap of single- and multi-layered amorphous germanium ultra-thin films. J. Appl. Phys. 2016, 119, 014304. [Google Scholar] [CrossRef]
- Mok, T.M.; O’Leary, S.K. The dependence of the Tauc and Cody optical gaps associated with hydrogenated amorphous silicon on the film thickness: αl Experimental limitations and the impact of curvature in the Tauc and Cody plots. J. Appl. Phys. 2007, 102, 113525. [Google Scholar] [CrossRef]
- Van de Walle, C.G. Band lineups and deformation potentials in the model-solid theory. Phys. Rev. B 1989, 39, 1871–1883. [Google Scholar] [CrossRef]
- Temkin, R.J.; Paul, W.; Connell, G.A.N. Amorphous germanium II. Structural properties. Adv. Phys. 1973, 22, 581–641. [Google Scholar] [CrossRef]
- Treacy, M.M.J.; Borisenko, K.B. The Local Structure of Amorphous Silicon. Science 2012, 335, 950–953. [Google Scholar] [CrossRef] [PubMed]
- Jaros, M. Electronic properties of semiconductor alloy systems. Rep. Prog. Phys. 1985, 48, 1091–1154. [Google Scholar] [CrossRef]
- Wang, X.-D.; Wang, H.-F.; Chen, B.; Li, Y.-P.; Ma, Y.-Y. A model for thickness effect on the band gap of amorphous germanium film. Appl. Phys. Lett. 2013, 102, 202102. [Google Scholar] [CrossRef]
- Goh, E.S.M.; Chen, T.P.; Sun, C.Q.; Liu, Y.C. Thickness effect on the band gap and optical properties of germanium thin films. J. Appl. Phys. 2010, 107, 024305. [Google Scholar] [CrossRef]








| Ref. No. | Material Platform | Cross-Sectional Parameter | Waveguide Type | Propagation Loss (dB/cm) |
|---|---|---|---|---|
| [13] (Sample A) | GeOI | 1 μm (w) × 0.3 μm (h) | Rib | 25.2 |
| [13] (Sample B) | GeOI | 1 μm (w) × 0.3 μm (h) | Rib | 10.7 |
| [14] | GeOI | 1 μm (w) × 0.27 μm (h) | Strip | 84 |
| [19] | GeOI | 2 μm (w) × 0.3 μm (h) | Rib | 14 |
| This work | Polymer | 4 μm (w) × ~40 nm (h) | Strip | 4.89 |
| Correction λ (nm) | 1500 | 1520 | 1540 | 1560 | 1580 | 1600 |
| Ge core absorption (dB/cm) | 20.56 | 18.55 | 16.50 | 14.57 | 12.93 | 11.75 |
| Measured n by ellipsometer | 4.251 | 4.241 | 4.232 | 4.225 | 4.218 | 4.210 |
| Probe κ | 3.39 × 10−2 | 3.17 × 10−2 | 3.00 × 10−2 | 2.79 × 10−2 | 2.62 × 10−2 | 2.49 × 10−2 |
| Fitted relation of κ vs. λ by Cauchy model | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zhang, Z. Polymer-Embedding Germanium Nanostrip Waveguide of High Polarization Extinction. Polymers 2023, 15, 4093. https://doi.org/10.3390/polym15204093
Liu J, Zhang Z. Polymer-Embedding Germanium Nanostrip Waveguide of High Polarization Extinction. Polymers. 2023; 15(20):4093. https://doi.org/10.3390/polym15204093
Chicago/Turabian StyleLiu, Jinyuan, and Ziyang Zhang. 2023. "Polymer-Embedding Germanium Nanostrip Waveguide of High Polarization Extinction" Polymers 15, no. 20: 4093. https://doi.org/10.3390/polym15204093
APA StyleLiu, J., & Zhang, Z. (2023). Polymer-Embedding Germanium Nanostrip Waveguide of High Polarization Extinction. Polymers, 15(20), 4093. https://doi.org/10.3390/polym15204093








