Dissipative Particle Dynamics Simulation for the Self-Assembly of Symmetric Pentablock Terpolymers Melts under 1D Confinements
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Neutral Wall
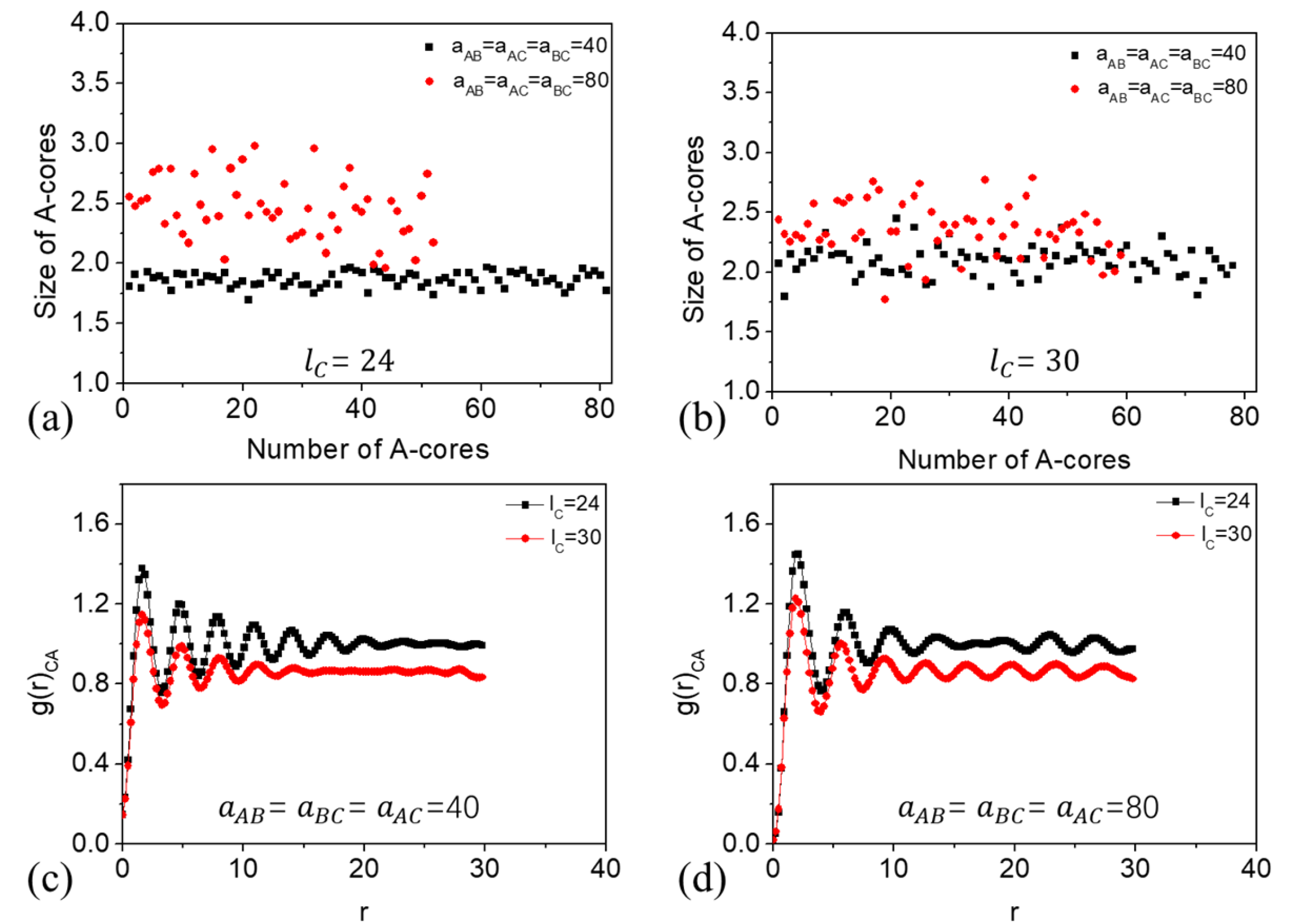
3.1.1. Influence of the -Block Length
Phase Behavior
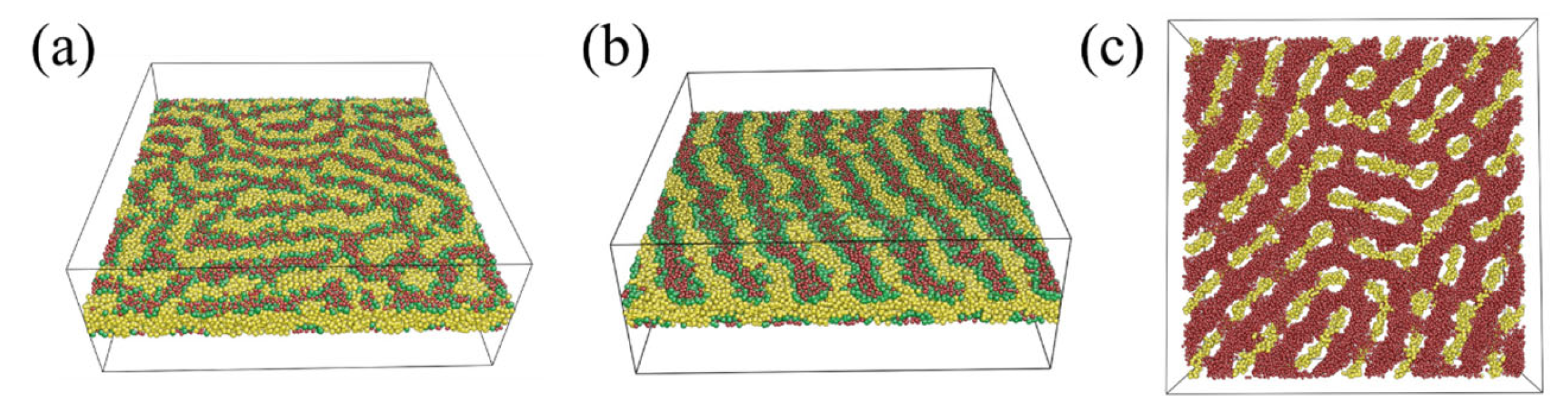
Characterization of C-Rich Perforated Lamellae
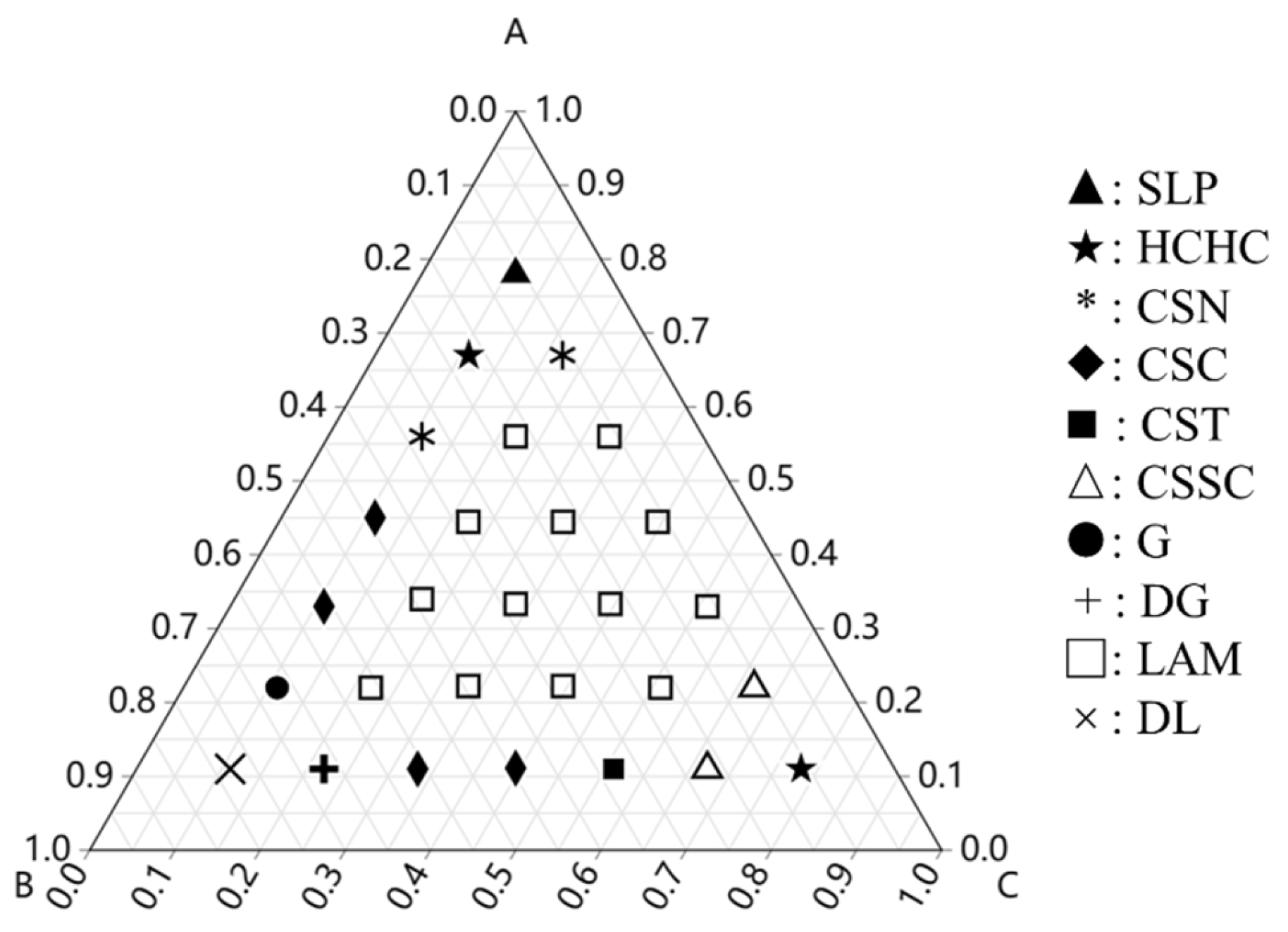
3.1.2. Influence of the Block Composition
3.2. Selective Wall
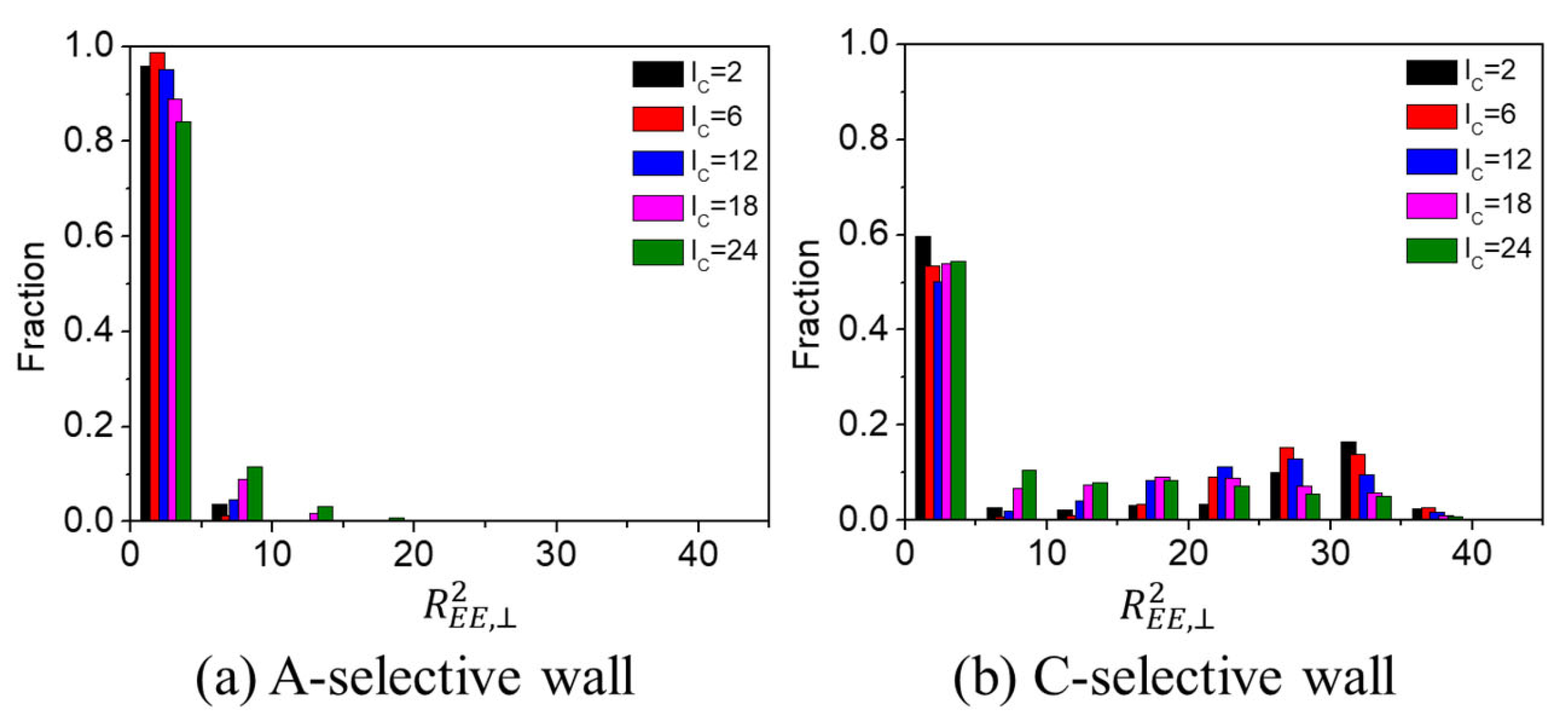
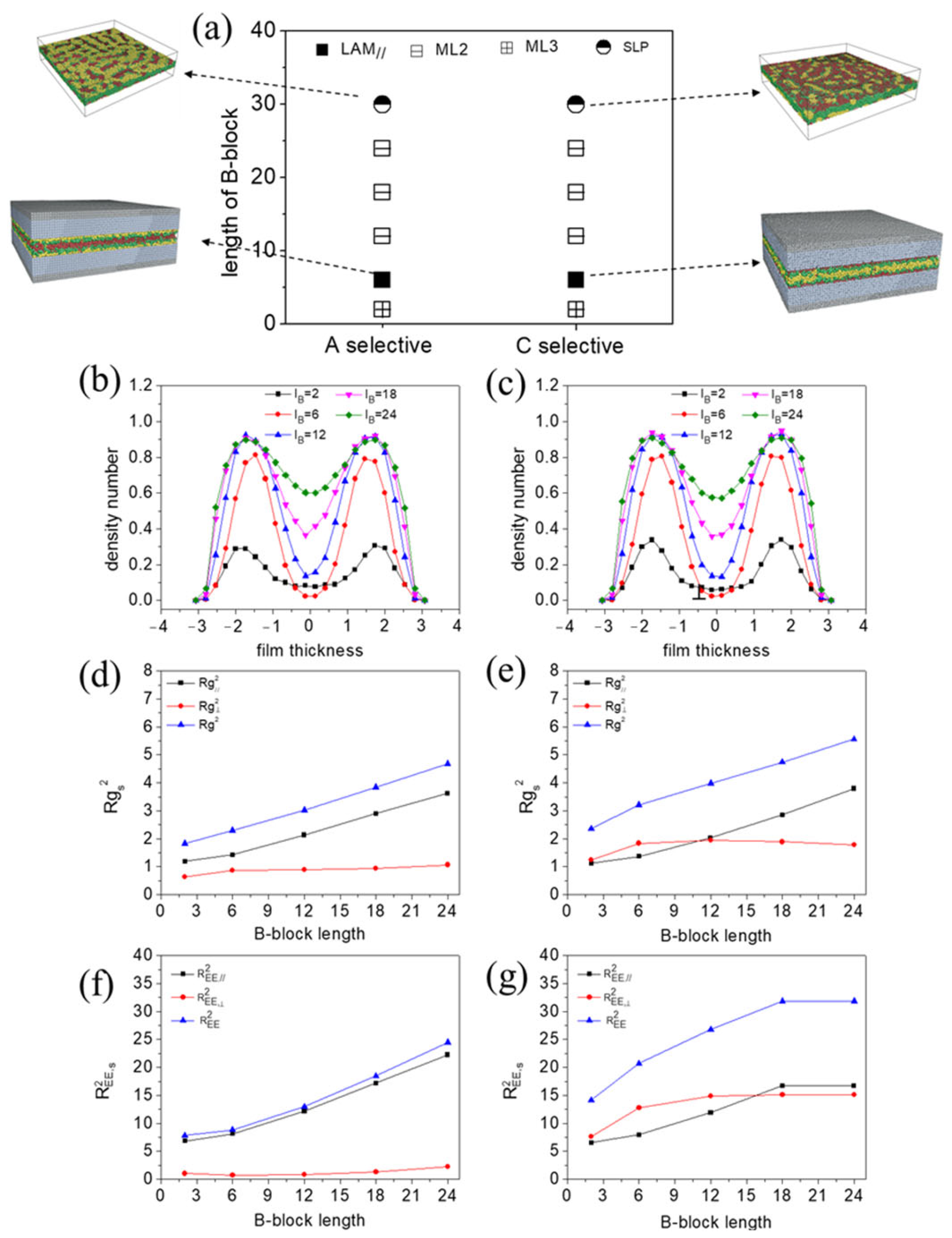
3.2.1. Influence of A(C)-Block Length
3.2.2. Influence of B-Block Length
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mendoza, C.; Nirwan, V.P.; Fahmi, A. Nanofabrication of hybrid nanomaterials: Macroscopically aligned nanoparticles pattern via directed self-assembly of block copolymers. J. Appl. Polym. Sci. 2023, 140, e53409. [Google Scholar] [CrossRef]
- Locarno, S.; Gallo, S.; Arosio, P.; Biordi, C.; Dallasega, D.; Gargano, M.; Ludwig, N.; Orsini, F.; Pignoli, E.; Veronese, M.; et al. Dosimetric Double Network Hydrogel Based on Poly(vinyl-alcohol)/Phenylalanine-Derivatives with Enhanced Mechanical Properties. ACS Appl. Polym. Mater. 2023, 5, 1902–1914. [Google Scholar] [CrossRef]
- Alvarez-Fernandez, A.; Cummins, C.; Saba, M.; Steiner, U.; Fleury, G.; Ponsinet, V.; Guldin, S. Block Copolymer Directed Metamaterials and Metasurfaces for Novel Optical Devices. Adv. Opt. Mater. 2021, 9, 2100175. [Google Scholar] [CrossRef]
- Guo, L.; Wang, Y.; Steinhart, M. Porous block copolymer separation membranes for 21st century sanitation and hygiene. Chem. Soc. Rev. 2021, 50, 6333–6348. [Google Scholar] [CrossRef] [PubMed]
- Kang, H.S.; Han, S.W. 3D touchless multiorder reflection structural color sensing display. Sci. Adv. 2020, 6, eabb5769. [Google Scholar] [CrossRef]
- Sadegh, F.; Akin, S.; Moghadam, M.; Keshavarzi, R.; Mirkhani, V.; Ruiz-Preciado, M.A.; Akman, E.; Zhang, H.; Amini, M.; Tangestaninejad, S.; et al. Copolymer-Templated Nickel Oxide for High-Efficiency Mesoscopic Perovskite Solar Cells in Inverted Architecture. Adv. Funct. Mater. 2021, 31, 2102237. [Google Scholar] [CrossRef]
- Jeong, S.-J.; Kim, J.Y.; Kim, B.H.; Moon, H.-S.; Kim, S.O. Directed self-assembly of block copolymers for next generation nanolithography. Mater. Today 2013, 16, 468–476. [Google Scholar] [CrossRef]
- Phillip, W.A.; O’neill, B.; Rodwogin, M.; Hillmyer, M.A.; Cussler, E.L. Self-Assembled Block Copolymer Thin Films as Water Filtration Membranes. ACS Appl. Mater. Interfaces 2010, 2, 847–853. [Google Scholar] [CrossRef]
- Liberman-Martin, A.L.; Chu, C.K.; Grubbs, R.H. Application of Bottlebrush Block Copolymers as Photonic Crystals. Macromol. Rapid Commun. 2017, 38, 1700058. [Google Scholar] [CrossRef]
- Wang, Z.K.; Lim, H.S.; Liu, H.Y.; Ng, S.C.; Kuok, M.H.; Tay, L.L.; Lockwood, D.J.; Cottam, M.G.; Hobbs, K.L.; Larson, P.R.; et al. Spin Waves in Nickel Nanorings of Large Aspect Ratio. Phys. Rev. Lett. 2005, 94, 137208. [Google Scholar] [CrossRef]
- Cummins, C.; Morris, M.A. Using block copolymers as infiltration sites for development of future nanoelectronic devices: Achievements, barriers, and opportunities. Microelectron. Eng. 2018, 195, 74–85. [Google Scholar] [CrossRef]
- Hu, X.-H.; Xiong, S. Fabrication of Nanodevices Through Block Copolymer Self-Assembly. Front. Nanotechnol. 2022, 4, 762996. [Google Scholar] [CrossRef]
- Huang, C.; Zhu, Y.; Man, X. Block copolymer thin films. Phys. Rep. 2021, 932, 1–36. [Google Scholar] [CrossRef]
- Hong, J.-W.; Chang, J.-H.; Chang, I.C.-Y.; Sun, Y.-S. Phase behavior in thin films of weakly segregated block copolymer/homopolymer blends. Soft Matter 2021, 17, 9189–9197. [Google Scholar] [CrossRef]
- Kim, D.H.; Suh, A.; Park, G.; Yoon, D.K.; Kim, S.Y. Nanoscratch-Directed Self-Assembly of Block Copolymer Thin Films. ACS Appl. Mater. Interfaces 2021, 13, 5772–5781. [Google Scholar] [CrossRef]
- Aviv, Y.; Altay, E.; Burg, O.; Müller, M.; Rzayev, J.; Shenhar, R. Bottlebrush Block Copolymer Assembly in Ultraconfined Films: Effect of Substrate Selectivity. Macromolecules 2021, 54, 2079–2089. [Google Scholar] [CrossRef]
- Michman, E.; Langenberg, M.; Stenger, R.; Oded, M.; Schvartzman, M.; Müller, M.; Shenhar, R. Controlled Spacing between Nanopatterned Regions in Block Copolymer Films Obtained by Utilizing Substrate Topography for Local Film Thickness Differentiation. ACS Appl. Mater. Interfaces 2019, 11, 35247–35254. [Google Scholar] [CrossRef]
- Mu, D.; Li, J.Q.; Feng, S.Y. One-dimensional Confinement Effect on the Self-assembly of Symmetric H-shaped Copolymers in a Thin Film. Sci. Rep. 2017, 7, 13610. [Google Scholar] [CrossRef]
- Choi, J.; Huh, J.; Carter, K.R.; Russell, T.P. Directed Self-Assembly of Block Copolymer Thin Films Using Minimal Topographic Patterns. ACS Nano 2016, 10, 7915–7925. [Google Scholar] [CrossRef]
- Kim, S.-W.; Kim, E.; Lee, H.; Berry, B.C.; Kim, H.-C.; Ryu, D.Y. Thickness-dependent ordering of perpendicularly oriented lamellae in PS-b-PMMA thin films. Polymer 2015, 74, 63–69. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Breen, C.; Zvelindovsky, A.; Pagonabarraga, I. Block Copolymer Nanocomposites under Confinement: Effect on Frustrated Phases. Macromolecules 2023, 56, 5010–5021. [Google Scholar] [CrossRef]
- Mu, D.; Li, J.-Q.; Cong, X.-S.; Zhang, H. Mesoscopic Detection of the Influence of a Third Component on the Self-Assembly Structure of A2B Star Copolymer in Thin Films. Polymers 2019, 11, 1636. [Google Scholar] [CrossRef] [PubMed]
- Spencer, R.K.; Matsen, M.W. Confinement effects on the miscibility of block copolymer blends. Eur. Phys. J. E 2016, 39, 43. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, L.; Zhang, L.; Lin, J.; Jiang, T. Controllable Hierarchical Microstructures Self-Assembled from Multiblock Copolymers Confined in Thin Films. Langmuir 2015, 31, 2533–2544. [Google Scholar] [CrossRef]
- Li, W.; Liu, M.; Qiu, F.; Shi, A.-C. Phase Diagram of Diblock Copolymers Confined in Thin Films. J. Phys. Chem. B 2013, 117, 5280–5288. [Google Scholar] [CrossRef]
- Jiang, Z.; Xu, C.; Qiu, Y.D.; Wang, X.; Zhou, D.; Xue, G. Complex microstructures of ABC triblock copolymer thin films directed by polymer brushes based on self-consistent field theory. Nanoscale Res. Lett. 2014, 9, 359. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Z.; Yin, Y.; Jiang, R.; Li, B. A simulation study of the self-assembly of ABC star terpolymers confined between two parallel surfaces. Soft Matter 2021, 17, 5336–5348. [Google Scholar] [CrossRef]
- Clothier, G.K.; Guimarães, T.R.; Thompson, S.W.; Rho, J.Y.; Perrier, S.; Moad, G.; Zetterlund, P.B. Multiblock copolymer synthesis via RAFT emulsion polymerization. Chem. Soc. Rev. 2023, 52, 3438–3469. [Google Scholar] [CrossRef]
- Zhang, Z.; Xiong, Y.; Yang, P.; Li, Y.; Tang, R.; Nie, X.; Chen, G.; Wang, L.; Hong, C.; You, Y. Easy Access to Diverse Multiblock Copolymers with On-Demand Blocks via Thioester-Relayed In-Chain Cascade Copolymerization. Angew. Chem. Int. Ed. 2023, 62, e202216685. [Google Scholar] [CrossRef]
- Guo, L.; Xu, J.; Du, B. Self-assembly of ABCBA Linear Pentablock Terpolymers. Polym. Rev. 2023, 1–35. [Google Scholar] [CrossRef]
- Gao, J.; Lv, C.; An, K.; Gu, X.; Nie, J.; Li, Y.; Xu, J.; Du, B. Observation of Double Gyroid and Hexagonally Perforated Lamellar Phases in ABCBA Pentablock Terpolymers. Macromolecules 2020, 53, 9641–9653. [Google Scholar] [CrossRef]
- Kopchick, J.G.; Storey, R.F.; Beyer, F.L.; Mauritz, K.A. Poly[acrylic acid-b-styrene-b-isobutylene-b-styrene-b-acrylic acid] pentablock terpolymers: 1. Morphological characterization. Polymer 2007, 48, 3739–3748. [Google Scholar] [CrossRef]
- Kopchick, J.G.; Storey, R.F.; Jarrett, W.L.; Mauritz, K.A. Morphology of poly[(t-butyl acrylate)-b-styrene-b-isobutylene-b-styrene-b-(t-butyl acrylate)] pentablock terpolymers and their thermal conversion to the acrylic acid form. Polymer 2008, 49, 5045–5052. [Google Scholar] [CrossRef]
- Meuler, A.J.; Fleury, G.; Hillmyer, M.A.; Bates, F.S. Structure and Mechanical Properties of an O70 (Fddd) Network-Forming Pentablock Terpolymer. Macromolecules 2008, 41, 5809–5817. [Google Scholar] [CrossRef]
- Nishiwaki, Y.; Masutani, K.; Kimura, Y.; Lee, C.W. Synthesis and mechanochemical properties of biobased ABCBA-type pentablock copolymers comprising poly-d-lactide (A), poly-l-lactide (B) and poly(1,2-propylene succinate) (C). J. Polym. Sci. 2022, 60, 2043–2054. [Google Scholar] [CrossRef]
- Dashtimoghadam, E.; Salimi-Kenari, H.; Motlaq, V.F.; Hasani-Sadrabadi, M.M.; Mirzadeh, H.; Zhu, K.; Knudsen, K.D.; Nyström, B. Synthesis and temperature-induced self-assembly of a positively charged symmetrical pentablock terpolymer in aqueous solutions. Eur. Polym. J. 2017, 97, 158–168. [Google Scholar] [CrossRef]
- Gao, J.; An, K.; Lv, C.; Nie, J.; Xu, J.; Du, B. Self-Assembly of Linear Amphiphilic Pentablock Terpolymer PAAx-PS48-PEO46-PS48-PAAxin Dilute Aqueous Solution. Polymers 2020, 12, 2183. [Google Scholar] [CrossRef]
- Liu, H.-H.; Huang, C.-I.; Shi, A.-C. Self-Assembly of Linear ABCBA Pentablock Terpolymers. Macromolecules 2015, 48, 6214–6223. [Google Scholar] [CrossRef]
- Lo, Y.; Chang, C.; Liu, H.; Huang, C.; Shi, A. Self-Assembly of Nonfrustrated ABCBA Linear Pentablock Terpolymers. Macromol. Theory Simul. 2021, 30, 2100014. [Google Scholar] [CrossRef]
- Ye, X.; Yu, X.; Shi, T.; Sun, Z.; An, L.; Tong, Z. A Self-Consistent Field Theory Study on the Morphologies of Linear ABCBA and H-Shaped (AB)2C(BA)2 Block Copolymers. J. Phys. Chem. B 2006, 110, 23578–23582. [Google Scholar] [CrossRef]
- Kim, T.-Y.; Hur, S.-M.; Ramírez-Hernández, A. Effect of Block Sequence on the Solution Self-Assembly of Symmetric ABCBA Pentablock Polymers in a Selective Solvent. J. Phys. Chem. B 2023, 127, 2575–2586. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.J.; Koelman, J.M.V.A. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Loo, Y.-L.; Register, R.A.; Adamson, D.H.; Ryan, A.J. A Highly Regular Hexagonally Perforated Lamellar Structure in a Quiescent Diblock Copolymer. Macromolecules 2005, 38, 4947–4949. [Google Scholar] [CrossRef]
- Bouzit, H.; Krusch, F.; Hermida-Merino, D.; Solano, E.; Cot, D.; Méricq, J.P.; Roualdes, S.; Semsarilar, M.; Quémener, D.; Aissou, K. Double stimuli-responsive perforated lamellar structure formed by linear ABC triblock terpolymer monoliths. J. Polym. Sci. 2023, 61, 1005–1014. [Google Scholar] [CrossRef]





| Formation Condition | |||
|---|---|---|---|
| Morphologies | Wall Properties | Block–Block Interaction Strength | Fraction of Blocks |
| Perpendicular lamellae | Nonselective wall | Not related | |
| Parallel lamellae | A-selective wall | Weak | |
| C-selective wall | Weak | ||
| Perforated lamellae | Nonselective wall | Not related | = 0.6~0.72 |
| = 0.6~0.72 | |||
| A-selective wall | Weak | = 0.60~0.68 | |
| C-selective wall | Weak | = 0.60~0.68 | |
| Cylinder | Nonselective wall | Weak | |
| Weak | |||
| Weak | |||
| Gyroid | Nonselective wall | Strong | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Bai, L. Dissipative Particle Dynamics Simulation for the Self-Assembly of Symmetric Pentablock Terpolymers Melts under 1D Confinements. Polymers 2023, 15, 3982. https://doi.org/10.3390/polym15193982
Guo Y, Bai L. Dissipative Particle Dynamics Simulation for the Self-Assembly of Symmetric Pentablock Terpolymers Melts under 1D Confinements. Polymers. 2023; 15(19):3982. https://doi.org/10.3390/polym15193982
Chicago/Turabian StyleGuo, Yingying, and Linqing Bai. 2023. "Dissipative Particle Dynamics Simulation for the Self-Assembly of Symmetric Pentablock Terpolymers Melts under 1D Confinements" Polymers 15, no. 19: 3982. https://doi.org/10.3390/polym15193982
APA StyleGuo, Y., & Bai, L. (2023). Dissipative Particle Dynamics Simulation for the Self-Assembly of Symmetric Pentablock Terpolymers Melts under 1D Confinements. Polymers, 15(19), 3982. https://doi.org/10.3390/polym15193982






