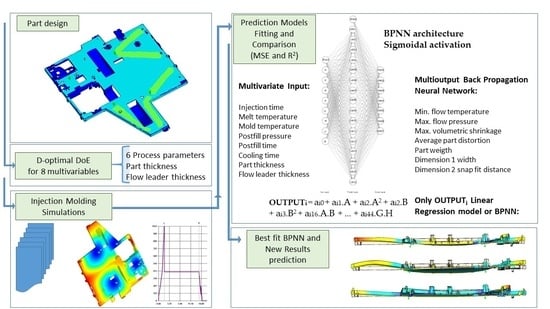
Predictive Methodology for Quality Assessment in Injection Molding Comparing Linear Regression and Neural Networks
Abstract
:1. Introduction
2. Methodology
2.1. Quality Features and Input Parameters Selection: Design of Experiments
2.2. Injection Molding Simulation and Results Extraction (Cadmould Software)
2.3. Obtention of Multivariate Linear Regression Prediction Model
2.4. Obtention of Artificial Neural Network Prediction Model
- Input, a vector with the independent variables.
- Input layer (Ii), where the components of the inputs vector are normalized between [−1,1];
- Hidden layer, where weights and bias are applied to inputs and sigmoid neurons (LWi) create newer inputs for the next layer;
- Output layer, where weights and bias are applied to hidden layer outputs and linear neurons (OWi) generate the outputs between [−1,1];
- Output, where a prediction vector is obtained after denormalizing the output layer;
2.5. Validation: Prediction Model Selection by Quality Features Prediction
3. Results and Discussion
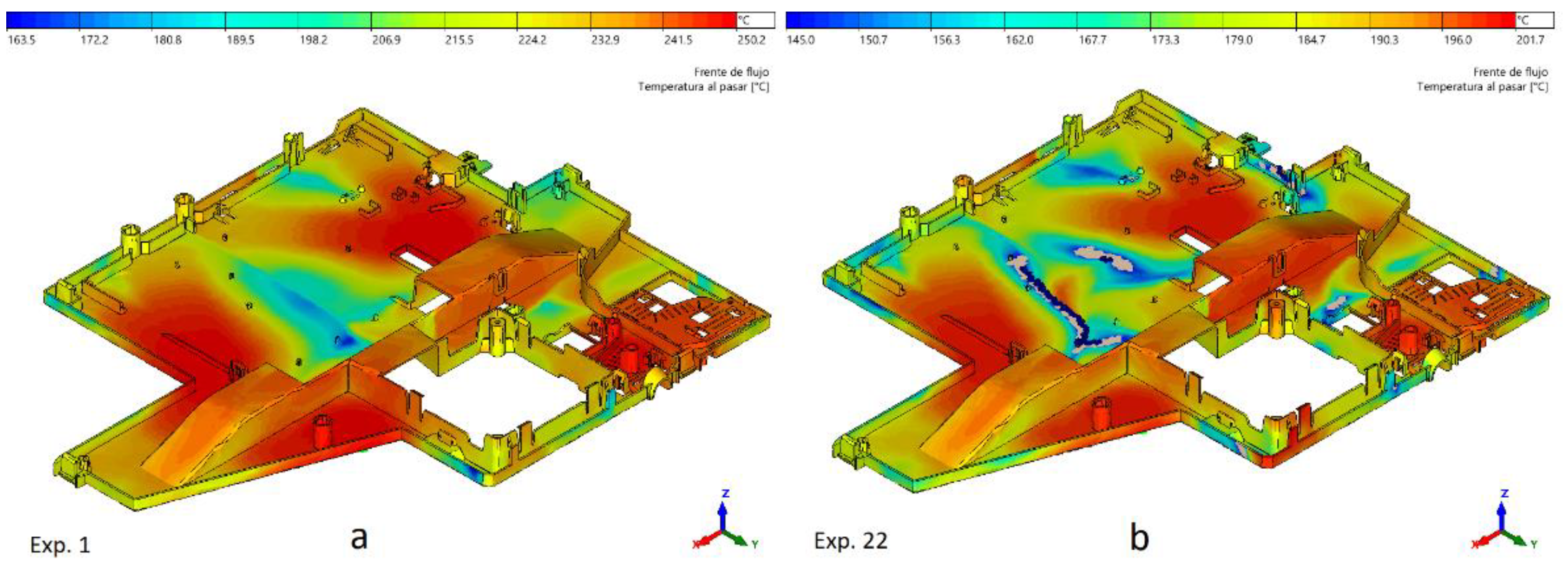
3.1. Injection Molding Simulation Results
3.2. Prediction Models Comparison and Discussion
4. Conclusions
- A new methodology has been developed and tested for the early design of complex plastic parts, making it possible to predict features of the final part by combining the optimal design of experiments, process simulation, regression, neural network fitting, and prediction model generation and application.
- Results present different prediction models for seven required output features simultaneously related to material, part, and process quality. These models predict newer results in real time, varying eight input molding and part thickness design parameters without launching additional time-consuming simulations.
- Simulation has shown the near unpredictable part dimensions due to the combination of thermo-volumetric and residual stress effects. The results of these could be additive or compensatory and then modify the dimensions of the part. A trial-and-error simulation process based on rules of thumb cannot overcome this situation. For this reason, the creation and application of a predictive model accounting for these effects is the fastest way to achieve an optimal solution.
- A multivariable and multicriteria prediction model based on BPNN is recommended for the prediction model. The prediction model obtained from a BPNN with 24 sigmoidal neurons in the hidden layer (BPNN3) has shown the best precision and highest correlation when predicting all 7 quality features with just one function. This number of neurons is a multiple of 8 because the 8 inputs are the independent variables. It is also a multiple of 3 because even though there are 7 output features, they have been selected from three distinct fields: process, material, and part quality. The product of these two figures explains the sufficient number of neurons. Results obtained from this model allow better design options complying with the restrictions defined for the outputs. For a future research study, the authors propose developing an optimization algorithm based on the selected predictive model. Additionally, deep research is needed to include new criteria in this methodology, taking into account inputs from active agents in the decision-making process: designers, mold makers, and converters. Moreover, research has to focus on including high-level variables to make this knowledge and application transferable.
- The main novelty of the paper lies in the fact that prediction models can define seven different outputs simultaneously from eight different input parameters. Input parameters are related not only to process conditions but also to design features such as part thickness and flow leader thickness. Outputs are related to process, material, and part quality, such as cavity temperature and pressure during injection, volumetric shrinkage, distortion after ambient conditions are reached, or weight and critical dimensions of the part.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Macht, M.L.; Rahm, W.E.; Paine, H.W. Injection molding. Ind. Eng. Chem. 1941, 33, 563–567. [Google Scholar] [CrossRef]
- Castany, F.J.; Serraller, F.; Clavería, I.; Javierre, C. Methodology in gas assisted moulding of Plastics. J. Mater. Process. Technol. 2003, 143, 214–218. [Google Scholar] [CrossRef]
- Turng, L.S.; Chiang, H.H.; Stevenson, J.F. Optimizing molding at low injection pressures. Plast. Eng. 1995, 51, 33–36. [Google Scholar]
- Park, S.J.; Lee, S.Y. Chapter 4 Injection molding for multicomponent materials. In Multicomponent Polymeric Materials; Kim, J.K., Thomas, S., Saha, P., Eds.; Springer: Dordrecht, The Netherlands, 2016. [Google Scholar]
- Jin, J.; Yu, H.Y.; Lv, S. Optimization of Plastic Injection Molding Process Parameters for Thin-Wall Plastics Injection Molding. Adv. Mater. Res. 2009, 69–70, 525–529. [Google Scholar]
- Cardozo, D. A brief history of the filling simulation of injection moulding. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2009, 223, 711–721. [Google Scholar] [CrossRef]
- Cuello, A.F.; Peinado, V. Software as Kommunikations plattform. Kunststoffe 2009, 99, 48–51. [Google Scholar]
- Nguyen, Q.; Babanezhad, M.; Nakhjiri, A.T.; Rezakazemi, M.; Shirazian, S. Prediction of thermal distribution and fluid flow in the domain with multi-solid structures using Cubic-Interpolated Pseudo-Particle model. PLoS ONE 2020, 15, e0233850. [Google Scholar] [CrossRef]
- Gordon, M.J., Jr. Chapter 8—Six Sigma Keys to Success are Control, Capability and Repeatability. In Six Sigma Quality for Business and Manufacture; Elsevier Science B.V.: Amsterdam, The Netherlands, 2002; pp. 333–392. [Google Scholar]
- Shi, H.; Xie, S.; Wang, X. A warpage optimization method for injection molding using artificial neural network with parametric sampling evaluation strategy. Int. J. Adv. Manuf. Tech. 2012, 65, 343–3523. [Google Scholar] [CrossRef]
- Cellere, A.; Lucchetta, G. Identification of crims model parameters for warpage prediction in injection molding simulation. Int. J. Mater. Form. 2010, 3, 37–40. [Google Scholar] [CrossRef]
- Wang, R.; Zeng, J.; Feng, X.; Xia, Y. Evaluation of Effect of Plastic Injection Molding Process Parameters on Shrinkage Based on Neural Network Simulation. J. Macromol. Sci. Part B 2013, 52, 206–221. [Google Scholar] [CrossRef]
- Roman, A.J.; Qin, S.; Zavala, V.M.; Osswald, T.A. Neural network feature and architecture optimization for injection molding surface defect prediction of model polypropylene. Polym. Eng. Sci. 2021, 61, 2376–2387. [Google Scholar] [CrossRef]
- Chen, W.J.; Lin, J.R. Application and Design of Artificial Neural Network for Multi-cavity Injection Molding Process Conditions. Adv. Futur. Comp. Contrl Syst. 2012, 160, 33–38. [Google Scholar] [CrossRef]
- Shen, C.; Wang, L.; Li, Q. Optimization of injection molding process parameters using combination of artificial neural network and genetic algorithm method. J. Mater. Proc. Tech. 2007, 183, 412–418. [Google Scholar] [CrossRef]
- Sun, Y.N.; Chen, Y.; Wang, W.Y.; Xu, H.W.; Qin, W. Modelling and prediction of Injection Molding Process Using Copula Entropy and Multi-Output SVR. In Proceedings of the 17th IEEE International Conference on Automation Science and Engineering (CASE), Lyon, France, 23–27 August 2021. [Google Scholar]
- Yang, Y.; Gao, F. Injection molding product weight: Online prediction and control based on a nonlinear principal component regression model. Polym. Eng. Sci. 2006, 46, 540–548. [Google Scholar] [CrossRef]
- Abdul, R.; Guo, G.; Chen, J.C.; Yoo, J.J.W. Shrinkage prediction of injection molded high density polyethylene parts with taguchi artificial neural network hybrid experimental design. Int. J. Interact. Des. Manuf. 2020, 14, 345–357. [Google Scholar] [CrossRef]
- Vagelatos, G.A.; Rigatos, G.G.; Tzafestas, S.G. Incremental fuzzy supervisory controller design for optimizing the injection molding process. Exp. Syst.Appl. 2001, 20, 207–216. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Durbin, R.; Golden, R.; Chauvin, Y. Backpropagation: Theory, Architecture, and Applications; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1995. [Google Scholar]
- Analytical Methods Committee, AMCTB No 55. Experimental design and optimisation (4): Plackett–Burman designs. Anal. Methods 2013, 5, 1901–1903. [Google Scholar] [CrossRef]
- Frohelich, C.; Kemmetmüller, W.; Kugi, A. Model Predictive Control for Velocity Tracking in full-motor Injection Molding. In Proceedings of the 3rd IEEE Conference on Control Technology and Applications, Hong Kong, China, 19–21 August 2019; Volume 28, pp. 1665–1680. [Google Scholar]
- Veligorskyi, O.; Khomenko, M.; Chakirov, R.; Vagapov, Y. Artificial Neural Network Motor Control for Full-Electric Injection Moulding Machine. In Proceedings of the 20th IEEE International Conference on Industrial Technology (IEEE ICIT), Melbourne, Australia, 13–15 February 2019. [Google Scholar]
- Kuo, C.F.J.; Li, Y.C.; Wu, Y.S. The Construction and Analysis of a Prediction Model for Combining the Taguchi Method and General Regression Neural Network for Injection Moulding. Polym. Polym. Compos. 2005, 13, 823–829. [Google Scholar]
- Tsai, K.M.; Luo, H.J. An inverse model for injection molding of optical lens using artificial neural network coupled with genetic algorithm. J. Intell. Manuf. 2017, 28, 473–487. [Google Scholar] [CrossRef]
- Tsai, K.M.; Luo, H.J. Comparison of injection molding process windows for plastic lens established by artificial neural network and response surface methodology. Int. J. Adv. Manuf. Technol. 2014, 77, 1599–1611. [Google Scholar] [CrossRef]
- Chen, J.C.; Guo, G.; Chang, Y.H. Intelligent dimensional prediction systems with real-time monitoring sensors for injection molding via statistical regression and artificial neural networks. Int. J. Interact. Des. Manuf. 2023, 17, 1265–1276. [Google Scholar] [CrossRef]
- Chen, J.C.; Guo, G.; Wang, W.N. Artificial neural network-based online defect detection system with in-mold temperature and pressure sensors for high precision injection molding. Int. J. Adv. Manuf. Technol. 2020, 110, 2023–2033. [Google Scholar] [CrossRef]
- Li, E.; Jia, L.; Yu, J. A genetic neural fuzzy system-based quality prediction model for injection process. Comput. Chem. Eng. 2022, 26, 1253–1263. [Google Scholar] [CrossRef]
- Shi, H.; Wang, X.; Xie, S. A Warpage Optimization method for Injection Molding Using Artificial Neural Network Combined Weighted Expected Improvement. Int. Polym. Process. 2012, 27, 341–347. [Google Scholar] [CrossRef]
- Li, K.; Yan, S.; Pan, W.; Zhao, G. Warpage optimization of fiber-reinforced composite injection molding by combining back propagation neural network and genetic algorithm. Int. J. Adv. Manuf. Technol. 2017, 90, 963–970. [Google Scholar] [CrossRef]
- Yan, T.; Mei, Y.; Wang, L. Optimization of FHB5.10 Electrical Appliance Shell Injection Molding Process Based on Moldflow and BP Neural Network. In Proceedings of the 3rd World Conference on Mechanical Engineering and Intelligent Manufacturing, Shanghai, China, 4–6 December 2020. [Google Scholar] [CrossRef]
- Song, Z.; Liu, S.; Wang, X.; Hu, Z. Optimization and prediction of volume shrinkage and warpage of injection-molded thin-walled parts based on neural network. Int. J. Adv. Manuf. Technol. 2020, 109, 755–769. [Google Scholar] [CrossRef]
- Guo, W.; Deng, F.; Meng, Z.; Hua, L.; Mao, H.; Su, J. A hybrid back-propagation neural network and intelligent algorithm combined algorithm for optimizing microcellular foaming injection molding process parameters. J. Manuf. Process. 2022, 50, 528–538. [Google Scholar] [CrossRef]
- Oliaei, E.; Heidari, B.S.; Davachi, S.M.; Bahrami, M.; Davoodi, S.; Hejazi, I.; Seyfi, J. Warpage and Shrinkage Optimization of Injection-Molded Plastic Spoon Parts for Biodegradable Polymers Using Taguchi, ANOVA and Artificial Neural Network Methods. J. Mater. Sci. Technol. 2016, 32, 710–720. [Google Scholar] [CrossRef]
- Lockner, Y.; Hoppman, C. Induced network-based transfer learning in injection molding for process modelling and optimization with artificial neural networks. Int. J. Adv. Manuf. Technol. 2021, 112, 3501–3513. [Google Scholar] [CrossRef]
- Lee, C.; Na, J.; Park, K.; Yu, H.; Kim, J.; Choi, K.; Park, D.; Park, S.; Rho, J.; Lee, S. Development of Artificial Neural Network System to Recommend Process Conditions of Injection Molding for Various Geometries. Adv. Intell. Syst. 2020, 2, 2000037. [Google Scholar] [CrossRef]
- Maarif, M.R.; Lystyanda, R.F.; Kang, Y.S.; Syafrudin, M. Artificial Neural Network Training Using Structural Learning with Forgetting for Parameter Analysis of Injection Molding Quality Prediction. Information 2022, 13, 488. [Google Scholar] [CrossRef]
- Zhou, H.; Li, D. Modelling and prediction of weld line location and properties based on injection moulding simulation. Int. J. Mater. Prod. Technol. 2004, 1, 526–538. [Google Scholar] [CrossRef]
- Sedighi, R.; Meiabadi, M.S.; Sedighi, M. Optimisation of gate location based on weld line in plastic injection moulding using computer-aided engineering, artificial neural network, and genetic algorithm. Int. J. Automot. Mech. Eng. 2017, 14, 4419–4431. [Google Scholar] [CrossRef]
- Mathivanan, D.; Parthasarathy, N.S. Prediction of sink depths using nonlinear modeling of injection molding variables. Int. J. Adv. Manuf. Technol. 2009, 43, 654–663. [Google Scholar] [CrossRef]
- Salamoni, T.D.; Wahjudi, A. Injection Molding Process Modeling Using Back Propagation Neural Network Method. In Proceedings of the 3rd International Conference on Mechanical Engineering, Surabaya, Indonesia; 2017; Volume 1983, p. 040009. [Google Scholar]
- Navarrete, J.; Calderón, M.; Zitzumbo, R.; Louvier, J.F. Optimization of Tensile Strain of Injection Molded Polyamid-6 Parts By Neural Networks And Nonlinear Programming Techniques. Dyna 2018, 93, 534–540. [Google Scholar] [CrossRef]
- Tzeng, C.J.; Yang, Y.K.; Lin, Y.H.; Tsai, C.H. A study of optimization of injection molding process parameters for SGF and PTFE reinforced PC composites using neural network and response surface methodology. Int. J. Adv. Manuf. Technol. 2012, 63, 691–704. [Google Scholar] [CrossRef]
- Li, K.; Yan, S.L.; Pan, W.F.; Zhao, G. Fiber orientation induced by injection molding of short-fiber-reinforced composites causes anisotropy in material properties and produces warping. Adv. Mech. Eng. 2017, 9, 1–11. [Google Scholar]
- Lockner, Y.; Hopmann, C.; Zhao, W. Transfer learning with artificial neural networks between injection molding processes and different polymer materials. J. Manuf. Process. 2022, 73, 395–408. [Google Scholar] [CrossRef]
- Tsai, C.C.; Lu, C.H. Adaptive Decoupling Predictive Temperature Control Using Neural Networks for Extrusion Barrels in Plastic Injection Molding Machines. In Proceedings of the 2015 IEEE International Conference on Systems, Man, and Cybernetics, Kowloon, Hong Kong, 9–12 October 2015; Curran Associates, Inc.: Red Hook, NY, USA, 2016; pp. 353–358. [Google Scholar] [CrossRef]
- Peng, Y.; Wei, W.; Wang, J. Model Predictive Synchronous Control of Barrel Temperature for Injection Molding Machine Based on Diagonal Recurrent Neural Networks. Mater. Manuf. Process. 2013, 28, 24–30. [Google Scholar] [CrossRef]
- Wang, R.; Feng, X.; Xia, Y.; Zeng, J. A Back Propagation Artificial Neural Network Prediction Model of the Gate Freeze Time for Injection Molded Polypropylenes. J. Macromol. Sci. Part B 2013, 52, 1414–1426. [Google Scholar] [CrossRef]
- Everett, S.E.; Dubay, R. A sub-space artificial neural network for mold cooling in injection molding. Expert Syst. Appl. 2017, 79, 358–371. [Google Scholar] [CrossRef]
- Bensingh, R.J.; Machavaram, R.; Boopathy, S.R.; Jebaraj, C. Injection molding process optimization of a bi-aspheric lens using hybrid artificial neural networks (ANNs) and particle swarm optimization (PSO). Measurement 2019, 134, 359–374. [Google Scholar] [CrossRef]
- Ke, K.C.; Huang, M.S. Quality Prediction for Injection Molding by Using a Multilayer Perceptron Neural Network. Polymers 2020, 12, 1812. [Google Scholar] [CrossRef]
- Lin, F.; Duan, J.; Lu, Q.; Li, X. Optimization of Injection Molding Quality Based on Bp Neural Network And Pso. Mater. Tehnol. 2022, 56, 491. [Google Scholar] [CrossRef]
- Moayyedian, M.; Dinc, A.; Mamedov, A. Optimization of Injection-Molding Process for Thin-Walled Polypropylene Part Using Artificial Neural Network and Taguchi Techniques. Polymers 2021, 13, 4158. [Google Scholar] [CrossRef]
- Heinish, J.; Lockner, Y.; Hopmann, C. Comparison of design of experiment methods for modeling injection molding experiments using artificial neural networks. J. Manuf. Process. 2021, 61, 357–368. [Google Scholar] [CrossRef]
- Galve, J.; Elduque, D.; Pina, C.; Clavería, I.; Javierre, C. Processability analysis of an injected part in virgin or recycled polypropylene. In Proceedings of the European Modeling and Simulation Symposium, Budapest, Hungary, 17–19 September 2018; pp. 241–247, ISBN 978-88-85741-03-4. [Google Scholar]
- Elduque, A.; Elduque, D.; Pina, C.; Clavería, I.; Javierrre, C. Electricity consumption estimation of the polymer material injection molding manufacturing process: Empirical model and application. Materials 2018, 11, 1740. [Google Scholar] [CrossRef]
- Galve, J.; Elduque, D.; Pina, C.; Clavería, I.; Acero, R.; Fernández, A.; Javierre, C. Dimensional stability and process capability of an industrial component injected with recycled polypropylene. Polymers 2019, 11, 1063. [Google Scholar] [CrossRef]
- Galve, J.; Elduque, D.; Pina, C.; Javierre, C. Life cycle assessment of a plastic part injected with recycled polypropylene: A comparison with alternative virgin materials. Int. J. Precis. Eng. Manuf. Green Technol. 2022, 9, 919–932. [Google Scholar] [CrossRef]
- Allen, T.T. DOE: Screening Using Fractional Factorials. In Introduction to Engineering Statistics and Lean Sigma; Springer: London, UK, 2010; pp. 289–313. [Google Scholar] [CrossRef]
- Montgomery, D.C. Appendix, X. In Design and Analysis of Experiments, 8th ed.; John Wiley and Sons: Hoboken, NJ, USA, 2013; Volume 1, pp. 706–717. [Google Scholar]
- McCullough, B.D. Custom design of experiments. In Business Experiments with R, 1st ed.; John Wiley and Sons: Hoboken, NJ, USA, 2021; Volume 1, pp. 305–340. [Google Scholar]
- Filz, P.; Kutschera, H.; Stöckmann., H.; Welter, F.; Roetgen, K. Simulation of Fluid Flow and Structural Analysis within Thin Walled Three Dimensional Geometries; EP 1 385 103 A1, Filed 23 July 2002, Issued 28 January 2004; European Patent Office: Munich, Germany.
- Osswald, T.A.; Rudolph, N. Polymer rheology. In Fundamentals and Applications; Hanser Publications: Cincinnati, OH, USA, 2015. [Google Scholar]
- Karrenberg, G.; Neubrech, B.; Wortberg, J. CFD-Simulation der Kunststoffplastifizierung in einem Extruder mit durchgehend genutetem Zylinder und Barriereschnecke. Z. Kunststofftechnik. 2013, 12, 205–238. [Google Scholar] [CrossRef]
- Nielsen, L.E.; Landel, R.F. Mechanical Properties of Polymers and Composites; Marcel Dekker: New York, NY, USA, 1994. [Google Scholar]
- Schmidt, T.W. Zur Abschätzung der Schwindung. Ph.D. Thesis, Rheinisch-Westfälische Technische Hochschule Aachen, Aachen, Germany, 1986. [Google Scholar]
- Fox, J.; Bouchet-Valat, M. Rcmdr: R Commander. R Package Version 2.7-2. 2021. Available online: https://socialsciences.mcmaster.ca/jfox/Misc/Rcmdr/ (accessed on 8 February 2022).
- Fox, J. The R Commander: A Basic Statistics Graphical User Interface to R. J. Stat. Softw. 2005, 14, 1–42. [Google Scholar] [CrossRef]
- Ryan, T.P. Modern Regression Methods; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 655. [Google Scholar]
- MATLAB, 9.9.0.1467703 (R2020b), The MathWorks Inc.: Natick, MA, USA, 2019.



| Parameters | Objective | Minimum | Maximum |
|---|---|---|---|
| Min. Flow Front Temperature (°C) | 160 | −15 | 40 |
| Max. Molding Pressure (Bar) | 700 | 500 | 725 |
| Max. Volumetric Shrinkage (%) | 12.5 | 11.5 | 13.5 |
| Average Linear Distortion (%) | 0.9 | 0.83 | 0.97 |
| Total Part Weight (g) | 320 | 313 | 327 |
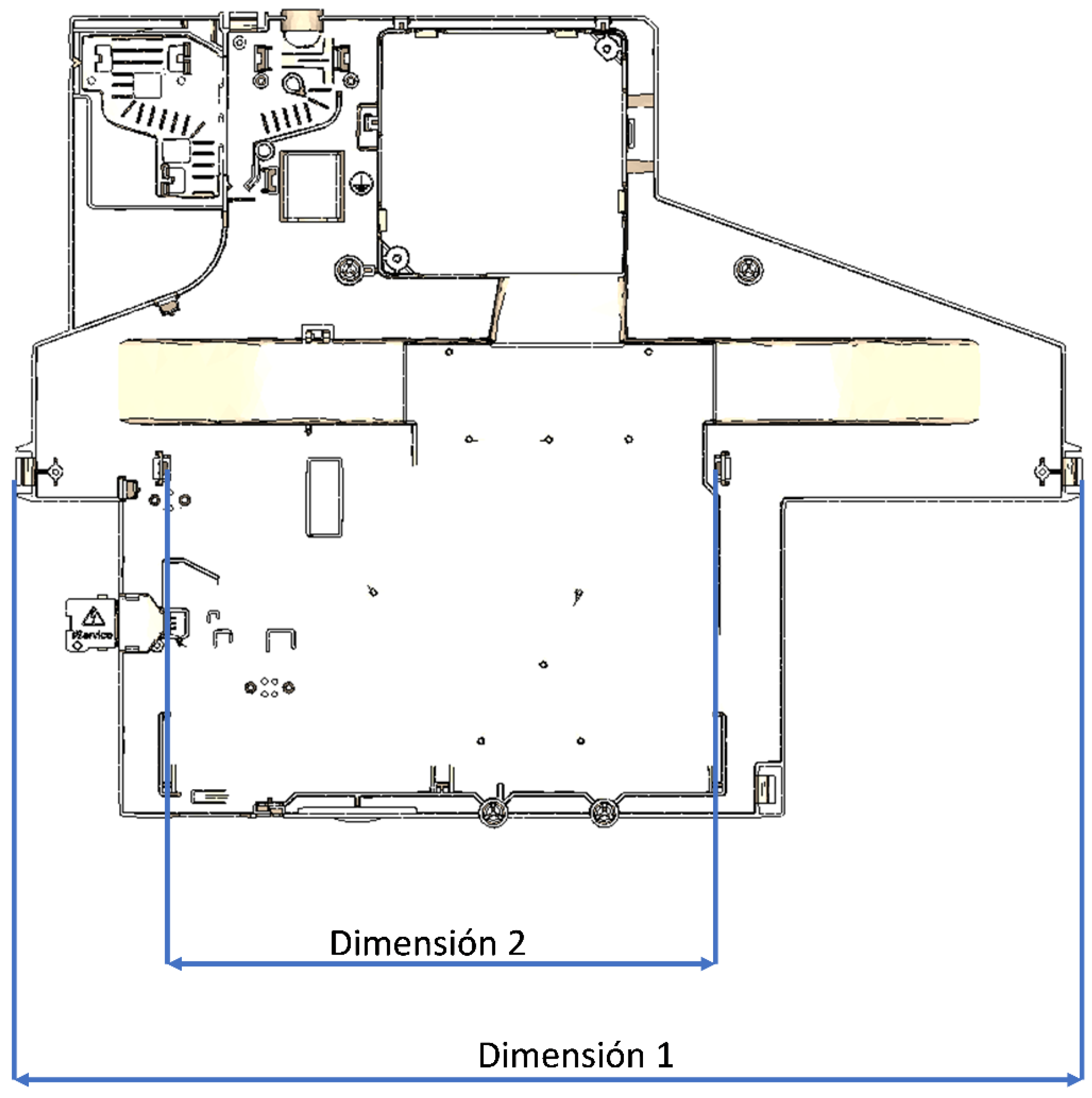
| Dimension 1 (mm) | 529.0 | 528.6 | 529.4 |
| Dimension 2 (mm) | 272.5 | 272.2 | 272.8 |
| Parameters | Lower | Center | Upper |
|---|---|---|---|
| A, Filling Time (s) | 1.4 | 1.75 | 2.1 |
| B, Melt Temperature (°C) | 200 | 250 | 300 |
| C, Cooling Time (s) | 28 | 35 | 42 |
| D, Mold Temperature (°C) | 40 | 50 | 60 |
| E, Post-pressure Time (s) | 9.6 | 12 | 14.4 |
| F, Post pressure (Bar) | 320 | 400 | 480 |
| G, Part Thickness (mm) | 1.0 | 1.1 | 1.2 |
| H, Flow Leaders Thickness (mm) | 1.5 | 1.6 | 1.7 |
| Experiment | A | B | C | D | E | F | G | H |
|---|---|---|---|---|---|---|---|---|
| 1 | 1.75 | 250 | 50 | 12 | 400 | 35 | 1.1 | 1.6 |
| 2 | 2.1 | 300 | 60 | 14.4 | 480 | 28 | 1.0 | 1.7 |
| 3 | 2.1 | 300 | 60 | 14.4 | 320 | 42 | 1.0 | 1.7 |
| 4 | 2.1 | 300 | 60 | 14.4 | 320 | 28 | 1.2 | 1.7 |
| 5 | 2.1 | 300 | 60 | 9.6 | 480 | 42 | 1.2 | 1.5 |
| 6 | 2.1 | 300 | 40 | 14.4 | 480 | 42 | 1.2 | 1.7 |
| 7 | 2.1 | 300 | 40 | 14.4 | 480 | 42 | 1.0 | 1.5 |
| 8 | 2.1 | 300 | 40 | 14.4 | 320 | 28 | 1.0 | 1.7 |
| 9 | 2.1 | 300 | 40 | 9.6 | 480 | 42 | 1.0 | 1.7 |
| 10 | 2.1 | 300 | 40 | 9.6 | 480 | 28 | 1.2 | 1.5 |
| 11 | 2.1 | 300 | 40 | 9.6 | 320 | 42 | 1.2 | 1.5 |
| 12 | 2.1 | 200 | 60 | 14.4 | 480 | 28 | 1.2 | 1.7 |
| 13 | 2.1 | 200 | 60 | 14.4 | 320 | 42 | 1.2 | 1.7 |
| 14 | 2.1 | 200 | 60 | 14.4 | 320 | 28 | 1.0 | 1.5 |
| 15 | 2.1 | 200 | 60 | 9.6 | 480 | 28 | 1.0 | 1.5 |
| 16 | 2.1 | 200 | 60 | 9.6 | 320 | 42 | 1.0 | 1.5 |
| 17 | 2.1 | 200 | 60 | 9.6 | 320 | 28 | 1.0 | 1.7 |
| 18 | 2.1 | 200 | 40 | 14.4 | 480 | 42 | 1.2 | 1.5 |
| 19 | 2.1 | 200 | 40 | 14.4 | 480 | 42 | 1.0 | 1.7 |
| 20 | 2.1 | 200 | 40 | 14.4 | 320 | 28 | 1.2 | 1.7 |
| 21 | 2.1 | 200 | 40 | 9.6 | 480 | 42 | 1.2 | 1.7 |
| 22 | 2.1 | 200 | 40 | 9.6 | 320 | 28 | 1.0 | 1.5 |
| 23 | 1.4 | 300 | 60 | 14.4 | 320 | 42 | 1.2 | 1.5 |
| 24 | 1.4 | 300 | 60 | 9.6 | 480 | 28 | 1.2 | 1.7 |
| 25 | 1.4 | 300 | 60 | 9.6 | 320 | 42 | 1.2 | 1.7 |
| 26 | 1.4 | 300 | 60 | 9.6 | 320 | 28 | 1.0 | 1.5 |
| 27 | 1.4 | 300 | 40 | 14.4 | 480 | 42 | 1.0 | 1.7 |
| 28 | 1.4 | 300 | 40 | 14.4 | 320 | 28 | 1.2 | 1.5 |
| 29 | 1.4 | 300 | 40 | 9.6 | 480 | 42 | 1.2 | 1.5 |
| 30 | 1.4 | 300 | 40 | 9.6 | 320 | 28 | 1.2 | 1.7 |
| 31 | 1.4 | 200 | 60 | 14.4 | 480 | 28 | 1.0 | 1.5 |
| 32 | 1.4 | 200 | 60 | 14.4 | 320 | 28 | 1.0 | 1.7 |
| 33 | 1.4 | 200 | 60 | 9.6 | 480 | 42 | 1.0 | 1.7 |
| 34 | 1.4 | 200 | 60 | 9.6 | 320 | 28 | 1.2 | 1.5 |
| 35 | 1.4 | 200 | 40 | 14.4 | 480 | 42 | 1.0 | 1.7 |
| 36 | 1.4 | 200 | 40 | 14.4 | 320 | 42 | 1.0 | 1.5 |
| 37 | 1.4 | 200 | 40 | 9.6 | 480 | 28 | 1.0 | 1.7 |
| 38 | 1.4 | 200 | 40 | 9.6 | 320 | 42 | 1.0 | 1.7 |
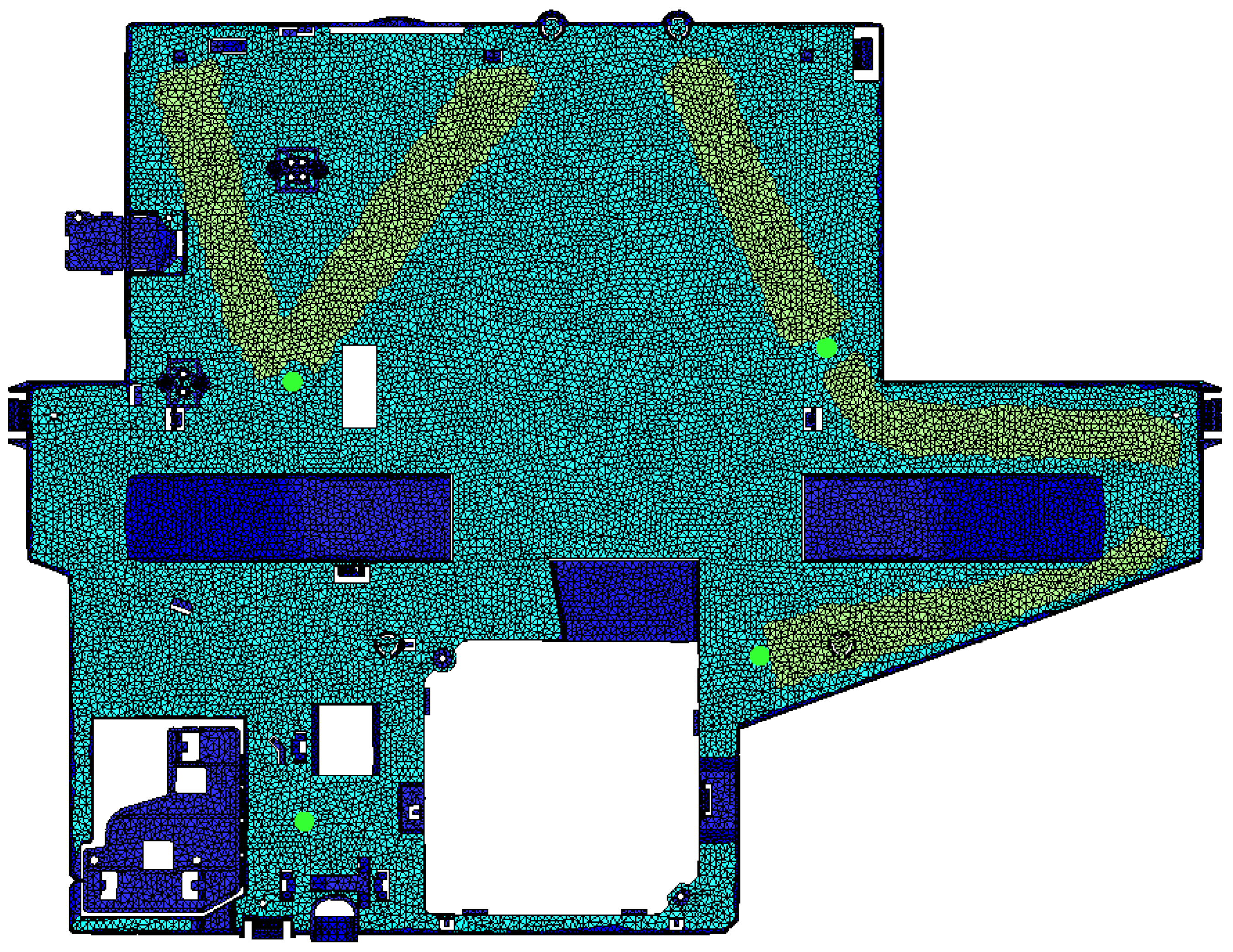
| Type of Element | Number of Elements | Number of Nodes | Averg. Element Area (mm2) | Averg. Side Length (mm) | Averg. Element Thickness (mm) |
|---|---|---|---|---|---|
| 10-N tetrahedra | 162,860 | 62,303 | 3.529 | 2.957 | 1.498 |
| Experiment Number | Tmin (°C) | Pmax (Bar) | VShrk (%) | Distor (%) | Weight (g) | Dim1 (mm) | Dim2 (mm) |
|---|---|---|---|---|---|---|---|
| 1 | 163.5 | 696.4 | 11.8 | 0.914 | 339.5 | 528.65 | 272.58 |
| 2 | 163.0 | 584.9 | 14.3 | 0.984 | 319.2 | 528.00 | 272.36 |
| 3 | 163.0 | 584.9 | 14.2 | 0.833 | 320.6 | 528.99 | 272.71 |
| 4 | 187.1 | 431.2 | 16.3 | 0.977 | 363.3 | 528.13 | 272.26 |
| 5 | 181.5 | 552.9 | 12.4 | 0.772 | 360.3 | 529.37 | 272.99 |
| 6 | 187.1 | 431.2 | 13.2 | 0.802 | 365.4 | 529.45 | 272.86 |
| 7 | 164.6 | 563.8 | 12.0 | 0.832 | 315.4 | 529.25 | 272.79 |
| 8 | 163.0 | 584.9 | 15.7 | 0.990 | 319.0 | 527.90 | 272.27 |
| 9 | 132.6 | 619.3 | 13.5 | 0.786 | 320.9 | 529.07 | 272.90 |
| 10 | 181.5 | 552.9 | 15.1 | 0.926 | 358.6 | 528.20 | 272.56 |
| 11 | 181.5 | 552.9 | 14.7 | 0.776 | 360.3 | 529.33 | 272.95 |
| 12 | 143.2 | 818.8 | 12.7 | 1.001 | 363.3 | 528.47 | 272.36 |
| 13 | 143.2 | 818.8 | 11.5 | 0.843 | 365.1 | 529.55 | 272.78 |
| 14 | 127.7 | 1081.8 | 12.7 | 0.986 | 313.8 | 528.21 | 272.36 |
| 15 | 127.0 | 1407.8 | 12.5 | 0.877 | 314.1 | 528.19 | 272.36 |
| 16 | 127.0 | 1407.8 | 11.6 | 0.760 | 315.6 | 529.09 | 272.71 |
| 17 | 127.9 | 1382.7 | 12.5 | 0.879 | 319.4 | 528.06 | 272.37 |
| 18 | 142.8 | 955.4 | 11.6 | 0.848 | 359.6 | 529.51 | 272.80 |
| 19 | 126.8 | 1019.8 | 11.5 | 0.838 | 320.5 | 529.33 | 272.73 |
| 20 | 143.2 | 818.8 | 12.5 | 0.993 | 363.3 | 528.50 | 272.38 |
| 21 | 130.0 | 908.7 | 11.5 | 0.805 | 365.3 | 529.51 | 272.91 |
| 22 | 127.0 | 1407.8 | 12.5 | 0.876 | 314.1 | 528.19 | 272.36 |
| 23 | 224.8 | 530.1 | 15.6 | 0.831 | 359.7 | 529.14 | 272.73 |
| 24 | 218.6 | 481.0 | 14.5 | 0.922 | 363.9 | 528.14 | 272.55 |
| 25 | 218.6 | 481.0 | 14.8 | 0.774 | 365.5 | 529.16 | 272.89 |
| 26 | 191.5 | 630.3 | 15.4 | 0.961 | 313.9 | 527.69 | 272.44 |
| 27 | 202.9 | 594.5 | 12.5 | 0.832 | 320.6 | 528.92 | 272.78 |
| 28 | 224.8 | 530.1 | 16.5 | 0.992 | 357.9 | 527.96 | 272.28 |
| 29 | 219.8 | 571.6 | 12.8 | 0.781 | 360.2 | 529.17 | 272.97 |
| 30 | 218.6 | 481.0 | 16.1 | 0.929 | 363.7 | 528.04 | 272.46 |
| 31 | 146.8 | 1030.4 | 12.7 | 1.054 | 313.2 | 527.18 | 272.24 |
| 32 | 148.7 | 1053.5 | 12.8 | 1.034 | 318.6 | 527.56 | 272.25 |
| 33 | 129.4 | 1121.8 | 11.7 | 0.831 | 320.4 | 528.65 | 272.78 |
| 34 | 156.6 | 1072.6 | 12.7 | 1.008 | 357.2 | 526.85 | 272.37 |
| 35 | 159.6 | 828.9 | 11.6 | 0.852 | 364.9 | 529.44 | 272.74 |
| 36 | 146.8 | 1030.4 | 11.5 | 0.886 | 314.8 | 529.24 | 272.69 |
| 37 | 129.4 | 1121.8 | 12.5 | 0.978 | 318.5 | 527.49 | 272.39 |
| 38 | 163.5 | 696.4 | 11.8 | 0.914 | 339.5 | 528.65 | 272.58 |
| Parameters | Oct.1 | Oct.2 | Oct.3 | Oct.5 | Oct.6 | Oct. 7 |
|---|---|---|---|---|---|---|
| A, Filling Time (s) | 1.5 | 1.575 | 1.65 | 1.85 | 1.925 | 2 |
| B, Melt Temperature (°C) | 215 | 225 | 240 | 260 | 275 | 285 |
| C, Cooling Time (s) | 29.5 | 31.5 | 33 | 37 | 38.5 | 40.5 |
| D, Mold Temperature (°C) | 42 | 45 | 48 | 52 | 55 | 58 |
| E, Post-pressure Time (s) | 10.2 | 10.8 | 11.4 | 12.6 | 13.2 | 13.8 |
| F, Post pressure (Bar) | 340 | 360 | 380 | 420 | 440 | 460 |
| Term | Regression | BPNN1 | BPNN2 | BPNN3 |
|---|---|---|---|---|
| Mean Squared Error (MSE) | 13.5456 | 7.74970 | 1.50553 | 0.03878 |
| Mean Percentage Error (MPE) | 2.64801 | 1.90270 | 0.80820 | 0.12848 |
| R-Squared (R2) | 0.982626 | 0.98730 | 0.99767 | 0.99993 |
| Term | Regression | BPNN1 | BPNN2 | BPNN3 |
|---|---|---|---|---|
| Mean Squared Error (MSE) | 1720.65 | 5.55311 | 2.11534 | 1.78237 |
| Mean Percentage Error (MPE) | 5.55165 | 0.29905 | 0.17997 | 0.19770 |
| R-Squared (R2) | 0.971839 | 0.99986 | 0.99994 | 0.99995 |
| Term | Regression | BPNN1 | BPNN2 | BPNN3 |
|---|---|---|---|---|
| Mean Squared Error (MSE) | 1.95318 | 0.98291 | 0.02160 | 0.05527 |
| Mean Percentage Error (MPE) | 10.1168 | 7.79060 | 1.12097 | 1.80582 |
| R-Squared (R2) | 0.296026 | 0.29579 | 0.98470 | 0.96033 |
| Term | Regression | BPNN1 | BPNN2 | BPNN3 |
|---|---|---|---|---|
| Mean Squared Error (MSE) | 0.00011 | 0.00517 | 1.3461 × 10−5 | 0.00022 |
| Mean Percentage Error (MPE) | 1.15390 | 8.12836 | 0.40936 | 1.72502 |
| R-Squared (R2) | 0.968651 | 0.060989 | 0.996164 | 0.940400 |
| Term | Regression | BPNN1 | BPNN2 | BPNN3 |
|---|---|---|---|---|
| Mean Squared Error (MSE) | 0.01159 | 0.27001 | 0.00471 | 0.00535 |
| Mean Percentage Error (MPE) | 0.03224 | 0.15546 | 0.02055 | 0.02160 |
| R-Squared (R2) | 0.999982 | 0.999438 | 0.999990 | 0.999989 |
| Term | Regression | BPNN1 | BPNN2 | BPNN3 |
|---|---|---|---|---|
| Mean Squared Error (MSE) | 0.02873 | 0.20477 | 0.00257 | 0.01626 |
| Mean Percentage Error (MPE) | 0.03210 | 0.08565 | 0.00960 | 0.02416 |
| R-Squared (R2) | 0.899864 | 0.240797 | 0.990435 | 0.93946 |
| Term | Regression | BPNN1 | BPNN2 | BPNN3 |
|---|---|---|---|---|
| Mean Squared Error (MSE) | 0.00215 | 0.03412 | 9.8153 × 10−5 | 0.00105 |
| Mean Percentage Error (MPE) | 0.01700 | 0.06777 | 0.00363 | 0.01189 |
| R-Squared (R2) | 0.929677 | 0.019345 | 0.996713 | 0.964266 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández, A.; Clavería, I.; Pina, C.; Elduque, D. Predictive Methodology for Quality Assessment in Injection Molding Comparing Linear Regression and Neural Networks. Polymers 2023, 15, 3915. https://doi.org/10.3390/polym15193915
Fernández A, Clavería I, Pina C, Elduque D. Predictive Methodology for Quality Assessment in Injection Molding Comparing Linear Regression and Neural Networks. Polymers. 2023; 15(19):3915. https://doi.org/10.3390/polym15193915
Chicago/Turabian StyleFernández, Angel, Isabel Clavería, Carmelo Pina, and Daniel Elduque. 2023. "Predictive Methodology for Quality Assessment in Injection Molding Comparing Linear Regression and Neural Networks" Polymers 15, no. 19: 3915. https://doi.org/10.3390/polym15193915
APA StyleFernández, A., Clavería, I., Pina, C., & Elduque, D. (2023). Predictive Methodology for Quality Assessment in Injection Molding Comparing Linear Regression and Neural Networks. Polymers, 15(19), 3915. https://doi.org/10.3390/polym15193915