2. Model Development
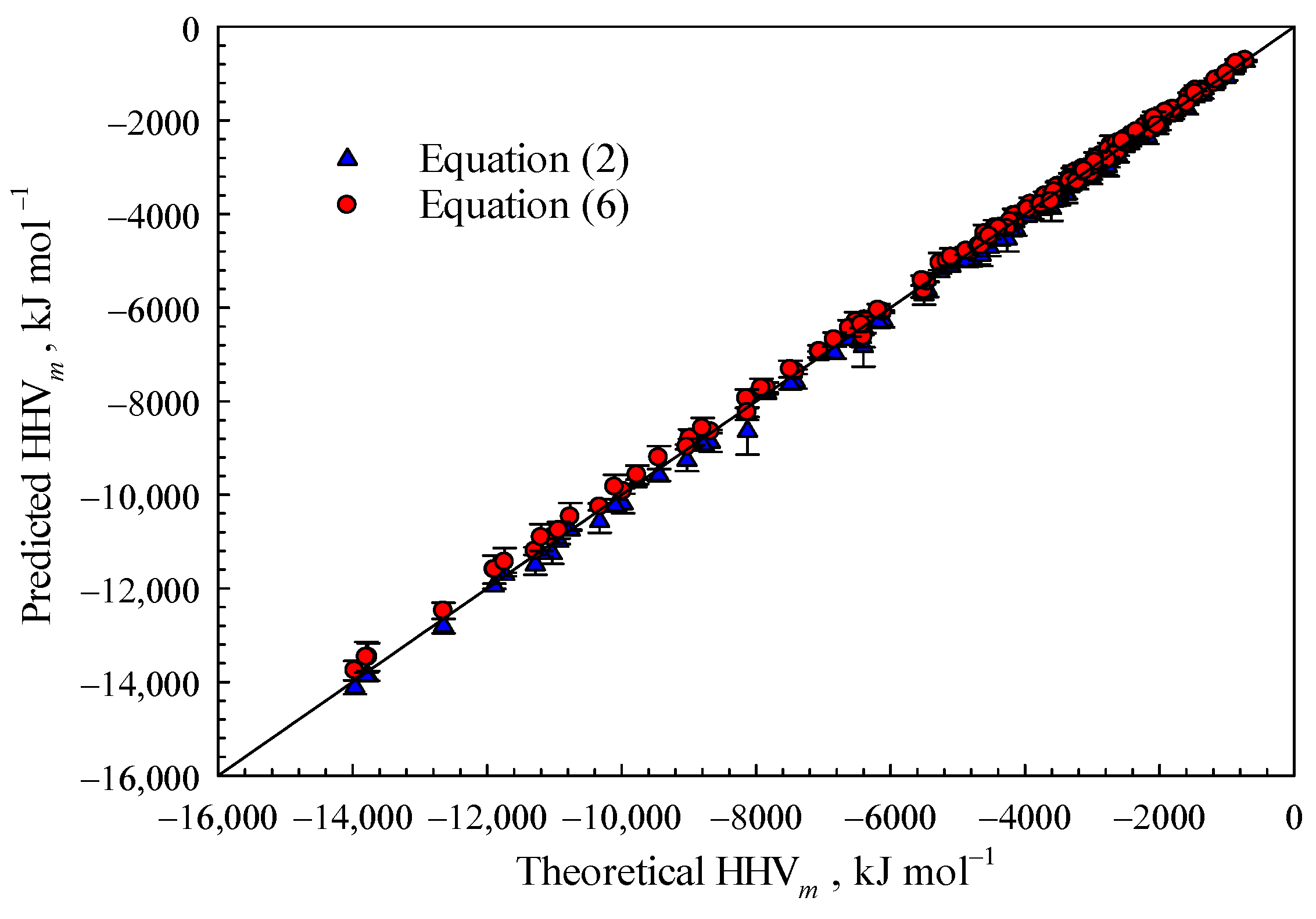
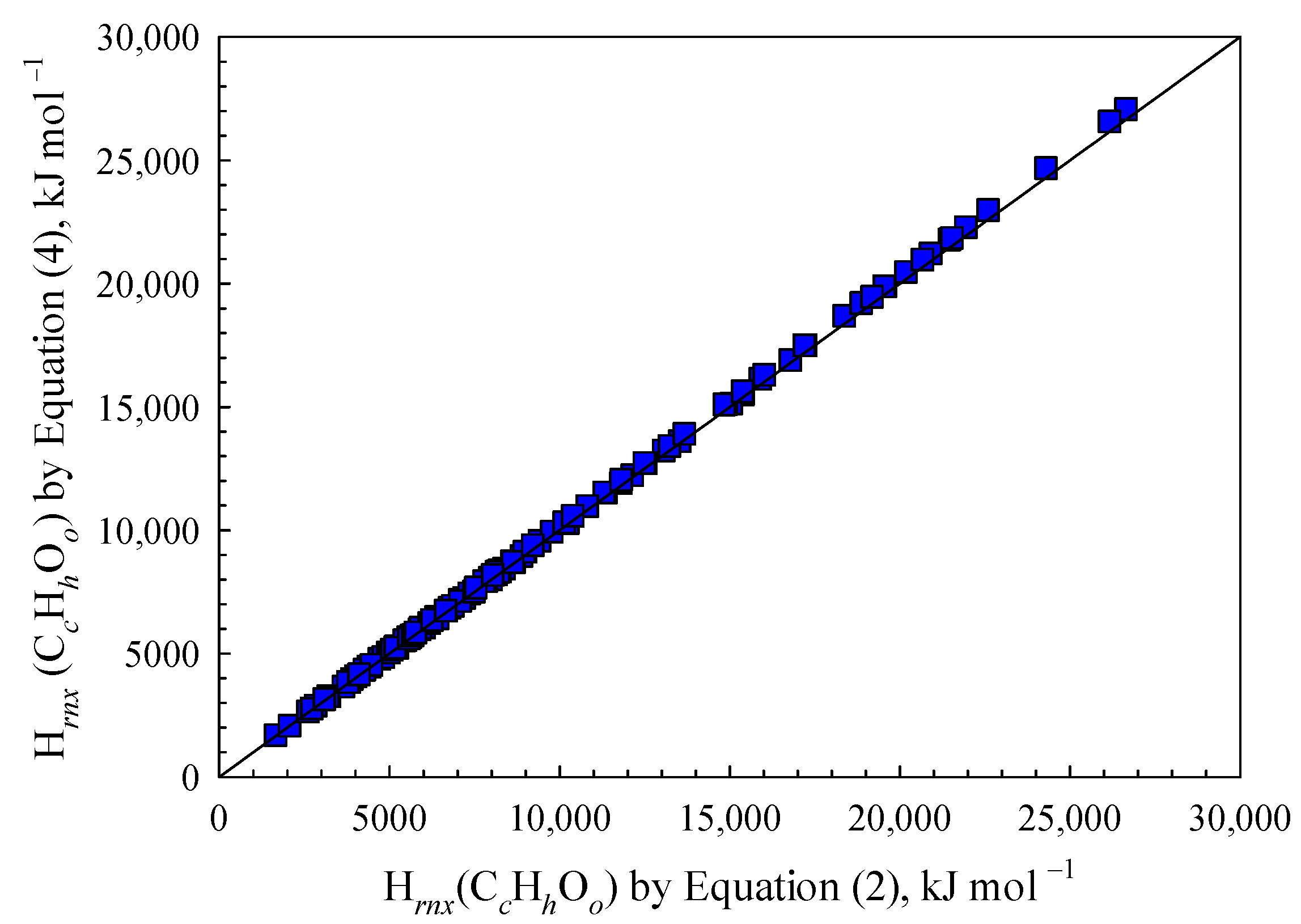
The combustion of organic materials with the genetic formula C
cH
hO
o can generally be described using the following reaction
where
=
c +
h/4 −
o/2,
= −
c, and
= −
h/2. The heat of a chemical reaction can be determined by considering the energies involved in bond breaking and bond making. The reaction heat of an exothermic reaction is usually defined as a negative value. Then, the bond dissociation energy (BDE) represents the amount of energy needed to break a bond and is expressed as a positive value. Thus, the products coefficients in Equation (1) are negative and represent that the formation process of combustion products is exothermic. Then, the combustion heat released by reaction (1) can then be accurately evaluated as the difference between the sum of bond dissociation energies (BDEs) of reactants and products [
4,
6].
where HHV
m refers to the higher heating value on a molar basis, at standard conditions (i.e., 100 kPa and 25 °C). H
rnx,i represents total bond dissociation energies of a substance
i, whereas
Di,m. signifies the BDE value of the chemical bond
m with respect to component
i. The value of H
rnx,H2O should include the molar heat of vaporization for water (40.7 kJ mol
−1).
The BDE values are always endothermic and have a positive enthalpy value, as shown in
Table 1. Significantly, the values of H
rnx,O2, H
rnx,CO2, and H
rnx,H2O remain constant, with the results of 498.0 kJ mol
−1, 1607.0 kJ mol
−1, and 969.8 kJ mol
−1, respectively. Taking CH
4 as an example, the total BDEs of CH
4 are approximately 1657.2 kJ mol
−1 by adding the average BDE values of four C-H bonds, i.e.,
. Then, the evaluation of Equation (2) yields −892.8 kJ mol
−1 for the combustion heat of CH
4, close to its actual value of −890.53 kJ mol
−1.
An empirical formula for the calculation to predict BDE values has been proposed by Tiggelen et al. [
21] as follows:
where
αA and
αB are constants characterizing radicals A and B. The value
αH for the H atom is definitely equal to unity, that is,
αH = 1.
αm stands for the smaller of the latter, i.e., min(
αA αB). Then, the typical values of
DH,
DC, and
DO were, respectively, 215.95 kJ mol
−1, 173.68 kJ mol
−1, 77.32 kJ mol
−1, and
αC = 1.20,
αO = 2.95 [
21]. The reliability of Equation (3) has been thoroughly discussed and demonstrated through a comparison between the calculated and experimental values of bond dissociation energy, as reported by Tiggelen et al. in 1965 [
21]. The discrepancies between calculated and experimental values are within a range of 8.37~12.56 kJ mol
−1, which can be considered negligible compared to the total value H
rxn(C
cH
hO
o) of organic materials.
Element C typically forms four electron-pair bonds, while element O forms two and element H only one. It is hypothesized here that a chemical bond can be simplified as either a single bond or a combination of such bonds. Then, in light of the empirical formula Equation (3), the total bond dissociation energies of an organic matter C
cH
hO
o can be determined using
where the symbol
refers to the summation for all the chemical bonds with atom C, and the number of bond R−C is 4
c. Similar definitions hold for another two accumulative symbols in Equation (4).
αC,m stands for the smaller of the latter, i.e., min(
αC,
αR), for C bonds in organic matter. For the organic compounds with established chemical structures, the carbon bonds have been simplified to C-C, C-H, and C-O, with corresponding bond numbers being determined through statistical analysis. For example, in the case of C-O bonds,
αC,m can be expressed as min(
αC,αO), with a value of 1.2. Similar connotations are attributed to other symbols. The first term on the right-hand side of Equation (4) can be determined by aggregating the outcomes. Analogous procedures are executed for the bonds involving oxygen and hydrogen.
For technical reasons, we rewrite Equation (4) as
where H
rnx,C is the average of α
CD
C/α
C,m for element C in an organic compounds, and similar definitions apply to H
rnx,H and H
rnx,O. Based on the assumption proposed above, the values of H
rnx,C, H
rnx,H, and H
rnx,O can be determined with the numbers of single bonds. By applying the rearrangement of Equation (5) to Equation (2), an analytical model for estimating combustion heat can be derived as
Formulas (6)–(9) describe the relationship between higher heating value and atom contents from the prescriptive of bond dissociation energies. The energy contribution of each element atom can be accurately calculated through further analysis, thereby enabling the determination of the reliability of traditional fitting equations.
4. Results and Discussion
The parameters H
rnx,C, H
rnx,H, and H
rnx,O in Equation (5) correspond to the contributions of individual elemental atoms toward the calculated bond dissociation energy values of an organic compound. These parameters are contingent upon the chemical structure of the compound. For instance, for carbon atoms in methane (CH
4), the value of α
C,m is consistently equal to 1, thereby resulting in an H
rnx,C value of 208.42 kJ mol
−1. In contrast, the carbon bond in methanol (CH
3OH) comprises three C-H bonds and one C-O bond, thereby enabling the determination of the H
rnx,C value as 199.73 kJ mol
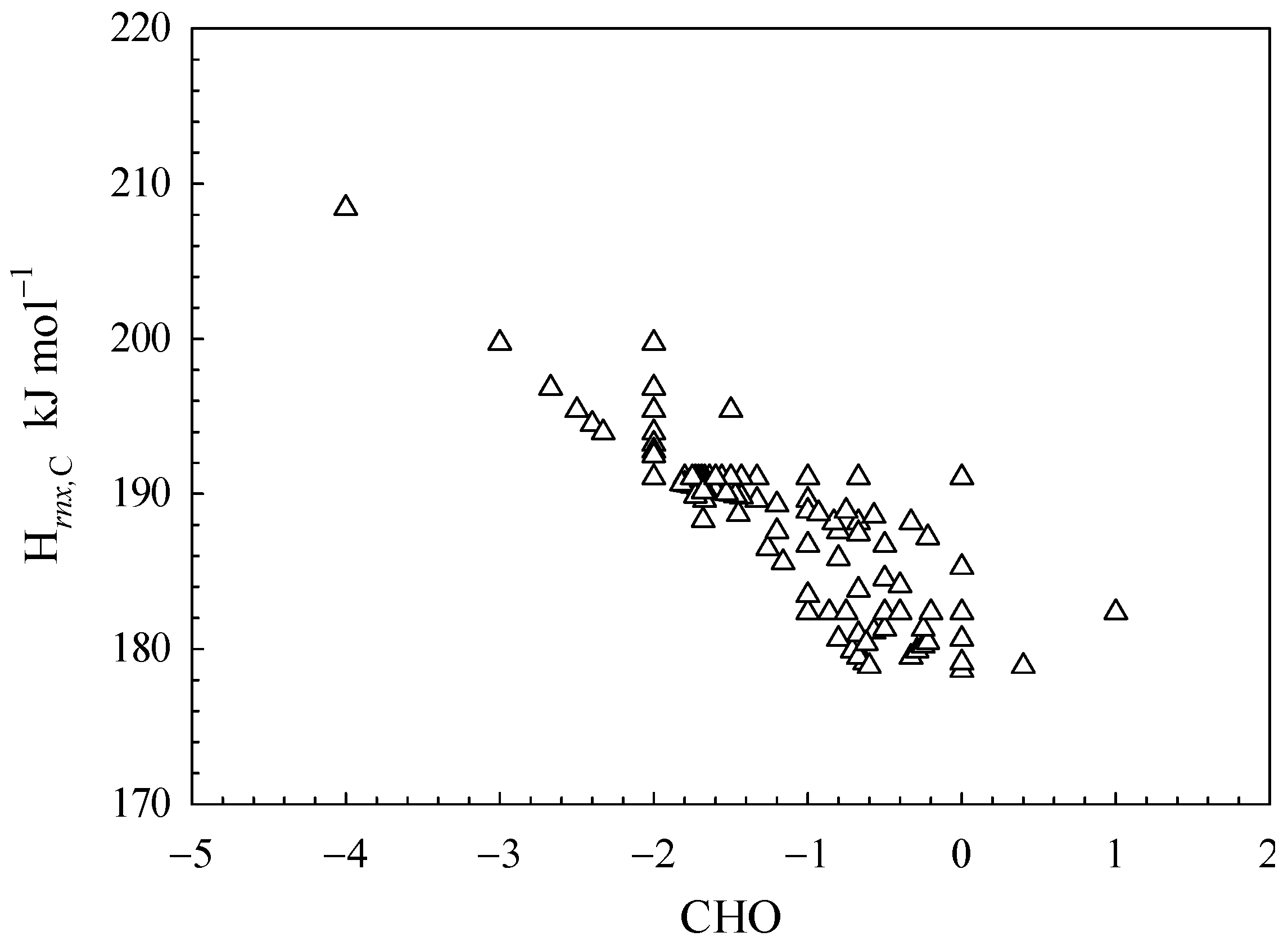
−1. As depicted in
Figure 3, the H
rnx,C value varies in the range of 178.63 to 208.42 kJ mol
−1.
As indicated by Equations (4) and (5), the H
rnx,C value increases with a decrease in average α
C,m value. As per Equation (3), the value of α
C,m can be either 1.2 or 1, resulting in a theoretical range for H
rnx,
C of 173.68 to 208.42 kJ mol
−1. The maximum H
rnx,
C value is equivalent to that of CH
4, as depicted in
Figure 3. However, the predicted minimum value is slightly lower than the experimental values, and no actual organic compound exhibits it. This is due to the indispensability of C-H bonds in the organic matter’s C bonds.
The CHO index, as depicted in
Figure 3, has been employed to characterize the status of carbon bonds. The H
rnx,C values display an inverse correlation with increasing CHO values. A higher value of the CHO index indicates a greater degree of carbon oxidation in organic matter, leading to a reduction in the proportion of C-H bonds within organic compounds’ C bonds. This results in the higher values of the average α
C,m of organic materials, due to the higher min(α
C, α
O) value compared to the min(α
C, α
H) value. In view of Equation (4), it is inevitable that the H
rnx,C value will decrease. From a chemical mechanism perspective, the breaking of C-O bonds is more facile than that of C-H bonds.
The experimental H
rnx,O values demonstrate a limited range of fluctuation, ranging from 190.07 to 209.09 kJ mol
−1 across a set of 154 organic compounds, as depicted in
Figure 4. The observed results align with the theoretical predictions, demonstrating consistency between theory and experiment. As the data samples do not contain any O-O bonds, the α
O,m value would be 1.2 or 1. When all oxygen bonds are either C-O or C=O bonds, the theoretical lower limit value is found to be consistent with the experimental data, i.e., α
ODO/α
C.
The αO,m value, however, would not be uniformly equal to 1 since the oxygen bonds in organic matters are not exclusively composed of O-H bonds. Theoretical maximum values of Hrnx,O can be deduced when an oxygen atom is bonded to both a hydrogen and a carbon, suggesting that alcohols are the most likely candidates in this group. Then, the upper limit value of Hrnx,O can be expressed as , where the calculated results align with the statistical findings from the experiments.
According to the definition of parameter
α [
21], the value of α for any radical is equal to or greater than unity. Therefore, irrespective of the nature of the hydrogen bond, the α
H,m value will consistently remain equal to 1. Consequently, this leads to H
rnx,H =
DH. Thus, the value of H
rnx,H remains a constant of 215.95 kJ mol
−1.
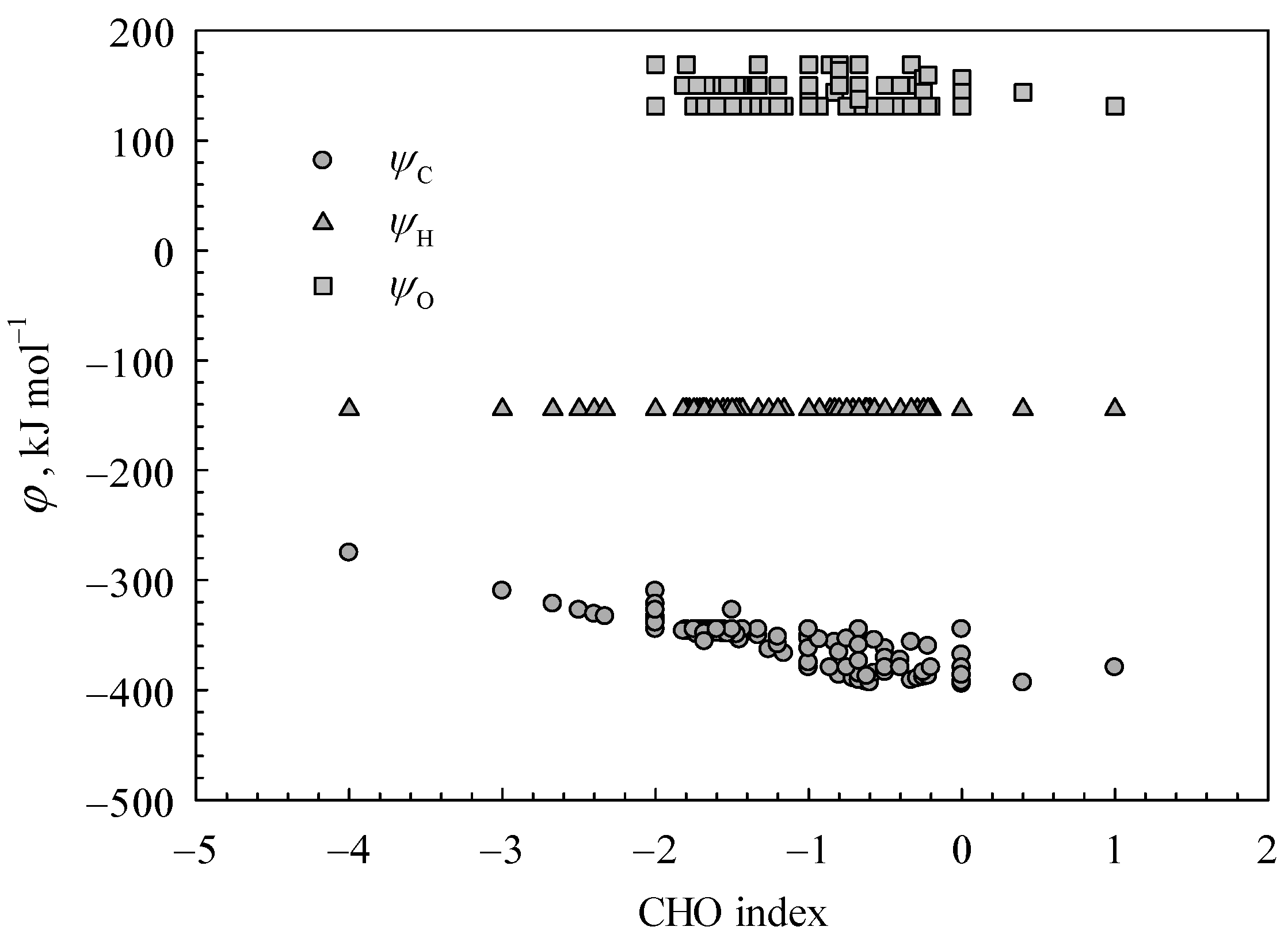
The variation trends of coefficients
φC,
φH, and
φO, along with the CHO values, are illustrated in
Figure 5. In accordance with the expression of Equation (6), the parameters
φC,
φH, and
φO characterize the energy output per mole of an elemental atom in relation to the higher heating values of organic substances. The
φH value has been determined as a constant of −144.44 kJ mol
−1, as H
rnx,O2 and H
rnx,H2O in Equation (8) are constants. Based on the empirical model presented in Equation (3), it is deduced that
DH ≈ 0.5·H
rnx (H
2). Considering Equation (8) and the hydrogen combustion reaction, it can be inferred that
φH is approximately equal to 0.5·HHV
m(H
2). The combustion heat of H
2 is approximately −142.30 kJ mol
−1 [
5], which closely aligns with the
φH.
As depicted in
Figure 5, the parameter
φC is observed to range from −394.50 to −275.34 kJ mol
−1 and exhibits a significant decrease with an increase in CHO index. The higher CHO index value indicates a reduced number of carbon atoms participating in the oxidation reaction during the combustion process. Accordingly, the contribution of carbon to the calorific value of combustion is reduced.
In consideration of the theoretical range (173.68, 208.42] kJ mol−1 for parameter Hrnx,C, it is theoretically anticipated that the coefficient φC would fall within the range (−414.30, −275.34] kJ mol−1. The decrease in energy released via carbon oxidation is remarkable as the Hrnx,C value increases. Therefore, achieving the minimum of φC is theoretically impossible.
Assuming all carbon bonds are C-C bonds, we can calculate that Hrnx,C = DC. Then, the estimated value of φC can be determined as −414.30 kJ mol−1, slightly exceeding the heat of combustion for elemental carbon (−393.5 kJ mol−1). The observed phenomenon is consistent with the fact that C-C bonds in carbon substances exhibit greater stability compared to those present in organic materials. The actual value of φC is typically significantly higher than the lower limit value, owing to the fact that the cleavage of C-H bonds requires a greater amount of energy absorption in comparison to C-C bonds.
According to Equation (9), the theoretical value of
φO would be between 131.13 and 169.17 kJ mol
−1, in light of the theoretical range [190.07, 209.09] kJ mol
−1 of the H
rnx,O value. This is consistent with the statistical results as shown in
Figure 5. Notably, Equation (9) denotes the difference in bond dissociation energy between O bonds in organic compounds and those in molecular oxygen O
2.
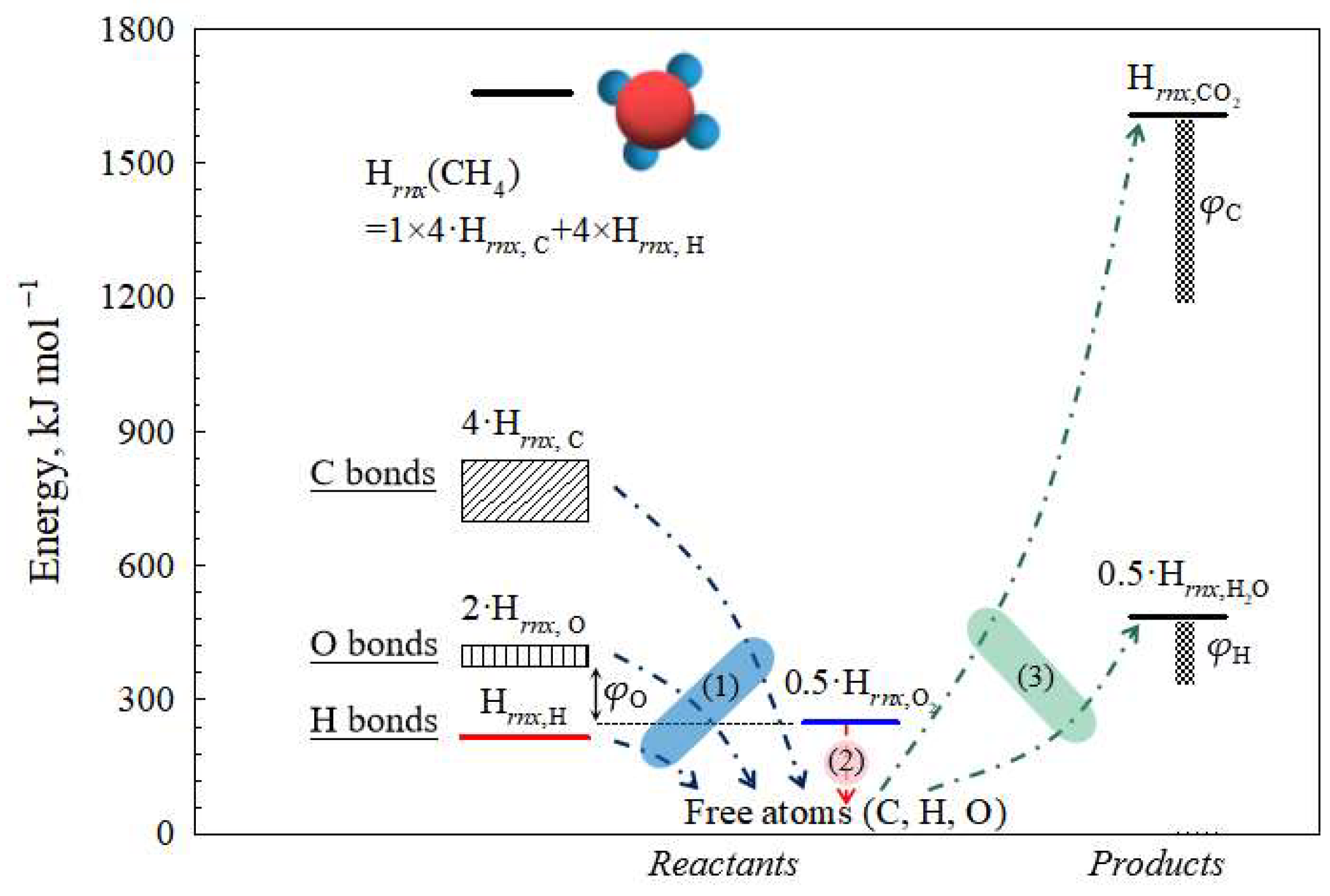
Based on the aforementioned analysis and Equations (6)–(9), the combustion process of organic compounds can be delineated into three distinct steps as shown in
Figure 6: (1) Thermal decomposition of organics yields isolated carbon, hydrogen, and oxygen atoms. (2) The molecular oxygen O
2 produces the free atom O. (3) The carbon and hydrogen atoms directly combine with oxygen atoms to produce carbon dioxide and water. The energy required for the formation of free O atoms in organic compounds is evidently higher compared to that needed for molecular oxygen.
The phenomenon of
φO > 0 demonstrates that the presence of oxygen in organic compounds has a negative impact on their combustion heat, which is consistent with statistical findings documented in the previous scholarly literature [
4,
5,
8,
23]. However, the current mathematical fittings occasionally adhere to the fundamental chemical principle regarding the role of element O in combustion heat.
By analyzing a significant amount of experimental data, previous research suggests that the heat released from burning organic fuels is approximately 418 kJ per mole of oxygen consumed, with water generated in the gas phase [
24,
25]. This empirical theory is commonly known as the oxygen consumption method [
4,
22]. By performing linear regression analysis, we have obtained HHV
m ≈ −437.81·
νO2 with a high
R2 value of 0.9988 for 154 different species of organic compounds. This can be further substantiated through theoretical deduction based on the proposed theoretical Equations (6)–(9). By utilizing the aforementioned hypothesis and Equation (3), Equation (6) can be rewritten as follows:
By substituting the given values, the coefficient (Hrnx,O2 − 4αODO) can be computed as −414.32 kJ mol−1. Equation (10) suggests that the heat released during the combustion process mainly depends on the bond recombination of atomic oxygen in oxygen molecules, regardless of changes in bond dissociation energies for atomic carbon, hydrogen, and oxygen in organic matter before and after reaction. This elegantly clarifies the correlation between combustion calorific value and oxygen consumption in terms of bond dissociation energy, providing a clear perspective.
For high-molecular polymers with complex constituents, the uncertainty surrounding their chemical structures hinders the applicability of Equation (2) in predicting H
rnx,i and HHV
m values. Consequently, empirical correlations are frequently established based on mass fractions of elemental composition. For high-molecular polymers with the chemical formula C
cH
hO
o, we define [C], [H], and [O] as the mass fractions of carbon, hydrogen, and oxygen elements, respectively. Then, we have [C] = 12
c/M
s, [H] =
h/M
s, and [O] = 16
o/M
s, where M
s = (12
c +
h+16
o). The higher heating values on a mass basis HHV
g can be expressed as HHV
m/M
s. On the basis, Equation (6) can be rewritten as
By employing a genetic algorithm optimization methodology in the 1stOpt 10.0 software, an analytical model is developed using data from a set of 154 organic matters [
22] while adhering to specific constraint conditions
φC∈(−414.30, −275.34],
φH = −144.44, and
φO∈[131.13, 169.17]. The fitting result has been listed as Equation (12) in
Table 2, demonstrating a significantly high correlation coefficient of
R2 = 0.9969.
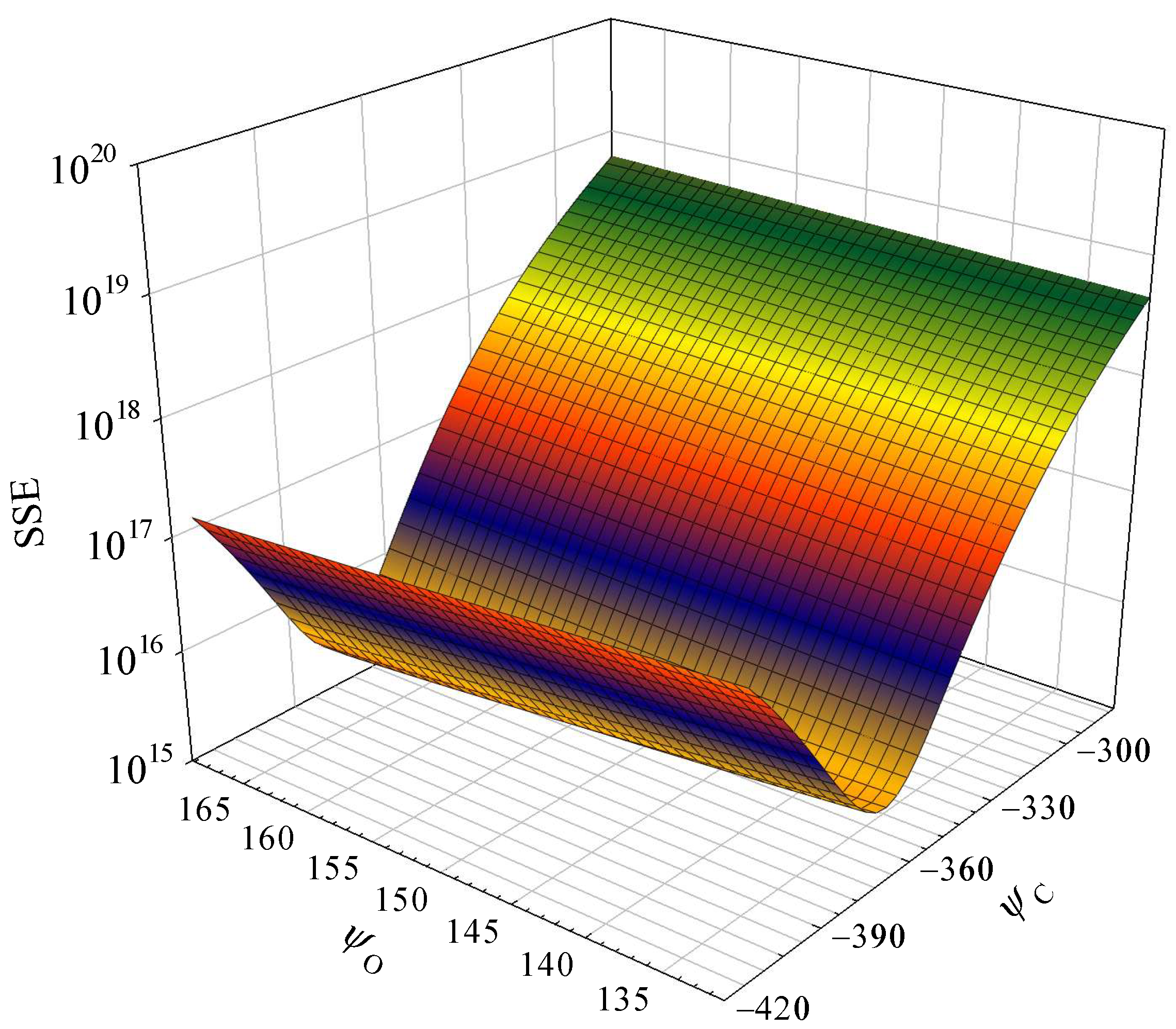
The sum of squares due to error (SSE) of parameters in Equation (12) is illustrated in
Figure 7. The SSE exhibits significant variations in response to changes in parameter
φC. The sensitivity values of
φC and
φO are calculated as 92.65% and 7.35%, respectively. Consequently, prior research has occasionally established a correlation between the higher heating value and carbon fractions using the equation HHV
g =
a·[C] +
b in the literature [
25,
26,
27]. The correlation for the organic compounds in the present work is listed as Equation (13) in
Table 2. The correlation coefficient exhibits a strong positive relationship with a value of 0.96.
Table 2 also presents other established correlations that share the same structure as Equation (11). The theoretical coefficients in Equation (11) prior to the mass fractions [C], [H], and [O] can be calculated as (−34.53, −22.95], −144.44, and [8.20, 10.57], respectively. The coefficients associated with [C] in Equations (14)–(18) consistently align with the expected theoretical range, while those connected to [H] exhibit noticeable variations. However, the observed empirical correlations sometimes challenge the established role of oxygen in the combustion process of organic substances, as demonstrated using Equations (14) and (15).
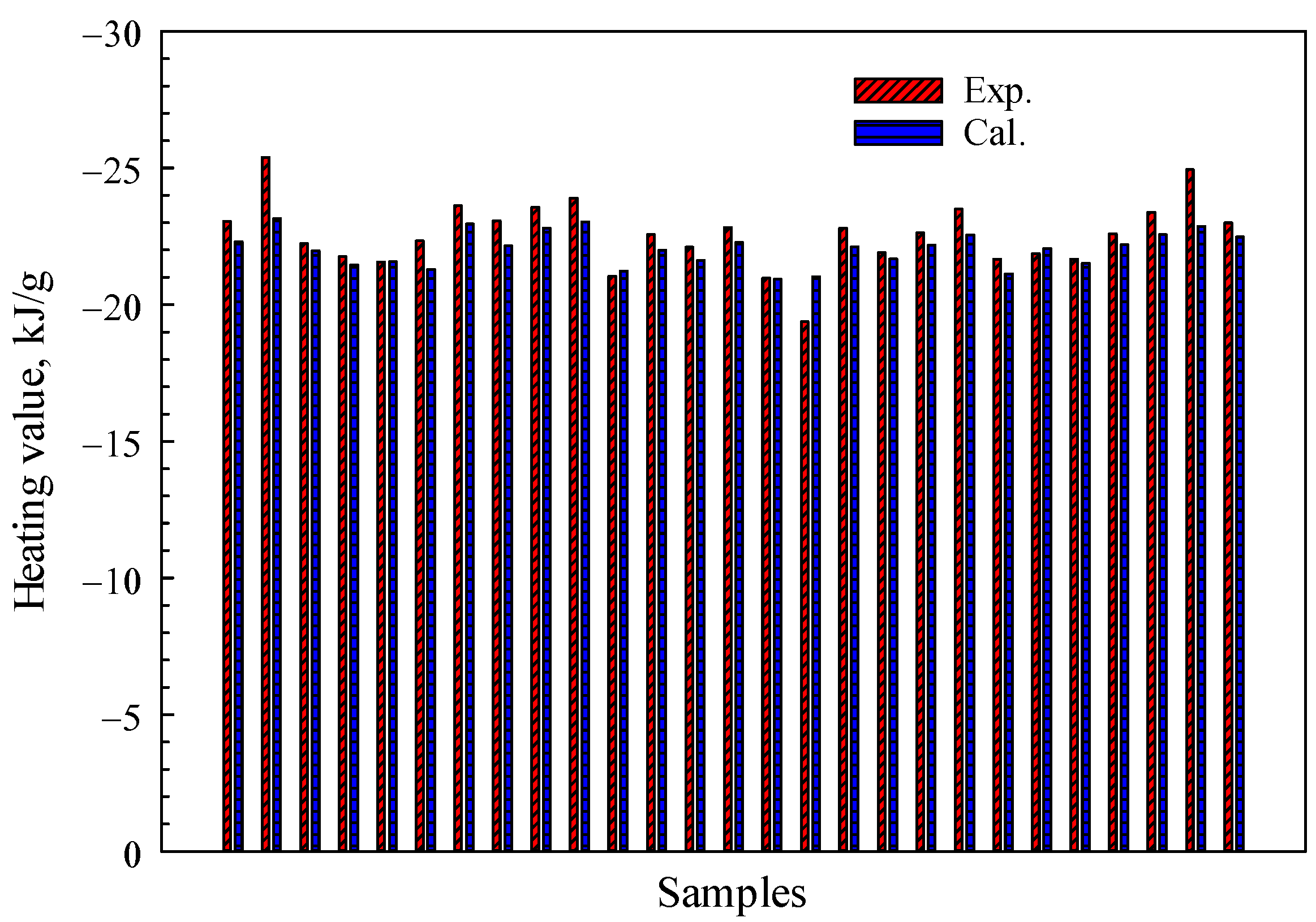
As shown in
Figure 8, to further investigate the robustness of the proposed theoretical models, we have compared the calculated results obtained from Equation (12) with experimental data collected from 27 different species of woody plant foliage [
18]. The test data adopted here are on a dry, ash-free basis. The average relative error, as depicted in
Figure 8, amounts to approximately 2%. The distinction arises from the fact that Equation (12) employs organic matter without benzene rings, whereas biomass primarily consists of cellulose, hemicellulose, and lignin, which contain a significant number of benzene rings. Theoretical models for Equations (6)–(9) do not take into account nitrogen and sulfur, which are other potential sources of error that should be considered.
For polymer materials with the chemical formula C
cH
hO
oN
nS
s, the combustion process can be expressed as
The heat of combustion of reaction (21) can be expressed using the extension Equation (6) according to the proposed theoretical model.
where
φN = 3·H
rnx,N − 0.5·H
rnx,N2,
φS = 4·H
rnx,S − H
rnx,SO2, and the values of H
rnx,N2 and H
rnx,SO2 are equivalent to 946 kJ mol
−1 and 1072.36 kJ mol
−1, respectively. The maximum values of H
rnx,N and H
rnx,S can be determined as α
ND
N and α
SD
S. The bond dissociation energies (BDE) of the N-H bond and S-H are reported as 390.80 kJ mol
−1 and 339.00 kJ mol
−1, respectively [
19,
20]. According to Equation (3), the values of H
rnx,N and H
rnx,S should be below 174.85 kJ mol
−1 and 123.05 kJ mol
−1, respectively. Subsequently, due to the aforementioned constrained condition, Equation (22) can be effectively fitted using a genetic algorithm in the 1stOpt 10.0 software as
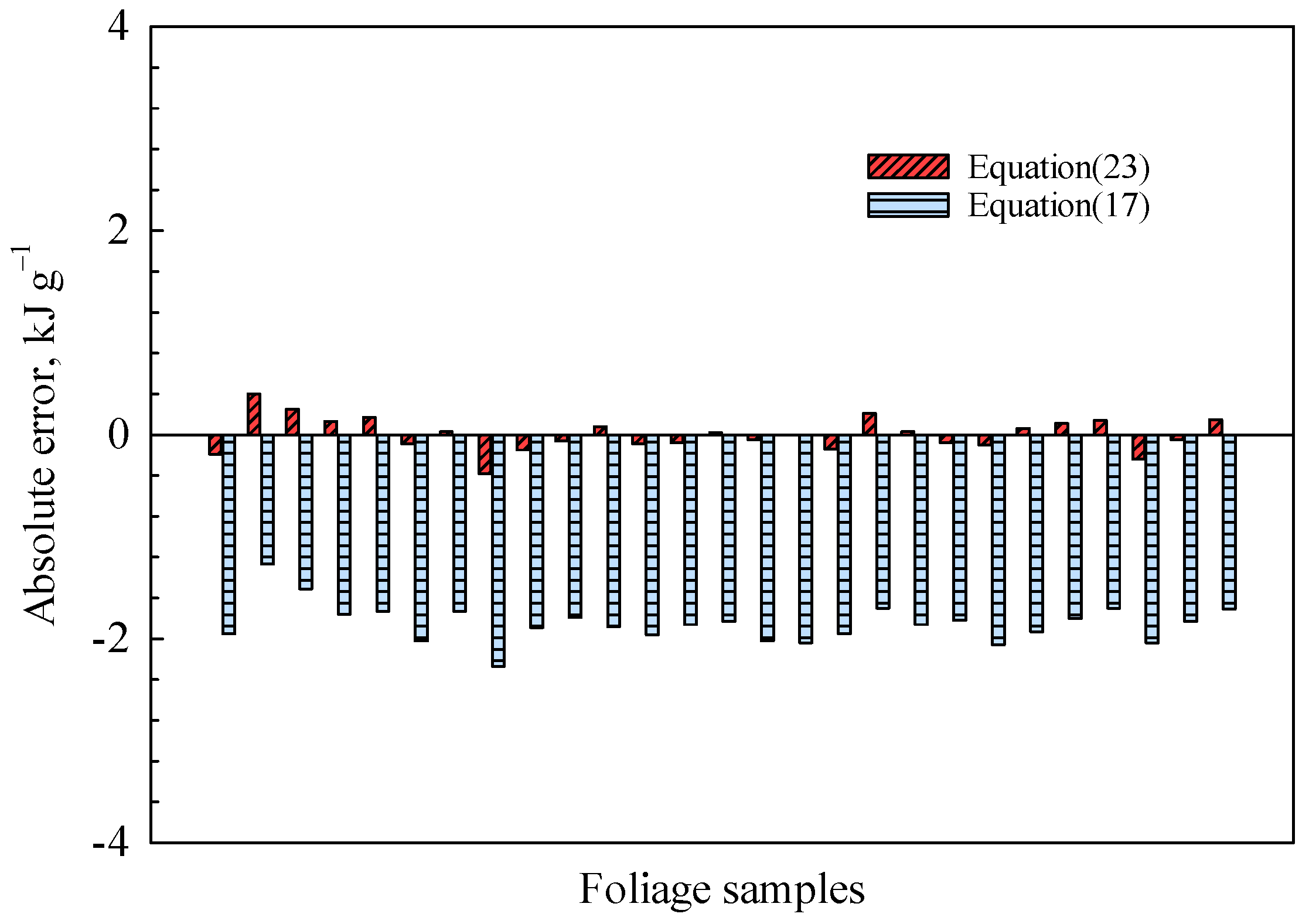
The present correlation, based on the theoretical model, evidently aligns with the mathematical fitting outcomes as listed in
Table 2. The absolute error between the experimental data and the results predicted with Equations (19) and (23) is depicted in
Figure 9. Equation (19) was initially proposed by Dulong and has since gained widespread utilization across various disciplines [
24]. The predictive model proposed in the present study clearly outperforms the existing model. The proposed model incorporates the influence of the element N, and the inclusion of conditional constraints enhances the rationality of coefficients. The influence of element contents on the accuracy of predicted results, however, necessitates further discussion. Hence, we have examined the parameter sensitivity of Equation (23) as illustrated in
Figure 10.
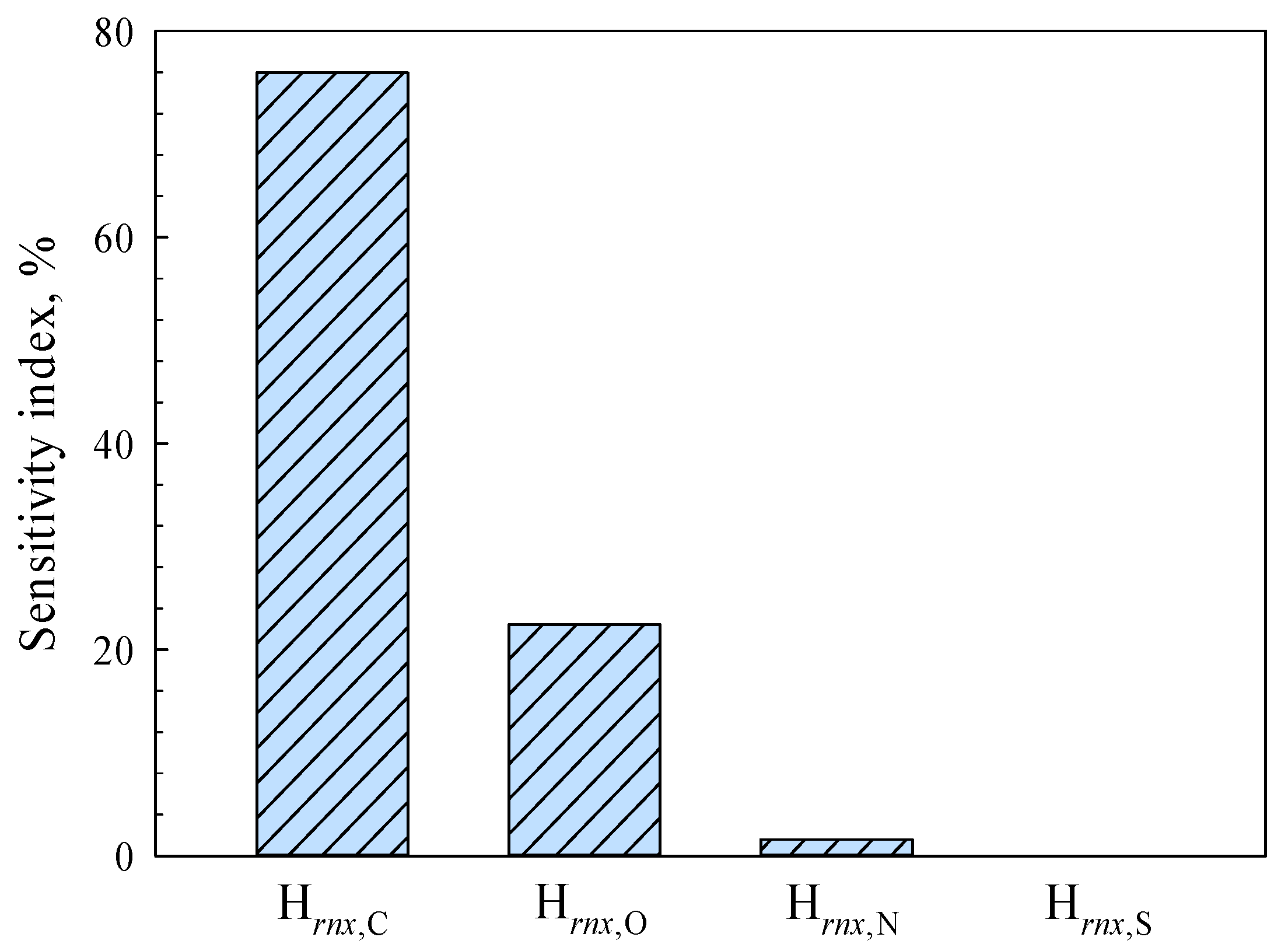
As shown in
Figure 10, the fitting parameters H
rnx,N and H
rnx,S have really small sensitivity index values, which means it is okay to ignore the mass fractions of element N and element S when predicting the higher heating values of lignocellulosic materials. This finding aligns with the comparative outcome illustrated in
Figure 9. The results of parameter sensitivity analysis critically depend on the numerical distribution of variables, which should be noted. Lignocellulosic biomass are essentially high-molecular polymers, mainly involving cellulose, hemicellulose, and lignin. According to the statistical data, lignocellulosic materials exhibit the highest carbon (C) content, followed by oxygen (O). The hydrogen (H) content is comparatively lower, while nitrogen (N) and sulfur (S) elements are present minimally or negligibly [
28]. Therefore,
Figure 10 implies that there is a potential risk of over-fitting when establishing empirical correlations involving the mass fractions of elements N and S in lignocellulosic materials. The efficacy of Equation (11) in predicting the performance of biomass materials and municipal solid wastes can be attributed to this observation.