A Phenomenological Model for Enthalpy Recovery in Polystyrene Using Dynamic Mechanical Spectra
Abstract
1. Introduction
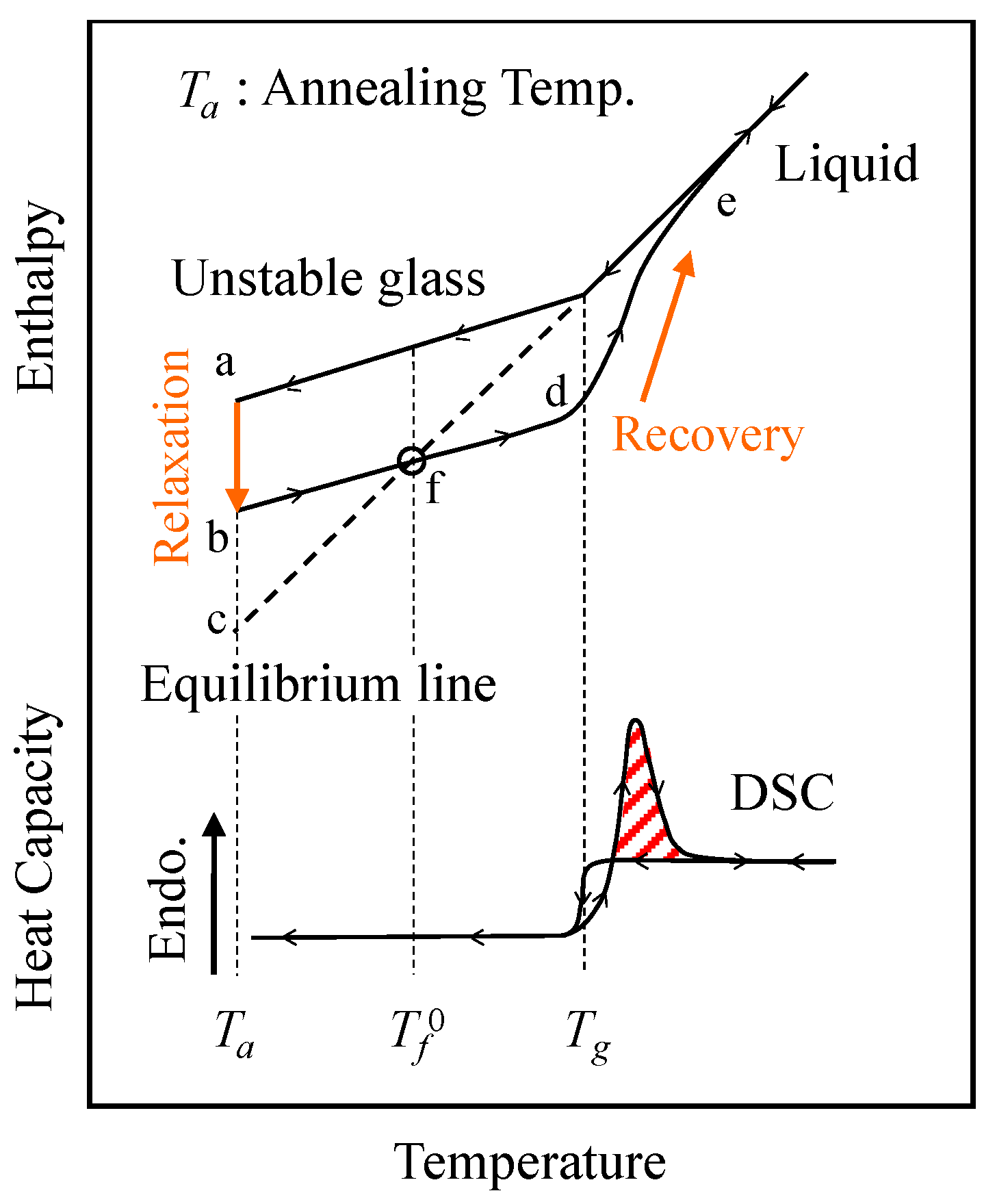
2. Theory
3. Experimental
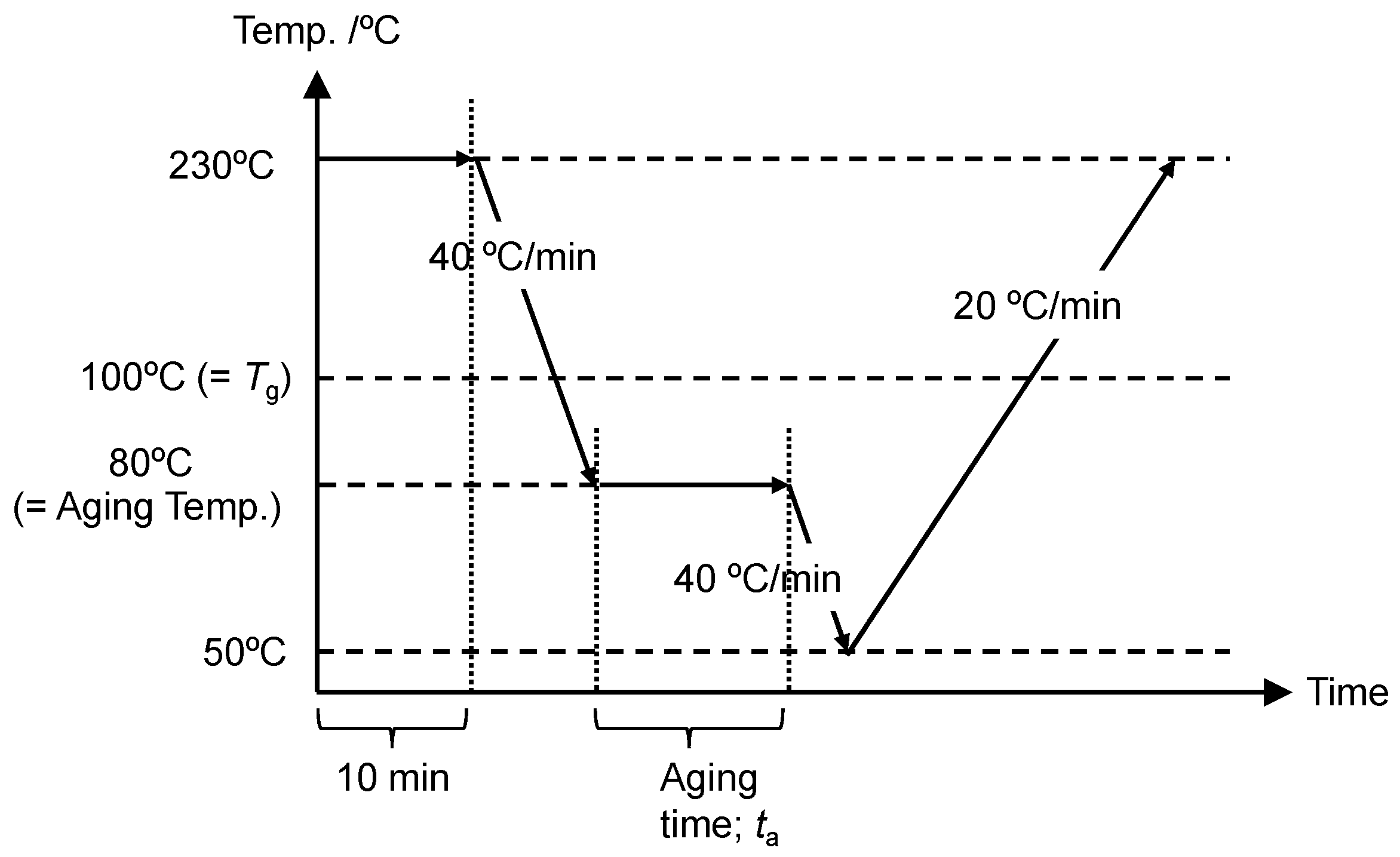
3.1. Sample Preparation
3.2. DSC Measurements
3.3. DMA Measurements
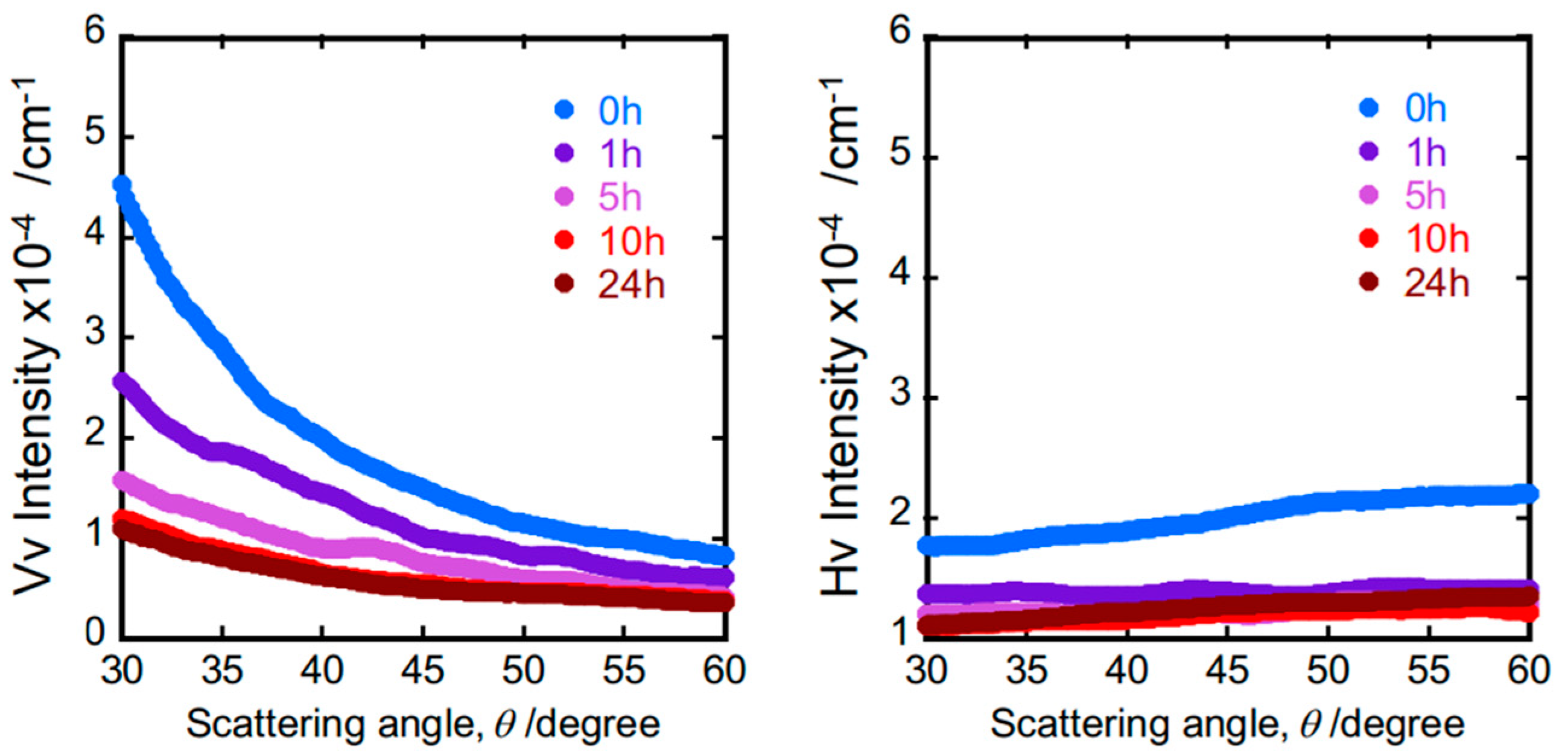
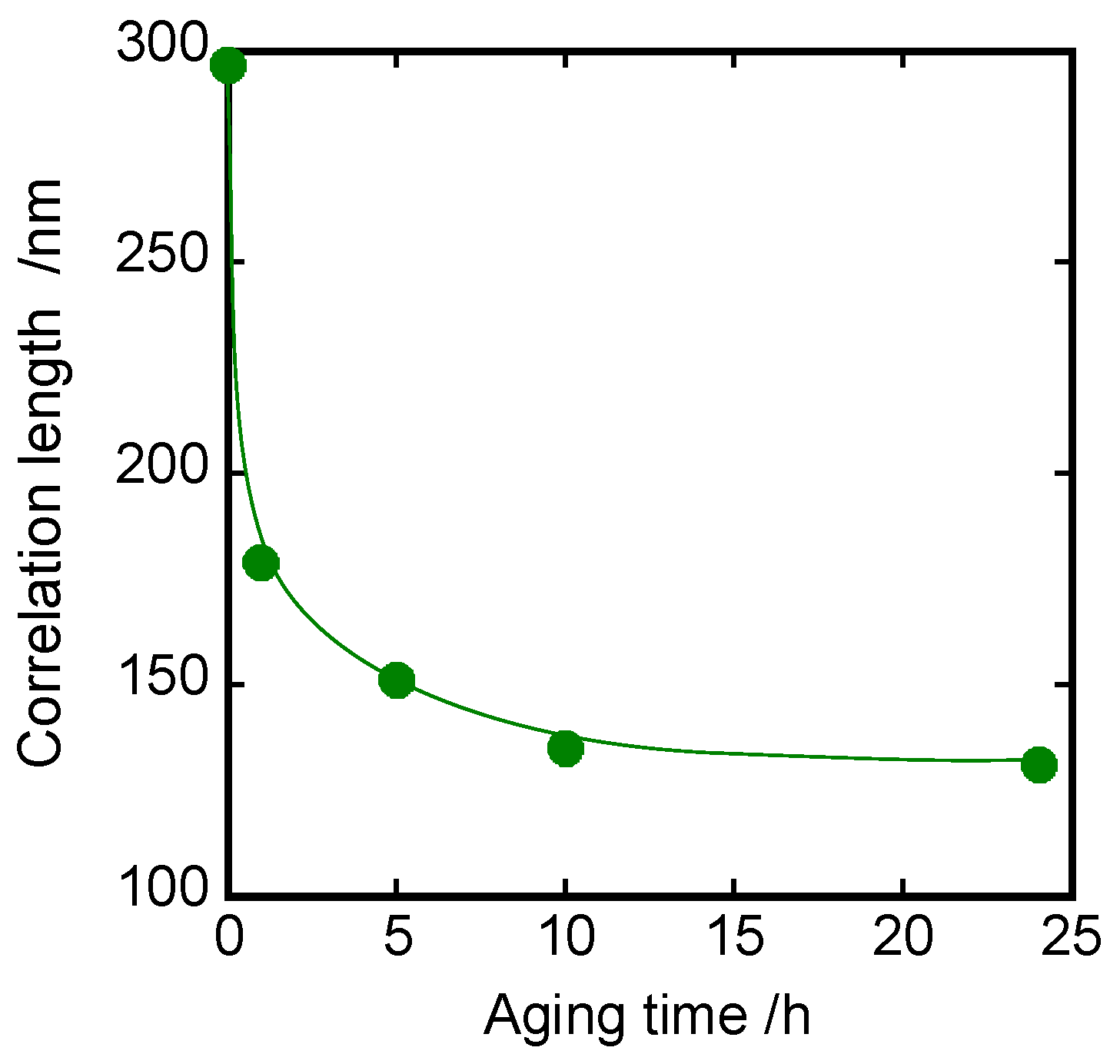
3.4. Light Scattering Measurements
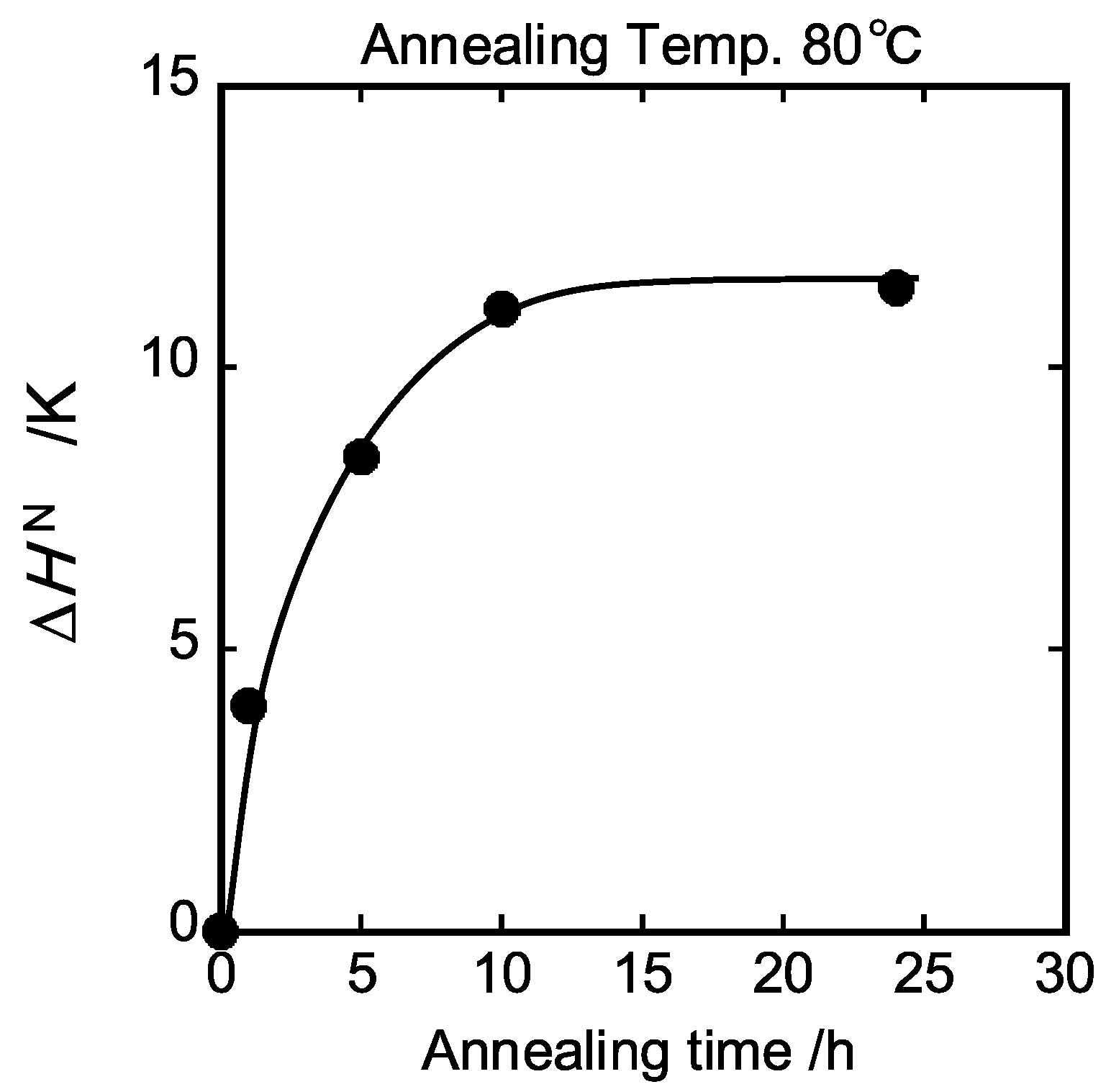
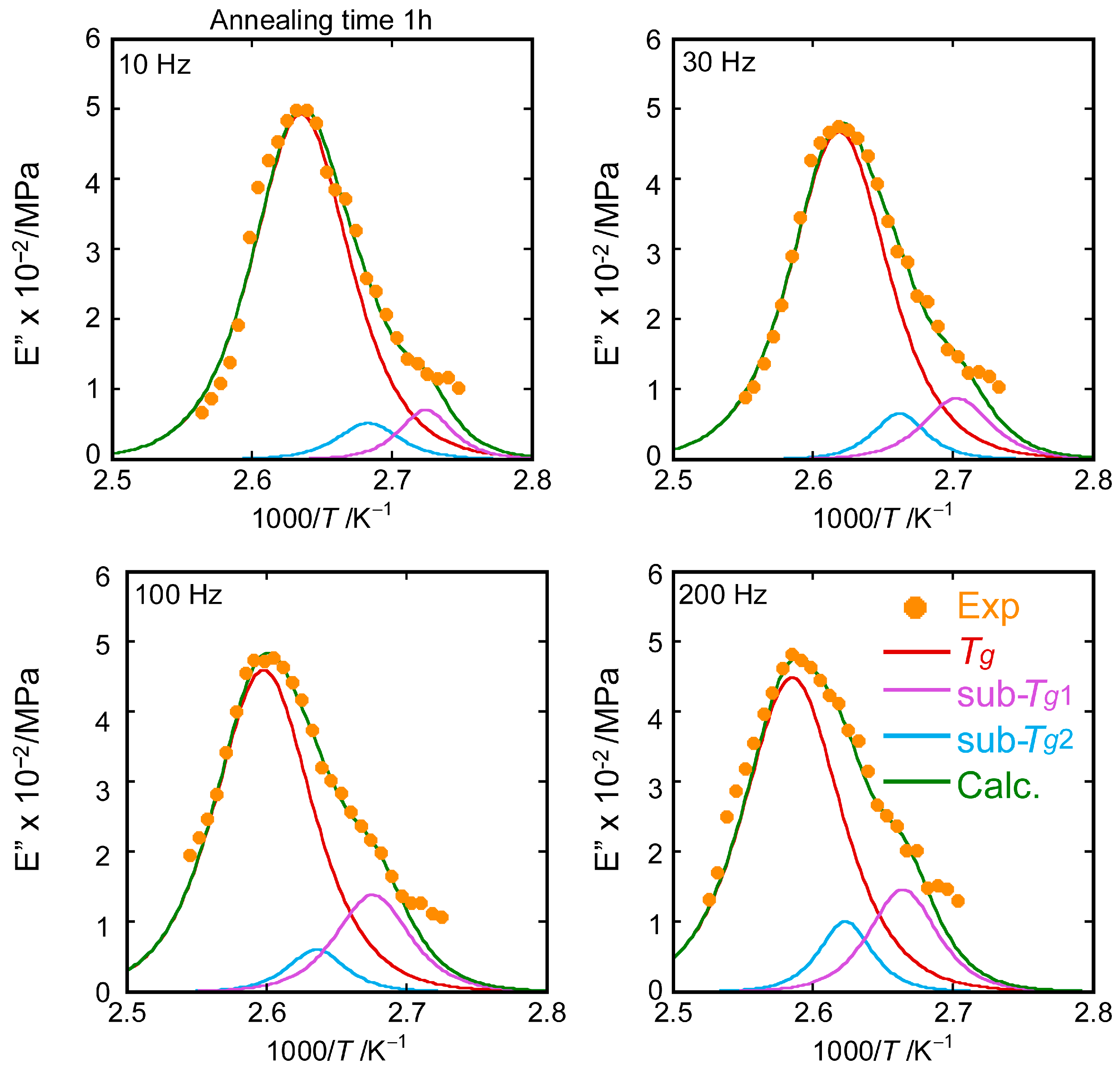
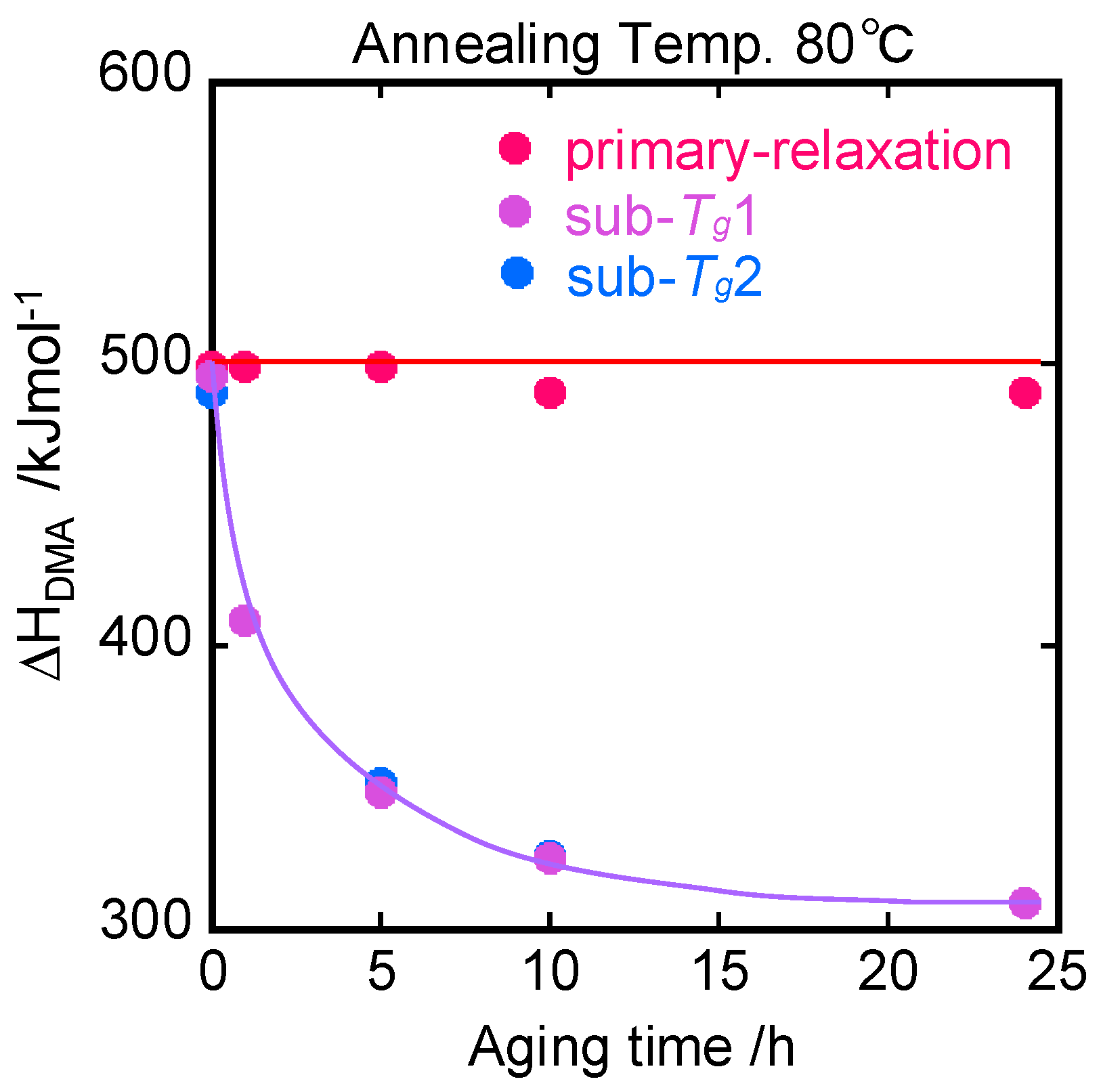
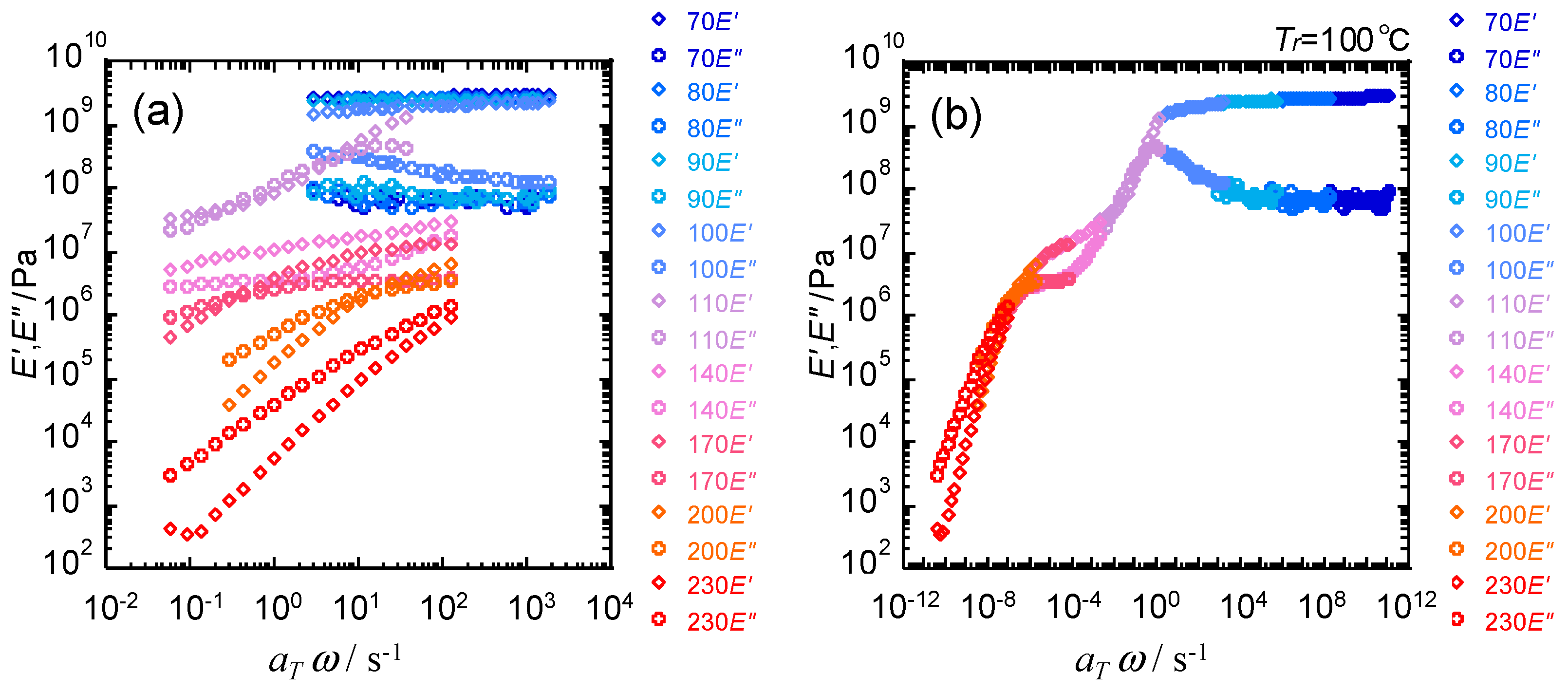
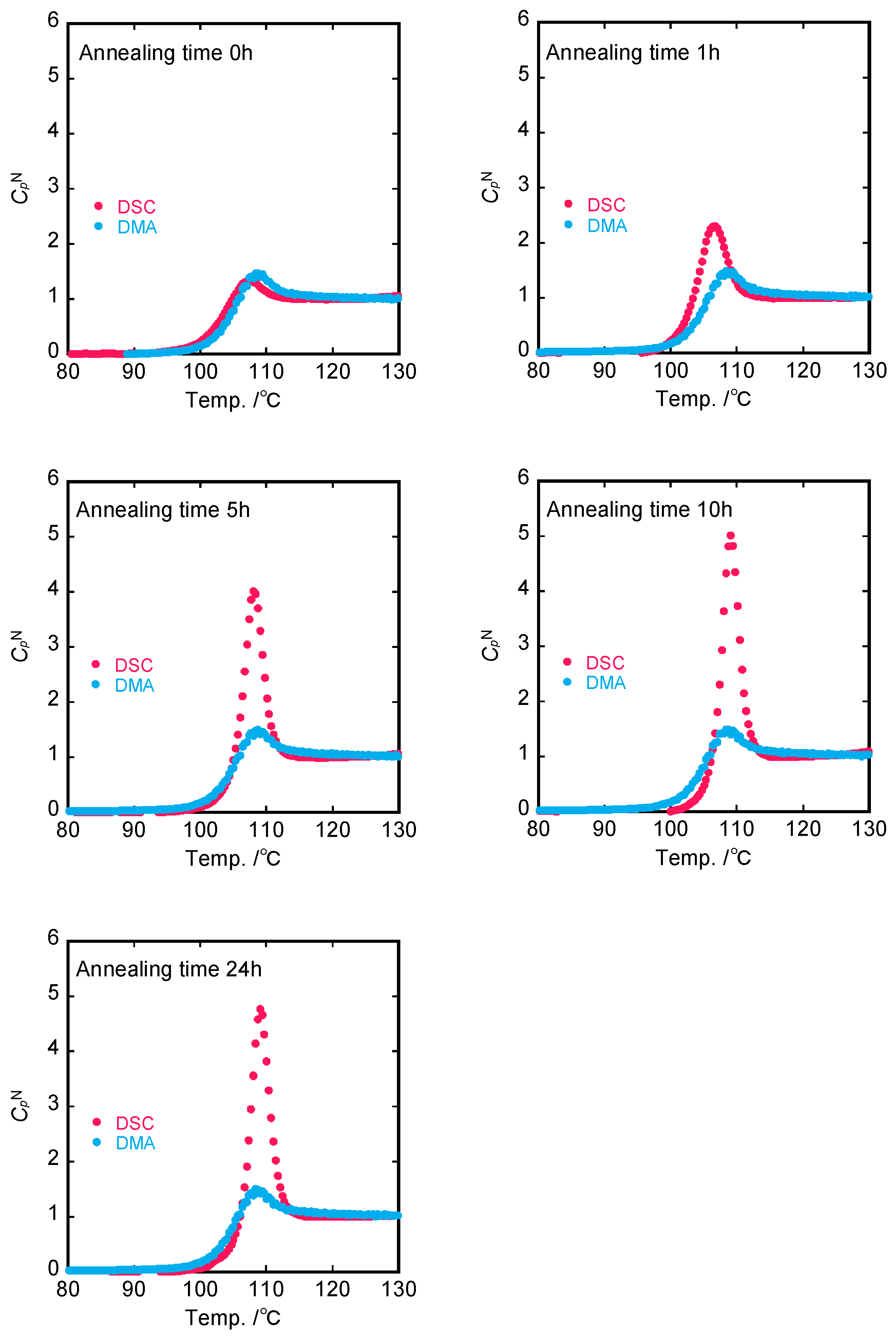
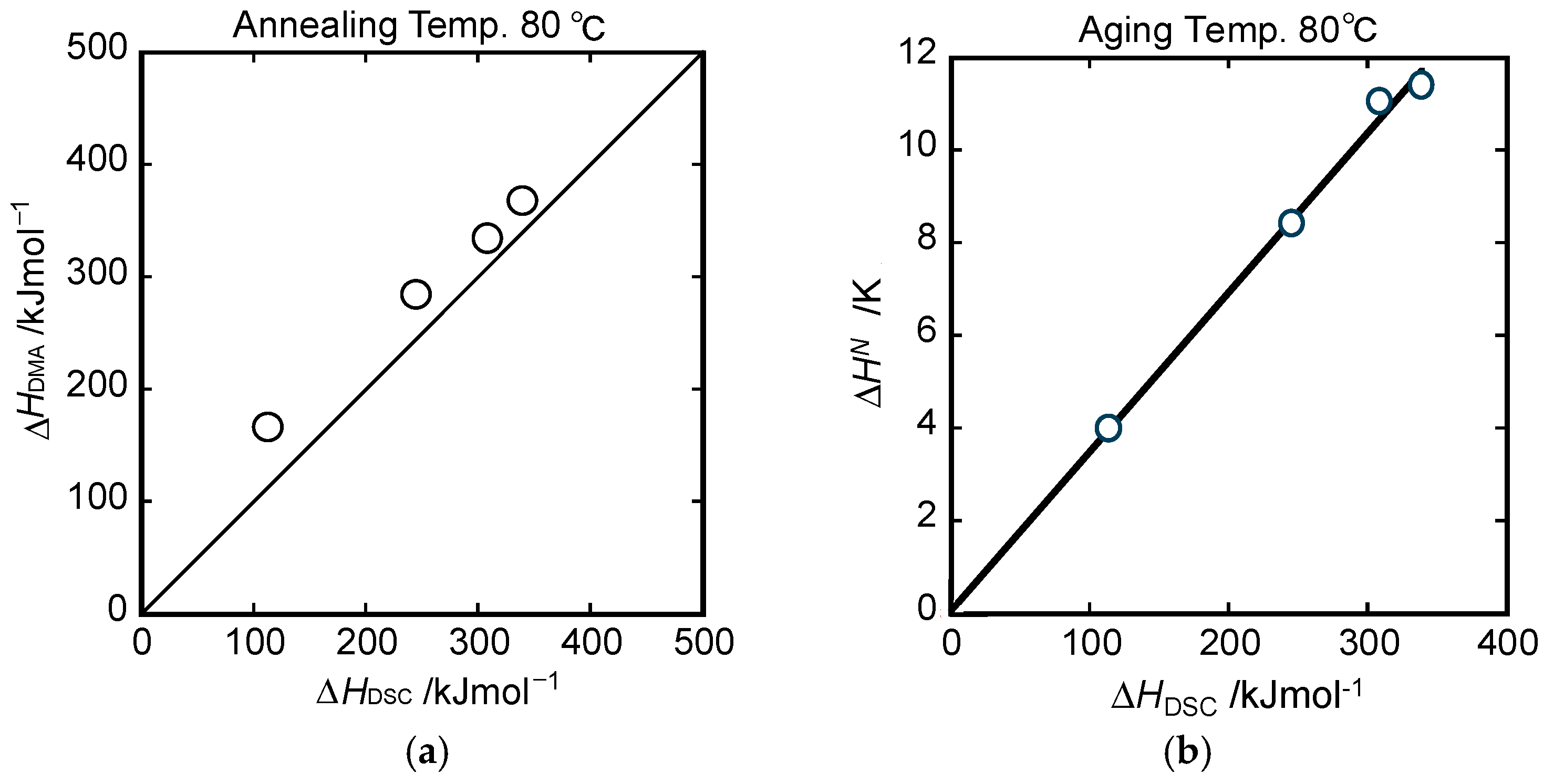
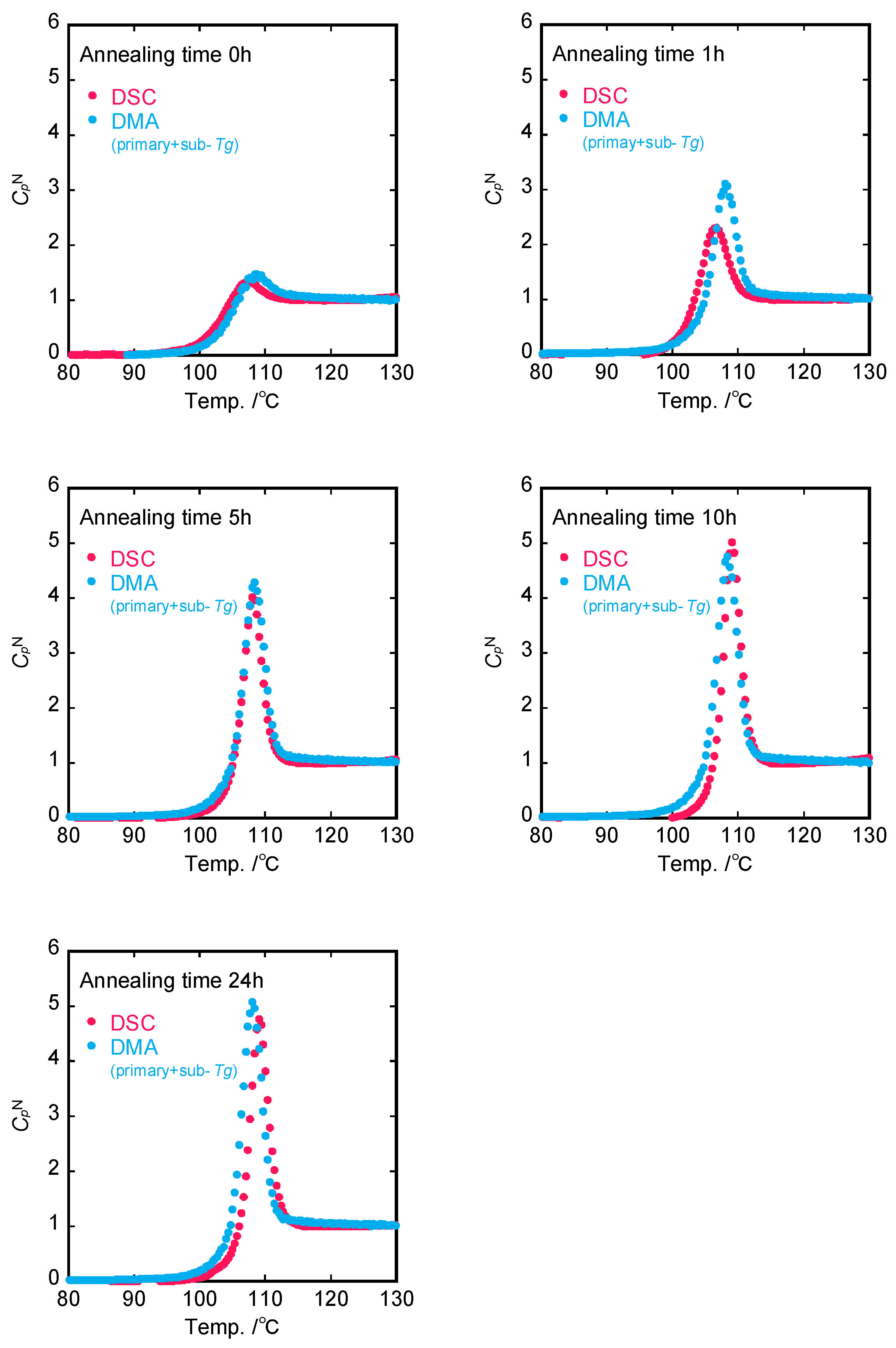
4. Results
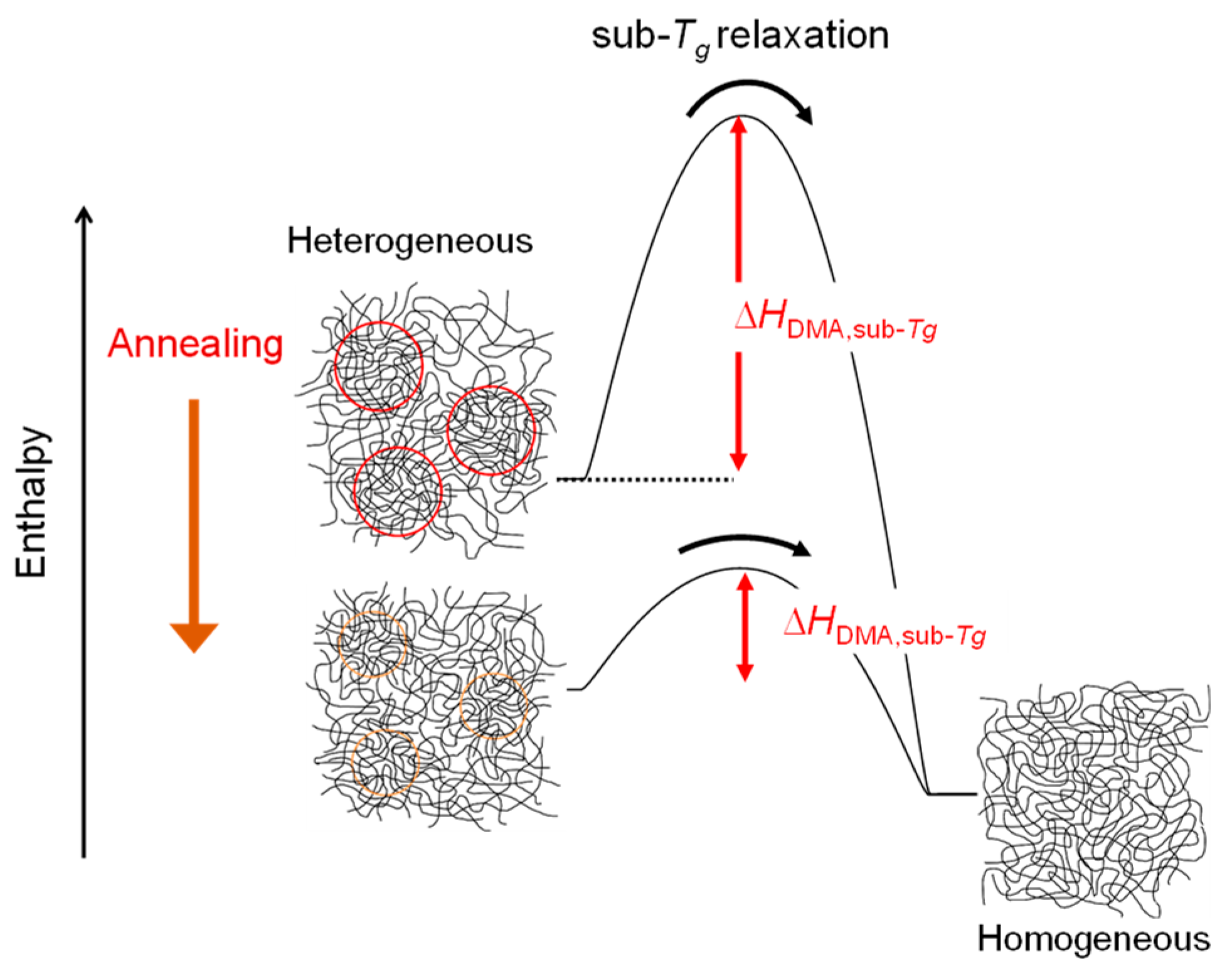
5. Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Struik, L.C.E. Physical Aging in Amorphous Polymers and Other Materials; Van Krevelen, D.W., Ed.; Elsevier Scientific Pub. Co.: Amsterdam, NY, USA, 1977. [Google Scholar]
- Struik, L.C.E. Physical aging in plastics and other glassy materials. Polym. Eng. Sci. 1977, 17, 165–173. [Google Scholar] [CrossRef]
- Grigoriadi, K.; Westrik, J.; Vogiatzis, G.G.; van Breemen, L.C.A.; Anderson, P.D.; Hutter, M. Physical Ageing of Polystyrene: Does Tacticity Play a Role? Macromolecules 2019, 52, 5948–5954. [Google Scholar] [CrossRef] [PubMed]
- Moynihan, C.T.; Macedo, P.B.; Montrose, C.J.; Montrose, C.J.; Gupta, P.K.; DeBolt, M.A.; Dill, J.F.; Dom, B.E.; Drake, P.W.; Easteal, A.J.; et al. Structural Relaxation in Vitreous Materials. Ann. N. Y. Acad. Sci. 1976, 279, 15–35. [Google Scholar] [CrossRef]
- Angell, C.A.; Ngai, K.L.; McKenna, G.B.; McMillan, P.F.; Martin, S.W. Relaxation in glassforming liquids and amorphous solids. J. Appl. Phys. 2000, 88, 3113–3157. [Google Scholar] [CrossRef]
- Weeks, E.R.; Crocker, J.C.; Levitt, A.C.; Schofield, A.; Weitz, D.A. Three-dimensional direct imaging of structural relaxation near the colloidal glass transition. Science 2000, 287, 627–631. [Google Scholar] [CrossRef]
- Torre, R.; Bartolini, P.; Righini, R. Structural relaxation in supercooled water by time-resolved spectroscopy. Nature 2004, 428, 296–299. [Google Scholar] [CrossRef] [PubMed]
- Hodge, I.M. Enthalpy relaxation and recovery in amorphous materials. J. Non-Cryst. Solids 1994, 169, 211–266. [Google Scholar] [CrossRef]
- Sakatusji, W.; Konishi, T.; Miyamoto, Y. Enthalpy relaxation and annealing effect in polystyrene. Phys. Rev. E 2013, 88, 012605. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Q.; Zhang, Y.; Montazerian, M.; Gulbiten, O.; Mauro, J.C.; Zanotto, E.D.; Yue, Y. Understanding Glass through Differential Scanning Calorimetry. Chem. Rev. 2019, 119, 7848–7939. [Google Scholar] [CrossRef]
- Kohlrausch, R. Theorie des elektrischen Rückstandes in der Leidener Flasche. Ann. Phys. Chem. 1854, 167, 179–214. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Kohlrausch, F. Ueber die elastische Nachwirkung bei der Torsion. Ann. Phys. Chem. 1863, 195, 337–368. [Google Scholar] [CrossRef]
- Tool, A.Q.; Eicitlin, C.G. Variations Caused in the Heating Curves of Glass by Heat Treatment1. J. Am. Ceram. Soc. 1931, 14, 276–308. [Google Scholar] [CrossRef]
- Tool, A.Q. Relation between Inelastic Deformability and Thermal Expansion of Glass in Its Annealing Range. J. Am. Ceram. Soc. 1946, 29, 240–253. [Google Scholar] [CrossRef]
- Hodge, I.M.; Berens, A.R. Effects of annealing and prior history on enthalpy relaxation in glassy polymers. 2. Mathematical modelingrelaxation in glassy polymers. 2. Mathematical modeling. Macromolecules 1982, 15, 762–770. [Google Scholar] [CrossRef]
- Hodge, I.M.; Huvard, G.S. Effects of annealing and prior history on enthalpy relaxation in glassy polymers. 3. Experimental and modeling studies of polystyrene. Macromolecules 1983, 16, 371–375. [Google Scholar] [CrossRef]
- Scherer, G.W. Use of the Adam-Gibbs Equation in the Analysis of Structural Relaxation. J. Am. Ceram. Soc. 1984, 67, 504–511. [Google Scholar] [CrossRef]
- Tribone, J.J.; O’Reilly, J.M.; Greener, J. Analysis of enthalpy relaxation in poly(methyl methacrylate): Effects of tacticity, deuteration, and thermal history. Macromolecules 1986, 19, 1732–1739. [Google Scholar] [CrossRef]
- Privalko, V.P.; Demchenko, S.S.; Lipatov, Y.S. Structure-dependent enthalpy relaxation at the glass transition of polystyrenes. Macromolecules 1986, 19, 901–904. [Google Scholar] [CrossRef]
- O’Reilly, J.M.; Hodge, I.M. Effects of heating rate on enthalpy recovery in polystyrene. J. Non-Cryst. Solids 1991, 131–133, 451–456. [Google Scholar] [CrossRef]
- Gomez Ribelles, J.L.; Monleon Pradas, M. Structural Relaxation of Glass-Forming Polymers Based on an Equation for Configurational Entropy. 1. DSC Experiments on Polycarbonate. Macromolecules 1995, 28, 5867–5877. [Google Scholar] [CrossRef]
- Brunacci, A.; Cowie, J.M.G.; Ferguson, R.; Gómez Ribelles, J.L.; Vidaurre Garayo, A. Structural Relaxation in Polystyrene and Some Polystyrene Derivatives. Macromolecules 1996, 29, 7976–7988. [Google Scholar] [CrossRef]
- Hutchinson, J.M.; Kumar, P. Enthalpy relaxation in polyvinyl acetate. Thermochim. Acta 2002, 391, 197–217. [Google Scholar] [CrossRef]
- Boucher, V.M.; Cangialosi, D.; Alegría, A.; Colmenero, J. Enthalpy Recovery of Glassy Polymers: Dramatic Deviations from the Extrapolated Liquidlike Behavior. Macromolecules 2011, 44, 8333–8342. [Google Scholar] [CrossRef]
- Narayanaswamy, O.S. A Model of Structural Relaxation in Glass. J. Am. Ceram. Soc. 1971, 54, 491–498. [Google Scholar] [CrossRef]
- Moynihan, C.T.; Easteal, A.J.; Bolt, M.A.; Tucker, J. Dependence of the Fictive Temperature of Glass on Cooling Rate. J. Am. Ceram. Soc. 1976, 59, 12–16. [Google Scholar] [CrossRef]
- Robertson, C.G.; Santangelo, P.G.; Roland, C.M. Comparison of glass formation kinetics and segmental relaxation in polymers. J. Non-Cryst. Solids 2000, 275, 153–159. [Google Scholar] [CrossRef]
- Mijović, J.; Ho, T. Proposed correlation between enthalpic and viscoelastic measurements of structural relaxation in glassy polymers. Polymer 1993, 34, 3865–3869. [Google Scholar] [CrossRef]
- Yoshida, H. Relationship between enthalpy relaxation and dynamic mechanical relaxation of engineering plastics. Thermochim. Acta 1995, 266, 119–127. [Google Scholar] [CrossRef]
- Simon, S.L.; Plazek, D.J.; Sobieski, J.W.; McGregor, E.T. Physical aging of a polyetherimide: Volume recovery and its comparison to creep and enthalpy measurements. J. Polym. Sci. Part B Polym. Phys. 1997, 35, 929–936. [Google Scholar] [CrossRef]
- Cowie, J.M.G. An ion conducted tour through some polymer electrolytes. Polym. Int. 1998, 47, 20–27. [Google Scholar] [CrossRef]
- Robertson, C.G.; Monat, J.E.; Wilkes, G.L. Physical aging of an amorphous polyimide: Enthalpy relaxation and mechanical property changes. J. Polym. Sci. Part B Polym. Phys. 1999, 37, 1931–1946. [Google Scholar] [CrossRef]
- Alves, N.M.; Mano, J.F.; Balaguer, E.; Meseguer Dueñas, J.M.; Gómez Ribelles, J.L. Glass transition and structural relaxation in semi-crystalline poly(ethylene terephthalate): A DSC study. Polymer 2002, 43, 4111–4122. [Google Scholar] [CrossRef]
- Dionísio, M.; Alves, N.M.; Mano, J.F. Molecular dynamics in polymeric systems. e-Polymers 2004, 4, 044. [Google Scholar] [CrossRef]
- Pan, P.; Zhu, B.; Inoue, Y. Enthalpy Relaxation and Embrittlement of Poly(l-lactide) during Physical Aging. Macromolecules 2007, 40, 9664–9671. [Google Scholar] [CrossRef]
- Illers, V.K.H. Einfluß der thermischen vorgeschichte auf die eigenschaften von polyvinylchlorid. Die Makromol. Chem. 1969, 127, 1–33. [Google Scholar] [CrossRef]
- Kovacs, A.J.; Aklonis, J.J.; Hutchinson, J.M.; Ramos, A.R. Isobaric volume and enthalpy recovery of glasses. II. A transparent multiparameter theory. J. Polym. Sci. Polym. Phys. Ed. 1979, 17, 1097–1162. [Google Scholar] [CrossRef]
- Tant, M.R.; Wilkes, G.L. An overview of the nonequilibrium behavior of polymer glasses. Polym. Eng. Sci. 1981, 21, 874–895. [Google Scholar] [CrossRef]
- Greaves, G.N.; Sen, S. Inorganic glasses, glass-forming liquids and amorphizing solids. Adv. Phys. 2007, 56, 1–166. [Google Scholar] [CrossRef]
- Weitz, A.; Wunderlich, B. Thermal analysis and dilatometry of glasses formed under elevated pressure. J. Polym. Sci. Polym. Phys. Ed. 1974, 12, 2473–2491. [Google Scholar] [CrossRef]
- Prest, W.M.; Roberts, F.J. Enthalpy Recovery in Pressure-Vitrified and Mechanically Stressed Polymeric Glasses. Ann. N. Y. Acad. Sci. 1981, 371, 67–86. [Google Scholar] [CrossRef]
- Tanaka, A.; Jono, Y.; Wakabayashi, N.; Nitta, K.-H.; Onogi, S. A Novel Mechanical Dispersion and Molecular Ordering in Styrene-Butadiene-Styrene Triblock Copolymer Films. Polym. J. 1991, 23, 1091–1097. [Google Scholar] [CrossRef][Green Version]
- Descamps, M.; Aumelas, A.; Desprez, S.; Willart, J.F. The amorphous state of pharmaceuticals obtained or transformed by milling: Sub-Tg features and rejuvenation. J. Non-Cryst. Solids 2015, 407, 72–80. [Google Scholar] [CrossRef]
- Wypych, A.; Duval, E.; Boiteux, G.; Ulanski, J.; David, L.; Mermet, A. Effect of physical aging on nano- and macroscopic properties of poly(methyl methacrylate) glass. Polymer 2005, 46, 12523–12531. [Google Scholar] [CrossRef]
- Ferri, D.; Laus, M. Activation Law Parameters of Viscoelastic Subglass Relaxations from Dynamic-Mechanical Moduli Measurements as a Function of Temperature. Macromolecules 1997, 30, 6007–6010. [Google Scholar] [CrossRef]
- Claiborne, C.; Crist, B. Light and X-ray scattering by polystyrene glasses. Colloid Polym. Sci. 1979, 257, 457–466. [Google Scholar] [CrossRef]
- Einstein, A. Theorie der Opaleszenz von homogenen Flüssigkeiten und Flüssigkeitsgemischen in der Nähe des kritischen Zustandes. Ann. Phys. 1910, 33, 1275–1295. [Google Scholar] [CrossRef]
- Debye, P.; Bueche, A.M. Scattering by an Inhomogeneous Solid. J. Appl. Phys. 1949, 20, 518–525. [Google Scholar] [CrossRef]
- Fujiki, M.; Oikawa, S. Light Scattering Study on the Structure of Pure Polystyrene. Polym. J. 1984, 16, 609–617. [Google Scholar] [CrossRef][Green Version]
- Schwarzl, F.; Staverman, A.J. Higher approximation methods for the relaxation spectrum from static and dynamic measurements of visco-elastic materials. Appl. Sci. Res. 1953, 4, 127–141. [Google Scholar] [CrossRef]
- Tschoegl, N.W. The Phenomenological Theory of Linear Viscoelastic Behavior an Introduction; Springer: Berlin/Heidelberg, Germany, 1989. [Google Scholar]
- Hutchinson, J.M.; Kovacs, A.J. A simple phenomenological approach to the thermal behavior of glasses during uniform heating or cooling. J. Polym. Sci. Polym. Phys. Ed. 1976, 14, 1575–1590. [Google Scholar] [CrossRef]
- Chen, H.S.; Wang, T.T. Sub-subTgstructural relaxation in glassy polymers. J. Appl. Phys. 1981, 52, 5898–5902. [Google Scholar] [CrossRef]
- Hutchinson, J.M.; Smith, S.; Horne, B.; Gourlay, G.M. Physical Aging of Polycarbonate: Enthalpy Relaxation, Creep Response, and Yielding Behavior. Macromolecules 1999, 32, 5046–5061. [Google Scholar] [CrossRef]
- Adolf, D.B.; Chambers, R.S.; Stavig, M.E.; Kawaguchi, S.T. Critical Tractions for Initiating Adhesion Failure at Interfaces in Encapsulated Components. J. Adhes. 2006, 82, 63–92. [Google Scholar] [CrossRef]
- Ohara, A.; Kodama, H. Correlation between enthalpy relaxation and mechanical response on physical aging of polycarbonate in relation to the effect of molecular weight on ductile-brittle transition. Polymer 2019, 181, 121720. [Google Scholar] [CrossRef]
- Sasaki, K.; Takatsuka, M.; Kita, R.; Shinyashiki, N.; Yagihara, S. Enthalpy and Dielectric Relaxation of Poly(vinyl methyl ether). Macromolecules 2018, 51, 5806–5811. [Google Scholar] [CrossRef]
- Pye, J.E.; Roth, C.B. Two simultaneous mechanisms causing glass transition temperature reductions in high molecular weight freestanding polymer films as measured by transmission ellipsometry. Phys. Rev. Lett. 2011, 107, 235701. [Google Scholar] [CrossRef] [PubMed]
- Cangialosi, D.; Boucher, V.M.; Alegria, A.; Colmenero, J. Direct evidence of two equilibration mechanisms in glassy polymers. Phys. Rev. Lett. 2013, 111, 095701. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nitta, K.-h.; Ito, K.; Ito, A. A Phenomenological Model for Enthalpy Recovery in Polystyrene Using Dynamic Mechanical Spectra. Polymers 2023, 15, 3590. https://doi.org/10.3390/polym15173590
Nitta K-h, Ito K, Ito A. A Phenomenological Model for Enthalpy Recovery in Polystyrene Using Dynamic Mechanical Spectra. Polymers. 2023; 15(17):3590. https://doi.org/10.3390/polym15173590
Chicago/Turabian StyleNitta, Koh-hei, Kota Ito, and Asae Ito. 2023. "A Phenomenological Model for Enthalpy Recovery in Polystyrene Using Dynamic Mechanical Spectra" Polymers 15, no. 17: 3590. https://doi.org/10.3390/polym15173590
APA StyleNitta, K.-h., Ito, K., & Ito, A. (2023). A Phenomenological Model for Enthalpy Recovery in Polystyrene Using Dynamic Mechanical Spectra. Polymers, 15(17), 3590. https://doi.org/10.3390/polym15173590







