Viscoelastic Response of Elastohydrodynamically Lubricated Compliant Contacts below Glass-Transition Temperature

Abstract

The widespread use of polymers in the high-performance engineering applications brings challenges in the field of liquid lubrication in order to separate the rubbing surfaces by the coherent fluid-film thickness relative to not only the inelastic material response of the polymers. The determination of the mechanical properties by the nanoindentation and the dynamic mechanical analysis represents the key methodology to identify the viscoelastic behavior with respect to the intense frequency and temperature dependance exhibited by polymers. The fluid-film thickness was examined by the optical chromatic interferometry on the rotational tribometer in the ball-on-disc configuration. Based on the experiments performed, first, the complex modulus and the damping factor for the PMMA polymer describing the frequency and temperature dependence were obtained. Afterwards, the central as well as minimum fluid-film thickness were investigated. The results revealed the operation of the compliant circular contact in the transition region very close to the boundary between the Piezoviscous-elastic and Isoviscous-elastic modes of the elastohydrodynamic lubrication regime, and a significant deviation of the fluid-film thickness from the prediction models for both modes in dependence on the inlet temperature.

1. Introduction

After the WW2, the first phase of the widespread use of polymers to many areas of industry was recorded [1,2]. Originally, the polymer machine elements, such as gears, were mainly operated under dry conditions or lubricated by greases and used to transfer the motion rather than to transmit torque. Conversely, the current research in the field of tribology of polymer materials is focused on the operation of machine elements under liquid lubrication conditions, especially, in the elastohydrodynamic lubrication (EHL) regime [3,4,5,6,7,8], where the rubbing surfaces are fully separated by a coherent film thickness of the lubricant.

Nowadays, the polymers in connection with the EHL regime make available the implementation into the high-performance applications where dynamics, tribology and extreme operating conditions interact. Transmissions, differentials and mechanisms with polymer gears are examples of the use in automotive, aviation, space industries, etc. One of the constrains of polymers is a significant dependence of mechanical properties on the temperature, which leads to the manifestation of viscoelastic behavior. In terms of tribology, the question arises, how the viscoelastic response of the polymer affects the formation of film thickness in compliant contacts operated in the EHL regime under operating conditions far from the glass-transition temperature of the polymer selected.

The current paper is concerned with the basic oriented research. The main aim of this paper is to investigate the formation of fluid-film thickness in the compliant circular contact operating in the EHL regime with respect to the temperature and time (or frequency), which characterize the viscoelastic response of the polymer. For validation, the amorphous transparent polymer Polymethyl-methacrylate (PMMA) and the reference synthetic lubricant 5P4E were employed. The results are presented in part A and part B where the former deals with the analysis of the material properties of PMMA by nanoindentation (nano-DMA) and the dynamic mechanical analysis (DMA). The latter is concerned with the analysis of the fluid-film thickness in compliant circular contact using the method of optical chromatic interferometry. The subject of this paper is further described in the Supplementary Information (SI)—A.

2. Materials and Methods

2.1. Selection of Materials

In part A, a plate-shaped PMMA polymer specimens of 10 (w) × 10 (l) × 0.5 (t) mm were used for determination of mechanical properties based on the nano-DMA. Moreover, the cylinder-shaped PMMA specimens of 3 mm in diameter and 8 mm in length for DMA were used. In Part B, a compliant contact was simulated between the flat PMMA polymer disc with a diameter of 120 mm, and the 100Cr6 bearing steel ball of 25.4 mm in external diameter. The purchased XT PMMA sheets (NUDEC, S. A (ES)) were manufactured by an extrusion process. The amorphous PMMA disposes of excellent light transmittance, over 90%, necessary for implementation of optical methods.

To achieve a sufficient interference of light, and to avoid the presence of parasitic light, the PMMA disc was coated with semi-reflective chromium and antireflective layers vapor-deposited on the bottom side (in contact with ball) and on the top side of disc, respectively. The mechanical properties of PMMA [9,10] are close in values to the engineering [11] and high-performance [12] polymers (PA66, POM, PEEK) frequently used to produce machine elements. Selected properties of specimens, such as RMS roughness (R_q) or E, are stated in

Table 1. Selected properties of specimens.

Specimen	Material	Rq (μm)	E (GPa)	$\mathit{\upsilon }$ (−)	Tg (°C)
Disc, plate and cylinder	PMMA	Rq1 < 0.005	3.3	0.39	105–110
Ball	100Cr6	Rq2 < 0.01	206	0.30	−

.

2.2. Selection of Lubricants

In part B, the compliant contact was lubricated with Santovac^® 5—Polyphenyl Ether (5P4E), a synthetic diffusion pump oil produced by SANTOLUBES LLC company (Spartanburg, SC, USA). The selected lubricant belongs to the API (American Petroleum Institute, Washington, DC, USA) Group V according to the base oil categories including synthetic lubricants such as polyglycols, silicones and esters. One of the main characteristics of 5P4E lubricant is its extreme viscosity, approximately η₀ ≈ 3 Pa s at 24 °C.

Hence, it is usually used in aviation and aerospace applications for extreme environmental and operating conditions. In addition, the 5P4E is frequently used as a reference lubricant in the field of EHL [7,13]. The rheological properties of 5P4E, such as the dynamic viscosity at atmospheric pressure (η₀) and pressure–viscosity coefficient (α) at 40 and 100 °C, are given in

Table 2. Properties of reference lubricant—5P4E.

Lubricant—5P4E	T (40 °C)	T (100 °C)
Dynamic viscosity, η0 (Pa s)	0.490	0.015
Pressure–viscosity coefficient, α (GPa−1)	39.0	16.1

.

2.3. Experimental Apparatus

Four commercial and one non-commercial experimental apparatuses were employed to determine the properties of PMMA, to evaluate the surface topography of selected specimens and the film thickness of the lubricant in compliant contact. In part A, Hysitron TI Premier Nanoindenter (Bruker) was used to analyze mechanical properties. For the chemical analysis, we employed the Raman spectroscopy using the Renishaw inVia Reflex Raman spectroscope and differential scanning colorimetry (DSC) by TA Instruments. DMA describing the viscoelastic properties of studied PMMA specimen was carried out in laboratories of the Centre of Polymer Systems (CPS) using a dynamic mechanical analyzer DMA1 (Mettler Toledo, Switzerland) equipped with clamps for compression testing mode.

In part B, the 3D optical profilometer Contour GT-X by Bruker was utilized for the surface texture analysis. For the analysis of the fluid-film thickness in compliant circular contact, the rotary optical tribometer in ball-on-disc configuration, developed by the tribology group of Brno University of Technology (BUT) in the Czech Republic, was employed. This experimental apparatus has recently been described by the authors in greater detail in [14,15].

2.4. Experimental Conditions and Methods

In part A, the nano-DMA experiments of PMMA were performed to determine the E′ and E″ moduli and the tan δ, see Equations (SA8) and (SA9). The experimental conditions for part A are stated in

Table 3. Experimental conditions for nano-DMA and DMA measurements—part A.

Parameter	Nano-DMA	DMA
Specimen	plate	cylinder
DMA loading mode	indentation	compression
Dimensions of specimen	10 (w) × 10 (l) × 0.5 (t) mm	Ø 3 × 8 mm
Frequency, f	1–250 Hz	10−3–102 Hz
Temperature, T	15, 20, 25, 30, 60, 80 °C	24, 40, 70, 80 °C

. The nanoindentation technique nanoDMA III on the Bruker Hysitron Premier Ti nano-indenter was used to measure the dynamic mechanical properties of PMMA. Two types of experiments were conducted with a maximum load (by normal force) of 13 mN at a temperature interval from 15 to 80 °C for the six discrete temperatures.

The first experiment consisted of a frequency sweep from 1 Hz to 250 Hz, and the second involved CMX to obtain a modulus at different indentation depths. The load rate was 1.3 mN/s, while an ideal Berkovich indenter with a tip radius of 150 nm was used for all tests. During each experiment, the sample was kept in the xSol temperature stage. Secondly, PMMA cylinder specimens were employed for the DMA frequency sweep analysis in the frequency range between 10⁻³ and 10² with five measuring points per decade. Based on the preliminary results of the amplitude dependent viscoelastic characterization, the linear viscoelastic region (deformation amplitude of 3 μm) was defined and applied for further experiments at specified temperatures.

Based on frequency sweep experiments, the TTSP principle was applied to obtain an MC that extends the frequency range beyond the measured frequency (f). Then, the MC was regressed according to the WLF equation (Equation (SA11)), and model parameters were derived. Besides this, the T_g region was measured by DSC at heating rate of 10 °C/min. Raman spectra of PMMA were collected before and after the tribological experiments as well. To obtain these spectra, the laser 785 nm was used.

In part B, prior to the film thickness experiments, the 3D optical profilometer was employed for the surface structure analysis. The PMMA disc has an optically smooth surface, see Table 1; however, the steel ball was repeatably polished to decrease the R_q and to get rid of parasitic optical reflectivity. After the preparation steps, the optical chromatic interferometry was implemented for evaluation of the h_c and h_m in the compliant contact. A detailed description of this method could be found in [16]. The fluid-film thickness was measured, calibrated, and evaluated in software Achilles (ver. 4.0.117, Radek Poliscuk, Brno University of Technology, Brno, Czech Republic).

The h_c and h_m formed in the compliant contact between the PMMA disc and the steel ball were evaluated under a single constant load, W = 35 N. Hence, the contact pair formed a circular contact with respect to the Hertzian theory corresponding to the ellipticity, k = 1. The temperature was controlled by thermocouples in the oil reservoir and thermocouples placed in the vicinity of inlet of the lubricant to the contact, which corresponds to the oil temperature and the inlet temperature (T), respectively. Four discrete inlet temperatures T from 24 to 80 °C below the widely used T_g interval (105–110 °C) [17] of PMMA were selected.

The experiments were carried out on the rotary optical tribometer under the pure rolling conditions where U₁ = U₂ (1 − disc, 2 − ball) corresponding to the sliding-rolling ratio SRR = 0. Therefore, the entrainment speed U_E is equal to the surface speed of the PMMA disc U₁ as well as of the steel ball U₂. Based on this, the frequency of loading f_L could be expressed by the ratio of U_E and the Hertzian contact radius a_H, see Equation (1), which corresponds to the state of loading and unloading of the contact during the one cycle.

$${\mathrm{f}}_{\mathrm{L}}=\frac{{\mathrm{U}}_{\mathrm{E}}}{{\mathrm{a}}_{\mathrm{H}}}$$

(1)

Utilizing the 5P4E lubricant, the influence of U_E and T on h_c and h_m was determined under the condition of isothermal full-film separation of contact surfaces. The film thickness was measured in the ascending order relative to the U_E. Four discrete values of h_c (100, 150, 200 and 250 nm) were selected for which the profiles of film thickness in transverse (x) and longitudinal (y) direction to U_E were assessed.

To detect a possible transition of h_m [18], the minimum film thickness was evaluated from interferograms at the exit of contact h_mr as well as at the side lobes h_ms of horseshoe. After collecting the experimental data, h_c and h_m were compared with the soft [18,19,20] and hard [5] EHL prediction models including Equations (SA4)–(SA7), and differences were discussed. Moreover, the operation region of the contact was identified relative to the EHL modes via a hydrodynamic map [21,22] by implementation of Equations (SA1)–(SA3).

The material response of the PMMA polymer was determined from the interferograms of initially circular contact at the individual T. Thus, the variations in R_c, ellipticity k and contact area A for static (U_E = 0) as well as running (U_E ≠ 0) contacts were evaluated. For the comparison, the maximal Hertzian contact pressures, p_H and a_H, were calculated according to Equations (2) and (3) as 56 MPa and 443 µm at 24 °C, respectively.

$${\mathrm{p}}_{\mathrm{H}}=\frac{3\mathrm{W}}{2{\mathsf{\pi } \mathrm{a}}_{\mathrm{H}}{}^2}$$

(2)

$${\mathrm{a}}_{\mathrm{H}}=\sqrt[3]{\frac{3\mathrm{WR}}{2{\mathrm{E}}_{\mathrm{R}}}}$$

(3)

$$\frac{2}{{\mathrm{E}}_{\mathrm{R}}}=\frac{\left(1-{\mathsf{\upsilon }}_1^2\right)}{{\mathrm{E}}_1}+\frac{\left(1-{\mathsf{\upsilon }}_2^2\right)}{{\mathrm{E}}_2}$$

(4)

Subsequently, the reduced elastic modulus (${\mathrm{E}}_{\mathrm{R}}$) and the elastic modulus of PMMA (E₁) were reversibly calculated from Equations (3) and (4) for individual T after the a_H was substituted by the experimentally obtained R_c. Nevertheless, these values were determined for the static contact (U_E = 0) assuming a pure elastic response of the PMMA disc, which did not manifest the effects of viscoelastic behavior under dynamic cyclic loading. The experimental conditions for part B are summarized in

Table 4. Experimental conditions for fluid-film thickness measurements—part B.

Parameter	Value
Entrainment speed, UE	0.00025–0.8 m/s
Loading frequency, fL	~0.3–900 Hz
Normal load, W	35 N
Inlet temperature, T	24, 40, 70, 80 °C
Sliding-rolling ratio, SRR	0
Ellipticity of contact, k	1

.

3. Results

3.1. Part A. Analysis of Material Properties of PMMA

From the part A, the frequency and temperature dependence of PMMA was determined employing the nanoindentation and the dynamic mechanical analysis considering the experimental conditions, see Table 3. To characterize the response of the material, five parameters—elastic E, storage E′, loss E″ and complex E^* (see Equation (SA8)) moduli and damping factor tan (δ) (see Equation (SA9))—were measured below T_g, which reflects the experimental conditions of tribological experiments in part B, see Table 4. The glass-transition for the PMMA specimens was determined by DSC corresponding to the interval ${\mathrm{T}}_{\mathrm{g} }\in ❬104, 115❭$ °C. This procedure was repeated before and after tribological experiments in part B together with acquisition of the Raman spectra to detect the possible changes in the PMMA structure. However, none of the measurements showed any significant variations during the tribological experiments.

The temperature dependence of E′ and E″ moduli and tan (δ) was determined at the constant reference frequency of 220 Hz and 1 Hz for nano-DMA and DMA, respectively, see Figure 1a,b. For the former and latter, frequency sweep and frequency as well as temperature sweep tests were performed. As expected, the values obtained from DMA are significantly lower compared to those from nano-DMA due to a different scale of the experiment. The E′ exhibited in both analyses a gradual linear decrease in the whole measured temperature range. The E″ obtained by nano-DMA demonstrated only a slight but gradual increase with temperature where for the DMA data, such increase begins only at 80 °C. The tan (δ) develops in similar manner relative to the E″ with minimal value of approx. 0.04.

In Figure 1b, using the DMA analysis, the E″ and tan (δ) data exhibit a significant fluctuation between 40–60 °C; however, E′ qualitatively corresponds to the nano-DMA data. Quantitatively, E′ and E″ moduli from nano-DMA overrated the data from the DMA temperature sweep tests several times. Conversely to E″ and E′, the data of tan (δ) were in accordance with the results in Figure 1a.

The nano-DMA and DMA frequency sweep experiments were also performed in the frequency interval of $f\in ❬1, 250❭$ Hz and $f\in ❬{10}^{-3}, {10}^2❭$ Hz for several discrete temperatures. This provided necessary input data to compose the MC by implementation of the TTSP. The MC were derived for E′, see Figure 2a,b, at ${ \mathrm{T}}_{\mathrm{R} }=60 °\mathrm{C}$ on account of the supplementation of this parameter into the tribological prediction models of h_c and h_m in part B.

After implementation of TTSP, the reduced frequency (f_red) extended the operating frequency range from ${10}^0$ to ${10}^7$ for the nano-DMA and from ${10}^{-7}$ to ${10}^4$ for the DMA analysis. However, the significant difference of nano-DMA and DMA data relative frequency (or temperature) is quite evident. The former corresponds to the increase in E′ from 3 to 7 GPa, for the latter, E′ was noticeable lower, ranging only between 0.5 and 1.5 GPa with increase in f_red.

The superposition of the data highlighted a difference between the operating frequency of nano-DMA as well as DMA experiments in part A (see Table 3) and tribological experiments in part B (see Table 4, evaluated according to Equation (1)). Hence, this justified using of the TTSP together with derivation of a_T that were regressed according to the WLF equation, see (Equation (SA11)). Then, the constants C₁ and C₂ were obtained, see Figure 2a,b.

3.2. Part B. Analysis of Fluid-Film Thickness in Compliant Contact

From the part B, data of the h_c and h_m were evaluated for experimental conditions, see Table 4. At first, interferograms were centered in x-y coordinates to determine the center of the contact at the intersection of horizontal and vertical paths according to the Newton’s fringes. Then, h_c was evaluated relative to the product of entrainment speed U_E and dynamic viscosity η₀, as Figure 3a (24 and 40 °C) and Figure 3b (70 and 80 °C) demonstrate.

From Figure 3a, it is evident that h_c qualitatively corresponds well, but it quantitatively differs with increase in U_Eη₀. On the other hand, in Figure 3b, h_c differs only slightly in the values, and the development of h_c at 70 and 80 °C in dependence on U_Eη₀ is practically identical. In both figures, the product of U_Eη₀ spans a similar range from ${10}^{-3}$ to ${10}^{-1}$ Pa·m in the entire temperature interval corresponding to h_c < 500 nm. Nevertheless, the absolute difference of h_c develops in a dissimilar manner between 24 and 40 °C as well as between 70 and 80 °C relative to the product of U_Eη₀.

The minimum film thickness was identified at the side lobes of the contact h_ms without no signs of transition of the minimum to the exit h_mr in all experiments, see Figure 4a,b. The difference between h_mr and h_ms gradually decreases with the increasing temperature. The increase in temperature (T ≥ 40 °C) at lower values of U_Eη₀ (up to 10⁻²) demonstrated a tendency of h_mr and h_ms to unify into a single curve; however, at higher values of U_Eη₀, this led to the increase in the variation between h_mr and h_ms.

In the next step, the film thickness profiles were investigated in the perpendicular and parallel direction relative to U_E along the center line of the contact for four discrete h_c (100, 150, 200 and 250 nm), see Figure 5 and Figure 6 showing dimensionless coordinates X and Y versus film thickness H. At 24 °C, the coherent film thickness is formed and the horseshoe shape with constriction at the side lobes is evident from the transverse profile in Figure 5a. An increase in U_E led to a more pronounced horseshoe film shape, so the difference between h_c and h_ms is more significant. In the parallel direction to U_E, the film thickness profile along the center line was almost constant except for the contact inlet (on the left) and for the exit from the contact (on the right) where, for the latter, significant variations in the wedge shape were observed, see Figure 5b.

Contrary to thickness profiles obtained at 24 °C, an increase in inlet temperature to 80 °C, see Figure 6a results in a reduction in the side lobes of horseshoe. Moreover, the gradual change in the film thickness in the transverse profile was observed in the direction from the side lobes to the central region along the center line, which corresponds to the increase in the ratio h_ms/h_c.

The film thickness profiles parallel to U_E, see Figure 6b, demonstrate a similar behavior such as at 24 °C, without inclination of film thickness profile with increasing U_E. In addition, the increase in T probably initializes the polymer constitutive variation in material stiffness connected with a change in the pressure distribution and thus the asymmetrical change in the radius of running contact R_c in the transverse and longitudinal profiles. However, for the former, this deviation is more noticeable. In the longitudinal profiles at the contact inlet, the secondary local minimum of film thickness was not recorded.

Further results represent the evaluation of interferograms of static contacts (U_E = 0) at different temperatures. The results summarized in

Table 5. Dimensional parameters of static contacts at different inlet temperatures.

Inlet Temperature T, °C	24	40	70	80
Contact radius Rcx, mm	0.439	0.466	0.503	0.528
Contact radius Rcy, mm	0.440	0.458	0.501	0.527
Average Rc, mm	0.439	0.462	0.502	0.527
Ellipticity k, −	0.997	1.015	1.002	1.001
Area A, mm2	0.606	0.671	0.788	0.874

showed a linear increase in R_c from 24 °C to 80 °C where the absolute difference represents the increase in R_c, approximately by 17%. Moreover, the difference of R_cx and R_cy in the transverse and longitudinal directions, respectively, was almost negligible.

Apart from R_c, the area of contact A demonstrated a significant enlargement (about 30%) when the inlet temperature increased from 24 °C to 80 °C. R_cx and R_cy were averaged and then substituted into Equations (3) and (4), from which the E_R and E₁ were calculated, see

Table 6. Reduced elastic modulus E_R and elastic modulus E₁ of PMMA calculated for static contacts at different inlet temperatures.

Inlet Temperature T, °C	24	40	70	80
Reduced elastic modulus ER, GPa	7.853	6.746	5.301	4.538
Elastic modulus of PMMA E1, GPa	3.388	2.903	2.274	1.943

.

On the other hand, the running contact (U_E ≠ 0) was always dimensionally smaller exhibiting a proportional difference of R_c between the transverse and longitudinal directions in the entire temperature interval relative to the static contact (U_E = 0) see Figure 7. This results in the ellipticity variation in the interval $k \in \left(1.03, 1.10\right)$ where higher values of k correspond with enhancement in inlet temperature. Only a slight transition from the circular (k = 1) to the wide elliptical contact (k > 1) was recorded. Despite the increase in ellipticity, the contact area of the running contact A was reduced in size by up to 12% in dependence on U_E for individual inlet temperatures. Contrary to this, the effect of temperature is more significant than U_E throughout the selected h_c (100, 150, 200 and 250 nm), which leads to the enlargement of contact area A of running contact in the interval from 0.5 to 20% relative to the contact area at 24 °C. However, this difference gradually decreases with increasing h_c, see Figure 7a,b.

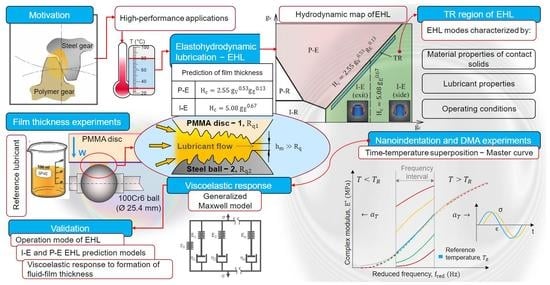
4. Discussion

One of the key attributes for operation of compliant contacts in demanding applications is sufficient lubrication of the rubbing surfaces. However, the interaction between viscous liquids and viscoelastic solids represents a complex problem not only relative to the state of the art in the soft EHL. Furthermore, the complexity of this interaction is even more enhanced by significantly different material properties of the rubbing surfaces forming a contact pair.

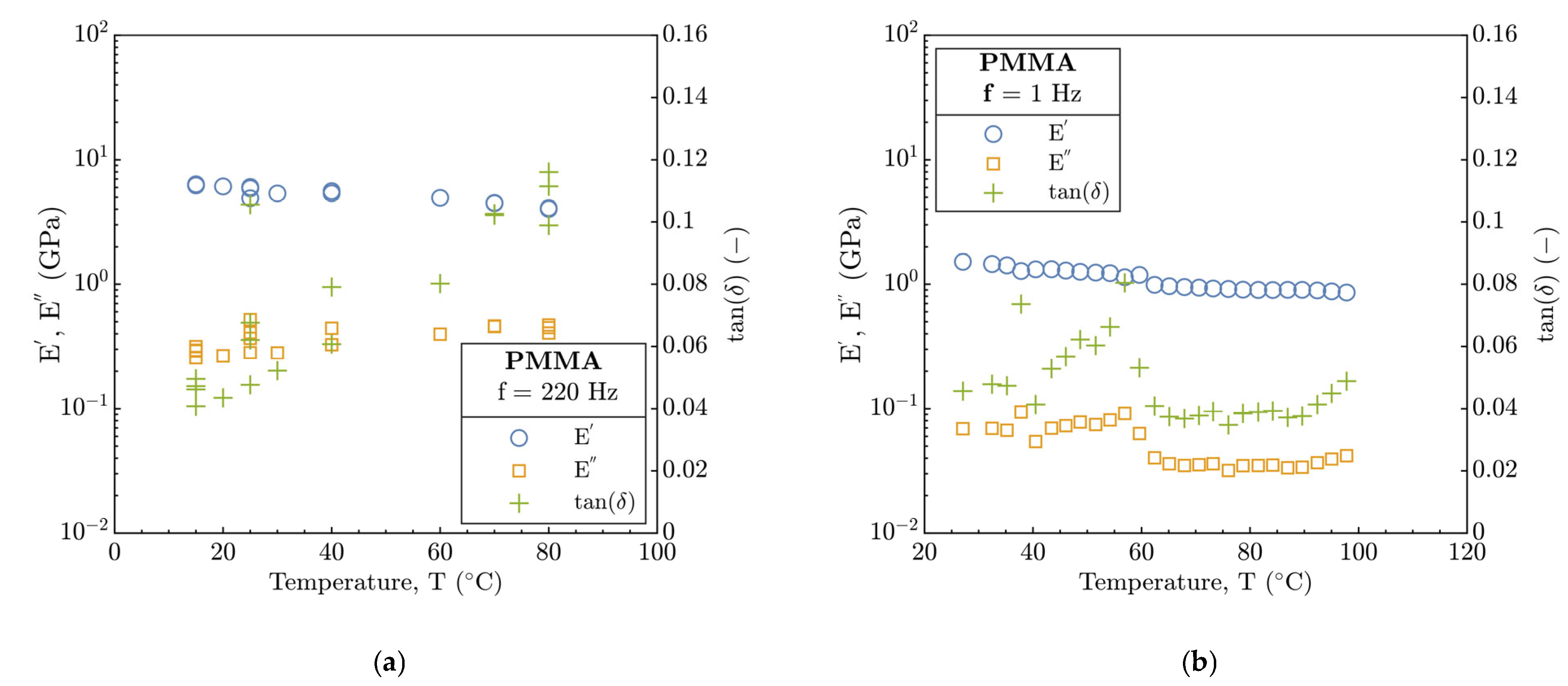
Generally, in the EHL regime, the constitutive material behavior is described according to the Hertzian theory by the elastic modulus E and the Poisson’s ratio v of the individual solids. In relation to the tribology, the Hertzian theory corresponds to the elastic response of the material and is usually compared with static contacts (U_E = 0) to evaluate the contact shape (Equation (3)) and magnitude (Equation (2)) and distribution of the contact pressure. To determine the elastic modulus of PMMA, the nanoindentation experiments in part A were performed and the obtained data were evaluated according to the Oliver and Pharr (O&P) [23] as well as the approach recently described by Mokhtari [24], see Figure 8. Since the data obtained from the nanoindentation may generally be overestimated, the elastic modulus of PMMA disc E₁ in part B was reversible calculated (see Equations (SA3) and (SA4)) from the radius of static contacts R_c (see Table 5) at the individual inlet temperatures T, see Table 6. However, the E₁ could be influenced by creep of PMMA after the contact is loaded, causing a gradual increase in the contact in size.

Moreover, the evaluation methodology by Mokhtari was included. This demonstrated the development of E in the similar manner as for O&P, but the E was quantitively underestimated considering the results from the tribological experiments in part B, see Figure 8. In comparison, at 24 °C, the E based on the Mokhtari method in part A and part B is in accordance with [10,25], nonetheless, the results of the O&P method in part A differ significantly.

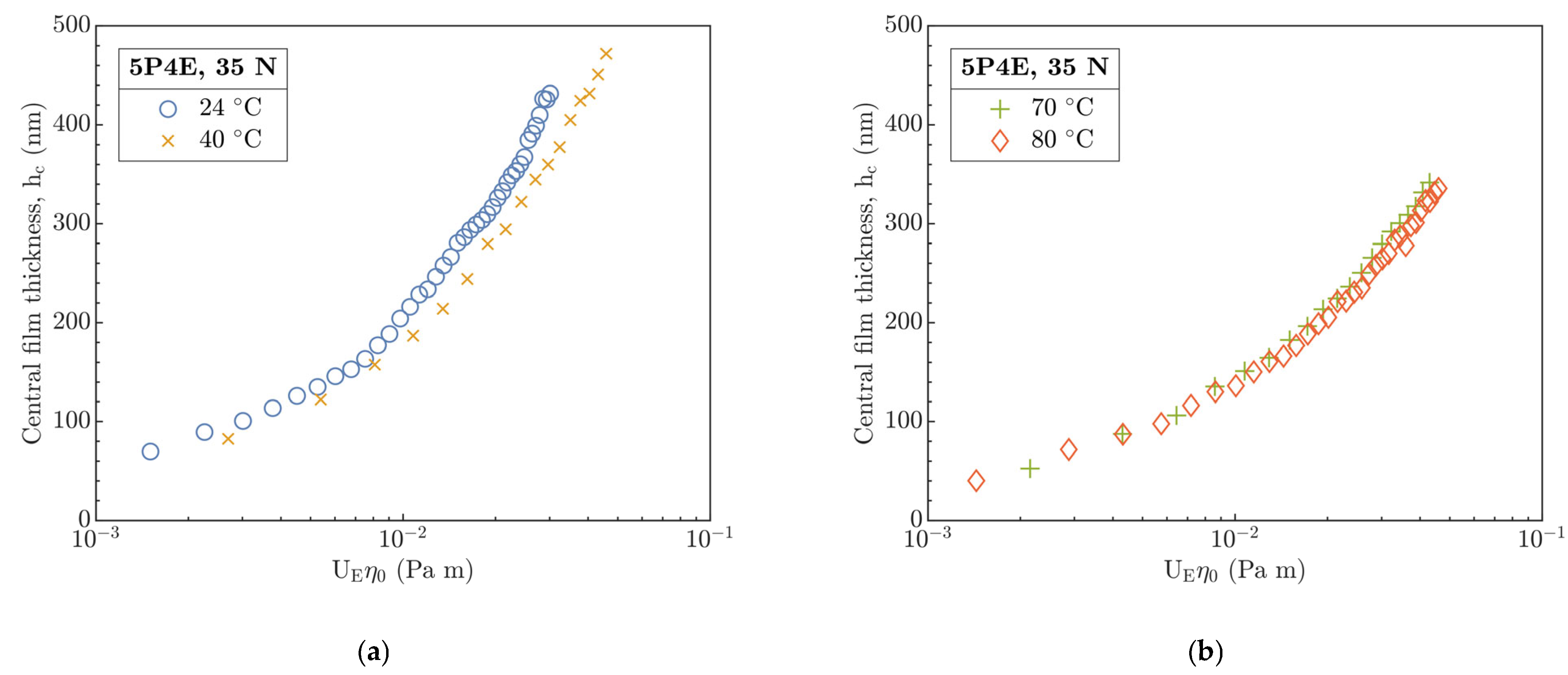
Based on the results in part B, the central (see Figure 3) and minimum (see Figure 4) film thickness in the contact of PMMA disc and steel ball were evaluated in dependence on the entrainment speed U_E and the inlet temperature T. A comparison of experimental data of central film thickness with the EHL prediction models by Hamrock and Dowson (H&D) for hard [5] (P-E, see Equation (SA4)) and soft [19] (I-E, see Equation (SA6)) EHL is demonstrated in Figure 9 and Figure 10 where the E₁ from Table 6 was integrated. Both figures show a dependence of H_c on the product of U_Eη₀.

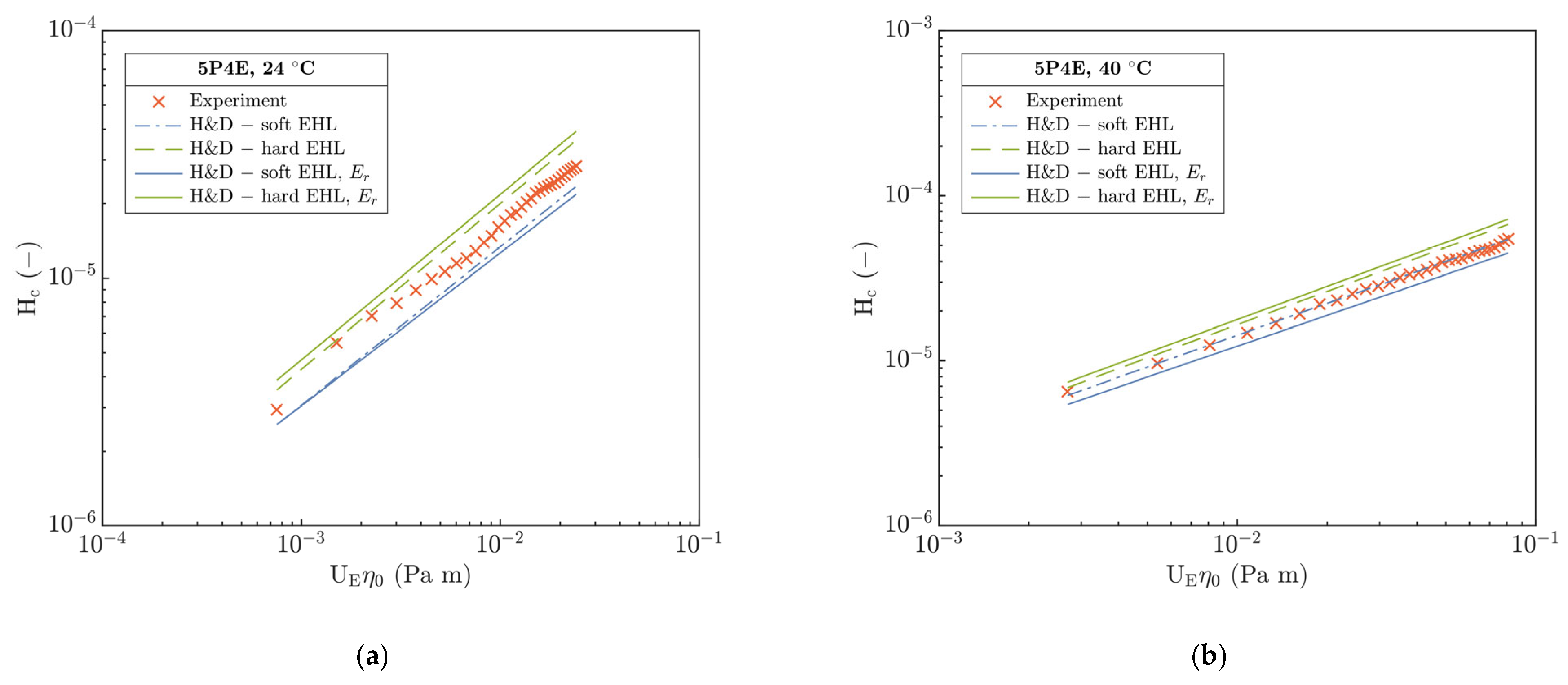
At 24 °C, Figure 9a clearly shows a non-predisposition of experimental data to the soft as well as hard H&D, though H_c qualitatively corresponds better with the soft H&D with a difference of 19%. The measured H_c relative to the soft model is overestimated; however, for the hard one, it is underestimated. This may result from a significant viscosity effect of used 5P4E lubricant (see Table 2) and only from a slight influence of temperature on the change in the mechanical properties of the polymer at 24 °C.

After the temperature increases to 40 °C, H_c correlates best with soft H&D by difference of ca. 2%. Moreover, the deviation of measured H_c from hard H&D slightly decreased as well as the deviation of predicted H_c between the soft and hard H&D. This could be a consequence of several interconnected effects—a decrease in η and the E with temperature and as a result of decrease in the contact pressure. One of other explanations for the difference between the experimental data and the soft H&D model especially at 24 °C may be a pressure–viscosity effect of the lubricant which correlates with the increase in the film thickness. However, for soft H&D, it is assumed that the effect of α is insufficient due to the expected low contact pressures in the I-E mode of EHL. Hence, $\overline{\mathrm{G}}$ (E_R α) parameter is omitted from the soft EHL models, see Equation (SA6).

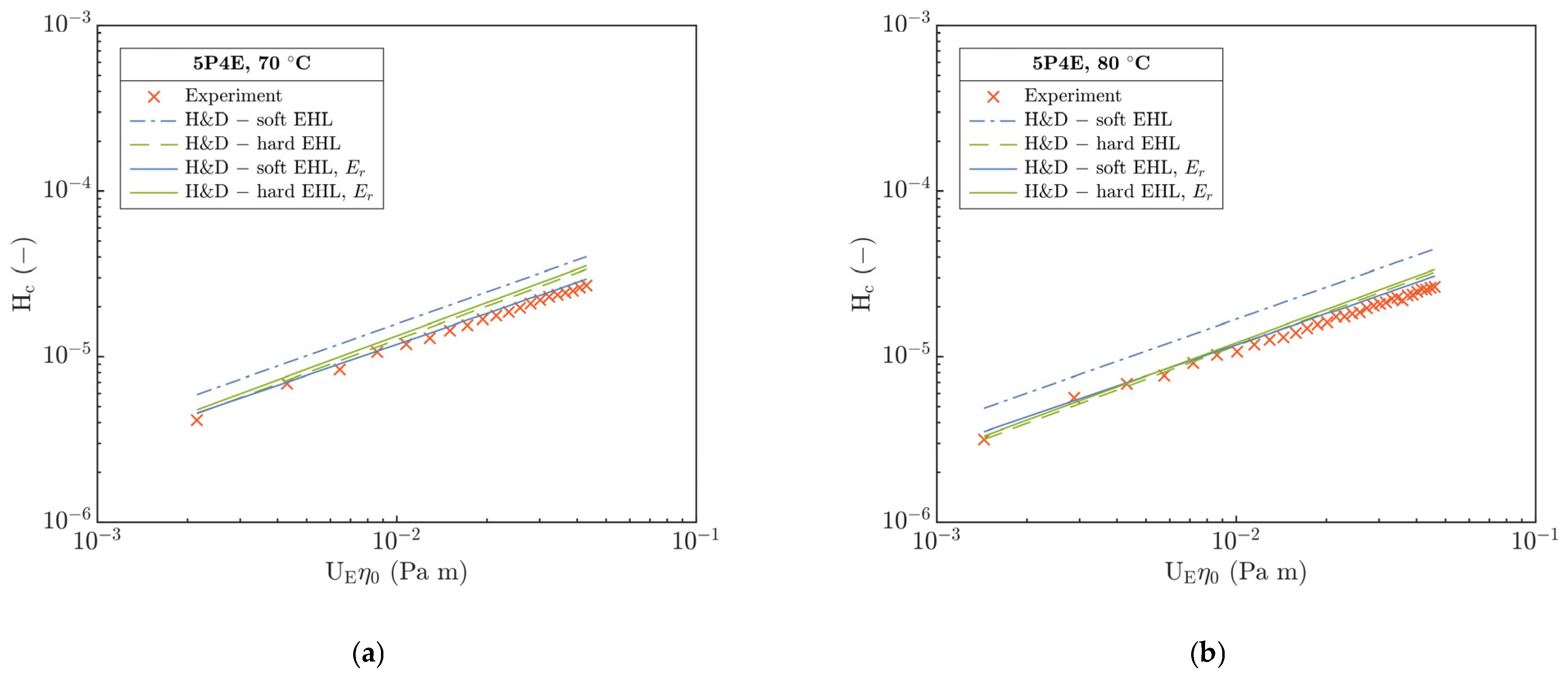
Interestingly, at temperatures of 70 and 80 °C in Figure 10a,b, a good qualitative and quantitative agreement of experimental H_c with hard H&D model was observed. However, relative to soft H&D, the measured H_c is several times lower than the predicted H_c, which is in contradiction to the expected behavior with respect to the enhanced compliance of the contact as the temperature increased. Moreover, the η decreased about two orders of magnitude relative to its value at 24 °C.

With the increase in temperature from 70 to 80 °C, the difference in H_c between the hard and soft H&D was even more emphasized. A difference between the experimental H_c and the hard H&D is only 16% on the average compared to soft H&D, where it exceeds 60%. This points out a discrepancy that, after the temperature increases, the contact of a steel ball and PMMA disc should become more compliant as a consequence of a decrease in E, which corresponds well with the operation in the I-E mode of EHL. However, a decrease in E and thus an increase in contact compliance should be reflected by an increase in H_c. The origin of this discrepancy seems to be not clear yet.

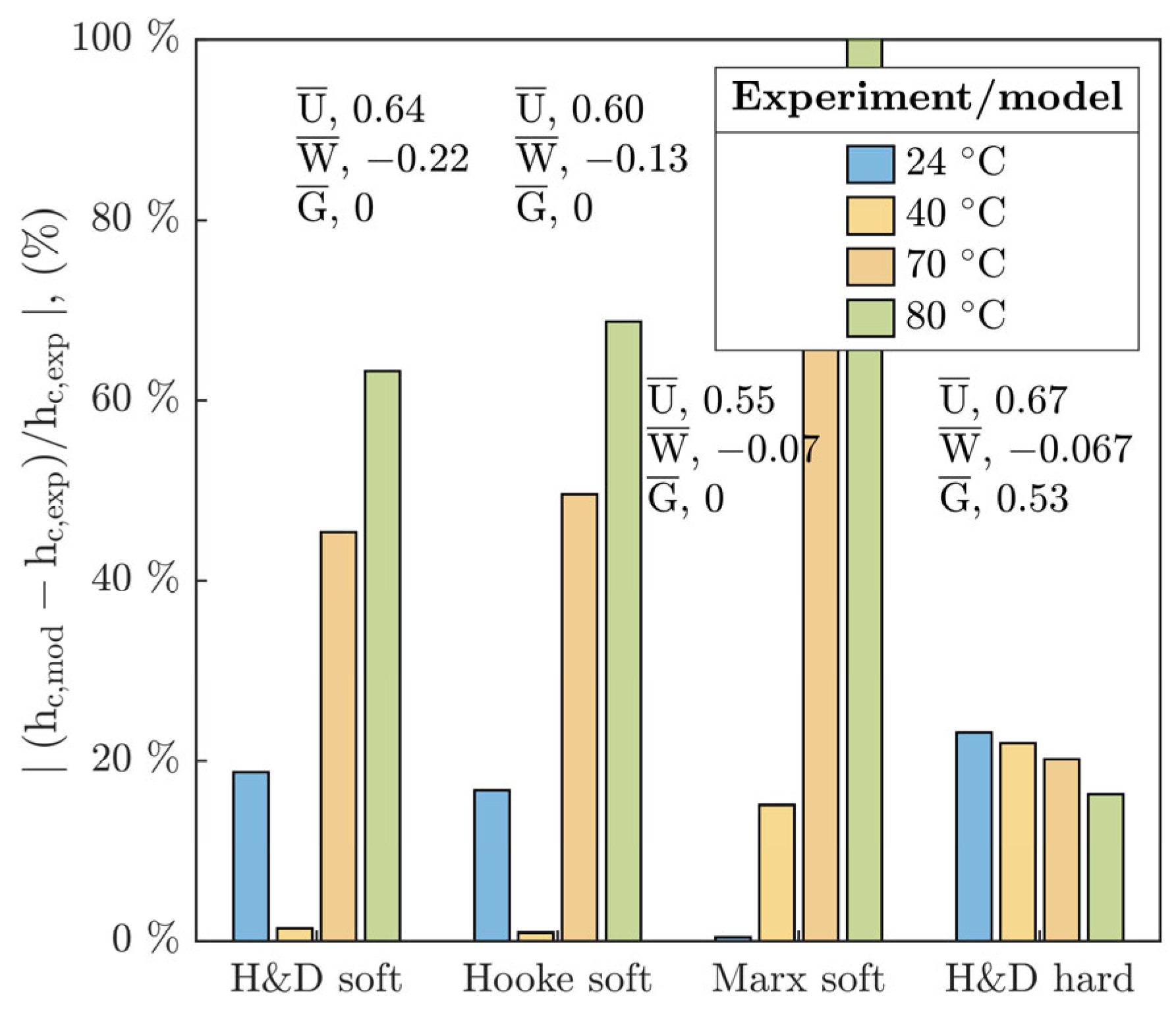
Besides the H&D models [5,19], the experimental data of h_c and h_m were compared with the Hooke et al. [18] and Marx et al. [20] soft EHL models. A discrete interpretation of the deviations of experiments relative to the prediction models is summarized in Figure 11. Here, the main deviation is manifested at 70 and 80 °C; however, it is considerably higher than for the hard H&D, especially for the soft Marx’s and Hooke’s models where it exceeds 50%. Opposite to this, at the temperature of 24 °C, the Marx’s model corresponds well with only a slight deviation up to 3% of the average.

Surprisingly, at 40 °C, the H&D and Hooke’s soft models best match with the experimental H_c. Generally, the best agreement is demonstrated by the hard H&D with deviation of ca. 15% in the entire temperature interval. In addition, a discrete evaluation of the deviations of the minimum film thickness at the exit of the contact h_mr,exp relative to h_mr,mod (for H&D see Equations (SA5) and (SA7)) demonstrated a higher deviation than for h_c,exp except for the hard H&D.

Comparing the results with EHL models, it is clear that, at high temperatures, the measured thicknesses are different from those predicted. There are several possibilities of how to explain this discrepancy. One of them may be the difference between the material properties and the assumptions of the models including the material parameters such as the E and the v, both defined for Hookean material. However, PMMA is a viscoelastic material whose properties are strongly dependent on time—loading rate, magnitude of strain under loading, and temperature. Nevertheless, these properties are not considered in the EHL models where their influence could be expected especially for the compliant contacts.

Observed deviations of h_c and h_m from the soft EHL models put into the contrast the operating conditions for which the individual prediction formulae were numerically derived or experimentally regressed and for which they are potentially valid. With respect to this, the operating region of experiments was compared with other works [19,20,26] in the field of soft EHL according to the speed $\overline{\mathrm{U}}$ and load $\overline{\mathrm{W}}$ parameters, see Figure 12. This figure shows a possible source of disagreement of fluid-film thickness between the current study and the H&D model [19], especially for temperature T ≥ 40 °C, where the increase in T corresponds with the increase in $\overline{\mathrm{W}}$ parameter. It is evident that the operation region does not match with soft H&D model.

The present study (purple rectangle) almost fully corresponds to the study by Myant et al. [27] according to the speed $\overline{\mathrm{U}}$ as well as load $\overline{\mathrm{W}}$ parameter. On the other hand, the current study is consistent with the results published by Fowell et al. [28] with respect to the $\overline{\mathrm{W}}$. However, relative to the $\overline{\mathrm{U}}$, it partially differs. The experimental conditions by de Vicente et al. [26] are shifted to higher values of $\overline{\mathrm{U}}$ as well as $\overline{\mathrm{W}}$ and thus they considerably differ, see Figure 12.

Nevertheless, the research of the other authors corresponds to a considerably different material configuration of contact pair, except for the study by Marx et al. [20], where the used elastomers and polymers, such as PDMS, exhibit a significant compliance. This reveals a difference from the current study as for mechanical properties of PMMA, see Table 1. Moreover, in these studies, the contact was often operated only up to 40 °C, where the E is not radically affected by temperature.

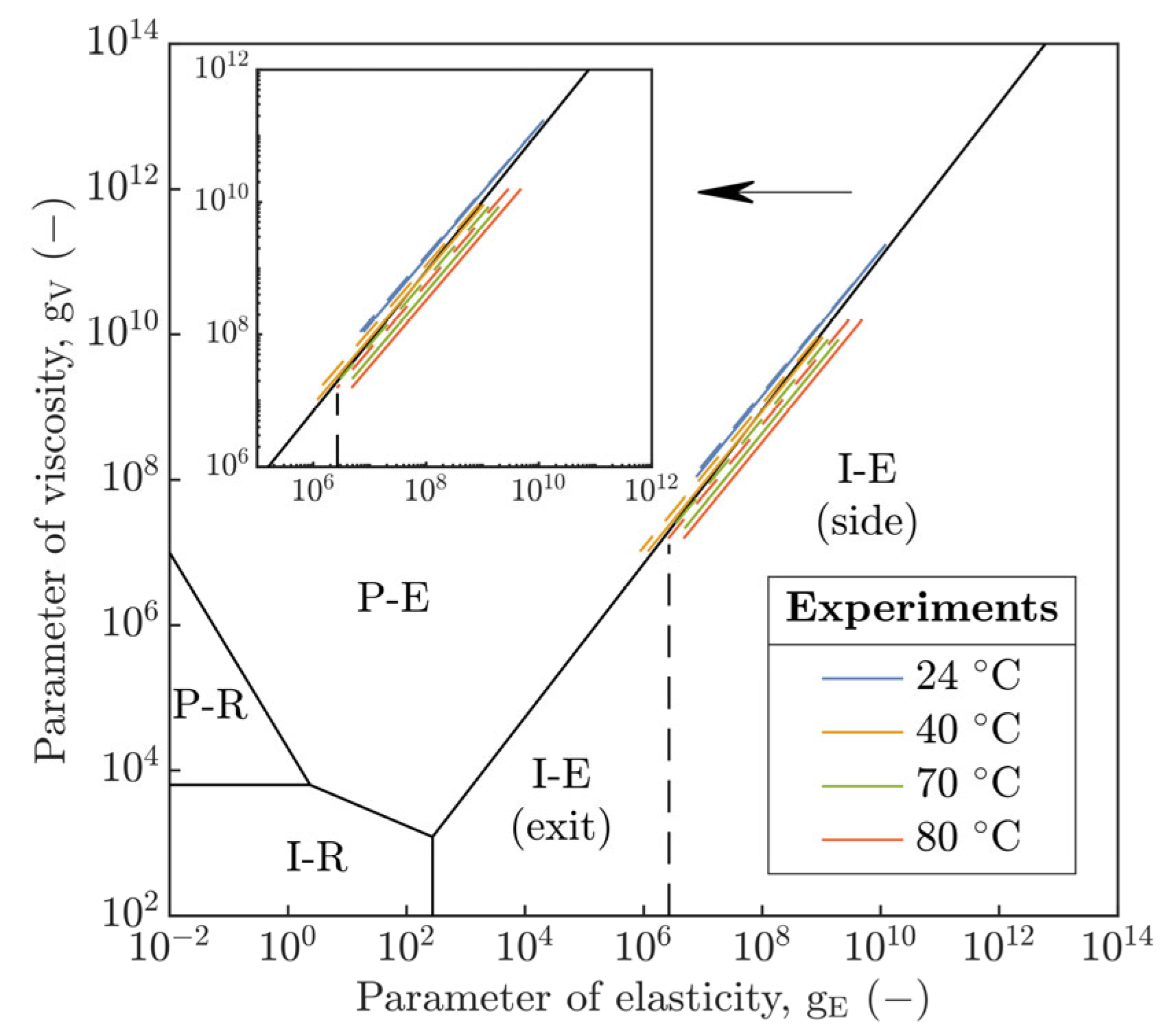
Except for $\overline{\mathrm{U}}$ and $\overline{\mathrm{W}}$ parameters, the operating conditions of the current study were compared relative to the Johnson’s parameters [21] of viscosity g_V (Equation (SA1)) and elasticity g_E (Equation (SA2)) in the hydrodynamic map of EHL, see Figure 13. According to the hydrodynamic map, the contact was operated in the TR region [29,30] between the P-E and I-E modes with predisposition to the former or latter mode in the dependence on T that affects the η of the lubricant (see Table 2) as well as the E of polymer (see Table 6).

Based on Figure 13, it is evident that, at 24 °C, the circular contact was operated in the P-E mode characteristic for rigid contacts and usually relevant to the steel–steel, steel–glass or steel–sapphire contact pairs that exhibit a high contact pressure in the field of EHL. This could explain a good agreement of h_c as well as h_m compared to the hard H&D model [5] rather than to the soft one [19] at this temperature, see Figure 9a. At 40 °C, the contact was closest to the boundary of both EHL modes where Equation (SA4) or Equation (SA6) should not be directly applicable; however, a very good agreement of H_c with two soft EHL models [18,19] was recorded, see Figure 11. At 70 and 80 °C, the contact was shifted in the TR region closer to the I-E mode, which could be related to the increase in compliance of the PMMA polymer with increasing temperature.

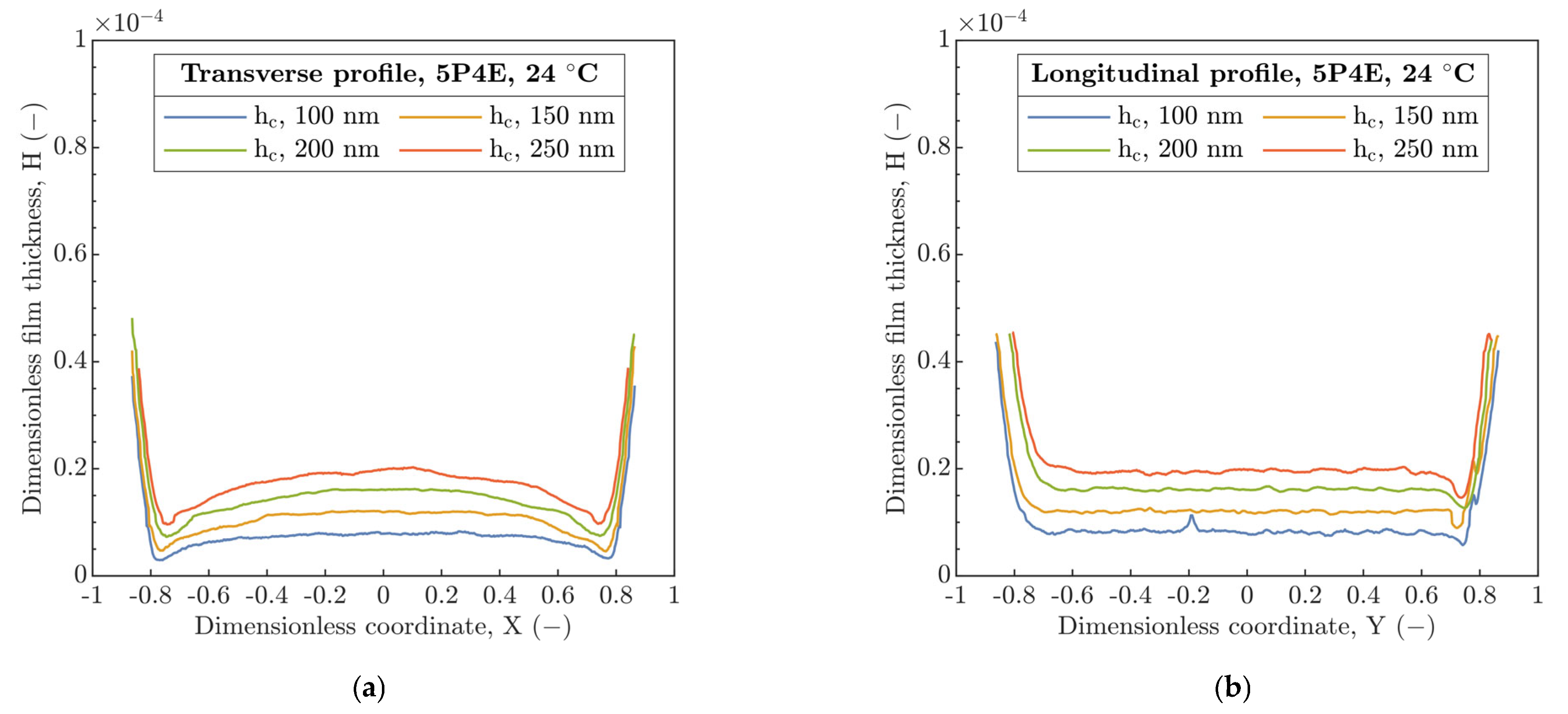
The transition of h_m assumed by Hooke et al. [18] from the side lobes to the exit of the contact with increase in U_E was not attained, see Figure 13. Thus, h_m was always located at the side lobes of the horseshoe, see Figure 4. Compared to [31], the film thickness profiles, see Figure 5 and Figure 6, did not show a transition of the secondary minimum from the exit to the inlet of the contact due to the increase in U_E considering the viscoelastic response of the material. Then, the increase in U_E causes a rather elastic than viscoelastic response of the material, which is in accordance with Figure 2a,b. Thus, the stiffness of the compliant material increases.

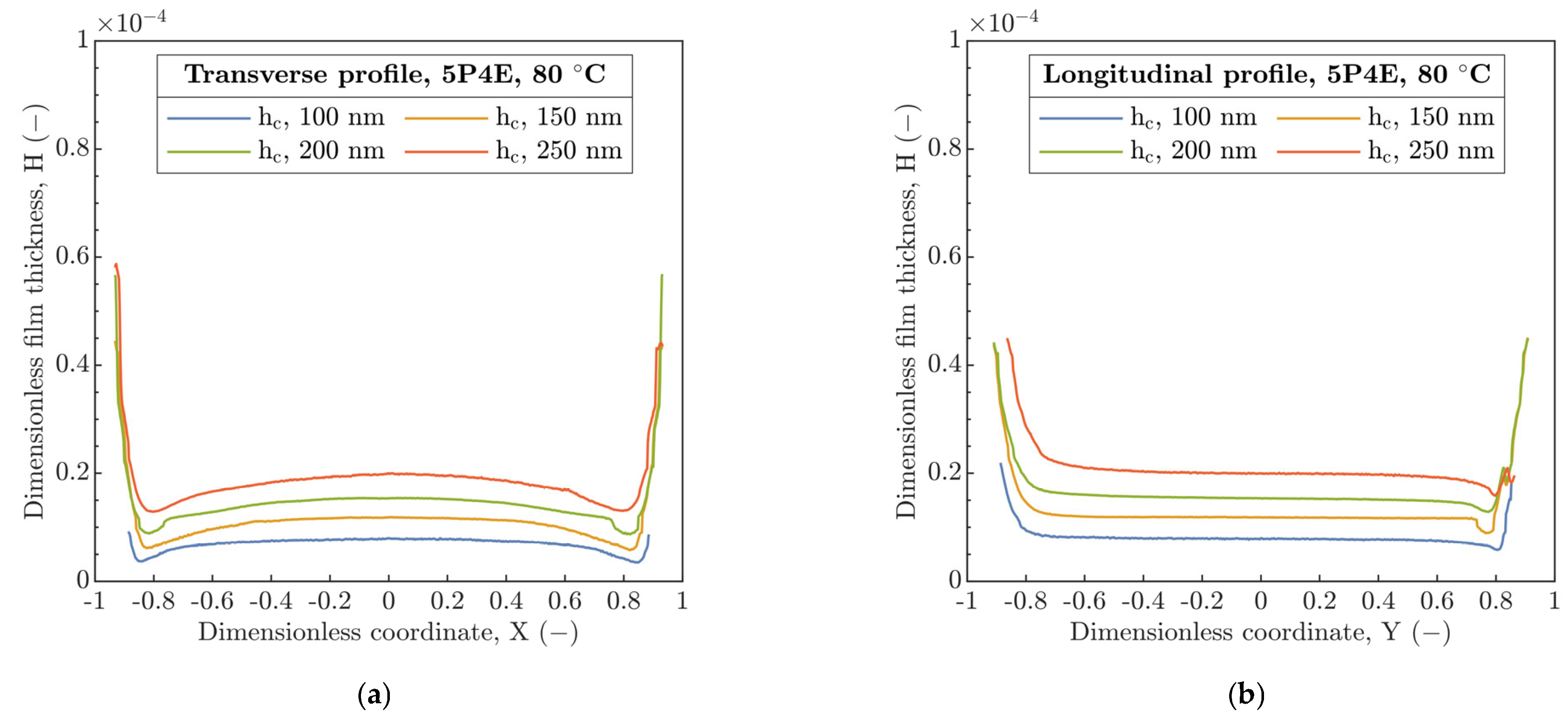
However, a shrinkage in the longitudinal film thickness profiles was discovered with respect to the U_E increase, see Figure 7a,b. Here, the increase in U_E corresponds to a higher film thickness, where the shrinkage effect is more pronounced. This corresponds to the variations in ellipticity and the contact area for running contacts, while, for static contacts, it was mainly unchanged, see Table 5. Based on this, the question arises, how a distribution of the contact pressure in the compliant contact was affected. Nevertheless, the experimental approach dealing with the distribution of the contact pressure is somewhat challenging in the connection with the analysis of fluid-film thickness.

The operating conditions of the experiments were compared not only for individual EHL modes but also for the expected TR region between the P-E and I-E modes in accordance with the research by Johnson [21], Jaffar [29] and Myers et al. [30]. Stated dimensionless parameters g_E (Equation (SA1)) and g_V (Equation (SA2)) were supplemented by the Archard’s parameter “of the system” g₄ [22] which bounds the TR region to the interval where $g_4\langle \in 0.1, 2.2\rangle$, see Equation (SA3). 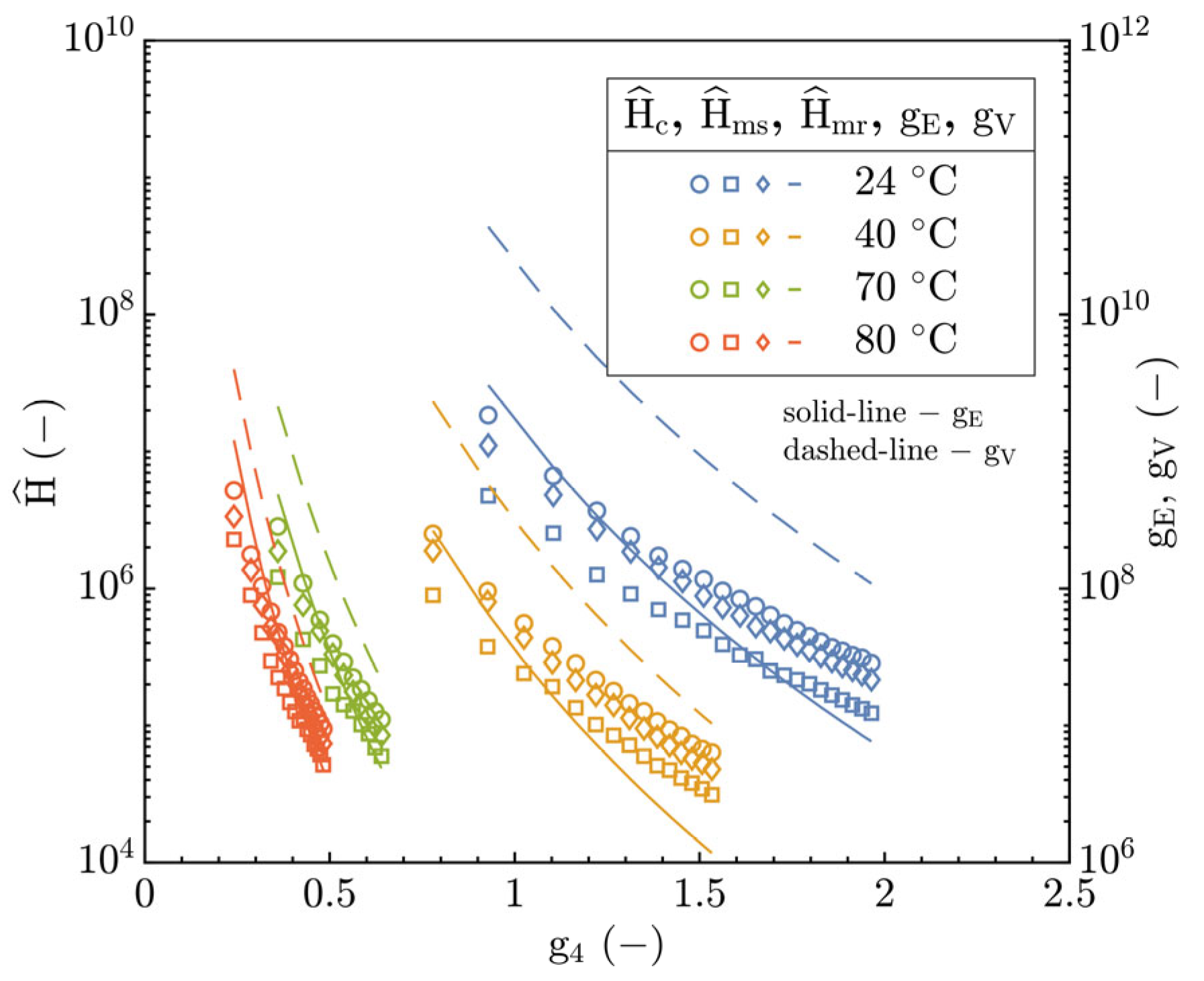In this connection, the film thickness prediction formulae were expressed using by g_E, g_V parameters and the film thickness parameter ($\widehat{H}=H {\left(\overline{W}/\overline{U}\right)}^2$). The central as well as minimum film thickness results expressed by ${\widehat{H}}_c$, ${\widehat{H}}_{mr}$ and ${\widehat{H}}_{ms}$ parameters in Figure 14 are well consistent with the assumed interval for the TR region based on the g₄ parameter in the interval from 0.2 to 1.95.

This could confirm the assumption of the operation of the contact in the TR region according to the hydrodynamic map of EHL, see Figure 13, and simultaneously, could justify the observed deviations of prediction models for the P-E and I-E modes of EHL applied to the TR region, see Figure 11. Relative to the g_E (right y-axis) in Figure 14, the film thickness development demonstrated a good quantitative agreement especially at T > 40 °C; however, at T ≤ 40 °C, it was significantly different. Contrary to the g_E parameter, the dependence of $\widehat{H}$ on the g_V is represented by a significant disagreement for all inlet temperatures. This may again point to the dominant effect of constitutive material behavior.

For polymers, the constitutive material behavior corresponds to the viscoelastic state where the material response in dependence on time (or frequency) and the temperature of loading is manifested. Relative to tribology, these phenomena are expected especially for U_E ≠ 0, when the polymer (PMMA) is dynamically loaded. However, except for P-E EHL models, the I-E models similarly presume only the elastic response of the material, which is in contradiction with viscoelastic response of polymers.

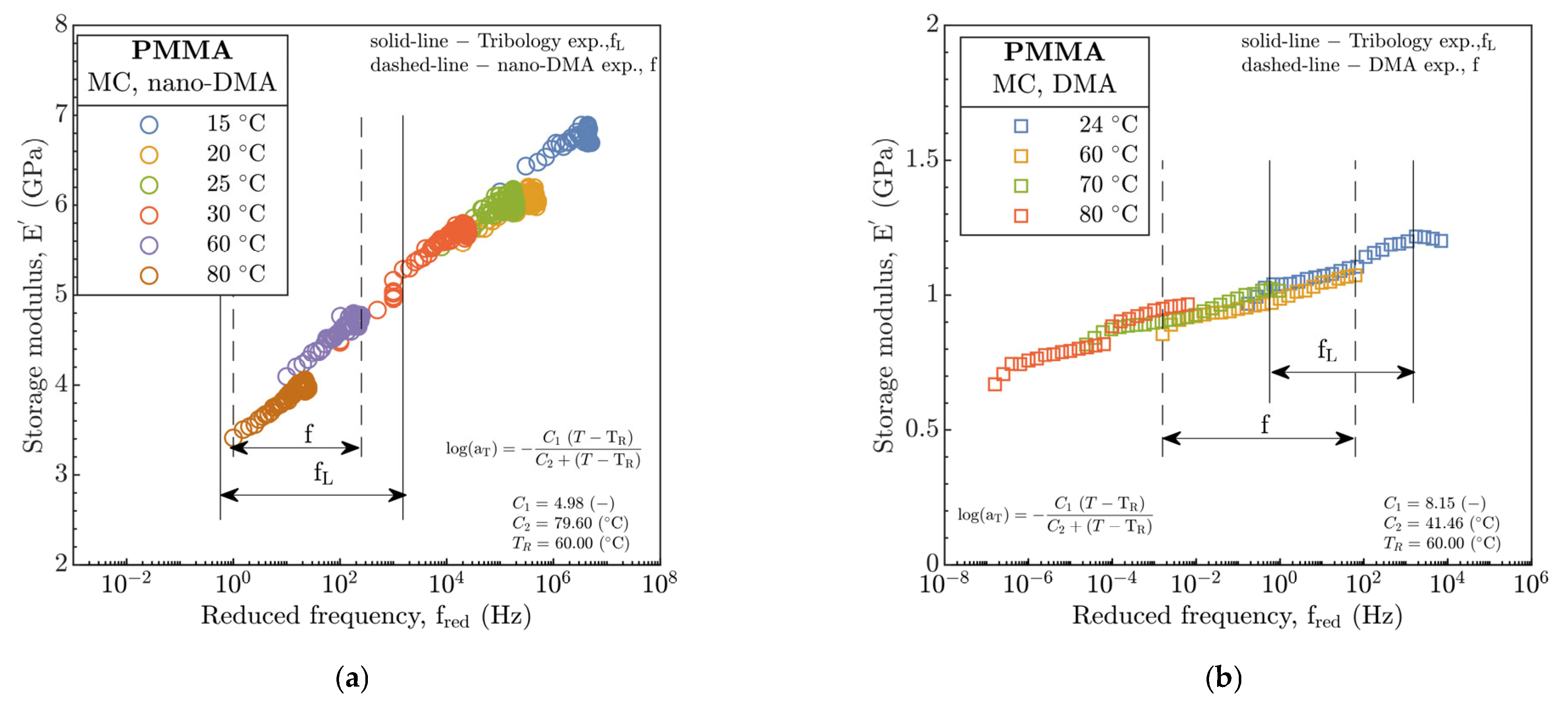
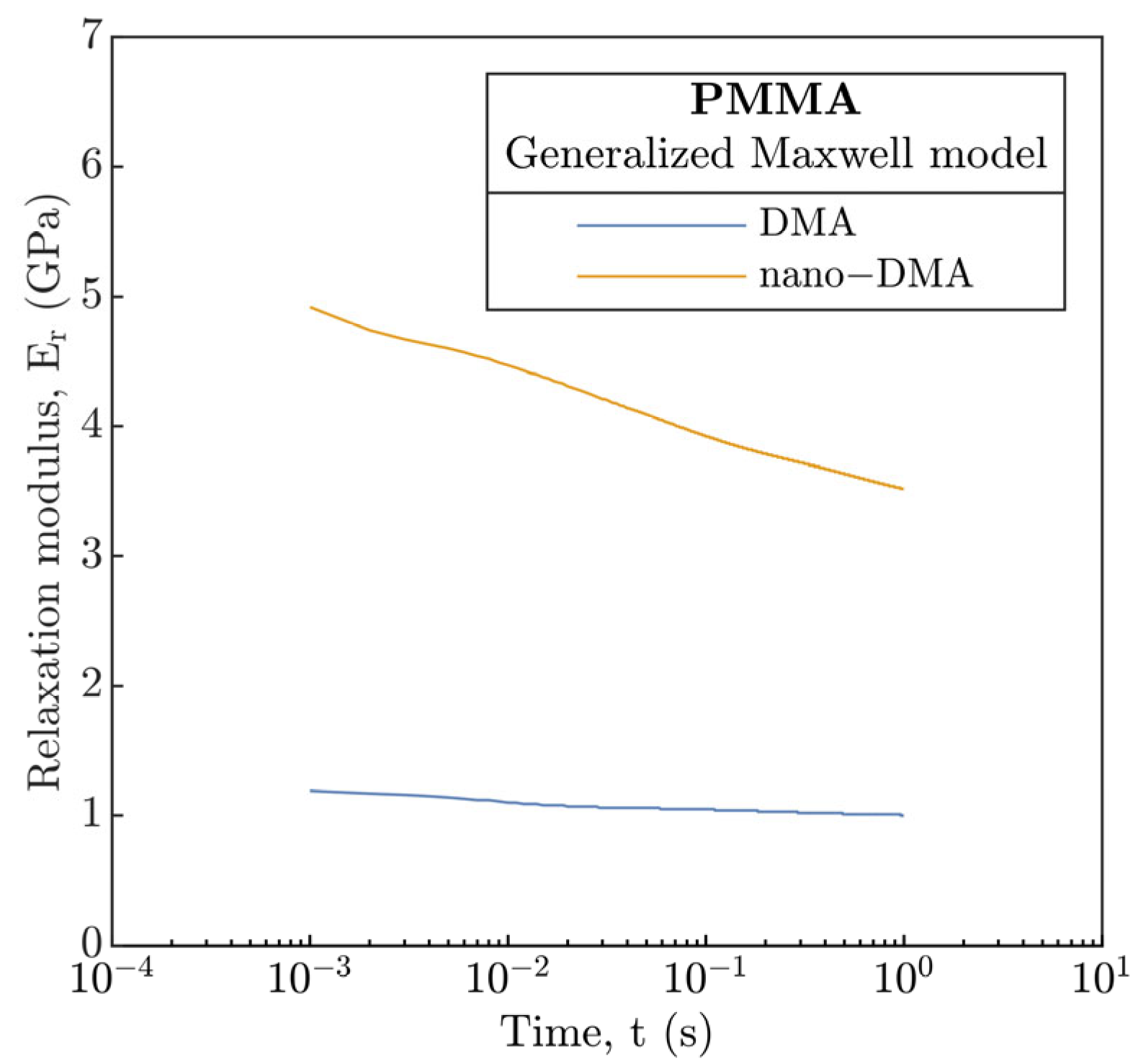
From part A, elastic E′ as well as viscous E″ parts of the E*and tan (δ) were obtained from frequency and temperature sweep experiments based on nano-DMA and DMA methods. However, for the implementation to the EHL models, the question arises whether the E in these models can somehow be replaced by the E* obtained by both methods. The problem results from the fact that the E* corresponds to the frequency domain relative to the experimental methods employed. Thus, the conversion from the storage to the relaxation modulus (E_r(t)), which characterizes viscoelastic properties in the time domain, is necessary.

Hence, the generalized Maxwell model was used. The parameters of the seven-branch model are given in Tables SB1 and SB2, see Supplementary Information (SI)—B. The number of branches corresponds with significant peaks of E″ during the DMA temperature sweep experiments, see Figure 2b. In order to obtain model parameters (stiffnesses and relaxation times of the individual elements), the Prony series were fitted using the least squares method for the master-curves obtained from DMA and nano-DMA in Figure 2. Consequently, the E_r from nano-DMA was integrated into the EHL prediction models as a time-dependent function, substituting the conventional E. A time dependence (time needed to reach a given point on the disc corresponding to the distance equal to the R_c) of the E_r is demonstrated in Figure 15.

The influence of E_r is evident from Figure 9 and Figure 10 where the H&D models for P-E and I-E mode of EHL were modified (H&D_m, dashed-line). At 24 and 40 °C, the difference H_c from the modified soft and hard H&D_m models remains mainly unchanged relative to H&D, and H_c correlates best with the soft and hard H&D for the former and latter temperature, respectively. However, for 70 and 80 °C, the experimental H_c demonstrated a very good agreement with modified soft H&D_m model with only a slight deviation not exceeding 10% relative to soft H&D where a deviation over 60% was previously recorded. Interestingly, although the viscoelastic response characterized by E_r was included, the H_c also corresponds well with hard H&D and H&D_m models, especially at a temperature of 80 °C.

It is evident that the inlet temperature leads to a significant decrease in H_c; however, the formation of film thickness in the TR region predominantly corresponds to the P-E mode rather than to the I-E mode. This is surprising relative to the constitutive material behavior of polymers, as well as the position of experiments close to the I-E mode, see Figure 13. However, this brings us back to the determination of the EHL mode, which may differ due to the integration of the E_r instead of the E.

The integration of the E_r in the hydrodynamic map, see Figure 13, shifts the operation conditions of the contact slightly toward the P-E mode of EHL in the TR region where the magnitude of shift with increasing temperature is enhanced. A similar shift would be seen in Figure 14 according to the Archard’s g₄ parameter as well, but in a different manner. Here, the development of ${\widehat{H}}_c$, ${\widehat{H}}_{mr}$ and ${\widehat{H}}_{ms}$ as well as g_E asymptotically approaches the boundary between the TR region and I-E mode of EHL and would converge to the value of 0.1 for g₄, which is derived in [21] as the boundary point of TR region. However, the above points out to a significant discrepancy between the expected operation mode of EHL and I-E EHL models. Simultaneously, the described behavior may be a consequence of the viscoelastic response of the polymer, which causes a decrease in fluid-film thickness, not considered by the I-E EHL models.

In addition, several reasons can be found to explain the described deviations. Another possibility may be strain hardening at high contact pressures, which may not be evident in the DMA analysis. Conversely, the DMA analysis may have shown softening due to cyclic loading of one spot on the specimen. Hence, there are several reasons why the stiffness could be even lower. One of them could be a decrease by about 10% in the E measured by nano-DMA at the rolling path after the tribological experiment was performed in part B. Nevertheless, the softening effect should only be particularly noticeable at the temperature close to the T_g interval.

5. Conclusions

In the present study, the constitutive viscoelastic response of PMMA was experimentally determined relative to the tribology of compliant contacts operated in the EHL regime below the glass-transition temperature of the polymer. The viscoelastic response was evaluated by the generalized Maxwell model and implemented in I-E and P-E EHL models where only a purely elastic response of the contact solids has been assumed so far. Hence, a significant deviation often revealed for these models, especially for I-E when the temperature increases, then fluid-film thickness is overestimated. The operating mode of EHL was identified by hydrodynamic map (g_E and g_V) and $\widehat{H}$ and g₄ parameters, and operating conditions of the formed circular contact were compared with research in the field of soft EHL. The main results can be summarized as follows:

The operating mode of the EHL has proved to be in the TR region close to the boundary between the P-E and I-E modes of the EHL according to the hydrodynamic map and the defined interval for the TR region via the Archard’s parameter g₄. The shift of operating conditions to the vicinity of the I-E mode is manifested by an increase in the compliance of the circular contact after the inlet temperature is enhanced.

The implementation of a viscoelastic response of PMMA in the prediction models through the relaxation modulus reduced the deviation between the measured fluid-film thickness and the H&D model for the I-E and P-E modes. A decrease in deviation corresponds to an increase in contact compliance and the proximity of the operating conditions to the boundary between the TR region and the I-E mode.

The minimum film thickness was always localized at the side lobes of the horseshoe of the contact without the expected transition to the exit of the contact with increasing entrainment speed. The secondary minimum of film thickness at the inlet to the contact was not manifested as a consequence of the viscoelastic response of the polymer.

For the TR region, the pressure-viscosity effect of the lubricant should be included reflecting the mixed behavior at the boundary between the P-E and I-E modes of EHL, especially at lower temperatures. For T > 40 °C, the I-E EHL models generally predict the film thickness which is considerably overestimated even though the pressure-viscosity effect of the lubricant is always neglected.

The constitutive viscoelastic behavior should be considered in I-E EHL models; however, the variation in the material properties of individual polymers can make the generalization very difficult. Moreover, considering the lubricant rheology, this may be even more complex. The obtained results could be applicable to the design of polymer gears as well as to the optimalization of the lubrication management in the engineering applications where the rubbing surfaces of compliant and rigid solids interact under liquid lubrication conditions. For future research, the fluid-film thickness could be investigated in more detail considering the viscoelastic response of PMMA relative to the rheology of the lubricant.