Numerical Conversion Method for the Dynamic Storage Modulus and Relaxation Modulus of Hydroxy-Terminated Polybutadiene (HTPB) Propellants
Abstract
1. Introduction
2. Materials and Experiments
2.1. Material Component and Sample Preparation
2.2. Experimental Conditions
3. Results and Analysis
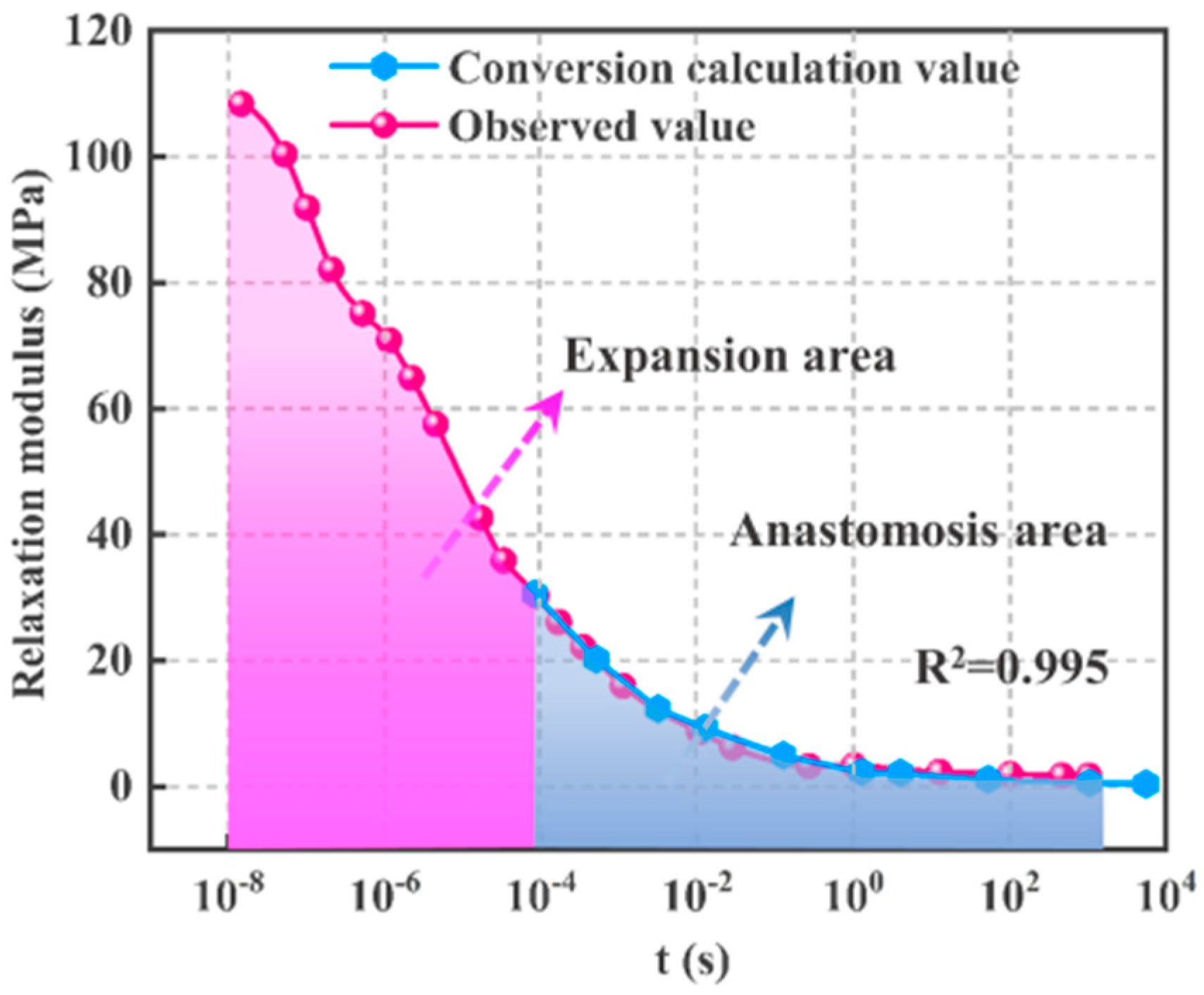
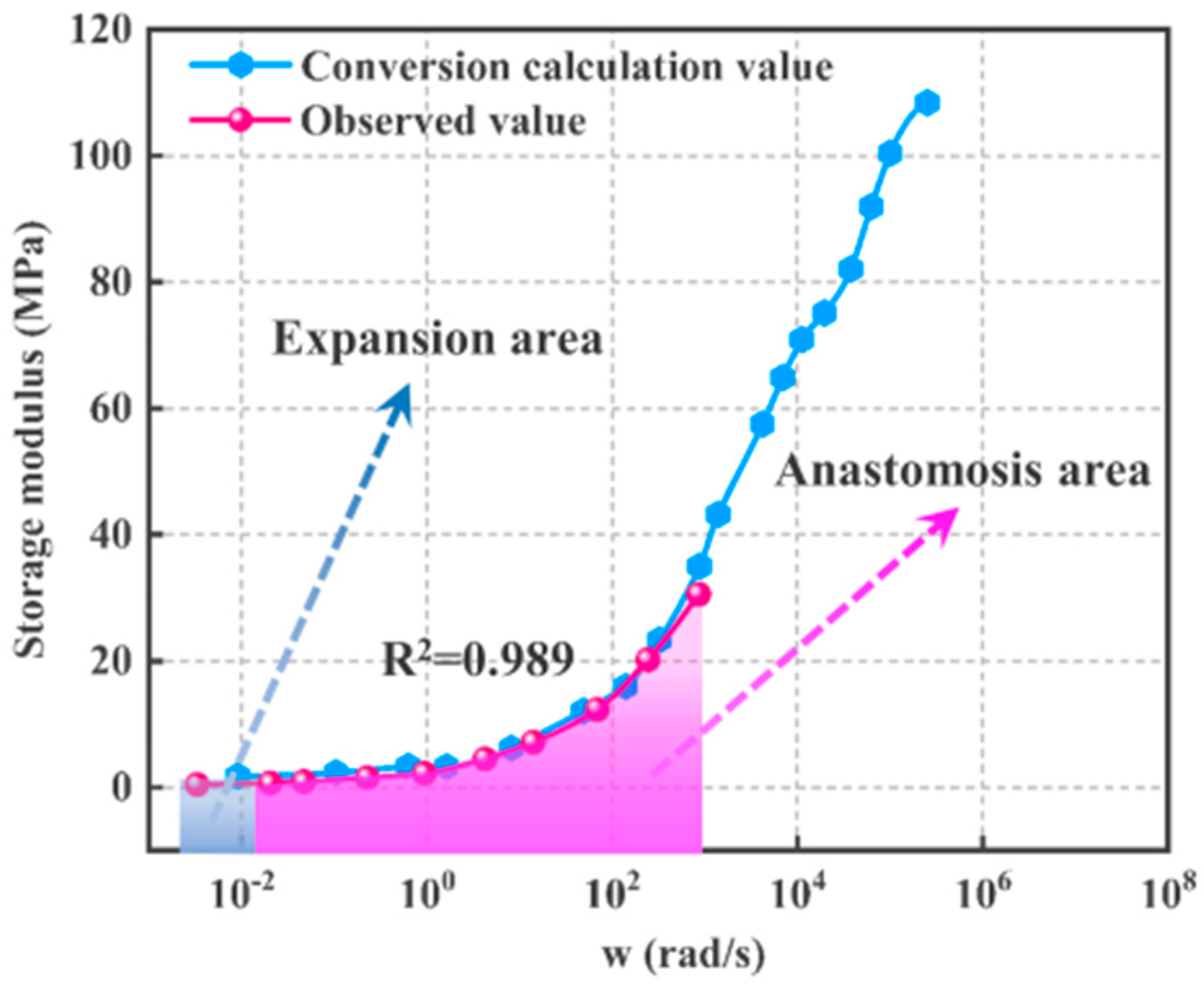
3.1. Experimental Results
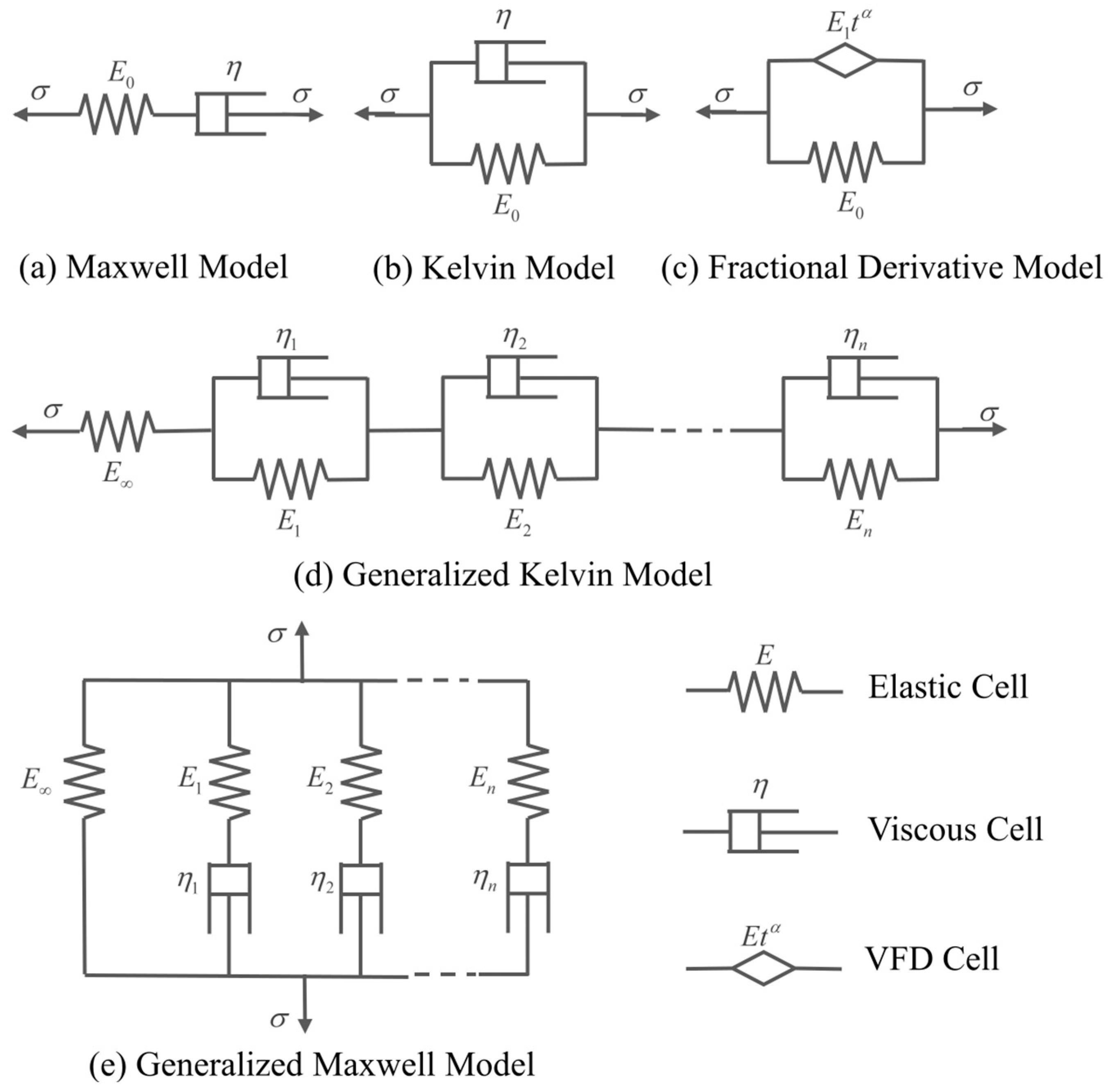
3.2. Theoretical Analysis of the Dynamic–static Modulus Conversion Method
3.3. Introduction of the “Catch-up Factor ” and “Waiting Factor ”
3.4. Specific Values Determination of the “Catch-Up Factor ” and “Waiting Factor ”
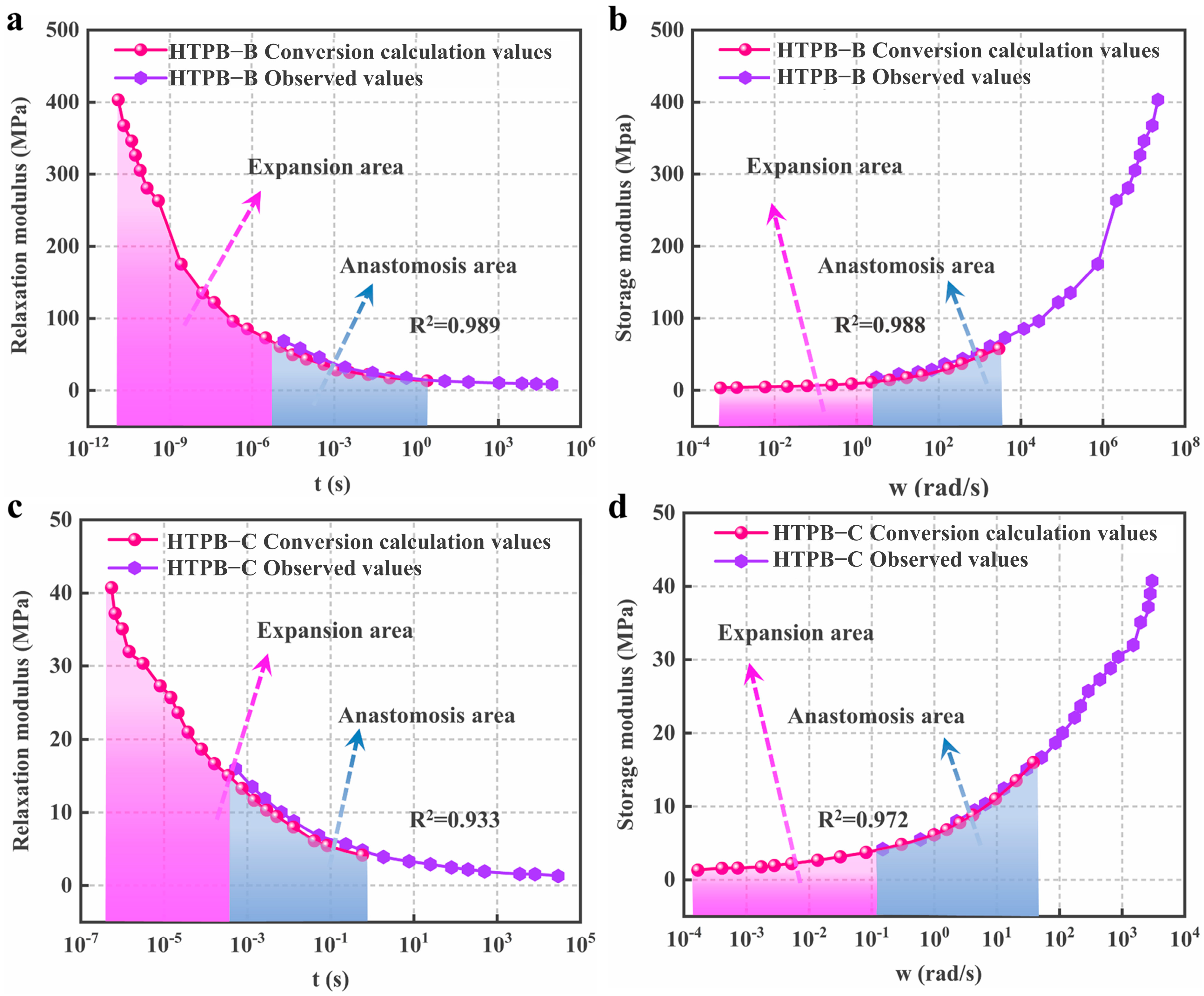
4. Applicability Verification
- Unavoidable measurement errors are introduced during the relaxation and dynamic modulus tests, such as errors in width and thickness measurement of the specimen, and errors in temperature conditions measured by the equipment.
- The time–temperature equivalent principle is used when dealing with experimental data for the relaxation modulus and dynamic modulus. This method itself is an equivalent approximation mean and also introduces errors.
- The overall modulus characteristics of the whole material are characterized by the individual characteristics of limited experimental specimens (3–5 specimens) rather than a large number of specimens, which also leaves considerable errors between the measured and real modulus values.
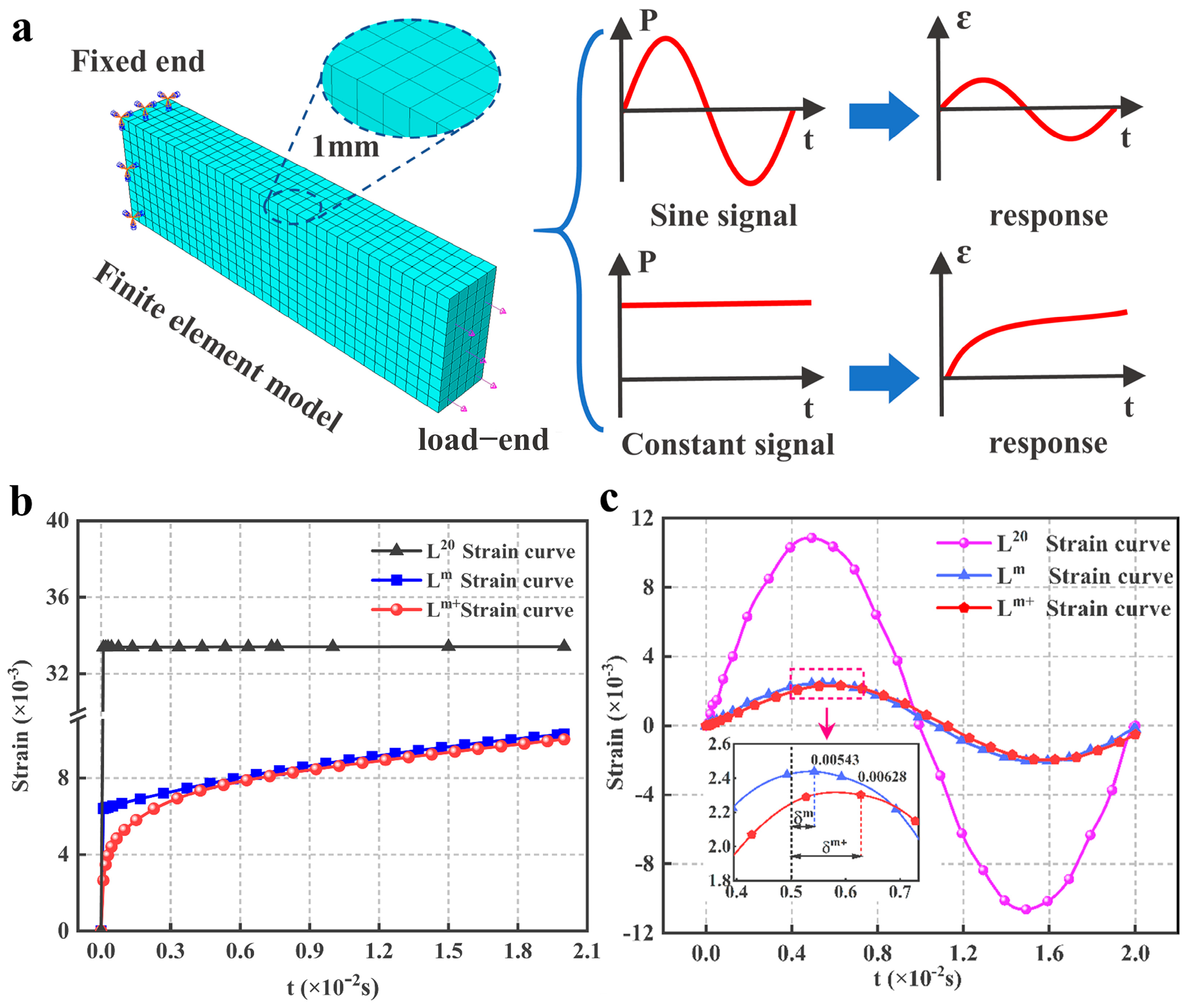
5. Finite Element Simulation Analysis of HTPB Propellants
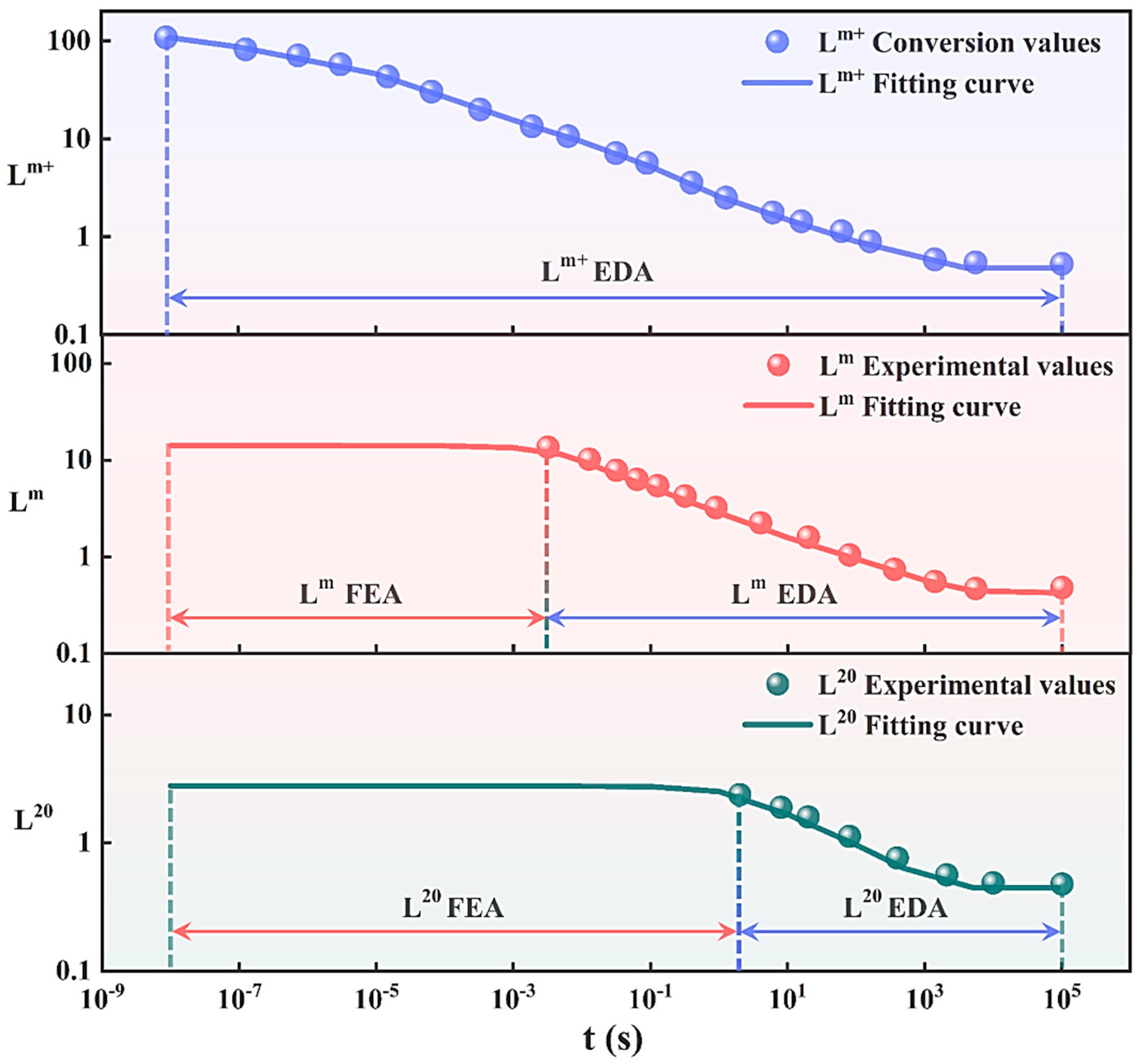
5.1. Fitting Analysis of the Model
5.2. Simulation and Its Result Analysis
- One end is fixed, and another is loaded with a sinusoidal excitation of 50 Hz;
- One end is fixed and another is loaded with a constant excitation.
6. Conclusions
- Based on the one-dimensional linear viscoelastic theory and the existing studies, the dynamic storage modulus and relaxation modulus conversion method of HTPB propellants is proposed by introducing the “catch-up factor ” and “waiting factor ”. The conversion method has a clear physical meaning, a simple form, and a high coefficient of determination between calculated and measured values (). It is also found that for different HTPB propellants, and have the same universal optimal value.
- The specific values of and are determined and they show a perfect reciprocal relationship.
- Using this conversion method, the relaxation modulus calculated from the dynamic storage modulus can expand the time range of the relaxation modulus master curve by about four orders of magnitude. Furthermore, the dynamic storage modulus converted from the relaxation modulus can avoid the problem that the dynamic loading frequency cannot be too small.
- The applicability of the conversion method and introduction of and for HTPB propellants with different component contents is well verified.
- This method has an obvious effect on the extension of the relaxation modulus master curve. The contribution of the Lm+ constitutive model obtained from this method is outstanding for instantaneous simulation calculations and long-term relaxation-creep simulations for propellants; the simulation results also keep consistent with existing relaxation modulus master curve models. This study has important reference value for computational studies accurate to the millisecond level in space launches and other fields.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kruyer, N.S.; Realff, M.J.; Sun, W.; Genzale, C.L.; Peralta-Yahya, P. Designing the bioproduction of Martian rocket propellant via a biotechnology-enabled in situ resource utilization strategy. Nat. Commun. 2021, 12, 6166. [Google Scholar] [CrossRef] [PubMed]
- Gibney, E. First private Moon lander sparks new lunar space race. Nature 2019, 566, 434–436. [Google Scholar] [CrossRef] [PubMed]
- Yuan, W.-L.; Zhang, L.; Tao, G.-H.; Wang, S.-L.; Wang, Y.; Zhu, Q.-H.; Zhang, G.-H.; Zhang, Z.; Xue, Y.; Qin, S.; et al. Designing high-performance hypergolic propellants based on materials genome. Sci. Adv. 2020, 6, eabb1899. [Google Scholar] [CrossRef] [PubMed]
- Duan, H.; Wu, Y.; Yang, K.; Maimaitituersun, W.; Wang, N.; Chen, J.s.; Huang, F. An experimental study on dynamic deformation and ignition response of a novel propellant under impact loading. Polym. Test. 2022, 107, 107472. [Google Scholar] [CrossRef]
- Kakavas, P.A. Mechanical properties of propellant composite materials reinforced with ammonium perchlorate particles. Int. J. Solids Struct. 2014, 51, 2019–2026. [Google Scholar] [CrossRef]
- Martínez, M.; López, R.; Rodríguez, J.; Salazar, A. Evaluation of the structural integrity of solid rocket propellant by means of the viscoelastic fracture mechanics approach at low and medium strain rates. Theor. Appl. Fract. Mech. 2022, 118, 103237. [Google Scholar] [CrossRef]
- Bentil, S.A.; Jackson, W.J.; Williams, C.; Miller, T.C. Viscoelastic Properties of Inert Solid Rocket Propellants Exposed to a Shock Wave. Propellants Explos. Pyrotech. 2022, 47, 1. [Google Scholar] [CrossRef]
- Hoffmann, L.F.S.; Bizarria, F.C.P.; Bizarria, J.W.P. Detection of liner surface defects in solid rocket motors using multilayer perceptron neural networks. Polym. Test. 2020, 88, 106559. [Google Scholar] [CrossRef]
- Xu, L.Z.; Du, Z.H.; Wang, J.B.; Cheng, C.; Du, C.X.; Gao, G.F. A viscoelastoplastic constitutive model of semi-crystalline polymers under dynamic compressive loading: Application to PE and PA66. Mech. Adv. Mater. Struct. 2020, 27, 1331–1341. [Google Scholar] [CrossRef]
- Zou, X.; Zhang, W.; Zhang, Z.; Gu, Y.; Fu, X.; Ge, Z.; Luo, Y. Study on Properties of Energetic Plasticizer Modified Double-Base Propellant. Propellants Explos. Pyrotech. 2021, 46, 1662–1671. [Google Scholar] [CrossRef]
- Rui, S.; Boyang, S.; Xinhui, L.; Weishang, Y.; Xiaowen, J.; Huimin, T.; Wen, L.; Haijun, X.; Yu, C. A mesoscopic damage model of solid propellants under thermo-mechanical coupling loads. Polym. Test. 2019, 79, 105927. [Google Scholar] [CrossRef]
- Naseem, H.; Yerra, J.; Murthy, H.; Ramakrishna, P.A. Ageing studies on AP/HTPB based composites solid propellants. Energetic Mater. Front. 2021, 2, 111–124. [Google Scholar] [CrossRef]
- de Francqueville, F.; Diani, J.; Gilormini, P.; Vandenbroucke, A. Use of a micromechanical approach to understand the mechanical behavior of solid propellants. Mech. Mater. 2021, 153, 103656. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, P.; Shen, Z. Research progress on structural health monitoring and testing technology for solid rocket motors. Eng. J. Wuhan Univ. 2021, 54, 95–101. [Google Scholar]
- He, P. Mechanical Properties of Polymers, 3rd ed.; Press of University of Science and Technology of China: Hefei, China, 1997; pp. 105–283. [Google Scholar]
- Serra-Aguila, A.; Puigoriol-Forcada, J.M.; Reyes, G.; Menacho, J. Estimation of Tensile Modulus of a Thermoplastic Material from Dynamic Mechanical Analysis: Application to Polyamide 66. Polymers 2022, 14, 1210. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, H.; Sun, M.; Lv, X. Tensile Mechanical Properties and Dynamic Constitutive Model of Polyurea Elastomer under Different Strain Rates. Polymers 2022, 14, 3579. [Google Scholar] [CrossRef]
- Evgin, T.; Mičušík, M.; Machata, P.; Peidayesh, H.; Preťo, J.; Omastová, M. Morphological, Mechanical and Gas Penetration Properties of Elastomer Composites with Hybrid Fillers. Polymers 2022, 14, 4043. [Google Scholar] [CrossRef]
- Kang, L.; Sun, C.; Liu, H.; Liu, B. Determination of Frequency-Dependent Shear Modulus of Viscoelastic Layer via a Constrained Sandwich Beam. Polymers 2022, 14, 3751. [Google Scholar] [CrossRef]
- Long, B.; Chen, X.; Wang, H. Low-temperature dynamic mechanical properties of thermal aging of hydroxyl-terminated polybutadiene-based propellant. Iran. Polym. J. 2021, 30, 453–462. [Google Scholar] [CrossRef]
- Sotomayor-del-Moral, J.A.; Pascual-Francisco, J.B.; Susarrey-Huerta, O.; Resendiz-Calderon, C.D.; Gallardo-Hernández, E.A.; Farfan-Cabrera, L.I. Characterization of Viscoelastic Poisson’s Ratio of Engineering Elastomers via DIC-Based Creep Testing. Polymers 2022, 14, 1837. [Google Scholar]
- Naseem, T.; Nazir, U.; Sohail, M.; Alrabaiah, H.; Sherif, E.-S.M.; Park, C. Numerical exploration of thermal transport in water-based nanoparticles: A computational strategy. Case Stud. Therm. Eng. 2021, 27, 101334. [Google Scholar] [CrossRef]
- Nazir, U.; Sohail, M.; Selim, M.M.; Alrabaiah, H.; Kumam, P. Finite element simulations of hybrid nano-Carreau Yasuda fluid with hall and ion slip forces over rotating heated porous cone. Sci. Rep. 2021, 11, 19604. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Nazir, U.; Sohail, M.; El-Zahar, E.R.; Park, C.; Thounthong, P. A Galerkin strategy for tri-hybridized mixture in ethylene glycol comprising variable diffusion and thermal conductivity using non-Fourier’s theory. Nanotechnol. Rev. 2022, 11, 834–845. [Google Scholar] [CrossRef]
- Zhao, B.; Liu, F.; Shen, Y. Study on stress relaxation modulus diagnosed by dynamic mechanics experiment. J. Beijing Inst. Technol. 1995, 3, 339–343. [Google Scholar]
- Zhang, H.N.; Liu, M.; Miao, Y.G.; Wang, H.; Chen, T.; Fan, X.Z.; Chang, H. Dynamic Mechanical Response and Damage Mechanism of HTPB Propellant under Impact Loading. Materials 2020, 13, 3031. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Wu, C.; Cheng, Y.; Ai, Y.; Li, H.; Tan, X. Comparative Analysis of Viscoelastic Properties of Open Graded Friction Course under Dynamic and Static Loads. Polymers 2021, 13, 1250. [Google Scholar] [CrossRef]
- Yang, G.; Peng, S.; Zhang, F.; Hua, H. Dynamic storage modulus of solid propellant main curve to calculate the stress relaxation modulus. J. Propuls. Technol. 2010, 31, 581–586. [Google Scholar] [CrossRef]
- Xie, W.B.; Zhang, W.; Yang, H.B.; Jiang, X.W.; Wang, L.N.; Gao, Y.B.; Cai, X.M. Mechanical behavior and damage kinetics of a unidirectional carbon/epoxy laminated composite under dynamic compressive loading. Polym. Compos. 2022, 43, 2909–2923. [Google Scholar] [CrossRef]
- Murcinkova, Z.; Postawa, P.; Winczek, J. Parameters Influence on the Dynamic Properties of Polymer-Matrix Composites Reinforced by Fibres, Particles, and Hybrids. Polymers 2022, 14, 3060. [Google Scholar] [CrossRef]
- Duan, F.Y.; Zhang, R.M.; Lei, J.F.; Liu, T.; Xuan, Y.; Wei, Z. Mechanical behavior and dynamic damage constitutive model of glass fiber-reinforced Vinyl Ester with different fiber contents. Sci. Prog. 2020, 103, 36850420961610. [Google Scholar] [CrossRef]
- Graziano, A.; Dias, O.A.T.; Petel, O. High-strain-rate mechanical performance of particle- and fiber-reinforced polymer composites measured with split Hopkinson bar: A review. Polym. Compos. 2021, 42, 4932–4948. [Google Scholar] [CrossRef]
- Lei, J.F.; Xuan, Y.; Liu, T.; Duan, F.Y.; Sun, H.; Wei, Z. Static and dynamic mechanical behavior and constitutive model of polyvinyl chloride elastomers for design processes of soft polymer materials. Adv. Mech. Eng. 2020, 12, 1687814020926788. [Google Scholar] [CrossRef]
- Kaya, Z.; Balcioglu, H.E.; Gun, H. The strain rate and temperature effects on the static and dynamic properties of S2 glass/epoxy composites. Appl. Phys. A-Mater. Sci. Processing 2020, 126, 665. [Google Scholar] [CrossRef]
- Zalewski, K.; Chyłek, Z.; Trzciński, W.A. Rheokinetic studies on the curing process of energetic systems containing RDX, HTPB with high content of 1,2-vinyl groups and hydantoin-based bonding agent. Polym. Test. 2022, 111, 107611. [Google Scholar] [CrossRef]
- Picquart, M.; Poirey, G. A multiscale approach for the development of a nonlinear viscoelastic friction-and-cavitation-based model for solid propellants. Int. J. Solids Struct. 2022, 251, 111749. [Google Scholar] [CrossRef]
- Venkategowda, T.; Manjunatha, L.H.; Anilkumar, P.R. Dynamic mechanical behavior of natural fibers reinforced polymer matrix composites-A review. Mater. Today Proc. 2022, 54, 395–401. [Google Scholar] [CrossRef]
- Miller, T.C.; Wojnar, C.S.; Louke, J.A. Measuring Propellant Stress Relaxation Modulus Using Dynamic Mechanical Analyzer. J. Propuls. Power 2017, 33, 1252–1259. [Google Scholar] [CrossRef]
- G. 770B-2005; Test Methods for Explosives. The National Military Standard GJB: Beijing, China, 2005; pp. 205–225.
- Long, S.C.; Yao, X.H.; Wang, H.R.; Zhang, X.Q. A dynamic constitutive model for fiber-reinforced composite under impact loading. Int. J. Mech. Sci. 2020, 166, 105226. [Google Scholar] [CrossRef]
- Christensen. Introduction to Viscoelastic Mechanics; Science Press: Beijing, China, 1990; pp. 58–106. [Google Scholar]
- Shen, T.; Gao, M.; Zhao, B. Engineering method for the conversion calculation of stress relaxation modulus and complex modulus. J. China Ordnance 1995, 3, 40–44. [Google Scholar]
- Li, Z. Advanced Econometrics, 3rd ed.; Tsinghua University Press: Beijing, China, 2000; pp. 66–154. [Google Scholar]
- Gao, Q.; Jian, Z. A ameliorative criterion for predicting the glass-forming ability of metallic glasses. J. Alloy. Compd. 2019, 771, 522–525. [Google Scholar] [CrossRef]
- Peng, X.H.; Yuan, J.; Wu, Z.D.; Lv, S.T.; Zhu, X.; Liu, J. Investigation on strength characteristics of bio-asphalt mixtures based on the time-temperature equivalence principle. Constr. Build. Mater. 2021, 309, 125132. [Google Scholar] [CrossRef]
- Park, S.W.; Schapery, R.A. Methods of interconversion between linear viscoelastic material functions. Part I—a numerical method based on Prony series. Int. J. Solids Struct. 1999, 36, 1653–1675. [Google Scholar] [CrossRef]
- Klanner, M.; Prem, M.S.; Ellermann, K. Steady-State Harmonic Vibrations of Viscoelastic Timoshenko Beams with Fractional Derivative Damping Models. Appl. Mech. 2021, 2, 797–819. [Google Scholar] [CrossRef]
- Permoon, M.R.; Rashidinia, J.; Parsa, A.; Haddadpour, H.; Salehi, R. Application of radial basis functions and sinc method for solving the forced vibration of fractional viscoelastic beam. J. Mech. Sci. Technol. 2016, 30, 3001–3008. [Google Scholar] [CrossRef]
- Pinnola, F.P.; Barretta, R.; de Sciarra, F.M.; Pirrotta, A. Analytical Solutions of Viscoelastic Nonlocal Timoshenko Beams. Mathematics 2022, 10, 477. [Google Scholar] [CrossRef]
- Wang, T.; Jiang, Z.; Zhu, A.; Yin, Z. A Mixed Finite Volume Element Method for Time-Fractional Damping Beam Vibration Problem. Fractal Fract. 2022, 6, 523. [Google Scholar] [CrossRef]
- Zhu, Z.Y.; Li, G.G.; Cheng, C.J. Quasi-static and dynamical analysis for viscoelastic Timoshenko beam with fractional derivative constitutive relation. Appl. Math. Mech.-Engl. Ed. 2002, 23, 1–12. [Google Scholar]
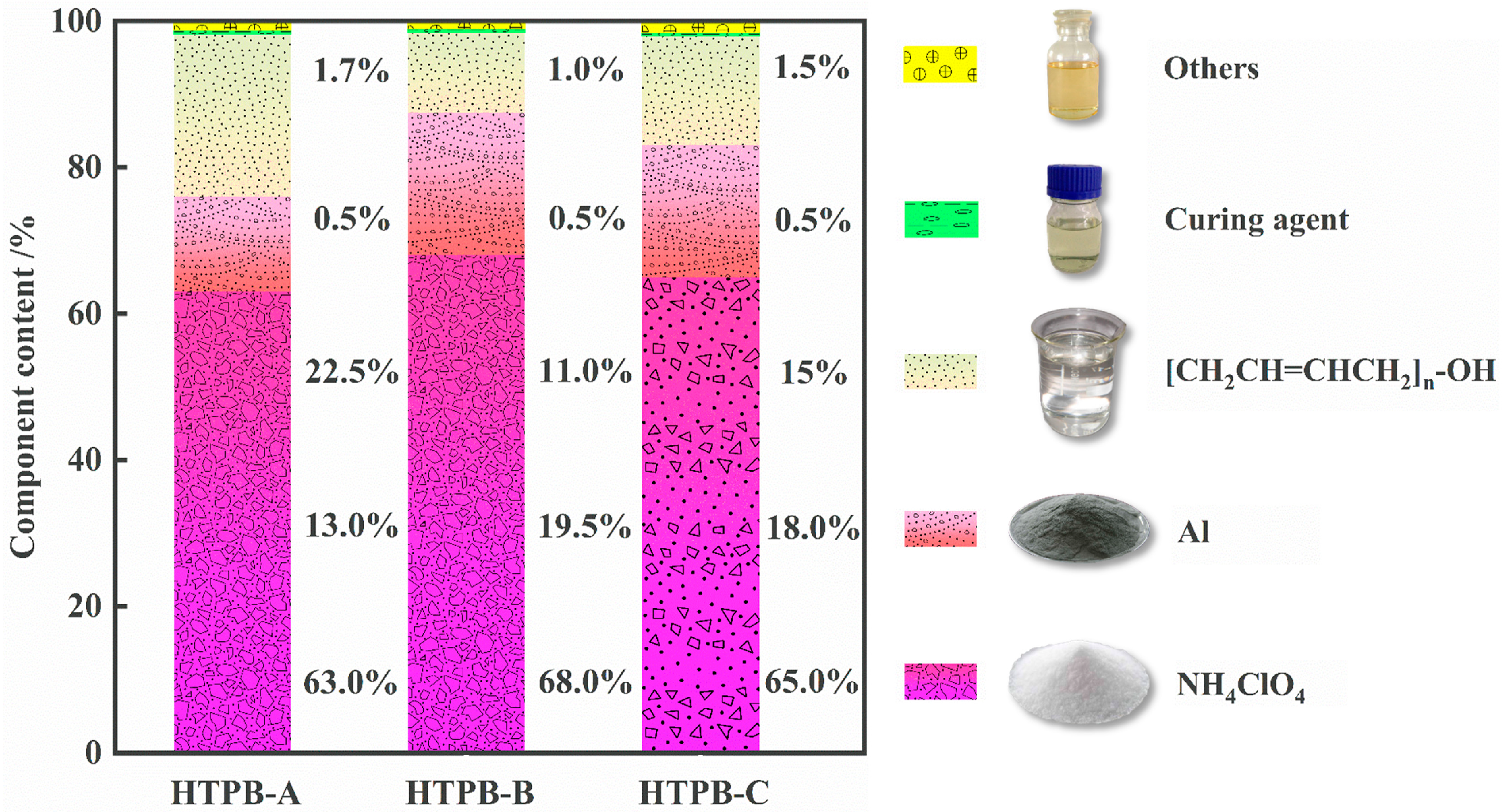
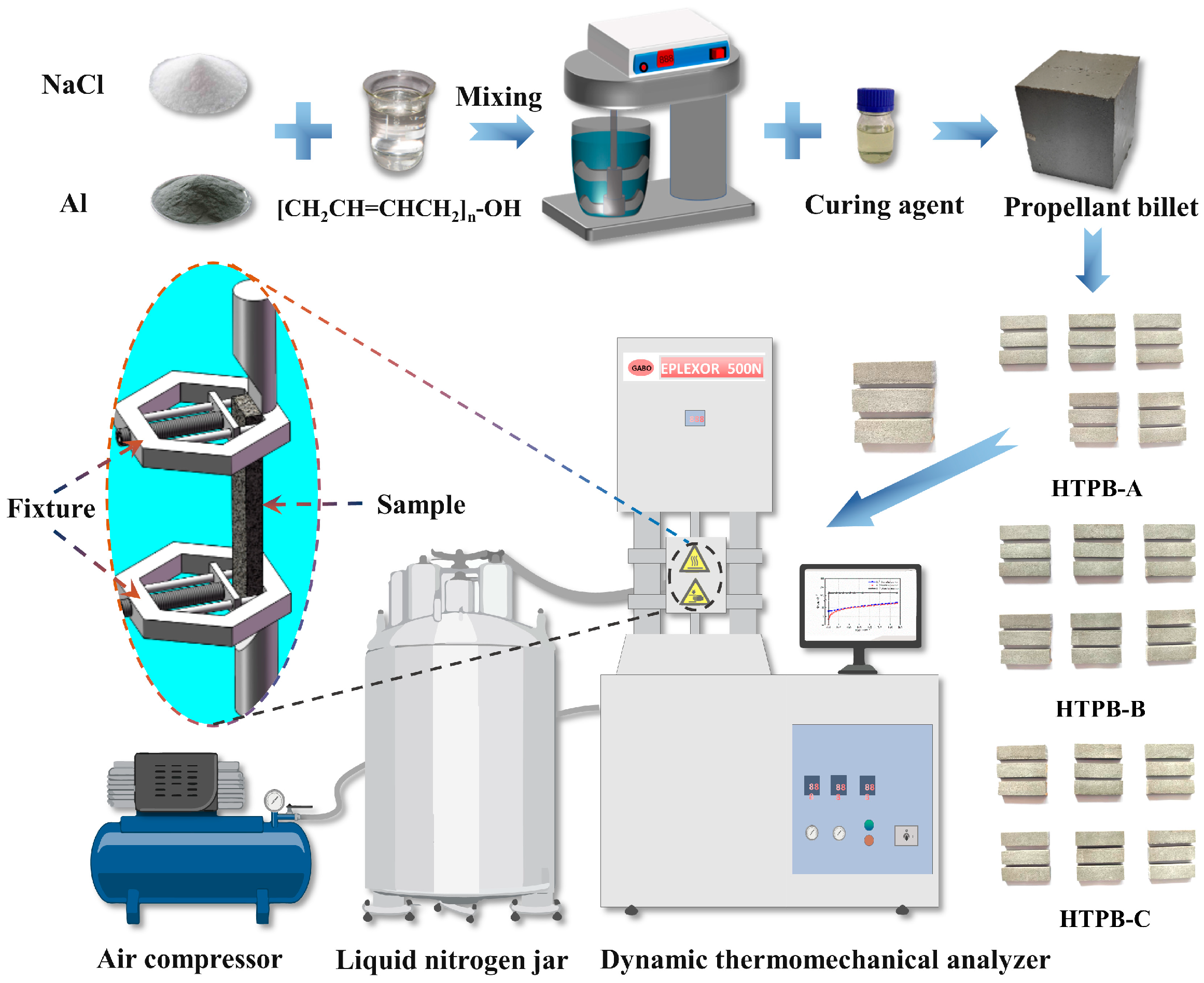

| Sample Type | Temperature (°C) | Relaxation Modulus Test | Dynamic Modulus Test | |||
|---|---|---|---|---|---|---|
| Time Range (s) | Strain | Frequency Range (Hz) | Static Strain | Dynamic Strain | ||
| HTPB-A | −20, −40, 25, 50, 70 | 0–1800 | 5% | 0.1–200 | 5% | 1% |
| HTPB-B | −20, −35, −55, 25, 40, 60 | 0–1800 | 5% | 1–200 | 5% | 1% |
| HTPB-C | −40, −20, 0, 20, 50, 70 | 0–1800 | 5% | 1–200 | 5% | 1% |
| Factor | HTPB-A | HTPB-B | HTPB-C | ||
|---|---|---|---|---|---|
| 1.445 | 1.445 | 1.429 | 1.445 | 1.351 | |
| 0.692 | 0.692 | 0.671 | 0.692 | 0.708 | |
| R2 | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, Y.; Cao, L.; Li, Z.; Chen, G.; Cao, P.; Liu, T. Numerical Conversion Method for the Dynamic Storage Modulus and Relaxation Modulus of Hydroxy-Terminated Polybutadiene (HTPB) Propellants. Polymers 2023, 15, 3. https://doi.org/10.3390/polym15010003
Ji Y, Cao L, Li Z, Chen G, Cao P, Liu T. Numerical Conversion Method for the Dynamic Storage Modulus and Relaxation Modulus of Hydroxy-Terminated Polybutadiene (HTPB) Propellants. Polymers. 2023; 15(1):3. https://doi.org/10.3390/polym15010003
Chicago/Turabian StyleJi, Yongchao, Liang Cao, Zhuo Li, Guoqing Chen, Peng Cao, and Tong Liu. 2023. "Numerical Conversion Method for the Dynamic Storage Modulus and Relaxation Modulus of Hydroxy-Terminated Polybutadiene (HTPB) Propellants" Polymers 15, no. 1: 3. https://doi.org/10.3390/polym15010003
APA StyleJi, Y., Cao, L., Li, Z., Chen, G., Cao, P., & Liu, T. (2023). Numerical Conversion Method for the Dynamic Storage Modulus and Relaxation Modulus of Hydroxy-Terminated Polybutadiene (HTPB) Propellants. Polymers, 15(1), 3. https://doi.org/10.3390/polym15010003








