Pyrolysis Kinetic Study of Polylactic Acid
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Proximate Analysis
2.3. Thermogravimetry
2.4. Determination of the Kinetic Triplets
3. Results and Discussion
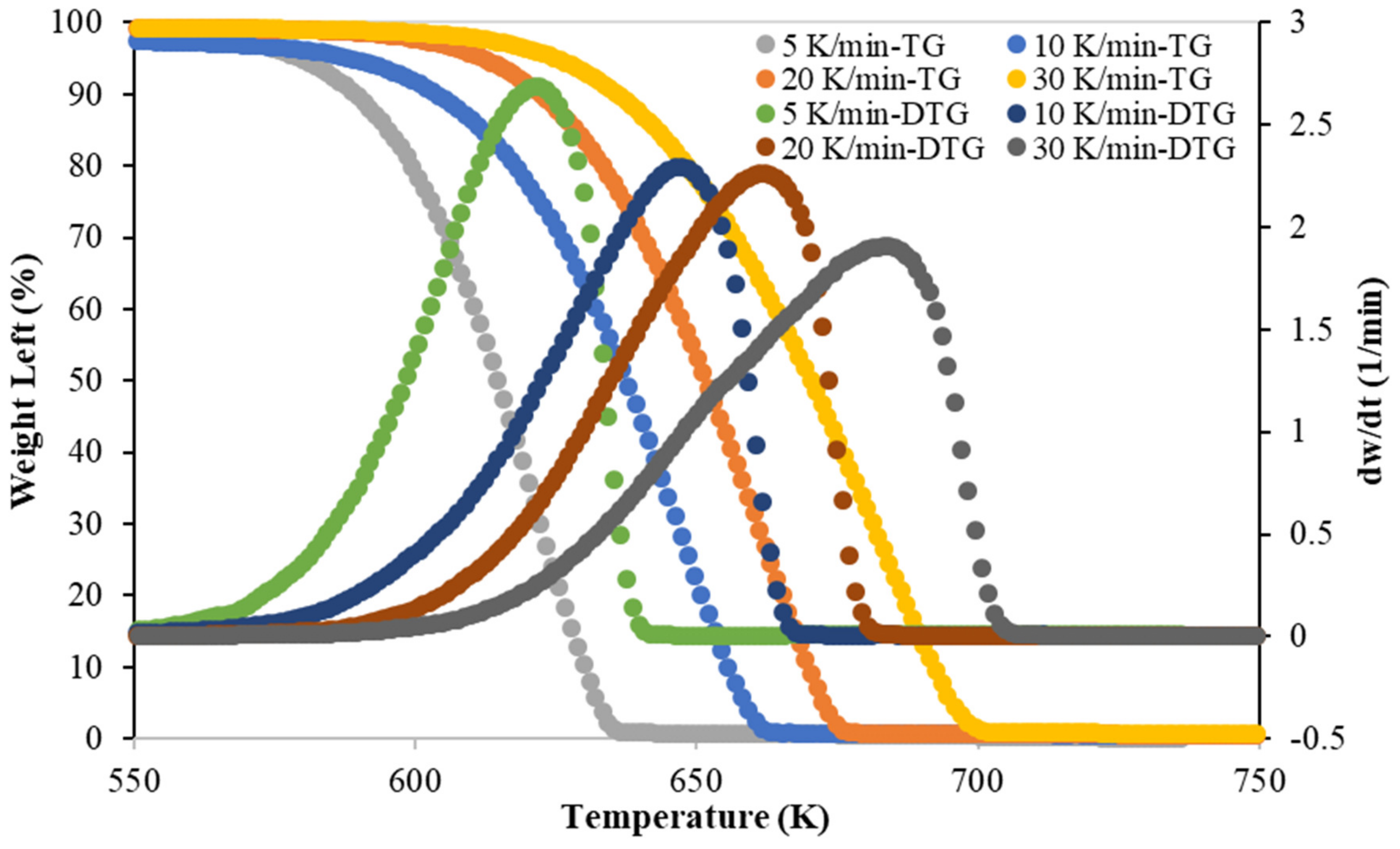
3.1. TG-DTG Analysis
3.2. Isoconversional Kinetics Models
3.3. Model-Fitting Kinetics Methods
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Halász, K.; Csóka, L. Plasticized biodegradable poly (lactic acid) based composites containing cellulose in micro-and nanosize. J. Eng. 2013, 2013, 329379. [Google Scholar] [CrossRef]
- Yuniarto, K.; Purwanto, Y.A.; Purwanto, S.; Welt, B.A.; Purwadaria, H.K.; Sunarti, T.C. Infrared and Raman studies on polylactide acid and polyethylene glycol-400 blend. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2016; Volume 1725, p. 020101. [Google Scholar] [CrossRef]
- Dhar, P.; Tarafder, D.; Kumar, A.; Katiyar, V. Effect of cellulose nanocrystal polymorphs on mechanical, barrier and thermal properties of poly (lactic acid) based bionanocomposites. RSC Adv. 2015, 5, 60426–60440. [Google Scholar] [CrossRef]
- Mortezaeikia, V.; Tavakoli, O.; Khodaparasti, M.S. A review on kinetic study approach for pyrolysis of plastic wastes using thermogravimetric analysis. J. Anal. Appl. Pyrolysis 2021, 160, 105340. [Google Scholar] [CrossRef]
- Saad, J.M.; Williams, P.T.; Zhang, Y.S.; Yao, D.; Yang, H.; Zhou, H. Comparison of waste plastics pyrolysis under nitrogen and carbon dioxide atmospheres: A thermogravimetric and kinetic study. J. Anal. Appl. Pyrolysis 2021, 156, 105135. [Google Scholar] [CrossRef]
- Pan, R.; Duque, J.V.F.; Debenest, G. Investigating Waste Plastic Pyrolysis Kinetic Parameters by Genetic Algorithm Coupled with Thermogravimetric Analysis. Waste Biomass Valorization 2021, 12, 2623–2637. [Google Scholar] [CrossRef]
- Zhang, Y.; Ahmad, M.S.; Boxiong Shen, B.; Yuan, P.; Shah, I.A.; Zhu, Q.; Ibrahim, M.; Bokhari, A.; Kleme, J.J.; Elkamel, A. Co-pyrolysis of lychee and plastic waste as a source of bioenergy through kinetic study and thermodynamic analysis. Energy 2022, 256, 124678. [Google Scholar] [CrossRef]
- Soufizadeh, M.; Doniavi, A.; Hasanzadeh, R. Assessment and optimization of plastic waste pyrolysis using quality control techniques based on kinetic modeling. Int. J. Environ. Sci. Technol. 2022, 19, 3897–3906. [Google Scholar] [CrossRef]
- Muravyev, N.V.; Vyazovkin, S. The Status of Pyrolysis Kinetics Studies by Thermal Analysis: Quality Is Not as Good as It Should and Can Readily Be. Thermo 2022, 2, 435–452. [Google Scholar] [CrossRef]
- Osman, A.I.; Fawzy, S.; Farrell, C.; Al-Muhtaseb, A.H.; Harrison, J.; Al-Mawali, S.; David, W.; Rooney, D.W. Comprehensive thermokinetic modelling and predictions of cellulose decomposition in isothermal, non-isothermal, and stepwise heating modes. J. Anal. Appl. Pyrolysis 2022, 161, 105427. [Google Scholar] [CrossRef]
- Koga, N.; Vyazovkin, S.; Burnham, A.K.; Favergeon, L.; Muravyev, N.V.; Pérez-Maqueda, L.A.; Saggese, C.; Sánchez-Jiménez, P.E. ICTAC Kinetics Committee recommendations for analysis of thermal decomposition kinetics. Thermochim. Acta 2023, 719, 179384. [Google Scholar] [CrossRef]
- Mróz, P.; Białas, S.; Mucha, M.; Kaczmarek, H. Thermogravimetric and DSC testing of poly (lactic acid) nanocomposites. Thermochim. Acta 2013, 573, 186–192. [Google Scholar] [CrossRef]
- Bhiogade, A.; Kannan, M.; Devanathan, S. Degradation kinetics study of Poly lactic acid (PLA) based biodegradable green composites. Mater. Today Proc. 2020, 24, 806–814. [Google Scholar] [CrossRef]
- Hayoune, F.; Chelouche, S.; Trache, D.; Zitouni, S.; Grohens, Y. Thermal decomposition kinetics and lifetime prediction of a PP/PLA blend supplemented with iron stearate during artificial aging. Thermochim. Acta 2020, 690, 178700. [Google Scholar] [CrossRef]
- Xiang, S.; Feng, L.; Bian, X.; Li, G.; Chen, X. Evaluation of PLA content in PLA/PBAT blends using TGA. Polym. Test. 2020, 81, 106211. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of Mixed Plastic Waste: I. Kinetic Study. Materials 2020, 13, 4912. [Google Scholar] [CrossRef]
- Aboulkas, A.; El Harfi, K.; El Bouadili, A. Thermal degradation behaviors of polyethylene and polypropylene. Part I Pyrolysis kinetics and mechanisms. Energy Convers. Manag. 2010, 51, 1363–1369. [Google Scholar] [CrossRef]
- Khodaparasti, M.S.; Shirazvatan, M.R.; Tavakoli, O.; Khodadadi, A.A. Co-pyrolysis of municipal sewage sludge and microalgae Chlorella Vulgaris: Products’ optimization; thermo-kinetic study, and ANN modeling. Energy Convers. Manag. 2022, 254, 115258. [Google Scholar] [CrossRef]
- Duque, J.V.; Martins, M.F.; Debenest, G.; Orlando, M.T.D. The influence of the recycling stress history on LDPE waste pyrolysis. Polym. Test. 2020, 86, 106460. [Google Scholar] [CrossRef]
- Mumbach, G.D.; Alves, J.L.F.; Silva, J.C.G.D.; Sena, R.F.D.; Marangoni, C.; Machado, R.A.F.; Bolzan, A. Thermal investigation of plastic solid waste pyrolysis via the deconvolution technique using the asymmetric double sigmoidal function: Determination of the kinetic triplet, thermodynamic parameters, thermal lifetime and pyrolytic oil composition for clean energy recovery. Energy Convers. Manag. 2019, 200, 112031. [Google Scholar] [CrossRef]
- Al-Yaari, M.; Dubdub, I. Application of artificial neural networks to predict the catalytic pyrolysis of HDPE using non-isothermal TGA data. Polymers 2020, 12, 1813. [Google Scholar] [CrossRef]
- Dubdub, I.; Al-Yaari, M. Pyrolysis of low-density polyethylene: A kinetic study using TGA data and ANN prediction. Polymers 2020, 12, 891. [Google Scholar] [CrossRef] [PubMed]
- Dubdub, I.; Al-Yaari, M. Thermal behavior of mixed plastics at different heating rates: I. Pyrolysis kinetics. Polymers 2021, 13, 3413. [Google Scholar] [CrossRef] [PubMed]
- Muravyev, N.; Pivkina, A.N.; Koga, N. Critical Appraisal of Kinetic Calculation Methods Applied to Overlapping Multistep Reactions. Molecules 2019, 24, 2298. [Google Scholar] [CrossRef] [PubMed]
- Aoyagi, Y.; Yamashita, K.; Doi, Y. Thermal degradation of poly [(R)-3-hydroxybutyrate], poly [ε-caprolactone], and poly [(S)-lactide]. Polym. Degrad. Stab. 2002, 76, 53–59. [Google Scholar] [CrossRef]
- Li, J.; Zheng, W.; Li, L.; Zheng, Y.; Lou, X. Thermal degradation kinetics of g-HA/PLA composite. Thermochim. Acta 2009, 493, 90–95. [Google Scholar] [CrossRef]
- McNeill, I.; Leiper, H. Degradation studies of some polyesters and polycarbonates—2. Polylactide: Degradation under isothermal conditions, thermal degradation mechanism, and photolysis of the polymer. Polym. Degrad. Stab. 1985, 11, 309–326. [Google Scholar] [CrossRef]



| Polymer/Composite | Findings | Reference |
|---|---|---|
| PLA, PLA/nano silver, PLA/nanoclay |
| Mróz et al. (2013) [12] |
| PLA, PLA/PEG, PLA/MCC * composites |
| Bhiogade et al. (2020) [13] |
| PP **/PLA blends |
| Hayoune et al. (2020) [14] |
| PLA/PBAT *** blends |
| Xiang et al. (2020) [15] |
| Polystyrene (PS) |
| Mortezaeikia et al. (2021) [4] |
| PLA |
| Mortezaeikia et al. (2021) [4] |
| LDPE |
| Saad et al. (2021) [5] |
| Polyethylene (PE) |
| Pan et al. (2021) [6] |
| Lychee and plastic wastes (LPW) |
| Zhang et al. (2022) [7] |
| Property | Value |
|---|---|
| Specific Gravity | 1.24 |
| Clarity | Transparent |
| Tensile Strength @ Break (MPa) | 53 |
| Tensile Yield Strength (MPa) | 60 |
| Tensile Modulus (GPa) | 3.5 |
| Tensile Elongation (%) | 6.0 |
| Melting Temperature (°C) | 145–160 |
| Glass Transition Temperature (°C) | 55–60 |
| Moisture | Volatile | Ash |
|---|---|---|
| 0.6 | 99.4 | 0 |
| Model | Equation | Comment |
|---|---|---|
| Friedman | The logarithm of Equation (2) | |
| Flynn-Wall-Qzawa (FWO) | Using Doyle’s approximation | |
| Kissinger-Akahira-Sunose (KAS) | Using Murry-White approximation | |
| Starink | Using Starink approximation |
| Model | Equation | Comment |
|---|---|---|
| Coats-Redfern | Applies an asymptotic series expansion. | |
| Criado * | Combination of Equation (1) and Coats-Redfern equation. |
| Run No. | Heating Rate (K/min) | Tonset (K) | Tpeak (K) | Tendset (K) |
|---|---|---|---|---|
| 1 | 5 | 534 | 623 | 642 |
| 2 | 10 | 543 | 647 | 668 |
| 3 | 20 | 566 | 663 | 682 |
| 4 | 30 | 580 | 684 | 707 |
| Ref. | This Work | Bhiogade et al. (2020) [13] | Mróz et al. (2013) [12] | Hayoune et al. (2022) [14] | Xiang et al. (2020) [15] |
|---|---|---|---|---|---|
| Tmax (K) | 647.0 | 638 | 625.3 | 622 | 657 |
| Conversion | Friedman | FWO | KAS | Starink | ||||
|---|---|---|---|---|---|---|---|---|
| E (kJ/mol) | R2 | E (kJ/mol) | R2 | E (kJ/mol) | R2 | E (kJ/mol) | R2 | |
| 0.1 | 115 | 0.9635 | 114 | 0.9944 | 110 | 0.9931 | 110 | 0.9932 |
| 0.2 | 109 | 0.9533 | 115 | 0.9944 | 111 | 0.9932 | 111 | 0.9933 |
| 0.3 | 99 | 0.9505 | 113 | 0.9904 | 109 | 0.9885 | 109 | 0.9886 |
| 0.4 | 94 | 0.9543 | 111 | 0.9870 | 106 | 0.9842 | 106 | 0.9842 |
| 0.5 | 89 | 0.9675 | 108 | 0.9843 | 103 | 0.9809 | 104 | 0.9811 |
| 0.6 | 90 | 0.9536 | 107 | 0.9824 | 101 | 0.9784 | 102 | 0.9786 |
| 0.7 | 91 | 0.9574 | 105 | 0.9809 | 100 | 0.9766 | 100 | 0.9768 |
| 0.8 | 92 | 0.9513 | 104 | 0.9794 | 99 | 0.9746 | 99 | 0.9748 |
| 0.9 | 91 | 0.9608 | 103 | 0.9777 | 98 | 0.9724 | 98 | 0.9726 |
| Average | 97 | 0.9569 | 109 | 0.9857 | 104 | 0.9824 | 104 | 0.9826 |
| References | E (kJ/mol) | Method |
|---|---|---|
| McNeill and Leiper (1985) [27] | 119 | |
| Aoyagi et al. (2002) [25] | 80–160 | |
| Li et al. (2009) [26] | 166.0 ± 6.3 174.7 ± 16.5 | FWO IKP + Coats–Redfern |
| Bhiogade et al. (2020) [13] | 79.21 | Coats–Redfern + Mampel |
| This work | 97 ± 8.76 | Friedman |
| 109 ± 4.25 | FWO | |
| 104 ± 4.72 | KAS | |
| 104 ± 4.64 | Starink |
| Reaction Mechanism | Heating Rates (K/min) | Average | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 5 | 10 | 20 | 30 | |||||||
| E | R2 | E | R2 | E | R2 | E | R2 | E | R2 | |
| (kJ/mol) | (kJ/mol) | (kJ/mol) | (kJ/mol) | (kJ/mol) | ||||||
| F1 | 256 | 0.9972 | 185 | 0.9995 | 197 | 1 | 177 | 0.9998 | 204 | 0.9991 |
| F2 | 533 | 0.983 | 253 | 0.9954 | 257 | 0.9996 | 274 | 0.9982 | 329 | 0.9941 |
| F3 | 899 | 0.9737 | 334 | 0.9895 | 327 | 0.9987 | 393 | 0.9964 | 488 | 0.9896 |
| D1 | 206 | 0.9938 | 271 | 0.9988 | 303 | 0.9993 | 223 | 0.9995 | 251 | 0.9979 |
| D2 | 278 | 0.9985 | 303 | 0.9997 | 333 | 0.9996 | 263 | 0.9999 | 294 | 0.9994 |
| D3 | 392 | 0.9998 | 341 | 1 | 368 | 0.9999 | 313 | 1 | 354 | 0.9999 |
| A2 | 123 | 0.997 | 87 | 0.9995 | 93 | 1 | 83 | 0.9998 | 97 | 0.9991 |
| A3 | 79 | 0.9967 | 55 | 0.9994 | 58 | 1 | 52 | 0.9997 | 61 | 0.999 |
| A4 | 56 | 0.9964 | 38 | 0.9994 | 41 | 1 | 36 | 0.9997 | 43 | 0.9989 |
| R1 | 98 | 0.9931 | 4 | 0.9996 | 146 | 0.9992 | 106 | 0.9994 | 89 | 0.9978 |
| R2 | 163 | 0.9999 | 4 | 0.9999 | 170 | 0.9998 | 139 | 1 | 119 | 0.9999 |
| R3 | 191 | 0.9998 | 4 | 0.9999 | 179 | 0.9999 | 151 | 1 | 131 | 0.9999 |
| P2 | 44 | 0.9914 | 60 | 0.9984 | 68 | 0.9991 | 47 | 0.9992 | 55 | 0.997 |
| P3 | 26 | 0.9888 | 36 | 0.998 | 41 | 0.9989 | 28 | 0.999 | 33 | 0.9962 |
| P4 | 17 | 0.985 | 25 | 0.9975 | 28 | 0.9987 | 18 | 0.9987 | 22 | 0.995 |
| Run No. | Heating Rate (K/min) | E (kJ/mol) | ln(A) | R2 | Reaction Mechanism |
|---|---|---|---|---|---|
| 1 | 5 | 163 | 29.33 | 0.9999 | Geometrical contraction model (R2) |
| 2 | 10 | 119 | 24.56 | 0.9999 | Geometrical contraction model (R2) |
| 3 | 20 | 170 | 30.12 | 0.9998 | Geometrical contraction model (R2) |
| 4 | 30 | 139 | 23.75 | 1.0000 | Geometrical contraction model (R2) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alhulaybi, Z.; Dubdub, I.; Al-Yaari, M.; Almithn, A.; Al-Naim, A.F.; Aljanubi, H. Pyrolysis Kinetic Study of Polylactic Acid. Polymers 2023, 15, 12. https://doi.org/10.3390/polym15010012
Alhulaybi Z, Dubdub I, Al-Yaari M, Almithn A, Al-Naim AF, Aljanubi H. Pyrolysis Kinetic Study of Polylactic Acid. Polymers. 2023; 15(1):12. https://doi.org/10.3390/polym15010012
Chicago/Turabian StyleAlhulaybi, Zaid, Ibrahim Dubdub, Mohammed Al-Yaari, Abdulrahman Almithn, Abdullah F. Al-Naim, and Haidar Aljanubi. 2023. "Pyrolysis Kinetic Study of Polylactic Acid" Polymers 15, no. 1: 12. https://doi.org/10.3390/polym15010012
APA StyleAlhulaybi, Z., Dubdub, I., Al-Yaari, M., Almithn, A., Al-Naim, A. F., & Aljanubi, H. (2023). Pyrolysis Kinetic Study of Polylactic Acid. Polymers, 15(1), 12. https://doi.org/10.3390/polym15010012









