Advanced Machine Learning Modeling Approach for Prediction of Compressive Strength of FRP Confined Concrete Using Multiphysics Genetic Expression Programming
Abstract
:1. Introduction
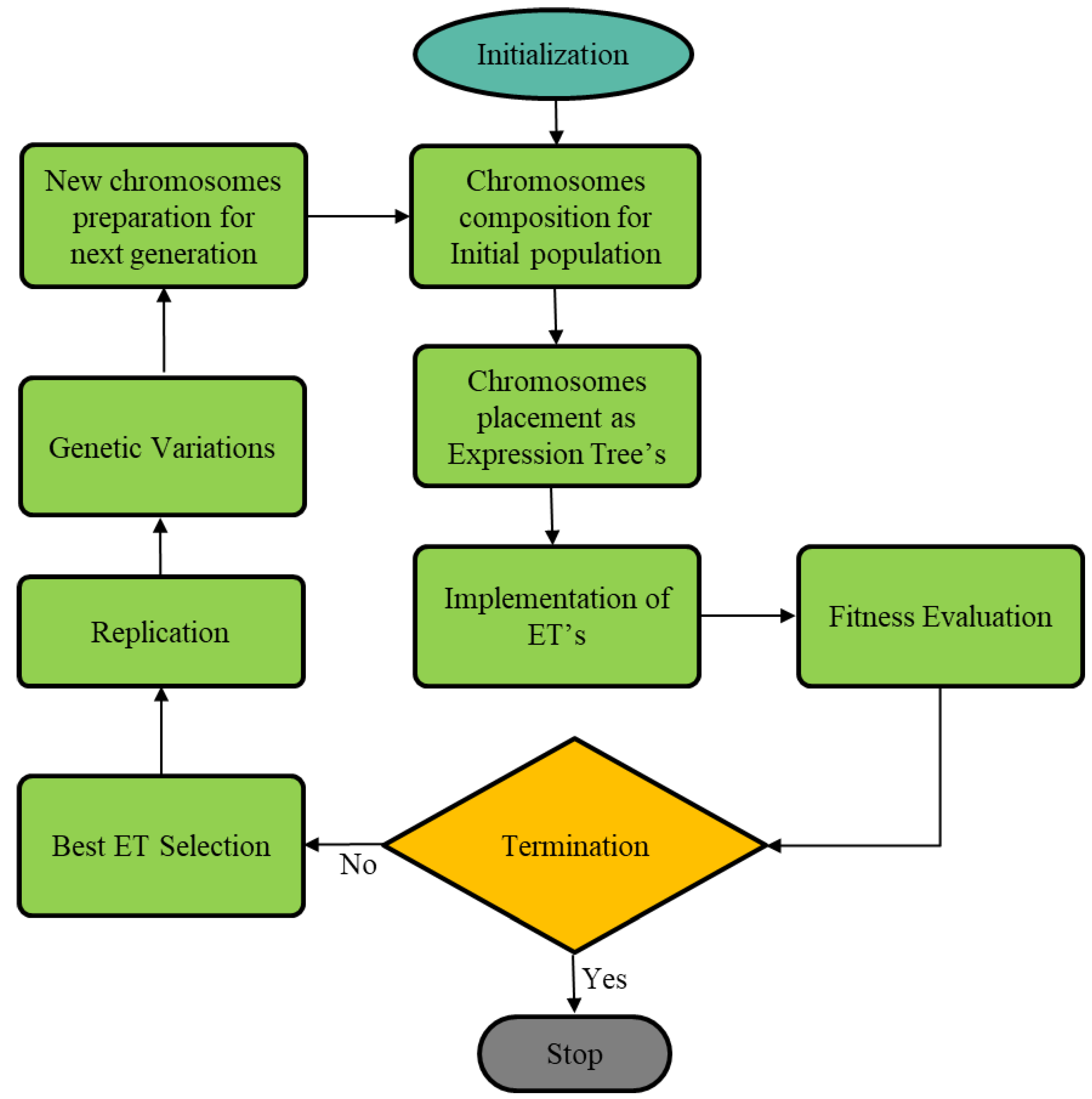
2. Gene Expression Programming
3. Research Methods
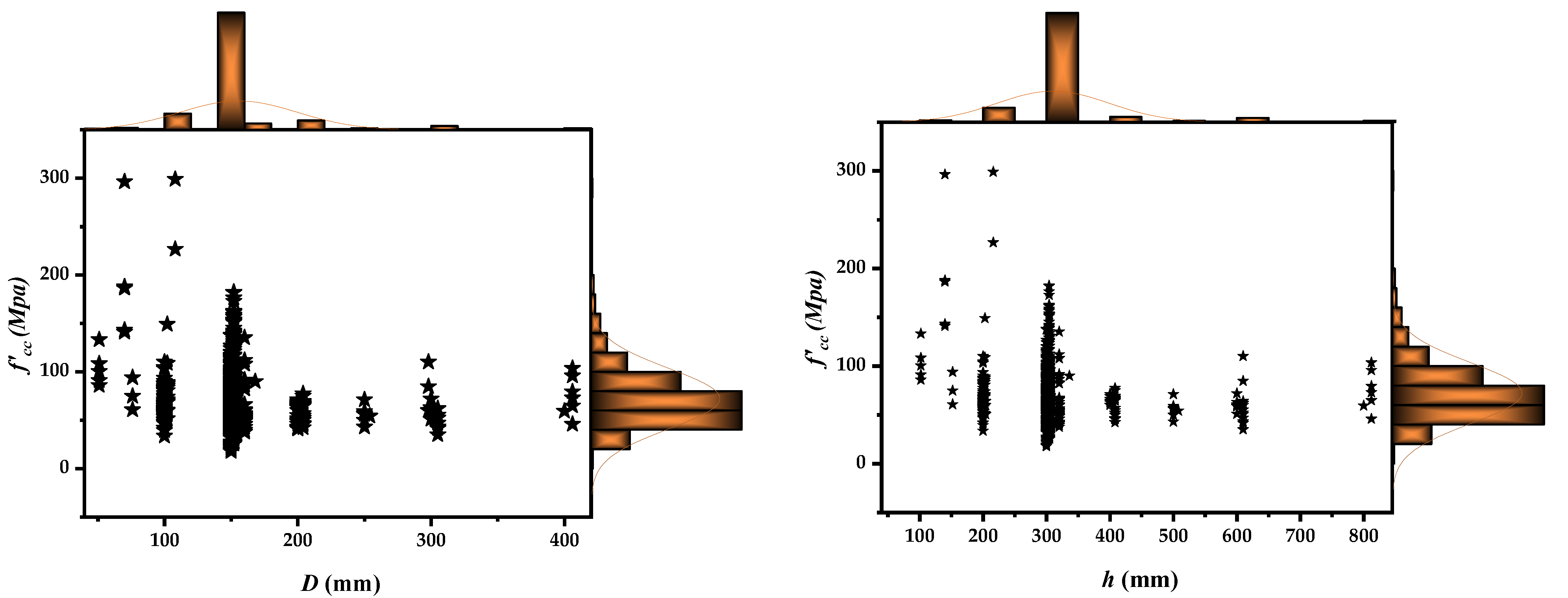
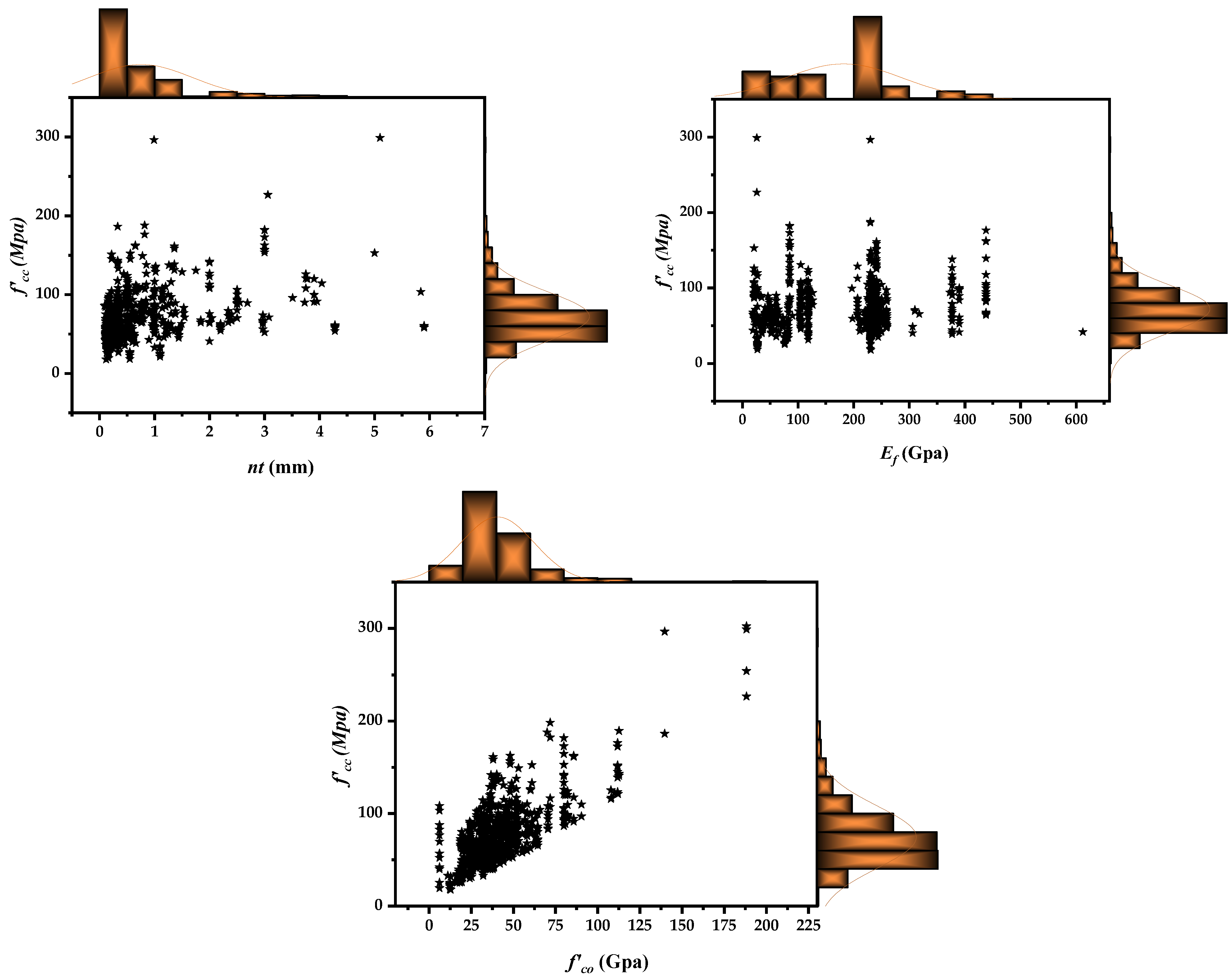
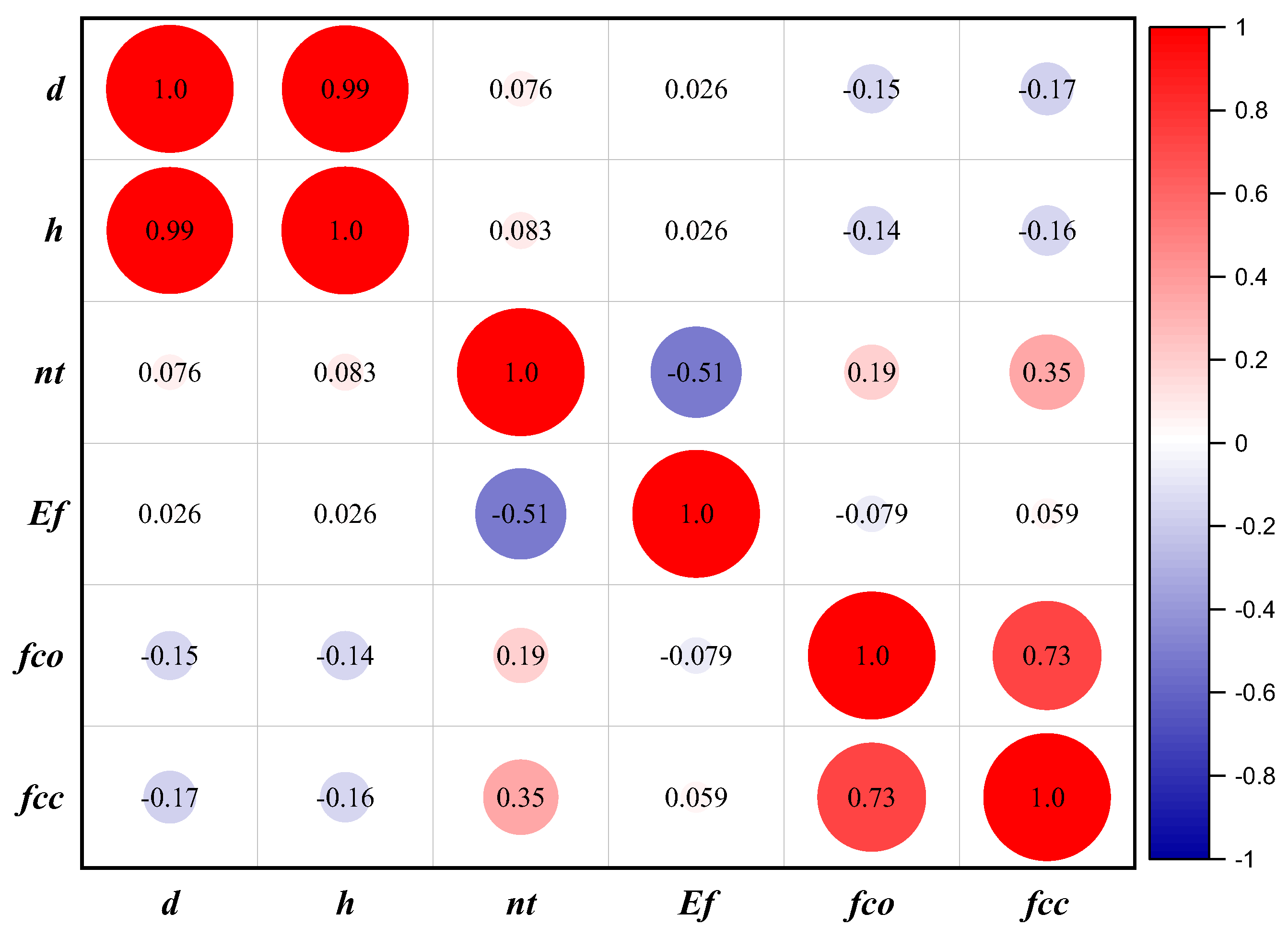
Database Establishment and Division
4. Modeling Approach
4.1. GEP Modelling
4.2. Regression Models
4.2.1. Multiple Non-Linear Regression (MNLR)
4.2.2. Multiple Linear Regression (MLR)
5. Results and Discussion
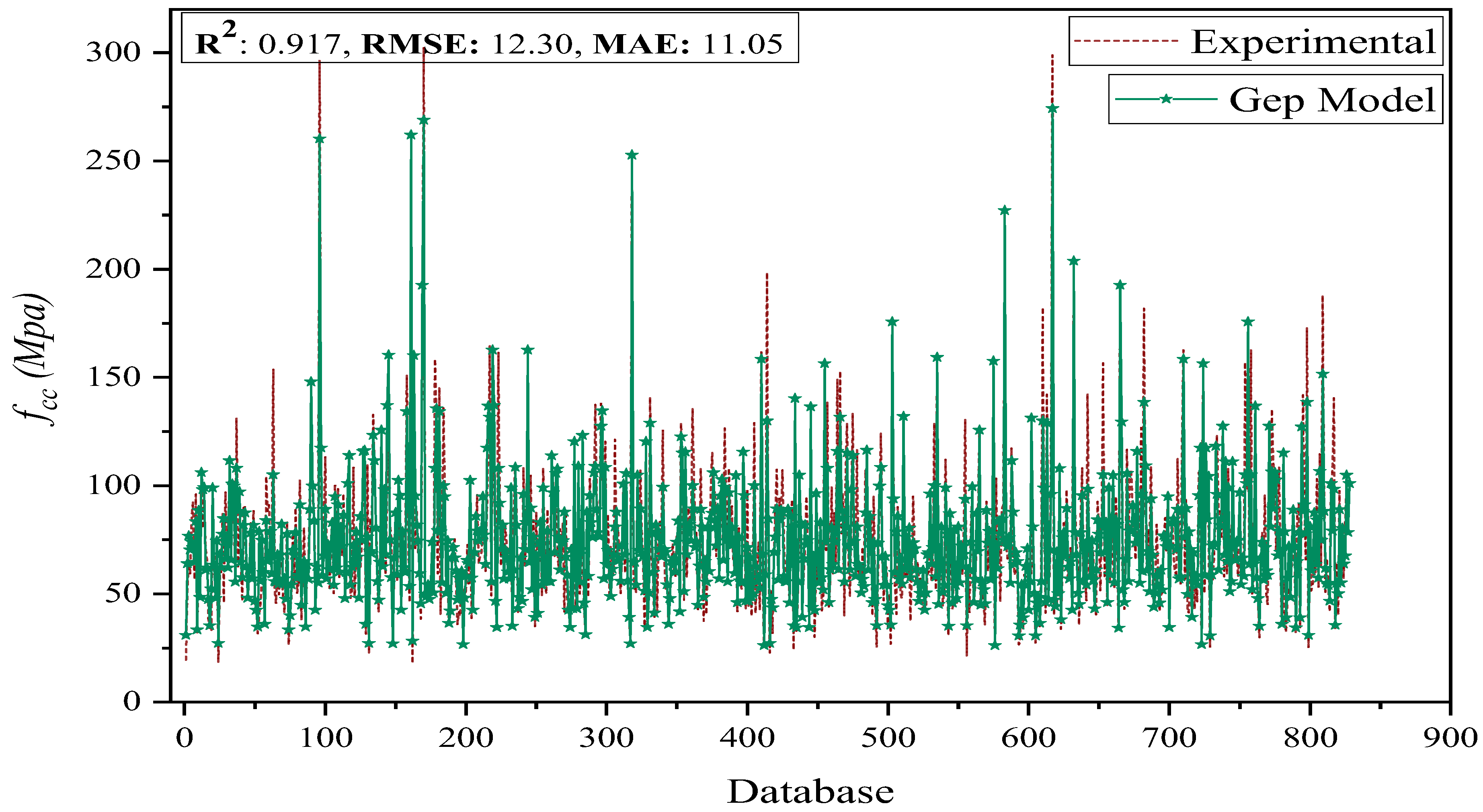
5.1. Model Performance and Evaluation
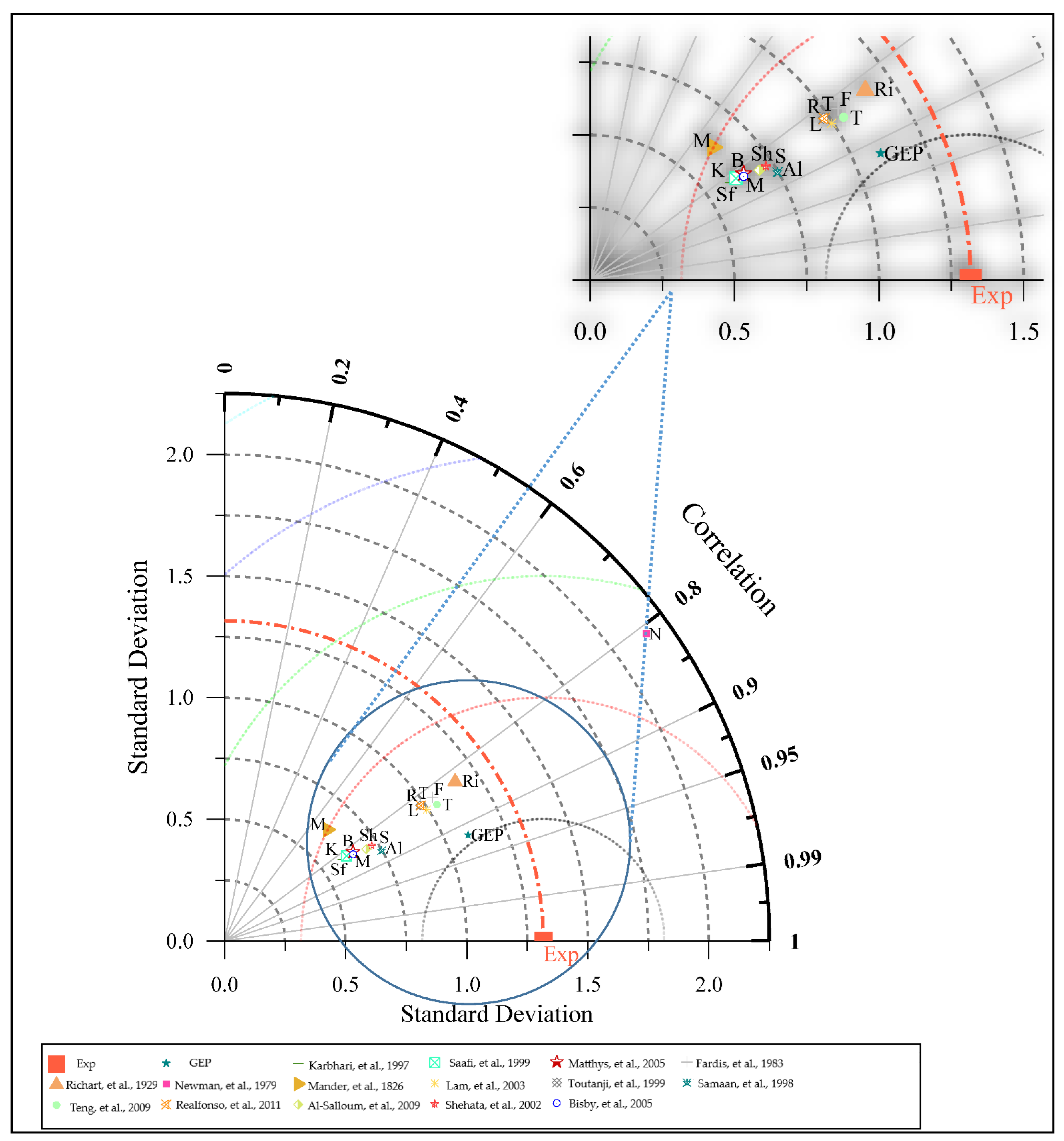
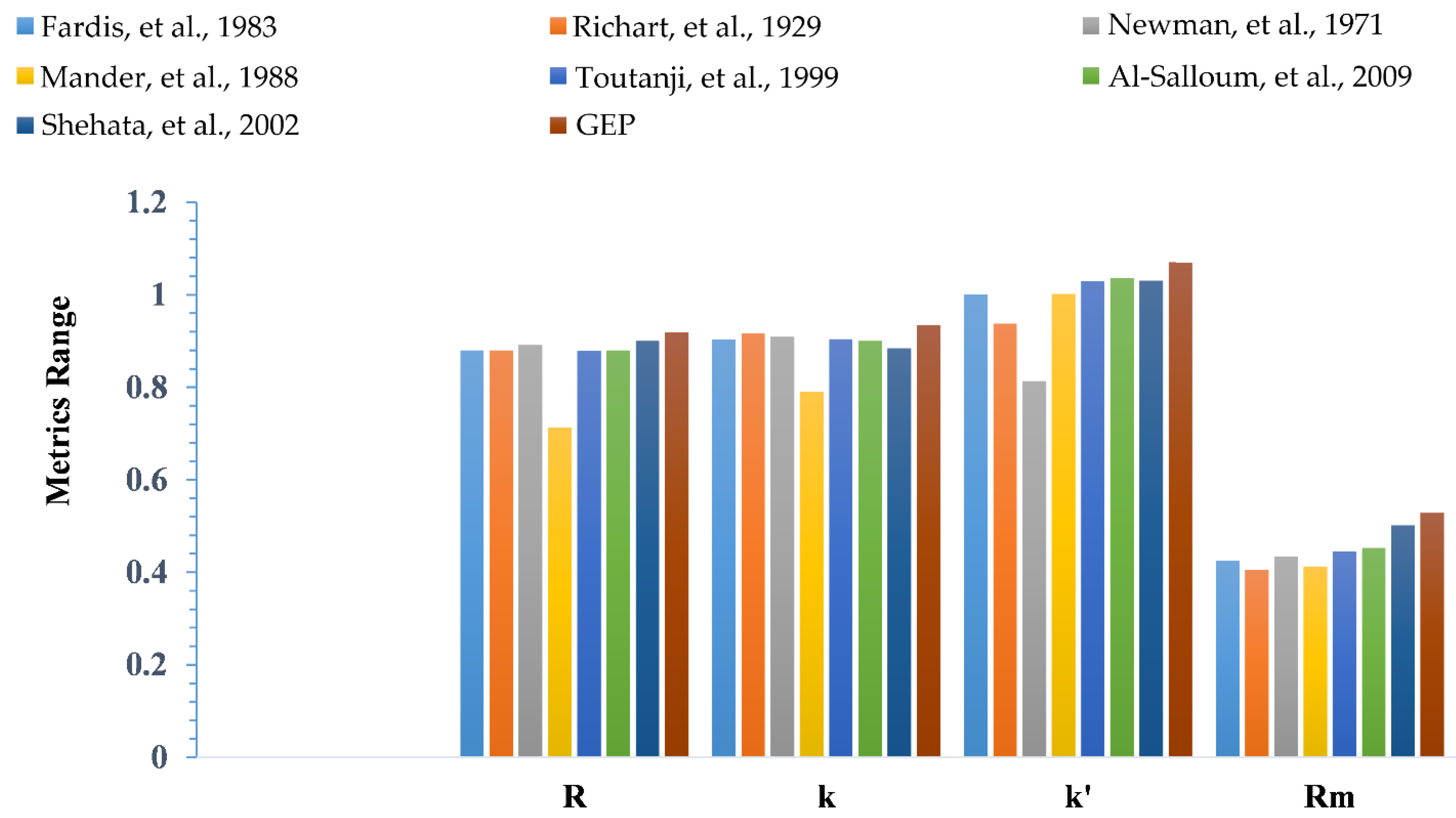
5.2. External Validation
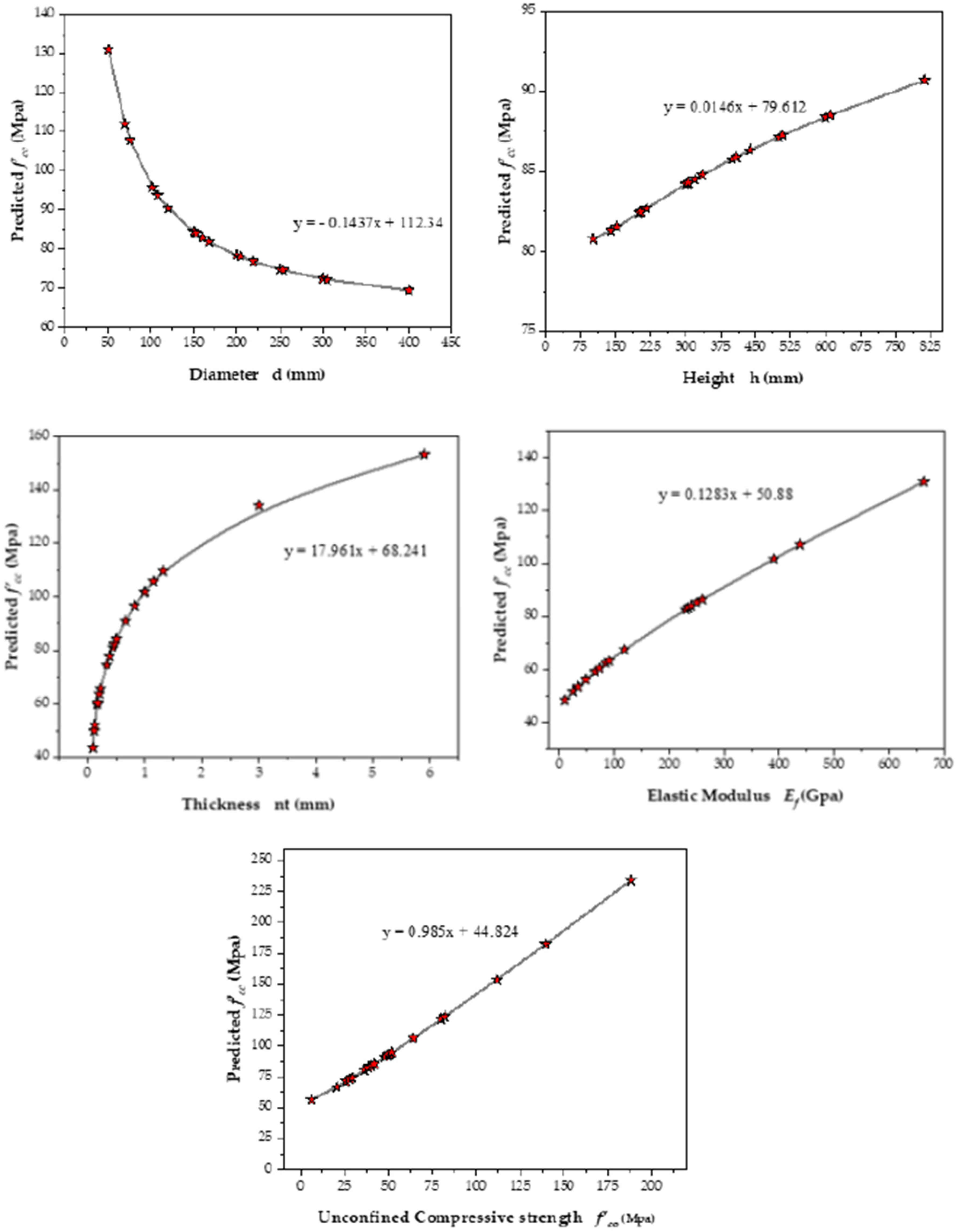
5.3. Parametric Study
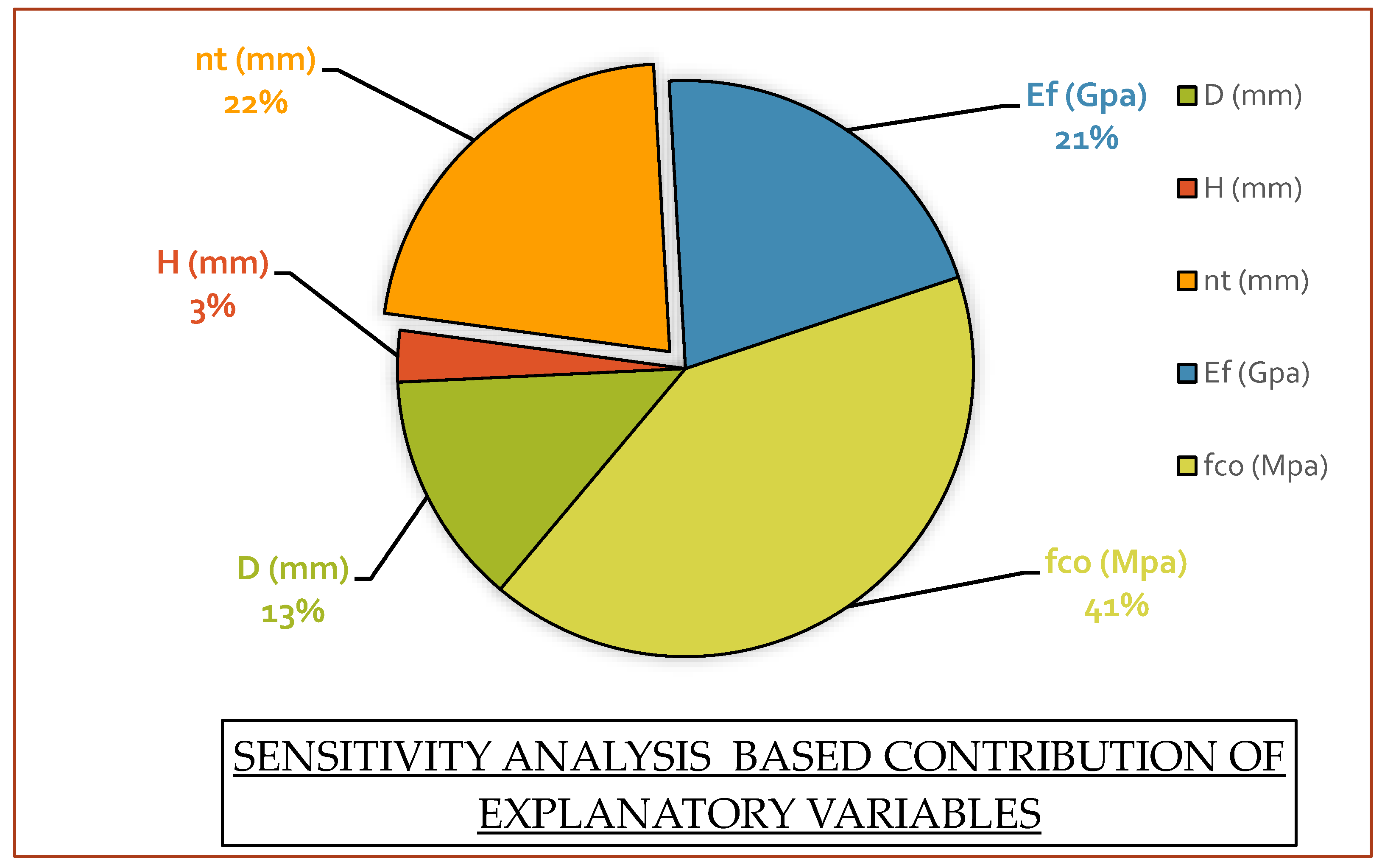
5.4. Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Li, S.; Bisby, L.; Ai, J. FRP rupture strains in the split-disk test. Compos. Part B Eng. 2011, 42, 962–972. [Google Scholar] [CrossRef]
- Castillo, E.D.R.; Griffith, M.; Ingham, J. Seismic behavior of RC columns flexurally strengthened with FRP sheets and FRP anchors. Compos. Struct. 2018, 203, 382–395. [Google Scholar] [CrossRef]
- Delgado, P.; Arêde, A.; Pouca, N.V.; Rocha, P.; Costa, A.; Delgado, R. Retrofit of RC hollow piers with CFRP sheets. Compos. Struct. 2012, 94, 1280–1287. [Google Scholar] [CrossRef]
- Geraldine, S.C.; William, C.S. Behavior of 1/6-Scale Model Bridge Columns Subjected to Inelastic Cyclic Loading. ACI Struct. J. 1990, 87, 630–638. [Google Scholar]
- Cevik, A.; Göğüş, M.T.; Güzelbey, I.H.; Filiz, H. Soft computing based formulation for strength enhancement of CFRP confined concrete cylinders. Adv. Eng. Softw. 2010, 41, 527–536. [Google Scholar] [CrossRef]
- Wu, Y.-B.; Jin, G.-F.; Ding, T.; Meng, D. Modeling Confinement Efficiency of FRP-Confined Concrete Column Using Radial Basis Function Neural Network. In 2010 2nd International Workshop on Intelligent Systems and Applications; IEEE: Piscataway, NJ, USA, 2010; pp. 1–6. [Google Scholar]
- Al Zand, A.W.; Badaruzzaman, W.H.W.; Mutalib, A.A.; Hilo, S.J. The enhanced performance of CFST beams using different strengthening schemes involving unidirectional CFRP sheets: An experimental study. Eng. Struct. 2016, 128, 184–198. [Google Scholar] [CrossRef]
- Güneyisi, E.M.; Nour, A.I. Axial compression capacity of circular CFST columns transversely strengthened by FRP. Eng. Struct. 2019, 191, 417–431. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, J.; Wang, Y.; Wang, F. Analytical modelling and design of partially CFRP-wrapped thin-walled circular NCFST stub columns under axial compression. Thin-Walled Struct. 2019, 144, 106276. [Google Scholar] [CrossRef]
- Farooq, F.; Jin, X.; Faisal Javed, M.; Akbar, A.; Izhar Shah, M.; Aslam, F.; Alyousef, R. Geopolymer concrete as sustainable material: A state of the art review. Constr. Build. Mater. 2021, 306, 124762. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Gao, Y. Composite Jacketed Concrete under Uniaxial Compression—Verification of Simple Design Equations. J. Mater. Civ. Eng. 1997, 9, 185–193. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Mirmiran, A. Analytical and Experimental Investigation of Reinforced Concrete Columns Encased in Fiberglass Tubular Jacket and Use of Fiber Jacket for Pile Splicing; Final Rep. Contract No. B-9135; Florida Department of Transportation: Tallahassee, FL, USA, 1996. [Google Scholar]
- Fardis, M.; Khalili, H.H.; Marshall, A.L. Discussion: FRP-encased concrete as a structural material. Mag. Concr. Res. 1983, 35, 242–243. [Google Scholar] [CrossRef]
- Richart, F.E.; Brandtzæg, A.; Brown, R.L. Failure of Plain and Spirally Reinforced Concrete in Compression; Bulletin (University of Illinois (Urbana-Champaign Campus). Engineering Experiment Station): Champaign, IL, USA, 1929; p. 74. [Google Scholar]
- Newman, K.; Newman, J.J.S. Failure theories and design criteria for plain concrete. Struct. Solid Mech. Eng. Des. Wiley-Intersci. Lond. Engl. 1971, 963–995. Available online: https://www.researchgate.net/publication/281365329_Failure_theories_and_design_criteria_for_plain_concrete (accessed on 22 April 2022).
- Sadeghian, P.; Fam, A. Improved design-oriented confinement models for FRP-wrapped concrete cylinders based on statistical analyses. Eng. Struct. 2015, 87, 162–182. [Google Scholar] [CrossRef]
- Keshtegar, B.; Ozbakkaloglu, T.; Gholampour, A. Modeling the behavior of FRP-confined concrete using dynamic harmony search algorithm. Eng. Comput. 2016, 33, 415–430. [Google Scholar] [CrossRef]
- Keshtegar, B.; Sadeghian, P.; Gholampour, A.; Ozbakkaloglu, T. Nonlinear modeling of ultimate strength and strain of FRP-confined concrete using chaos control method. Compos. Struct. 2017, 163, 423–431. [Google Scholar] [CrossRef]
- Bisby, L.A.; Dent, A.J.S.; Green, M.F. Comparison of confinement models for fiber-reinforced polymer-wrapped concrete. ACI Struct. J. 2005, 102, 62–72. [Google Scholar]
- De Lorenzis, L.; Tepfers, R. Comparative Study of Models on Confinement of Concrete Cylinders with Fiber-Reinforced Polymer Composites. J. Compos. Constr. 2003, 7, 219–237. [Google Scholar] [CrossRef]
- Lam, L.; Teng, J. Design-oriented stress–strain model for FRP-confined concrete. Constr. Build. Mater. 2003, 17, 471–489. [Google Scholar] [CrossRef]
- Soudki, K.; Alkhrdaji, T. Guide for the Design and Construction of Externally Bonded FRP Systems for Strengthening Concrete Structures (ACI 440.2R-02). In Tructures Congress 2005: Metropolis and Beyond; American Society of Civil Engineers: Reston, VA, USA, 2005; pp. 1627–1633. [Google Scholar]
- Farooq, F.; Ahmed, W.; Akbar, A.; Aslam, F.; Alyousef, R. Predictive modeling for sustainable high-performance concrete from industrial wastes: A comparison and optimization of models using ensemble learners. J. Clean. Prod. 2021, 292, 126032. [Google Scholar] [CrossRef]
- Khan, M.A.; Zafar, A.; Akbar, A.; Javed, M.; Mosavi, A. Application of Gene Expression Programming (GEP) for the Prediction of Compressive Strength of Geopolymer Concrete. Materials 2021, 14, 1106. [Google Scholar] [CrossRef]
- Aslam, F.; Elkotb, M.A.; Iqtidar, A.; Khan, M.A.; Javed, M.F.; Usanova, K.I.; Alamri, S.; Musarat, M.A. Compressive strength prediction of rice husk ash using multiphysics genetic expression programming. Ain Shams Eng. J. 2021, 13, 101593. [Google Scholar] [CrossRef]
- Khan, M.A.; Farooq, F.; Javed, M.F.; Zafar, A.; Ostrowski, K.A.; Aslam, F.; Malazdrewicz, S.; Maślak, M. Simulation of Depth of Wear of Eco-Friendly Concrete Using Machine Learning Based Computational Approaches. Materials 2021, 15, 58. [Google Scholar] [CrossRef]
- Javed, M.F.; Farooq, F.; Memon, S.A.; Akbar, A.; Khan, M.A.; Aslam, F.; Alyousef, R.; Alabduljabbar, H.; Rehman, S.K.U.; Rehman, S.K.U.; et al. New Prediction Model for the Ultimate Axial Capacity of Concrete-Filled Steel Tubes: An Evolutionary Approach. Crystals 2020, 10, 741. [Google Scholar] [CrossRef]
- Khan, S.; Khan, M.A.; Zafar, A.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predicting the Ultimate Axial Capacity of Uniaxially Loaded CFST Columns Using Multiphysics Artificial Intelligence. Materials 2021, 15, 39. [Google Scholar] [CrossRef]
- Khan, M.A.; Shah, M.I.; Javed, M.F.; Rasheed, S.; El-Shorbagy, M.; El-Zahar, E.R.; Malik, M. Application of random forest for modelling of surface water salinity. Ain Shams Eng. J. 2021, 13, 101635. [Google Scholar] [CrossRef]
- Naderpour, H.; Kheyroddin, A.; Amiri, G.G. Prediction of FRP-confined compressive strength of concrete using artificial neural networks. Compos. Struct. 2010, 92, 2817–2829. [Google Scholar] [CrossRef]
- Elsanadedy, H.; Al-Salloum, Y.; Abbas, H.; Alsayed, S. Prediction of strength parameters of FRP-confined concrete. Compos. Part B Eng. 2012, 43, 228–239. [Google Scholar] [CrossRef]
- Jiang, K.; Han, Q.; Bai, Y.; Du, X. Data-driven ultimate conditions prediction and stress-strain model for FRP-confined concrete. Compos. Struct. 2020, 242, 112094. [Google Scholar] [CrossRef]
- Sharifi, Y.; Moghbeli, A. New empirical approaches for compressive strength assessment of CFRP confined rectangular concrete columns. Compos. Struct. 2021, 262, 113373. [Google Scholar] [CrossRef]
- Chen, W.; Xu, J.; Dong, M.; Yu, Y.; Elchalakani, M.; Zhang, F. Data-driven analysis on ultimate axial strain of FRP-confined concrete cylinders based on explicit and implicit algorithms. Compos. Struct. 2021, 268, 113904. [Google Scholar] [CrossRef]
- Chou, J.-S.; Pham, A.-D. Enhanced artificial intelligence for ensemble approach to predicting high performance concrete compressive strength. Constr. Build. Mater. 2013, 49, 554–563. [Google Scholar] [CrossRef]
- Noori, R.; Hoshyaripour, G.; Ashrafi, K.; Araabi, B.N. Uncertainty analysis of developed ANN and ANFIS models in prediction of carbon monoxide daily concentration. Atmos. Environ. 2010, 44, 476–482. [Google Scholar] [CrossRef]
- Sebaaly, H.; Varma, S.; Maina, J.W. Optimizing asphalt mix design process using artificial neural network and genetic algorithm. Constr. Build. Mater. 2018, 168, 660–670. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Zafar, A.; Farooq, F.; Javed, M.F.; Alyousef, R.; Alabduljabbar, H. Geopolymer Concrete Compressive Strength via Artificial Neural Network, Adaptive Neuro Fuzzy Interface System, and Gene Expression Programming With K-Fold Cross Validation. Front. Mater. 2021, 8, 621163. [Google Scholar] [CrossRef]
- Zhao, T.H.; Khan, M.I.; Chu, Y.M. Artificial neural networking (ANN) analysis for heat and entropy generation in flow of non-Newtonian fluid between two rotating disks. Math. Methods Appl. Sci. 2021. [CrossRef]
- Zha, T.-H.; Castillo, O.; Jahanshahi, H.; Yusuf, A.; Alassafi, M.O.; Alsaadi, F.E.; Chu, Y.-M. A Fuzzy-Based Strategy to Suppress the Novel Coronavirus (2019-NCOV) Massive Outbreak. Appl. Comput. Math. 2021, 20, 160–176. [Google Scholar]
- Nazeer, M.; Hussain, F.; Khan, M.I.; Asad-ur-Rehman; El-Zahar, E.R.; Chu, Y.-M.; Malik, M. Theoretical study of MHD electro-osmotically flow of third-grade fluid in micro channel. Appl. Math. Comput. 2021, 420, 126868. [Google Scholar] [CrossRef]
- Chu, H.-H.; Zhao, T.-H.; Chu, Y.-M. Sharp bounds for the Toader mean of order 3 in terms of arithmetic, quadratic and contraharmonic means. Math. Slovaca 2020, 70, 1097–1112. [Google Scholar] [CrossRef]
- Zhao, T.-H.; He, Z.-Y.; Chu, Y.-M. On some refinements for inequalities involving zero-balanced hypergeometric function. AIMS Math. 2020, 5, 6479–6495. [Google Scholar] [CrossRef]
- Zhao, T.-H.; Wang, M.-K.; Chu, Y.-M. A sharp double inequality involving generalized complete elliptic integral of the first kind. AIMS Math. 2020, 5, 4512–4528. [Google Scholar] [CrossRef]
- Zhao, T.-H.; Zhou, B.-C.; Wang, M.-K.; Chu, Y.-M. On approximating the quasi-arithmetic mean. J. Inequal. Appl. 2019, 2019, 42. [Google Scholar] [CrossRef]
- Zhao, T.-H.; Wang, M.-K.; Zhang, W.; Chu, Y.-M. Quadratic transformation inequalities for Gaussian hypergeometric function. J. Inequal. Appl. 2018, 2018, 1–15. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gandomi, A.H.; Babanajad, S.K.; Alavi, A.H.; Farnam, Y. Novel Approach to Strength Modeling of Concrete under Triaxial Compression. J. Mater. Civ. Eng. 2012, 24, 1132–1143. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Yun, G.J.; Alavi, A.H. An evolutionary approach for modeling of shear strength of RC deep beams. Mater. Struct. 2013, 46, 2109–2119. [Google Scholar] [CrossRef]
- Chu, H.-H.; Khan, M.A.; Javed, M.; Zafar, A.; Alabduljabbar, H.; Qayyum, S. Sustainable use of fly-ash: Use of gene-expression programming (GEP) and multi-expression programming (MEP) for forecasting the compressive strength geopolymer concrete. Ain Shams Eng. J. 2021, 12, 3603–3617. [Google Scholar] [CrossRef]
- Khan, M.A.; Memon, S.A.; Farooq, F.; Javed, M.F.; Aslam, F.; Alyousef, R. Compressive Strength of Fly-Ash-Based Geopolymer Concrete by Gene Expression Programming and Random Forest. Adv. Civ. Eng. 2021, 2021, 6618407. [Google Scholar] [CrossRef]
- Ferreira, C. Gene Expression Programming: Mathematical Modeling by an Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; Volume 21. [Google Scholar]
- Aval, S.B.; Ketabdari, H.; Gharebaghi, S.A. Estimating Shear Strength of Short Rectangular Reinforced Concrete Columns Using Nonlinear Regression and Gene Expression Programming. Structures 2017, 12, 13–23. [Google Scholar] [CrossRef]
- Behnia, D.; Ahangari, K.; Noorzad, A.; Moeinossadat, S.R. Predicting crest settlement in concrete face rockfill dams using adaptive neuro-fuzzy inference system and gene expression programming intelligent methods. J. Zhejiang Univ. A 2013, 14, 589–602. [Google Scholar] [CrossRef] [Green Version]
- Khan, M.A.; Aslam, F.; Javed, M.F.; Alabduljabbar, H.; Deifalla, A.F. New prediction models for the compressive strength and dry-thermal conductivity of bio-composites using novel machine learning algorithms. J. Clean. Prod. 2022, 350, 131364. [Google Scholar] [CrossRef]
- Ilyas, I.; Zafar, A.; Javed, M.F.; Farooq, F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Forecasting Strength of CFRP Confined Concrete Using Multi Expression Programming. Materials 2021, 14, 7134. [Google Scholar] [CrossRef] [PubMed]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Javed, M.F.; Jamhiri, B. Predictive modeling of swell-strength of expansive soils using artificial intelligence approaches: ANN, ANFIS and GEP. J. Environ. Manag. 2021, 289, 112420. [Google Scholar] [CrossRef] [PubMed]
- Cevik, A.; Cabalar, A.F. A genetic-programming-based formulation for the strength enhancement of fiber-reinforced-polymer-confined concrete cylinders. J. Appl. Polym. Sci. 2008, 110, 3087–3095. [Google Scholar] [CrossRef]
- Gandomi, A.; Alavi, A.H.; Arjmandi, P.; Aghaeifar, A.; Seyednour, R. Genetic programming and orthogonal least squares: A hybrid approach to modeling the compressive strength of CFRP-confined concrete cylinders. J. Mech. Mater. Struct. 2010, 5, 735–753. [Google Scholar] [CrossRef]
- Ozbakkaloglu, T.; Lim, J.C. Axial compressive behavior of FRP-confined concrete: Experimental test database and a new design-oriented model. Compos. Part B Eng. 2013, 55, 607–634. [Google Scholar] [CrossRef] [Green Version]
- Ferreira, C. Gene expression programming: A new adaptive algorithm for solving problems. arXiv 2001. preprint. [Google Scholar] [CrossRef]
- Gholampour, A.; Gandomi, A.; Ozbakkaloglu, T. New formulations for mechanical properties of recycled aggregate concrete using gene expression programming. Constr. Build. Mater. 2017, 130, 122–145. [Google Scholar] [CrossRef]
- Kiani, B.; Gandomi, A.H.; Sajedi, S.; Liang, R.Y. New Formulation of Compressive Strength of Preformed-Foam Cellular Concrete: An Evolutionary Approach. J. Mater. Civ. Eng. 2016, 28, 04016092. [Google Scholar] [CrossRef]
- Ozturan, M.; Kutlu, B.; Ozturan, T. Comparison of concrete strength prediction techniques with artificial neural network approach. Build. Res. J. 2008, 56, 23–36. [Google Scholar]
- Özcan, F.; Atis, C.; Karahan, O.; Uncuoğlu, E.; Tanyildizi, H. Comparison of artificial neural network and fuzzy logic models for prediction of long-term compressive strength of silica fume concrete. Adv. Eng. Softw. 2009, 40, 856–863. [Google Scholar] [CrossRef]
- Ahmadi, M.; Naderpour, H.; Kheyroddin, A. ANN Model for Predicting the Compressive Strength of Circular Steel-Confined Concrete. Int. J. Civ. Eng. 2017, 15, 213–221. [Google Scholar] [CrossRef]
- Naderpour, H.; Nagai, K.; Fakharian, P.; Haji, M. Innovative models for prediction of compressive strength of FRP-confined circular reinforced concrete columns using soft computing methods. Compos. Struct. 2019, 215, 69–84. [Google Scholar] [CrossRef]
- Ziegel, E.R.; Frank, I.; Todeschini, R. Data Analysis Handbook. Technometrics 1996, 38, 193. [Google Scholar] [CrossRef]
- Azim, I.; Yang, J.; Javed, M.F.; Iqbal, M.F.; Mahmood, Z.; Wang, F.; Liu, Q.-F. Prediction model for compressive arch action capacity of RC frame structures under column removal scenario using gene expression programming. Structures 2020, 25, 212–228. [Google Scholar] [CrossRef]
- Benjamin, J.R.; Cornell, C.A. Probability, Statistics and Decision for Civil Engineers; Courier Cooperation, Dover Publication, Mineola: New York, NY, USA, 2014; p. 244. [Google Scholar]
- Sadrossadat, E.; Soltani, F.; Mousavi, S.M.; Marandi, S.M.; Alavi, A.H. A new design equation for prediction of ultimate bearing capacity of shallow foundation on granular soils. J. Civ. Eng. Manag. 2014, 19, S78–S90. [Google Scholar] [CrossRef] [Green Version]
- Jalal, F.E.; Xu, Y.; Iqbal, M.; Jamhiri, B.; Javed, M.F. Predicting the compaction characteristics of expansive soils using two genetic programming-based algorithms. Transp. Geotech. 2021, 30, 100608. [Google Scholar] [CrossRef]
- Sadrossadat, E.; Heidaripanah, A.; Ghorbani, B. Towards application of linear genetic programming for indirect estimation of the resilient modulus of pavements subgrade soils. Road Mater. Pavement Des. 2016, 19, 139–153. [Google Scholar] [CrossRef]
- Sadrossadat, E.; Heidaripanah, A.; Osouli, S. Prediction of the resilient modulus of flexible pavement subgrade soils using adaptive neuro-fuzzy inference systems. Constr. Build. Mater. 2016, 123, 235–247. [Google Scholar] [CrossRef]
- Shahin, M.A.; Maier, H.R.; Jaksa, M.B. Data Division for Developing Neural Networks Applied to Geotechnical Engineering. J. Comput. Civ. Eng. 2004, 18, 105–114. [Google Scholar] [CrossRef]
- Tajeri, S.; Sadrossadat, E.; Bazaz, J.B. Indirect estimation of the ultimate bearing capacity of shallow foundations resting on rock masses. Int. J. Rock Mech. Min. Sci. 2015, 80, 107–117. [Google Scholar] [CrossRef]
- Li, P.; Khan, M.A.; Galal, A.M.; Awan, H.H.; Zafar, A.; Javed, M.F.; Qayyum, S.; Malik, M.; Wang, F. Sustainable use of chemically modified tyre rubber in concrete: Machine learning based novel predictive model. Chem. Phys. Lett. 2022, 793, 139478. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. Atmos. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Al-Salloum, Y.; Siddiqui, N. Compressive strength prediction model for FRP-confined concrete. In Proceedings of the Ninth International Symposium on Fiber Reinforced Polymer Reinforcement for Concrete Structures, Sydney, Australia, 13–15 July 2009. [Google Scholar]
- Matthys, S.; Toutanji, H.; Audenaert, K.; Taerwe, L. Axial load behavior of large-scale columns confined with fiber-reinforced polymer composites. ACI Struct. J. 2005, 102, 258. [Google Scholar]
- Realfonzo, R.; Napoli, A. Concrete confined by FRP systems: Confinement efficiency and design strength models. Compos. Part B Eng. 2011, 42, 736–755. [Google Scholar] [CrossRef]
- Saafi, M.; Toutanji, H.; Li, Z. Behavior of concrete columns confined with fiber reinforced polymer tubes. Mater. J. 1999, 96, 500–509. [Google Scholar]
- Samaan, M.; Mirmiran, A.; Shahawy, M. Model of Concrete Confined by Fiber Composites. J. Struct. Eng. 1998, 124, 1025–1031. [Google Scholar] [CrossRef]
- Shehata, I.A.; Carneiro, L.A.; Shehata, L.C. Strength of short concrete columns confined with CFRP sheets. Mater. Struct. 2002, 35, 50–58. [Google Scholar] [CrossRef]
- Teng, J.G.; Jiang, T.; Lam, L.; Luo, Y.Z. Refinement of a Design-Oriented Stress–Strain Model for FRP-Confined Concrete. J. Compos. Constr. 2009, 13, 269–278. [Google Scholar] [CrossRef] [Green Version]
- Toutanji, H. Stress-strain characteristics of concrete columns externally confined with advanced fiber composite sheets. Mater. J. 1999, 96, 397–404. [Google Scholar]
- Roy, P.P.; Roy, K. On Some Aspects of Variable Selection for Partial Least Squares Regression Models. QSAR Comb. Sci. 2008, 27, 302–313. [Google Scholar] [CrossRef]
- Golbraikh, A.; Tropsha, A. Beware of q2! J. Mol. Graph. Model. 2002, 20, 269–276. [Google Scholar] [CrossRef]
| Sr. # | Generalized Setting | |
|---|---|---|
| 1 |
| 120 |
| 2 |
| 3 |
| 3 |
| 8 |
| 4 |
| Addition |
| 5 |
| +, /, −, ×, 3√ |
| Constants Configurations | ||
| 6 |
| 10 |
| 7 |
| Floating |
| 8 |
| −10 to +10 |
| GEP Operators | ||
| 9 |
| 0.00138 |
| 10 |
| 0.00206 |
| 11 |
| 0.00476 |
| 12 |
| 0.00548 |
| 13 |
| 0.00496 |
| 14 |
| 0.00548 |
| 15 |
| 0.00157 |
| 16 |
| 0.0026 |
| 17 |
| 0.00123 |
| Recombination Rates | ||
| 18 |
| 0.00755 |
| 19 |
| 0.00277 |
| 20 |
| 0.00189 |
| 21 |
| 0.00277 |
| Sr. #. | Equation | Range | Model | Output | Reference |
|---|---|---|---|---|---|
| 1 | R > 0.8 | GEP | 0.917 | ||
| MLR | 0.788 | ||||
| MNLR | 0.856 | ||||
| 2 | GEP | 0.528 | (Roy and Roy, 2008) [87] | ||
| MLR | 0.244 | ||||
| MNLR | 0.398 | ||||
| where | GEP | 0.980 | |||
| MLR | 0.987 | ||||
| MNLR | 0.977 | ||||
| GEP | 0.998 | ||||
| MLR | 0.997 | ||||
| MNLR | 0.988 | ||||
| 3 | GEP | 0.934 | (Golbraikh and Tropsha, 2002) [88] | ||
| MLR | 0.965 | ||||
| MNLR | 0.952 | ||||
| 4 | GEP | 1.019 | |||
| MLR | 0.980 | ||||
| MNLR | 1.014 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ilyas, I.; Zafar, A.; Afzal, M.T.; Javed, M.F.; Alrowais, R.; Althoey, F.; Mohamed, A.M.; Mohamed, A.; Vatin, N.I. Advanced Machine Learning Modeling Approach for Prediction of Compressive Strength of FRP Confined Concrete Using Multiphysics Genetic Expression Programming. Polymers 2022, 14, 1789. https://doi.org/10.3390/polym14091789
Ilyas I, Zafar A, Afzal MT, Javed MF, Alrowais R, Althoey F, Mohamed AM, Mohamed A, Vatin NI. Advanced Machine Learning Modeling Approach for Prediction of Compressive Strength of FRP Confined Concrete Using Multiphysics Genetic Expression Programming. Polymers. 2022; 14(9):1789. https://doi.org/10.3390/polym14091789
Chicago/Turabian StyleIlyas, Israr, Adeel Zafar, Muhammad Talal Afzal, Muhammad Faisal Javed, Raid Alrowais, Fadi Althoey, Abdeliazim Mustafa Mohamed, Abdullah Mohamed, and Nikolai Ivanovich Vatin. 2022. "Advanced Machine Learning Modeling Approach for Prediction of Compressive Strength of FRP Confined Concrete Using Multiphysics Genetic Expression Programming" Polymers 14, no. 9: 1789. https://doi.org/10.3390/polym14091789
APA StyleIlyas, I., Zafar, A., Afzal, M. T., Javed, M. F., Alrowais, R., Althoey, F., Mohamed, A. M., Mohamed, A., & Vatin, N. I. (2022). Advanced Machine Learning Modeling Approach for Prediction of Compressive Strength of FRP Confined Concrete Using Multiphysics Genetic Expression Programming. Polymers, 14(9), 1789. https://doi.org/10.3390/polym14091789








