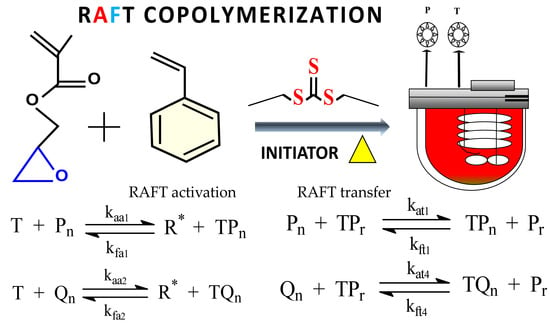
Mathematical Description of the RAFT Copolymerization of Styrene and Glycidyl Methacrylate Using the Terminal Model
Abstract
:1. Introduction
2. Experimental
2.1. Reagents
2.2. Size Exclusion Chromatography (SEC) Characterization Method
2.3. 1H-NMR Characterization Method
2.4. Copolymerization Reactions
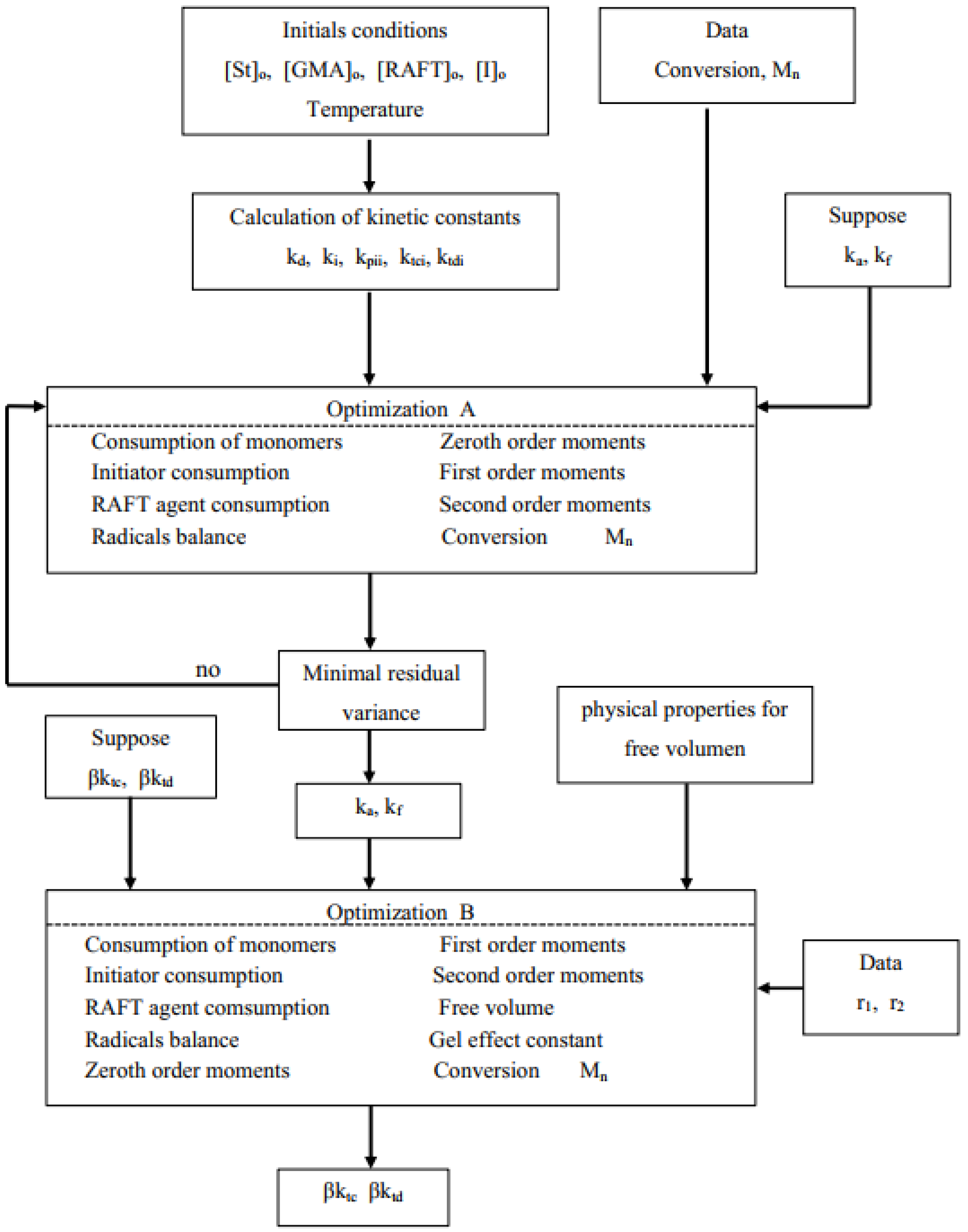
3. Model Development
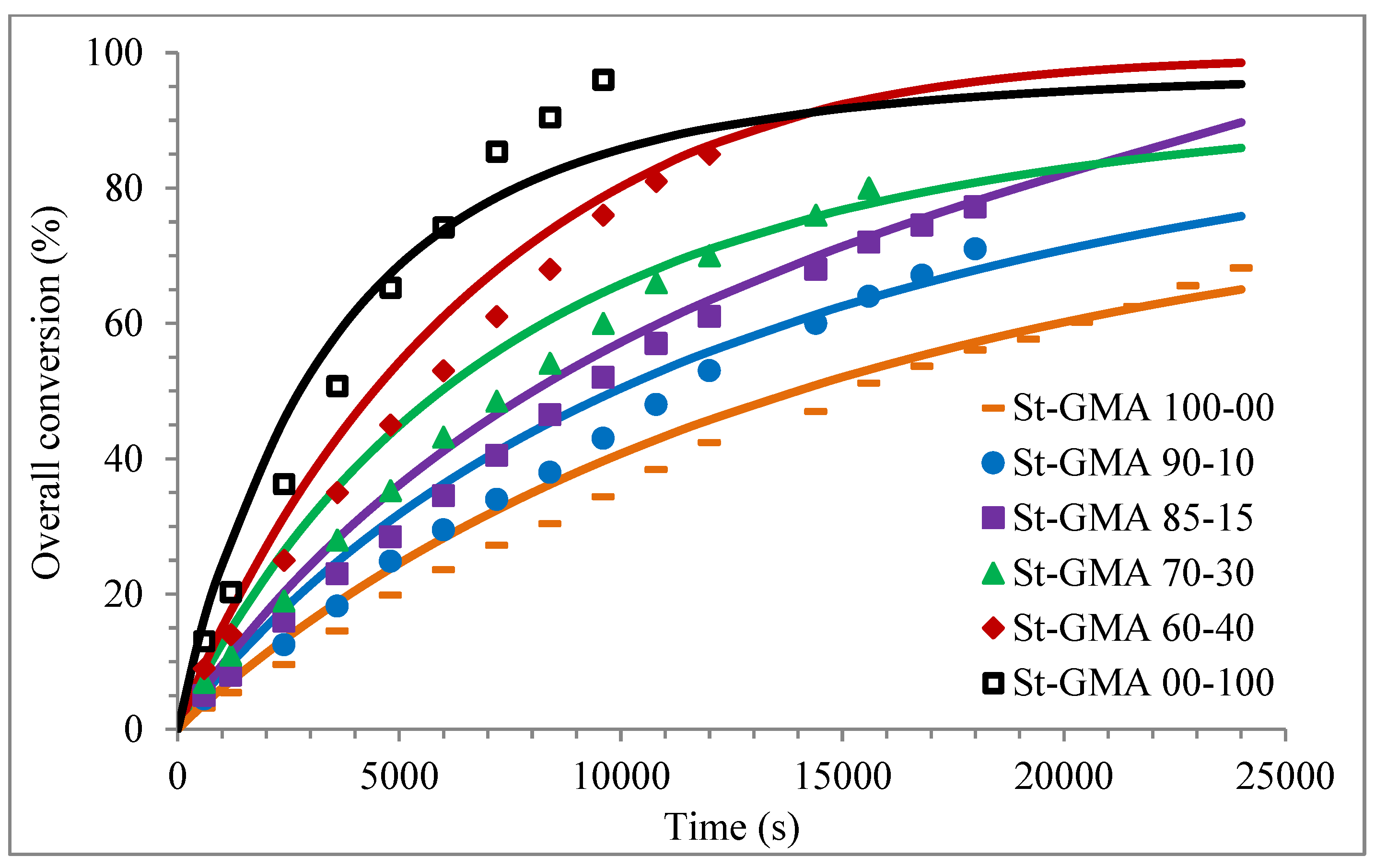
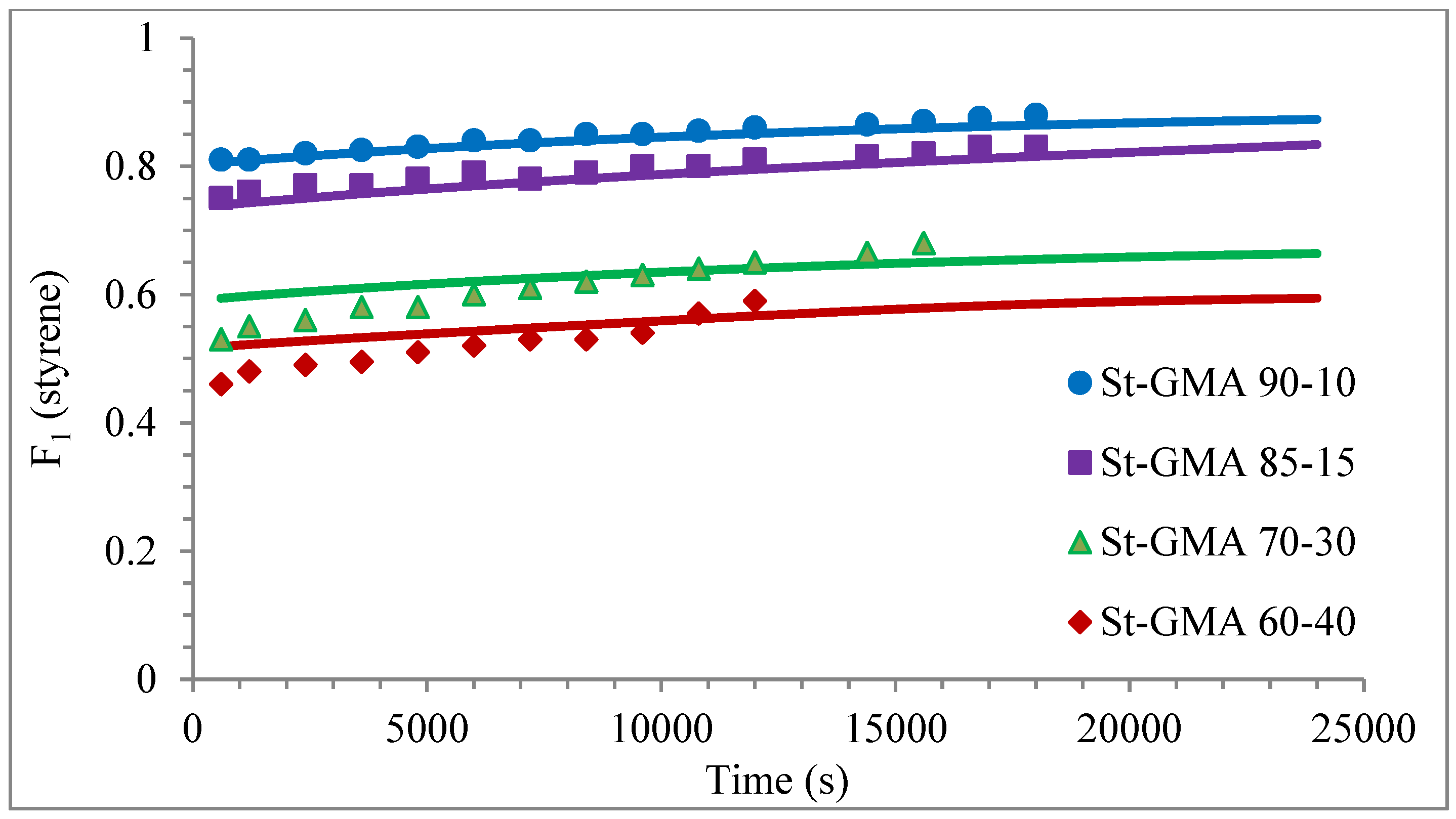
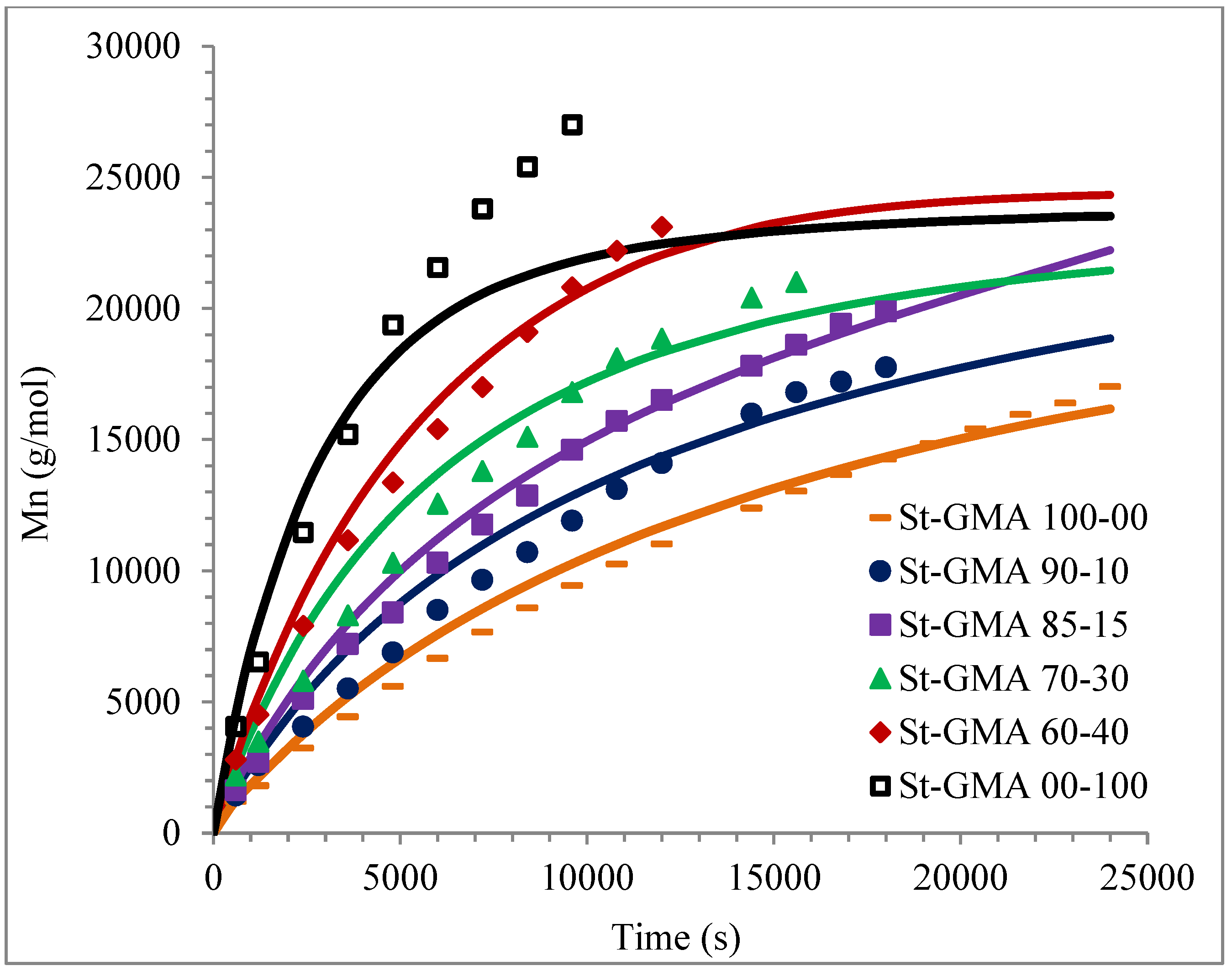
4. Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hainey, P.; Sherrington, D.C. Oligoamine-functionalised poly(glycidyl methacrylate ethyleneglycol dimethacrylate) resins as moderate base extractants for gold from cyanide solutions. React. Funct. Polym. 2000, 43, 195–210. [Google Scholar] [CrossRef]
- Zhang, H.; Ruckenstein, E. One-pot three-step synthesis of amphiphilic comb-like copolymers with hydrophilic backbone and hydrophobic side chains. Macromolecules 2000, 33, 814–819. [Google Scholar] [CrossRef]
- Martin, P.; Devaux, J.; Legras, R.; Gurp, M.V.; Duin, M.V. Competitive reactions during compatibilization of blends of polybutyleneterephthalate with epoxide-containing rubber. Polymer 2000, 42, 2463–2478. [Google Scholar] [CrossRef]
- Bondar, Y.; Kim, H.J.; Yoon, S.H.; Lim, Y.J. Synthesis of cation-exchange adsorbent for anchoring metal ions by modification of poly(glycidyl methacrylate) chains grafted onto polypropylene fabric. React. Funct. Polym. 2004, 58, 43–51. [Google Scholar] [CrossRef]
- Benvenuta-Tapia, J.J.; Tenorio-López, J.A.; Martínez-Estrada, A.; Guerrero-Sánchez, C. Application of RAFT-synthesized reactive tri-block copolymers for the recycling of post-consumer R-PET by melt processing. Mater. Chem. Phys. 2019, 229, 474–481. [Google Scholar] [CrossRef]
- Benvenuta-Tapia, J.J.; Champagne, P.; Tenorio-López, J.A.; Vivaldo-Lima, E.; Guerrero-Santos, R. Improving recycled poly(lactic acid) biopolymer properties by chain Extension using block copolymers synthesized by nitroxide-mediated polymerization (NMP). Polymers 2021, 13, 2791. [Google Scholar] [CrossRef]
- Maa, C.-T.; Chang, F.-C. In situ compatibilization of PET/PS blends through reactive copolymers. J. Appl. Polym. Sci. 1993, 49, 913–924. [Google Scholar] [CrossRef]
- Fakirov, S. (Ed.) Handbook of Thermoplastic Polyesters; Wiley-VCH: Weinheim, Germany, 2002. [Google Scholar]
- Lee, H.; An, S.; Kim, S.; Jeon, B.; Kim, M.; Kim, I.S. Readily Functionalizable and Stabilizable Polymeric Particles with Controlled Size and Morphology by Electrospray. Sci. Rep. 2018, 8, 15725. [Google Scholar] [CrossRef] [Green Version]
- Barner-Kowollik, C. Handbook of RAFT Polymerization; Wiley-VCH: Weinheim, Germany, 2008; pp. 110–122. [Google Scholar]
- Nicolas, J.; Guillaneuf, Y.; Lefay, C.; Bertin, D.; Gigmes, D.; Charleux, B. Charleux; Nitroxide-mediated polymerization. Prog. Polym. Sci. 2013, 38, 63–235. [Google Scholar] [CrossRef]
- Vivaldo-Lima, E.; Jaramillo-Soto, G.; Penlidis, A. Nitroxide-mediated polymerization (NMP). In Encyclopedia of Polymer Science and Technology, Herman; Mark, F., Ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; pp. 1–48. [Google Scholar] [CrossRef]
- Matyjaszewski, K.; Xia, J. Atom transfer radical polymerization. Chem. Rev. 2001, 101, 2921–2990. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Davis, T.P.; Heuts, J.P.A.; Stenzel, M.H.; Vana, P.; Whittaker, M. RAFTing Down under: Tales of missing radicals, fancy architectures, and mysterious holes. J. Polym. Sci. Part A Polym. Chem. 2003, 41, 365–375. [Google Scholar] [CrossRef]
- Zhu, Y.; Liu, Y.; Miller, K.A.; Zhu, H.; Egap, E. Lead Halide Perovskite Nanocrystals as Photocatalysts for PET-RAFT Polymerization under Visible and Near-Infrared Irradiation. ACS Macro Lett. 2020, 9, 725–730. [Google Scholar] [CrossRef]
- Wan, J.; Fan, B.; Liu, Y.; Hsia, T.; Qin, K.; Junkers, T.; Teo, B.M.; Thang, S.H. Room temperature synthesis of block copolymer nano-objects with different morphologies via ultrasound initiated RAFT polymerization-induced self-assembly (sono-RAFT-PISA). Polym. Chem. 2020, 11, 3564–3572. [Google Scholar] [CrossRef]
- Benvenuta-Tapia, J.J.; Tenorio-López, J.A.; Vivaldo-Lima, E. Estimation of reactivity ratios in the RAFT copolymerization of styrene and glycidyl methacrylate. Macromol. React. Eng. 2018, 12, 5. [Google Scholar] [CrossRef]
- Brar, A.S.; Kumar, A.A.; Goyal, A.K. Characterization and optimization of poly (glycidyl methacrylate-co-styrene) synthesized by atom transfer radical polymerization. Eur. Polym. J. 2008, 44, 4082–4091. [Google Scholar] [CrossRef]
- Moayeri, A.; Lessard, B.; Maric, M. Nitroxide mediated controlled synthesis of glycidyl methacrylate-rich copolymers enabled by SG1-based alkoxyamines bearing succinimidyl ester groups. Polym. Chem. 2011, 2, 2084–2092. [Google Scholar] [CrossRef]
- Stenzel-Rosenbaum, M.H.; Davis, T.P.; Fane, A.G.; Chen, V. Porous polymer films and honeycomb structures made by the self-organization of well-defined macromolecular structures created by living radical polymerization techniques. Angew. Chem. 2001, 40, 3428–3432. [Google Scholar] [CrossRef]
- Favier, A.; D’Agosto, F.; Charreyre, M.-T.; Pichot, C. Synthesis of N-acryloxysuccinimide copolymers by RAFT polymerization, as reactive building blocks with full control of composition and molecular weights. Polymer 2004, 45, 7821–7830. [Google Scholar] [CrossRef]
- Feldermann, A.; Toy, A.A.; Phan, H.; Stenzel, M.; Davis, T.; Barner-Kowollik, C. Reversible addition fragmentation chain transfer copolymerization: Influence of the RAFT process on the copolymer composition. Polymer 2004, 45, 3997–4007. [Google Scholar] [CrossRef]
- Benvenuta-Tapia, J.J.; Vivaldo-Lima, E.; Guerrero-Santos, R. Effect of copolymers synthesized by nitroxide-mediated polymerization as chain extenders of postconsumer poly (ethylene terephthalate) waste. Polym. Eng. Sci. 2019, 59, 2255–2264. [Google Scholar] [CrossRef]
- Braunecker, W.A.; Matyjaszewski, K. Controlled/living radical polymerization: Features, developments, and perspectives. Prog. Polym. Sci. 2007, 32, 93–146. [Google Scholar] [CrossRef]
- Chernikova, E.; Morozov, A.; Leonova, E.; Garina, E.; Golubev, V.; Bui, C.; Charleux, B. Controlled free-radical polymerization of n-butyl acrylate by reversible addition−fragmentation chain transfer in the presence of tert-butyl dithiobenzoate. A kinetic study. Macromolecules 2004, 37, 6329–6339. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Coote, M.L.; Davis, T.P.; Radom, L.; Vana, P. The reversible addition-fragmentation chain transfer process and the strength and limitations of modeling: Comment on “the magnitude of the fragmentation rate coefficient. J. Polym. Sci. Part A Polym. Chem. 2003, 41, 2828–2832. [Google Scholar] [CrossRef]
- Zargar, A.; Schork, F.J. Copolymer sequence distributions in controlled radical polymerization. Macromol. React. Eng. 2009, 3, 118–130. [Google Scholar] [CrossRef]
- Dixon, K.W. Decomposition rates of organic free radical initiatiors. In Polymer Handbook, 4th ed.; Brandrup, J., Immergut, E.H., Grulke, E.A., Abe, A., Bloch, D.R., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 1998; pp. II/1–II/76. ISBN 9780471166283. [Google Scholar]
- Buback, M.; Gilbert, R.G.; Hutchinson, R.A.; Klumperman, B.; Kuchta, F.-D.; Manders, B.G.; O’Driscoll, K.F.; Russell, G.T.; Schweer, J. Critically evaluated rate coefficients for free-radical polymerization, 1. Propagation rate coefficient for styrene. J. Macromol. Chem. Phys. 1995, 196, 3267–3280. [Google Scholar] [CrossRef] [Green Version]
- Wang, W.; Hutchinson, R.A. PLP/SEC/NMR study of free copolymerization of styrene and glycidyl methacrylate. Macromolecules 2008, 41, 9011–9018. [Google Scholar] [CrossRef]
- Hui, A.W.; Hamielec, A.E. Thermal polymerization of styrene at high conversions and temperatures. An experimental study. J Appl. Polym. Sci. 1972, 16, 749–769. [Google Scholar] [CrossRef]
- Beuermann, S.; Buback, M.; Schmaltz, C. Termination rate coefficients of butyl acrylate free-radical homopolymerization in supercritical CO2 and in bulk. Ind. Eng. Chem. Res. 1999, 38, 3338–3344. [Google Scholar] [CrossRef]
- Achilias, D.; Kiparissides, C. Modeling of diffusion-controlled free-radical polymerization reactions. J. Appl. Polym. Sci. 1988, 35, 1303–1323. [Google Scholar] [CrossRef]
- Fox, T.G.; Flory, P.J. Second-order transition temperatures and related properties of polystyrene. J. Appl. Phys. 1950, 21, 581–591. [Google Scholar] [CrossRef]
- Li, D.; Li, N.; Hutchinson, R.A. High-temperature free Radical copolymerization of styrene and butyl methacrylate with depropagation and penultimate kinetic effects. Macromolecules 2006, 39, 4366–4373. [Google Scholar] [CrossRef]
- Hutchinson, R.A.; Beuermann, S.; Paquet, D.A.; McMinn, J.H.; Jackson, C. Determination of free-Radical propagation rate coefficients for cycloalkyl and functional methacrylates by pulsed-laser polymerization. Macromolecules 1998, 31, 1542–1547. [Google Scholar] [CrossRef]
- Bhattacharya, D.; Hamielec, A. Bulk thermal copolymerization of styrene p-methylstyrene: Modelling diffusion-controlled termination and propagation using free-volume theory. Polymer 1986, 27, 611–618. [Google Scholar] [CrossRef]
- Dow The Materials Science Company Explore Products. Available online: https://www.dow.com (accessed on 12 October 2015).
- Soh, S.K.; Sundberg, D.C. Diffusion-controlled vinyl polymerization. I. The gel effect. J. Polym. Sci. Polym. Chem. Ed. 1982, 20, 1299–1313. [Google Scholar] [CrossRef]
- Narasimhaswamy, T.; Sumathi, S.C.; Reddy, B.S.R. 2,4,6-Tribromophenyl acrylate-co-glycidyl methacrylate polymers: Synthesis, characterization, and reactivity ratios. J. Polym. Sci. Part A Polym. Chem. 1992, 30, 2165–2172. [Google Scholar] [CrossRef]
- Dube, M.A.; Rilling, K.; Penlidis, A. A kinetic investigation of butyl acrylate polymerization. J. Appl. Polym. Sci. 1991, 43, 2137–2145. [Google Scholar] [CrossRef]
- Keramopoulos, A.; Kiparissides, C. Mathematical modeling of diffusion-controlled free-radical terpolymerization reactions. J. Appl. Polym. Sci. 2003, 88, 161–176. [Google Scholar] [CrossRef]
- Marten, F.L.; Hamielec, A.E. High conversion diffusion Controlled polymerization. ACS Symp. Ser. 1979, 104, 43–70. [Google Scholar] [CrossRef]
- Marten, F.L.; Hamielec, A.E. High conversion diffusion controlled polymerization of styrene I. J. Appl. Polym. Sci. 1982, 27, 489–505. [Google Scholar] [CrossRef]
- Vivaldo-Lima, E.; Hamielec, A.; Wood, P. Auto-acceleration effect in free radical polymerization. A Comparison of the CCS and MH models. Polym. React. Eng. 1994, 2, 17–85. [Google Scholar] [CrossRef]
- Moad, G.; Rizzardo, E.; Thang, S.H. Living radical polymerization by the RAFT process–A second update. Aust. J. Chem. 2009, 82, 1402–1472. [Google Scholar] [CrossRef]
- Chernikova, E.; Golubev, V.; Filippov, A.; Lin, C.Y.; Coote, M.L. Use of spin traps to measure the addition and fragmentation rate coefficients of small molecule RAFT-aducts radicals. Polym. Chem. 2010, 1, 1437–1440. [Google Scholar] [CrossRef]
- Perrier, S.; Takolpuckdee, P. Macromolecular design via reversible addition-fragmentation chain transfer (RAFT)/xanthates (MACIX) polymerization. J. Polym. Chem. 2005, 43, 5347–5393. [Google Scholar] [CrossRef]
- De Rybel, N.; Van Steenberge, P.H.M.; Reyniers, M.-F.; Barner-Kowollik, C.; D’Hooge, D.R.; Marin, G.B. An update on the pivotal role of kinetic modeling for the mechanistic understanding and design of bulk and RAFT polymerization. Macromol. Theory Simul. 2017, 26, 1. [Google Scholar] [CrossRef]
- Zapata-González, I.; Saldívar-Guerra, E.; Ortiz-Cisneros, J. Full molecular in RAFT polymerization. New mechanistic insight by direct integration of the equations. Macromol. Theory Simul. 2011, 20, 370–388. [Google Scholar] [CrossRef]
- Zapata-González, I.; Saldívar-Guerra, E.; Licea-Claverie, A. A kinetic modeling of RAFT polymerization via dithiobenzoate agents considering the missing step. Theory. Chem. Eng. J. 2017, 326, 1242–1254. [Google Scholar] [CrossRef]
- Fortunatti, C.; Sarmonia, C.; Brandolin, A.; Asteasuain, M. Modeling of RAFT polymerization using probability generating functions. Detailed prediction of full molecular weigth distributions and sensitivity analysis. Macromol. React. Eng. 2014, 8, 781–795. [Google Scholar] [CrossRef]
- Mayo, F.R.; Lewis, F.M. Copolymerization. I. A Basis for comparing the behavior of monomers in copolymerization; the copolymerization of styrene and methyl Methacrylate. J. Am. Chem. Soc. 1944, 66, 1594–1601. [Google Scholar] [CrossRef]
- Meeter, D.A.; Wolfe, P.J. UWHAUS Nonlinear Least Squares Fitting and Function Minimization; University of Wisconsin Computing Center: Madison, WI, USA, 1965. [Google Scholar]
- Breman, K.E.; Campbell, S.L.; Petzold, L.R. Numerical Solution of Initial-Value Problems in Differential-Algebraic Equations; Elsevier Science Publishing Company: New York, NY, USA, 1989. [Google Scholar]
- Bitsch, B.; Barner-Kowollik, C.; Zhu, S. Modeling the effects of reactor backmixing on RAFT polymerization. Macromol. React. Eng. 2011, 5, 55–68. [Google Scholar] [CrossRef]
- Wang, A.R.; Zhu, S. Modeling the reversible addition-fragmentation transfer polymerization process. J. Polym. Sci. Part A Polym. Chem. 2003, 41, 1553–1566. [Google Scholar] [CrossRef]
- Gao, X.; Zhu, S. Modeling analysis of chain transfer in reversible addition-fragmentation chain transfer polymerization. J. Appl. Polym. Sci. 2011, 12, 497–508. [Google Scholar] [CrossRef]
- Sun, X.; Luo, Y.; Wang, R.; Li, B.-G.; Liu, A.B.; Zhu, S. Programmed synthesis of composition with controlled chain Composition distribution via semibatch RAFT copolymerization. Macromolecules 2007, 40, 849–859. [Google Scholar] [CrossRef]
- Jiang, J.; Wang, W.-J.; Li, B.-G.; Zhu, S. Modeling and experimentation of RAFT solution copolymerization of styrene and butyl acrylate effect of chain transfer reaction on polymer molecular weight distribution. Macromol. React. Eng. 2017, 11, 6. [Google Scholar] [CrossRef]
- Wang, R.; Luo, Y.; Li, B.; Sun, X.; Zhu, S. Design and control of copolymer composition distribution in living radical polymerization using semi-batch feeding police: A model simulation. Macromol. Theory Simul. 2006, 15, 356–368. [Google Scholar] [CrossRef]
- Pallares, J.; Jaramillo-Soto, G.; Flores-Cataño, C.; Vivaldo-Lima, E.; Lona, L.M.F.; Penlidis, A. A comparison of reaction mechanisms for reversible addition-fragmentation chain transfer polymerization using modeling tools. J. Macromol. Sci. Part A Pure Appl. Chem. 2006, 43, 1293–1322. [Google Scholar] [CrossRef]
- Moad, G.; Chiefari, J.; Chong, Y.K.; Krstina, J.; Mayadunne, R.T.A.; Postma, A.; Thang, S.H. Living free radical polymerization with reversible addition–Fragmentation chain transfer (the life of RAFT). Polym. Int. 2000, 49, 993–1001. [Google Scholar] [CrossRef]
- Kwak, Y.; Goto, A.; Tsujii, Y.; Murata, Y.; Komatsu, K.; Fukuda, T. A kinetic study on the rate retardation in radical polymerization of styrene with addition−fragmentation chain transfer. Macromolecules 2002, 35, 3026–3029. [Google Scholar] [CrossRef]
- Kwak, Y.; Goto, A.; Fukuda, T. Rate retardation in reversible addition−Fragmentation chain transfer (RAFT) polymerization: Further evidence for cross-termination producing 3-arm star chain. Macromolecules 2004, 37, 1219–1225. [Google Scholar] [CrossRef]
- Barner-Kowollik, C.; Quinn, J.; Morsley, D.R.; Davis, T.P. Modeling the reversible addition–Fragmentation chain transfer process in cumyl dithiobenzoate-mediated styrene homopolymerizations: Assessing rate coefficients for the addition–fragmentation equilibrium. J. Polym. Sci. Polym. Chem. 2001, 39, 1353–1365. [Google Scholar] [CrossRef]
- Feldermann, A.; Coote, M.L.; Stenzel, M.H.; Davis, T.P.; Barner-Kowollik, C. Consistent experimental and theoretical evidence for long-lived intermediate radicals in living free radical polymerization. J. Am. Chem. Soc. 2004, 126, 15915–15923. [Google Scholar] [CrossRef]
- Wang, A.R.; Zhu, S.; Kwak, Y.; Goto, A.; Fukuda, T.; Monteiro, M.S. A difference of six orders of magnitude: A reply to “the magnitude of the fragmentation rate coefficient”. J. Polym. Sci. Part A Polym. Chem. 2003, 41, 2833–2839. [Google Scholar] [CrossRef]
- Wang, A.R.; Zhu, S. Effects of diffusion-controlled radical reactions on RAFT polymerization. Macromol. Theory Simul. 2003, 12, 196–208. [Google Scholar] [CrossRef]
- Bellotti, V.; Simonutti, R. New Light in Polymer Science: Photoinduced Reversible Addition-Fragmentation Chain Transfer Polymerization (PET-RAFT) as Innovative Strategy for the Synthesis of Advanced Materials. Polymers 2021, 13, 1119. [Google Scholar] [CrossRef] [PubMed]
- Doerr, A.M.; Burroughs, J.M.; Gitter, S.R.; Yang, X.; Boydston, A.J.; Long, B.K. Advances in Polymerizations Modulated by External Stimuli. ACS Catal. 2020, 10, 14457–14515. [Google Scholar] [CrossRef]
- Zhu, Y.; Egap, E. Light-Mediated Polymerization Induced by Semiconducting Nanomaterials: State-of-the-Art and Future Perspectives. ACS Polym. Au 2021, 1, 76–99. [Google Scholar] [CrossRef]
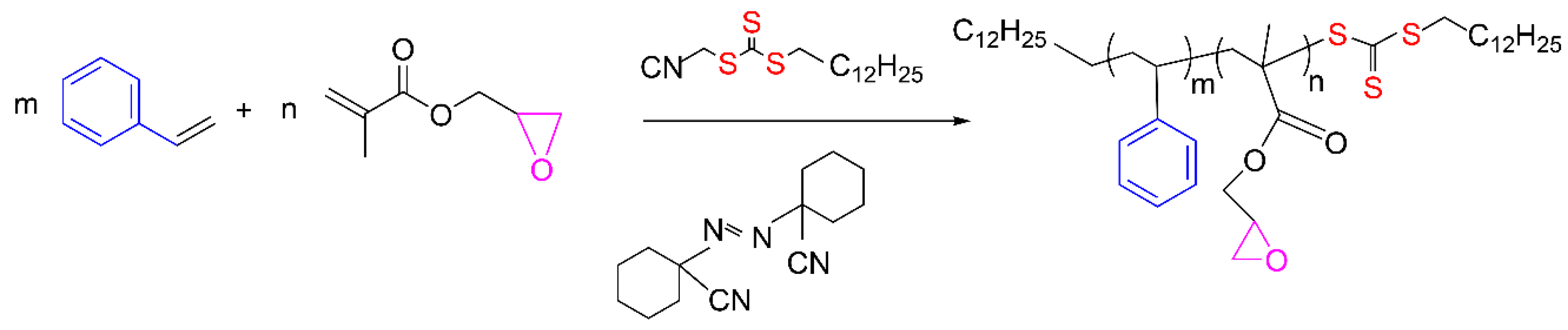






| Initiation | Propagation |
|---|---|
| I 2 | |
| + A P1 Pn + A Pn+1 Qn + A Pn+1 | |
| + B Q1 Pn + B Qn+1 Qn + B Qn+1 | |
| RAFT activation T + R• + TPn T + Qn R• + TQn | RAFT transfer Pn + TPr TPn + Pr Pn + TQr TPn + Qr Qn + TQr TQn + Qr Qn + TPr TQn + Pr |
| Termination | |
| Pn + Pr Mn+r Pn + Pr Mn + Mr | |
| Qn + Qr Mn+r Qn + Qr Mn + Mr | |
| Pn + Qr Mn+r Pn + Qr Mn + Mr | |
| = [Pn] = [TPn] = [Mn] |
| = [Qn] = [TQn] i = 0, 1, 2 |
| = −ki1[ ][A] − kp11[A][ ] − kp21[A][ ] St monomer | (1) |
| = −ki2[ ][B] − kp12[B][ ] − kp22[B][ ] GMA monomer | (2) |
| = −kd[I] initiator | (3) |
| = 2kdf[I] − ki1[A][ R•] − ki2[B][ ] − kfa1[ ][ ] + kaa1[ ][T] − kfa2[ ][R*] + kaa2[ ][T] | (4) |
| = kfa2[ ][ ] − kaa2[T][ ] + kfa1[ ][ ] − kaa1[T][ ] RAFT agent | (5) |
| = ki1[ ][A] + kfa1[ ][TPn] − kaa1[T][Pn] − kat3[ ] [Pn] + kft3[ ][TPn] + kft1[ ][TPn] − kat1[ ][Pn] − kp11[A][Pn] − kp12[B][Pn] + kp11[A][Pn−1] + kp21[A][Qn−1] − ktc3[ ][Pn] −ktd3[ ][Pn] − ktc1[ ][Pn] − ktd1[ ][Pn] | (6) |
| = ki2[ ][B] + kfa2[R*][TQn] − kaa2[T][Qn] – kat4[ ][Qn] + kft4[ ][TQn] + kft2[ ][TQn] − kat2[ ][Qn] − kp21[A][Qn] − kp22[B][Qn] + kp12[B][Pn−1] + kp22[B][Qn−1] − ktc3[ ][Qn] − ktd3[ ][Qn] − ktc2[ ][Qn] − ktd2[ ][Qn] | (7) |
| = −kfa1[ ][TPn] + kaa1[T][Pn] + kat3[ ][Pn] – kft3[ ][TPn] + kat1[ ][Pn] − kft1[ ][TPn] | (8) |
| = −kfa2[ ][TQn] + kaa2[T][Qn] − kft2[ ][TQn] + kat2[ ][Qn] + kat4[ ][Qn] − kft4[ ][TQn] | (9) |
| = ktc3 + ktc1 + ktc2 + ktd3[ ][Pn] + ktd1[ ][Pn] + ktd2[ ][Qn] + ktd3[ ][Qn] | (10) |
| Zeroth-order moments | |
| = ki1[][A] + kfa1[][] − kaa1[T][] − kat3[][] + kft3[][] + kft1[][] − kat1[][] − kp11[A][] − kp12[B][] + kp11[A][] + kp21[A][] − ktc3[][] − ktd3[][] − ktc1[][] − ktd1[][] | (11) |
| = ki2[][B] + kfa2[][] − kaa2[T][] − kat4[][] + kft4[][] + kft2[][] − kat2[][] − kp21[A][] − kp22[B][] + kp12[B][] + kp22[B][] − ktc3[][] − ktd3[][] − ktc2[][] − ktd2[][] | (12) |
| = −kfa1[][] + kaa1[T][] + kat3[][] − kft3[][] + kat1[][] − kft1[][] | (13) |
| = −kfa2[][] + kaa2[T][] − kft2[][] + kat2[]] + kat4[][] − kft4[][] | (14) |
| ] | (15) |
| First-order moments | |
| = ki1[][A] + kfa1[][] − kaa1[T][] − kat3[][] + kft3[][] + kft1[][] − kat1[]] − kp11[A][] − kp12[B][] + kp11[A][ + ] + kp21[A][ + ] − ktc3[][] − ktd3[][] − ktc1[][] − ktd1[][] | (16) |
| = ki2[][B] + kfa2[][] − kaa2[T][] − kat4[][] + kft4[][] + kft2[][] − kat2[][] − kp21[A][] − kp22[B][] + kp12[B][ + ] + kp22[B][ + ] − ktc3[][] − ktd3[][] − ktc2[][] − ktd2[][] | (17) |
| = −kfa1[][] + kaa1[T][] + kat3[][] − kft3[][] + kat1[][] − kft1[][] | (18) |
| = −kfa2[][] + kaa2[T][] − kft2[][] + kat2[][] + kat4[][]− kft4[][] | (19) |
| ] | (20) |
| Second-order moments | |
| = ki1[][A] + kfa1[][] − kaa1[T][] − kat3[][] + kft3[][] + kft1[][] − kat1[][] − kp11[A][] − kp12[B][] + kp11[A][ + 2 + ] + kp21[A][ + 2 + ] − ktc3[][] − ktd3[][] − ktc1[][] − ktd1[][] | (21) |
| = ki2[][B] + kfa2[][] − kaa2[T][] − kat4[][] + kft4[][] + kft2[][] − kat2[][] − kp21[A][] − kp22[B][] + kp12[B][ + 2 + ] + kp22[B][ + 2 + ] − ktc3[][] − ktd3[][] − ktc2[][] − ktd2[][] | (22) |
| = −kfa1[][] + kaa1[T][] + kat3[][] − kft3[][] + kat1[][] − kft1[][ | (23) |
| = −kfa2[][] + kaa2[T][] − kft2[][] + kat2[][] + kat4[][] − kft4[][] | (24) |
| ] | (25) |
| PM1 = 104.15 gmol−1 | |
| PM2 = 142.20 gmol−1 | |
| kd (s−1) = 2.2798 × 1019 exp(−166.9 kJmol−1/RT) initiator | [28] |
| f = 0.60 | |
| kp11 (L mol−1 s−1) = 4.266 × 107 exp(−3909.61/T) St | [29] |
| kp22 (L mol−1 s−1) = 5.100 × 106 exp(−2754/T) GMA | [30] |
| ki1 (L mol−1 s−1) = kp11 | |
| ki2 (L mol−1 s−1) = kp22 | |
| r1 (kp11/kp12) = 0.3724 | [19] |
| r2 (kp22/kp21) = 0.6834 | [19] |
| ktc1 (L mol−1 s−1) = 2.0 × 1010 exp(−1553.01/T) St | [31] |
| ktc2 (L mol−1 s−1) = 2.57 × 108 exp(−292.0/T) (a) GMA | [32] |
| ktd = ktc |
| (g mL−1) = 0.9193 − 0.000665 T/°C | [35] |
| (g mL−1) = 1.09428 − 0.001041 T/°C | [36] |
| (g mL−1) = 1.09926 − 2.65 × 10−4 T/°C | [35] |
| (g mL−1) = 1.08 | This work |
| (K) = 156.15 | [37] |
| (K) = 348.15 | [38] |
| (K) = 373.15 | [39] |
| (K) = 347.0 | [40] |
| (K−1) = 0.00062 | [41] |
| (K−1) = 0.0004 | This work |
| (K−1) = 0.00045 | [39] |
| (K−1) = 0.00048 (a) | [41] |
| (K−1) = F1 + F2 | [42] |
| St homopolymerization | ||||
| RAFT activation | kaa1 = kfa1 | RAFT transfer | kat1 = kft1 | kaa1 = kat1 |
| GMA homopolymerization | ||||
| RAFT activation | kaa2 = kfa2 | RAFT transfer | kat2 = kft2 | kaa2 = kat2 |
| Copolymer Identifier | Styrene [St]o | GMA [GMA]o | RAFT [CPDT]o | Initiator [ACHN]o | R3:R2:R1 |
|---|---|---|---|---|---|
| (mol L−1) | (mol L−1) | (mol L−1) | (mol L−1) | ||
| St-GMA 100-00 | 8.6445 | – | 0.0297 | 0.0074 | 291:4:1 |
| St-GMA 90-10 | 7.6091 | 0.8455 | 0.0304 | 0.0076 | 278:4:1 |
| St-GMA 85-15 | 7.1370 | 1.2595 | 0.0307 | 0.0077 | 273:4:1 |
| St-GMA 70-30 | 5.7546 | 2.4662 | 0.0316 | 0.0079 | 260:4:1 |
| St-GMA 60-40 | 4.8669 | 3.2446 | 0.0322 | 0.0080 | 251:4:1 |
| St-GMA 00-100 | – | 7.5949 | 0.0360 | 0.0090 | 211:4:1 |
| RAFT activation, L mol−1 s−1 | |
| kfa1 = 101,113 ± 2690 | kaa1 = 101,113 ± 2690 |
| kfa2 = 484,000 ± 1200 | kaa2 = 484,000 ± 1200 |
| RAFT transfer, L mol−1 s−1 | |
| kft1 = 101,113 ± 2690 | kat1 = 101,113 ± 2690 |
| kft2 = 484,000 ± 1200 | kat2 = 484,000 ± 1200 |
| kft3 = 271,517 ± 7223 | kat3 = 708,224 ± 1756 |
| kft4 = 708,224 ± 1756 | kat4 = 271,517 ± 7223 |
| Sample | St-GMA | |||||
|---|---|---|---|---|---|---|
| 100-00 | 90-10 | 85-15 | 70-30 | 60-40 | 00-100 | |
| βktc = βktd | 0.3836 ± 0.0023 | 0.3581 ± 0.0214 | 0.3979 ± 0.0001 | 0.23045 ± 5 × 10−5 | 0.2925 ± 5 × 10−5 | 0.00081 ± 7 × 10−7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tenorio-López, J.A.; Benvenuta-Tapia, J.J.; García-Navarro, N.; Vivaldo-Lima, E.; Champagne, P.; Saldívar-Guerra, E. Mathematical Description of the RAFT Copolymerization of Styrene and Glycidyl Methacrylate Using the Terminal Model. Polymers 2022, 14, 1448. https://doi.org/10.3390/polym14071448
Tenorio-López JA, Benvenuta-Tapia JJ, García-Navarro N, Vivaldo-Lima E, Champagne P, Saldívar-Guerra E. Mathematical Description of the RAFT Copolymerization of Styrene and Glycidyl Methacrylate Using the Terminal Model. Polymers. 2022; 14(7):1448. https://doi.org/10.3390/polym14071448
Chicago/Turabian StyleTenorio-López, José Alfredo, Juan José Benvenuta-Tapia, Norma García-Navarro, Eduardo Vivaldo-Lima, Pascale Champagne, and Enrique Saldívar-Guerra. 2022. "Mathematical Description of the RAFT Copolymerization of Styrene and Glycidyl Methacrylate Using the Terminal Model" Polymers 14, no. 7: 1448. https://doi.org/10.3390/polym14071448
APA StyleTenorio-López, J. A., Benvenuta-Tapia, J. J., García-Navarro, N., Vivaldo-Lima, E., Champagne, P., & Saldívar-Guerra, E. (2022). Mathematical Description of the RAFT Copolymerization of Styrene and Glycidyl Methacrylate Using the Terminal Model. Polymers, 14(7), 1448. https://doi.org/10.3390/polym14071448