A Density-Dependent Modified Doraivelu Model for the Cold Compaction of Poly (Ether Ketone Ketone) Powders
Abstract
:1. Introduction
2. Establishing the Constitutive Model of PEKK Powders
2.1. PEKK Powder Performance
2.2. Modified Doraivelu Constitutive Model
2.3. Numerical Implementation of Stress-Integration Algorithm
3. Experiment and Simulation
3.1. Experimental Method
3.2. Cold-Compaction Simulation
4. Results and Discussion
4.1. Parameter Identification
4.2. Verification of Modified Doraivelu Model
4.3. Influence of Initial Density on the Prediction Accuracy of the Model
5. Conclusions
- (1)
- The modified Doraivelu model based on PEKK powder was developed by introducing the material parameters m and n. A substepping method for the constitutive model was developed using UMAT in ABAQUS/Standard and applied to the finite-element model.
- (2)
- Through experiments and numerical calculations, it was determined that when m = 0, n = 4 and the initial relative density was 0.4485, the error was the smallest and the prediction accuracy was the highest. Therefore, the modified model can accurately describe the change law of density during cold compaction.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mehr, F.R.; Salavati, M.; Morgenthal, A.; Kamrani, S.; Fleck, C. Computational analysis and experimental calibration of cold isostatic compaction of Mg-SiC nanocomposite powders. Mater. Today Commun. 2021, 27, 102321. [Google Scholar] [CrossRef]
- Olsson, E.; Larsson, P.L. A numerical analysis of cold powder compaction based on micromechanical experiments. Powder Technol. 2013, 243, 71–78. [Google Scholar] [CrossRef] [Green Version]
- Güner, F.; Ömer, N.C.; Sofuoğlu, H. Numerical modeling of cold powder compaction using multi particle and continuum media approaches. Powder Technol. 2015, 271, 238–247. [Google Scholar] [CrossRef]
- Parilak, L.; Dudrova, E.; Bidulsky, R.; Kabatova, M. Derivation, testing and application of a practical compaction equation for cold die-compacted metal powders. Powder Technol. 2017, 322, 447–460. [Google Scholar] [CrossRef]
- Stupkiewicz, S.; Piccolroaz, A.; Bigoni, D. Elastoplastic coupling to model cold ceramic powder compaction. J. Eur. Ceram. Soc. 2014, 34, 2839–2848. [Google Scholar] [CrossRef] [Green Version]
- Han, L.H.; Elliott, J.; Best, S.M.; Cameron, R.; Bentham, A.C.; Mills, A.; Amidon, G.E.; Hancock, B.C. Numerical Simulation on Pharmaceutical Powder Compaction. Mater. Sci. Forum. 2008, 575–578, 560–565. [Google Scholar] [CrossRef]
- Hu, G.; Zhou, B.; Fu, R.; Guo, Y.; Han, C.; Lv, K. Discrete element modeling of the compression molding of polymer–crystal composite particles. Powder Technol. 2021, 390, 112–125. [Google Scholar] [CrossRef]
- Es-Saheb, M.H.H. The Cold Compaction of Polyvinyl Chloride (PVC) Powders. J. King Saud Univ.-Eng. Sci. 1994, 6, 99–112. [Google Scholar] [CrossRef]
- Crawford, R.J.; Sprevak, D. Cold compaction of polymeric powders in tapered dies. Eur. Polym. J. 1984, 20, 441–446. [Google Scholar] [CrossRef]
- Kupkova, M. Modification of the Density-Pressure Relationship due to the Internal Friction and Cohesion of a Powder Mass Undergoing Closed Die Compaction. Key Eng. Mater. 2009, 409, 334–337. [Google Scholar] [CrossRef]
- Kang, C.S.; Lee, S.C.; Kim, K.T.; Rozenberget, O. Densification Behavior of Iron Powder during Cold Stepped Compaction. Mater. Sci. Forum 2007, 534–536, 257–260. [Google Scholar] [CrossRef]
- Xu, Y.; Musser, J.; Li, T.; Padding, J.T.; Rogers, W.A. Particles climbing along a vertically vibrating tube: Numerical simulation using the Discrete Element Method (DEM). Powder Technol. 2017, 320, 304–312. [Google Scholar] [CrossRef]
- Song, Y. Modeling and Numerical Simulation of Fe-Based Powder Forming in Thermal-Electrical-Mechanical Coupled Fields; South China University of Technology: Guangzhou, China, 2011. [Google Scholar]
- Heckel, R.W. Density-pressure relationships in powder compaction. Trans. Metall. Soc. AIME 1961, 221, 671–675. [Google Scholar]
- Harthong, B.; Jérier, J.F.; Richefeu, V.; Chareyre, B.; Dorémus, P.; Imbault, D.; Donzé, F.V. Contact impingement in packings of elastic–plastic spheres, application to powder compaction. Int. J. Mech. Sci. 2012, 61, 32–43. [Google Scholar] [CrossRef]
- Jerier, J.F.; Hathong, B.; Richefeu, V.; Chareyre, B.; Imbault, D.; Donze, F.V.; Doremus, P. Study of cold powder compaction by using the discrete element method. Powder Technol. 2011, 208, 537–541. [Google Scholar] [CrossRef]
- Kim, G.T.; Kim, J.S. Stage 1 Compaction Behavior of Tool Steel under Die Pressing; John Wiley & Sons: New York, NY, USA, 1997. [Google Scholar]
- Simo, J.C.; Ju, J.W.; Pister, K.S.; Taylor, R.L. Assessment of Cap Model: Consistent Return Algorithms and Rate-Dependent Extension. J. Eng. Mech. 1988, 114, 191–218. [Google Scholar] [CrossRef]
- Zhou, M.; Huang, S.; Hu, J.; Lei, Y.; Xiao, Y.; Li, B.; Yan, S.; Zou, F. A density-dependent modified Drucker-Prager Cap model for die compaction of Ag57.6-Cu22.4-Sn10-In10 mixed metal powders. Powder Technol. 2017, 305, 183–196. [Google Scholar] [CrossRef]
- Oyane, M.; Shima, S.; Tabata, T. Consideration of basic equations, and their application, in the forming of metal powders and porous metals. J. Mech. Work. Technol. 1978, 1, 325–341. [Google Scholar] [CrossRef]
- Gurson, A.L. Continuum Theory of Ductile Rupture by Void Nucleation and Growth: Part I—Yield Criteria and Flow Rules for Porous Ductile Media. J. Eng. Mater.-Technol. 1977, 99, 297–300. [Google Scholar] [CrossRef]
- Doraivelu, S.M.; Gegel, H.L.; Gunasekera, J.S.; Malas, J.C.; Morgan, J.T. A new yield function for compressible PM materials. Int. J. Mech. Sci. 1984, 26, 527–535. [Google Scholar] [CrossRef]
- Huang, C.M.; Chen, P.Q.; Shao, M.; Li, Y.Y. Numerical simulation in powder compaction of metallurgy component. Trans. Nonferrous Met. Soc. 2006, 6, 111–115. [Google Scholar] [CrossRef]
- Tszeng, T.C.; Wu, W.T. A study of the coefficients in yield functions modeling metal powder deformation. Acta Mater. 1996, 44, 3543–3552. [Google Scholar] [CrossRef]
- Kim, H.S.; Estrin, Y.; Gutmanas, E.Y. A constitutive model for densification of metal compacts: The case of copper. Mat. Sci. Eng. R 2001, 307, 67–73. [Google Scholar] [CrossRef]
- Pérez-Martín, H.; Mackenzie, P.; Baidak, A.; Brádaigh, C.M.Ó.; Ray, D. Crystallinity studies of PEKK and carbon fibre/PEKK composites: A review. Compos. Part B 2021, 223, 109127. [Google Scholar] [CrossRef]
- Pedoto, G.; Grandidier, J.C.; Gigliotti, M.; Vinet, A. Characterization and modelling of the PEKK thermomechanical and creep behavior above the glass transition temperature. Mech. Mater. 2021, 166, 104189. [Google Scholar] [CrossRef]
- OXPEKK® IG300 physical property table. Available online: https://www.soliao.com/item/69055-oxpekkig300.html (accessed on 13 February 2022).
- Zhdanovich, G.M.; Sidorov, V.A.; Yakubovskii, C.A. Distribution of pressure and density in powder compacts of complex configuration. Sov. Powder Metall. Met. Ceram. 1982, 21, 369–372. [Google Scholar] [CrossRef]
- Wang, J.; Li, C. Modelling of metal powder compacting process. Met. Mach. 1996, 31, 3. [Google Scholar]
- Song, Y.; Li, Y.; Zhou, Z.; Zheng, Z.; Chen, P. Improved model and 3D simulation of densification process for iron powder. Chin. J. Nonferrous Met. 2010, 20, 1470–1475. [Google Scholar] [CrossRef]
- Liao, D.; Yang, Z.X.; Xu, T.T. J2-deformation-type soil model coupled with state-dependent dilatancy and fabric evolution: Multiaxial formulation and FEM implementation. Comput. Geotech. 2021, 129, 103674. [Google Scholar] [CrossRef]
- Sloan, S.W. Substepping schemes for the numerical integration of elastoplastic stress-strain relations. Int. J. Numer. Meth. Eng. 1987, 24, 893–911. [Google Scholar] [CrossRef]
- Potts, D.M.; Gens, A. A critical assessment of methods of correcting for drift from the yield surface in elasto-plastic finite element analysis. Int. J. Numer. Anal. Met. 1985, 9, 149–159. [Google Scholar] [CrossRef]





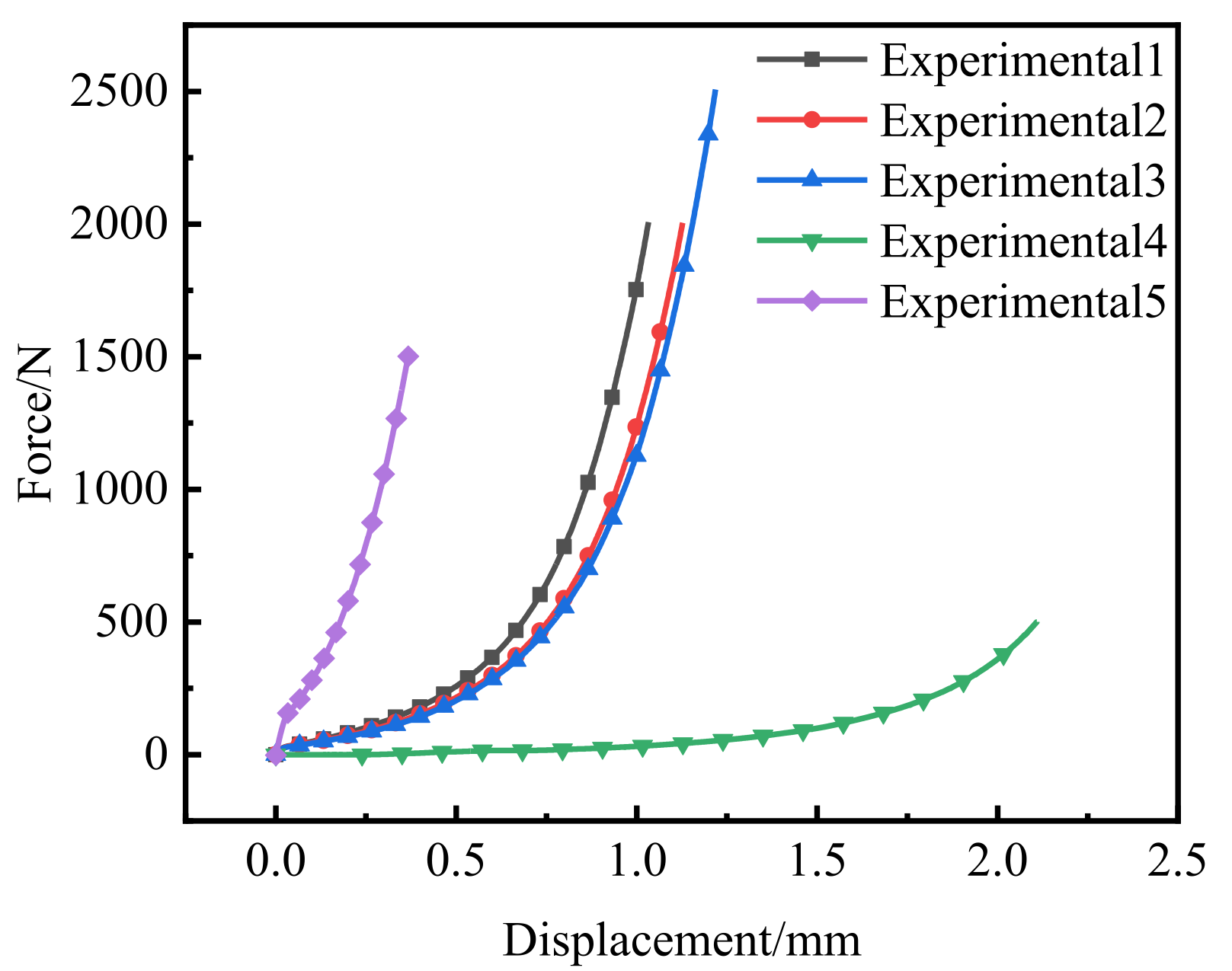

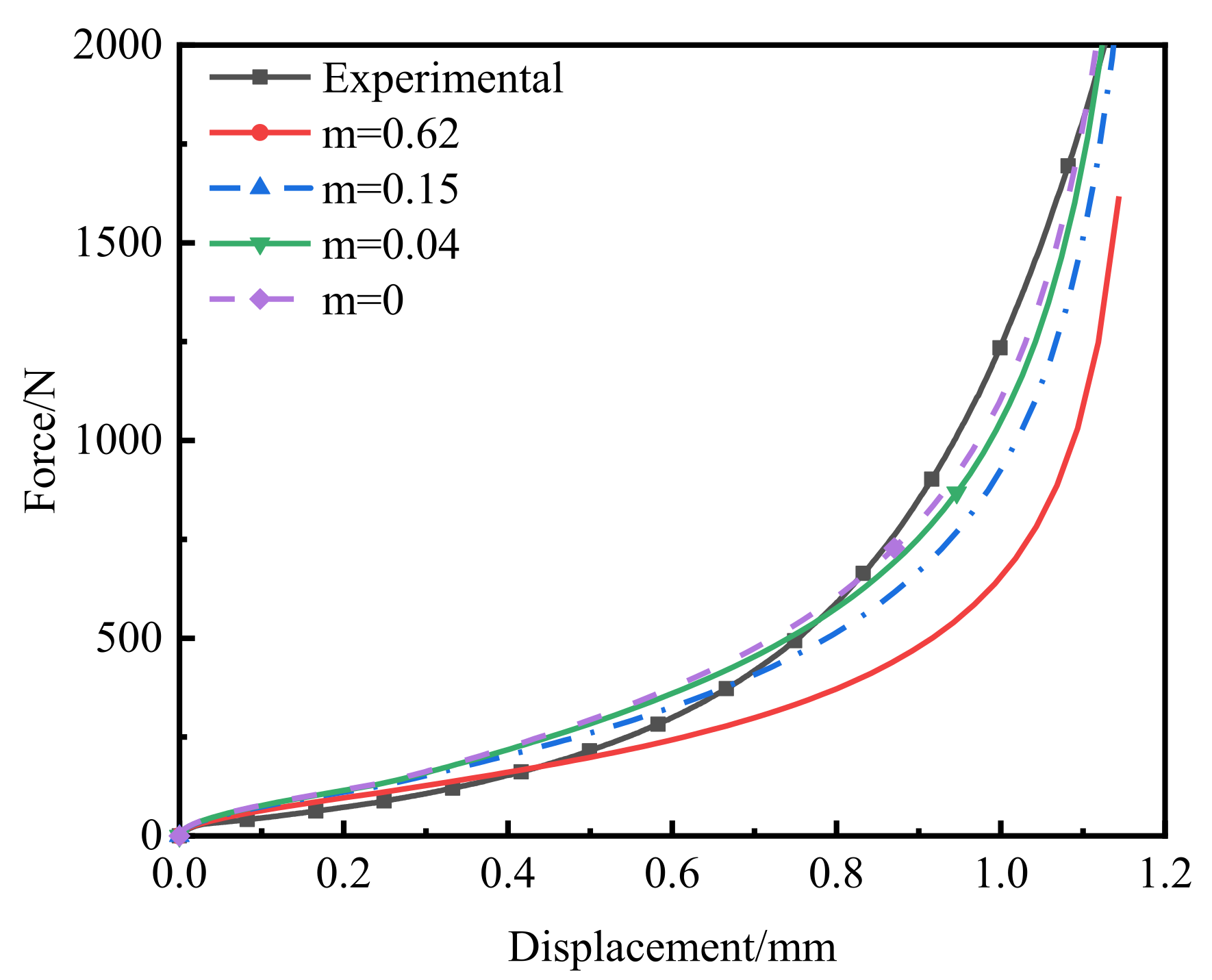


| Num. | Quality/mg | Initial Relative Density | Density | Compaction Terminal Force/N |
|---|---|---|---|---|
| 1 | 5.44 | 0.4352 | 0.9415 | 2000 |
| 2 | 6.22 | 0.4485 | 0.9719 | 2000 |
| 3 | 6.37 | 0.4377 | 0.9837 | 2500 |
| 4 | 5.56 | 0.2558 | 0.7165 | 500 |
| 5 | 5.38 | 0.6767 | 0.9667 | 1500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, F.; Wang, H.; Wu, X.; Ye, Z.; Liu, H. A Density-Dependent Modified Doraivelu Model for the Cold Compaction of Poly (Ether Ketone Ketone) Powders. Polymers 2022, 14, 1270. https://doi.org/10.3390/polym14061270
Xu F, Wang H, Wu X, Ye Z, Liu H. A Density-Dependent Modified Doraivelu Model for the Cold Compaction of Poly (Ether Ketone Ketone) Powders. Polymers. 2022; 14(6):1270. https://doi.org/10.3390/polym14061270
Chicago/Turabian StyleXu, Fan, Huixiong Wang, Xuelian Wu, Zihao Ye, and Hong Liu. 2022. "A Density-Dependent Modified Doraivelu Model for the Cold Compaction of Poly (Ether Ketone Ketone) Powders" Polymers 14, no. 6: 1270. https://doi.org/10.3390/polym14061270
APA StyleXu, F., Wang, H., Wu, X., Ye, Z., & Liu, H. (2022). A Density-Dependent Modified Doraivelu Model for the Cold Compaction of Poly (Ether Ketone Ketone) Powders. Polymers, 14(6), 1270. https://doi.org/10.3390/polym14061270






