Variable Offset Computation Space for Automatic Cooling Dimensioning
Abstract
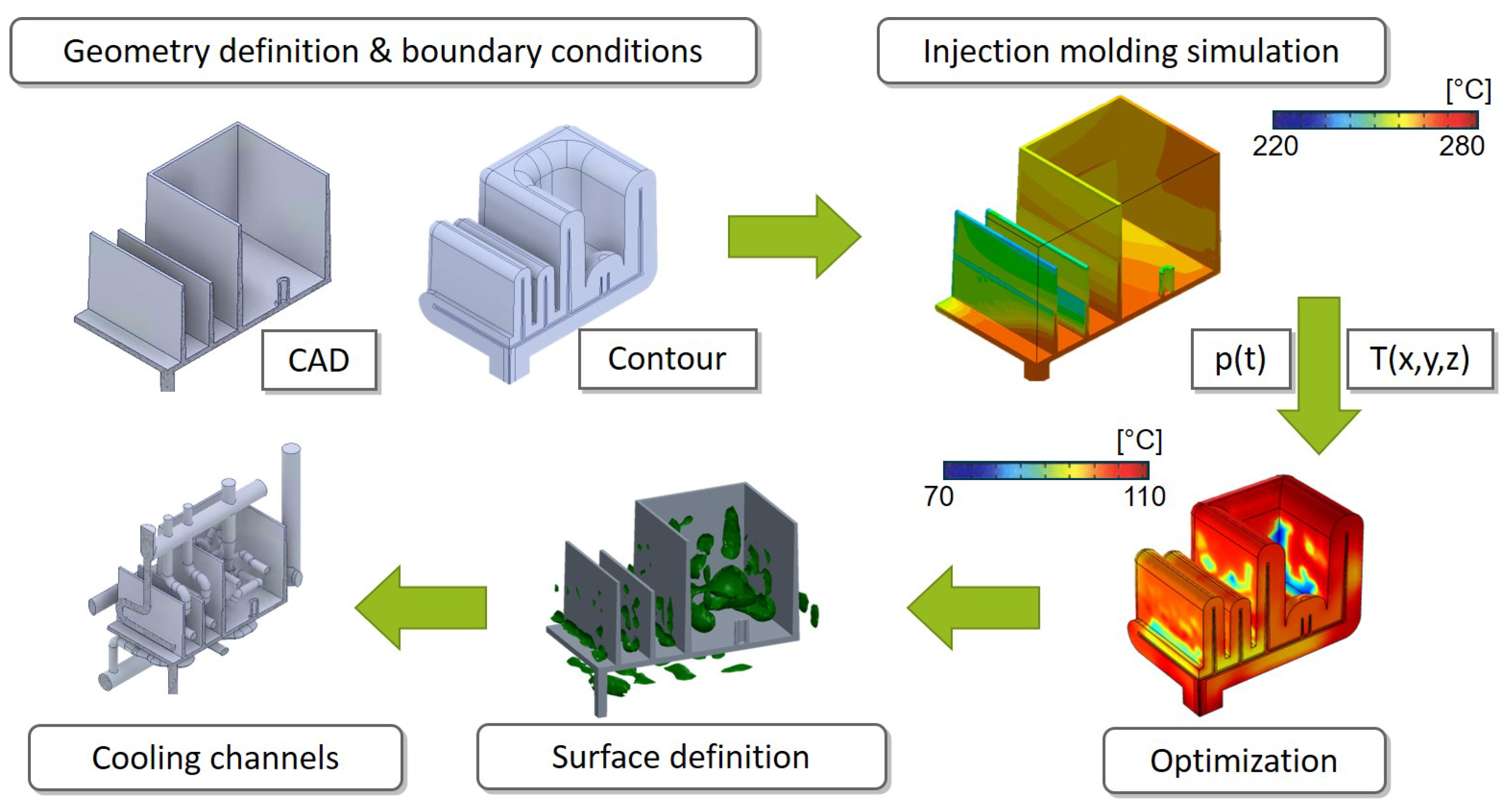
:1. Introduction
- Experiment-based design;
- Design and optimization based on the conformal cooling line;
- Optimization using expert algorithms;
- Modular/parametrical design of conformal cooling channels;
- Solid modelling based on topology optimization.
2. Related Work
2.1. Methodology of an Inverse Thermal Mold Design
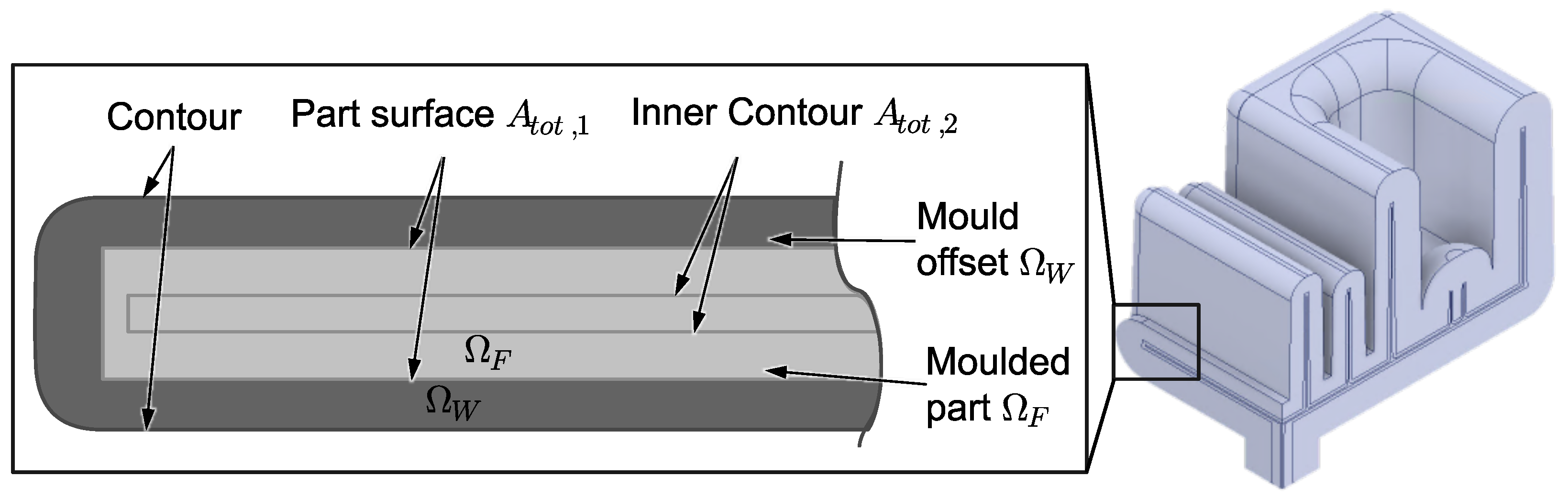
2.2. Offsets
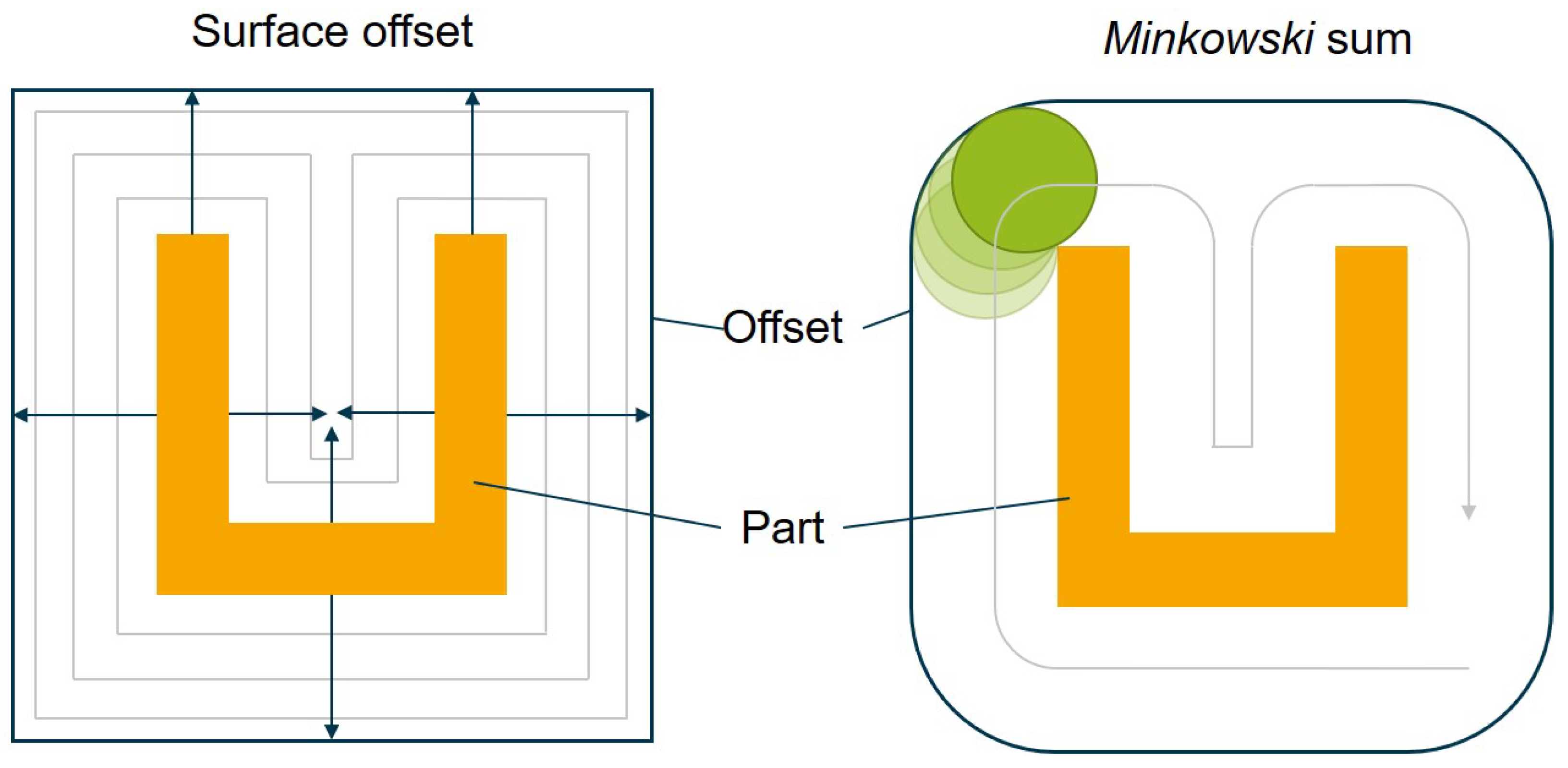
Variable Offsets
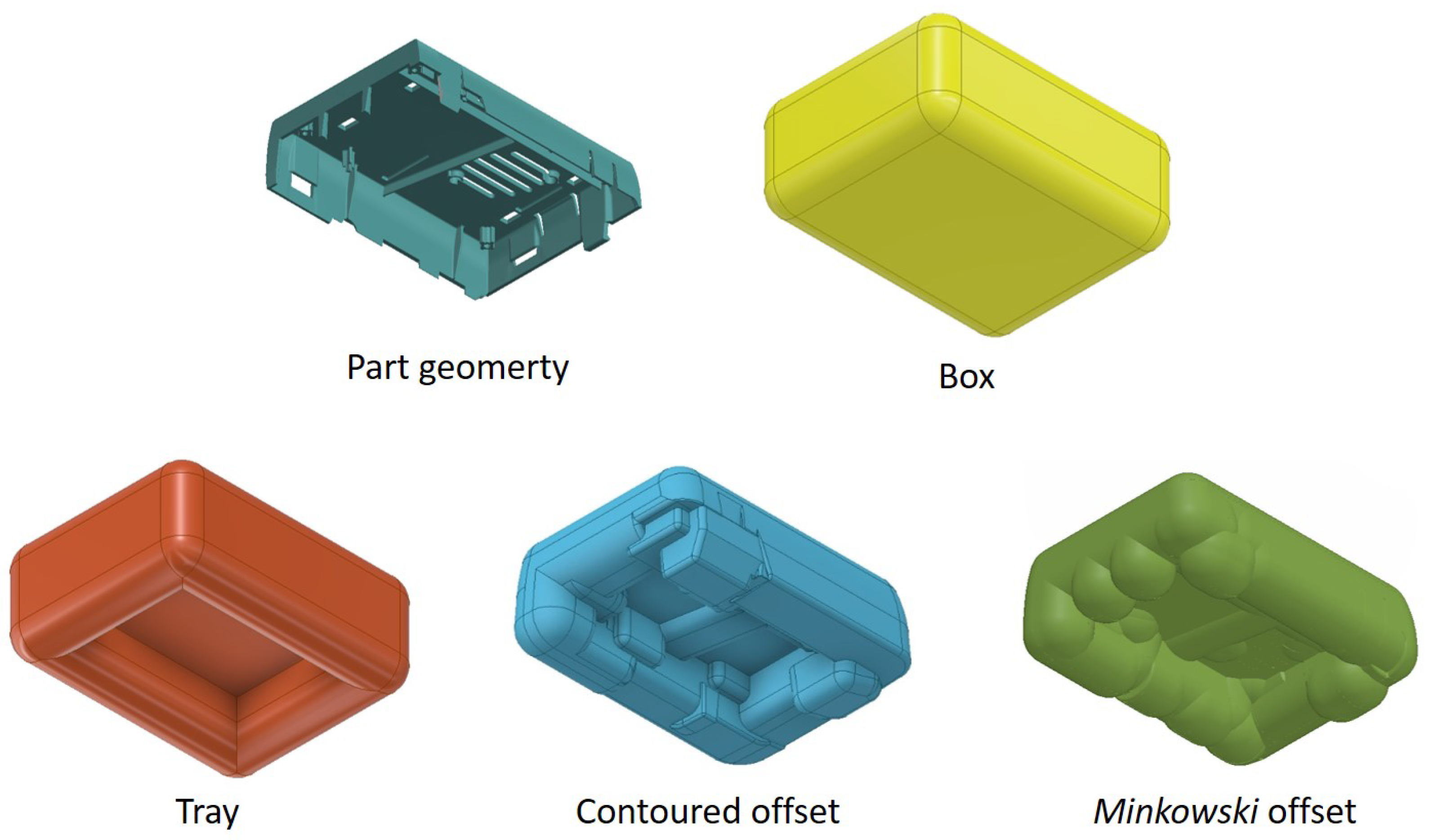
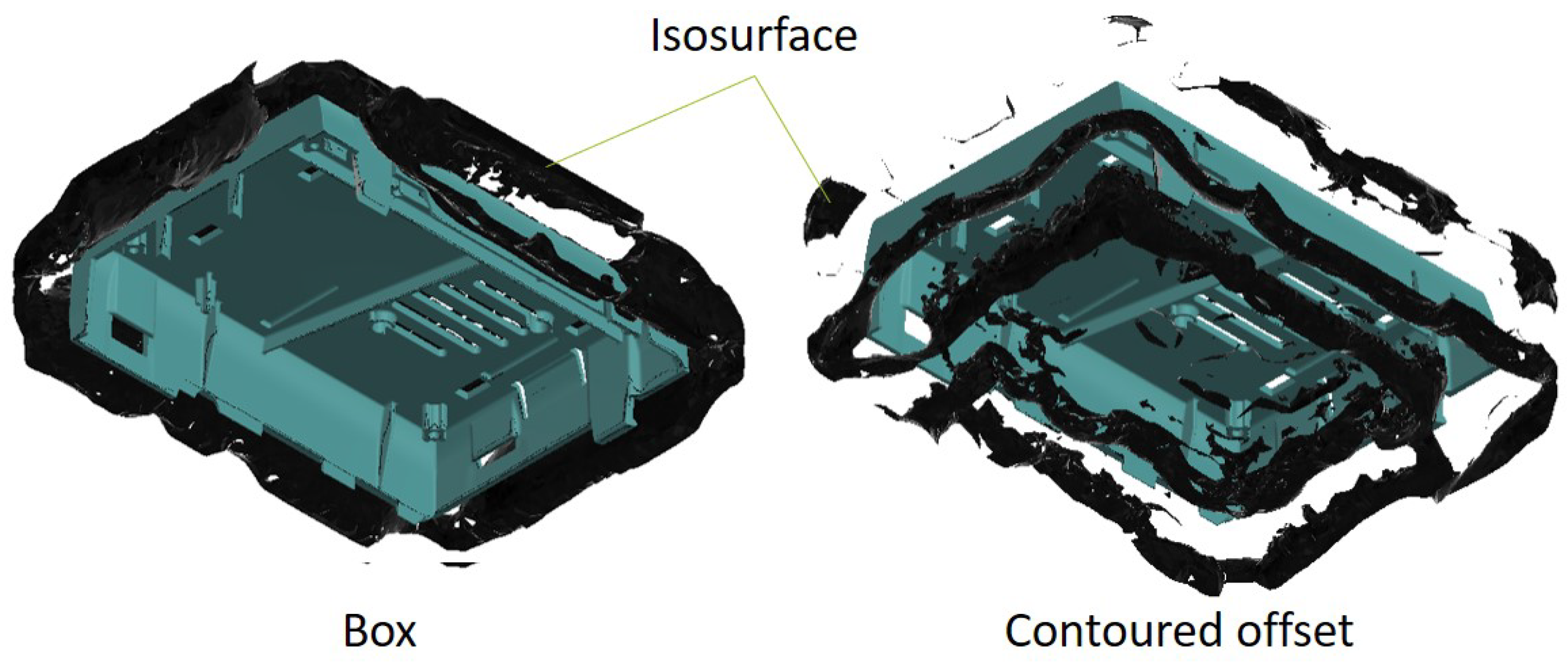
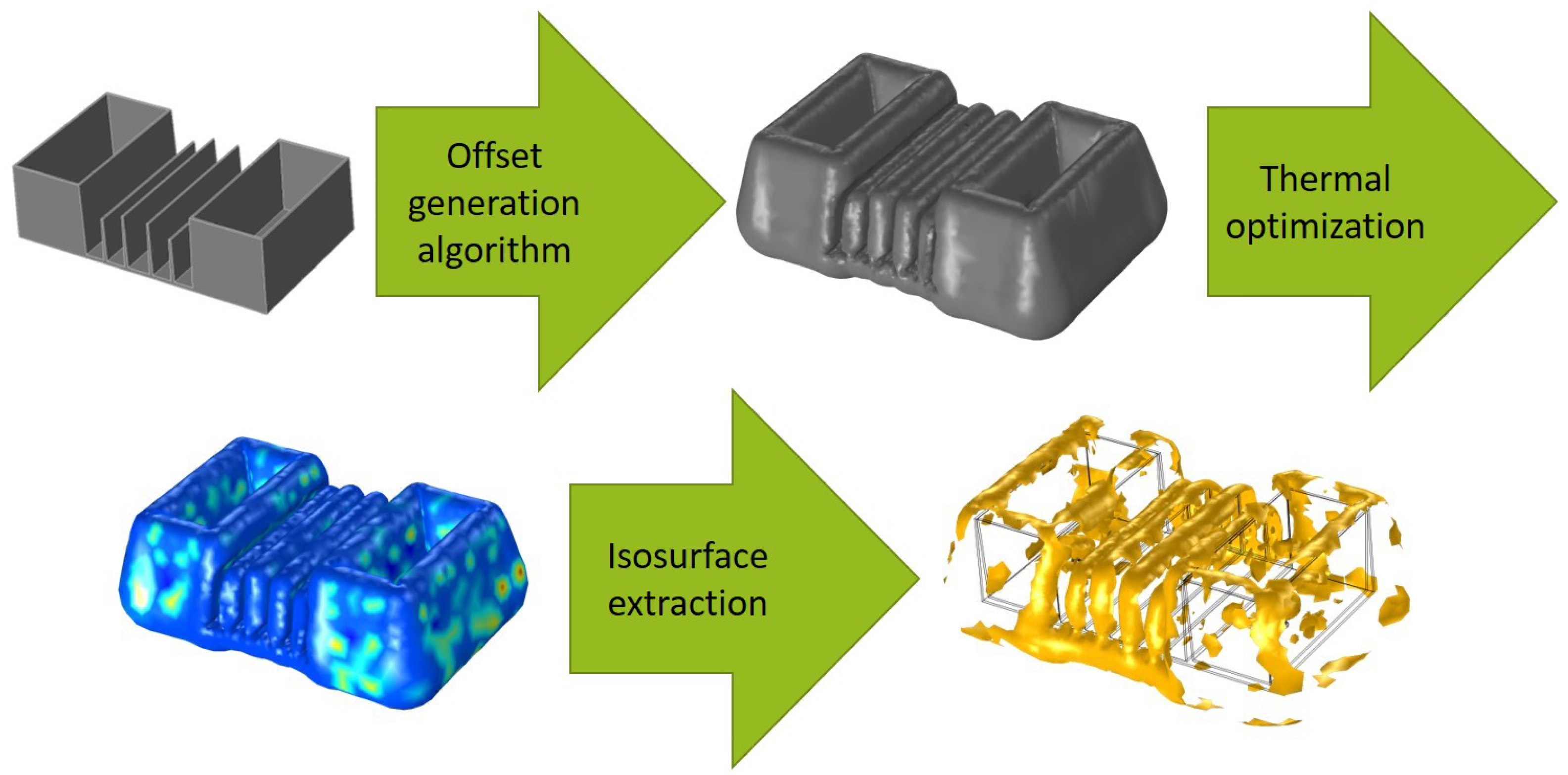
3. Creation of Offsets for Complex Molded Parts
4. Investigation of the Influence of the Offset on the Calculated Optimum
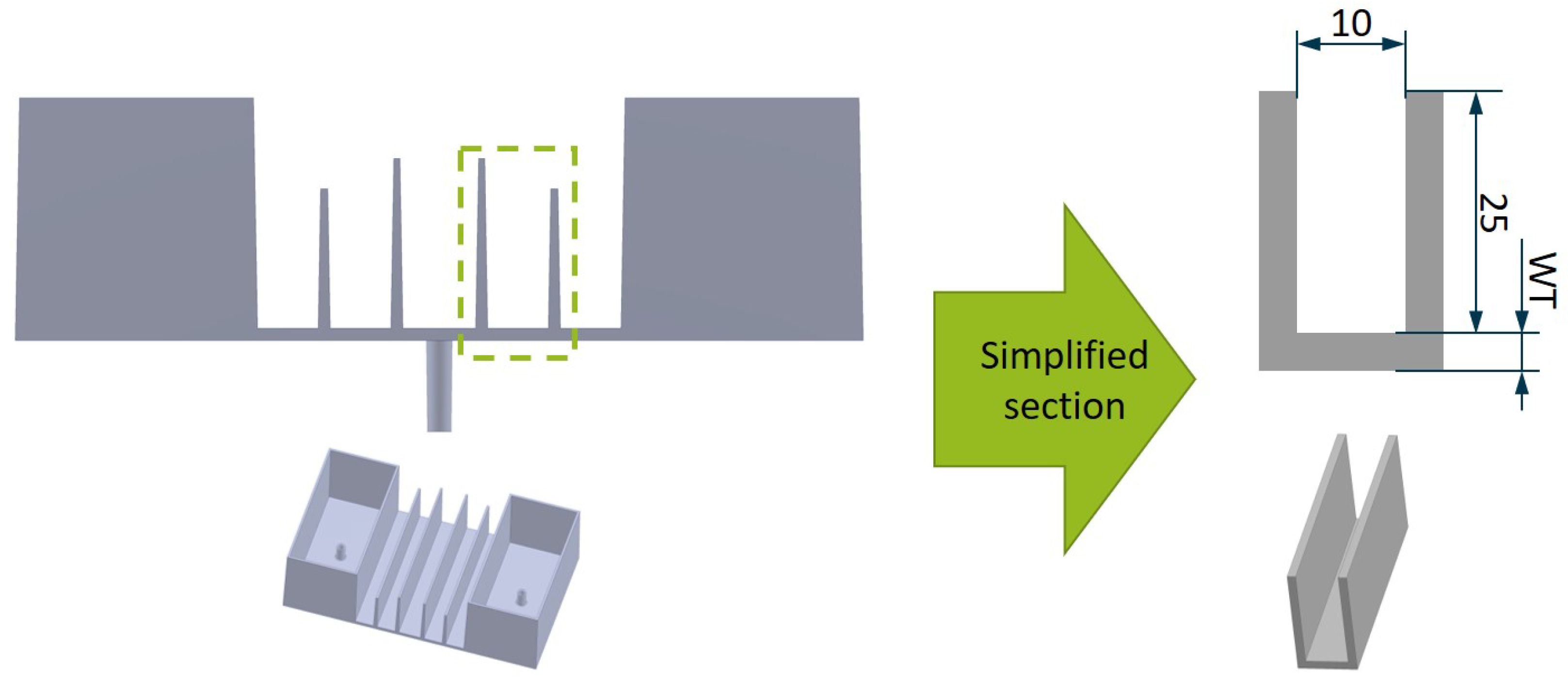
4.1. Design of Experiment
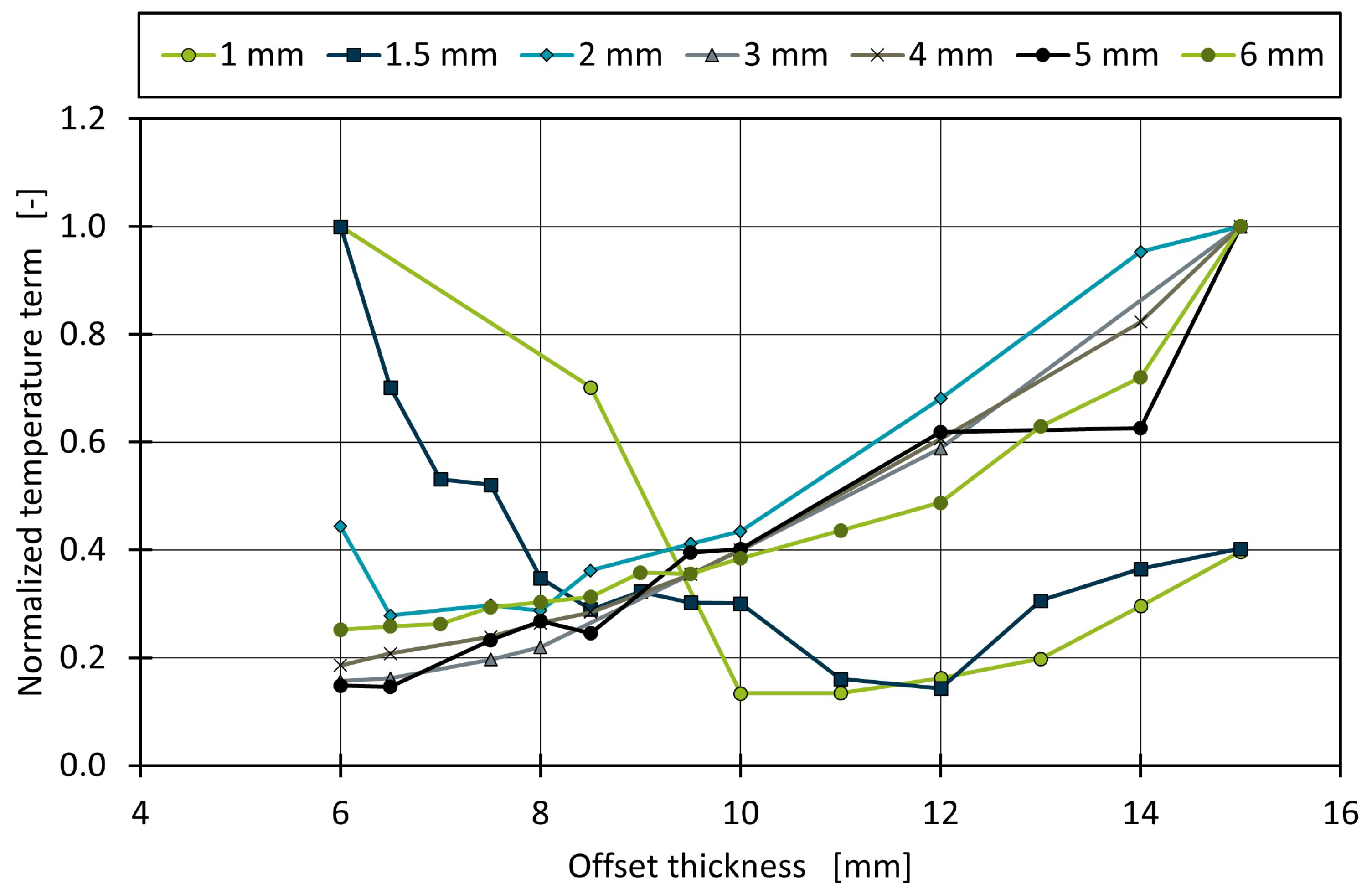
4.2. Influence of the Offset Thickness
4.3. Influence of an Extended Optimization Surface
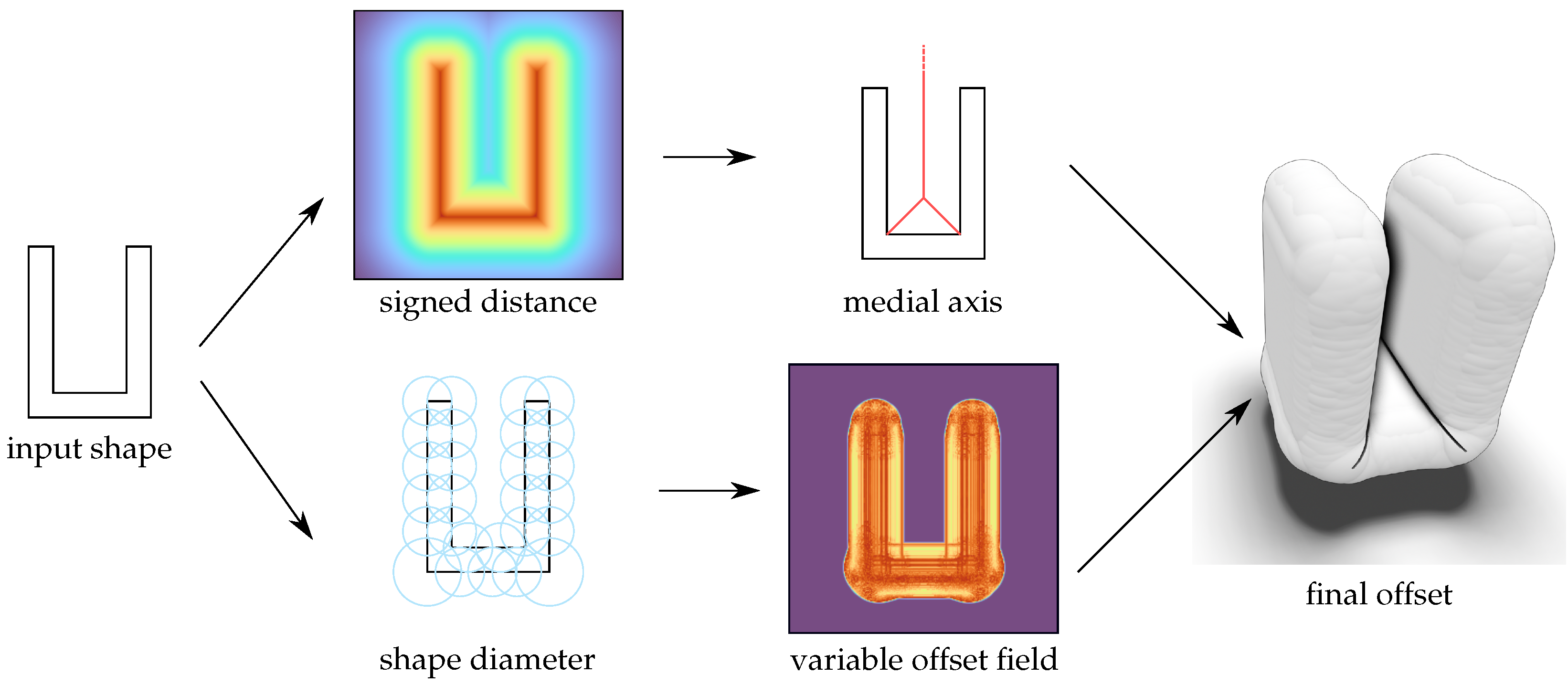
5. Variable Offsets
- The offset distance from the surface depends on the thickness of the local part geometry.
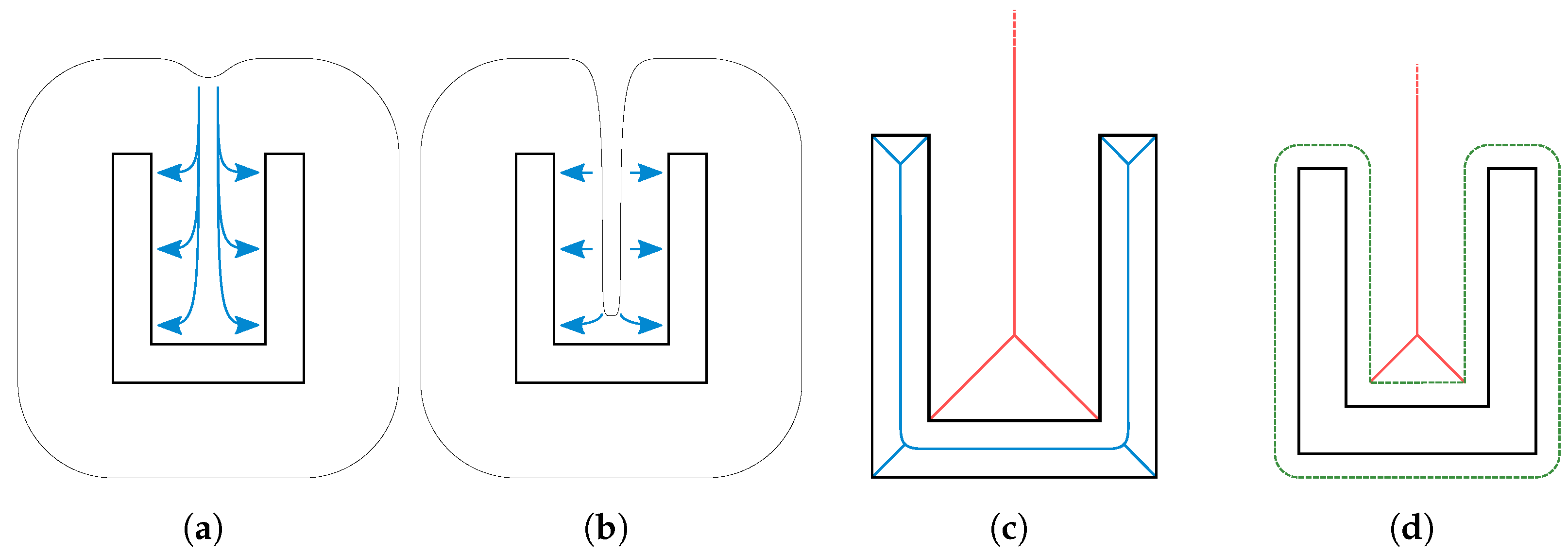
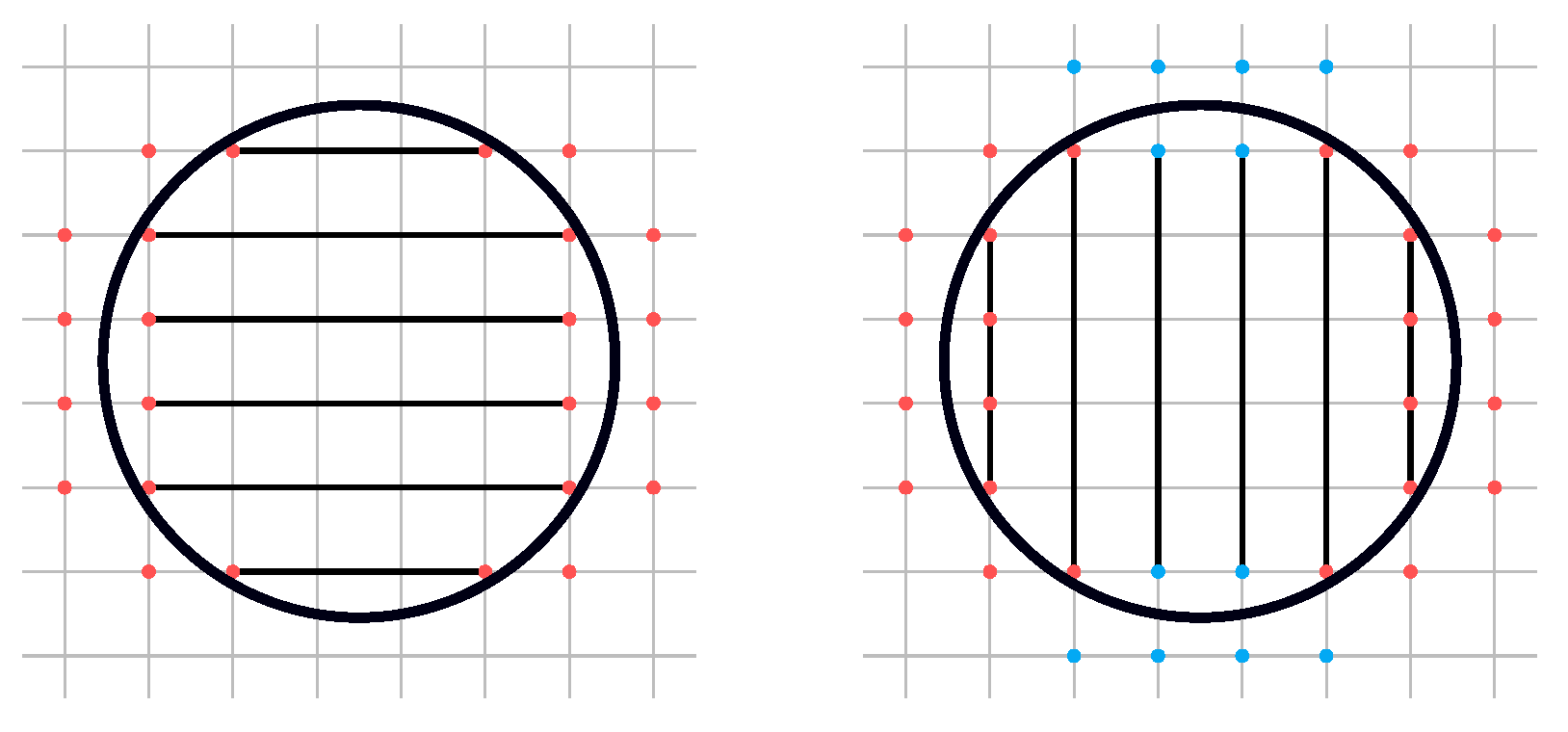
- Offsets should not connect at concave surfaces, as shown in Figure 10, to offer the optimization algorithm better control over temperatures closer to the part surface.
5.1. Shape Diameter Function
5.2. Medial Axis
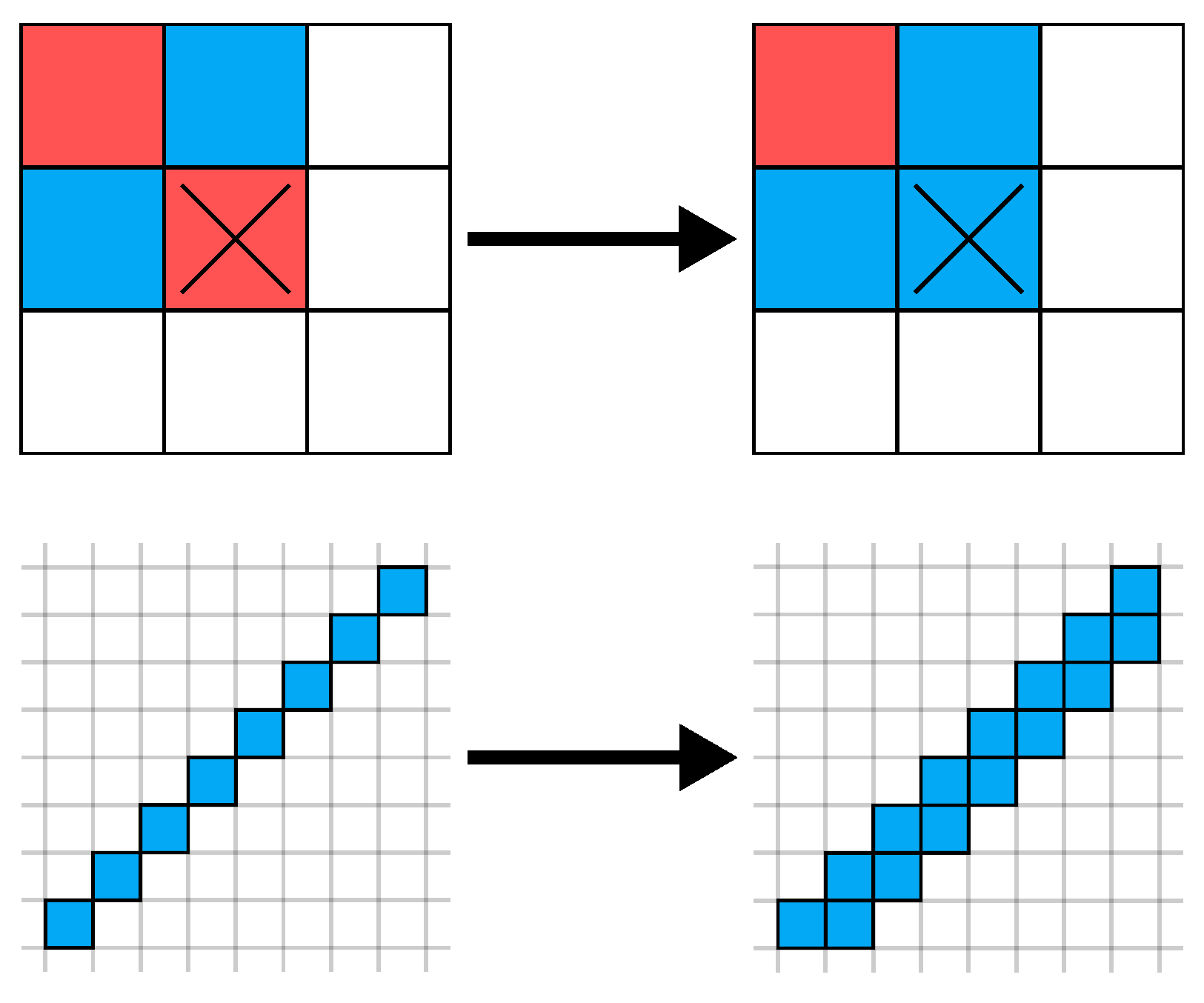
5.3. Efficient Offset Extraction
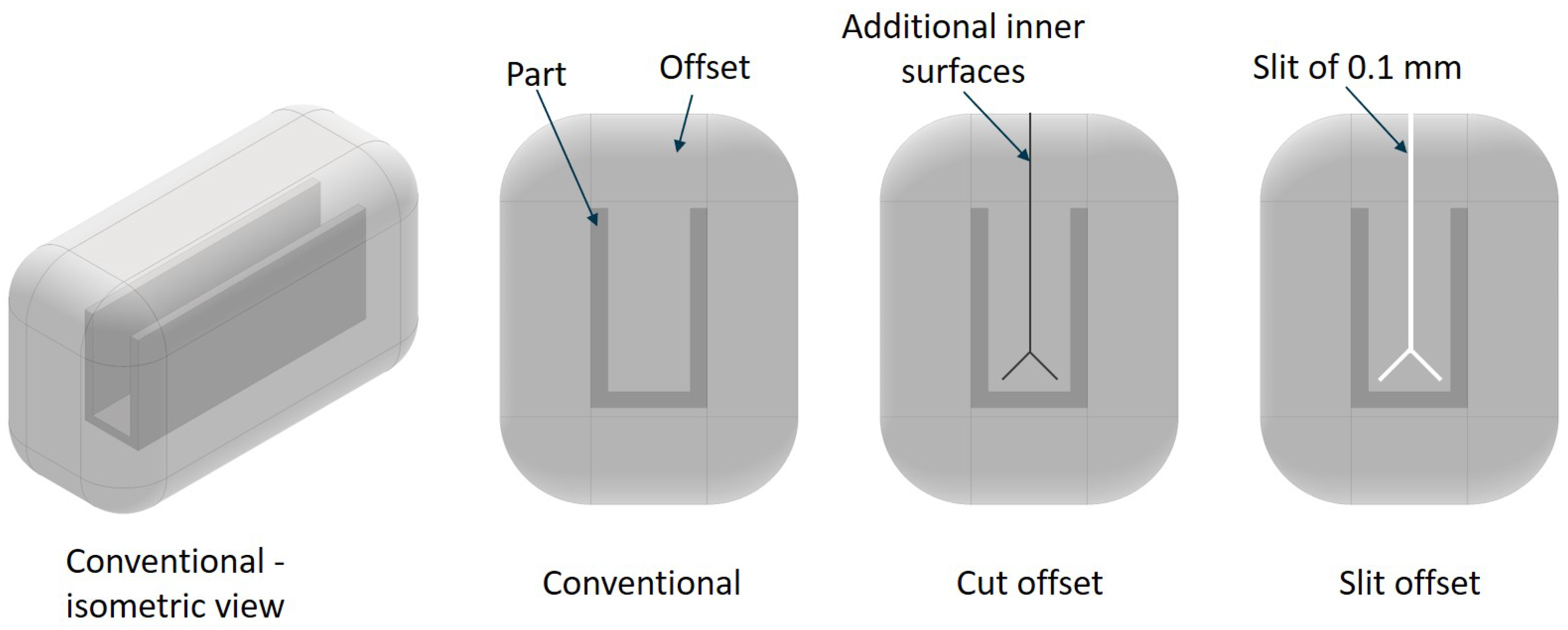
5.4. Post-Processing
6. Evaluation
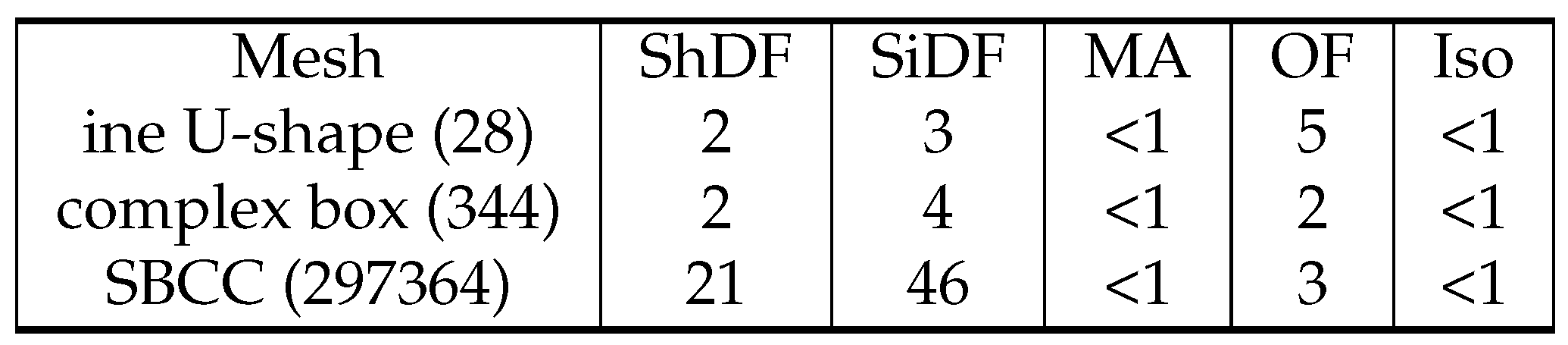
6.1. Performance
6.2. Qualitative Results
6.3. Validation of the Automatically Generated Offset in Thermal Optimization
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hopmann, C.; Menges, G.; Michaeli, W.; Mohren, P. Spritzgießwerkzeuge—Auslegung, Bau, Anwendung; Carl Hanser Verlag München: Munich, Germany, 2018; Volume 7. [Google Scholar]
- Menges, G.; Haberstroh, E.; Michaeli, W.; Schmachtenberg, E. Menges Werkstoffkunde Kunststoffe; Carl Hanser Verlag München: Munich, Germany, 2011; Volume 6. [Google Scholar]
- Feng, S.; Kamat, A.M.; Pei, Y. Design and fabrication of conformal cooling channels in molds: Review and progress updates. Int. J. Heat Mass Transf. 2021, 171, 121082. [Google Scholar] [CrossRef]
- He, B.; Ying, L.; Li, X.; Hu, P. Optimal design of longitudinal conformal cooling channels in hot stamping tools. Appl. Therm. Eng. 2016, 106, 1176–1189. [Google Scholar] [CrossRef]
- Hu, P.; He, B.; Ying, L. Numerical investigation on cooling performance of hot stamping tool with various channel designs. Appl. Therm. Eng. 2016, 96, 338–351. [Google Scholar] [CrossRef]
- Li, H.; Mei, Y.; Lin, B.; Xiao, H.Q. Design and optimization of conformal cooling system of an injection molding chimney. In Materials Science Forum; Trans Tech Publ.: Freienbach, Switzerland, 2016; Volume 850, pp. 679–686. [Google Scholar] [CrossRef]
- Agazzi, A.; Sobotka, V.; Le Goff, R.; Garcia, D.; Jarny, Y. A Methodology for the Design of Effective Cooling System in Injection Moulding. Int. J. Mater. Form. 2010, 3, 13–16. [Google Scholar] [CrossRef]
- Wang, Y.; Yu, K.M.; Wang, C.C. Spiral and conformal cooling in plastic injection molding. Comput.-Aided Des. 2015, 63, 1–11. [Google Scholar] [CrossRef]
- Li, C.G.; Li, C.L.; Liu, Y.; Huang, Y. A new C-space method to automate the layout design of injection mould cooling system. Comput.-Aided Des. 2012, 44, 811–823. [Google Scholar] [CrossRef]
- Li, C.; Li, C.; Mok, A. Automatic layout design of plastic injection mould cooling system. Comput.-Aided Des. 2005, 37, 645–662. [Google Scholar] [CrossRef]
- Au, K.M.; Yu, K.M. A scaffolding architecture for conformal cooling design in rapid plastic injection moulding. Int. J. Adv. Manuf. Technol. 2007, 34, 496–515. [Google Scholar] [CrossRef]
- Au, K.M.; Yu, K.M. Modeling of multi-connected porous passageway for mould cooling. Comput.-Aided Des. 2011, 43, 989–1000. [Google Scholar] [CrossRef]
- Huang, J.; Fadel, G.M. Bi-Objective Optimization Design of Heterogeneous Injection Mold Cooling Systems. J. Mech. Des. 2001, 123, 226–239. [Google Scholar] [CrossRef]
- Shin, K.H. A method for representation and analysis of conformal cooling channels in molds made of functionally graded tool steel/Cu materials. J. Mech. Sci. Technol. 2019, 33, 1743–1750. [Google Scholar] [CrossRef]
- Path-planning algorithm for the automatic generation of a cooling channel layout in injection moulds. In Proceedings of the ANTEC Conference, Online, 10–21 May 2021.
- Hohlweck, T. Inverse Thermische Optimierung zur Wissensbasierten Thermischen Spritzgießwerkzeugauslegung. Ph.D. Thesis, RWTH Aachen University, Aachen, Germany, 2022. [Google Scholar]
- Reisgen, U.; Drummer, D.; Marschall, H. (Eds.) Thermal Optimisation of Injection Moulds by Solving an Inverse Heat Conduction Problem. In EMPOrIA-International Joint Conference; Springer: Cham, Switzerland, 2020. [Google Scholar]
- Nikoleizig, P. Inverse Thermische Spritzgießwerkzeugauslegung auf Basis des Lokalen Kühlbedarfs. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 2018. [Google Scholar]
- Hopmann, C.; Gerads, J.; Hohlweck, T. Investigation of an inverse thermal injection mould design methodology in dependence of the part geometry. Int. J. Mater. Form. 2021, 14, 209–321. [Google Scholar] [CrossRef]
- Hopmann, C.; Theunissen, M.; Schneppe, T.; Schmitz, M. Automatic cooling channel design forinjection moulds. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2019; Volume 2139, p. 030004. [Google Scholar] [CrossRef]
- Dahmen, W.; Reusken, A. Numerik für Ingenieure und Naturwissenschaftler; Springer: Berlin, Germany, 2008; Volume 2. [Google Scholar]
- Dantas, L.; Orlande, H.R.B. A function estimation approach for determining temperature-dependent thermophysical properties. Inverse Probl. Eng. 1996, 3, 261–279. [Google Scholar] [CrossRef]
- Campen, M.; Kobbelt, L. Polygonal boundary evaluation of minkowski sums and swept volumes. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2010; Volume 29, pp. 1613–1622. [Google Scholar] [CrossRef]
- Kim, S.J.; Yang, M.Y. Triangular mesh offset for generalized cutter. Comput.-Aided Des. 2005, 37, 999–1014. [Google Scholar] [CrossRef]
- Pavić, D.; Kobbelt, L. High-resolution volumetric computation of offset surfaces with feature preservation. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2008; Volume 27, pp. 165–174. [Google Scholar]
- Kim, S.J.; Lee, D.Y.; Yang, M.Y. Offset triangular mesh using the multiple normal vectors of a vertex. Comput.-Aided Des. Appl. 2004, 1, 285–291. [Google Scholar] [CrossRef]
- Jung, W.; Shin, H.; Choi, B.K. Self-intersection removal in triangular mesh offsetting. Comput.-Aided Des. Appl. 2004, 1, 477–484. [Google Scholar] [CrossRef]
- Rossignac, J.R.; Requicha, A.A. Offsetting operations in solid modelling. Comput. Aided Geom. Des. 1986, 3, 129–148. [Google Scholar] [CrossRef] [Green Version]
- Forsyth, M. Shelling and offsetting bodies. In Proceedings of the Third ACM Symposium on Solid Modeling and Applications, Salt Lake City, UT, USA, 17–19 May 1995; pp. 373–381. [Google Scholar]
- Boschetto, A.; Bottini, L. Triangular mesh offset aiming to enhance Fused Deposition Modeling accuracy. Int. J. Adv. Manuf. Technol. 2015, 80, 99–111. [Google Scholar] [CrossRef]
- Lorensen, W.E.; Cline, H.E. Marching cubes: A high resolution 3D surface construction algorithm. ACM Siggraph Comput. Graph. 1987, 21, 163–169. [Google Scholar] [CrossRef]
- Musialski, P.; Auzinger, T.; Birsak, M.; Wimmer, M.; Kobbelt, L. Reduced-order shape optimization using offset surfaces. ACM Trans. Graph. 2015, 34, 102:1–102:9. [Google Scholar] [CrossRef]
- Ross, E.; Hambleton, D.; Aish, R. Face-offsetting polygon meshes with variable offset rates. In Advances in Architectural Geometry; VDF Hochschulverlag AG Zurich: Zurich, Switzerland, 2016; pp. 40–61. [Google Scholar]
- Woerl, A.C.; Schoemer, E.; Schwanecke, U. Variable-Radius Offset Surface Approximation on the GPU. J. WSCG 2020, 28, 99–108. [Google Scholar]
- Varadhan, G.; Manocha, D. Accurate Minkowski Sum Approximation of Polyhedral Models. In Proceedings of the 12th Pacific Conference on Computer Graphics and Applications, Seoul, Korea, 6–8 October 2004. [Google Scholar]
- Schürmann, E. Abschätzmethoden für die Auslegung von Spritzgießwerkzeugen. Ph.D. Thesis, RWTH Aachen, Aachen, Germany, 1979. [Google Scholar]
- Shapira, L.; Shamir, A.; Cohen-Or, D. Consistent mesh partitioning and skeletonisation using the shape diameter function. Vis. Comput. 2008, 24, 249–259. [Google Scholar] [CrossRef]
- Yan, Y.; Letscher, D.; Ju, T. Voxel cores: Efficient, robust, and provably good approximation of 3d medial axes. ACM Trans. Graph. (TOG) 2018, 37, 1–13. [Google Scholar] [CrossRef]
- Xia, H.; Tucker, P.G. Distance solutions for medial axis transform. In Proceedings of the 18th International Meshing Roundtable; Springer: Berlin/Heidelberg, Germany, 2009; pp. 247–265. [Google Scholar] [CrossRef] [Green Version]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, PAMI-9, 532–550. [Google Scholar] [CrossRef]
- Trettner, P.; Kobbelt, L. Fast and Robust QEF Minimization using Probabilistic Quadrics. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 2020; Volume 39, pp. 325–334. [Google Scholar]
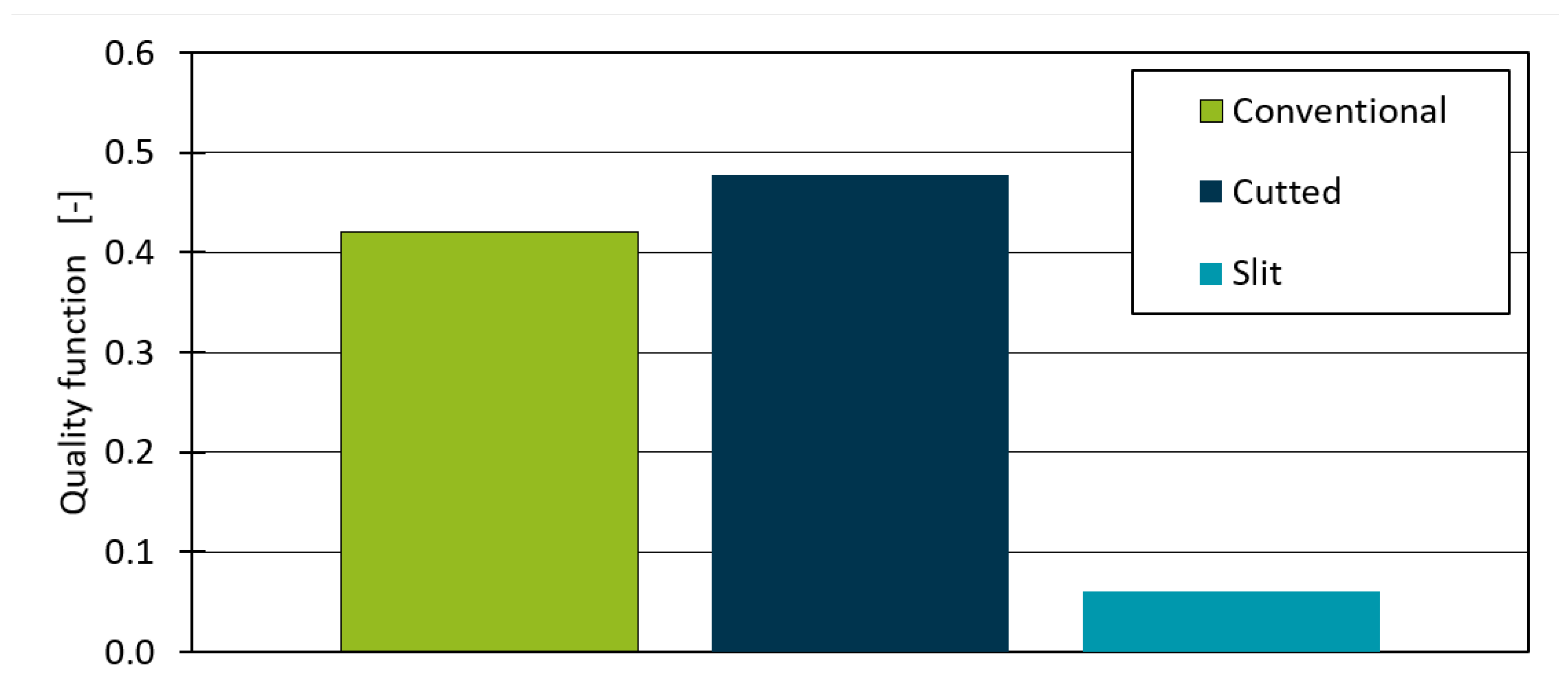


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hopmann, C.; Fritsche, D.C.; Hohlweck, T.; Nehring-Wirxel, J. Variable Offset Computation Space for Automatic Cooling Dimensioning. Polymers 2022, 14, 762. https://doi.org/10.3390/polym14040762
Hopmann C, Fritsche DC, Hohlweck T, Nehring-Wirxel J. Variable Offset Computation Space for Automatic Cooling Dimensioning. Polymers. 2022; 14(4):762. https://doi.org/10.3390/polym14040762
Chicago/Turabian StyleHopmann, Christian, Daniel Colin Fritsche, Tobias Hohlweck, and Julius Nehring-Wirxel. 2022. "Variable Offset Computation Space for Automatic Cooling Dimensioning" Polymers 14, no. 4: 762. https://doi.org/10.3390/polym14040762
APA StyleHopmann, C., Fritsche, D. C., Hohlweck, T., & Nehring-Wirxel, J. (2022). Variable Offset Computation Space for Automatic Cooling Dimensioning. Polymers, 14(4), 762. https://doi.org/10.3390/polym14040762





