Monothetic Analysis and Response Surface Methodology Optimization of Calcium Alginate Microcapsules Characteristics
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
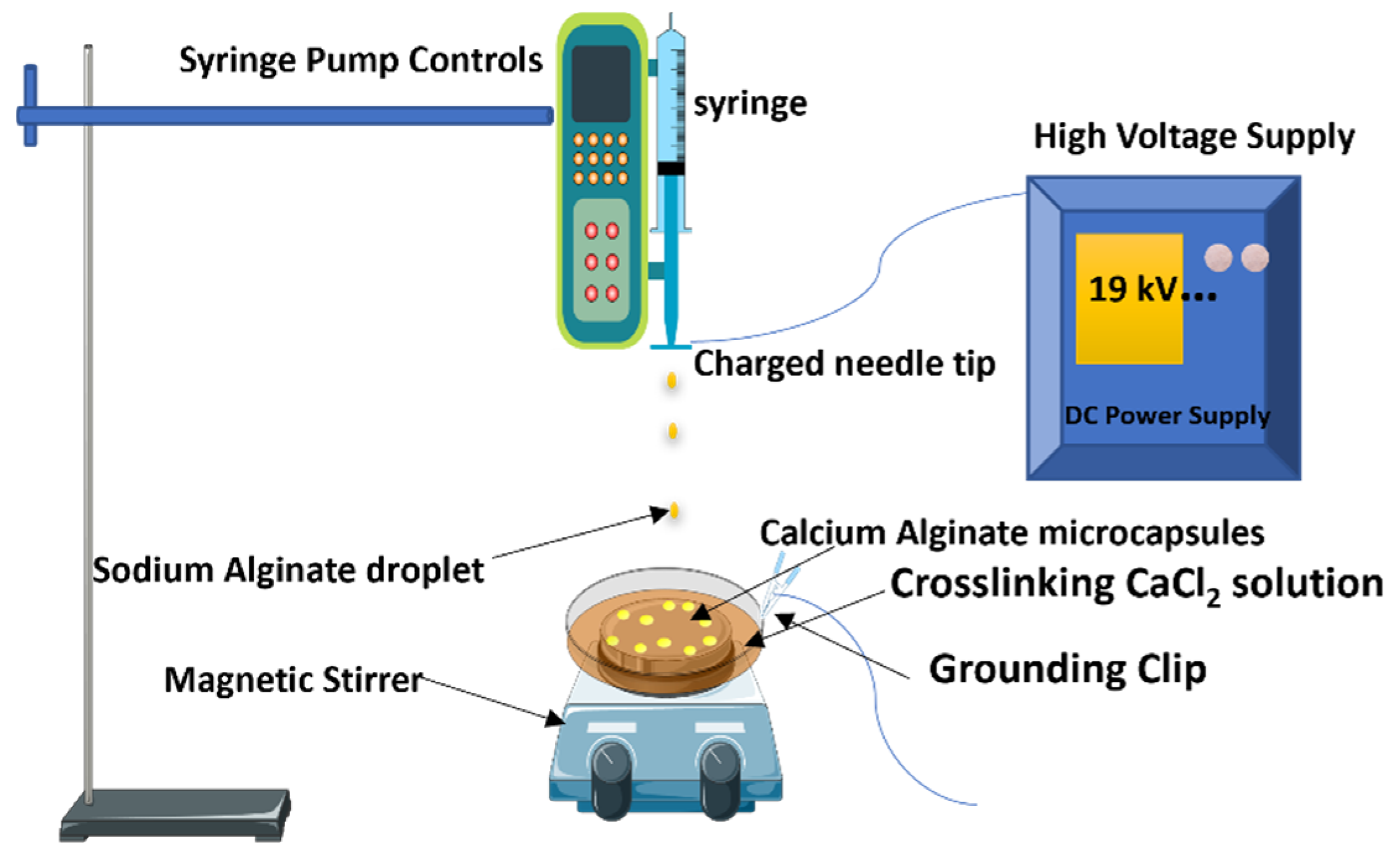
2.2. Synthesis of Calcium Alginates Using Electrospray Technique
2.3. Microcapsule Size Distribution Determination
2.4. Sphericity Coefficient Determination
2.5. Experimental Size and Sphericity Optimization
2.6. Model Validation
2.7. Optimization
3. Results
3.1. OFAT Analysis of Independent Parameters
3.1.1. Effect of Sodium Alginate Concentration
3.1.2. Effect of Voltage
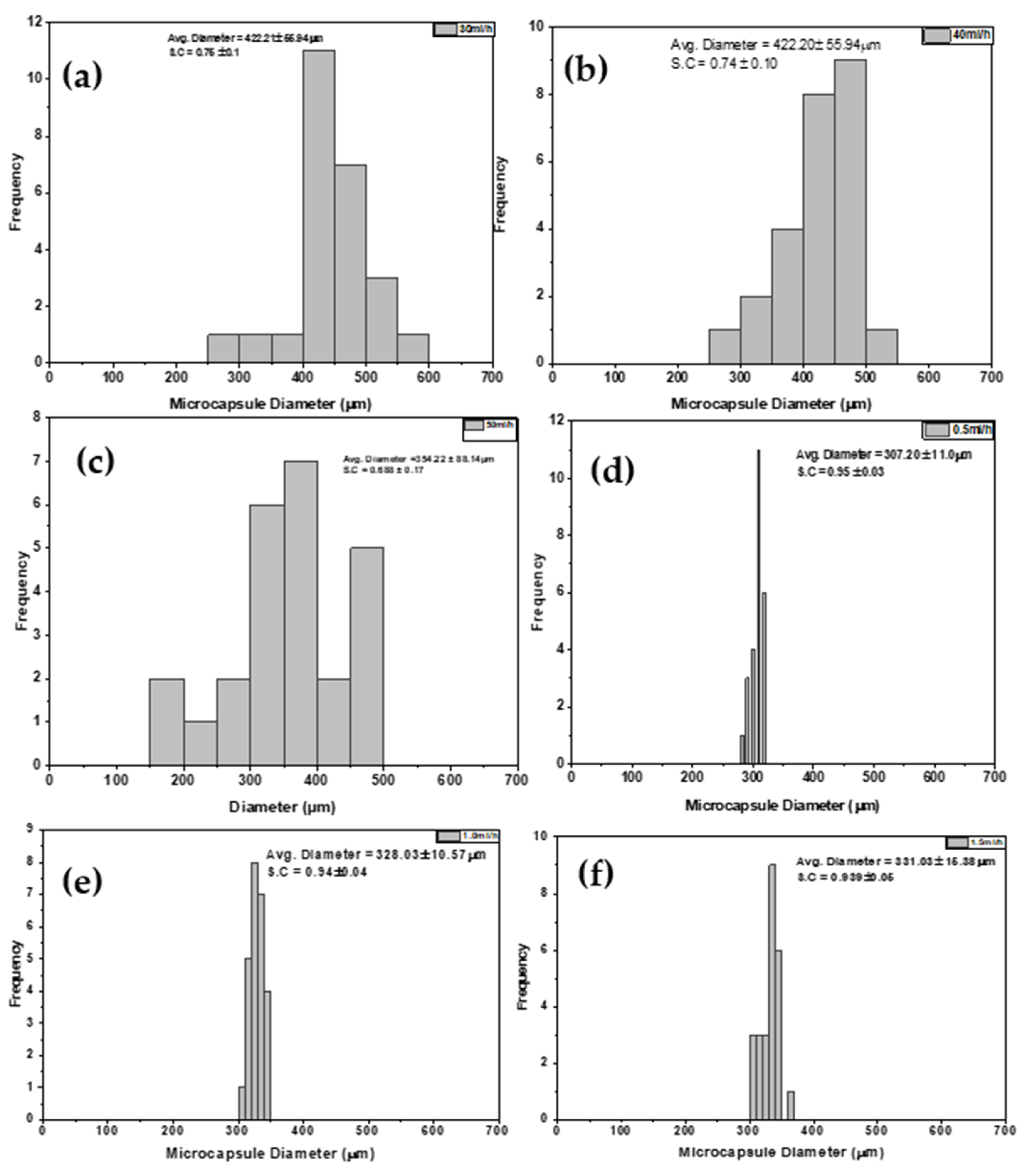
3.1.3. Effect of Flowrate
3.1.4. Effect of Calcium Chloride Concentration
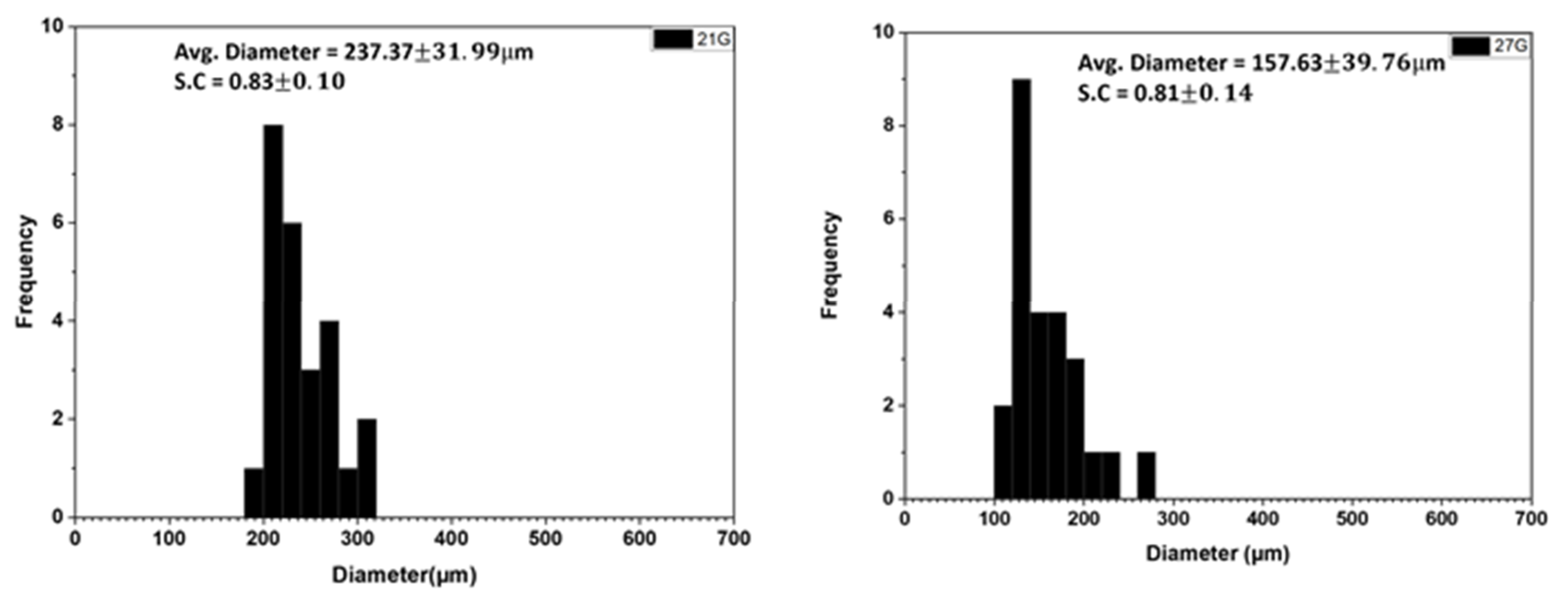
3.1.5. Effect of Needle Size
3.2. ANOVA and Model Generation
3.2.1. Linear Variable Effect on Microcapsule Size and Sphericity
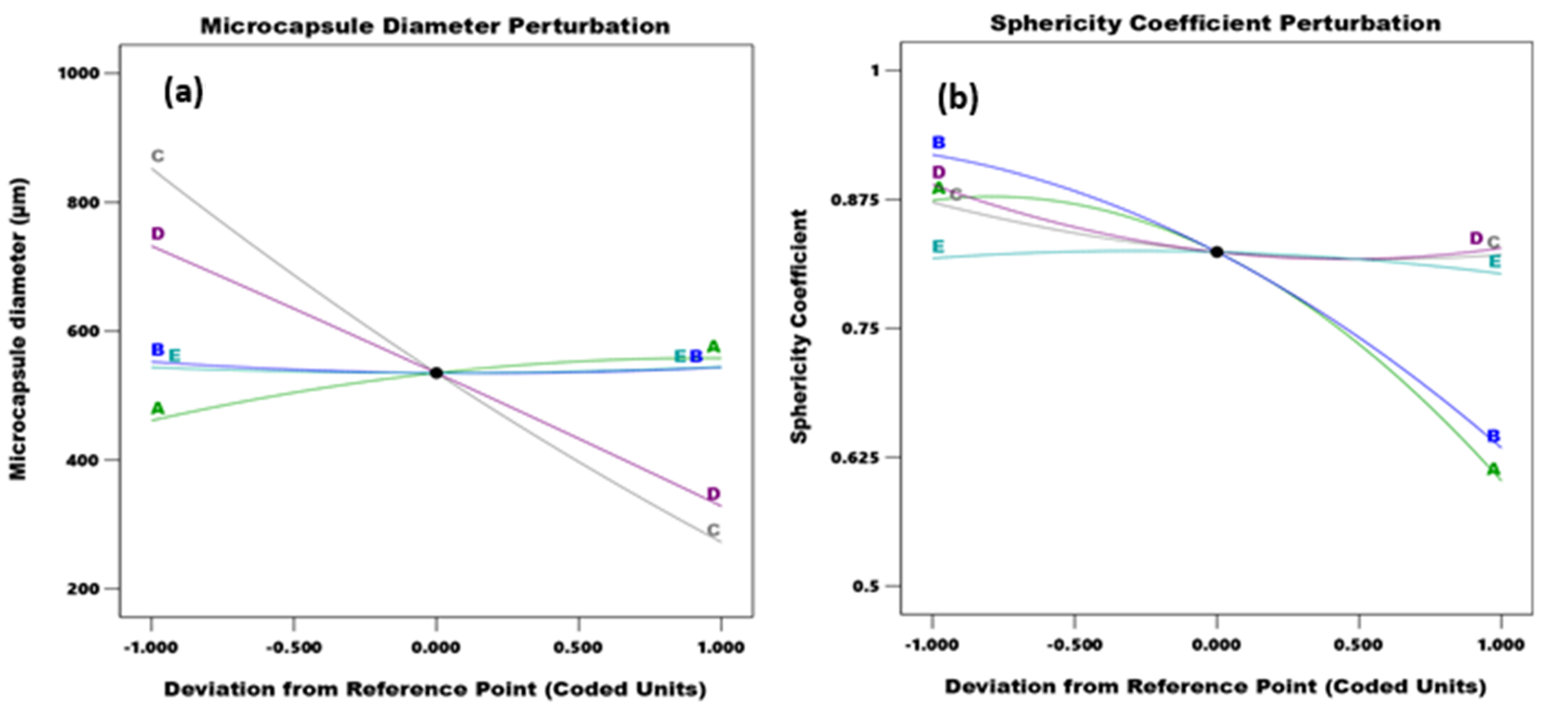
3.2.2. Effect of Independent Variable Interaction on Microcapsule Particle Size and Sphericity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pawar, S.N.; Edgar, K.J. Alginate Derivatization: A Review of Chemistry, Properties and Applications. Biomaterials 2012, 33, 3279–3305. [Google Scholar] [CrossRef] [PubMed]
- Sharmila, A.; Mardera, M.S.; Soundarya, H.P.; Shreyas, M. Treatment of Textile Wastewater Using Sodium Alginate Beads. J. Phys. Conf. Ser. 2021, 1979, 012005. [Google Scholar] [CrossRef]
- Yan, M.; Shi, J.; Liu, L.; Zhu, H.; Tang, S.; Zhou, G.; Zeng, J.; Zhang, H.; Yu, Y.; Guo, J. Preparation of High-Strength and High-Toughness Sodium Alginate Fibers Based on the Study of Multi-Ion Diffusion Kinetics in a Low Temperature Dissolution System. New J. Chem. 2021, 45, 5981–5991. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, X.; Guo, H. Preparation and Properties of a Novel Sodium Alginate Microcapsule. J. Phys. Conf. Ser. 2021, 1893. [Google Scholar] [CrossRef]
- Atanase, L.I. Micellar Drug Delivery Systems Based on Natural Biopolymers. Polymers 2021, 13, 477. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Wang, W.; Liu, A.; Fan, W.J.; Ding, R.; Tian, H.; Han, P.; Li, W.H. Self-Healing and Anti-Corrosion Performances of 1, 2, 4—Triazole Modified Nano-Silica Hydrogels. Colloids Interface Sci. Commun. 2018, 27, 11–17. [Google Scholar] [CrossRef]
- Wen, J.; Lei, J.; Chen, J.; Gou, J.; Li, Y.; Li, L. An Intelligent Coating Based on PH-Sensitive Hybrid Hydrogel for Corrosion Protection of Mild Steel. Chem. Eng. J. 2020, 392, 123742. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Tian, L.; Pan, C. Study on Preparation Technology of Self-Healing Micro-Nano Capsule Based on Calcium Alginate. In Proceedings of the 2018 IEEE International Conference on Manipulation, Manufacturing and Measurement on the Nanoscale (3M-NANO), Hangzhou, China, 13–17 August 2018; pp. 151–154. [Google Scholar]
- Costa, A.B.; Graham Cooks, R. Simulated Splashes: Elucidating the Mechanism of Desorption Electrospray Ionization Mass Spectrometry. Chem. Phys. Lett. 2008, 464, 1–8. [Google Scholar] [CrossRef]
- Khosroyar, S. Ferric—Saccharate Capsulation with Alginate Coating Using the Emulsification Method. Afr. J. Microbiol. Res. 2012, 6, 2455–2461. [Google Scholar]
- Poncelet, D.; Lencki, R.; Beaulieu, C.; Halle, J.P.; Neufeld, R.J.; Fournier, A. Production of Alginate Beads by Emulsification/Internal Gelation. I. Methodology. Appl. Microbiol. Biotechnol. 1992, 38, 39–45. [Google Scholar] [CrossRef]
- Uyen, N.T.T.; Hamid, Z.A.A.; Tram, N.X.T.; Ahmad, N. Fabrication of Alginate Microspheres for Drug Delivery: A Review. Int. J. Biol. Macromol. 2020, 153, 1035–1046. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Q.; Kang, H.; Bielec, M.; Wu, X.; Cheng, Q.; Wei, W.; Dai, H. Influence of Different Divalent Ions Cross-Linking Sodium Alginate-Polyacrylamide Hydrogels on Antibacterial Properties and Wound Healing. Carbohydr. Polym. 2018, 197, 292–304. [Google Scholar] [CrossRef] [PubMed]
- Grant, G.T.; Morris, E.R.; Rees, D.A.; Smith, P.J.C.; Thom, D. Biological Interactions between Polysaccharides and Divalent Cations: The Egg-Box Model. FEBS Lett. 1973, 32, 195–198. [Google Scholar] [CrossRef] [Green Version]
- Klokk, T.I.; Melvik, J.E. Controlling the Size of Alginate Gel Beads by Use of a High Electrostatic Potential. J. Microencapsul. 2002, 19, 415–424. [Google Scholar] [CrossRef]
- Elkady, M.; Hassan, H.S.; Hashim, A. Immobilization of magnetic nanoparticles onto amine-modified nano-silica gel for copper ions remediation. Materials 2016, 9, 460. [Google Scholar] [CrossRef] [PubMed]
- Cassidy, M.B.; Lee, H.; Trevors, J.T. Environmental Applications of Immobilized Microbial Cells: A Review. J. Ind. Microbiol. 1996, 16, 79–101. [Google Scholar] [CrossRef]
- Lee, B.B.; Ravindra, P.; Chan, E.S. Size and Shape of Calcium Alginate Beads Produced by Extrusion Dripping. Chem. Eng. Technol. 2013, 36, 1627–1642. [Google Scholar] [CrossRef]
- Partovinia, A.; Vatankhah, E. Experimental Investigation into Size and Sphericity of Alginate Micro-Beads Produced by Electrospraying Technique: Operational Condition Optimization. Carbohydr. Polym. 2019, 209, 389–399. [Google Scholar] [CrossRef]
- Nedović, V.A.; Obradović, B.; Leskošek-Čukalović, I.; Trifunović, O.; Pešić, R.; Bugarski, B. Electrostatic Generation of Alginate Microbeads Loaded with Brewing Yeast. Process Biochem. 2001, 37, 17–22. [Google Scholar] [CrossRef]
- Zakeri, M.; Moghadam, H.; Samimi, A.; Mohebbi-Kalhori, D. Optimization of Calcium Alginate Beads Production by Electrospray Using Response Surface Methodology. Mater. Res. Express, 2019, 6, 095412. [Google Scholar] [CrossRef]
- Poncelet, D. Production of Alginate Beads by Emulsification/Internal Gelation. Ann. N. Y. Acad. Sci. 2001, 944, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Mehregan Nikoo, A.; Kadkhodaee, R.; Ghorani, B.; Razzaq, H.; Tucker, N. Controlling the Morphology and Material Characteristics of Electrospray Generated Calcium Alginate Microhydrogels. J. Microencapsul. 2016, 33, 605–612. [Google Scholar] [CrossRef] [PubMed]
- Lotfipour, F.; Mirzaeei, S.; Maghsoodi, M. Evaluation of the Effect of Cacl2 and Alginate Concentrations and Hardening Time on the Characteristics of Lactobacillus Acidophilus Loaded Alginate Beads Using Response Surface Analysis. Adv. Pharm. Bull. 2012, 2, 71–78. [Google Scholar] [PubMed]
- Shi, P.; He, P.; Teh, T.K.H.; Morsi, Y.S.; Goh, J.C.H. Parametric Analysis of Shape Changes of Alginate Beads. Powder Technol. 2011, 210, 60–66. [Google Scholar] [CrossRef]
- Zhang, S.; Campagne, C.; Salaün, F. Influence of Solvent Selection in the Electrospraying Process of Polycaprolactone. Appl. Sci. 2019, 9, 402. [Google Scholar] [CrossRef] [Green Version]
- Fukui, Y.; Maruyama, T.; Iwamatsu, Y.; Fujii, A.; Tanaka, T.; Ohmukai, Y.; Matsuyama, H. Preparation of Monodispersed Polyelectrolyte Microcapsules with High Encapsulation Efficiency by an Electrospray Technique. Colloids Surfaces A Physicochem. Eng. Asp. 2010, 370, 28–34. [Google Scholar] [CrossRef]
- Huang, K.S.; Yang, C.H.; Lin, Y.S.; Wang, C.Y.; Lu, K.; Chang, Y.F.; Wang, Y.L. Electrostatic Droplets Assisted Synthesis of Alginate Microcapsules. Drug Deliv. Transl. Res. 2011, 1, 289–298. [Google Scholar] [CrossRef] [PubMed]
- Moghaddam, M.K.; Mortazavi, S.M.; Khaymian, T. Micro/Nano-Encapsulation of a Phase Change Material by Coaxial Electrospray Method. Iran. Polym. J. 2015, 24, 759–774. [Google Scholar] [CrossRef]


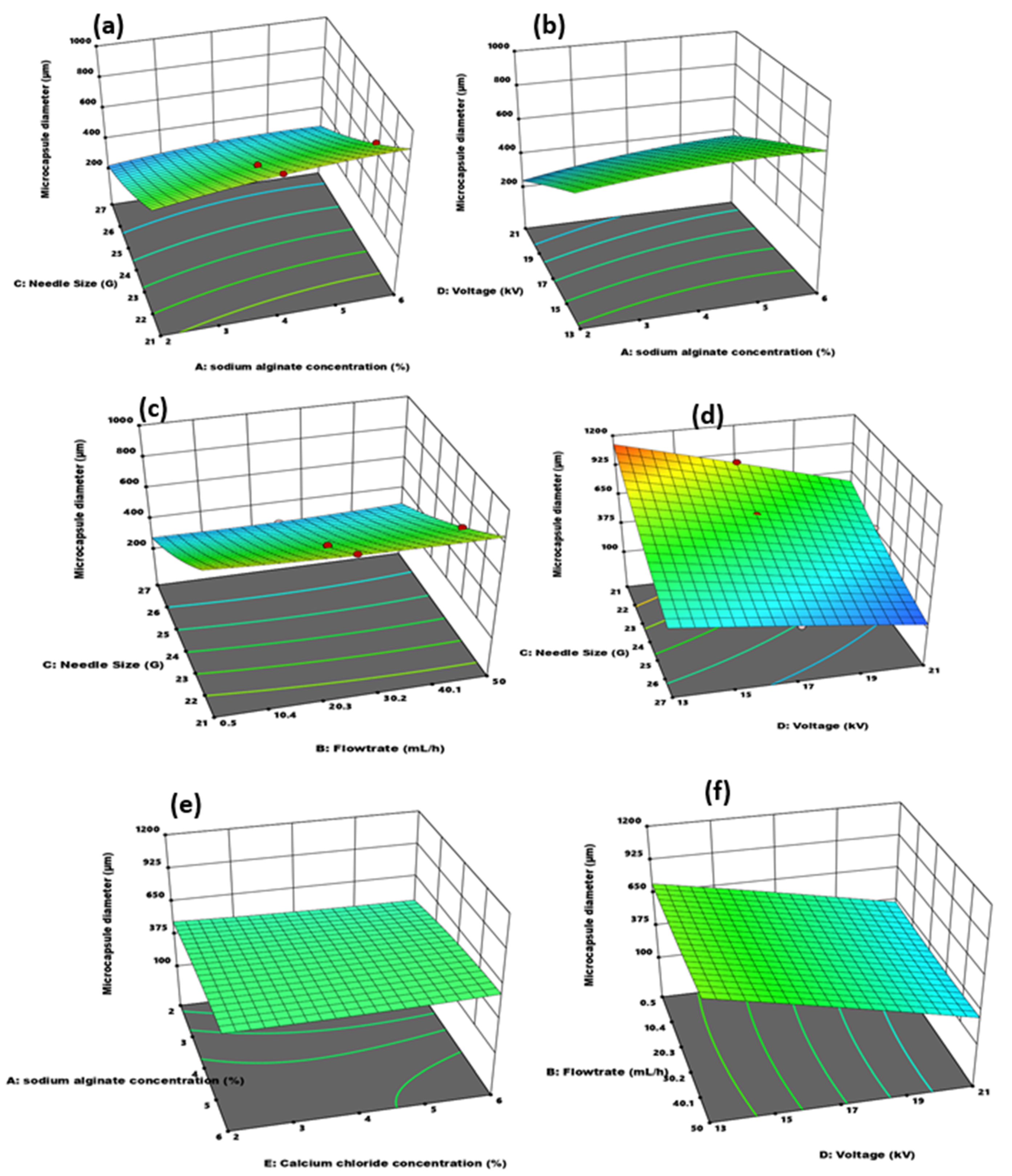
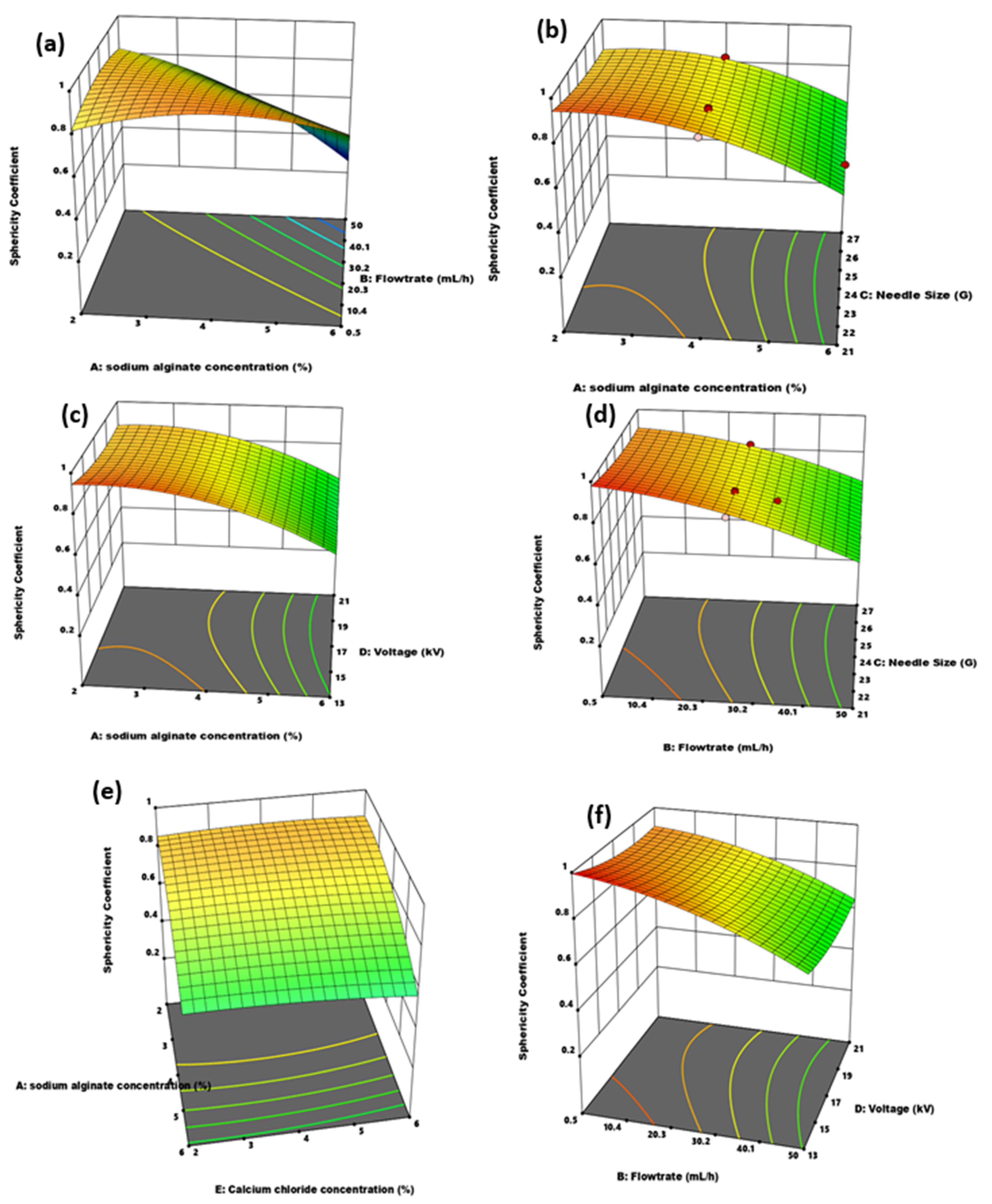
| Factor | Name | Units | Coded Low | Coded High |
|---|---|---|---|---|
| A(X1) | Sodium alginate concentration | % | 2.00 | 6.00 |
| B(X2) | Flowrate | mL/h | 0.50 | 50.00 |
| C(X3) | Needle size | G | 21.00 | 27.00 |
| D(X4) | Voltage | kV | 13.00 | 21.00 |
| E(X5) | Calcium chloride concentration | % | 2.00 | 6.00 |
| Response | Name | Units | Observations | Minimum | Maximum | Mean | Std. Dev. | Ratio |
|---|---|---|---|---|---|---|---|---|
| R1 | Microcapsule diameter | µm | 50.00 | 75.253 | 1193.15 | 523.87 | 326.21 | 15.86 |
| R2 | sphericity coefficient | N/A | 50.00 | 0.29632 | 0.9956 | 0.7731 | 0.1865 | 3.36 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 5.212 × 106 | 20 | 2.606 × 105 | 3219.25 | <0.0001 |
| A(X1)-sodium alginate concentration | 57,254.67 | 1 | 57,254.67 | 707.30 | <0.0001 |
| B(X2)-Flowrate | 424.16 | 1 | 424.16 | 5.24 | 0.0295 |
| C(X3)-Needle Size | 2.153 × 106 | 1 | 2.153 × 106 | 26,602.98 | <0.0001 |
| D(X4)-Voltage | 9.512 × 105 | 1 | 9.512 × 105 | 11,751.21 | <0.0001 |
| E(X5)-Calcium chloride concentration | 3.13 | 1 | 3.13 | 0.0386 | 0.8456 |
| AB(X1X2) | 320.66 | 1 | 320.66 | 3.96 | 0.0561 |
| AC(X1X3) | 4144.28 | 1 | 4144.28 | 51.20 | <0.0001 |
| AD(X1X4) | 6493.40 | 1 | 6493.40 | 80.22 | <0.0001 |
| AE(X1X5) | 4650.78 | 1 | 4650.78 | 57.45 | <0.0001 |
| BC(X2X3) | 4288.83 | 1 | 4288.83 | 52.98 | <0.0001 |
| BD(X2X4) | 3390.96 | 1 | 3390.96 | 41.89 | <0.0001 |
| CD(X3X4) | 76,976.49 | 1 | 76,976.49 | 950.94 | <0.0001 |
| CE(X3X5) | 1514.59 | 1 | 1514.59 | 18.71 | 0.0002 |
| DE(X4X5) | 3414.89 | 1 | 3414.89 | 42.19 | <0.0001 |
| 1566.25 | 1 | 1566.25 | 19.35 | 0.0001 | |
| 647.87 | 1 | 647.87 | 8.00 | 0.0084 | |
| 1459.96 | 1 | 1459.96 | 18.04 | 0.0002 | |
| Residual | 2347.49 | 29 | 80.95 | ||
| Lack of Fit | 1568.52 | 22 | 71.30 | 0.6407 | 0.8006 |
| Pure Error | 778.96 | 7 | 111.28 | ||
| Cor Total | 5.214 × 106 | 49 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 1.69 | 20 | 0.0847 | 253.24 | <0.0001 |
| A(X1)-sodium alginate concentration | 0.4518 | 1 | 0.4518 | 1350.64 | <0.0001 |
| B(X2)-Flowrate | 0.4692 | 1 | 0.4692 | 1402.38 | <0.0001 |
| C(X3)-Needle Size | 0.0165 | 1 | 0.0165 | 49.20 | <0.0001 |
| D(X4)-Voltage | 0.0222 | 1 | 0.0222 | 66.32 | <0.0001 |
| E(X5)-Calcium chloride concentration | 0.0014 | 1 | 0.0014 | 4.28 | 0.0475 |
| AB(X1X2) | 0.4440 | 1 | 0.4440 | 1327.09 | <0.0001 |
| AC(X1X3) | 0.0070 | 1 | 0.0070 | 21.02 | <0.0001 |
| AE(X1X5) | 0.0021 | 1 | 0.0021 | 6.36 | 0.0174 |
| BC(X2X3) | 0.0041 | 1 | 0.0041 | 12.21 | 0.0015 |
| BD(X2X4) | 0.0027 | 1 | 0.0027 | 8.15 | 0.0079 |
| BE(X2X5) | 0.0080 | 1 | 0.0080 | 23.95 | <0.0001 |
| CE(X3X5) | 0.0072 | 1 | 0.0072 | 21.54 | <0.0001 |
| DE(X4X5) | 0.0040 | 1 | 0.0040 | 11.90 | 0.0017 |
| A2(X12) | 0.0179 | 1 | 0.0179 | 53.42 | <0.0001 |
| B2(X22) | 0.0089 | 1 | 0.0089 | 26.60 | <0.0001 |
| D2(X42) | 0.0032 | 1 | 0.0032 | 9.57 | 0.0044 |
| Residual | 0.0097 | 29 | 0.0003 | ||
| Lack of Fit | 0.0083 | 22 | 0.0004 | 1.83 | 0.2093 |
| Pure Error | 0.0014 | 7 | 0.0002 | ||
| Cor Total | 1.70 | 49 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anani, J.; Noby, H.; Zkria, A.; Yoshitake, T.; ElKady, M. Monothetic Analysis and Response Surface Methodology Optimization of Calcium Alginate Microcapsules Characteristics. Polymers 2022, 14, 709. https://doi.org/10.3390/polym14040709
Anani J, Noby H, Zkria A, Yoshitake T, ElKady M. Monothetic Analysis and Response Surface Methodology Optimization of Calcium Alginate Microcapsules Characteristics. Polymers. 2022; 14(4):709. https://doi.org/10.3390/polym14040709
Chicago/Turabian StyleAnani, Joshua, Hussien Noby, Abdelrahman Zkria, Tsuyoshi Yoshitake, and Marwa ElKady. 2022. "Monothetic Analysis and Response Surface Methodology Optimization of Calcium Alginate Microcapsules Characteristics" Polymers 14, no. 4: 709. https://doi.org/10.3390/polym14040709
APA StyleAnani, J., Noby, H., Zkria, A., Yoshitake, T., & ElKady, M. (2022). Monothetic Analysis and Response Surface Methodology Optimization of Calcium Alginate Microcapsules Characteristics. Polymers, 14(4), 709. https://doi.org/10.3390/polym14040709









