DMA of TPU Films and the Modelling of Their Viscoelastic Properties for Noise Reduction in Jet Engines
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
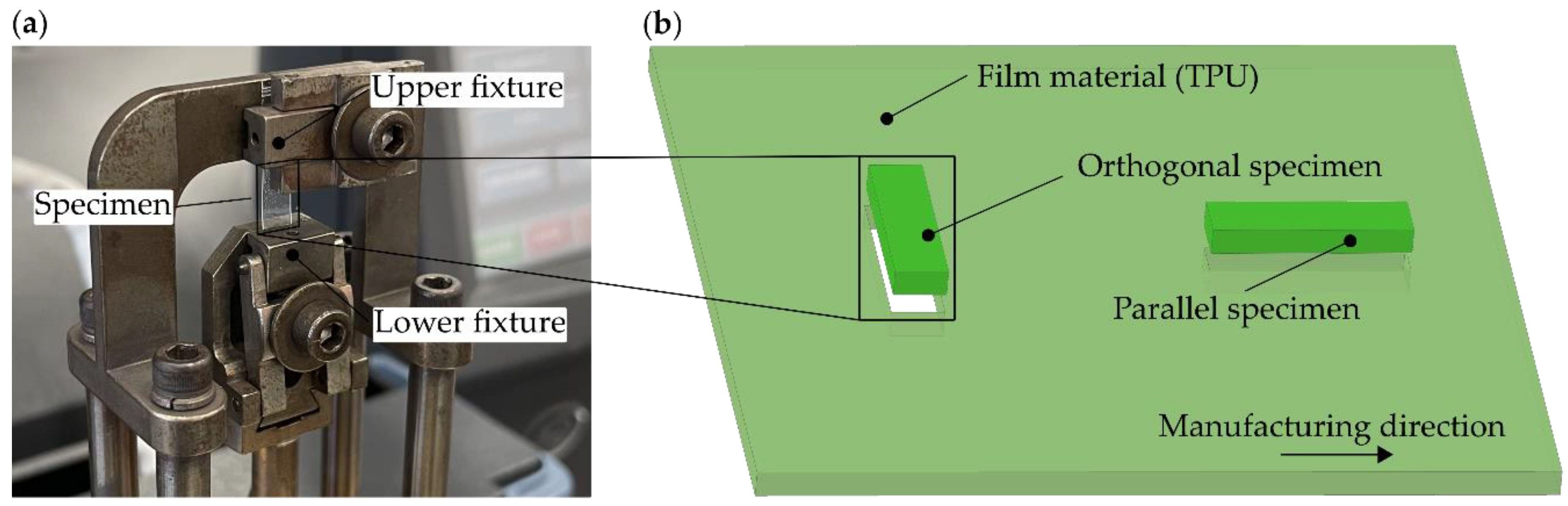
2.2. Experimental Apparatus and Procedure
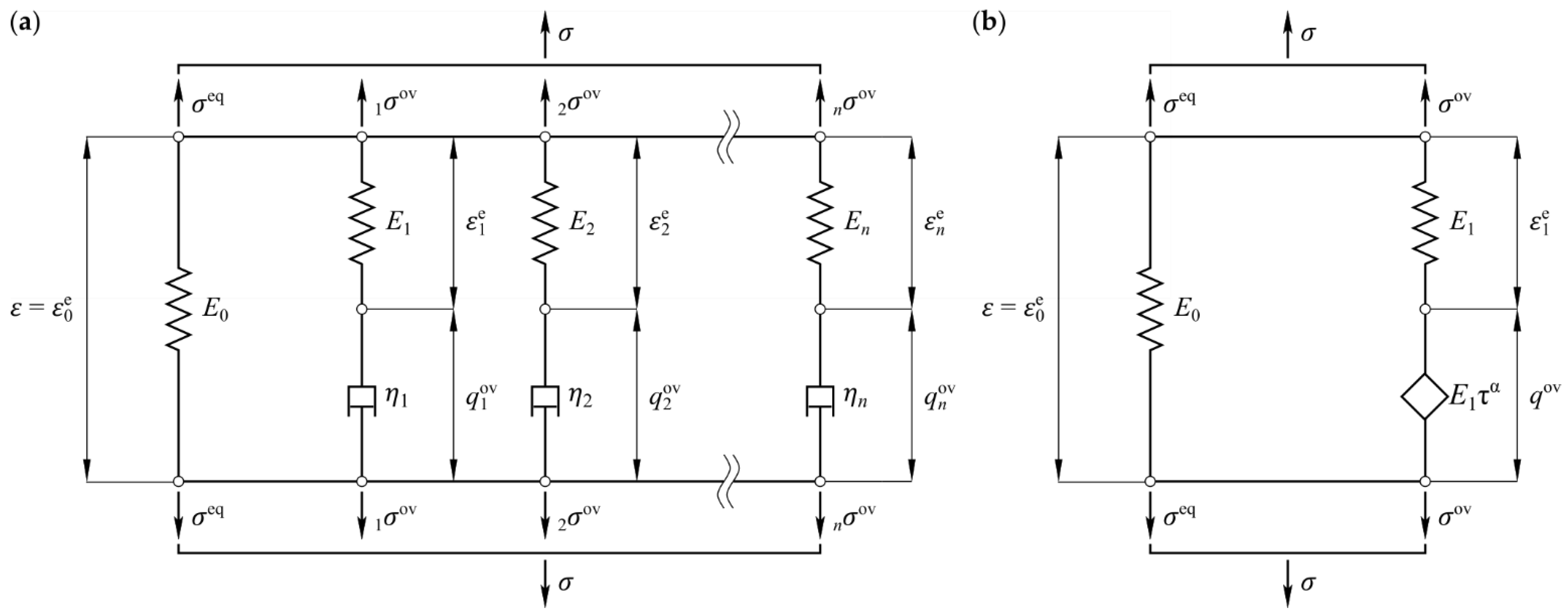
2.3. Viscoelastic Material Modelling
3. Results and Discussion
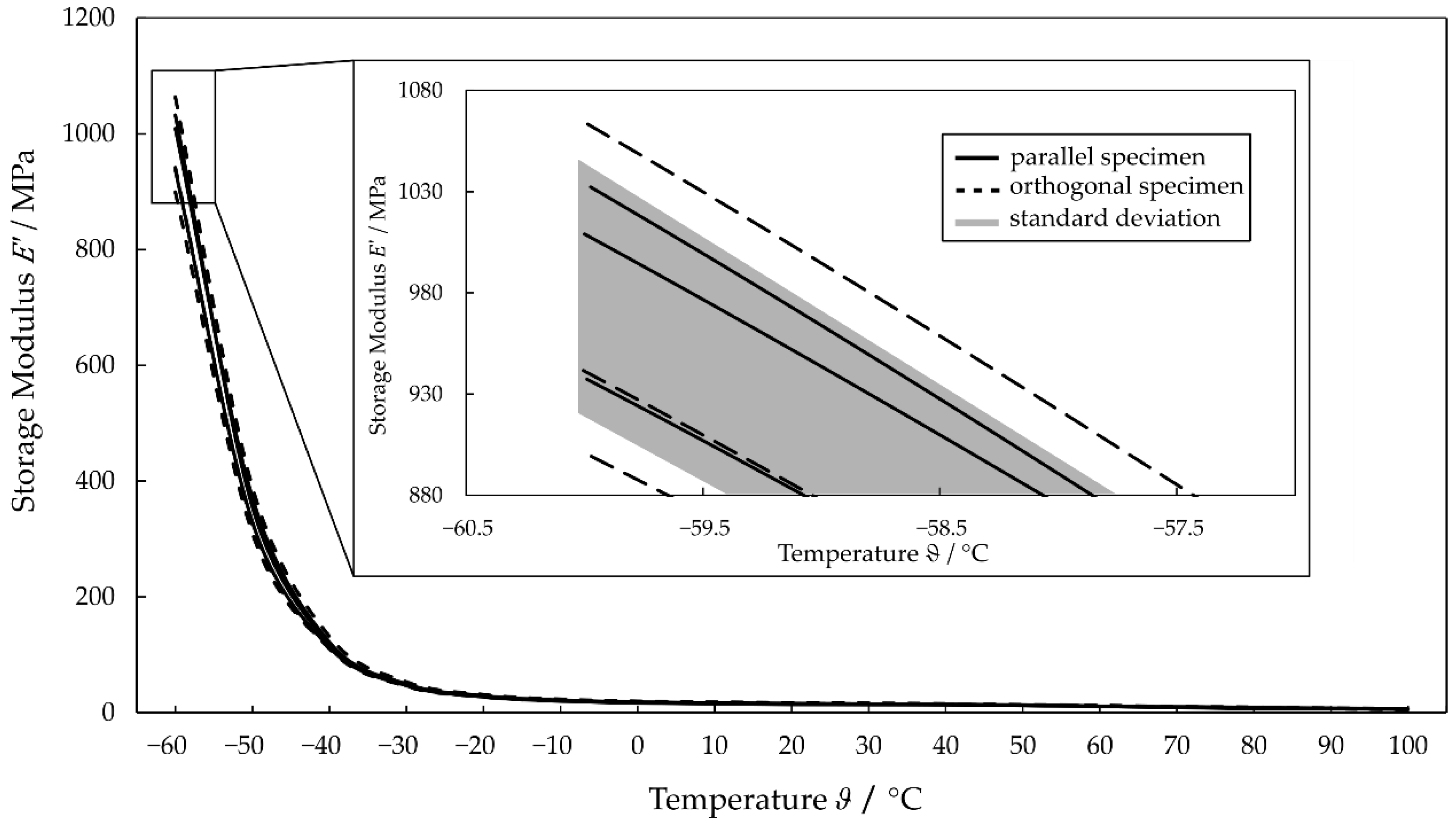
3.1. Analysys of Production-Related Material Orthotropy
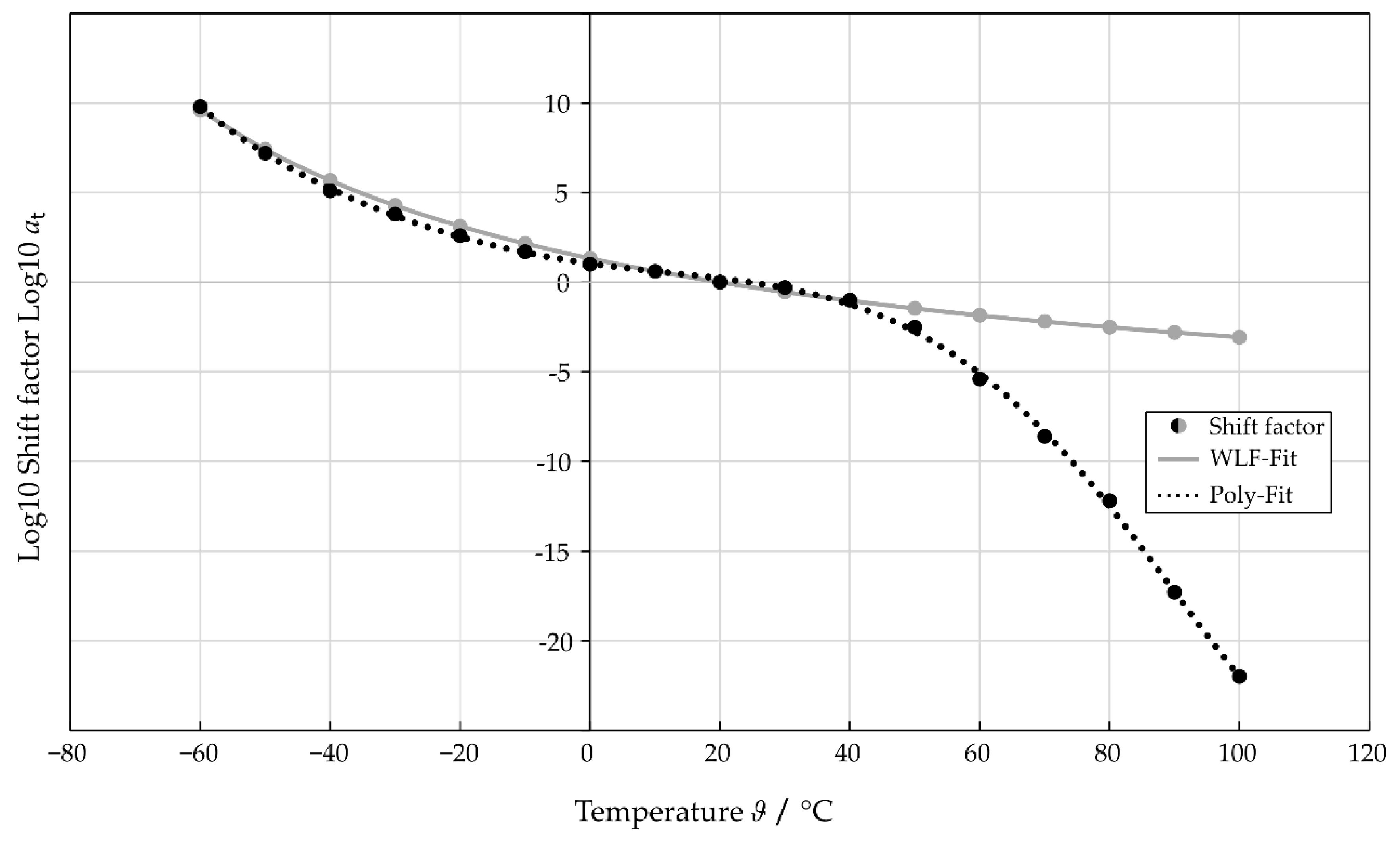
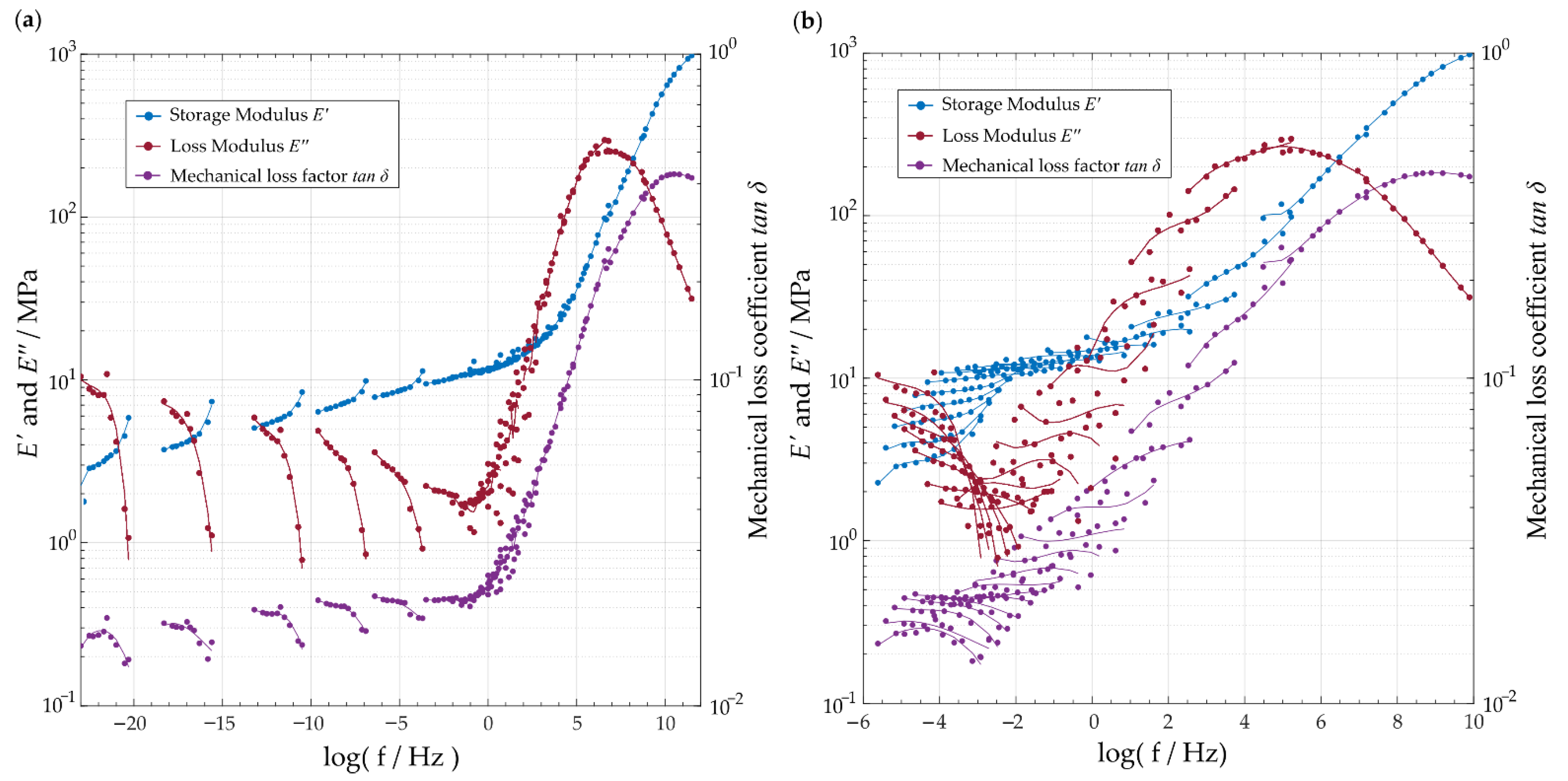
3.2. Frequency Dependent Complex Modulus
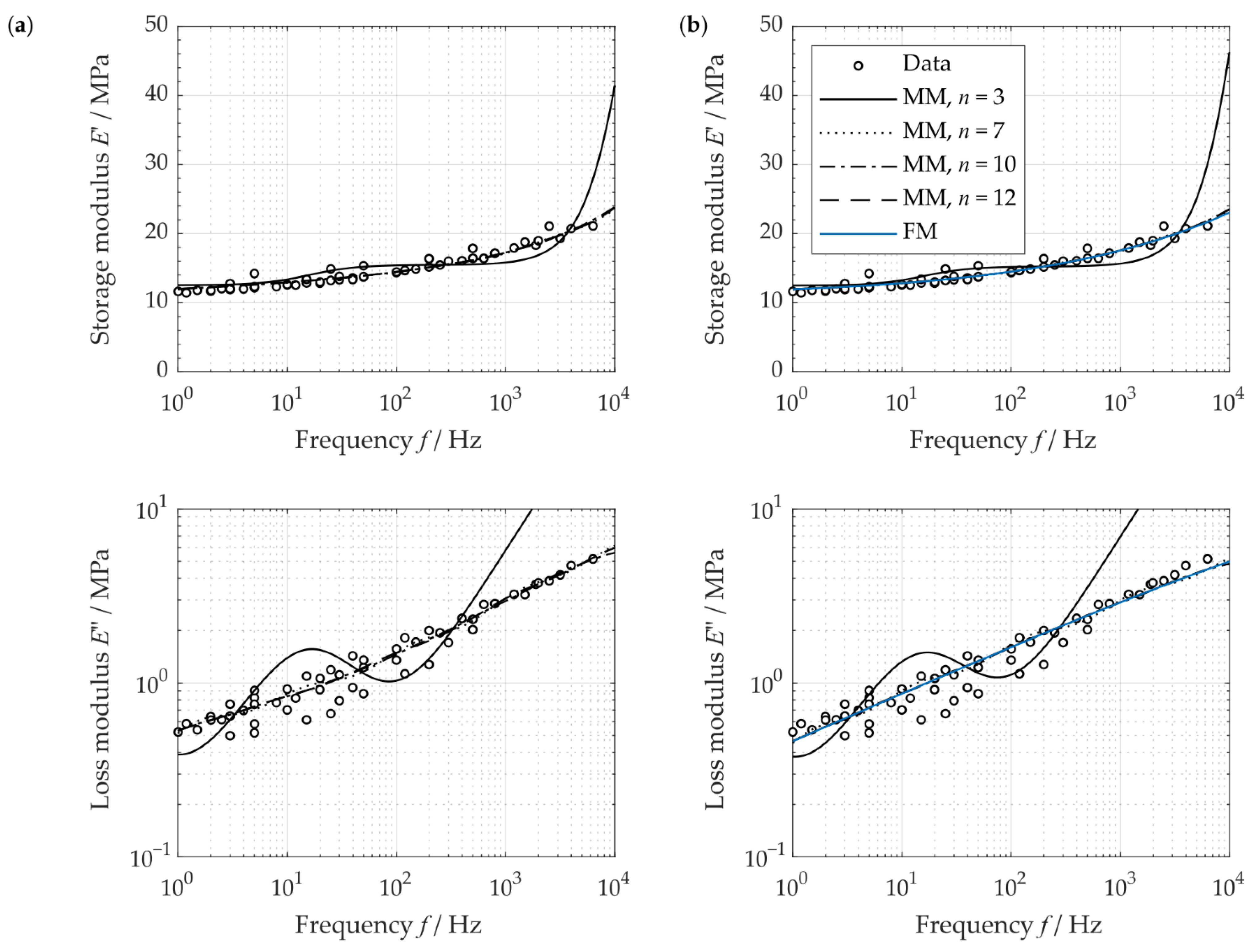
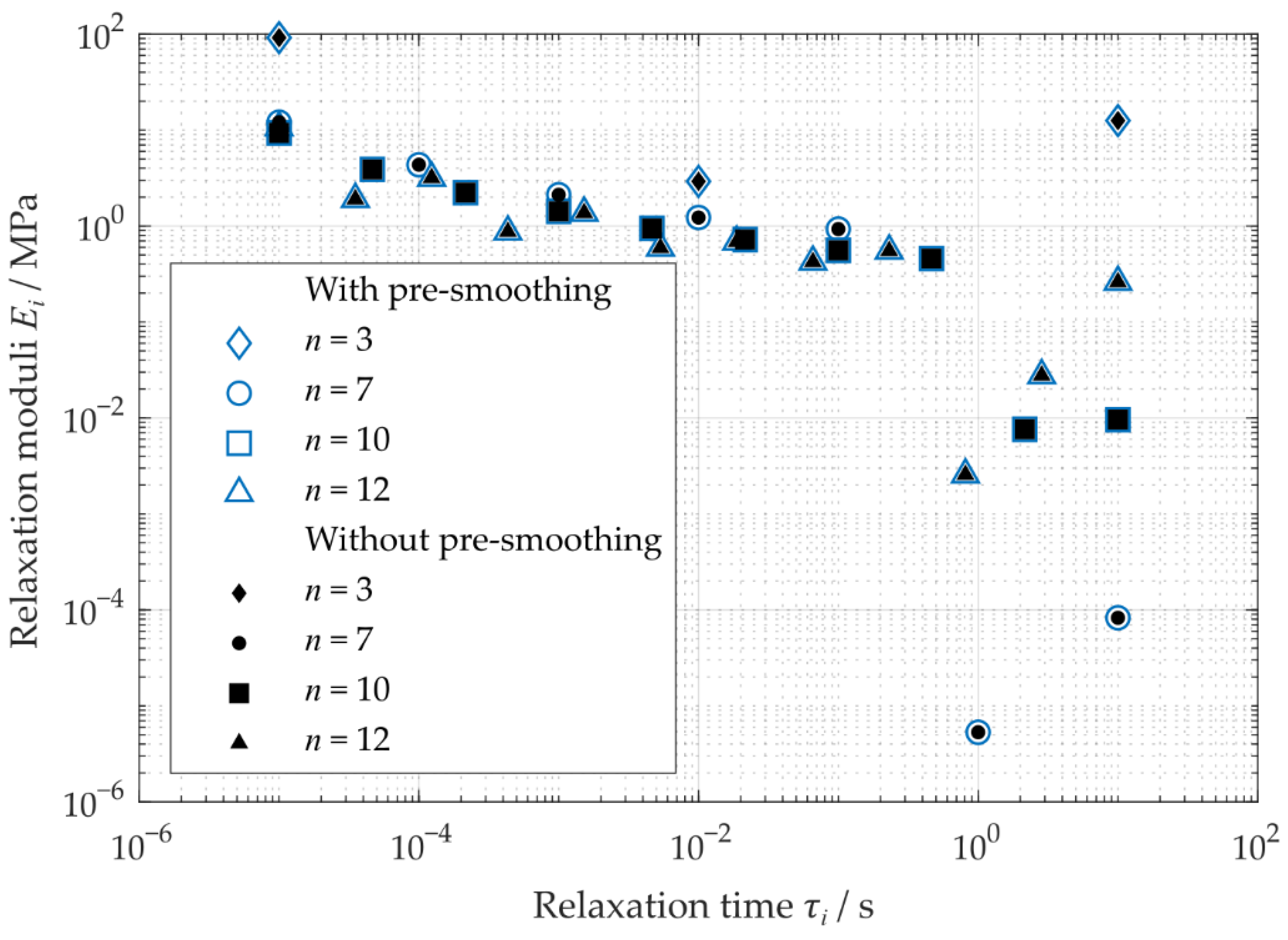
3.3. Identified Viscoelastic Material Parameter
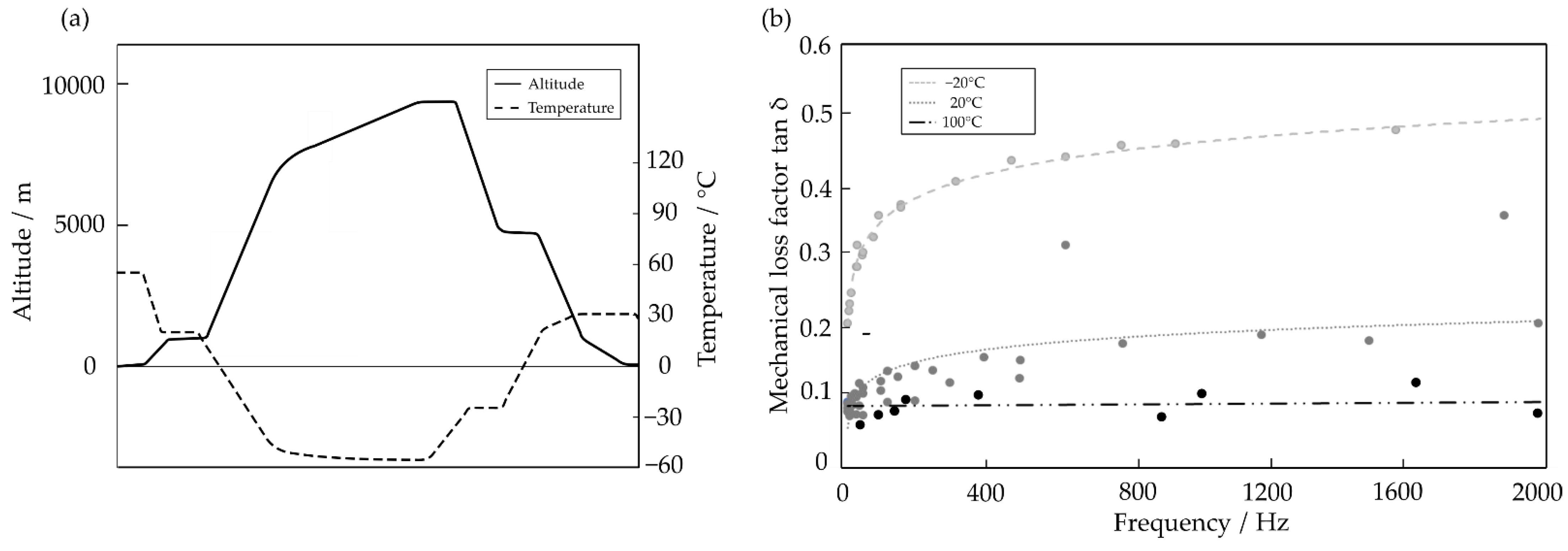
3.4. Effect of Flight Cycle Conditions on Mechanical Properties
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- European Safety Agency. Certification Specification and Acceptable Means of Compliance and Guidance Material for Aircraft Noise CS-36; European Safety Agency: Cologne, Germany, 2016. [Google Scholar]
- Kurzke, J. Fundamental Differences Between Conventional and Geared Turbofans. In Volume 1: Aircraft Engine; Ceramics; Coal, Biomass and Alternative Fuels; Controls, Diagnostics and Instrumentation; Education; Electric Power; Awards and Honors; ASME Turbo Expo: Orlando, FL, USA, 2009; pp. 145–153. ISBN 978-0-7918-4882-1. [Google Scholar]
- Carolus, T.; Schneider, M.; Reese, H. Axial flow fan broad-band noise and prediction. J. Sound Vib. 2007, 300, 50–70. [Google Scholar] [CrossRef]
- Rolls-Royce Public Limited Company. The Jet Engine, 6th ed.; John Wiley & Sons Ltd. on Behalf of Rolls-Royce Plc: Chichester, UK, 2015; ISBN 9781119065999. [Google Scholar]
- Li, L.; Liu, Y.; Zhang, F.; Sun, Z. Several explanations on the theoretical formula of Helmholtz resonator. Adv. Eng. Softw. 2017, 114, 361–371. [Google Scholar] [CrossRef]
- Sugimoto, R.; Murray, P.; Astley, R.J. Folded Cavity Liners for Turbofan Engine Intakes. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference (33rd AIAA Aeroacoustics Conference), Colorado Springs, CO, USA, 4–6 June 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012; p. 06042012, ISBN 978-1-60086-932-7. [Google Scholar]
- Hoeschler, K.; Sarradj, E.; Modler, N.; Enghardt, L. Novel Jet Engine Acoustic Liner with improved Broadband Noise Absorption. In Proceedings of the 31st Congress of the International Council of the Aeronautical Sciences, Belo Horizonte, Brazil, 9–14 September 2018. [Google Scholar]
- Dannemann, M.; Kucher, M.; Kunze, E.; Modler, N.; Knobloch, K.; Enghardt, L.; Sarradj, E.; Höschler, K. Experimental Study of Advanced Helmholtz Resonator Liners with Increased Acoustic Performance by Utilising Material Damping Effects. Appl. Sci. 2018, 8, 1923. [Google Scholar] [CrossRef]
- Knobloch, K.; Enghardt, L.; Bake, F. Helmholtz Resonator Liner with Flexible Walls. In Proceedings of the 2018 AIAA/CEAS Aeroacoustics Conference, Atlanta, GA, USA, 25–29 June 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA; p. 06252018, ISBN 978-1-62410-560-9. [Google Scholar]
- Neubauer, M.; Dannemann, M.; Herzer, N.; Schwarz, B.; Modler, N. Analysis of a Film Forming Process through Coupled Image Correlation and Infrared Thermography. Polymers 2022, 14, 1231. [Google Scholar] [CrossRef] [PubMed]
- Read, B.E.; Dean, G.D. The Determination of Dynamic Properties of Polymers and Composites, 1st ed.; Wiley: New York, NY, USA, 1978; ISBN 0-470-26543-4. [Google Scholar]
- Menard, K.P.; Menard, N.R. Dynamic Mechanical Analysis, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2020; ISBN 9780429190308. [Google Scholar]
- Govorčin Bajsić, E.; Rek, V.; Ćosić, I. Preparation and Characterization of Talc Filled Thermoplastic Polyurethane/Polypropylene Blends. J. Polym. 2014, 2014, 1–8. [Google Scholar] [CrossRef]
- Strankowski, M.; Korzeniewski, P.; Strankowska, J.; S, A.A.; Thomas, S. Morphology, Mechanical and Thermal Properties of Thermoplastic Polyurethane Containing Reduced Graphene Oxide and Graphene Nanoplatelets. Materials 2018, 11, 82. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; He, M.; Qin, S.; Yu, J.; Guo, J.; Xu, G. Study on dynamic mechanical, thermal, and mechanical properties of long glass fiber reinforced thermoplastic polyurethane/poly(butylene terephthalate) composites. Polym. Compos. 2018, 39, 63–72. [Google Scholar] [CrossRef]
- Salem, T.F.; Tirkes, S.; Akar, A.O.; Tayfun, U. Enhancement of mechanical, thermal and water uptake performance of TPU/jute fiber green composites via chemical treatments on fiber surface. e-Polymers 2020, 20, 133–143. [Google Scholar] [CrossRef]
- Beloshenko, V.; Beygelzimer, Y.; Chishko, V.; Savchenko, B.; Sova, N.; Verbylo, D.; Voznyak, A.; Vozniak, I. Mechanical Properties of Flexible TPU-Based 3D Printed Lattice Structures: Role of Lattice Cut Direction and Architecture. Polymers 2021, 13, 2986. [Google Scholar] [CrossRef] [PubMed]
- Neubauer, M.; Schwaericke, F.; Radmann, V.; Sarradj, E.; Modler, N.; Dannemann, M. Material Selection Process for Acoustic and Vibration Applications Using the Example of a Plate Resonator. Materials 2022, 15, 2935. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The Temperature Dependence of Relaxation Mechanisms in Amorphous Polymers and Other Glass-forming Liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Chae, S.-H.; Zhao, J.-H.; Edwards, D.R.; Ho, P.S. Characterization of the Viscoelasticity of Molding Compounds in the Time Domain. J. Electron. Mater. 2010, 39, 419–425. [Google Scholar] [CrossRef]
- Trivedi, A.R.; Siviour, C.R. A novel methodology for predicting the high rate mechanical response of polymers from low rate data: Application to (plasticised) poly(vinyl chloride). Mech. Time-Depend Mater. 2021, 25, 383–409. [Google Scholar] [CrossRef]
- Lakes, R.S. Viscoelastic Materials; Cambridge University Press: Cambridge, UK, 2009; ISBN 978-0-521-88568-3. [Google Scholar]
- Nasdala, L. FEM-Formelsammlung Statik und Dynamik: Hintergrundinformationen, Tipps und Tricks, 1st ed.; Vieweg+Teubner Verlag/Springer Fachmedien Wiesbaden GmbH Wiesbaden: Wiesbaden, Germany, 2010. [Google Scholar]
- Schiessel, H.; Metzler, R.; Blumen, A.; Nonnenmacher, T.F. Generalized viscoelastic models: Their fractional equations with solutions. J. Phys. A: Math. Gen. 1995, 28, 6567–6584. [Google Scholar] [CrossRef]
- Koeller, R.C. Applications of Fractional Calculus to the Theory of Viscoelasticity. J. Appl. Mech. 1984, 51, 299–307. [Google Scholar] [CrossRef]
- Mainardi, F.; Gorenflo, R. Time-fractional derivatives in relaxation processes: A tutorial survey. Fract. Calc. Appl. Anal. 2007, 10, 269–308. [Google Scholar]
- Monje, C.A.; Chen, Y.; Vinagre, B.M.; Xue, D.; Feliu, V. Fractional-Order Systems and Controls: Fundamentals and Applications, 1st ed.; Springer: London, UK, 2010; ISBN 978-1-84996-334-3. [Google Scholar]
- Park, S.W.; Kim, Y.R. Fitting Prony-Series Viscoelastic Models with Power-Law Presmoothing. J. Mater. Civ. Eng. 2001, 13, 26–32. [Google Scholar] [CrossRef]
- Elastollan, N.N. Physical Properties. Available online: https://plastics-rubber.basf.com/global/assets/en/Performance_Polymers/Brochures/Elastollan/Elastollan_Properties-Physical-Properties.pdf (accessed on 27 October 2022).
- Kucher, M.; Dannemann, M.; Böhm, R.; Modler, N. An Experimental Approach for the Determination of the Mechanical Properties of Base-Excited Polymeric Specimens at Higher Frequency Modes. Vibration 2022, 5, 429–441. [Google Scholar] [CrossRef]
- Capps, R.N. Dynamic Young’s moduli of some commercially available polyurethanes. J. Acoust. Soc. Am. 1983, 73, 2000–2005. [Google Scholar] [CrossRef]

| Temperature [°C] | |||||||
|---|---|---|---|---|---|---|---|
| Specimen 1 Parallel | Specimen 2 Parallel | Specimen 3P arallel | Specimen 4 Orthogonal | Specimen 5 Orthogonal | Specimen 6 Orthogonal | Relative Standard Deviation [%] | |
| −60 | 1032.22 | 1009.03 | 937.32 | 1063.32 | 899.23 | 941.61 | 5.94 |
| −40 | 118.79 | 121.74 | 112.63 | 131.49 | 111.11 | 109.92 | 6.37 |
| −20 | 28.10 | 29.06 | 27.22 | 31.07 | 28.11 | 26.83 | 4.90 |
| 0 | 17.17 | 18.40 | 16.76 | 19.75 | 17.96 | 17.17 | 5.61 |
| 20 | 14.41 | 15.79 | 14.24 | 17.07 | 15.55 | 15.08 | 6.17 |
| 40 | 13.68 | 14.40 | 13.54 | 15.28 | 14.23 | 14.19 | 3.97 |
| 60 | 10.81 | 11.44 | 10.70 | 12.30 | 11.41 | 11.33 | 4.61 |
| 80 | 6.98 | 8.93 | 8.26 | 9.43 | 8.51 | 8.41 | 8.92 |
| 100 | 0.00 | 6.44 | 5.98 | 6.55 | 5.56 | 4.74 | 11.25 |
| 3 | 7 | 10 | 12 | |
|---|---|---|---|---|
| Without pre-smoothing | ||||
| Error measure | 0.294 | 0.111 | 0.109 | 0.109 |
| With pre-smoothing | ||||
| Error measure | 0.298 | 0.124 | 0.122 | 0.122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Neubauer, M.; Pohl, M.; Kucher, M.; Böhm, R.; Höschler, K.; Modler, N. DMA of TPU Films and the Modelling of Their Viscoelastic Properties for Noise Reduction in Jet Engines. Polymers 2022, 14, 5285. https://doi.org/10.3390/polym14235285
Neubauer M, Pohl M, Kucher M, Böhm R, Höschler K, Modler N. DMA of TPU Films and the Modelling of Their Viscoelastic Properties for Noise Reduction in Jet Engines. Polymers. 2022; 14(23):5285. https://doi.org/10.3390/polym14235285
Chicago/Turabian StyleNeubauer, Moritz, Michael Pohl, Michael Kucher, Robert Böhm, Klaus Höschler, and Niels Modler. 2022. "DMA of TPU Films and the Modelling of Their Viscoelastic Properties for Noise Reduction in Jet Engines" Polymers 14, no. 23: 5285. https://doi.org/10.3390/polym14235285
APA StyleNeubauer, M., Pohl, M., Kucher, M., Böhm, R., Höschler, K., & Modler, N. (2022). DMA of TPU Films and the Modelling of Their Viscoelastic Properties for Noise Reduction in Jet Engines. Polymers, 14(23), 5285. https://doi.org/10.3390/polym14235285







