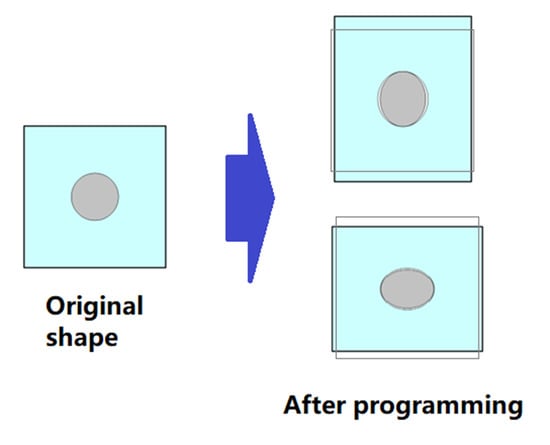
Evolution of Shore Hardness under Uniaxial Tension/Compression in Body-Temperature Programmable Elastic Shape Memory Hybrids
Abstract
1. Introduction
2. Materials, Samples Preparation and Experimental
2.1. Materials
2.2. Sample Preparation
2.3. Experimental Procedure
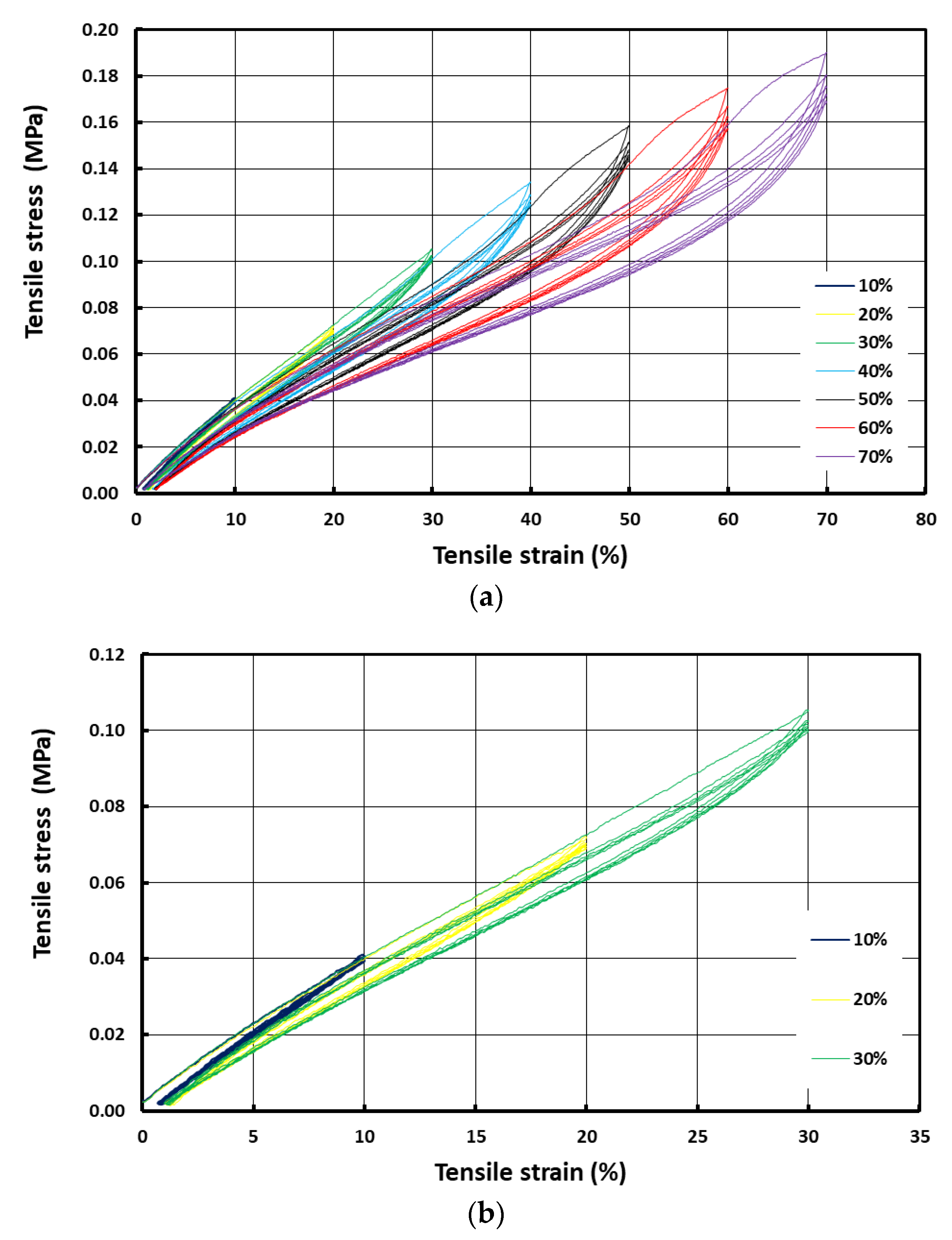
3. Results and Analysis
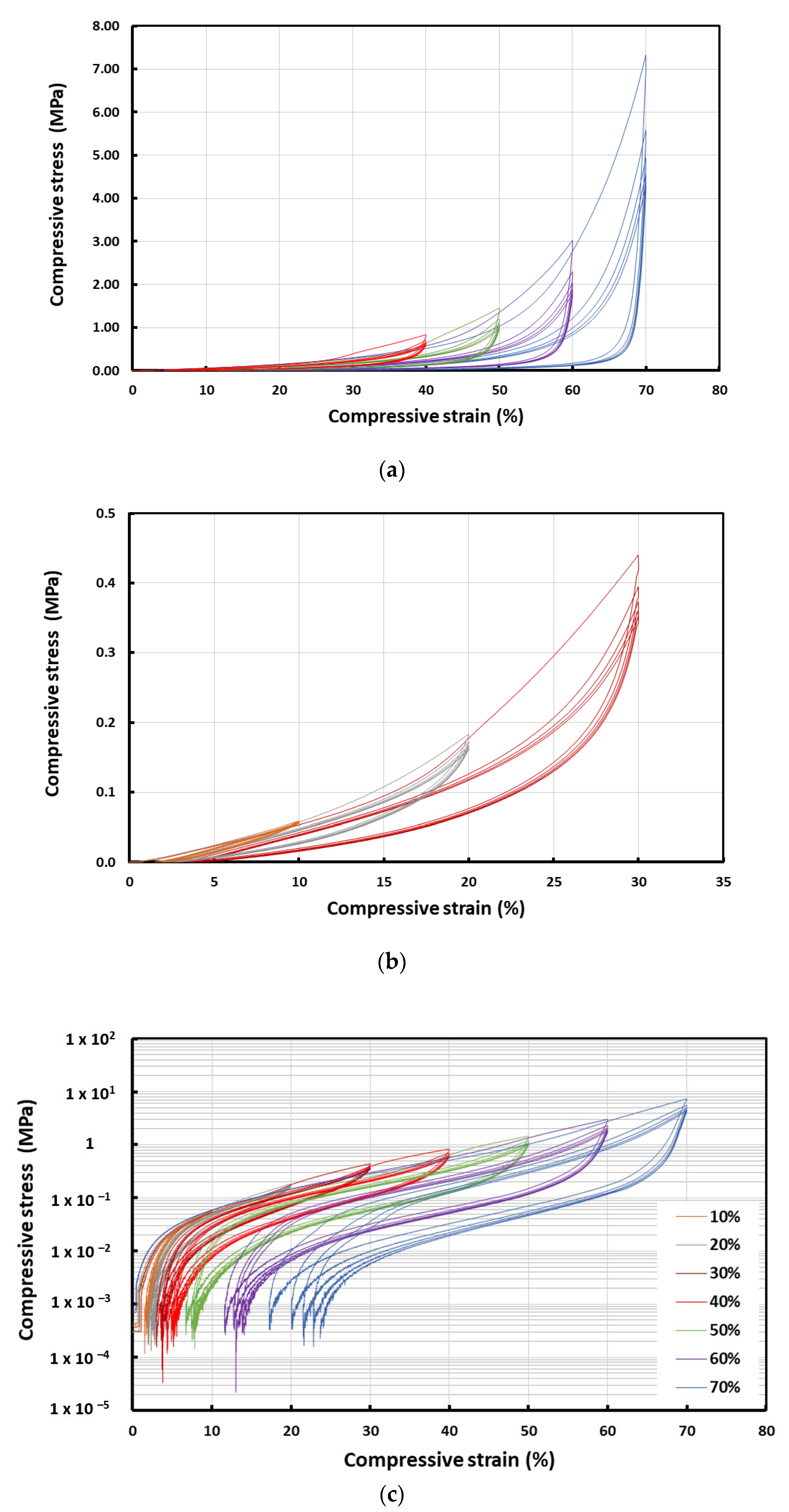
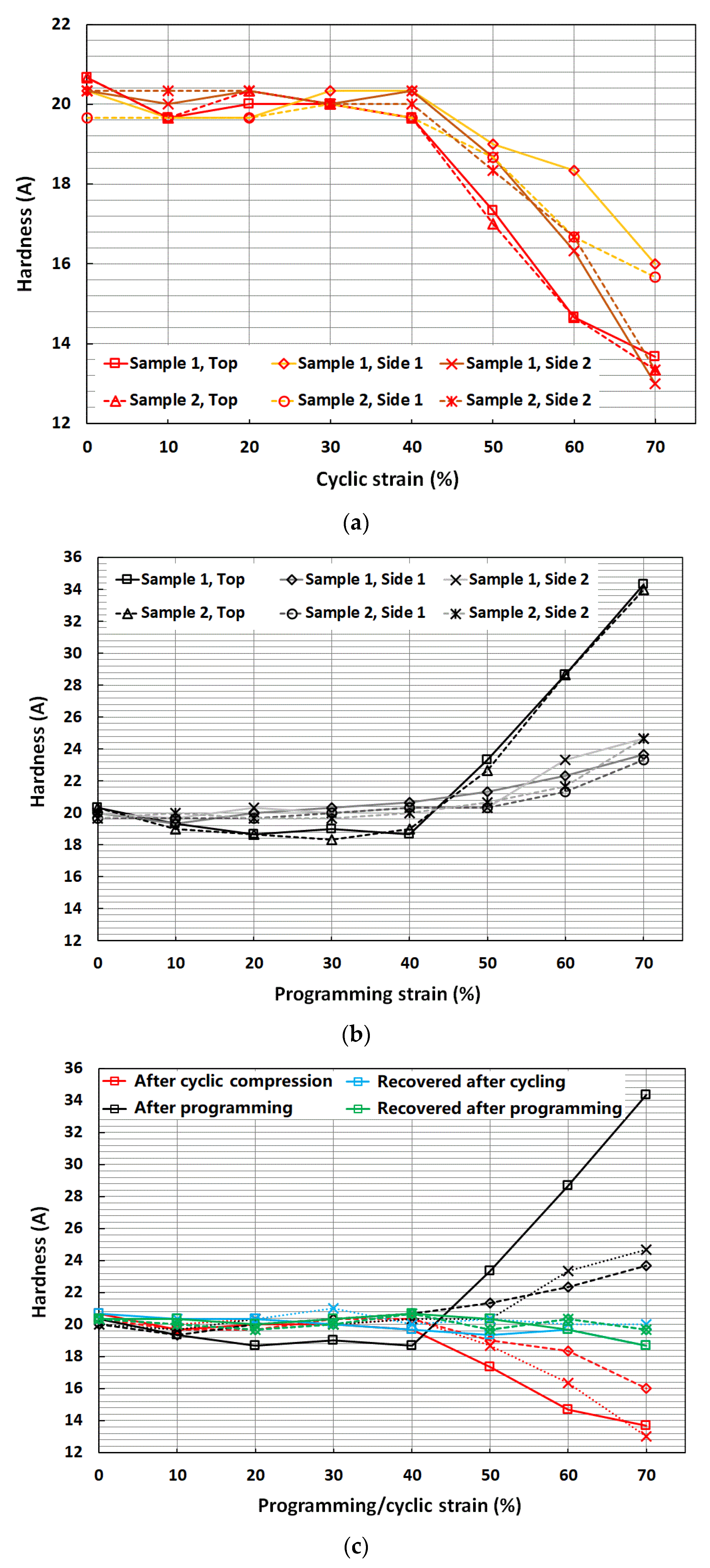
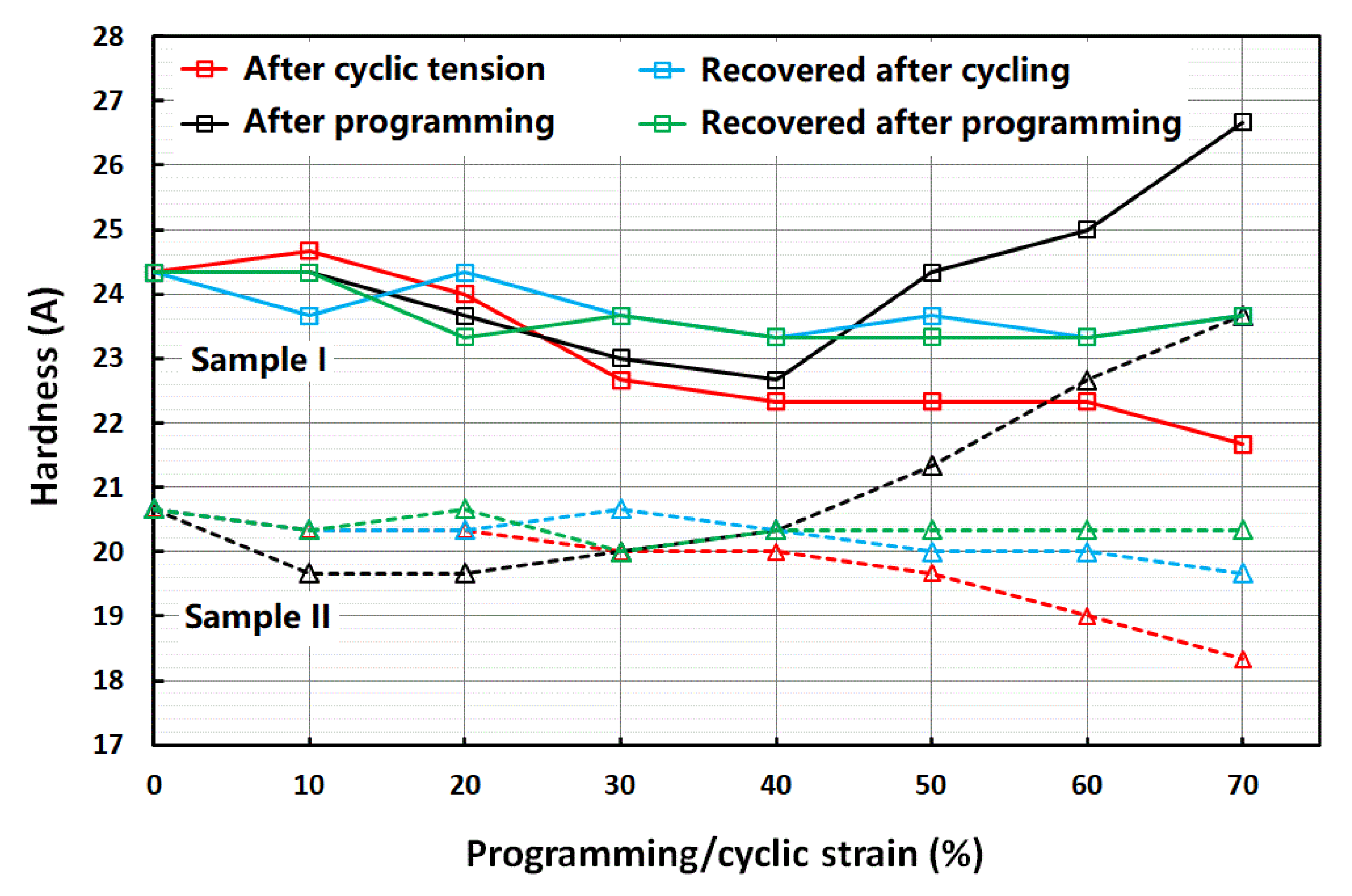
- After subjection to cyclic compression tests at 10, 20, 30, 40, 50, 60 and 70% strains;
- After the recovery of the samples that were subjected to cyclic compression in i;
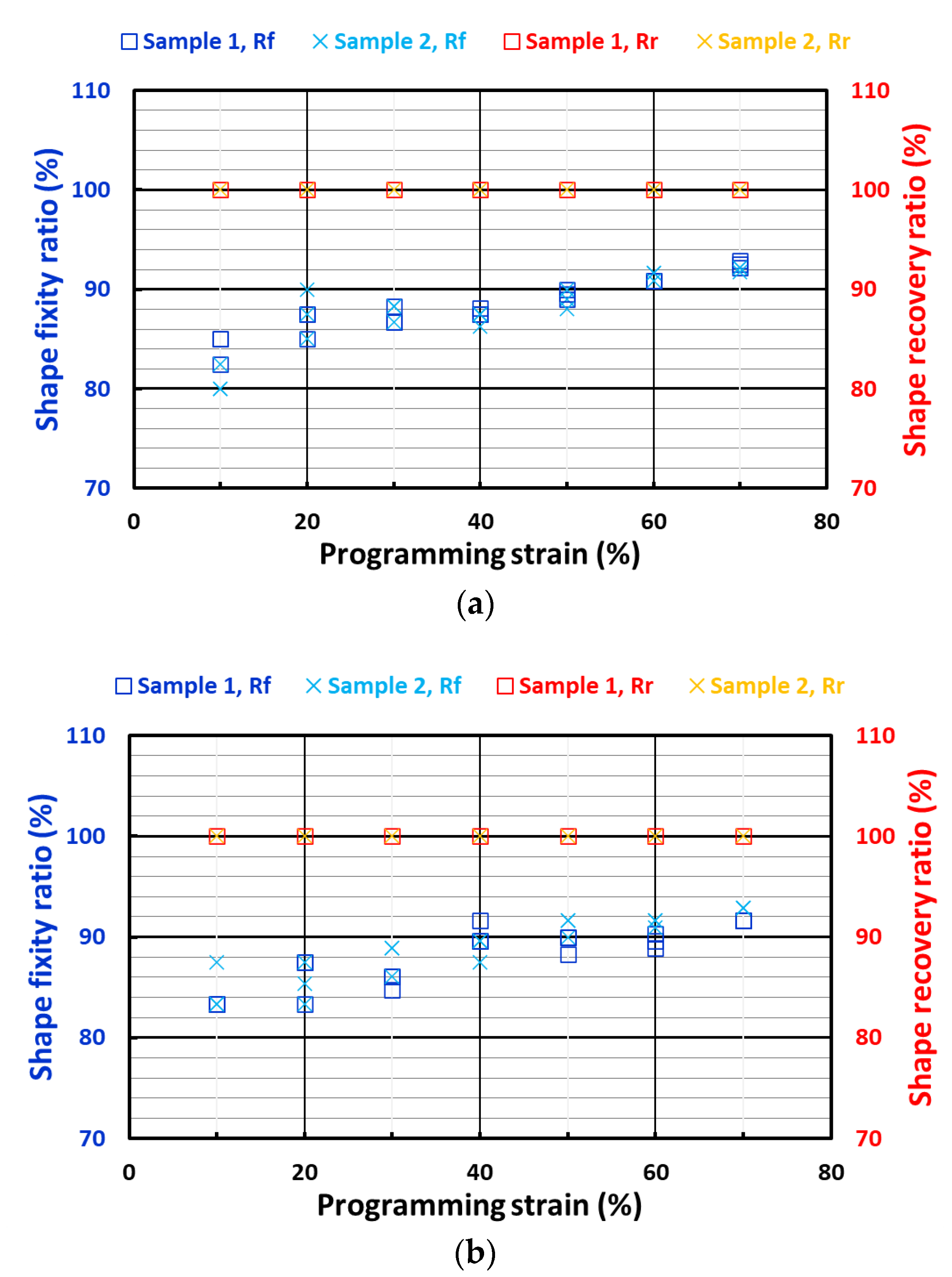
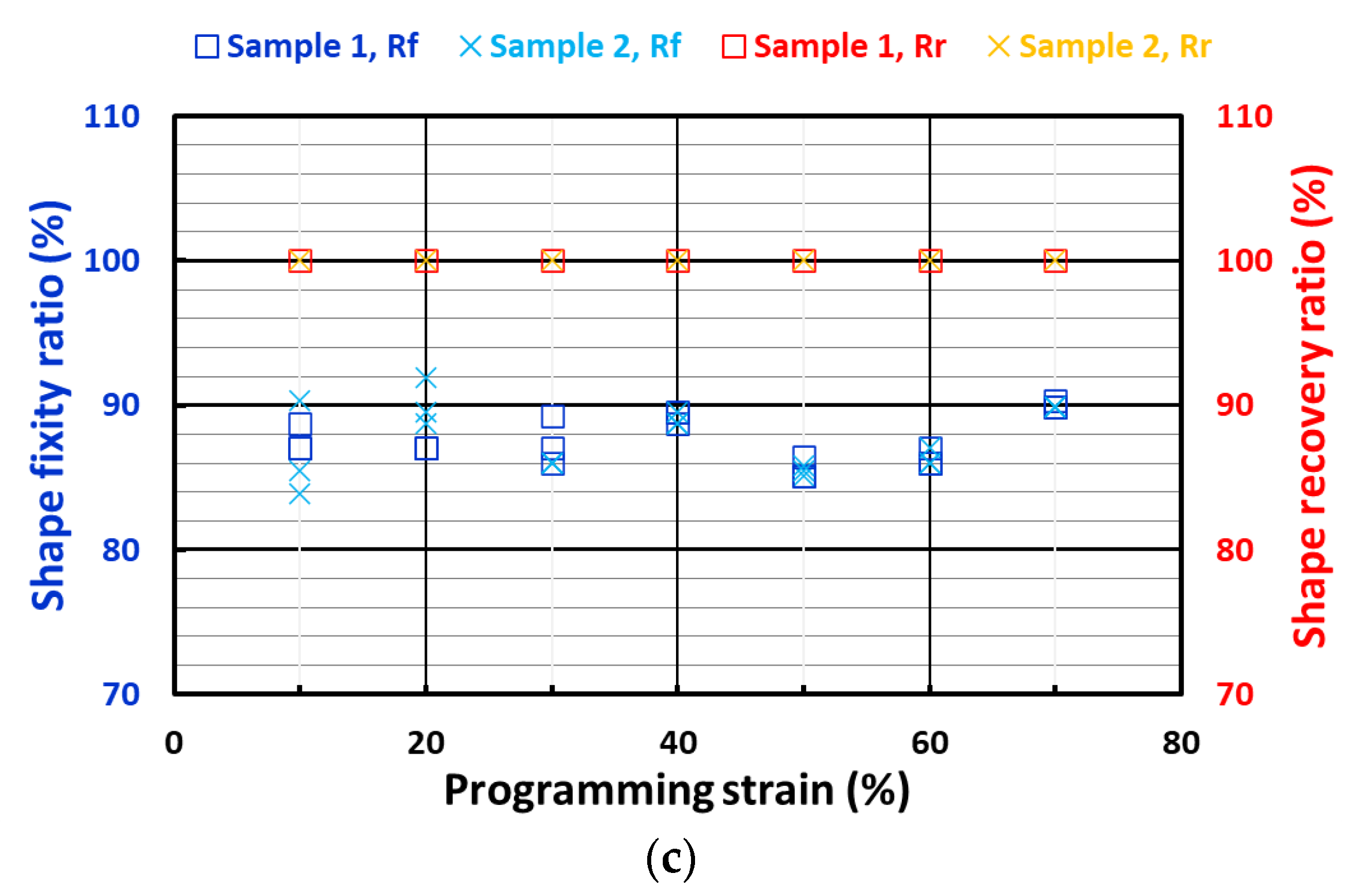
- After subjection to programming tests at 10, 20, 30, 40, 50, 60 and 70% strains;
- After the recovery of the samples that were subjected to programming in iii.
4. Mechanisms for Evolution of Hardness
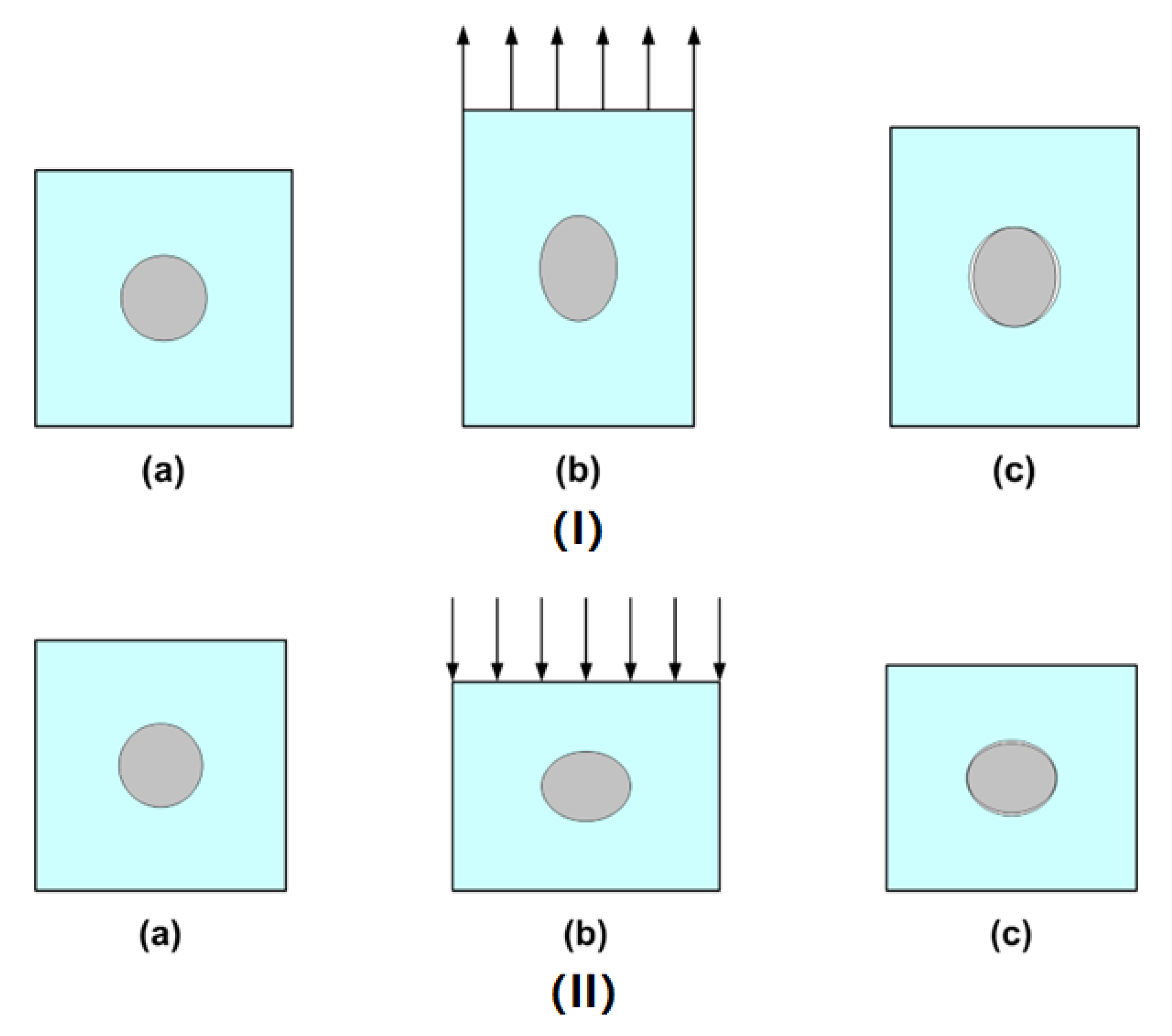
4.1. Debonding upon Loading
4.2. Hardness after Programming
5. Further Discussion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Otsuka, K.; Wayman, C.M. (Eds.) Shape Memory Materials; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Huang, W.M.; Ding, Z.; Wang, C.C.; Wei, J.; Zhao, Y.; Purnawali, H. Shape memory materials. Mater. Today 2010, 13, 54–61. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.; Ding, Z.; Zhao, Y.; Wang, C.; Purnawali, H.; Tang, C. Stimulus-responsive shape memory materials: A review. Mater. Des. 2012, 33, 577–640. [Google Scholar] [CrossRef]
- Huang, W.M.; Song, C.; Fu, Y.; Wang, C.; Zhao, Y.; Purnawali, H.; Lu, H.; Tang, C.; Ding, Z.; Zhang, J. Shaping tissue with shape memory materials. Adv. Drug Deliv. Rev. 2013, 65, 515–535. [Google Scholar] [CrossRef]
- Huang, W.M.; Zhao, Y.; Wang, C.C.; Ding, Z.; Purnawali, H.; Tang, C.; Zhang, J.L. Thermo/chemo-responsive shape memory effect in polymers: A sketch of working mechanisms, fundamentals and optimization. J. Polym. Res. 2012, 19, 9952. [Google Scholar] [CrossRef]
- Fan, K.; Huang, W.M.; Wang, C.C.; Ding, Z.; Zhao, Y.; Purnawali, H.; Liew, K.C.; Zheng, L.X. Water-responsive shape memory hybrid: Design concept and demonstration. Express Polym. Lett. 2011, 5, 409–416. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.; Wang, T.; Chen, H.; Renata, C.; He, L.; Lv, P.; Wang, C. An overview of elastic polymeric shape memory materials for comfort fitting. Mater. Des. 2017, 136, 238–248. [Google Scholar] [CrossRef]
- Ahmad, M.; Luo, J.; Xu, B.; Purnawali, H.; King, P.J.; Chalker, P.R.; Fu, Y.; Huang, W.; Miraftab, M. Synthesis and Characterization of Polyurethane-Based Shape-Memory Polymers for Tailored T-g around Body Temperature for Medical Applications. Macromol. Chem. Phys. 2011, 212, 592–602. [Google Scholar] [CrossRef]
- Wang, T.X.; Renata, C.; Chen, H.M.; Huang, W.M. Elastic shape memory hybrids programmable at around body-temperature for comfort fitting. Polymers 2017, 9, 674. [Google Scholar] [CrossRef]
- Naveen, B.S.; Naseem, A.B.M.; Ng, C.J.L.; Chan, J.W.; Lee, R.Z.X.; Teo, L.E.T.; Wang, T.; Nripan, M.; Huang, W.M. Body-Temperature Programmable Soft-Shape Memory Hybrid Sponges for Comfort Fitting. Polymers 2021, 13, 3501. [Google Scholar] [CrossRef]
- Zhu, G.; Xu, S.; Wang, J.; Zhang, L. Shape memory behaviour of radiation-crosslinked PCL/PMVS blends. Radiat. Phys. Chem. 2006, 75, 443–448. [Google Scholar] [CrossRef]
- Salvekar, A.V.; Zhou, Y.; Huang, W.M.; Wong, Y.S.; Venkatraman, S.S.; Shen, Z.; Zhu, G.; Cui, H.P. Shape/temperature memory phenomena in un-crosslinked poly-ɛ-caprolactone (PCL). Eur. Polym. J. 2015, 72, 282–295. [Google Scholar] [CrossRef]
- Chern, M.-J.; Yang, L.-Y.; Shen, Y.-K.; Hung, J.-H. 3D scaffold with PCL combined biomedical ceramic materials for bone tissue regeneration. Int. J. Precis. Eng. Manuf. 2013, 14, 2201–2207. [Google Scholar] [CrossRef]
- Wang, T.X.; Huang, W.M.; Aw, J.E.; He, L.W.; Vettorello, M. Comfort fitting using shape memory polymeric foam. J. Test. Eval. 2017, 45, 1201–1212. [Google Scholar] [CrossRef]
- Wang, C.C.; Huang, W.M.; Ding, Z.; Zhao, Y.; Purnawali, H.; Zheng, L.; Fan, H.; He, C.B. Rubber-like shape memory polymeric materials with repeatable thermal-assisted healing function. Smart Mater. Struct. 2012, 21, 115010. [Google Scholar] [CrossRef]
- Mullins, L. Softening of rubber by deformation. Rubber Chem. Technol. 1969, 42, 339–362. [Google Scholar] [CrossRef]
- Diani, J.; Fayolle, B.; Gilormini, P. A review on the Mullins effect. Eur. Polym. J. 2009, 45, 601–612. [Google Scholar] [CrossRef]
- Amin, A.; Alam, M.; Okui, Y. An improved hyperelasticity relation in modeling viscoelasticity response of natural and high damping rubbers in compression: Experiments, parameter identification and numerical verification. Mech. Mater. 2002, 34, 75–95. [Google Scholar] [CrossRef]
- Rickaby, S.; Scott, N. Cyclic stress-softening model for the Mullins effect in compression. Int. J. Non-Linear Mech. 2013, 49, 152–158. [Google Scholar] [CrossRef]
- Beatty, M.F. The Mullins Effect in a Pure Shear, in Advances in Continuum Mechanics and Thermodynamics of Material Behavior; Springer: Berlin/Heidelberg, Germany, 2000; pp. 369–392. [Google Scholar]
- Plagge, J.; Klüppel, M. Mullins effect revisited: Relaxation, recovery and high-strain damage. Mater. Today Commun. 2019, 20, 100588. [Google Scholar] [CrossRef]
- Dorfmann, A. Stress softening of elastomers in hydrostatic tension. Acta Mech. 2003, 165, 117–137. [Google Scholar] [CrossRef]
- Ragni, L.; Tubaldi, E.; Dall’Asta, A.; Ahmadi, H.; Muhr, A. Biaxial shear behaviour of HDNR with Mullins effect and deformation-induced anisotropy. Eng. Struct. 2018, 154, 78–92. [Google Scholar] [CrossRef]
- Mars, W.; Fatemi, A. Observations of the constitutive response and characterization of filled natural rubber under monotonic and cyclic multiaxial stress states. J. Eng. Mater. Technol. 2004, 126, 19–28. [Google Scholar] [CrossRef]
- Machado, G.; Chagnon, G.; Favier, D. Analysis of the isotropic models of the Mullins effect based on filled silicone rubber experimental results. Mech. Mater. 2010, 42, 841–851. [Google Scholar] [CrossRef]
- Mai, T.-T.; Morishita, Y.; Urayama, K. Induced anisotropy by Mullins effect in filled elastomers subjected to stretching with various geometries. Polymer 2017, 126, 29–39. [Google Scholar] [CrossRef]
- Machado, G.; Chagnon, G.; Favier, D. Induced anisotropy by the Mullins effect in filled silicone rubber. Mech. Mater. 2012, 50, 70–80. [Google Scholar] [CrossRef]
- Fu, W.; Wang, L.; Huang, J.; Liu, C.; Peng, W.; Xiao, H.; Li, S. Mechanical properties and Mullins effect in natural rubber reinforced by grafted carbon black. Adv. Polym. Technol. 2019, 2019, 4523696. [Google Scholar] [CrossRef]
- Rault, J.; Marchal, J.; Judeinstein, P.; Albouy, P.A. Stress-induced crystallization and reinforcement in filled natural rubbers: 2H NMR study. Macromolecules 2006, 39, 8356–8368. [Google Scholar] [CrossRef]
- Kitey, R.; Upadhyay, C. Effect of Carbon Black Content on Quasi-Static Compression Behaviour of Filled Rubber, in Aerospace and Associated Technology; Routledge: London, UK, 2022; pp. 305–310. [Google Scholar]
- Allen, V.; Chen, L.; Englert, M.; Moussaoui, A.; Pisula, W. Control of Mullins stress softening in silicone elastomer composites by rational design of fumed silica fillers. Compos. Sci. Technol. 2021, 214, 108955. [Google Scholar] [CrossRef]
- Persson, A.-M.M.R.; Andreassen, E. Cyclic Compression Testing of Three Elastomer Types—A Thermoplastic Vulcanizate Elastomer, a Liquid Silicone Rubber and Two Ethylene-Propylene-Diene Rubbers. Polymers 2022, 14, 1316. [Google Scholar] [CrossRef]
- Krpovic, S.; Dam-Johansen, K.; Skov, A.L. Importance of Mullins effect in commercial silicone elastomer formulations for soft robotics. J. Appl. Polym. Sci. 2021, 138, 50380. [Google Scholar] [CrossRef]
- Dorfmann, A.; Ogden, R.W. A constitutive model for the Mullins effect with permanent set in particle-reinforced rubber. Int. J. Solids Struct. 2004, 41, 1855–1878. [Google Scholar] [CrossRef]
- Zhu, P.; Zhong, Z. Constitutive modelling for the mullins effect with permanent set and induced anisotropy in particle-filled rubbers. Appl. Math. Model. 2021, 97, 19–35. [Google Scholar] [CrossRef]
- Boyce, M.C.; Kear, K.; Socrate, S.; Shaw, K. Deformation of thermoplastic vulcanizates. J. Mech. Phys. Solids 2001, 49, 1073–1098. [Google Scholar] [CrossRef]
- Maiti, A.; Small, W.; Gee, R.H.; Weisgraber, T.H.; Chinn, S.C.; Wilson, T.S.; Maxwell, R.S. Mullins effect in a filled elastomer under uniaxial tension. Phys. Rev. E 2014, 89, 012602. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, S.K.; Mishra, Y.K. Nanocarbon reinforced rubber nanocomposites: Detailed insights about mechanical, dynamical mechanical properties, payne, and mullin effects. Nanomaterials 2018, 8, 945. [Google Scholar] [CrossRef] [PubMed]
- Houwink, R. Slipping of molecules during the deformation of reinforced rubber. Rubber Chem. Technol. 1956, 29, 888–893. [Google Scholar] [CrossRef]
- Rigbi, Z. Reinforcement of rubber by carbon black. In Properties of Polymers; Springer: Berlin/Heidelberg, Germany, 1980; pp. 21–68. [Google Scholar]
- Corby, M.; de Focatiis, D.S. Reversibility of the Mullins effect for extending the life of rubber components. Plast. Rubber Compos. 2019, 48, 24–31. [Google Scholar] [CrossRef]
- Yan, L.; Dillard, D.A.; West, R.L.; Lower, L.D.; Gordon, G.V. Mullins effect recovery of a nanoparticle-filled polymer. J. Polym. Sci. Part B Polym. Phys. 2010, 48, 2207–2214. [Google Scholar] [CrossRef]
- Wang, S.; Chester, S.A. Modeling thermal recovery of the Mullins effect. Mech. Mater. 2018, 126, 88–98. [Google Scholar] [CrossRef]
- Sun, Y.; Yang, L.; Liu, F.; Wang, Z. Mullins Effect and Its Reversibility for Thermoplastic Vulcanizates Based on Ethylene–Acrylic Acid Copolymer/Nitrile–Butadiene Rubber Blends. Polym. Sci. Ser. A 2020, 62, 670–679. [Google Scholar]
- Zhao, J.; Wang, C.; Wang, Z. Mullins effect and its reversibility of compatibilised thermoplastic vulcanisates based on high impact polystyrene/high vinyl polybutadiene rubber blend. Plast. Rubber Compos. 2015, 44, 155–161. [Google Scholar] [CrossRef]
- Wineman, A.; Shaw, J. Combined deformation-and temperature-induced scission in a rubber cylinder in torsion. Int. J. Non-Linear Mech. 2007, 42, 330–335. [Google Scholar] [CrossRef]
- Harwood, J.; Payne, A.R. Stress softening in natural rubber vulcanizates. Part III. Carbon black-filled vulcanizates. J. Appl. Polym. Sci. 1966, 10, 315–324. [Google Scholar] [CrossRef]
- Zhao, H.; Allanson, D.; Ren, X. Use of shore hardness tests for in-process properties estimation/monitoring of silicone rubbers. J. Mater. Sci. Chem. Eng. 2015, 3, 142–147. [Google Scholar] [CrossRef] [PubMed]
- Qi, H.; Joyce, K.; Boyce, M. Durometer hardness and the stress-strain behavior of elastomeric materials. Rubber Chem. Technol. 2003, 76, 419–435. [Google Scholar] [CrossRef]
- Meththananda, I.M.; Parker, S.; Patel, M.P.; Braden, M. The relationship between Shore hardness of elastomeric dental materials and Young’s modulus. Dent. Mater. 2009, 25, 956–959. [Google Scholar] [CrossRef]
- Prem, N.; Schale, F.; Zimmermann, K.; Gowda, D.K.; Odenbach, S. Synthesis and characterization of the properties of thermosensitive elastomers with thermoplastic and magnetic particles for application in soft robotics. J. Appl. Polym. Sci. 2021, 138, 51296. [Google Scholar] [CrossRef]
- Eshraghi, S.; Das, S. Mechanical and microstructural properties of polycaprolactone scaffolds with one-dimensional, two-dimensional, and three-dimensional orthogonally oriented porous architectures produced by selective laser sintering. Acta Biomat. 2010, 6, 2467–2476. [Google Scholar] [CrossRef]
- Wu, X.L.; Huang, W.M.; Lu, H.B.; Wang, C.C.; Cui, H.P. Characterization of polymeric shape memory materials. J. Polym. Eng. 2017, 37, 1–20. [Google Scholar] [CrossRef]
- Wu, X.; Huang, W.; Tan, H. Characterization of shape recovery via creeping and shape memory effect in ether-vinyl acetate copolymer (EVA). J. Polym. Res. 2013, 20, 150. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.M.; Wang, C.C.; Zhao, Y.; Ding, Z.; Purnawali, H. Optimization of the shape memory effect in shape memory polymers. J. Polym. Sci. Part A Polym. Chem. 2011, 49, 3574–3581. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W.M.; Lu, H.; Lim, K.J.; Zhou, Y.; Wang, T.X.; Gao, X.Y. Heating-responsive shape-memory effect in thermoplastic polyurethanes with low melt-flow index. Macromol. Chem. Phys. 2014, 215, 2430–2436. [Google Scholar] [CrossRef]


| Samples | Pictures | Dimensions | Tests |
|---|---|---|---|
| Cylindrical |  | Diameter—1.8 cm Height—2 cm | 1. Cyclic compression 2. Programming (compression) |
| Cuboid |  | Length—2.7 cm Width—1.6 cm Height—1.2 cm | 1. Cyclic compression 2. Programming (compression) |
| Strip |  | Length—3.2 cm Width—1.2 cm Thickness—0.5 cm | 1. Cyclic tension 2. Programming (tension) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naveen, B.S.; Jose, N.T.; Krishnan, P.; Mohapatra, S.; Pendharkar, V.; Koh, N.Y.H.; Lim, W.Y.; Huang, W.M. Evolution of Shore Hardness under Uniaxial Tension/Compression in Body-Temperature Programmable Elastic Shape Memory Hybrids. Polymers 2022, 14, 4872. https://doi.org/10.3390/polym14224872
Naveen BS, Jose NT, Krishnan P, Mohapatra S, Pendharkar V, Koh NYH, Lim WY, Huang WM. Evolution of Shore Hardness under Uniaxial Tension/Compression in Body-Temperature Programmable Elastic Shape Memory Hybrids. Polymers. 2022; 14(22):4872. https://doi.org/10.3390/polym14224872
Chicago/Turabian StyleNaveen, Balasundaram Selvan, Nivya Theresa Jose, Pranav Krishnan, Subham Mohapatra, Vivek Pendharkar, Nicholas Yuan Han Koh, Woon Yong Lim, and Wei Min Huang. 2022. "Evolution of Shore Hardness under Uniaxial Tension/Compression in Body-Temperature Programmable Elastic Shape Memory Hybrids" Polymers 14, no. 22: 4872. https://doi.org/10.3390/polym14224872
APA StyleNaveen, B. S., Jose, N. T., Krishnan, P., Mohapatra, S., Pendharkar, V., Koh, N. Y. H., Lim, W. Y., & Huang, W. M. (2022). Evolution of Shore Hardness under Uniaxial Tension/Compression in Body-Temperature Programmable Elastic Shape Memory Hybrids. Polymers, 14(22), 4872. https://doi.org/10.3390/polym14224872