Inverse Finite Element Approach to Identify the Post-Necking Hardening Behavior of Polyamide 12 under Uniaxial Tension
Abstract
:1. Introduction
2. Materials and Methods
- Necking followed by stable neck propagation until fracture (23 °C ambient, conditioned) (Group I);
- Necking followed by strain hardening (37 °C ambient and conditioned, 50 °C ambient) (Group II);
- Without necking (50 °C conditioned, 80 °C ambient and conditioned, 100 °C) (Group III).
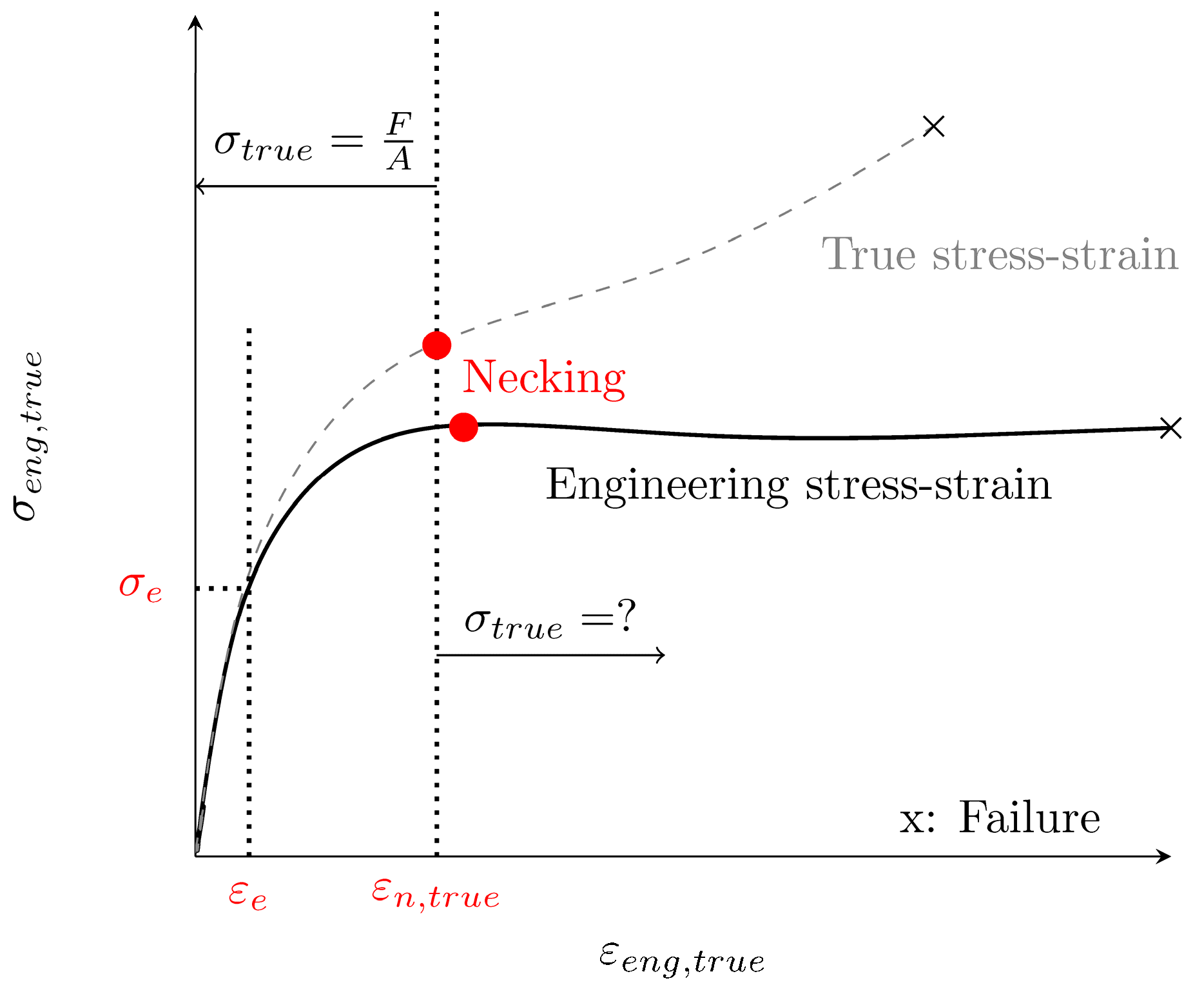
2.1. Stress and Strain Conversion
- = 0: no fit
- = 1: perfect fit
- 0 < < 1: partial correct fit
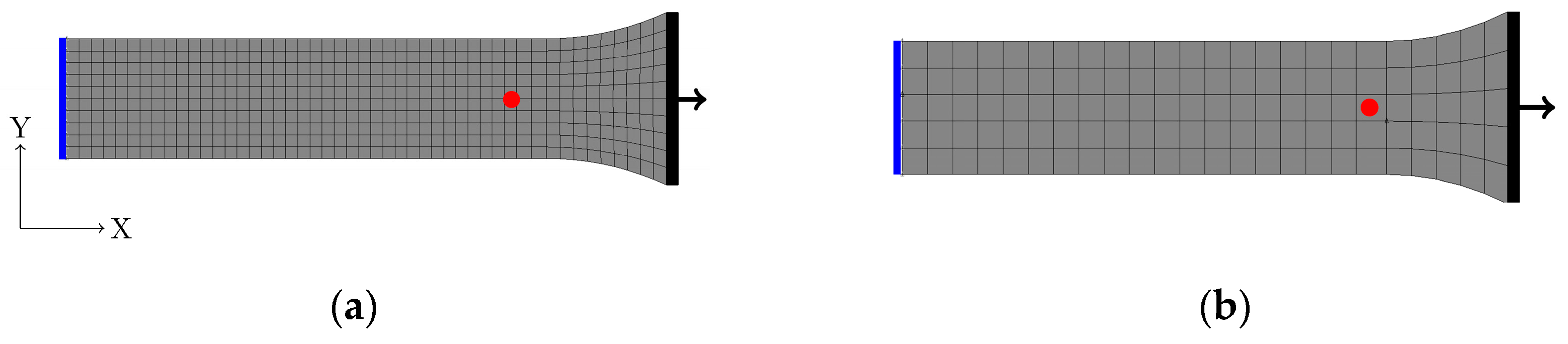
2.2. Elastoplastic Constitutive Model and Inverse Identification Approach
2.2.1. Hardening Model until Necking
2.2.2. Hardening Model Post Necking
3. Results
3.1. Linear Elastic Values
3.2. Curve Fitting until Necking
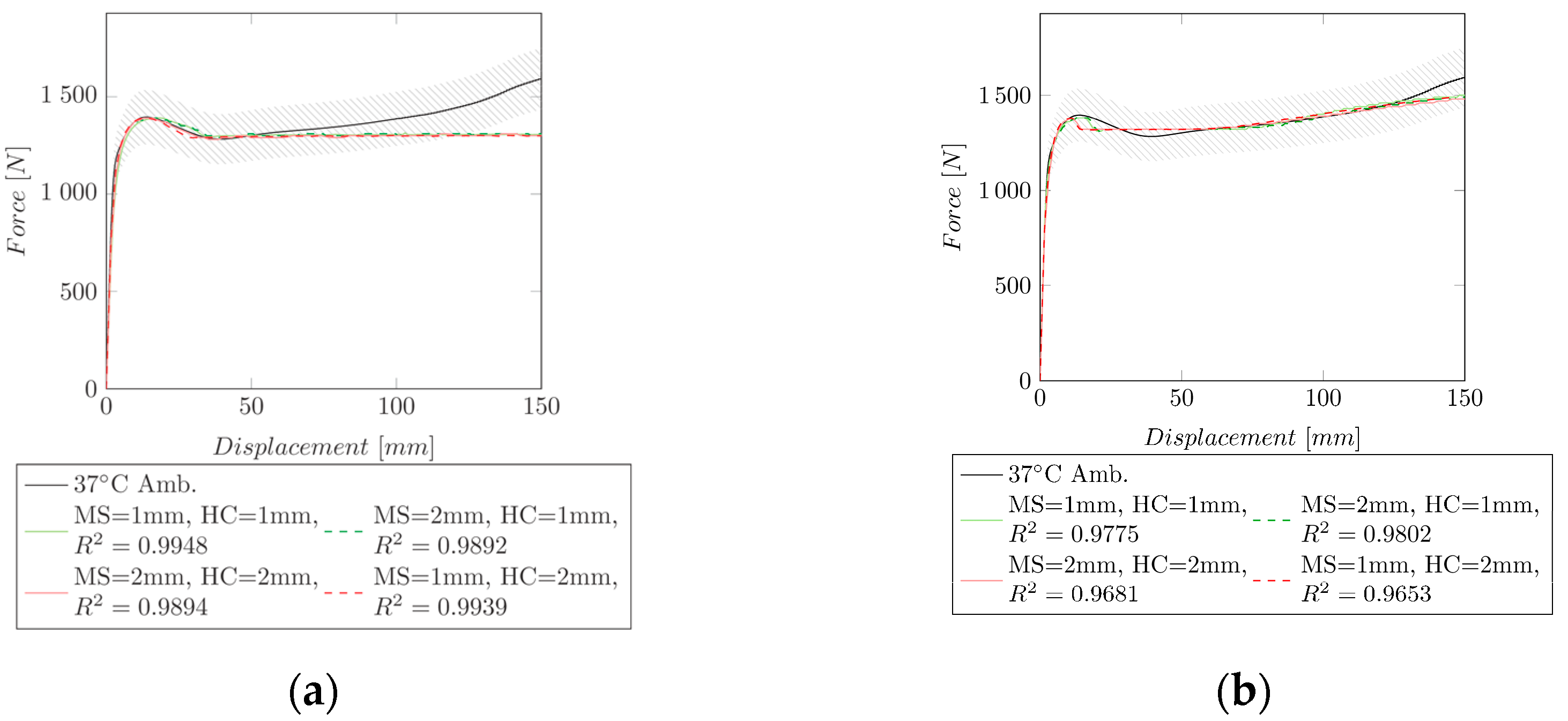
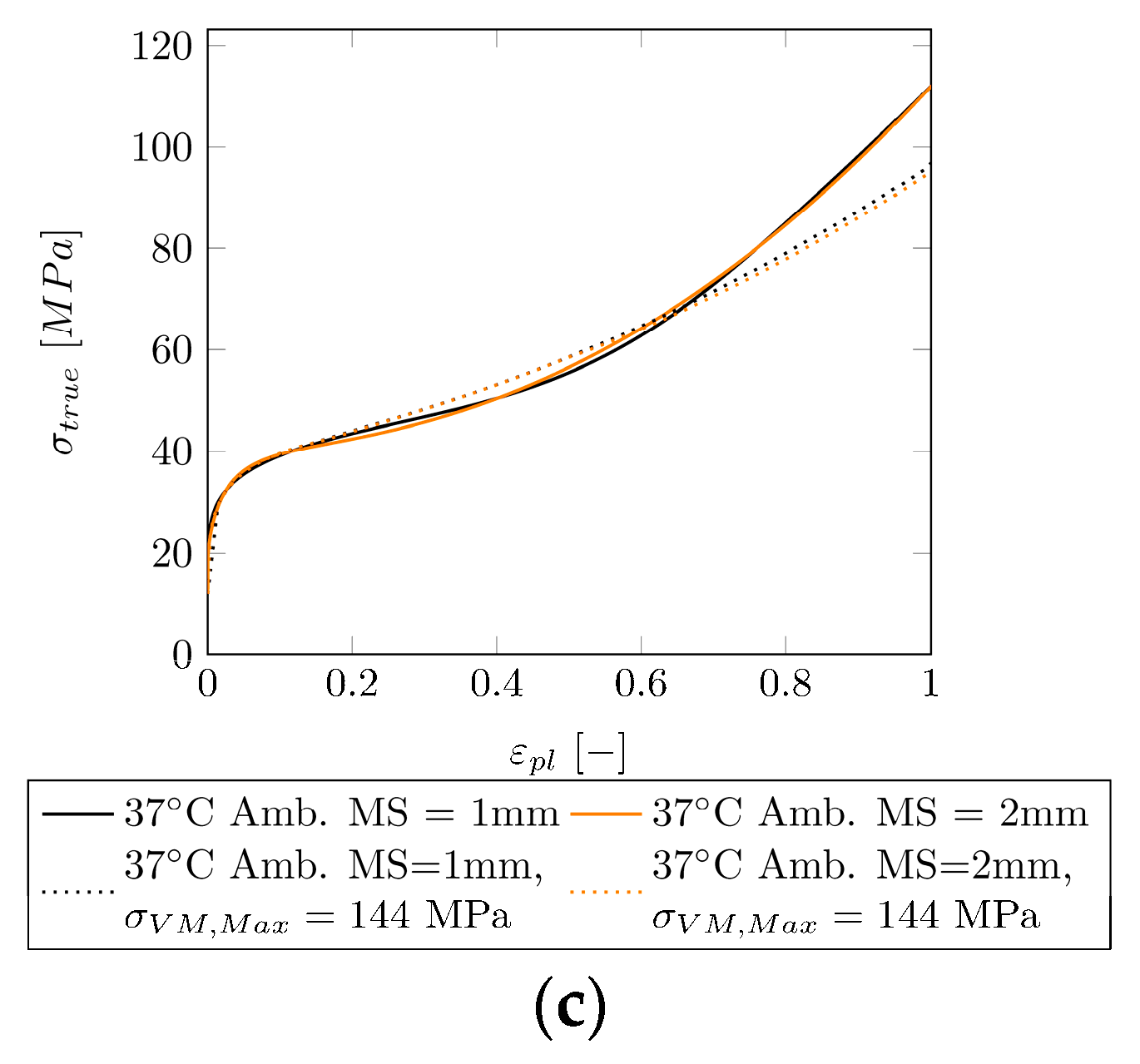
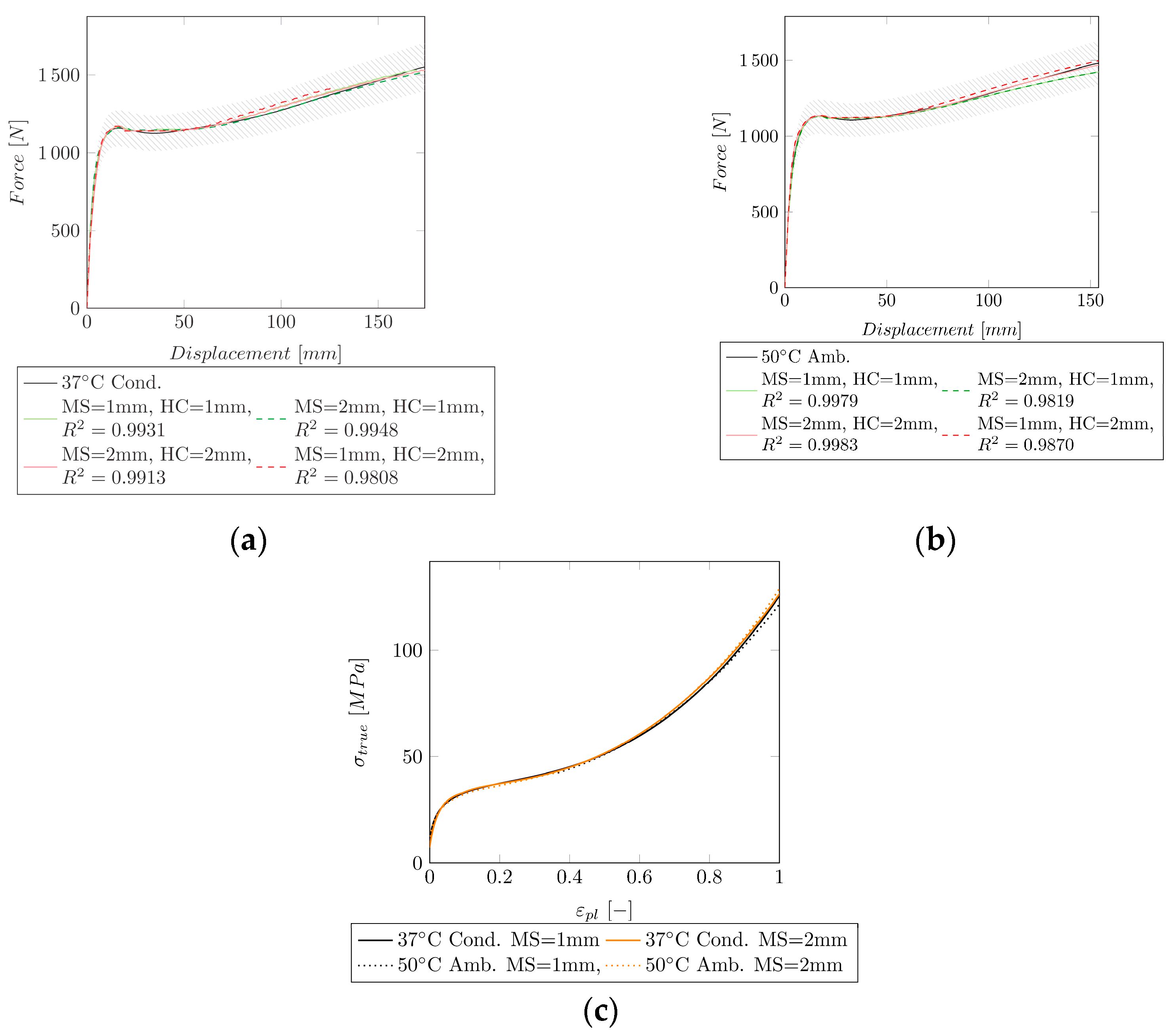
3.3. Curve Fitting Post-Necking
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
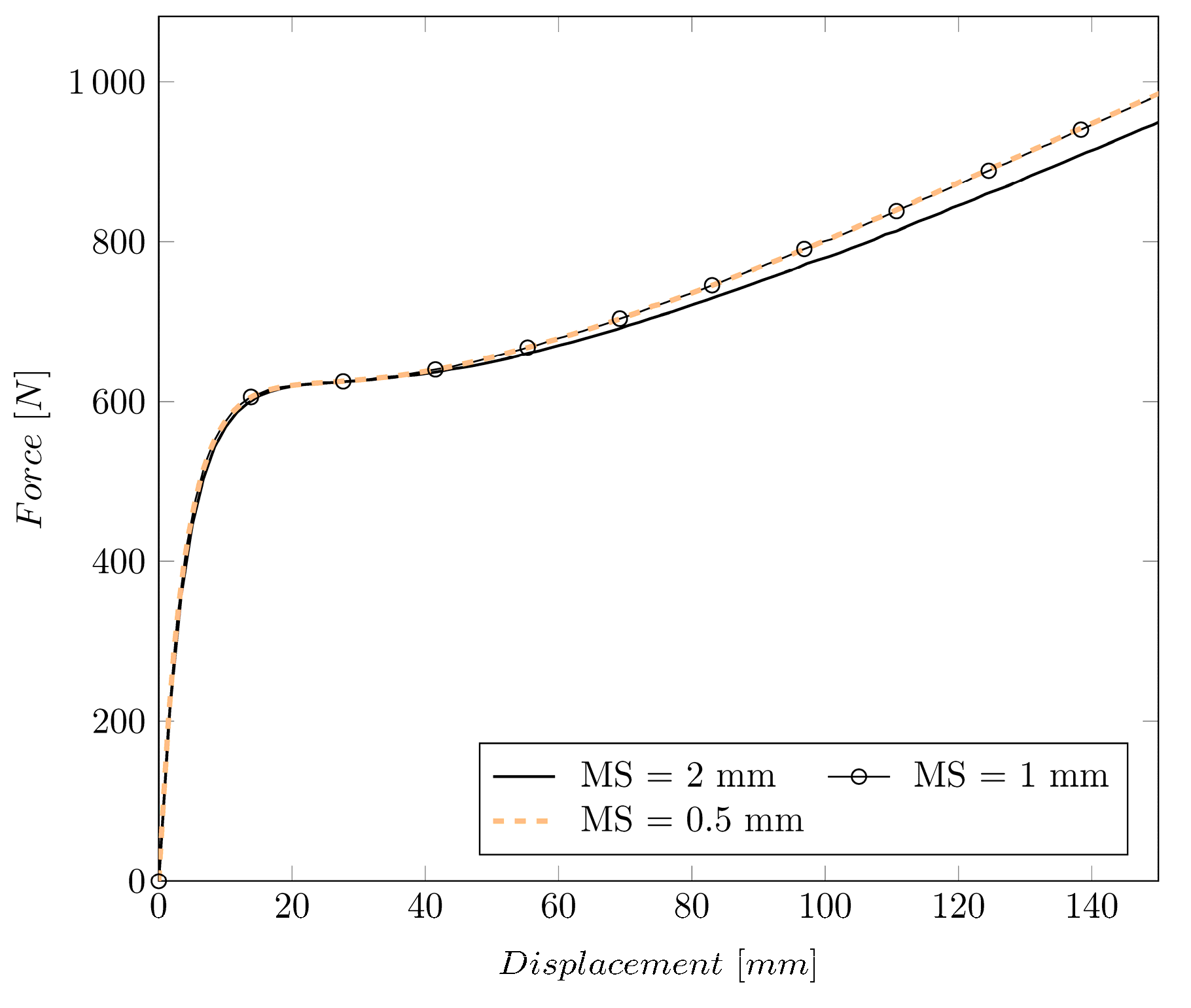
Appendix B
| Temp. (°C) | Variable | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Amb | Cond | Amb | Cond | Amb | Cond | Amb | Cond | ||
| ) | − | − | 1.155 × 10−4 | 2.92 × 10−5 | 2.34 × 10−14 | 2.34 × 10−14 | − | − | |
| 159.2 | 49.21 | − | − | 159.2 | 49.21 | 902.9 | 69.34 | ||
| 0.426 | 0.2328 | 0.1149 | 0.1494 | 0.426 | 0.2328 | − | − | ||
| − | − | − | − | − | − | 15.46 | 29.3 | ||
| 0.9629 | 0.9760 | 0.992 | 0.9923 | 0.9629 | 0.9760 | 0.9881 | 0.8632 | ||
| ) | − | − | 4.23 × 10−5 | 1.193 × 10−4 | 2.34 × 10−14 | 2.33 × 10−14 | - | − | |
| 47.82 | 49.94 | − | − | 47.82 | 49.94 | 60.91 | 34.98 | ||
| 0.2467 | 0.3017 | 0.1515 | 0.2156 | 0.2467 | 0.3017 | - | - | ||
| − | − | − | − | − | − | 27.36 | 27.31 | ||
| 0.9852 | 0.9853 | 0.9959 | 0.9947 | 0.9852 | 0.9853 | 0.8319 | 0.9395 | ||
| ) | − | − | 1.059 × 10-4 | − | 2.34 × 10-14 | − | − | − | |
| 48.86 | − | − | − | 48.85 | − | 34.9 | − | ||
| 0.2987 | − | 0.2163 | − | − | − | − | − | ||
| − | − | − | − | − | − | 27.04 | − | ||
| 0.9844 | − | 0.9941 | − | 0.9844 | − | 0.9396 | − | ||
References
- Menary, G.H.; Armstrong, C.G. Experimental Study and Numerical Modelling of Injection Stretch Blow Moulding of Angioplasty Balloons. Plast. Rubber Compos. 2006, 35, 348–354. [Google Scholar] [CrossRef]
- Hutchinson, J.W.; Neale, K.W. Neck Propagation. J. Mech. Phys. Solids 1983, 31, 405–426. [Google Scholar] [CrossRef]
- Knysh, P.; Korkolis, Y.P. Identification of the Post-Necking Hardening Response of Rate- and Temperature-Dependent Metals. Int. J. Solids Struct. 2017, 115–116, 149–160. [Google Scholar] [CrossRef]
- Kim, J.H.; Serpantié, A.; Barlat, F.; Pierron, F.; Lee, M.G. Characterization of the Post-Necking Strain Hardening Behavior Using the Virtual Fields Method. Int. J. Solids Struct. 2013, 50, 3829–3842. [Google Scholar] [CrossRef]
- Zhao, K.; Wang, L.; Chang, Y.; Yan, J. Identification of Post-Necking Stress-Strain Curve for Sheet Metals by Inverse Method. Mech. Mater. 2016, 92, 107–118. [Google Scholar] [CrossRef]
- Coppieters, S.; Kuwabara, T. Identification of Post-Necking Hardening Phenomena in Ductile Sheet Metal. Exp. Mech. 2014, 54, 1355–1371. [Google Scholar] [CrossRef]
- G’sell, C.; Aly-Helal, N.A.; Jonas, J.J. Effect of Stress Triaxiality on Neck Propagation during the Tensile Stretching of Solid Polymers. J. Mater. Sci. 1983, 18, 1731–1742. [Google Scholar] [CrossRef]
- Kwon, H.J.; Jar, P.Y.B. On the Application of FEM to Deformation of High-Density Polyethylene. Int. J. Solids Struct. 2008, 45, 3521–3543. [Google Scholar] [CrossRef]
- G’sell, C.; Jonas, J.J. Determination of the Plastic Behaviour of Solid Polymers at Constant True Strain Rate. J. Mater. Sci. 1979, 14, 583–591. [Google Scholar] [CrossRef]
- Kwon, H.J.; Jar, P.Y.B. Application of Essential Work of Fracture Concept to Toughness Characterization of High-Density Polyethylene. Polym. Eng. Sci. 2007, 47, 1327–1337. [Google Scholar] [CrossRef]
- Xu, M.M.; Huang, G.Y.; Feng, S.S.; McShane, G.J.; Stronge, W.J. Static and Dynamic Properties of Semi-Crystalline Polyethylene. Polymers 2016, 8, 77. [Google Scholar] [CrossRef] [PubMed]
- Fesko, D.G. Post-Yield Behavior of Thermoplastics and the Application to Finite Element Analysis. Polym. Eng. Sci. 2000, 40, 1190–1199. [Google Scholar] [CrossRef]
- Arriaga, A.; Lazkano, J.M.; Pagaldai, R.; Zaldua, A.M.; Hernandez, R.; Atxurra, R.; Chrysostomou, A. Finite-Element Analysis of Quasi-Static Characterisation Tests in Thermoplastic Materials: Experimental and Numerical Analysis Results Correlation with ANSYS. Polym. Test. 2007, 26, 284–305. [Google Scholar] [CrossRef]
- Shin, D.S.; Kim, Y.S.; Jeon, E.S. Approximation of Non-Linear Stress-Strain Curve for GFRP Tensile Specimens by Inverse Method. Appl. Sci. 2019, 9, 3474. [Google Scholar] [CrossRef]
- Zhang, H.; Coppieters, S.; Jiménez-Peña, C.; Debruyne, D. Inverse Identification of the Post-Necking Work Hardening Behaviour of Thick HSS through Full-Field Strain Measurements during Diffuse Necking. Mech. Mater. 2019, 129, 361–374. [Google Scholar] [CrossRef]
- Massey, L.K.; McKeen, L.W. Film Properties of Plastics and Elastomers; Elsevier: Amsterdam, The Netherlands, 2004; pp. 157–188. [Google Scholar] [CrossRef]
- IndustryARC. Balloon Catheter Market—Industry Analysis, Market Size, Share, Trends, Application Analysis, Growth and Forecast 2021–2026. Available online: https://www.industryarc.com/Research/Balloon-Catheter-Market-Research-504252 (accessed on 20 June 2022).
- Amstutz, C.; Weisse, B.; Valet, S.; Haeberlin, A.; Burger, J.; Zurbuchen, A. Temperature-Dependent Tensile Properties of Polyamide 12 for the Use in Percutaneous Transluminal Coronary Angioplasty Balloon Catheters. Biomed. Eng. Online 2021, 20, 1–19. [Google Scholar] [CrossRef]
- Mahieux, C.A.; Reifsnider, K.L. Property Modeling across Transition Temperatures in Polymers: Application to Thermoplastic Systems. J. Mater. Sci. 2002, 37, 911–920. [Google Scholar] [CrossRef]
- Wang, S.; Zhou, Z.; Zhang, J.; Fang, G.; Wang, Y. Effect of Temperature on Bending Behavior of Woven Fabric-Reinforced PPS-Based Composites. J. Mater. Sci. 2017, 52, 13966–13976. [Google Scholar] [CrossRef]
- Ludwik, P. Elemente Der Technologischen Mechanik; Springer: Berlin/Heidelberg, Germany, 1909. [Google Scholar] [CrossRef]
- Swift, H.W. Plastic Instability under Plane Stress. J. Mech. Phys. Solids 1952, 1, 1–18. [Google Scholar] [CrossRef]
- Ghosh, A.K. Tensile Instability and Necking in Materials with Strain Hardening and Strain-Rate Hardening. Acta Metall. 1977, 25, 1413–1424. [Google Scholar] [CrossRef]
- Voce, E. The Relationship between Stress and Strain from Homogenous Deformation. J. Inst. Met. 1948, 74, 537–562. [Google Scholar]
- Hockett, J.E.; Sherby, O.D. Large Strain Deformation of Polycrystalline Metals at Low Homologous Temperatures. J. Mech. Phys. Solids 1975, 23, 87–98. [Google Scholar] [CrossRef]
- Cook, R.D.; Nachtsheim, C.J. A Comparison of Algorithms for Constructing Exact D-Optimal Designs. Technometrics 1980, 22, 315. [Google Scholar] [CrossRef]
- Goel, T.; Stander, N. Adaptive Simulated Annealing for Global Optimization in LS-OPT. In Proceedings of the 7th European LS-DYNA Conference, Palm Springs, CA, USA, 4 May 2009; pp. 1–8. [Google Scholar]
- Stander, N.; Basudhar, A.; Roux, W.; Witowski, K.; Eggleston, T.; Goel, T.; Craig, K. LS-OPT User ’s Manual: A Design Optimization and Probabilistic Analysis Tool for the Engineering Analyst; Livermore Software Technology Corporation: Livermore, CA, USA, 2019; p. 802. [Google Scholar]
- Helbig, M.; Koch, D. An Introduction to Material Characterization. Available online: https://www.dynamore.de/de/download/presentation/2020/copy_of_dynamore-express-introduction-to-material-characterization (accessed on 15 August 2022).
- Mohammad Amjadi; Ali Fatemi Tensile Behavior of High-Density Polyethylene Including the Effects of Processing Technique. Polymers 2020, 12, 1857. [CrossRef] [PubMed]
- Rösler, J.; Harders, H.; Bäker, M. Mechanical Behaviour of Engineering Materials: Metals, Ceramics, Polymers, and Composites; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2007; ISBN 9783540734468. [Google Scholar]


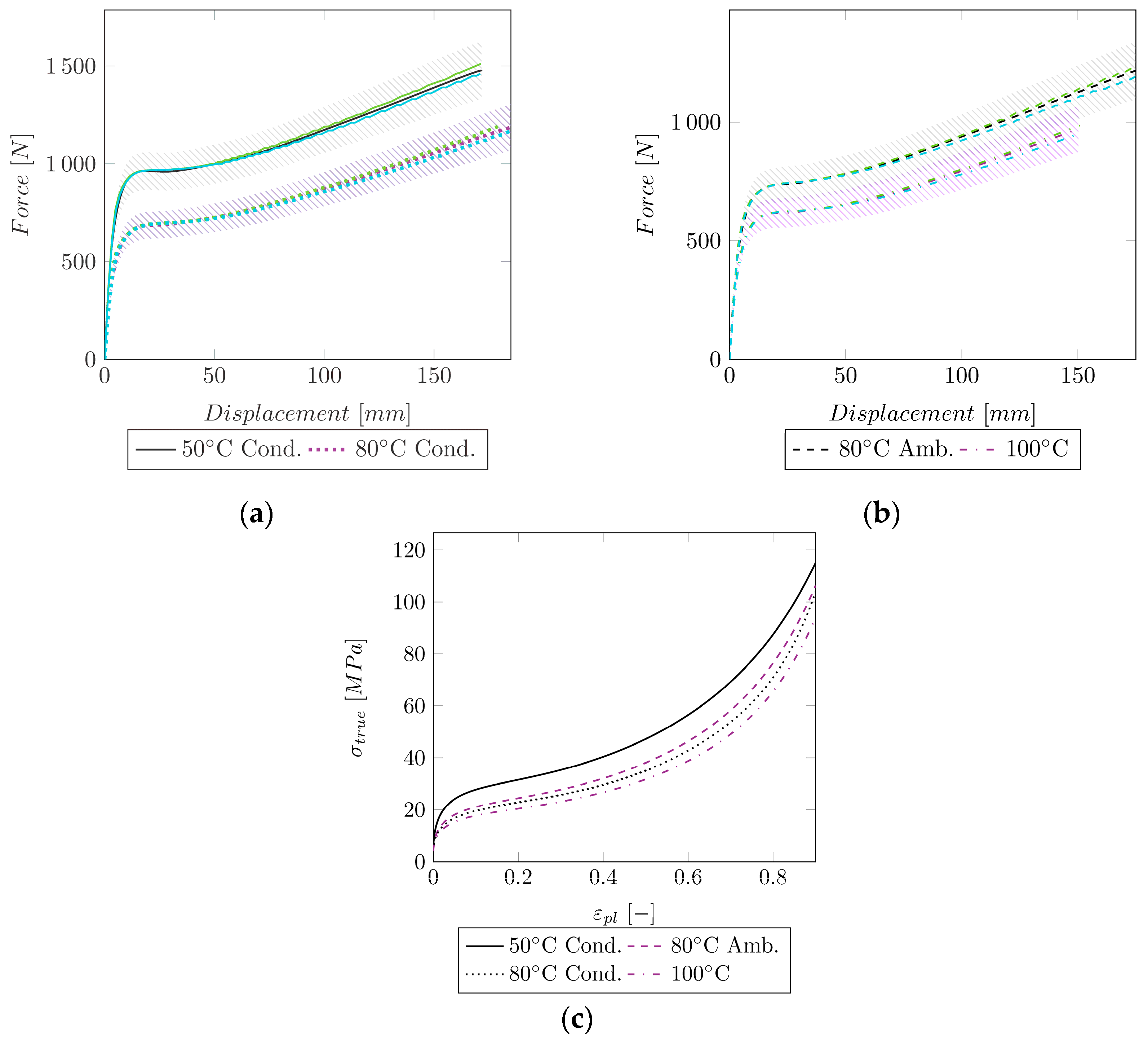

| Temp (°C) | (MPa) | (-) | (MPa) | (-) | ||
|---|---|---|---|---|---|---|
| Ambient | Conditioned | |||||
| 23 | 1553.5 | 29.76 | 0.37 | 882.0 | 11.38 | 0.31 |
| 37 | 1036.3 | 11.86 | 0.44 | 641.5 | 7.67 | 0.46 |
| 50 | 606.2 | 7.26 | 0.46 | 446.4 | 5.32 | 0.46 |
| 80 | 315.2 | 4.69 | 0.47 | 297.6 | 4.42 | 0.47 |
| 100 | 272.1 | 4.04 | 0.47 | - | - | - |
| Variable | (MPa) | |||
|---|---|---|---|---|
| Ambient | Conditioned | Ambient | Conditioned | |
| 1952 | 1103 | 5857 | 18.57 | |
| 395 | 310.0 | 4.722 | 4.575 | |
| 401.3 | 411 | 408 | 408.8 | |
| 312.8 | 312.7 | 200 | 302.1 | |
| 21.17 | 19.13 | 4.328 | 15.96 | |
| 12.8 | 18.16 | 21.2 | 22.84 | |
| 0.9994 | 0.9995 | 0.99958 | 1 | |
| Temp. (°C) | Variable | ||
|---|---|---|---|
| Amb | Cond | ||
| 23 (valid up to , ) | 195.6 | 4.149 | |
| 0.8 | 0.4159 | ||
| 46.46 | 48.8 | ||
| 0.996 | 0.9946 | ||
| 37 (valid up to , ) | 2.539 | 4.56 | |
| 0.3681 | 0.519 | ||
| 53.43 | 41.74 | ||
| 0.9925 | 0.9997 | ||
| 50 (valid up to ) | 4.646 | - | |
| 0.5207 | - | ||
| 40.67 | - | ||
| 0.9997 | - | ||
| Variable | 50 °C Cond | 80 °C Amb | 80 °C Cond | 100 °C |
|---|---|---|---|---|
| 30.98 | 24.52 | 25.08 | 20.66 | |
| 7.389 | 6.309 | 4.429 | 6.088 | |
| 0.5794 | 0.5784 | 0.5298 | 0.563 | |
| 48.01 | 62.16 | 76.34 | 63.99 | |
| 7.512 | 8.015 | 2.803 | 8.499 | |
| 79.43 | 70.78 | 79.21 | 61.12 | |
| 2.296 | 2.379 | 12.04 | 2.457 | |
| –HC | 1 | 1 | 1 | 1 |
| –FD, MS = 1 mm | 0.994 | 0.9971 | 0.9961 | 0.9976 |
| –FD, MS = 2 mm | 0.9958 | 0.9929 | 0.9937 | 0.9927 |
| Variable | 23 °C Cond | 37 °C Amb | 37 °C Cond | 50 °C Amb | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MS (mm) | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 | ||
| 34.96 | 39.9 | 43.42 | 37.88 | 41.72 | 32.2 | 39.40 | 36.26 | 36.06 | 37.57 | |
| 23.36 | 6.967 | 4.961 | 3.395 | 5.908 | 14.5 | 5.94 | 14.45 | 8.047 | 6.316 | |
| 3.494 | 0.4335 | 0.4241 | 4.579 | 0.4479 | 0.7373 | 0.57 | 0.7913 | 0.6062 | 0.5632 | |
| 10.16 | 3.494 | 52.94 | 30.76 | 2.184 | 8.742 | 36.98 | 38.38 | 0.8628 | 90.57 | |
| 4.373 | 0.7256 | 1.719 | 4.015 | 6.024 | 0.031366 | 2.79 | 2.385 | 4.171 | 2.661 | |
| 41.96 | 88 | 0.4477 | 44.26 | 51.04 | 71.01 | 49.30 | 51.83 | 84.64 | 0.8859 | |
| 1.232 | 2.596 | 8.613 | 0.2106 | 1.588 | 2.172 | 2.79 | 2.694 | 2.469 | 15.07 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Amstutz, C.; Weisse, B.; Haeberlin, A.; Burger, J.; Zurbuchen, A. Inverse Finite Element Approach to Identify the Post-Necking Hardening Behavior of Polyamide 12 under Uniaxial Tension. Polymers 2022, 14, 3476. https://doi.org/10.3390/polym14173476
Amstutz C, Weisse B, Haeberlin A, Burger J, Zurbuchen A. Inverse Finite Element Approach to Identify the Post-Necking Hardening Behavior of Polyamide 12 under Uniaxial Tension. Polymers. 2022; 14(17):3476. https://doi.org/10.3390/polym14173476
Chicago/Turabian StyleAmstutz, Cornelia, Bernhard Weisse, Andreas Haeberlin, Jürgen Burger, and Adrian Zurbuchen. 2022. "Inverse Finite Element Approach to Identify the Post-Necking Hardening Behavior of Polyamide 12 under Uniaxial Tension" Polymers 14, no. 17: 3476. https://doi.org/10.3390/polym14173476
APA StyleAmstutz, C., Weisse, B., Haeberlin, A., Burger, J., & Zurbuchen, A. (2022). Inverse Finite Element Approach to Identify the Post-Necking Hardening Behavior of Polyamide 12 under Uniaxial Tension. Polymers, 14(17), 3476. https://doi.org/10.3390/polym14173476






