Compressive Strength Properties Perpendicular to the Grain of Hollow Glue-Laminated Timber Elements
Abstract
1. Introduction
1.1. State-of-the-Art
1.2. Objectives
2. Materials and Methods
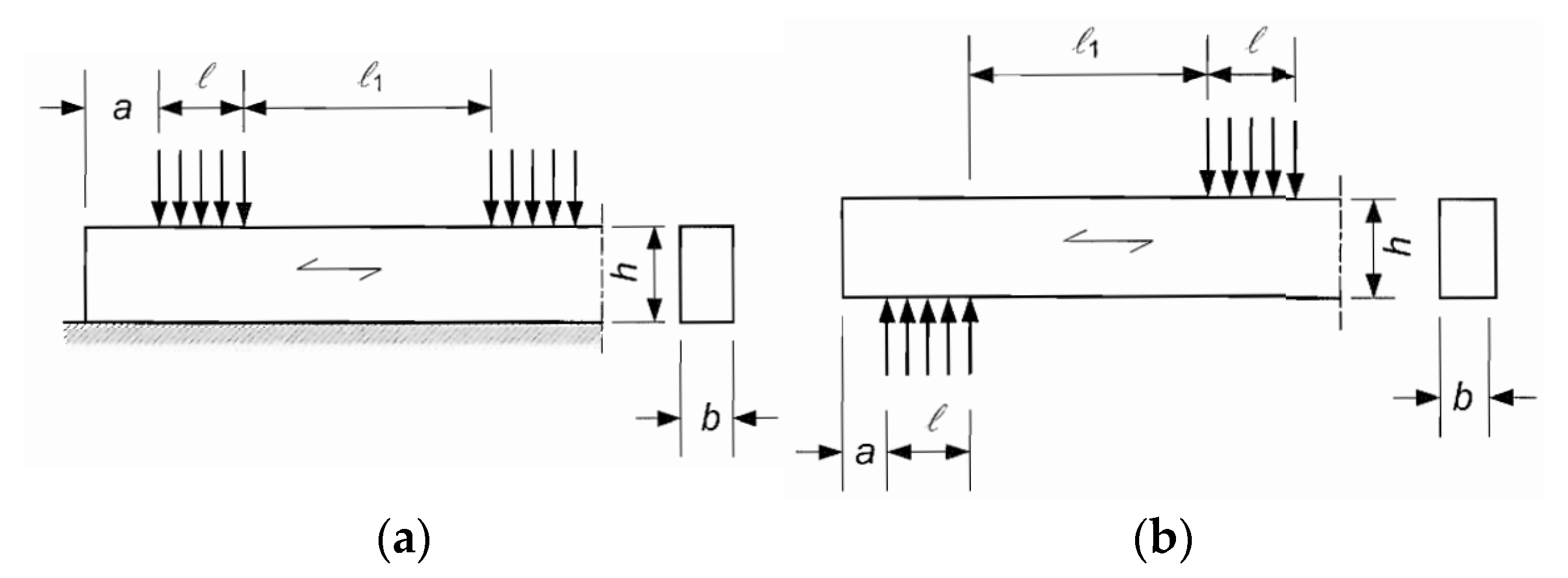
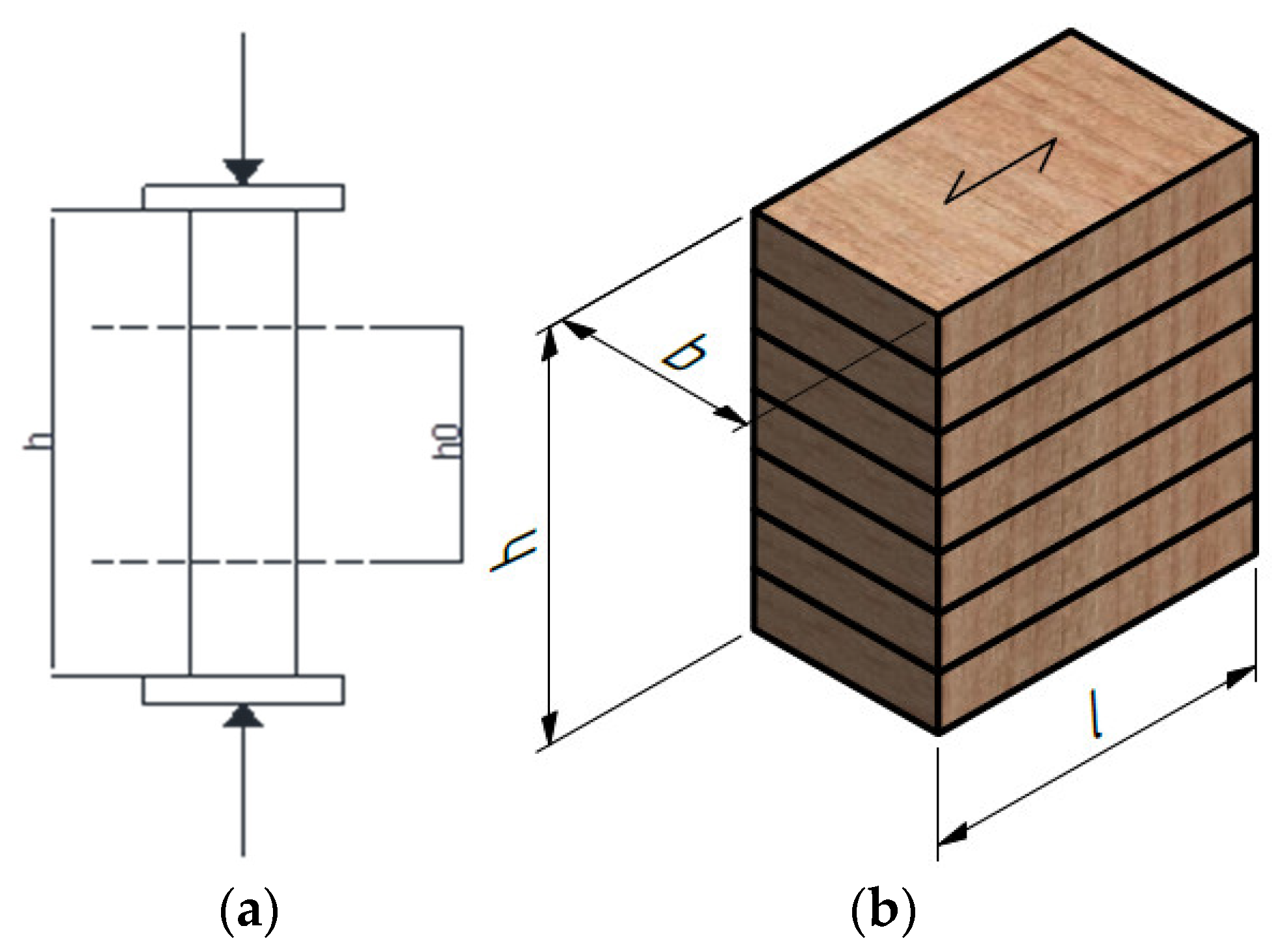
2.1. Test Setup
- fc,90—compression strength (N/mm2)
- Fc,90,max—maximal compression load parallel to the grain (N)
- b—width (mm)
- l—length (mm)
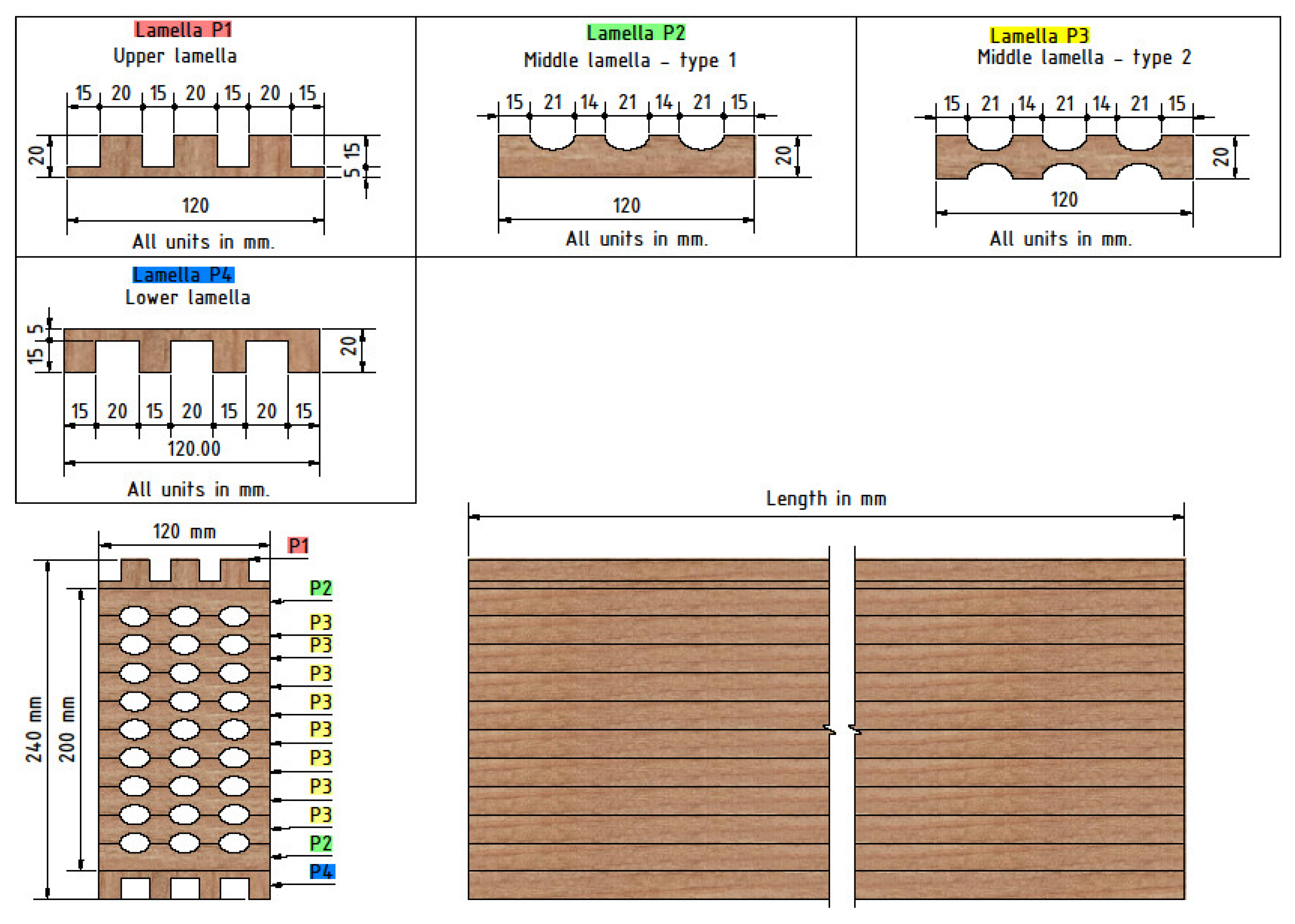
2.2. Type and Number of Samples
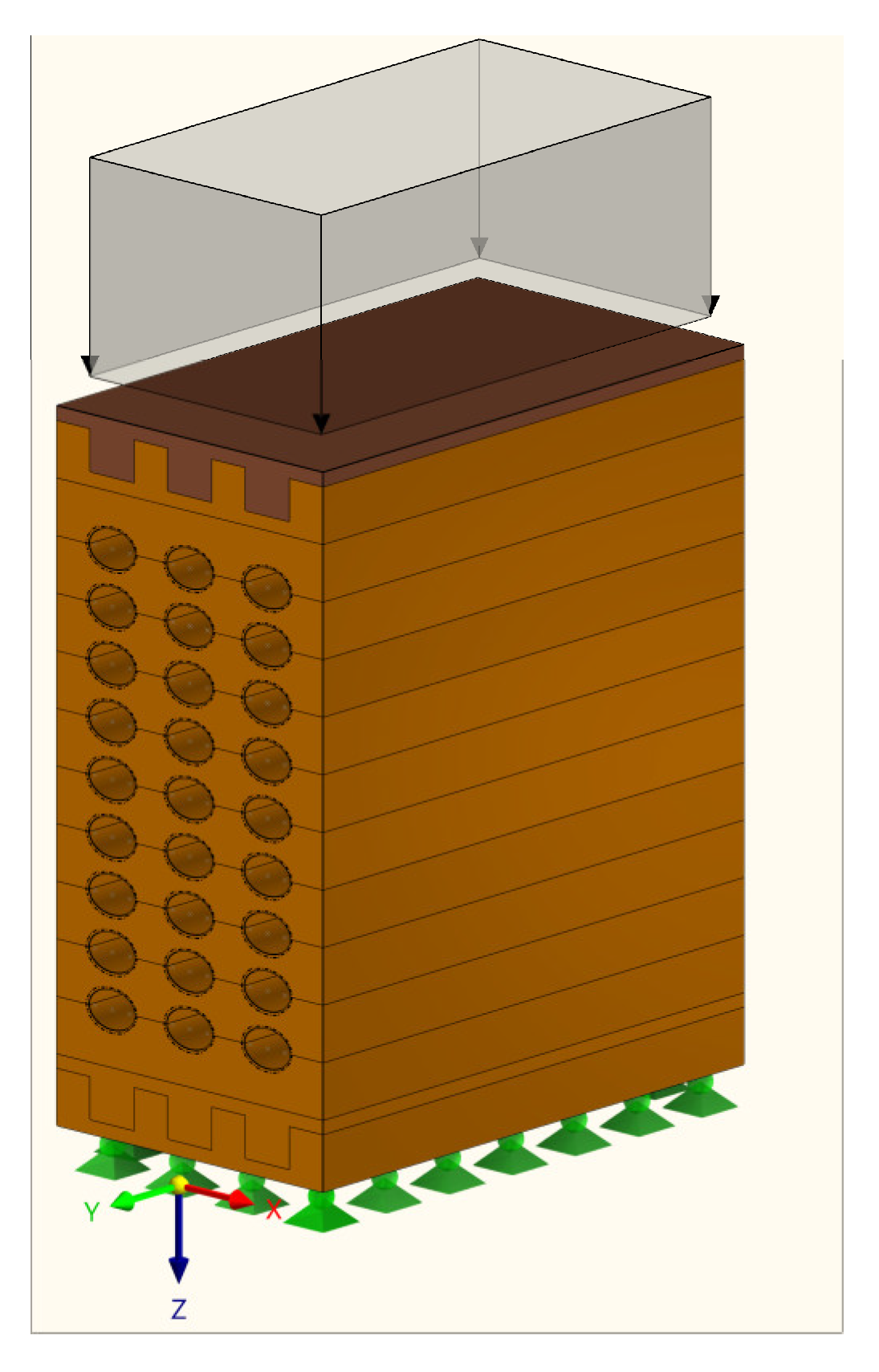
2.3. FEM Description
3. Results
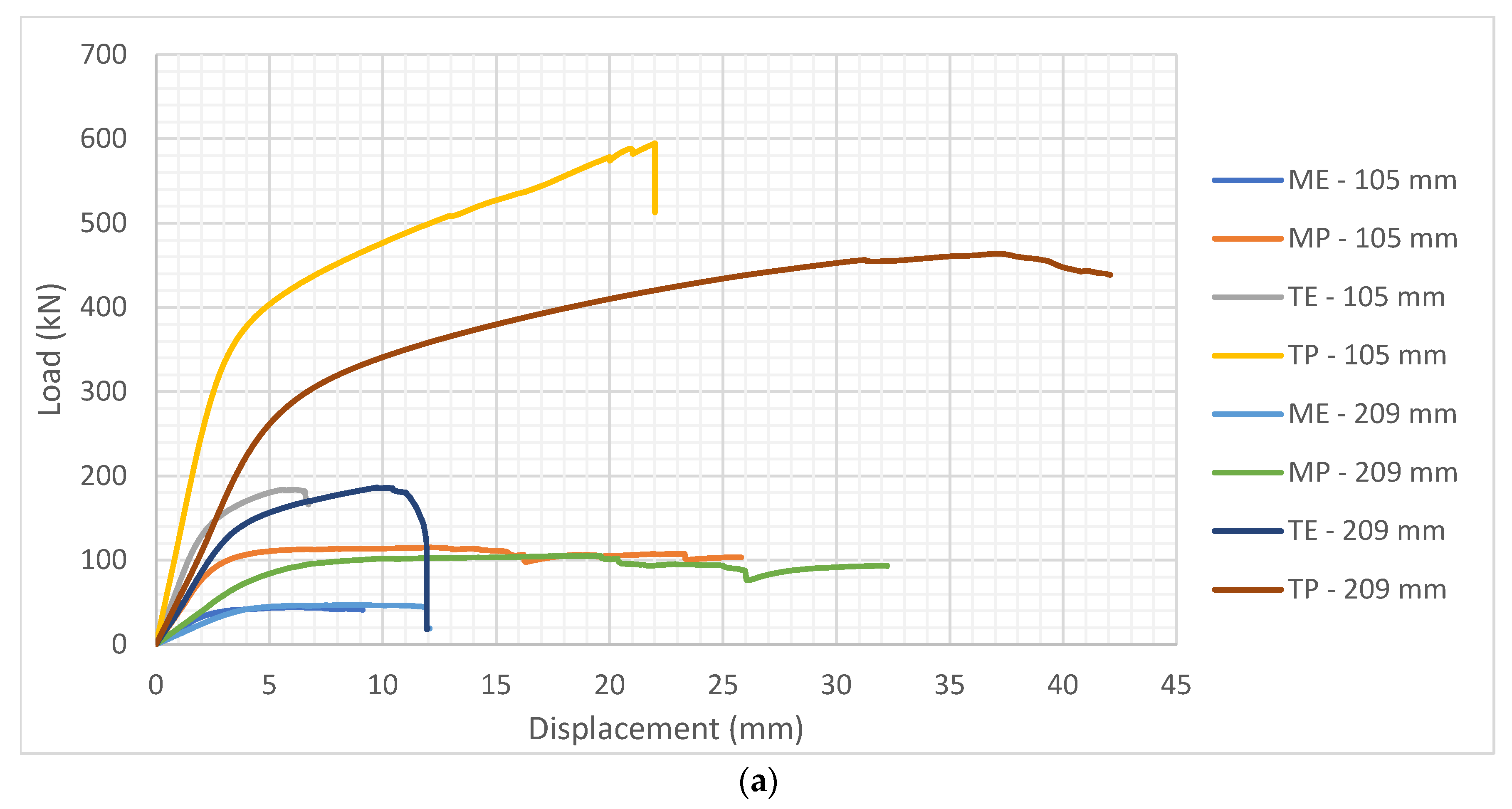
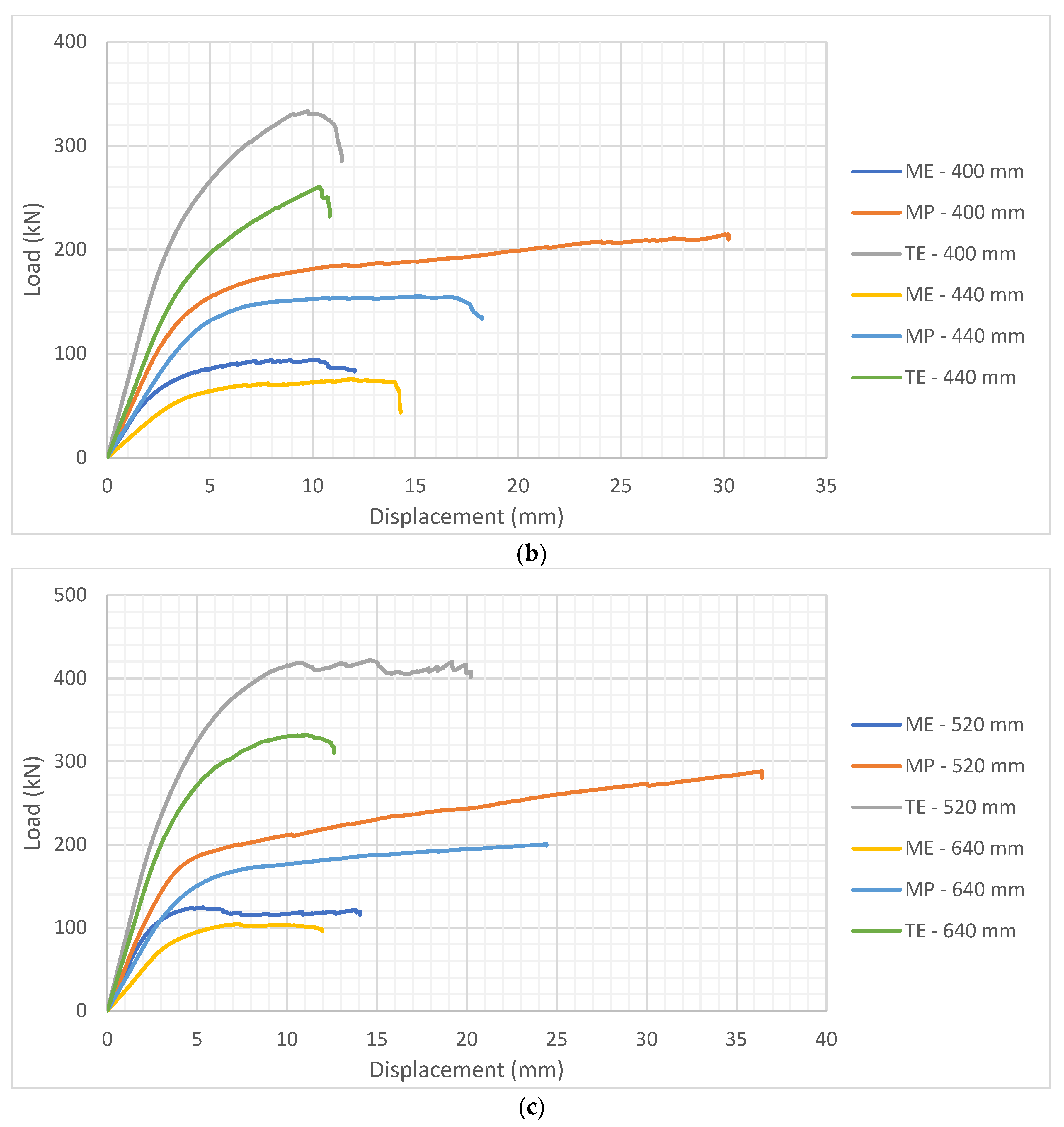
3.1. Experimental Work
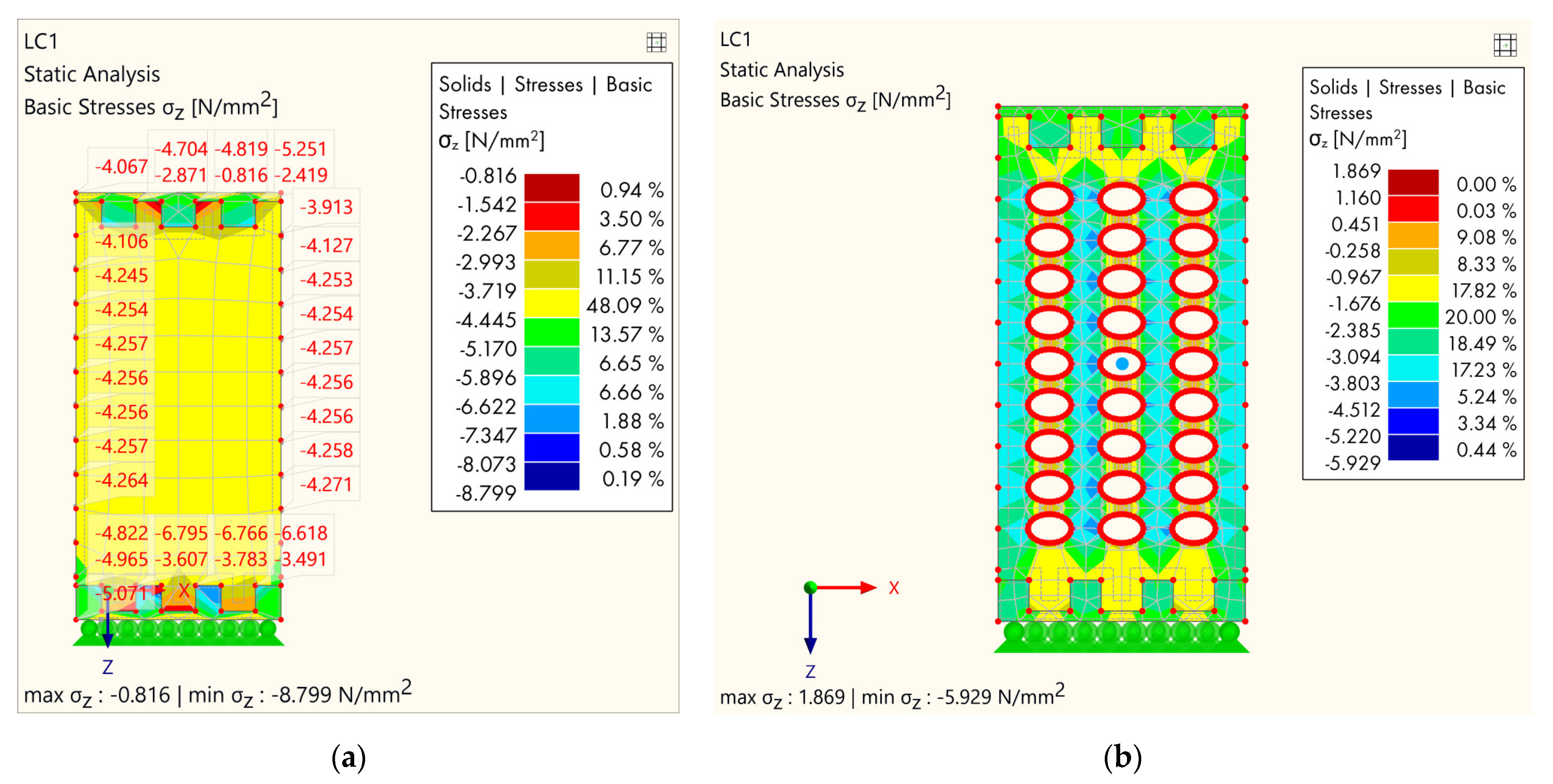
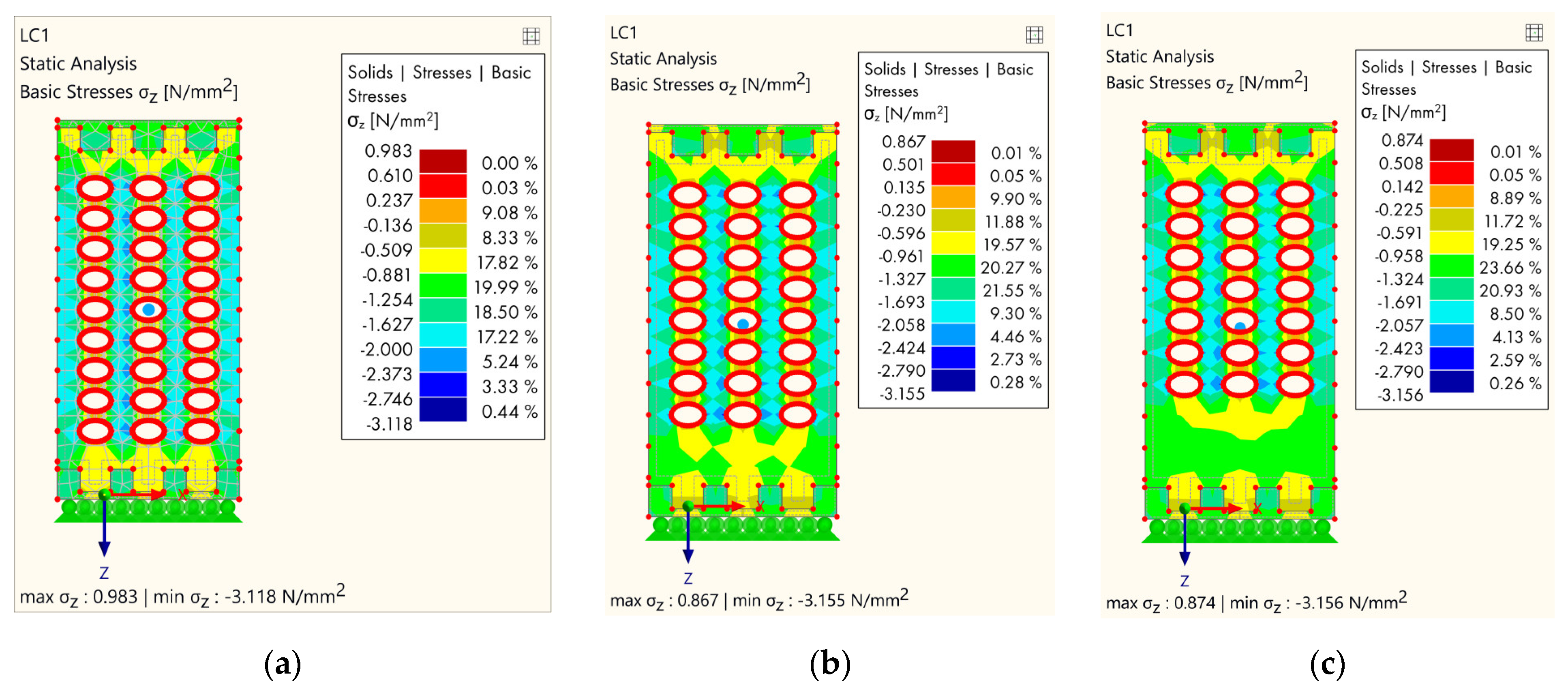
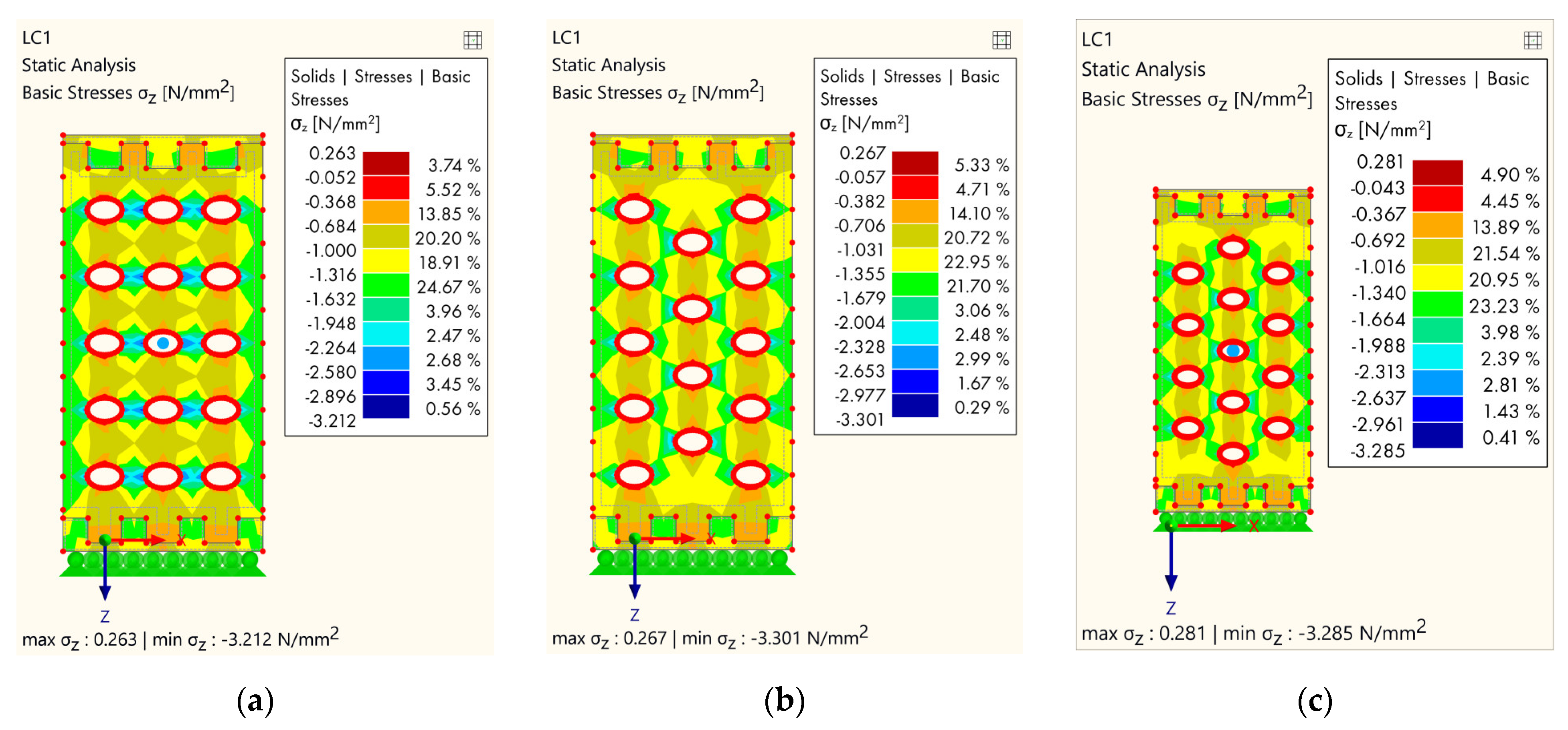
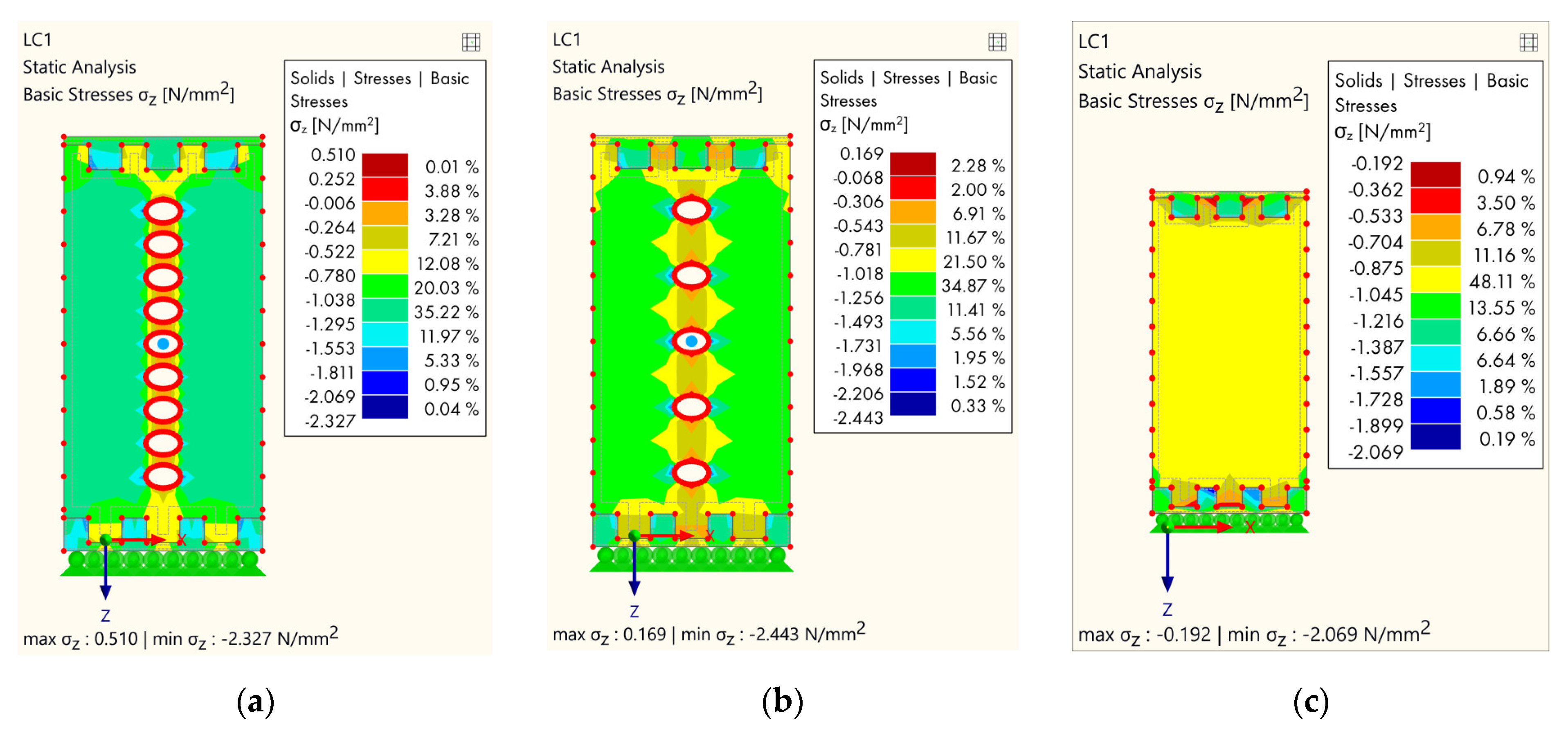
3.2. FEM Analysis
4. Discussion
4.1. Experimental Work
4.2. FEM Analysis
5. Conclusions
6. Patents
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sciomenta, M.; Bedon, C.; Fragiacomo, M.; Luongo, A. Shear Performance Assessment of Timber Log-House Walls under In-Plane Lateral Loads via Numerical and Analytical Modelling. Buildings 2018, 8, 99. [Google Scholar] [CrossRef]
- Perković, N.; Rajčić, V.; Pranjić, M. Behavioral Assessment and Evaluation of Innovative Hollow Glue-Laminated Timber Elements. Materials 2021, 14, 6911. [Google Scholar] [CrossRef] [PubMed]
- EN 1995-1-1:2004/A2:2014; Eurocode 5: Design of Timber Structures—Part 1-1: General—Common Rules and Rules for Buildings. CEN: Brussels, Belgium, 2004.
- Leijten, A.J.M.; Larsen, H.J.; van der Put, T.A.C.M. Structural Design for Compression Strength Perpendicular to the Grain of Timber Beams. Constr. Build. Mater. 2010, 24, 252–257. [Google Scholar] [CrossRef]
- Madsen, B.; Leijten, A.J.M.; Gehri, E.; Mischler, A.; Jorissen, A.J.M. Behaviour of Timber Connections; Vancouver Ltd.: Vancouver, BC, Canada, 2000. [Google Scholar]
- Blass, H.J.; Görlacher, I.R. Compression Perpendicular to the Grain. In Proceedings of the 8th World Conference of Timber Engineering, Lahti, Finland, 14–17 June 2004; Finnish Association of Civil Engineers RIL: Lathi, Finland, 2004; pp. 435–440. [Google Scholar]
- Roh Werkst, H.; van der Put, T.A.C.M. Derivation of the Bearing Strength Perpendicular to the Grain of Locally Loaded Timber Blocks. Holz Roh-Werkst. 2008, 66, 409–417. [Google Scholar]
- Pozgaj, A.; Chovanec, D.; Kurjatko, S.; Babiak, M. Struktúra a Vlastnosti Dreva; Priroda: Bratislava, Slovakia, 1993. [Google Scholar]
- Tabarsa, T.; Chui, Y.H. Characterizing Mircroscopic Behaviour of Wood in Radial Compression. Part 2: Effect of Species and Loading Direction. Wood Fiber Sci. 2001, 33, 223–232. [Google Scholar]
- Kretschmann, D.E. Influence of Juvenile Wood Content on Shear Parallel, Compression, and Tension Transverse to Grain Strength and Mode I Fracture Toughness for Loblolly Pine; Research Paper FPL-RP-647; U.S. Department of Agriculture, Forest Service, Forest Products Laboratory: Madison, WI, USA, 2008; Volume 647, p. 27. [Google Scholar]
- Hoffmeyer, P.; Damkilde, L.; Pedersen, T.N. Structural Timber and Glulam in Compression Perpendicular to Grain. Holz Roh-Werkst. 2000, 58, 73–80. [Google Scholar] [CrossRef]
- Gehri, E. Timber in Compression Perpendicular to the Grain. In Proceedings of the International Conference of IUFRO S5.02 Timber Engineering, Copenhagen, Denmark, 18–20 June 1997; BKM: Copenhagen, Denmark, 1997; pp. 16–17. [Google Scholar]
- Verbist, M.; Branco, J.M.; Nunes, L. Characterization of the Mechanical Performance in Compression Perpendicular to the Grain of Insect-Deteriorated Timber. Buildings 2020, 10, 14. [Google Scholar] [CrossRef]
- Bodig, J.; Jayne, B.A. Mechanics of Wood and Wood Composites; Van Nostrand Reinhold Company Inc.: New York, NY, USA, 1982. [Google Scholar]
- Dinwoodie, J.M. Timber: Its Nature and Behavior; E & FN Spon: New York, NY, USA, 2000. [Google Scholar]
- EN 384:2016; Structural Timber-Determination of Characteristic Values of Mechanical Properties and Density. CEN: Brussels, Belgium, 2016.
- Kunesh, R.H. Strength and Elastic Properties of Wood in Transverse Compression. For. Prod. J. 1967, 18, 65–72. [Google Scholar]
- Madsen, B.; Hooley, R.F.; Hall, C.P. A Design Method for Bearing Stresses in Wood. Can. J. Civ. Eng. 2011, 9, 338–349. [Google Scholar] [CrossRef]
- Leijten, A.J.M. The Bearing Strength Capacity Prediction by Eurocode 5 and Other Potential Design Code Models. In Proceedings of the World Conference on Timber Engineering (WCTE 2016), Vienna, Austria, 22–25 August 2016; Vienna University of Technology: Vienna, Austria, 2016; pp. 1–8. [Google Scholar]
- Leijten, A.J.M.; Jorissen, A.J.M.; de Leijer, B.J.C. The Local Bearing Capacity Perpendicular to Grain of Structural Timber Elements. Constr. Build. Mater. 2012, 27, 54–59. [Google Scholar] [CrossRef][Green Version]
- Serrano, E.; Enquist, B. Compression Strength Perpendicular to Grain in Cross-Laminated Timber (CLT). In Proceedings of the World Conference on Timber Engineering (WCTE 2010), Trentino, Italy, 20–24 June 2010; Trees and Timber Institute, National Research Council: Trentino, Italy, 2010; pp. 1–8. [Google Scholar]
- Brandner, R. Cross Laminated Timber (CLT) in Compression Perpendicular to Plane: Testing, Properties, Design and Recommendations for Harmonizing Design Provisions for Structural Timber Products. Eng. Struct. 2018, 171, 944–960. [Google Scholar] [CrossRef]
- Gasparri, E.; Lam, F.; Liu, Y. Compression Perpendicular to Grain Behavior for the Design of a Prefabricated CLT Façade Horizontal Joint. In Proceedings of the WCTE 2016—World Conference on Timber Engineering, Vienna, Austria, 22–25 August 2016; Vienna University of Technology: Vienna, Austria, 2016. [Google Scholar]
- Brandner, R.; Schickhofer, G. Properties of Cross Laminated Timber (CLT) in Compression Perpendicular to Grain. In Proceedings of the International Network on Timber Engineering Research (INTER), Bath, UK, 1–4 September 2014; KIT: Karlsruhe, Germany, 2014; pp. 1–13. [Google Scholar]
- Franzoni, L.; Lebée, A.; Lyon, F.; Forêt, G. Elastic Behavior of Cross Laminated Timber and Timber Panels with Regular Gaps: Thick-Plate Modeling and Experimental Validation. Eng. Struct. 2017, 141, 402–416. [Google Scholar] [CrossRef]
- Tian, Z.; Gong, Y.; Xu, J.; Li, M.; Wang, Z.; Ren, H. Predicting the Average Compression Strength of CLT by Using the Average Density or Compressive Strength of Lamina. Forests 2022, 13, 591. [Google Scholar] [CrossRef]
- EN 408:2012; Timber Structures—Structural Timber and Glued Laminated Timber—Determination of Some Physical and Mechanical Properties. CEN: Brussels, Belgium, 2012. Available online: https://standards.iteh.ai/catalog/standards/cen/6ffae6c9-5eaf-4c84-8bf3-5132cbfc563c/en-408-2010a1-2012 (accessed on 2 July 2022).
- Kollmann, F.F.P.; Côté, W.A. Principles of Wood Science and Technology; Springer: Berlin/Heidelberg, Germany, 1968. [Google Scholar]
- Brol, J.; Kubica, J.; Weglorz, M. The Problem of Compressive Strength in Direction Perpendicular to the Grains on Example of Tests of the Load-Bearing Capacity of the Continuously Supported Timber-Frame Sill Plates. Materials 2020, 13, 1160. [Google Scholar] [CrossRef] [PubMed]
- Basta, C.T.; Gupta, R.; Leichti, R.J.; Sinha, A. Characterizing Perpendicular-to-Grain Compression (C) Behavior in Wood Construction. Holzforschung 2011, 65, 845–853. [Google Scholar] [CrossRef]
- Kathem, A.; Tajdar, H.; Arman, K. Compression Perpendicular to Grain in Timber—Bearing Strength for a Sill Plate; Linnaeus University: Växjö, Sweden, 2014. [Google Scholar]
- Leijten, A.J.M.; Jorissen, A.J.M. Global Test Standards and Code Design Rules for Compressive Strength Perpendicular to Grain. In Proceedings of the World Conference of Timber Engineering (WCTE 2010), Trento, Italy, 20–24 June 2010; CNR-IVALSA: Trento, Italy, 2010. [Google Scholar]
- Stoilov, G.; Pashkouleva, D.; Kavardzhikov, V. Digital Image Correlation for Monitoring of Timber Walls. Int. J. NDT Days 2019, II, 417–422. [Google Scholar]
- Speranzini, E.; Marsili, R.; Moretti, M.; Rossi, G. Image Analysis Technique for Material Behavior Evaluation in Civil Structures. Materials 2017, 10, 770. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Johansson, M.; Olsson, A.; Oscarsson, J.; Enquist, B. Local Variation of Modulus of Elasticity in Timber Determined on the Basis of Non-Contact Deformation Measurement and Scanned Fibre Orientation. Eur. J. Wood Wood Prod. 2014, 73, 17–27. [Google Scholar] [CrossRef]
- Kleiberit. Deutsches Institut fur Bautechnik. Available online: https://www.kleiberit.com/fileadmin/Content/Documents/EN/Info_Sheets/510_Tragender_Holzbau_GB_US.pdf (accessed on 13 July 2022).
- Structural Analysis Software. Dlubal. Available online: https://www.dlubal.com/en (accessed on 13 July 2022).
- RSECTION: Section Properties and Stress Analysis. Dlubal Software. Available online: https://www.dlubal.com/en/products/cross-section-properties-software/rsection (accessed on 13 July 2022).








| Width (mm) | Length (mm) | Height (mm) | Weight (g) | Density (kg/m3) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Avg. | CoV. (%) | St. Dev. | Avg. | CoV. (%) | St. Dev. | Avg. | CoV. (%) | St. Dev. | Avg. | CoV (%) | St. Dev. | Avg. | CoV. (%) | St. Dev. | |
| Softwood M1–M12 | 119.3 | 0.19 | 0.22 | 120.1 | 0.30 | 0.36 | 119.0 | 0.22 | 0.27 | 657.9 | 1.52 | 9.99 | 385.7 | 1.42 | 5.47 |
| Hardwood T1–T12 | 119.3 | 0.21 | 0.25 | 119.9 | 0.35 | 0.42 | 118.5 | 0.89 | 1.06 | 1337.4 | 1.35 | 18.08 | 789.4 | 1.60 | 12.60 |
| Moduli | Symbol | Value (N/mm2) |
|---|---|---|
| Modulus of elasticity parallel | E0, mean | 11,500 |
| Modulus of elasticity perpendicular | E90, mean | 300 |
| Shear modulus | Gmean | 650 |
| Modulus of elasticity parallel | E0,05 | 9600 |
| Modulus of elasticity perpendicular | E90,05 | 250 |
| Shear modulus | G05 | 540 |
| Type of Cross-Section | MP | ME | TE | TP | ||||
|---|---|---|---|---|---|---|---|---|
| Specimen Length (mm) | fc,90, k (MPa) | kc, 90 | fc,90, k (MPa) | kc, 90 | fc,90, k (MPa) | kc, 90 | fc,90, k (MPa) | kc, 90 |
| 105 | 4.17 | 1.00 | 1.90 | 1.00 | 6.75 | 1.00 | 15.08 | 1.00 |
| 209 | 4.07 | 1.00 | 1.83 | 1.00 | 6.58 | 1.00 | 12.96 | 1.00 |
| 400 | 5.90 | 1.42 | 2.67 | 1.40 | 9.59 | 1.42 | / | / |
| 440 | 5.03 | 1.24 | 5.90 | 1.45 | 8.16 | 1.24 | / | / |
| 520 | 6.08 | 1.46 | 2.95 | 1.55 | 10.42 | 1.54 | / | / |
| 640 | 5.90 | 1.45 | 2.78 | 1.51 | 9.72 | 1.48 | / | / |
| Specimen Length (mm) | Type of Cross-Section | Average Failure Force (kN) | CoV. (%) | St. Dev. | Fmax-Ratio in Relation to ME | Fmax-Ratio in Relation to TE |
|---|---|---|---|---|---|---|
| 105 | ME | 45.2 | 9.07 | 4.1 | 1.00 | 0.54 |
| MP | 118.4 | 7.09 | 8.4 | 2.62 | 1.41 | |
| TE | 185.2 | 8.26 | 15.3 | 4.10 | 2.21 | |
| TP | 622.19 | 6.22 | 38.7 | 13.77 | 7.43 | |
| 209 | ME | 47.7 | 5.03 | 2.4 | 1.00 | 0.54 |
| MP | 106.7 | 9.09 | 9.7 | 2.24 | 1.22 | |
| TE | 184.1 | 1.90 | 3.5 | 3.86 | 2.10 | |
| TP | 453.80 | 2.29 | 10.4 | 9.51 | 5.17 | |
| 400 | ME | 87.3 | 9.51 | 8.3 | 1.00 | 0.31 |
| MP | 219.3 | 8.76 | 19.2 | 2.51 | 0.78 | |
| TE | 320.2 | 6.09 | 19.5 | 3.67 | 1.15 | |
| TP | / | / | / | / | / | |
| 440 | ME | 75.3 | 1.73 | 1.3 | 1.00 | 0.39 |
| MP | 157.4 | 8.64 | 13.6 | 2.09 | 0.82 | |
| TE | 255.3 | 10.77 | 27.5 | 3.39 | 1.33 | |
| TP | / | / | / | / | / | |
| 520 | ME | 126.5 | 5.06 | 6.4 | 1.00 | 0.24 |
| MP | 282.4 | 5.24 | 14.8 | 2.23 | 0.54 | |
| TE | 413.7 | 3.50 | 14.5 | 3.27 | 0.79 | |
| TP | / | / | / | / | / | |
| 640 | ME | 106.9 | 8.70 | 9.3 | 1.00 | 0.31 |
| MP | 196.0 | 4.23 | 8.3 | 1.83 | 0.57 | |
| TE | 323.8 | 6.61 | 21.4 | 3.03 | 0.94 | |
| TP | / | / | / | / | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Perković, N.; Barbalić, J.; Rajčić, V.; Duvnjak, I. Compressive Strength Properties Perpendicular to the Grain of Hollow Glue-Laminated Timber Elements. Polymers 2022, 14, 3403. https://doi.org/10.3390/polym14163403
Perković N, Barbalić J, Rajčić V, Duvnjak I. Compressive Strength Properties Perpendicular to the Grain of Hollow Glue-Laminated Timber Elements. Polymers. 2022; 14(16):3403. https://doi.org/10.3390/polym14163403
Chicago/Turabian StylePerković, Nikola, Jure Barbalić, Vlatka Rajčić, and Ivan Duvnjak. 2022. "Compressive Strength Properties Perpendicular to the Grain of Hollow Glue-Laminated Timber Elements" Polymers 14, no. 16: 3403. https://doi.org/10.3390/polym14163403
APA StylePerković, N., Barbalić, J., Rajčić, V., & Duvnjak, I. (2022). Compressive Strength Properties Perpendicular to the Grain of Hollow Glue-Laminated Timber Elements. Polymers, 14(16), 3403. https://doi.org/10.3390/polym14163403









