The Local Topological Free Energy of the SARS-CoV-2 Spike Protein
Abstract
1. Introduction
2. Materials and Methods
2.1. Measures of Topological/Geometrical Complexity
2.2. Topological/Geometrical Free Energy
3. Results
3.1. Local Topological Free Energy of SARS-CoV-2 Variants
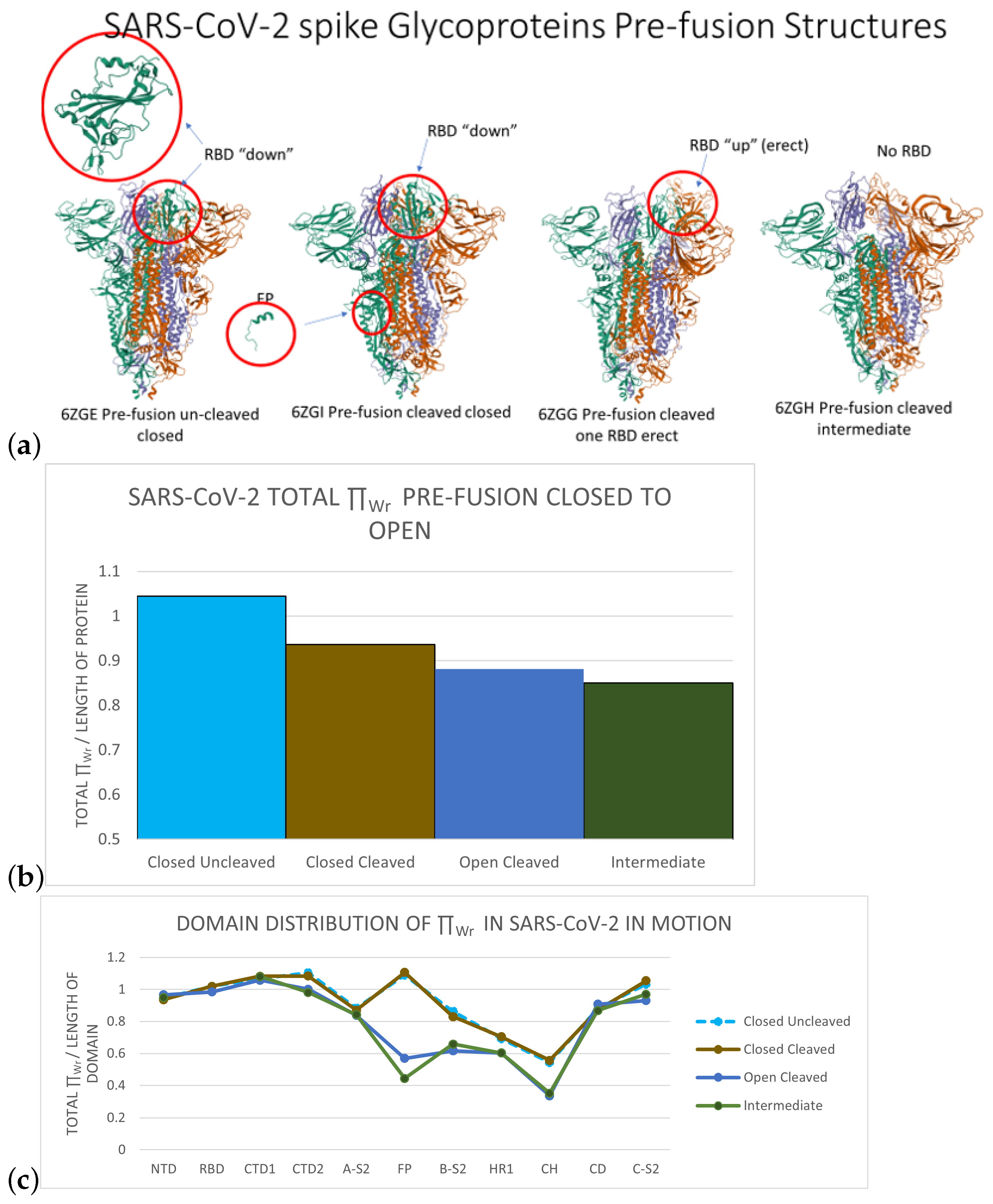
3.1.1. The Distribution of the Total Local Topological Free Energy in the SARS-CoV-2 Spike Protein Domains from Closed to Open Conformation
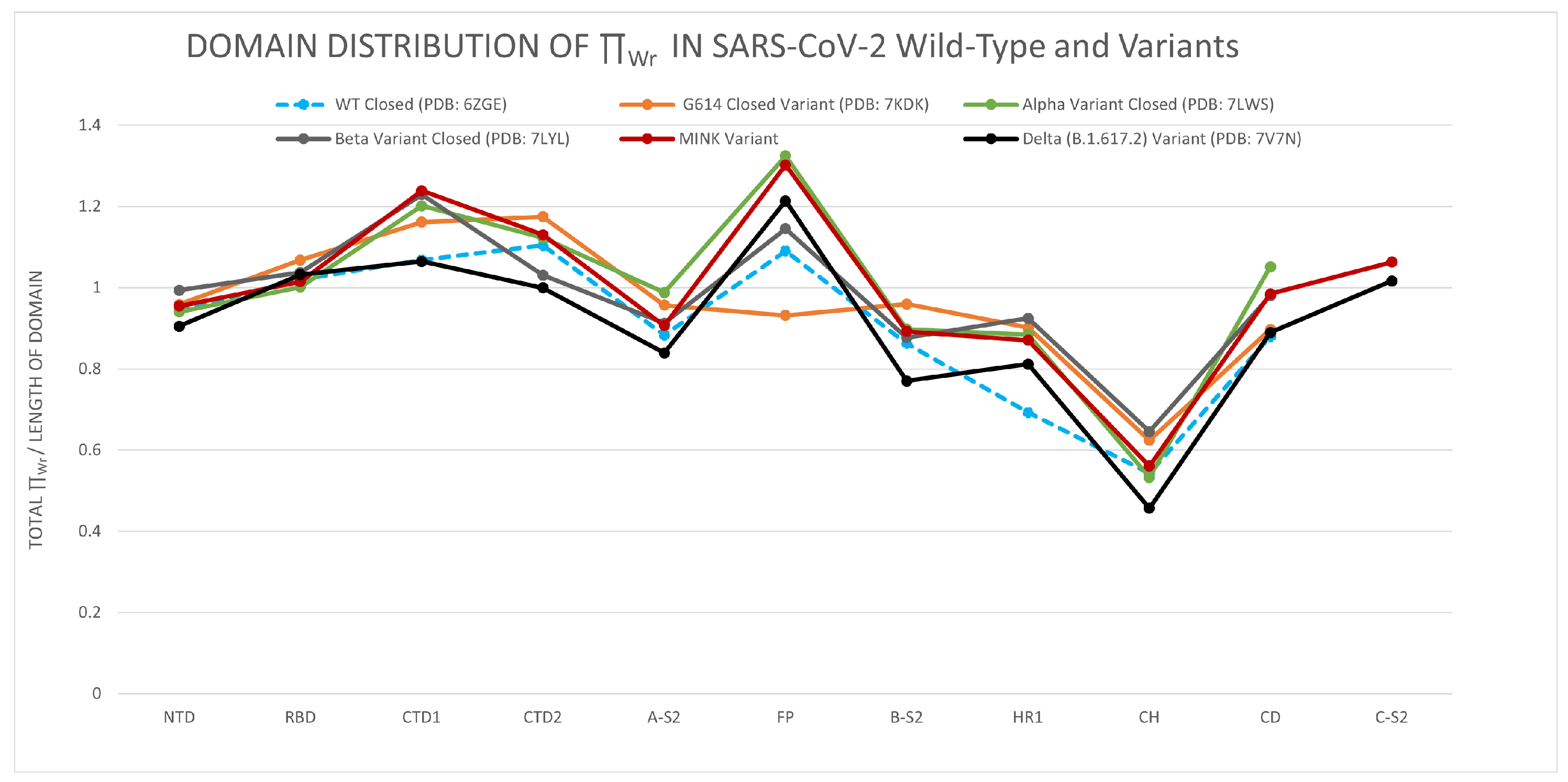
3.1.2. The Distribution of the Total Local Topological Free Energy in SARS-CoV-2 Protein Variants’ Domains
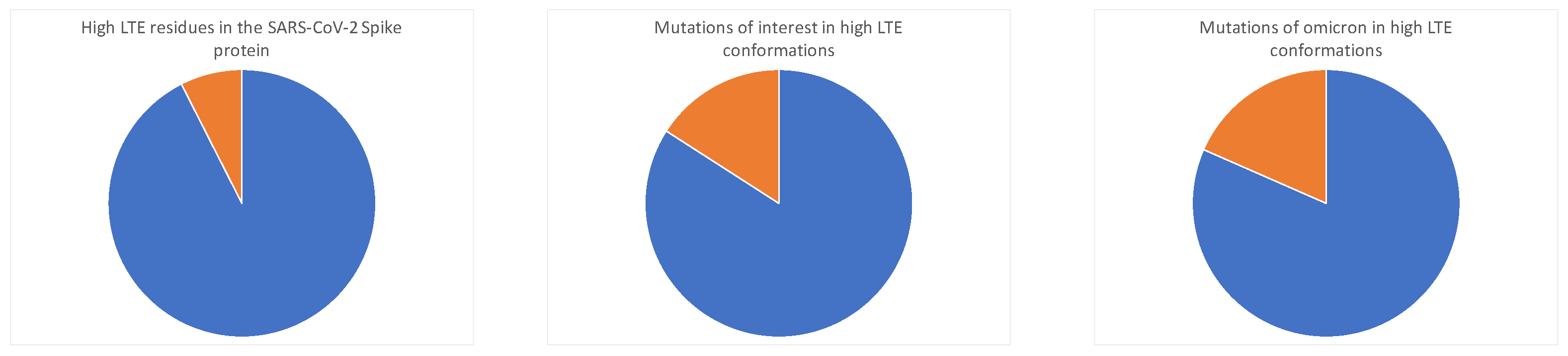
3.2. High Local Topological Free Energy Conformations in SARS-CoV-2
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Belouzard, S.; Millet, J.K.; Licitra, B.N.; Whittaker, G.R. Mechanisms of coronavirus cell entry mediated by the viral spike protein. Viruses 2012, 4, 1011–1033. [Google Scholar] [CrossRef] [PubMed]
- Cai, Y.; Zhang, J.; Xiao, T.; Peng, H.; Sterling, S.M.; Walsh, R.M., Jr.; Rawson, S.; Rits-Volloch, S.; Chen, B. Distinct conformational states of SARS-CoV-2 spike protein. Science 2020, 369, 1586–1592. [Google Scholar] [CrossRef] [PubMed]
- Earp, L.J.; Delos, S.E.; Park, H.E.; White, J.M. The many mechanisms of viral membrane fusion proteins. Curr. Top. Microbiol. Immunol. 2005, 285, 25–66. [Google Scholar] [PubMed]
- Harrison, S.C. Mechanism of membrane fusion by viral envelope proteins. Adv. Virus Res. 2005, 64, 231–361. [Google Scholar]
- Weissenhorn, W.; Hinz, A.; Gaudin, Y. Virus membrane fusion. FEBS Lett. 2007, 581, 2150–2155. [Google Scholar] [CrossRef]
- White, J.M.; Delos, S.E.; Brecher, M.; Schornberg, K. Structures and mechanisms of viral membrane fusion proteins: Multiple variations on a common theme. Crit. Rev. Biochem. Mol. Biol. 2008, 43, 189–219. [Google Scholar] [CrossRef]
- Nisole, S.; Saïb, A. Early steps of retrovirus replicative cycle. Retrovirology 2004, 1, 9. [Google Scholar] [CrossRef]
- Penner, R.C. Backbone free energy estimator applied to viral glycoproteins. J. Comput. Biol. 2020, 27, 1–14. [Google Scholar] [CrossRef]
- Berman, H.M.; Westbrook, J.; Feng, Z.; Gilliland, G.; Bhat, T.N.; Weissig, H.; Shindyalov, I.N.; Bourne, P.E. Magnetic helicity in a periodic domain. Nucleic Acids Res. 2000, 28, 235–242. [Google Scholar] [CrossRef]
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell; Garland Science: New York, NY, USA, 2002. [Google Scholar]
- Pouokam, M.; Cruz, B.; Burgess, S.; Segal, M.; Vazquez, M.; Arsuaga, J. The Rabl configuration limits topological entanglement of chromosomes in budding yeast. Sci. Rep. 2019, 9, 6795. [Google Scholar] [CrossRef]
- Rawdon, E.J.; Kern, J.C.; Piatek, M.; Plunkett, P.; Stasiak, A.; Millett, K.C. Effect of knotting on the shape of polymers. Macromolecules 2008, 41, 8281–8287. [Google Scholar] [CrossRef]
- Trigueros, S.; Arsuaga, J.; Vazquez, M.E.; Sumners, D.W.; Roca, J. Novel Display of knotted DNA molecules by two-dimensional gel electrophoresis. Nucleic Acids Res. 2001, 29, e67. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; Trigueros, S.; Sumners, D.W.; Roca, J. Knotting probability of DNA molecules confined in restricted volumes: DNA knotting in phage capsids. Proc. Natl. Acad. Sci. USA 2002, 99, 5373–5377. [Google Scholar] [CrossRef] [PubMed]
- Arsuaga, J.; Vazquez, M.; McGuirk, P.; Trigueros, S.; Sumners, D.W.; Roca, J. DNA knots reveal a chiral organization of DNA in phage capsids. Proc. Natl. Acad. Sci. USA 2005, 102, 9165–9169. [Google Scholar] [CrossRef]
- Arsuaga, J.; Diao, Y.; Kaplan, T.; Vazquez, M. The effects of density on the topological structure of the mitochondrial DNA from trypanosomes. J. Math. Biol. 2012, 64, 1087–1108. [Google Scholar]
- Hua, X.; Raghavan, B.; Nguyen, D.; Arsuaga, J.; Vazquez, M. Random State Transitions of Knots: A first step towards modeling unknotting by type II topoisomerases. Topol. Appl. 2007, 157, 1381–1397. [Google Scholar] [CrossRef] [PubMed]
- Stolz, R.; Yoshida, M.; Brasher, R.; Flanner, M.; Ishihara, K.; Sheratt, D.J.; Shimokawa, K.; Vazquez, M. Pathways of DNA unlinking: A story of stepwise simplification. Sci. Rep. 2017, 7, 12420. [Google Scholar] [CrossRef]
- Sumners, D.W.; Whittington, S.G. Untangling DNA. Math. Intelligencer. 1990, 12, 71–80. [Google Scholar] [CrossRef]
- Marenduzo, D.; Orlandini, E.; Stasiak, A.; Sumners, D.W.; Tubiana, L.; Micheletti, C. DNA-DNA interactions in bacteriophage capsids are responsible for the observed DNA knotting. Proc. Natl. Acad. Sci. USA 2009, 106, 22269–22274. [Google Scholar] [CrossRef]
- Micheletti, C.; Marenduzzo, D.; Orlandini, E.; Sumners, D.W. Knotting of random ring polymers in confined spaces. J. Chem. Phys. 2006, 124, 64903. [Google Scholar] [CrossRef]
- Micheletti, C.; Orland, H. Efficient Sampling of Knotting-Unknotting Pathways for Semiflexible Gaussian Chains. Polymers 2017, 9, 196. [Google Scholar] [CrossRef] [PubMed]
- Buck, D.; Erica, F. A topological characterization of knots and links arising from site-specific recombination. J. Phys. A Math. Theor. 2007, 40, 12377–12395. [Google Scholar] [CrossRef]
- Buck, D.; Erica, F. Predicting Knot or Catenane Type of Site-Specific Recombination Products. J. Mol Biol. 2007, 374, 1186–1199. [Google Scholar] [CrossRef] [PubMed]
- Flapan, E.; He, A.; Wong, H. Topological descriptions of protein folding. Proc. Natl. Acad. Sci. USA 2019, 116, 9360–9369. [Google Scholar] [CrossRef] [PubMed]
- Darcy, I.; Luecke, J.; Vazquez, M. Tangle analysis of difference topology experiments: Applications to a Mu protein-DNA complex. Algebr. Geom. Topol. 2009, 9, 2247–2309. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Trovato, A.; Seno, F. Linking in domain-swapped protein dimers. Sci. Rep. 2016, 6, 33872. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Seno, F.; Trovato, A. Exploring the correlation between the folding rates of proteins and the entanglement of their native state. J. Phys. A Math. Theor. 2017, 50, 504001. [Google Scholar] [CrossRef]
- Baiesi, M.; Orlandini, E.; Seno, F.; Trovato, A. Sequence and structural patterns detected in entangled proteins reveal the importance of co-translational folding. Sci. Rep. 2019, 9, 8426. [Google Scholar] [CrossRef]
- Panagiotou, E.; Plaxco, K.W. A topological study of protein folding kinetics. Topol. Geom. Biopolym. AMS Contemp. Math. Ser. 2020, 746, 223–233. [Google Scholar]
- Sulkowska, J.I.; Rawdon, E.J.; Millett, K.C.; Onuchic, J.N.; Stasiak, A. Conservation of complex knotting and slipknotting in patterns in proteins. Proc. Natl. Acad. Sci. USA 2012, 109, E1715. [Google Scholar] [CrossRef]
- Shimokawa, K.; Ishihara, K.; Grainge, I.; Sherratt, D.; Vazquez, M. FtsK-dependent XerCD-dif recombination unlinks replication catenanes in a stepwise manner. Proc. Natl. Acad. Sci. USA 2013, 110, 20906–20911. [Google Scholar] [CrossRef] [PubMed]
- Niemyska1, W.; Dabrowski-Tumanski, D.; Kadlof, M.; Haglund, E.; Sułkowski, P.; Sulkowska, J.I. Complex lasso: New entangled motifs in proteins. Sci. Rep. 2016, 6, 36895. [Google Scholar] [CrossRef] [PubMed]
- Jamroz, M.; Niemyska, W.; Rawdon, E.J.; Stasiak, A.; Millett, K.C.; Sulkowski, P.; Sulkowska, J. KnotProt: A database of proteins with knots and slipknots. Nucleic Acids Res. 2015, 43, D306–D314. [Google Scholar] [CrossRef] [PubMed]
- Dabrowski-Tumanski, P.; Piejko, M.; Niewieczerzal, S.; Stasiak, A.; Sulkowska, J.I. Protein Knotting by Active Threading of Nascent Polypeptide Chain Exiting from the Ribosome Exit Channel. J. Phys. Chem. B 2018, 122, 11616–11625. [Google Scholar] [CrossRef] [PubMed]
- Goundaroulis, D.; Gügümcu, N.; Lambropoulou, S.; Dorier, J.; Stasiak, A.; Kauffman, L.H. Topological methods for open-knotted protein chains using the concepts of knotoids and bonded knotoids. Polymers 2017, 9, 444. [Google Scholar] [CrossRef]
- Levitt, M. Protein Folding by Restrained EnergyMinimization and Molecular Dynamics. J. Mol. Biol. 1983, 170, 723–764. [Google Scholar] [CrossRef]
- Arteca, G.A. Overcrossing Spectra of Protein Backbones—Characterization of 3-Dimensional Molecular Shape and Global Structural Homologies. Biopolymers 1993, 33, 1829–1841. [Google Scholar] [CrossRef]
- Arteca, G.A. Scaling Behavior of Some Molecular Shape Descriptors of Polymer Chains and Protein Backbones. Phys. Rev. E 1994, 49, 2417–2428. [Google Scholar] [CrossRef] [PubMed]
- Arteca, G.A. Scaling Regimes Self-Entanglements in Very Compact Proteins. Phys. Rev. E 1995, 51, 2600–2610. [Google Scholar] [CrossRef]
- Arteca, G.A.; Tapia, O. Characterization of Fold Diversity among Proteins with the Same Number of Amino Acid Residues. J. Chem. Inf. Comput. Sci. 1999, 39, 642–649. [Google Scholar] [CrossRef]
- Reimann, C.T.; Arteca, G.A.; Tapia, O. A Connection between Mean Overcrossing Number and Orientationally-Averaged Collision Cross Section. Phys. Chem. Chem. Phys. 2002, 4, 4058–4064. [Google Scholar] [CrossRef]
- Rogen, P.; Bohr, H. A New Family of Global Protein Shape Descriptors. Math. Biosci. 2003, 182, 167–181. [Google Scholar] [CrossRef]
- Baldwin, Q.; Panagiotou, E. The local topological free energy of proteins. J. Theor. Biol. 2021, 529, 110854. [Google Scholar] [CrossRef] [PubMed]
- Harrison, S.C. Viral membrane fusion. Virology 2015, 479–480, 498–507. [Google Scholar] [CrossRef]
- McCallum, M.; Walls, A.C.; Bowen, J.E.; Corti, D.; Veesler, D. Structure-guided covalent stabilization of coronavirus spike protein trimers in the closed conformation. Nat. Struct. Biol. 2020, 27, 942–949. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Yang, C.; Xu, X.; Xu, W.; Liu, S. Structural and functional properties of SARS-CoV-2 spike protein: Potential antivirus drug development for COVID-19. Acta Pharmacol. Sin. 2020, 41, 1141–1149. [Google Scholar] [CrossRef]
- Fan, X.; Cao, D.; Kong, L.; Zhang, X. Cryo-EM analysis of the post-fusion structure of the SARS-CoV spike glycoprotein. Nat. Commun. 2020, 11, 3618. [Google Scholar] [CrossRef]
- Shah, M.; Ahmad, B.; Choi, S.; Woo, H.G. Mutations in the SARS-CoV-2 spike RBD are responsible for stronger ACE2 binding and poor anti-SARS-CoV mAbs cross-neutralization. Comp. Struct. Biotech. J. 2020, 18, 3402–3414. [Google Scholar] [CrossRef]
- Henderson, R.; Edwards, R.J.; Mansouri, K.; Janowska, K.; Stalls, V.; Gobeil, S.M.C.; Kopp, M.; Li, D.; Parks, R.; Hsu, A.L.; et al. Controlling the SARS-CoV-2 spike glycoprotein conformation. Nat. Strut. Mol. Biol. 2020, 27, 925–933. [Google Scholar] [CrossRef]
- Giron, C.C.; Laaksonen, A.; Barroso da Silva, F.L. Up State of the SARS-COV-2 Spike Homotrimer Favors an Increased Virulence for New Variants. Front. Med. Technol. 2021, 3, 29. [Google Scholar] [CrossRef]
- Gobeil, S.M.C.; Janowska, K.; McDowell, S.; Mansouri, K.; Parks, R.; Manne, K.; Stalls, V.; Kopp, M.; Henderson, R.; Edwards, R.J.; et al. Effect of natural mutations of SARS-CoV-2 on spike structure, conformation and antigenicity. Science 2021, 373, eabi6226. [Google Scholar] [CrossRef] [PubMed]
- Panagiotou, E.; Kauffman, L. Knot polynomials of open and closed curves. Proc. R. Soc. Math. Phys. Eng. Sci. 2020, 476, 20200124. [Google Scholar] [CrossRef] [PubMed]
- Plaxco, K.W.; Simons, K.T.; Baker, D. Contact order, transiton state placement and the refolding rates of single domain proteins. J. Mol. Biol. 1998, 277, 985–994. [Google Scholar] [CrossRef] [PubMed]
- Diao, Y.; Dobay, A.; Stasiak, A. The average inter-crossing number of equilateral random walks and polygons. J. Phys. A Math. Gen. 2005, 38, 7601–7616. [Google Scholar] [CrossRef][Green Version]
- Diao, Y.; Ernst, C.; Hinson, K.; Ziegler, U. The mean-squared writhe of alternating random knot diagrams. J. Phys. A Math. Theor. 2010, 43, 495202. [Google Scholar] [CrossRef]
- Arsuaga, J.; Blackstone, T.; Diao, Y.; Karadayi, E.; Saito, M. The linking of uniform random polygons in confined spaces. J. Phys. A Math. Theor. 2007, 40, 1925–1936. [Google Scholar] [CrossRef]
- Millett, K.C.; Dobay, A.; Stasiak, A. Linear random knots and their scaling behavior. Macromolecules 2005, 38, 601–606. [Google Scholar] [CrossRef]
- Portillo, J.; Diao, Y.; Scharein, R.; Arsuaga, J.; Vazquez, M. On the mean and variance of the writhe of random polygons. J. Phys. A Math. Theor. 2011, 44, 275004. [Google Scholar] [CrossRef]
- Panagiotou, E.; Millett, K.C.; Atzberger, P.J. Topological methods for polymeric materials: Characterizing the relationship between polymer entanglement and viscoelasticity. Polymers 2019, 11, 437. [Google Scholar] [CrossRef]
- Panagiotou, E.; Kröger, M.; Millett, K.C. Writhe and mutual entanglement combine to give the entanglement length. Phys. Rev. E 2013, 88, 062604. [Google Scholar] [CrossRef]
- Panagiotou, E.; Kröger, M. Pulling-force-induced elongation and alignment effects on entanglement and knotting characteristics of linear polymers in a melt. Phys. Rev. E 2014, 90, 042602. [Google Scholar] [CrossRef] [PubMed]
- Panagiotou, E.; Tzoumanekas, C.; Lambropoulou, S.; Millett, K.C.; Theodorou, D.N. A Study of the Entanglement in Systems with Periodic Boundary Conditions. Progr. Theor. Phys. Suppl. 2011, 191, 172–181. [Google Scholar] [CrossRef]
- Banchoff, T. Self-linking numbers of space polygons. Indiana Univ. Math. J. 1976, 25, 1171–1188. [Google Scholar] [CrossRef]
- Wang, J.; Panagiotou, E. The protein folding rate and the geometry and topology of the native state. Sci. Rep. 2022, 12, 6384. [Google Scholar] [CrossRef] [PubMed]
- Herschberg, T.; Pifer, K.; Panagiotou, E. A computational package for measuring Topological Entanglement in Polymers, Proteins and Periodic systems (TEPPP). Comp. Prog. Phys. 2022, in press.
- Wang, G.; Dunbrack, R.L.J. PISCES: A protein sequence culling server. Bioinformatics 2003, 19, 1589–1591. [Google Scholar] [CrossRef]
- Wrapp, D.; Wang, N.; Corbett, K.S.; Goldsmith, J.A.; Hsieh, C.L.; Abiona, O.; Graham, B.S.; McLellan, J.S. Cryo-EM structure of the 2019-nCoV spike in the prefusion conformation. Science 2020, 367, 1260–1263. [Google Scholar] [CrossRef]
- Wrobel, A.; Benton, D.; Xu, P.E.A. SARS-CoV-2 and bat RaTG13 spike glycoprotein structures inform on virus evolution and furin-cleavage effects. Nat. Struct. Mol. Biol. 2020, 27, 763–767. [Google Scholar] [CrossRef]
- Ray, D.; Le, L.; Andricioaei, I. Distant residues modulate conformational opening in SARS-CoV-2 spike protein. Proc. Natl. Acad. Sci. USA 2021, 118, e2100943118. [Google Scholar] [CrossRef]
- Hsieh, C.L.; Goldsmith, J.A.; Schaub, J.M.; DiVenere, A.M.; Kuo, H.-C.; Javanmardi, K.; Le, K.C.; Wrapp, D.; Lee, A.G.; Liu, Y.; et al. Structure-based design of prefusion-stabilized SARS-CoV-2 spikes. Science 2020, 369, 1501–1505. [Google Scholar] [CrossRef] [PubMed]
- Juraszek, J.; Rutten, L.; Blokland, S.; Bouchier, P.; Voorzaat, R.; Ritschel, T.; Bakkers, M.J.G.; Renault, L.L.R.; Langedijk, J.P.M. Stabilizing the closed SARS-CoV-2 spike trimer. Nat. Commun. 2021, 12, 244. [Google Scholar] [CrossRef] [PubMed]
- Alai, S.; Gujar, N.; Joshi, M.; Gautam, M.; Gairola, S. Pan-India novel coronavirus SARS-CoV-2 genomics and global diversity analysis in spike protein. Heliyon 2021, 7, E06564. [Google Scholar] [CrossRef] [PubMed]
- Carroll, T.; Fox, D.; van Doremalen, N.; Ball, E.; Morris, M.K.; Sotomayor-Gonzalez, A.; Servellita, V.; Rustagi, A.; Yinda, C.K.; Fritts, L.; et al. The B.1.427/1.429 (epsilon) SARS-CoV-2 variants are more virulent than ancestral B.1 (614G) in Syrian hamsters. bioRxiv 2021. [Google Scholar] [CrossRef] [PubMed]
- Deng, X.; Garcia-Knight, M.A.; Khalid, M.M.; Servellita, V.; Wang, C.; Morris, M.K.; Sotomayor-González, A.; Glasner, D.R.; Reyes, K.R.; Gliwa, A.S.; et al. Transmission, infectivity, and neutralization of a spike L452R SARS-CoV-2 variant. Cell 2021, 184, 3426–3437.e8. [Google Scholar] [CrossRef] [PubMed]
- European Centre for Disease Prevention and Control. Rapid Increase of a SARS-CoV-2 Variant with Multiple Spike Protein Mutations Observed in the United Kingdom; European Centre for Disease Prevention and Control: Solna, Sweden, 2020. [Google Scholar]
- Hoffmann, M.; Kleine-Wber, H.; Pohlmann, S. A multibasic cleavage site in the spike protein of SARS-CoV-2 is essential for infection of human lung cells. Mol. Cell 2020, 78, 779–784.e5. [Google Scholar] [CrossRef]
- Kirchdoerfer, R.N.; Wang, N.; Pallesen, J.; Wrapp, D.; Turner, H.L.; Cottrell, C.A.; Corbett, K.S.; Graham, B.S.; McLellan, J.S.; Ward, A.B. Stabilized coronavirus spikes are resistant to conformational changes induced by receptor recognition of proteolysis. Sci. Rep. 2018, 8, 15701. [Google Scholar] [CrossRef]
- Will, B.K.; Fischer, M.; Gnanakaran, S.; Yoon, H.; Theiler, J.; Abfalterer, W.; Hengartner, N.; Giorgi, E.E.; Bhattacharya, T.; Foley, B.; et al. Tracking changes in SARS-CoV-2 spike: Evidence that d614g increases infectivity of the COVID-19 virus. Cell 2020, 182, 812–827.e19. [Google Scholar]
- Tegally, H.; Wilkinson, E.; Giovanetti, M.; Iranzadeh, A.; Fonseca, V.; Giandhari, J.; Doolabh, D.; Pillay, S.; San, E.J.; Msomi, N.; et al. Emergence and rapid spread of a new severe acute respiratory syndrome-related coronavirus 2 (SARS-CoV-2) lineage with multiple spike mutations in South Africa. medRxiv 2020. [Google Scholar] [CrossRef]
- Wang, P.; Casner, R.; Nair, M.; Huang, Y.; Shapiro, L.; Ho, D. Increased resistance of SARS-CoV-2 variant P.1 to antibody neutralization. Cell Host Microbe 2021, 29, 747–751. [Google Scholar] [CrossRef]
- Wang, R.; Hozumi, Y.; Yin, C.; Wei, G.W. Decoding SARS-CoV-2 transmission and evolution and ramifications for COVID-19 diagnosis, vaccine, and medicine. J. Chem. Inf. Model. 2020, 60, 5853–5865. [Google Scholar] [CrossRef]


| Spike Glycoprotein pre-fusion (6VSB), Closed chain A |
|---|
| Writhe 95–100% 86, 121, 197, 281, 296, 542, 569, 687, 688, 749, 753, 796, 797, 908, 969, |
| 984, 1083, 1097 |
| Torsion 95–100% 107, 543, 741, 756, 884 |
| Spike Glycoprotein post-fusion (6XRA, chain A) |
| Writhe 95–100% 754, 917, 965, 1083, 1124, 1188, 1192, 1193 |
| Torsion 95–100% 743, 1039, 1090, 1153 |
| Spike Glycoprotein pre-fusion (6VYB, Open Chain B) |
| Writhe 95–100% 281, 302, 337, 569, 601, 667, 796, 797, 855, 908, 942, 969 |
| Torsion 95–100% 31, 86, 122, 462, 543, 612, 743, 756, 884 |
| Closed Spike Glycoprotein pre-fusion (6VXX, Open Chain B) |
| Writhe 95–100% 97, 110, 197, 281, 302, 543, 569, 601, 667, 796, 797, 855, 908, 969 |
| Torsion 95–100% 31, 86, 122, 612, 743, 756, 884 |
| Uncleavable Closed Spike Glycoprotein pre-fusion (6ZGE, chain A) |
| Writhe 95–100% 31, 68, 110, 197, 281, 365, 480, 543, 569, 645, 667, 796, 797, 822, 855, |
| 905, 908, 969 |
| Torsion 95–100% 107, 743, 821, 822, 823 |
| Cleaved Closed Spike Glycoprotein pre-fusion (6ZGI, chain A) |
| Writhe 95–100% 31, 110, 197, 281, 365, 480, 543, 569, 667, 796, 797, 822, 855, 908, 969, |
| 1018, 1083, 1097 |
| Torsion 95–100% 107, 743, 821, 822, 823, 1017, 1018, 1019, 1039, 1056, 1082, 1090 |
| One RBD Erect(open) Spike Glycoprotein pre-fusion (6ZGG, chain B) |
| Writhe 95–100% 110, 197, 281, 543, 569, 667, 796, 855, 908, 969 |
| Torsion 95–100% 480, 884 |
| Cleaved Intermediate Spike Glycoprotein pre-fusion (6ZGH, chain A) |
| Writhe 95–100% 97, 110, 197, 281, 543, 569, 796, 855, 908, 985 |
| Torsion 95–100% 107, 741, 969 |
| Spike Glycoprotein pre-fusion G614 Variant, Minus RBD (6XS6, chain A) |
|---|
| Writhe 95–100% 110, 121, 197, 281, 559, 561, 562, 569, 601, 667, 743, 796, 797, 855, |
| 908, 913, 963, 964, 969, 1083, 1097 |
| Torsion 95–100% 107, 196, 612, 1056 |
| Spike Glycoprotein pre-fusion Closed G614 Variant (7KDK, Chain A) |
| Writhe 95–100% 110, 121, 197, 281, 302, 337, 365, 543, 559, 569, |
| 601, 645, 667, 743, 753, 796, 797, 855, 865, 908, 913, 964, 969, 1083, 1097 |
| Torsion 95–100% 107, 612, 1039, 1056 |
| Open South African (B.1.351) Spike Glycoprotein Variant pre-fusion (7LYL, chain A) |
| Writhe 95–100% 97, 110, 121, 136, 197, 281, 302, 338, 368, 480, 525, 543, 568, 569, |
| 601, 667, 743, 753, 796, 797, 855, 908, 913, 964, 969 |
| Torsion 95–100% 31, 212, 462, 612 |
| Open Brazil (P.1) Spike Glycoprotein Variant pre-fusion, (7M8K, Chain A) |
| Writhe 95–100% 67, 110, 197, 281, 543, 569, 601, |
| 612, 667, 743, 753, 796, 797, 855, 908, 969 |
| Torsion 95–100% 122, 462, 485, 611, 613, 884 |
| Open N501Y Spike Glycoprotein Variant pre-fusion (7MJG, Chain B) |
| Writhe 95–100% 97, 197, 281, 480, 543, 569, 601, 667, 796, 797, 908, 969, |
| 988, 1083, 1097 |
| Torsion 95–100% 612, 743 |
| Open D614G substitution Variant pre-fusion (7KRQ, Chain A) |
| Writhe 95–100% 97, 110, 146, 148, 197, 281, 406, 543, 569, |
| 601, 623, 667, 753, 796, 797, 830, 855, 908, 964, 969 |
| Torsion 95–100% 841 |
| Closed UK (B.1.1.7) SARS-CoV-2 S-GSAS-D614G Variant Spike |
| protein pre-fusion (7LWS, Chain A) |
| Writhe 95–100% 110, 121, 197, 281, 365, 386, 406, 480, 525, 543, 569, 601, 667, 742, |
| 743, 796, 797, 908, 913, 963, 969, 1097 |
| Torsion 95–100% 96, 462, 485, 568, 612 |
| Open UK (B.1.1.7) S-GSAS-D614G Variant Spike Glycoprotein (7LWT, Chain A) |
| Writhe 95–100% 121, 197, 281, 302, 338, 365, 406, |
| 480, 543, 569, 667, 743, 796, 797, 811, 855, 908, 913, 963, 964, 969 |
| Torsion 95–100% 107, 462 |
| Open South African (B.1.351) Spike protein Variant S-GSAS-B.1.351 (7LYN, Chain A) |
| Writhe 95–100% 121, 197, 281, 302, 337, 365, 480, 543, 559, 569, 601, 667, |
| 743, 796, 797, 855, 908, 913, 963, 964, 969 |
| Torsion 95–100% 462, 485 |
| Open Brazilian (B.1.1.28) Spike protein Variant, S-GSAS-B.1.1.28, pre-fusion |
| (7LWW, Chain A) |
| Writhe 95–100% 121, 138, 139, 197, 281, 365, 406, 480, 543, |
| 559, 569, 589, 601, 645, 667, 743, 752, 796, 797, 811, 855, 908, 913, |
| 963, 964, 969 |
| Torsion 95–100% 462, 485, 612 |
| Closed Delta Variant pre-fusion (7V7N, Chain A) |
| Writhe 95–100% 97, 195, 279, 363 |
| 478, 541, 567, 599, 665, 794, 795, 853, 906, 967, 1081, 1095 |
| Torsion 95–100% 96, 610, 1037, 1054, 1088 |
| Open Delta Variant (open) pre-fusion (7V7O, Chain A) |
| Writhe 95–100% 97, 195, 279, 478, 515, 541, 557, |
| 567, 665, 741, 794, 795, 906, 967, 986, 1081, 1095 |
| Torsion 95–100% 610, 1037, 1088 height |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baldwin, Q.; Sumpter, B.; Panagiotou, E. The Local Topological Free Energy of the SARS-CoV-2 Spike Protein. Polymers 2022, 14, 3014. https://doi.org/10.3390/polym14153014
Baldwin Q, Sumpter B, Panagiotou E. The Local Topological Free Energy of the SARS-CoV-2 Spike Protein. Polymers. 2022; 14(15):3014. https://doi.org/10.3390/polym14153014
Chicago/Turabian StyleBaldwin, Quenisha, Bobby Sumpter, and Eleni Panagiotou. 2022. "The Local Topological Free Energy of the SARS-CoV-2 Spike Protein" Polymers 14, no. 15: 3014. https://doi.org/10.3390/polym14153014
APA StyleBaldwin, Q., Sumpter, B., & Panagiotou, E. (2022). The Local Topological Free Energy of the SARS-CoV-2 Spike Protein. Polymers, 14(15), 3014. https://doi.org/10.3390/polym14153014






