Large Scale Hydrodynamically Coupled Brownian Dynamics Simulations of Polymer Solutions Flowing through Porous Media
Abstract
:1. Introduction
2. Method
2.1. Equation of Motion for the Polymer Blobs
2.2. Equation of Motion for the Fluid Blobs
2.3. Solutions of the Equations of Motion
3. Force Fields
3.1. The Conservative Potentials
3.2. The Transient Potential
3.3. The Equation of State
4. Interaction of the Fluid with the Solid
5. Weights and System Parameters
6. Results and Discussion
6.1. Flow through Cylindrical Porous Media
6.1.1. Pressure Drop in the Positive x Direction
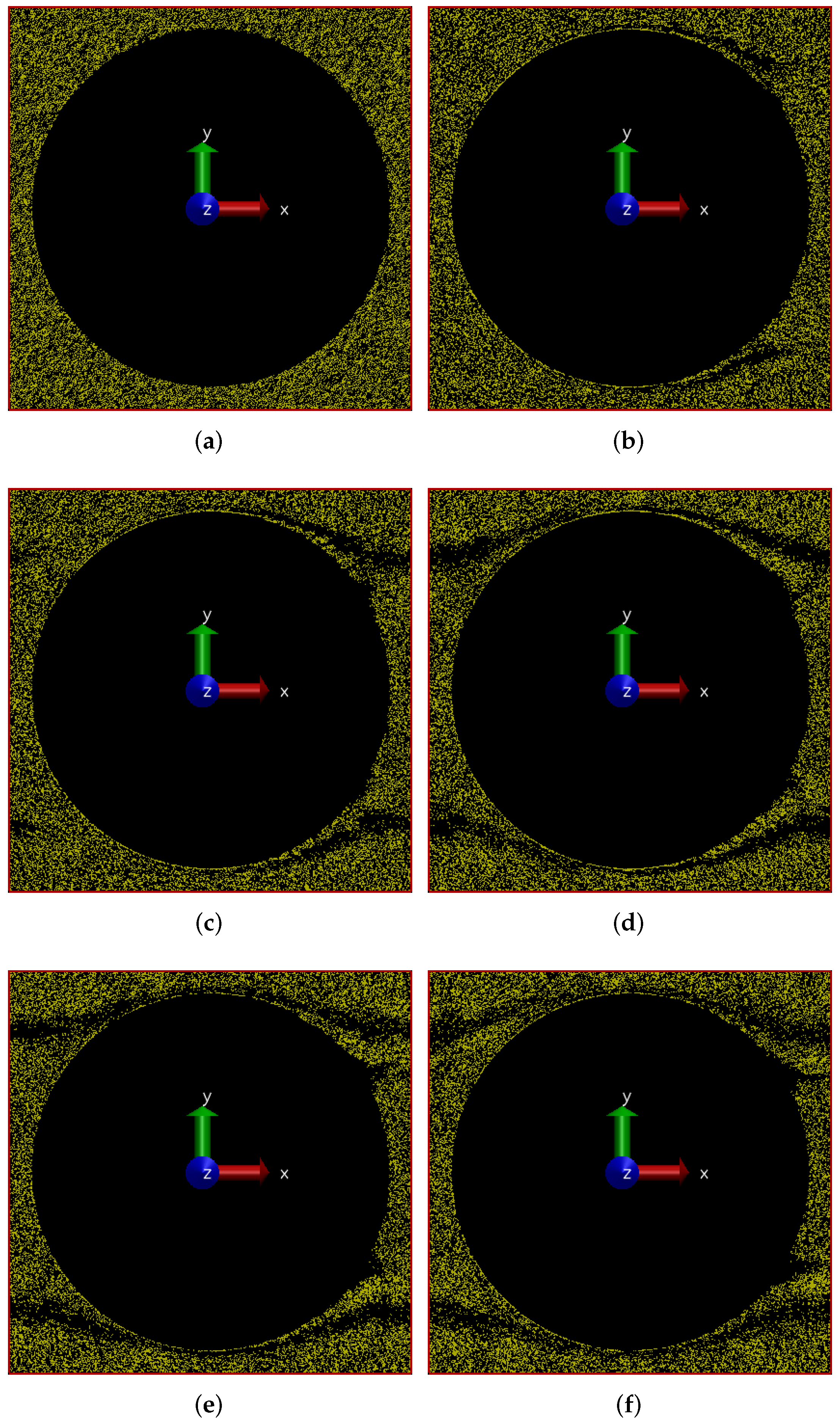
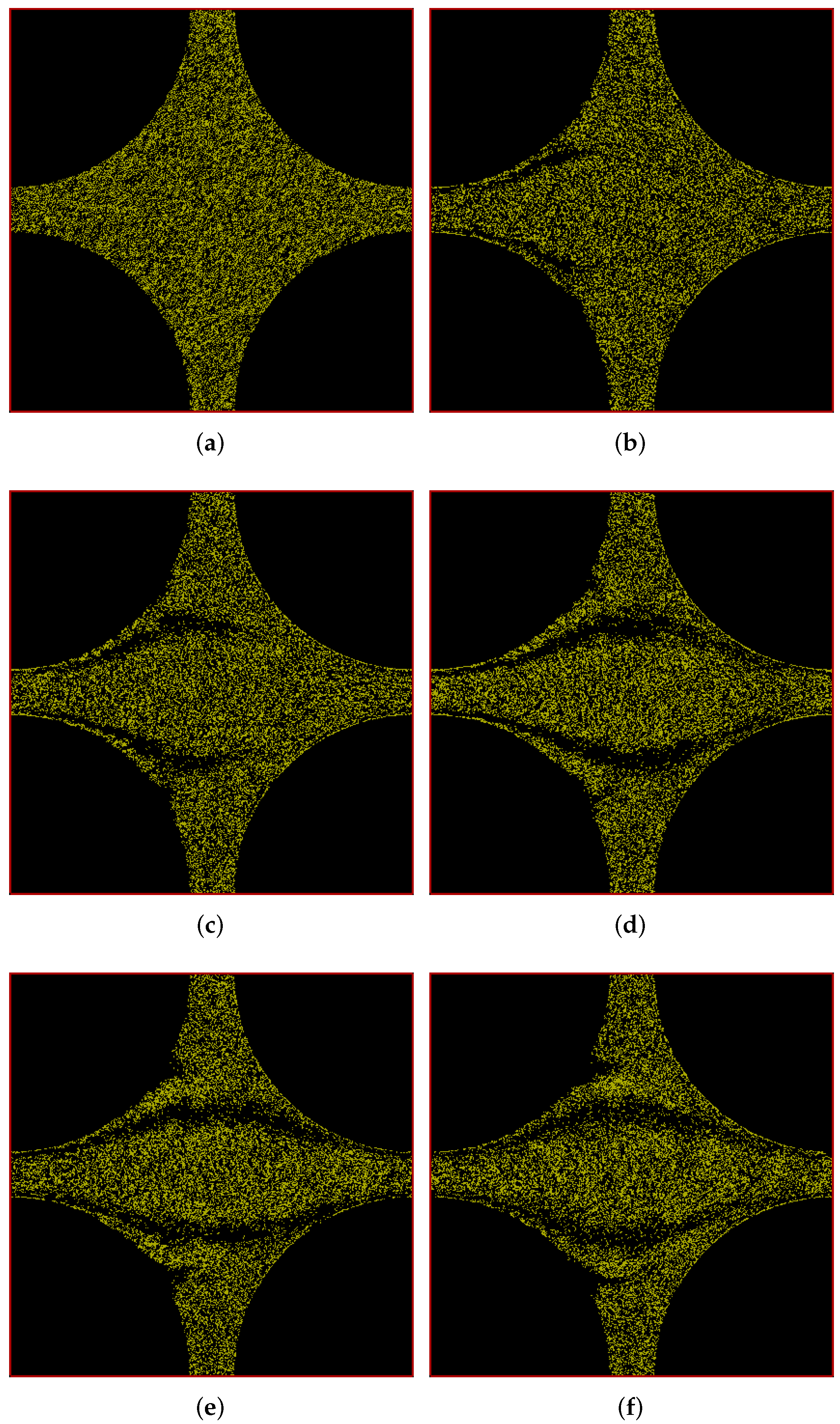
6.1.2. Pressure Drop along the Positive x-y Diagonal
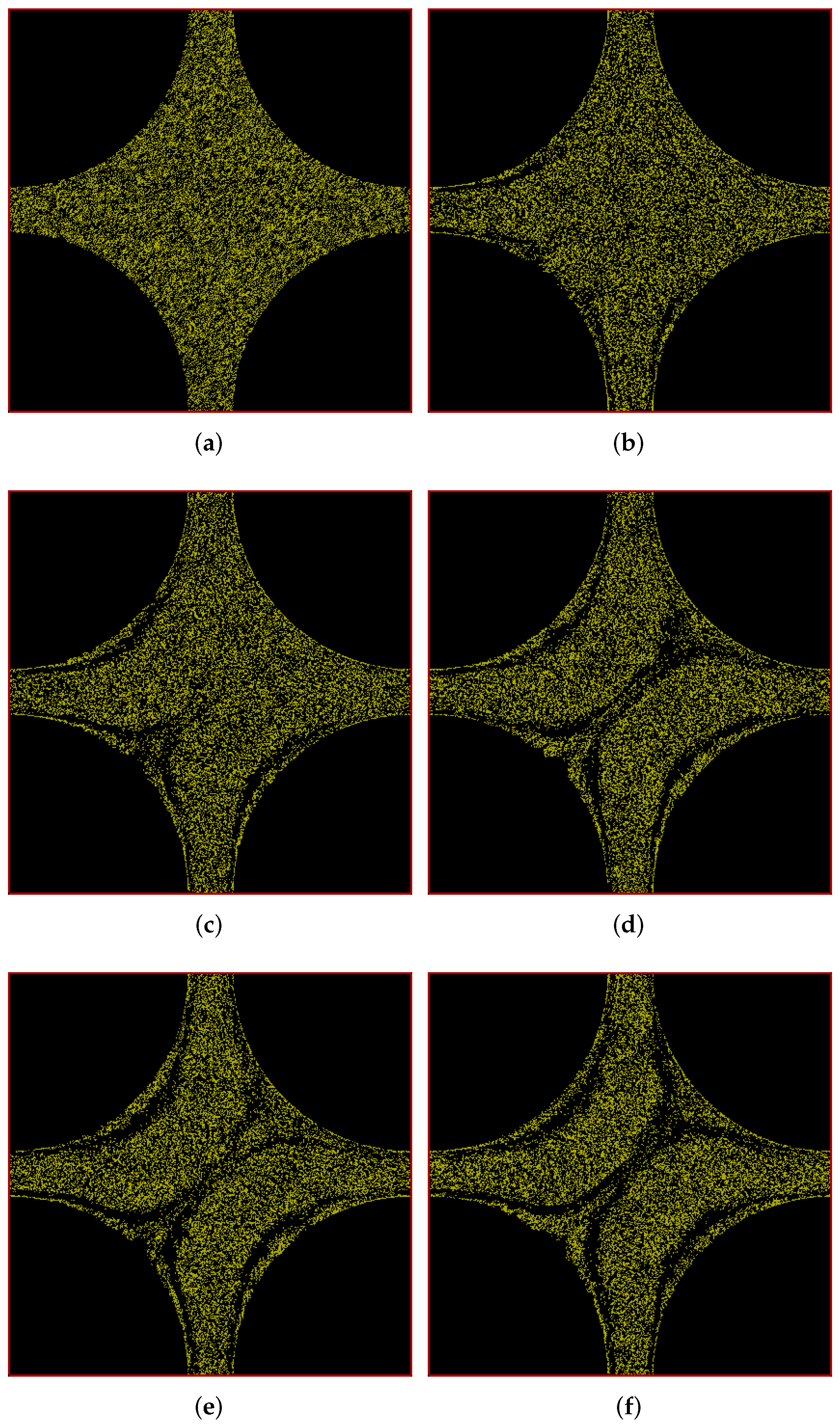
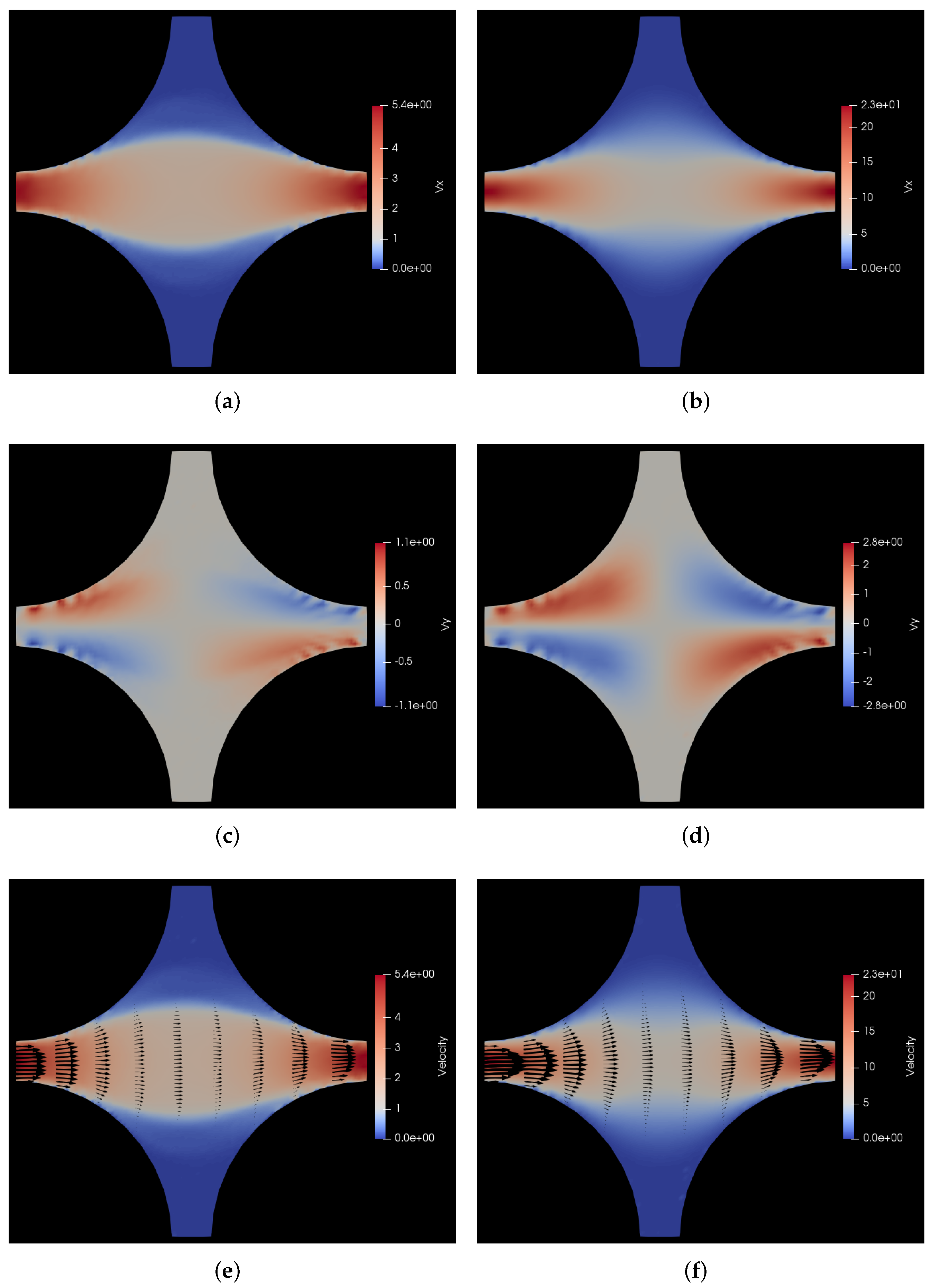
6.2. Flow through Cuboidal Porous Media
6.2.1. Pressure Drop in the Positive x Direction
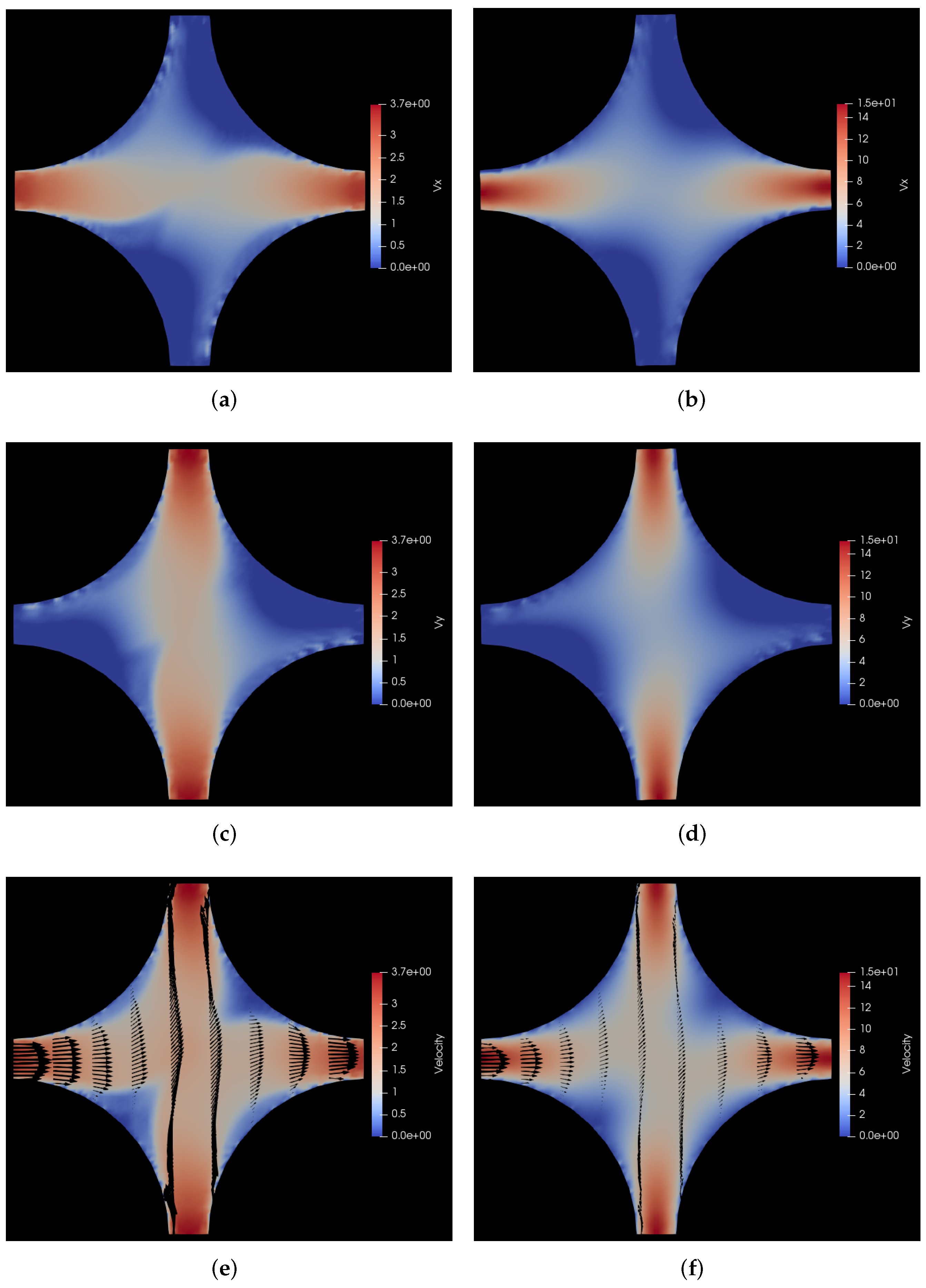

6.2.2. Pressure Drop along the Positive x-y Diagonal

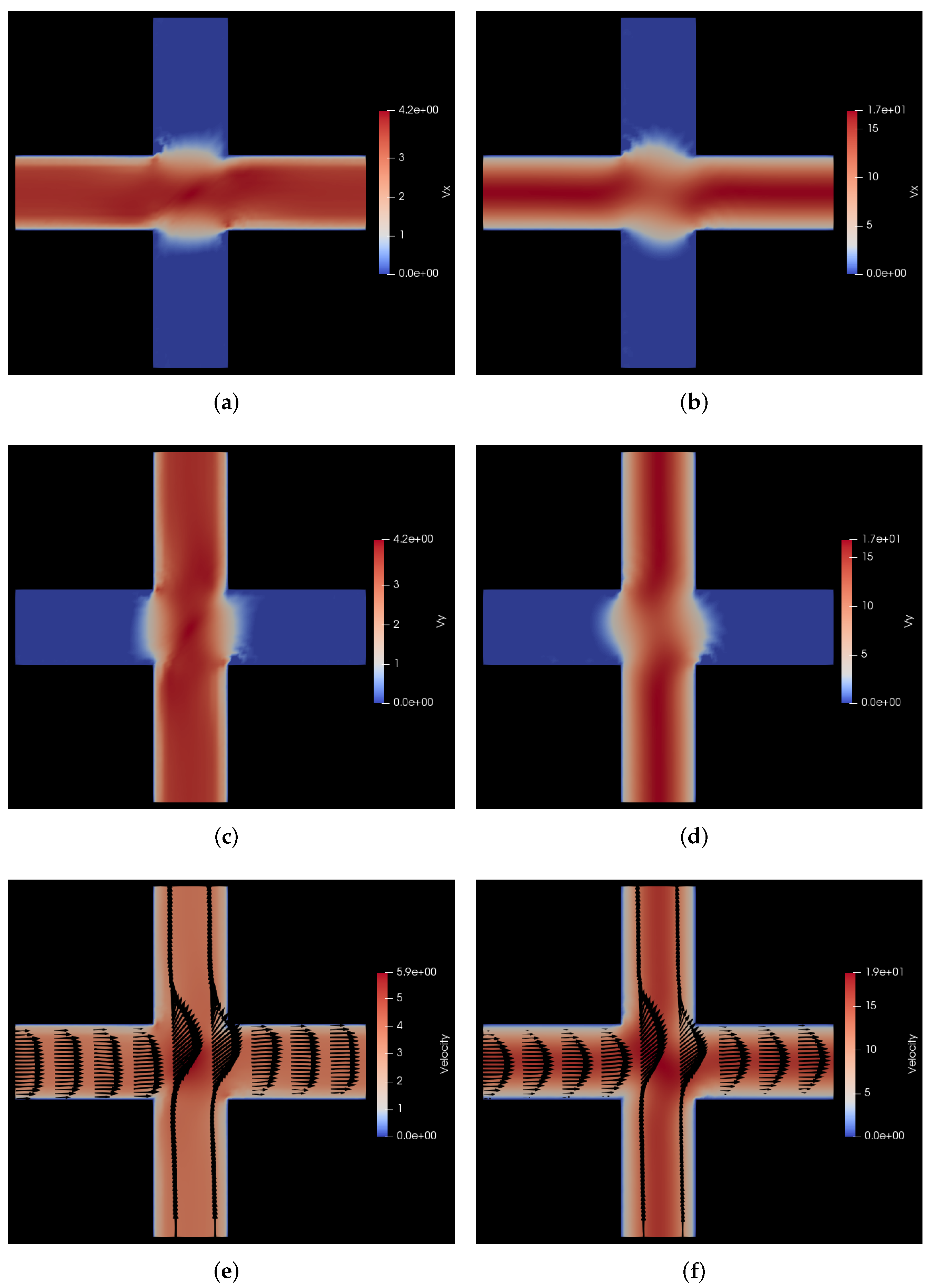
7. Conclusions and Scope for Further Research
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Thomas, S. Enhanced oil recovery—An overview. Oil Gas Sci. Technol. 2008, 63, 9–19. [Google Scholar] [CrossRef] [Green Version]
- Nilsson, M.A.; Kulkarni, R.; Gerberich, L.; Hammond, R.; Singh, R.; Baumhoff, E.; Rothstein, J.P. Effect of fluid rheology on enhanced oil recovery in a microfluidic sandstone device. J. Non-Newton. Fluid Mech. 2013, 202, 112–119. [Google Scholar] [CrossRef]
- Thomas, A.; Gaillard, N.; Favero, C. Some key features to consider when studying acrylamide-based polymers for chemical enhanced oil recovery. Oil Gas Sci. Technol. 2012, 67, 887–902. [Google Scholar] [CrossRef] [Green Version]
- Sorbie, K.S. Polymer-Improved Oil Recovery; CRC Press Inc.: Boca Raton, FL, USA, 1991. [Google Scholar]
- Squires, T.M.; Quake, S.R. Microfluidics: Fluid physics at the nanoliter scale. Rev. Mod. Phys. 2005, 77, 977. [Google Scholar] [CrossRef] [Green Version]
- Divoux, T.; Fardin, M.A.; Manneville, S.; Lerouge, S. Shear banding of complex fluids. Annu. Rev. Fluid Mech. 2016, 48, 81–103. [Google Scholar] [CrossRef] [Green Version]
- Lerouge, S.; Olmsted, P.D. Non-local effects in shear banding of polymeric flows. Front. Phys. 2020, 246. [Google Scholar] [CrossRef]
- Groisman, A.; Steinberg, V. Elastic turbulence in a polymer solution flow. Nature 2000, 405, 53–55. [Google Scholar] [CrossRef] [Green Version]
- Marshall, R.; Metzner, A. Flow of viscoelastic fluids through porous media. Ind. Eng. Chem. Fundam. 1967, 6, 393–400. [Google Scholar] [CrossRef]
- James, D.F.; McLaren, D. The laminar flow of dilute polymer solutions through porous media. J. Fluid Mech. 1975, 70, 733–752. [Google Scholar] [CrossRef]
- Rodriguez, S.; Romero, C.; Sargenti, M.; Müller, A.; Sáez, A.; Odell, J. Flow of polymer solutions through porous media. J. Non-Newton. Fluid Mech. 1993, 49, 63–85. [Google Scholar] [CrossRef]
- Chmielewski, C.; Jayaraman, K. Elastic instability in crossflow of polymer solutions through periodic arrays of cylinders. J. Non-Newton. Fluid Mech. 1993, 48, 285–301. [Google Scholar] [CrossRef]
- Talwar, K.K.; Khomami, B. Flow of viscoelastic fluids past periodic square arrays of cylinders: Inertial and shear thinning viscosity and elasticity effects. J. Non-Newton. Fluid Mech. 1995, 57, 177–202. [Google Scholar] [CrossRef]
- Sousa, P.; Pinho, F.; Oliveira, M.; Alves, M. Efficient microfluidic rectifiers for viscoelastic fluid flow. J. Non-Newton. Fluid Mech. 2010, 165, 652–671. [Google Scholar] [CrossRef] [Green Version]
- Galindo-Rosales, F.J.; Campo-Deano, L.; Pinho, F.T.; Van Bokhorst, E.; Hamersma, P.; Oliveira, M.S.; Alves, M.A. Microfluidic systems for the analysis of viscoelastic fluid flow phenomena in porous media. Microfluid. Nanofluid. 2012, 12, 485–498. [Google Scholar] [CrossRef] [Green Version]
- Ekanem, E.M.; Berg, S.; De, S.; Fadili, A.; Bultreys, T.; Rücker, M.; Southwick, J.; Crawshaw, J.; Luckham, P.F. Signature of elastic turbulence of viscoelastic fluid flow in a single pore throat. Phys. Rev. E 2020, 101, 042605. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1988; Volume 73. [Google Scholar]
- Graessley, W.W. Polymeric Liquids and Networks: Dynamics and Rheology; Garland Science: New York, NY, USA, 2008. [Google Scholar]
- Olmsted, P.D. Perspectives on shear banding in complex fluids. Rheol. Acta 2008, 47, 283–300. [Google Scholar] [CrossRef]
- Peterson, J.D.; Cromer, M.; Fredrickson, G.H.; Gary Leal, L. Shear banding predictions for the two-fluid Rolie-Poly model. J. Rheol. 2016, 60, 927–951. [Google Scholar] [CrossRef]
- Liu, A.W.; Bornside, D.E.; Armstrong, R.C.; Brown, R.A. Viscoelastic flow of polymer solutions around a periodic, linear array of cylinders: Comparisons of predictions for microstructure and flow fields. J. Non-Newton. Fluid Mech. 1998, 77, 153–190. [Google Scholar] [CrossRef]
- Hulsen, M.A.; Fattal, R.; Kupferman, R. Flow of viscoelastic fluids past a cylinder at high Weissenberg number: Stabilized simulations using matrix logarithms. J. Non-Newton. Fluid Mech. 2005, 127, 27–39. [Google Scholar] [CrossRef] [Green Version]
- Richter, D.; Iaccarino, G.; Shaqfeh, E.S. Simulations of three-dimensional viscoelastic flows past a circular cylinder at moderate Reynolds numbers. J. Fluid Mech. 2010, 651, 415–442. [Google Scholar] [CrossRef] [Green Version]
- De, S.; Kuipers, J.; Peters, E.; Padding, J. Viscoelastic flow simulations in model porous media. Phys. Rev. Fluids 2017, 2, 053303. [Google Scholar] [CrossRef] [Green Version]
- De, S.; Kuipers, J.; Peters, E.; Padding, J. Viscoelastic flow simulations in random porous media. J. Non-Newton. Fluid Mech. 2017, 248, 50–61. [Google Scholar] [CrossRef]
- Berk Usta, O.; Ladd, A.J.; Butler, J.E. Lattice-Boltzmann simulations of the dynamics of polymer solutions in periodic and confined geometries. J. Chem. Phys. 2005, 122, 094902. [Google Scholar] [CrossRef] [PubMed]
- Boek, E.S.; Venturoli, M. Lattice-Boltzmann studies of fluid flow in porous media with realistic rock geometries. Comput. Math. Appl. 2010, 59, 2305–2314. [Google Scholar] [CrossRef] [Green Version]
- Bird, R.; Stewart, W.; Lightfoot, E. Transport Phenomena; Wiley International edition; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Müller-Plathe, F. Coarse-graining in polymer simulation: From the atomistic to the mesoscopic scale and back. ChemPhysChem 2002, 3, 754–769. [Google Scholar] [CrossRef]
- Baschnagel, J.; Binder, K.; Doruker, P.; Gusev, A.A.; Hahn, O.; Kremer, K.; Mattice, W.L.; Müller-Plathe, F.; Murat, M.; Paul, W.; et al. Bridging the gap between atomistic and coarse-grained models of polymers: Status and perspectives. In Viscoelasticity, Atomistic Models, Statistical Chemistry; Springer: Berlin, Germany, 2000; pp. 41–156. [Google Scholar]
- Marrink, S.J.; Risselada, H.J.; Yefimov, S.; Tieleman, D.P.; De Vries, A.H. The MARTINI force field: Coarse grained model for biomolecular simulations. J. Phys. Chem. B 2007, 111, 7812–7824. [Google Scholar] [CrossRef] [Green Version]
- Monticelli, L.; Kandasamy, S.K.; Periole, X.; Larson, R.G.; Tieleman, D.P.; Marrink, S.J. The MARTINI coarse-grained force field: Extension to proteins. J. Chem. Theory Comput. 2008, 4, 819–834. [Google Scholar] [CrossRef]
- Risken, H. Fokker-planck equation. In The Fokker–Planck Equation; Springer: Berlin, Germany, 1984; pp. 63–95. [Google Scholar]
- Akkermans, R.L.; Briels, W.J. Coarse-grained dynamics of one chain in a polymer melt. J. Chem. Phys. 2000, 113, 6409–6422. [Google Scholar] [CrossRef]
- Klippenstein, V.; Tripathy, M.; Jung, G.; Schmid, F.; van der Vegt, N.F. Introducing memory in coarse-grained molecular simulations. J. Phys. Chem. B 2021, 125, 4931–4954. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057–5086. [Google Scholar] [CrossRef]
- Padding, J.; Briels, W.J. Time and length scales of polymer melts studied by coarse-grained molecular dynamics simulations. J. Chem. Phys. 2002, 117, 925–943. [Google Scholar] [CrossRef] [Green Version]
- Padding, J.T.; Boek, E.S.; Briels, W.J. Dynamics and rheology of wormlike micelles emerging from particulate computer simulations. J. Chem. Phys. 2008, 129, 074903. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masubuchi, Y.; Takimoto, J.I.; Koyama, K.; Ianniruberto, G.; Marrucci, G.; Greco, F. Brownian simulations of a network of reptating primitive chains. J. Chem. Phys. 2001, 115, 4387–4394. [Google Scholar] [CrossRef]
- Uneyama, T.; Masubuchi, Y. Multi-chain slip-spring model for entangled polymer dynamics. J. Chem. Phys. 2012, 137, 154902. [Google Scholar] [CrossRef]
- Van den Noort, A.; den Otter, W.K.; Briels, W.J. Coarse graining of slow variables in dynamic simulations of soft matter. EPL Europhys. Lett. 2007, 80, 28003. [Google Scholar] [CrossRef]
- Briels, W.J. Transient forces in flowing soft matter. Soft Matter 2009, 5, 4401–4411. [Google Scholar] [CrossRef]
- Bird, R.B.; Curtiss, C.F.; Armstrong, R.C.; Hassager, O. Dynamics of Polymeric Liquids, Volume 2: Kinetic Theory; Wiley: Hoboken, NJ, USA.
- Monaghan, J.J. Smoothed particle hydrodynamics. Rep. Prog. Phys. 2005, 68, 1703. [Google Scholar] [CrossRef]
- Ahuja, V.; van der Gucht, J.; Briels, W. Hydrodynamically Coupled Brownian Dynamics: A coarse-grain particle-based Brownian dynamics technique with hydrodynamic interactions for modeling self-developing flow of polymer solutions. J. Chem. Phys. 2018, 148, 034902. [Google Scholar] [CrossRef] [Green Version]
- Ahuja, V.R.; van der Gucht, J.; Briels, W.J. Coarse-grained simulations for flow of complex soft matter fluids in the bulk and in the presence of solid interfaces. J. Chem. Phys. 2016, 145, 194903. [Google Scholar] [CrossRef]
- Cho, H.W.; Kim, H.; Sung, B.J.; Kim, J.S. Tracer diffusion in tightly-meshed homogeneous polymer networks: A brownian dynamics simulation study. Polymers 2020, 12, 2067. [Google Scholar] [CrossRef]
- Djordjevich, A.; Savović, S.; Janićijević, A. Explicit finite-difference solution of two-dimensional solute transport with periodic flow in homogenous porous media. J. Hydrol. Hydromech. 2017, 65, 426–432. [Google Scholar] [CrossRef] [Green Version]
- Djordjevich, A.; Savović, S. Solute transport with longitudinal and transverse diffusion in temporally and spatially dependent flow from a pulse type source. Int. J. Heat Mass Transf. 2013, 65, 321–326. [Google Scholar] [CrossRef]
- Sahmani, S.; Fattahi, A.M.; Ahmed, N. Develop a refined truncated cubic lattice structure for nonlinear large-amplitude vibrations of micro/nano-beams made of nanoporous materials. Eng. Comput. 2020, 36, 359–375. [Google Scholar] [CrossRef]
- Sahmani, S.; Fattahi, A. Development of efficient size-dependent plate models for axial buckling of single-layered graphene nanosheets using molecular dynamics simulation. Microsyst. Technol. 2018, 24, 1265–1277. [Google Scholar] [CrossRef]
- Sahmani, S.; Fattahi, A. Development an efficient calibrated nonlocal plate model for nonlinear axial instability of zirconia nanosheets using molecular dynamics simulation. J. Mol. Graph. Model. 2017, 75, 20–31. [Google Scholar] [CrossRef]
- Padding, J.; Briels, W.J. Momentum conserving Brownian dynamics propagator for complex soft matter fluids. J. Chem. Phys. 2014, 141, 244108. [Google Scholar] [CrossRef] [Green Version]
- Santos de Oliveira, I.S.; van den Noort, A.; Padding, J.T.; den Otter, W.K.; Briels, W.J. Alignment of particles in sheared viscoelastic fluids. J. Chem. Phys. 2011, 135, 104902. [Google Scholar] [CrossRef] [Green Version]
- Santos de Oliveira, I.S.; den Otter, W.K.; Briels, W.J. The origin of flow-induced alignment of spherical colloids in shear-thinning viscoelastic fluids. J. Chem. Phys. 2012, 137, 204908. [Google Scholar] [CrossRef]
- Santos de Oliveira, I.S.; Fitzgerald, B.W.; den Otter, W.K.; Briels, W.J. Mesoscale modeling of shear-thinning polymer solutions. J. Chem. Phys. 2014, 140, 104903. [Google Scholar] [CrossRef]
- Briels, W.J. Responsive Particle Dynamics for modeling solvents on the mesoscopic scale. In Computational Trends in Solvation and Transport in Liquids; Sutman, G., Grotendorst, J., Gompper, G., Marx, D., Eds.; Schriften des Forschungszentrum Jülich: Jülich, Germany, 2015; pp. 557–597. [Google Scholar]
- Batchelor, G.K. An Introduction to Fluid Dynamics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Cole, R.H. Underwater Explosions; Dover Publications: New York, NY, USA, 1965. [Google Scholar]
- Morris, J.P.; Fox, P.J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, 136, 214–226. [Google Scholar] [CrossRef]
- Whitworth, A.P.; Bhattal, A.; Turner, J.; Watkins, S. Estimating density in smoothed particle hydrodynamics. Astron. Astrophys. 1995, 301, 929. [Google Scholar]
- Van den Noort, A.; Briels, W.J. Brownian dynamics simulations of concentration coupled shear banding. J. Non-Newton. Fluid Mech. 2008, 152, 148–155. [Google Scholar] [CrossRef]
| System Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Solute length scale | 5.0 | m | |
| Friction coefficient | 1.0 × | kg/s | |
| Number of Kuhn segments | p | 300,000 | - |
| Concentration of polymers | C | 2.5 | C * |
| Maximum number density of polymers | 1.0 × | C * | |
| Number of polymers | 33,062 | - | |
| Flory Huggins interaction parameter | 0.5 | - | |
| Strength of polymer interactions | 500 | ||
| Relaxation time | 1.0 | s | |
| Spring constant | k | 50 | |
| Solvent length scale | h | 10.0 | m |
| Resolution of fluid | 1.9099 | particles/ | |
| Number of fluid blobs | 13,228 | - | |
| Density of fluid | 1000 | kg/ | |
| Viscosity of fluid | 1.0 | mPa·s | |
| Pressure coefficient | 0.13 | Pa | |
| Time step | 10.0 | s | |
| Temperature | T | 300 | K |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahuja, V.R.; van der Gucht, J.; Briels, W. Large Scale Hydrodynamically Coupled Brownian Dynamics Simulations of Polymer Solutions Flowing through Porous Media. Polymers 2022, 14, 1422. https://doi.org/10.3390/polym14071422
Ahuja VR, van der Gucht J, Briels W. Large Scale Hydrodynamically Coupled Brownian Dynamics Simulations of Polymer Solutions Flowing through Porous Media. Polymers. 2022; 14(7):1422. https://doi.org/10.3390/polym14071422
Chicago/Turabian StyleAhuja, Vishal Raju, Jasper van der Gucht, and Wim Briels. 2022. "Large Scale Hydrodynamically Coupled Brownian Dynamics Simulations of Polymer Solutions Flowing through Porous Media" Polymers 14, no. 7: 1422. https://doi.org/10.3390/polym14071422
APA StyleAhuja, V. R., van der Gucht, J., & Briels, W. (2022). Large Scale Hydrodynamically Coupled Brownian Dynamics Simulations of Polymer Solutions Flowing through Porous Media. Polymers, 14(7), 1422. https://doi.org/10.3390/polym14071422








