Modeling the Effect of Stress Ratio, Loading Frequency and Fiber Orientation on the Fatigue Response of Composite Materials
Abstract
:1. Introduction
2. Effect of Stress Ratio, Fiber Orientation and Loading Frequency on Fatigue Life of Composite Laminate
2.1. Effect of Stress Ratio
2.2. Effect of Fiber Orientation
2.3. Effect of Frequency
3. Modelling
4. Validation Examples
4.1. Fatigue Life Prediction for Variable Stress Ratios
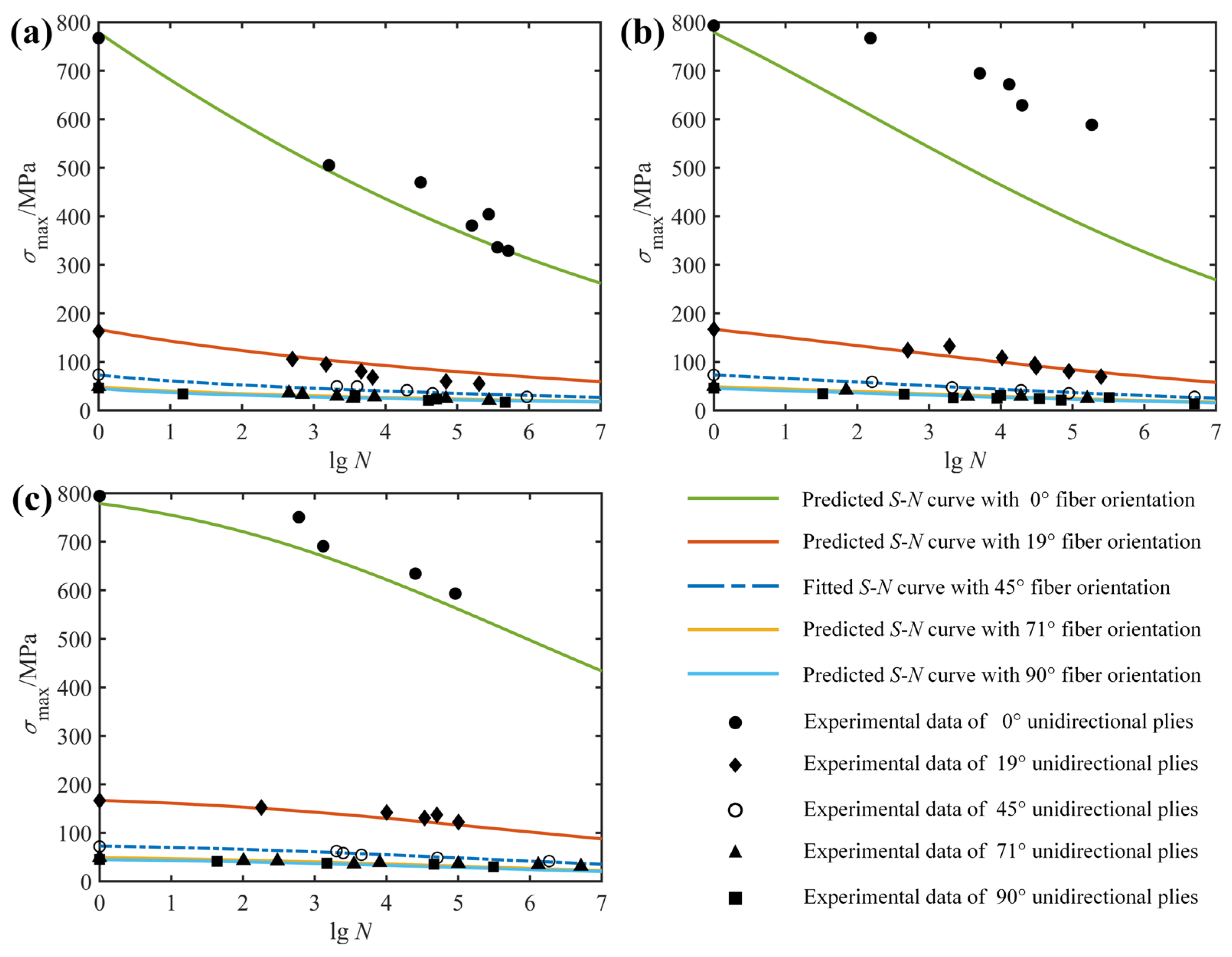
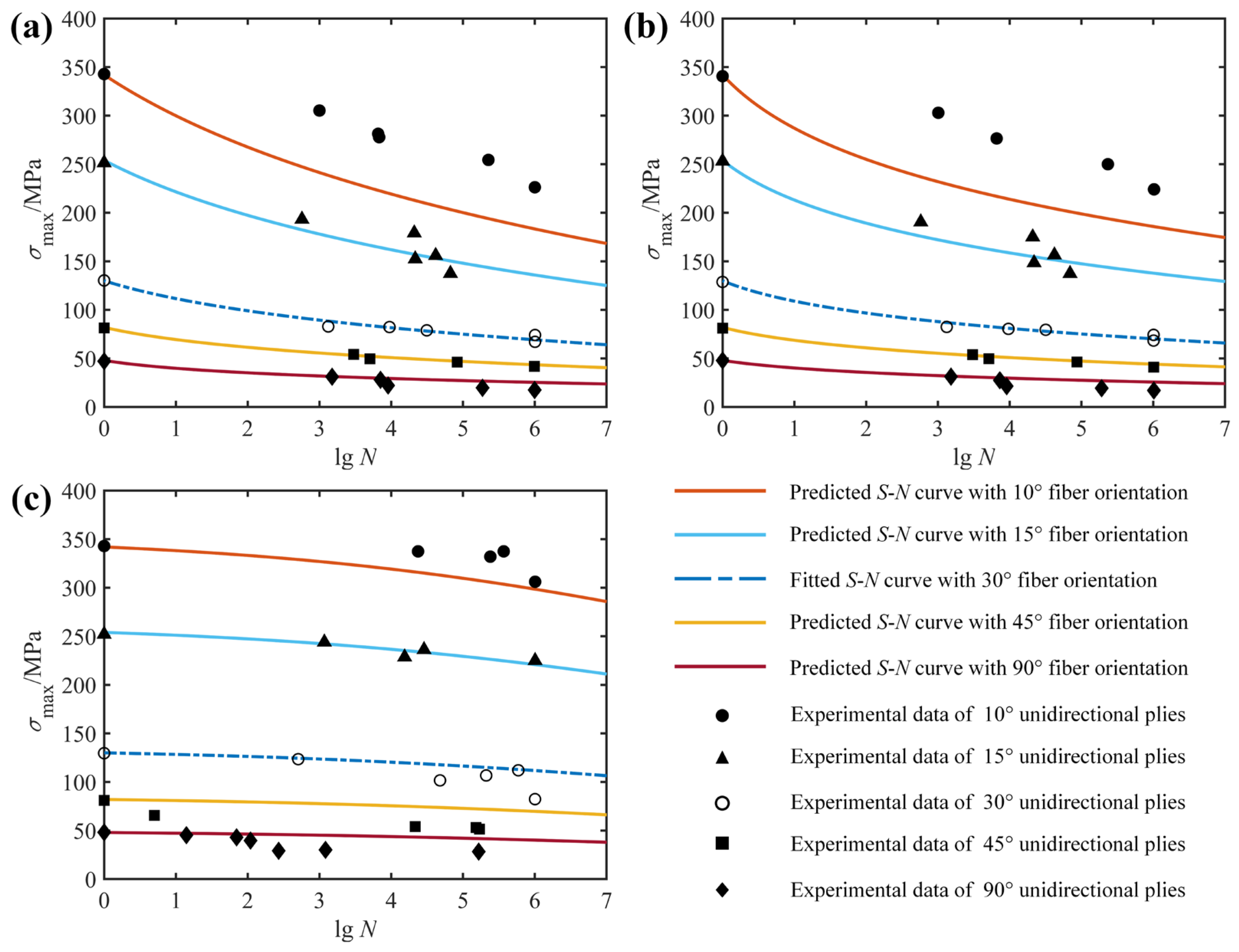
4.2. Fatigue Life Prediction for Variable Fiber Orientations
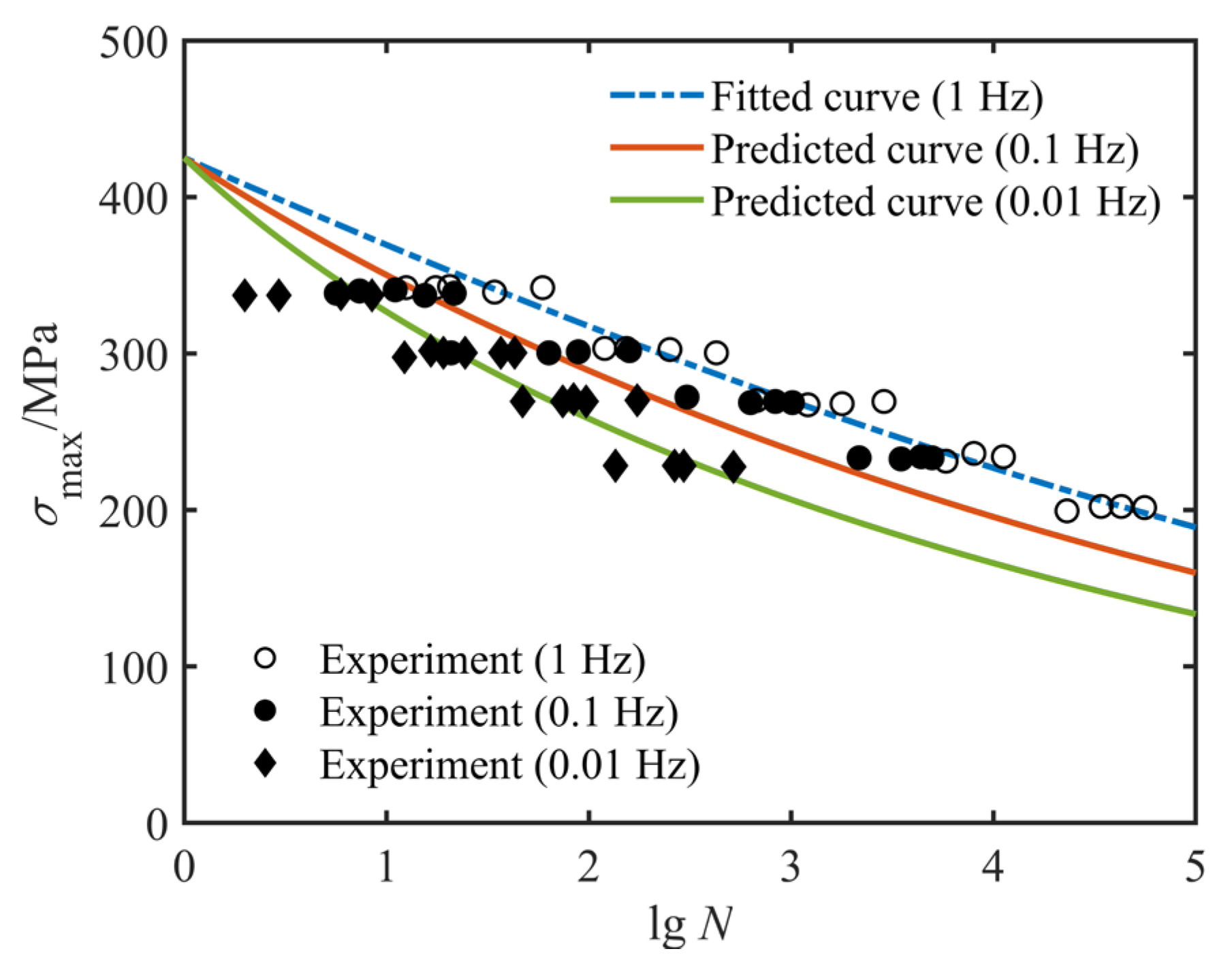
4.3. Fatigue Life Prediction for Variable Frequencies
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shabani, P.; Taheri-Behrooz, F.; Samareh-Mousavi, S.S.; Shokrieh, M.M. Very high cycle and gigacycle fatigue of fiber-reinforced composites: A review on experimental approaches and fatigue damage mechanisms. Prog. Mater. Sci. 2020, 118, 100762. [Google Scholar] [CrossRef]
- Skinner, T.; Datta, S.; Chattopadhyay, A.; Hall, A. Fatigue damage behavior in carbon fiber polymer composites under biaxial loading. Compos. Part B Eng. 2019, 174, 106942. [Google Scholar] [CrossRef]
- Wu, F.; Yao, W. A fatigue damage model of composite materials. Int. J. Fatigue 2010, 32, 134–138. [Google Scholar] [CrossRef]
- Alam Ansari, T.; Singh, K.K.; Azam, M.S. Fatigue damage analysis of fiber-reinforced polymer composites—A review. J. Reinf. Plast. Compos. 2018, 37, 636–654. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P.; Manshadi, B.D.; Keller, T. Influence of the constant life diagram formulation on the fatigue life prediction of composite materials. Int. J. Fatigue 2010, 32, 659–669. [Google Scholar] [CrossRef]
- Philippidis, T.; Passipoularidis, V. Residual strength after fatigue in composites: Theory vs. experiment. Int. J. Fatigue 2007, 29, 2104–2116. [Google Scholar] [CrossRef]
- Post, N.; Case, S.; Lesko, J. Modeling the variable amplitude fatigue of composite materials: A review and evaluation of the state of the art for spectrum loading. Int. J. Fatigue 2008, 30, 2064–2086. [Google Scholar] [CrossRef]
- D’Amore, A.; Giorgio, M.; Grassia, L. Modeling the residual strength of carbon fiber reinforced composites subjected to cyclic loading. Int. J. Fatigue 2015, 78, 31–37. [Google Scholar] [CrossRef]
- Gaurav, A.; Singh, K.K. Fatigue behavior of FRP composites and CNT-Embedded FRP composites: A review. Polym. Compos. 2016, 39, 1785–1808. [Google Scholar] [CrossRef]
- Vieira, P.R.; Carvalho, E.M.L.; Vieira, J.D.; Filho, R.D.T. Experimental fatigue behavior of pultruded glass fibre reinforced polymer composite materials. Compos. Part B Eng. 2018, 146, 69–75. [Google Scholar] [CrossRef]
- Capela, C.; Oliveira, S.; Ferreira, J. Fatigue behavior of short carbon fiber reinforced epoxy composites. Compos. Part B Eng. 2018, 164, 191–197. [Google Scholar] [CrossRef]
- Fan, W.; Dang, W.; Liu, T.; Li, J.; Xue, L.; Yuan, L.; Dong, J. Fatigue behavior of the 3D orthogonal carbon/glass fibers hybrid composite under three-point bending load. Mater. Des. 2019, 183, 108112. [Google Scholar] [CrossRef]
- Vassilopoulos, A.P. The history of fiber-reinforced polymer composite laminate fatigue. Int. J. Fatigue 2020, 134, 105512. [Google Scholar] [CrossRef]
- Sendeckyj, G.P. Life Prediction for Resin-Matrix Composite Materials. Compos. Mater. Ser. 1991, 4, 431–483. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A Fatigue Failure Criterion for Fiber Reinforced Materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef] [Green Version]
- Park, T.; Kim, M.; Jang, B.; Lee, J.; Park, J. A nonlinear constant life model for the fatigue life prediction of composite structures. Adv. Compos. Mater. 2014, 23, 337–350. [Google Scholar] [CrossRef]
- Hwang, W.; Han, K. Fatigue of Composites—Fatigue Modulus Concept and Life Prediction. J. Compos. Mater. 1986, 20, 154–165. [Google Scholar] [CrossRef]
- Singh, C.V.; Talreja, R. A synergistic damage mechanics approach for composite laminates with matrix cracks in multiple orientations. Mech. Mater. 2009, 41, 954–968. [Google Scholar] [CrossRef]
- Fawaz, Z.; Ellyin, F. Fatigue Failure Model for Fibre-Reinforced Materials under General Loading Conditions. J. Compos. Mater. 1994, 28, 1432–1451. [Google Scholar] [CrossRef]
- Philippidis, T.P.; Vassilopoulos, A. Life prediction methodology for GFRP laminates under spectrum loading. Compos. Part A Appl. Sci. Manuf. 2004, 35, 657–666. [Google Scholar] [CrossRef]
- DorMohammdi, S.; Godines, C.; Abdi, F.; Huang, D.; Repupilli, M.; Minnetyan, L. Damage-tolerant composite design principles for aircraft components under fatigue service loading using multi-scale progressive failure analysis. J. Compos. Mater. 2017, 51, 2181–2202. [Google Scholar] [CrossRef]
- Pidaparti, R.; Vogt, A. Experimental investigation of Poisson’s ratio as a damage parameter for bone fatigue. J. Biomed. Mater. Res. 2002, 59, 282–287. [Google Scholar] [CrossRef] [PubMed]
- Lecompte, D.; Smits, A.; Sol, H.; Vantomme, J.; Van Hemelrijck, D. Mixed numerical–experimental technique for orthotropic parameter identification using biaxial tensile tests on cruciform specimens. Int. J. Solids Struct. 2007, 44, 1643–1656. [Google Scholar] [CrossRef] [Green Version]
- Van Paepegem, W.; De Baere, I.; Degrieck, J. Modelling the nonlinear shear stress–strain response of glass fibre-reinforced composites. Part I: Experimental results. Compos. Sci. Technol. 2006, 66, 1455–1464. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Progressive fatigue damage modeling of composite materials, Part II: Material characterization and model verification. J. Compos. Mater. 2000, 34, 1081–1116. [Google Scholar] [CrossRef]
- Stojković, N.; Folić, R.; Pasternak, H. Mathematical model for the prediction of strength degradation of composites subjected to constant amplitude fatigue. Int. J. Fatigue 2017, 103, 478–487. [Google Scholar] [CrossRef]
- Kaminski, M.; Laurin, F.; Maire, J.-F.; Rakotoarisoa, C.; Hemon, E. Fatigue damage modeling of composite structures: The Onera viewpoint. AerospaceLab 2015, 6, 1–12. [Google Scholar] [CrossRef]
- Shokrieh, M.M.; Lessard, L.B. Multiaxial fatigue behaviour of unidirectional plies based on uniaxial fatigue experiments—I. Modelling. Int. J. Fatigue 1997, 19, 201–207. [Google Scholar] [CrossRef]
- Ma, H.; Ma, Q.; Bai, X.; Xu, J.; An, Z. A material property degradation model of composite laminates considering stress level. Mech. Adv. Mater. Struct. 2021, 1–12. [Google Scholar] [CrossRef]
- Kawai, M. A phenomenological model for off-axis fatigue behavior of unidirectional polymer matrix composites under different stress ratios. Compos. Part A Appl. Sci. Manuf. 2004, 35, 955–963. [Google Scholar] [CrossRef]
- Andersen, S.I.; Bach, P.W.; Bonnee, W.J.A.; Kensche, C.W.; Lilholt, H.; Lystrup, A.; Sys, W. Fatigue of Materials and Components for Wind Turbine Rotor Blades; OPOCE: Luxembourg, 1996. [Google Scholar]
- El Kadi, H.; Ellyin, F. Effect of stress ratio on the fatigue of unidirectional glass fibre/epoxy composite laminae. Composites 1994, 25, 917–924. [Google Scholar] [CrossRef]
- ASTM D3039/D3039M—08; Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2008.
- ASTM D3479/D3479M—12; Standard Test Method for Tension-Tension Fatigue of Polymer Matrix Composite Materials. ASTM: West Conshohocken, PA, USA, 2008.
- Justo, J.; Marin, J.; Paris, F.; Canas, J. The effect of frequency on fatigue behavior of graphite epoxy composites. In Proceedings of the ECCM16-16th European Conference on Composite Materials, Seville, Spain, 22–26 June 2014. [Google Scholar]
- Kharrazi, M.R.; Sarkani, S. Frequency-dependent fatigue damage accumulation in fiber-reinforced plastics. J. Compos. Mater. 2001, 35, 1924–1953. [Google Scholar] [CrossRef]
- D’Amore, A.; Grassia, L. A method to predict the fatigue life and the residual strength of composite materials subjected to variable amplitude (VA) loadings. Compos. Struct. 2019, 228, 111338. [Google Scholar] [CrossRef]
- Perreux, D.; Joseph, E. The effect of frequency on the fatigue performance of filament-wound pipes under biaxial loading: Experimental results and damage model. Compos. Sci. Technol. 1997, 57, 353–364. [Google Scholar] [CrossRef]
- Hertzberg, R.W.; Manson, J.A. Fatigue of Engineering Plastics; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Broutman, L.; Sahu, S. A New Theory to Predict Cumulative Fatigue Damage in Fiberglass Reinforced Plastics. In Proceedings of the Second Conference on Composite Materials: Testing and Design, Anaheim, CA, USA, 20–22 April 1971. [Google Scholar]
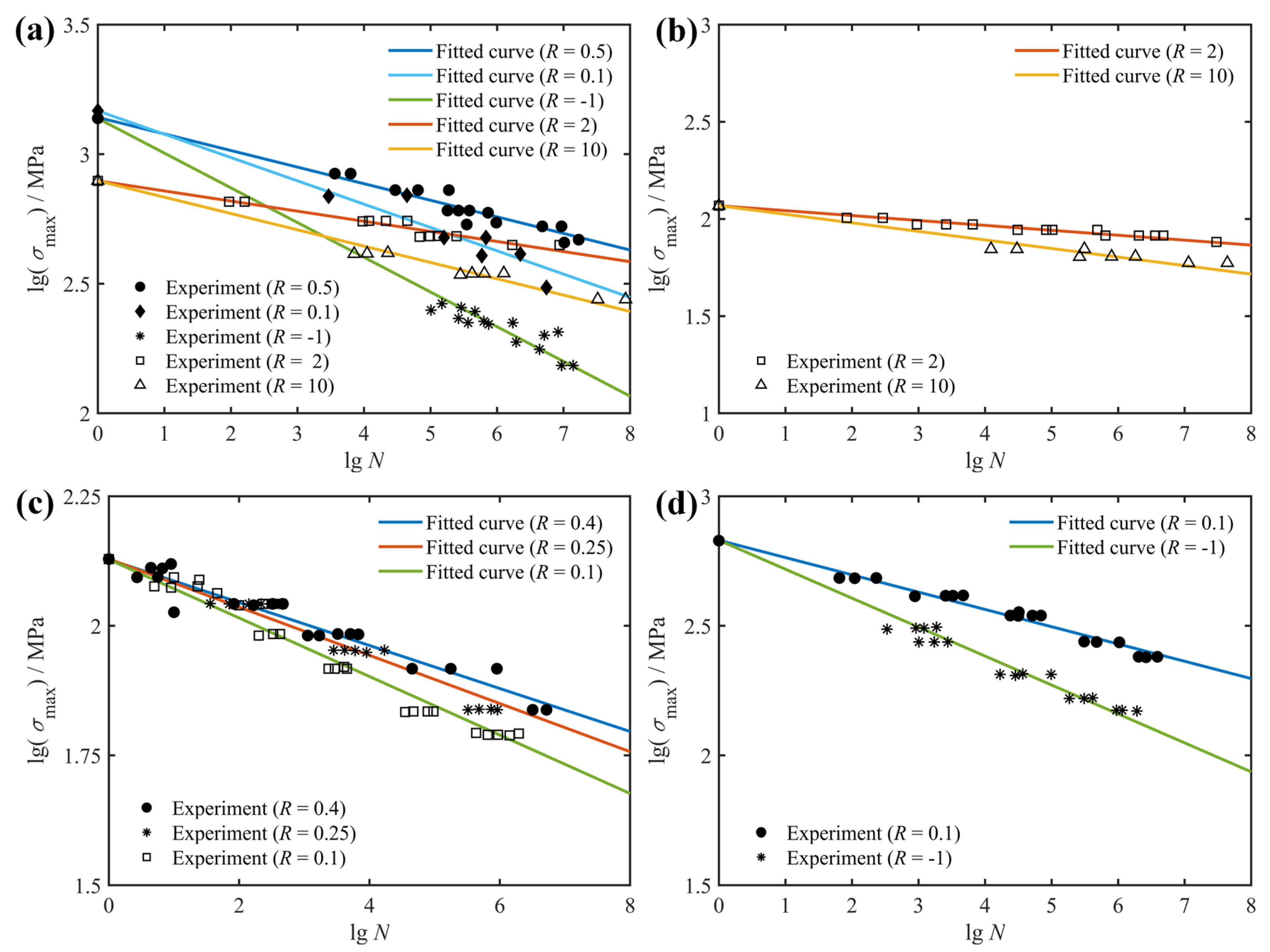
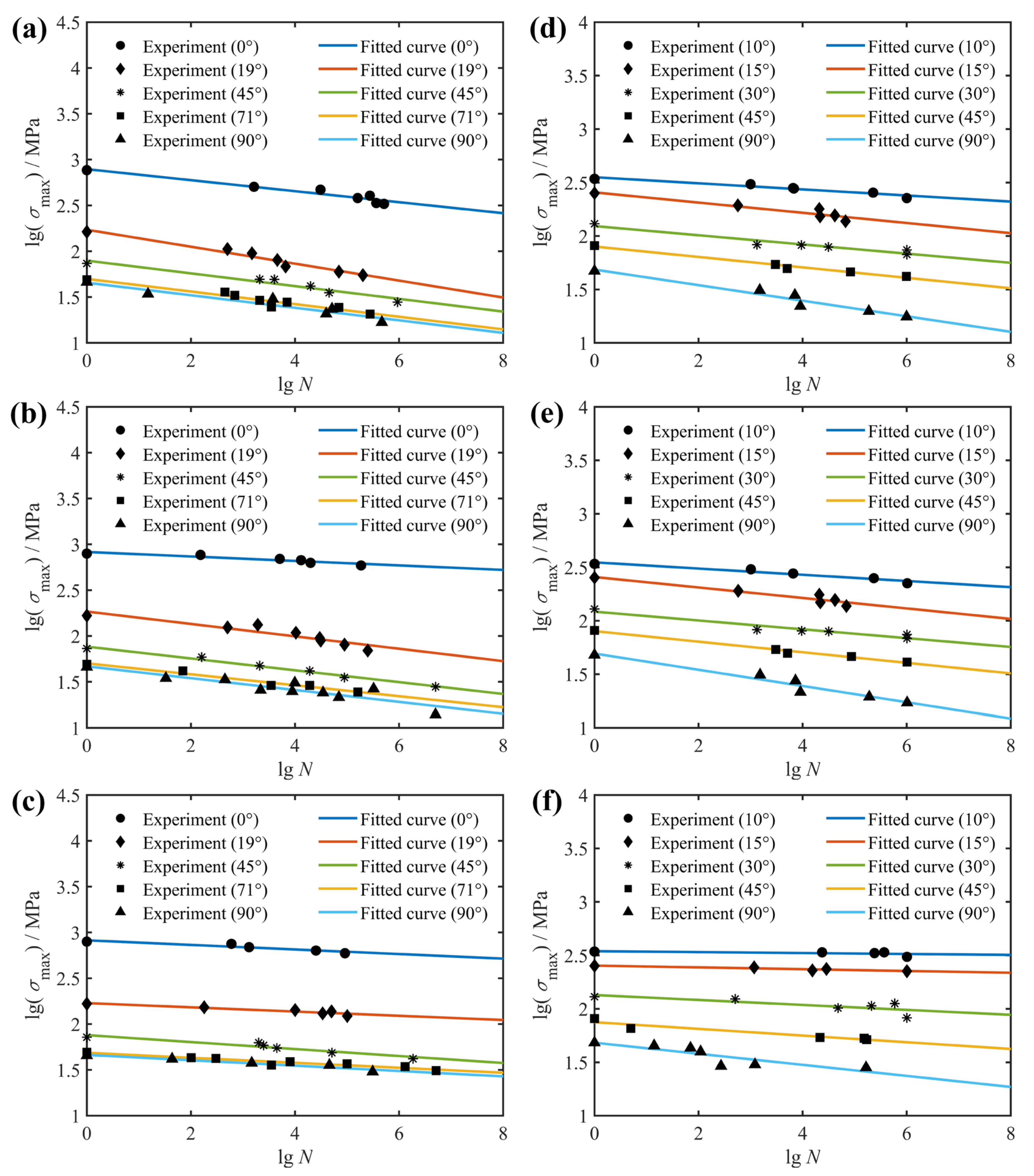
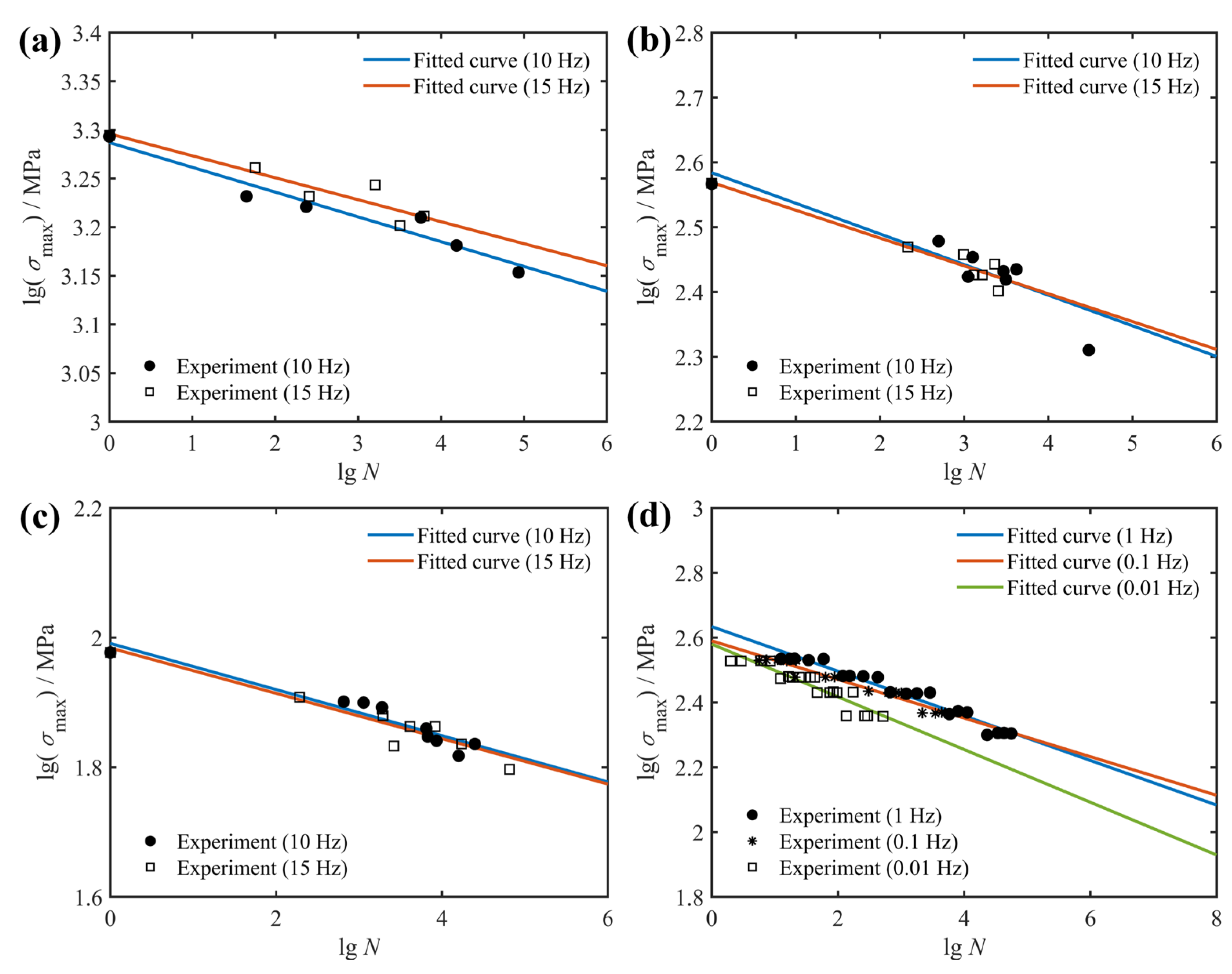
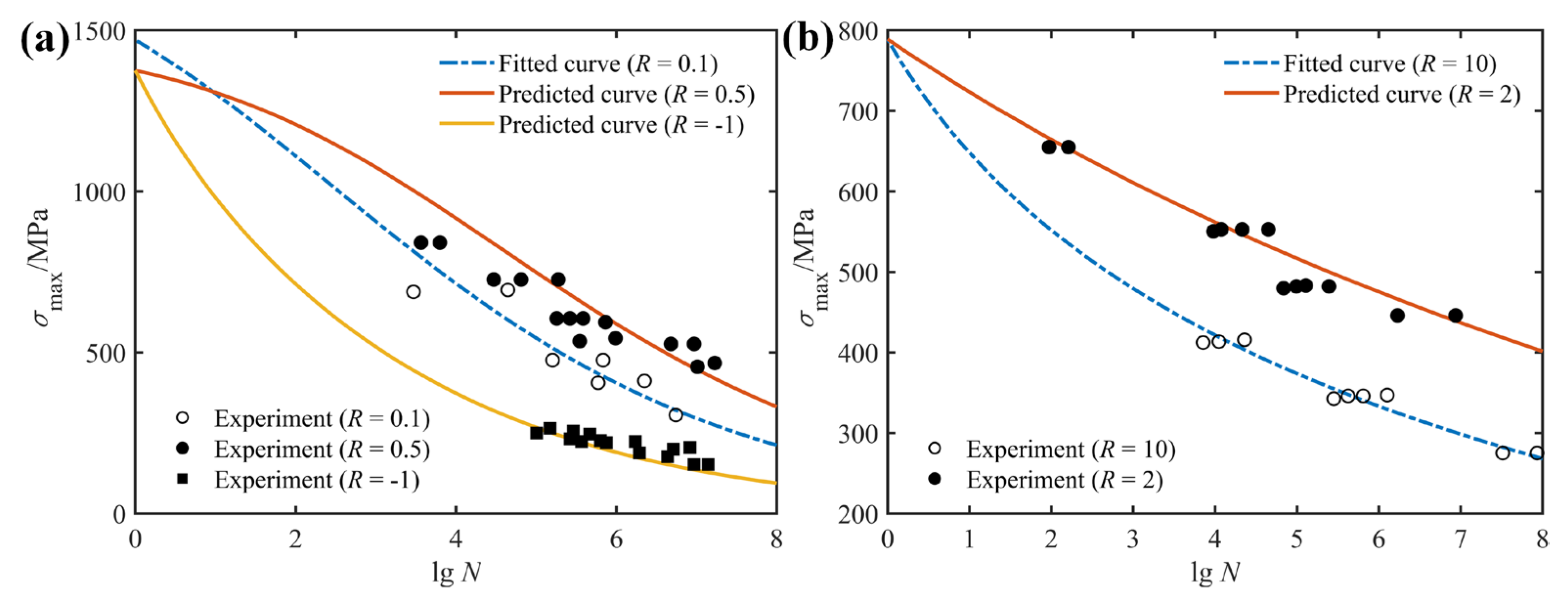
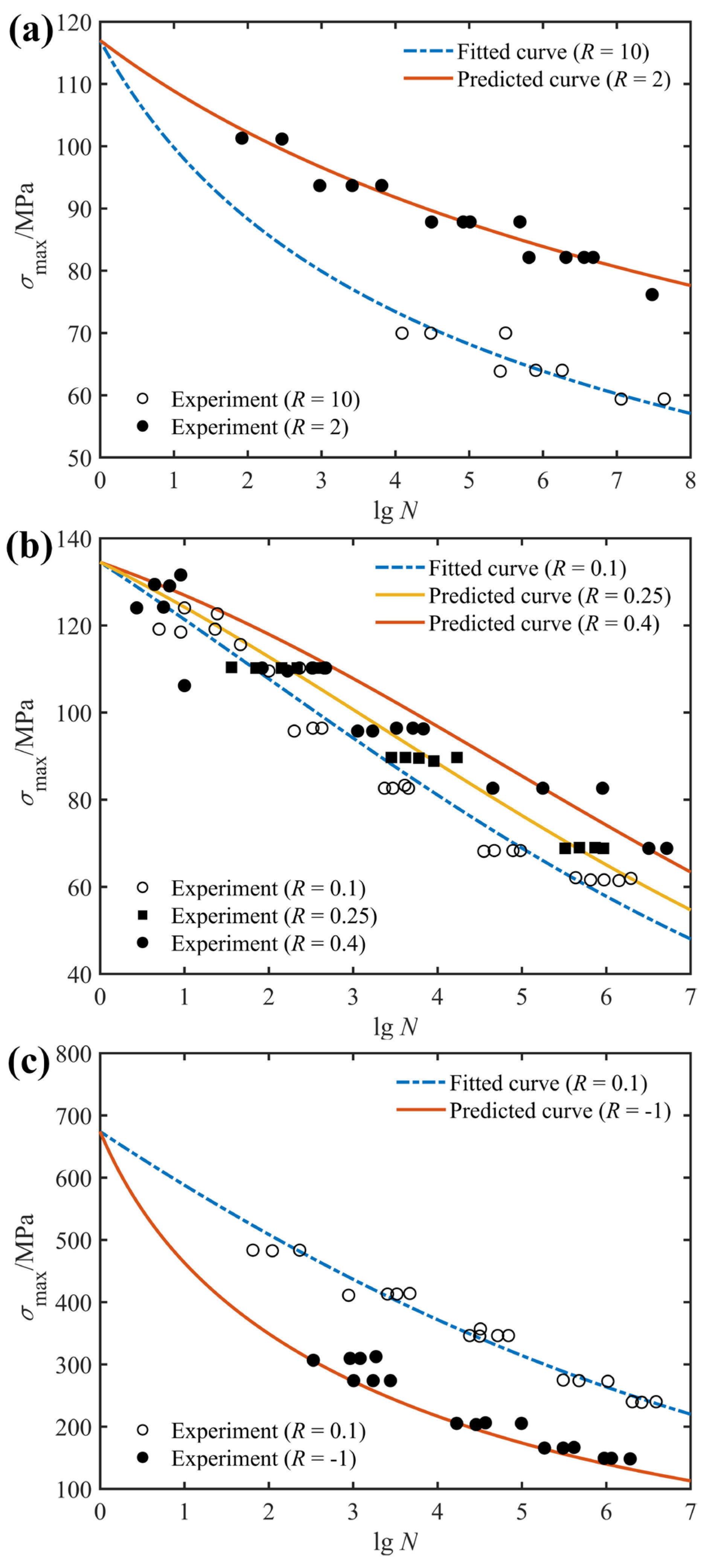

| Material | Layup Configuration | Stress Ratio R | Ultimate Strength /MPa |
|---|---|---|---|
| Glass/Polyester | [0°]8 | 0.1 | 1470 |
| 0.5 | 1375 | ||
| −1 | 1375 | ||
| 10 | 789 | ||
| 2 | 789 | ||
| Glass/Polyester | [90°]4 | 10 | 117 |
| 2 | 117 | ||
| S2/Glass/Epoxy | [±45°]S | 0.1 | 134.5 |
| 0.25 | 134.5 | ||
| 0.4 | 134.5 | ||
| DD5E-Glass/Epoxy | [0°/±45°/0°]S | 0.1 | 674 |
| −1 | 674 |
| Data Source | Material Type | Loading Frequency/Hz | Stress Ratio R | Fiber Orientation/° | Ultimate Strength of each Orientation/MPa |
|---|---|---|---|---|---|
| Ref. [32] | E-Glass/Epoxy | 3.3 | 0 | 0, 19, 45, 71, 90 | 779, 167, 73, 49, 45 |
| 0.5 | |||||
| −1 | |||||
| Ref. [30] | T800H/2500 | 10 | 0.1 | 10, 15, 30, 45, 90 | 342, 254, 130, 82, 48 |
| 0.5 | |||||
| −1 |
| Data Source | Material Type | Layup Configuration | Tensile Strength /MPa | Frequency /Hz |
|---|---|---|---|---|
| Ref. [31] | E-Glass/Epoxy | [0°/90°]S | 425 | 1 |
| 0.1 | ||||
| 0.01 | ||||
| Ref. [35] | Graphite/Epoxy (AS4/8552) | [0°]4 | 1948 | 10 |
| 15 | ||||
| [15°]4 | 369 | 10 | ||
| 18 | ||||
| [45°]4 | 95 | 10 | ||
| 18 | ||||
| [0°/90°]3 | 798.3 | 10 | ||
| 15 |
| Materials and Layup Configuration | Stress Ratio R | Model Parameters | ||
|---|---|---|---|---|
| Fitting | Prediction | α | β | |
| Glass/Polyester [0°]8 | 0.1 | 0.5, −1 | 0.202 | 0.256 |
| 10 | 2 | 1.631 | 0.07089 | |
| Glass/Polyester [90°]4 | 10 | 2 | 125 | 0.0007594 |
| S2/Glass/Epoxy [±45°]S | 0.1 | 0.25, 0.4 | 0.3033 | 0.1593 |
| DD5E-Glass/Epoxy [0°/±45°/0°]S | 0.1 | −1 | 0.446 | 0.1527 |
| Materials and Layup Configuration | Stress Ratio | Fiber Angle θ/° | Model Parameters | ||
|---|---|---|---|---|---|
| Fitting | Prediction | α | β | ||
| Unidirectional E-Glass/Epoxy | −1 | 45 | 0, 19, 71, 90 | 0.15 | 0.1485 |
| 0 | 0.2896 | 0.1729 | |||
| 0.5 | 0.1879 | 0.2354 | |||
| Unidirectional T800H/2500 | −1 | 30 | 10, 15, 45, 90 | 0.3263 | 0.06516 |
| 0.1 | 2.3 | 0.06035 | |||
| 0.5 | 0.1182 | 0.1405 | |||
| Materials and Layup Configuration | Loading Frequency f/Hz | Model Parameters | ||
|---|---|---|---|---|
| Fitting | Prediction | α | β | |
| E-Glass/Epoxy cross-ply | 1 | 0.1, 0.01 | 0.4146 | 0.1665 |
| Graphite/Epoxy [0°]4 | 10 | 15 | 0.3201 | 0.1 |
| Graphite/Epoxy [15°]4 | 10 | 18 | 0.22 | 0.2098 |
| Graphite/Epoxy [45°]4 | 10 | 18 | 0.2 | 0.1647 |
| Graphite/Epoxy [0°/90°]3 | 10 | 15 | 0.02888 | 0.2585 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, H.; Bai, X.; Ran, Y.; Wei, X.; An, Z. Modeling the Effect of Stress Ratio, Loading Frequency and Fiber Orientation on the Fatigue Response of Composite Materials. Polymers 2022, 14, 2772. https://doi.org/10.3390/polym14142772
Ma H, Bai X, Ran Y, Wei X, An Z. Modeling the Effect of Stress Ratio, Loading Frequency and Fiber Orientation on the Fatigue Response of Composite Materials. Polymers. 2022; 14(14):2772. https://doi.org/10.3390/polym14142772
Chicago/Turabian StyleMa, Huidong, Xuezong Bai, Yawei Ran, Xubing Wei, and Zongwen An. 2022. "Modeling the Effect of Stress Ratio, Loading Frequency and Fiber Orientation on the Fatigue Response of Composite Materials" Polymers 14, no. 14: 2772. https://doi.org/10.3390/polym14142772
APA StyleMa, H., Bai, X., Ran, Y., Wei, X., & An, Z. (2022). Modeling the Effect of Stress Ratio, Loading Frequency and Fiber Orientation on the Fatigue Response of Composite Materials. Polymers, 14(14), 2772. https://doi.org/10.3390/polym14142772






