Steady State of Motion of Two Particles in Poiseuille Flow of Power-Law Fluid
Abstract
1. Introduction
2. Numerical Model
2.1. Lattice Boltzmann Method
2.2. Fluid-Particle Coupling and Boundary Treatment
2.3. Repulsive Force
2.4. Problem Definition
3. Validation
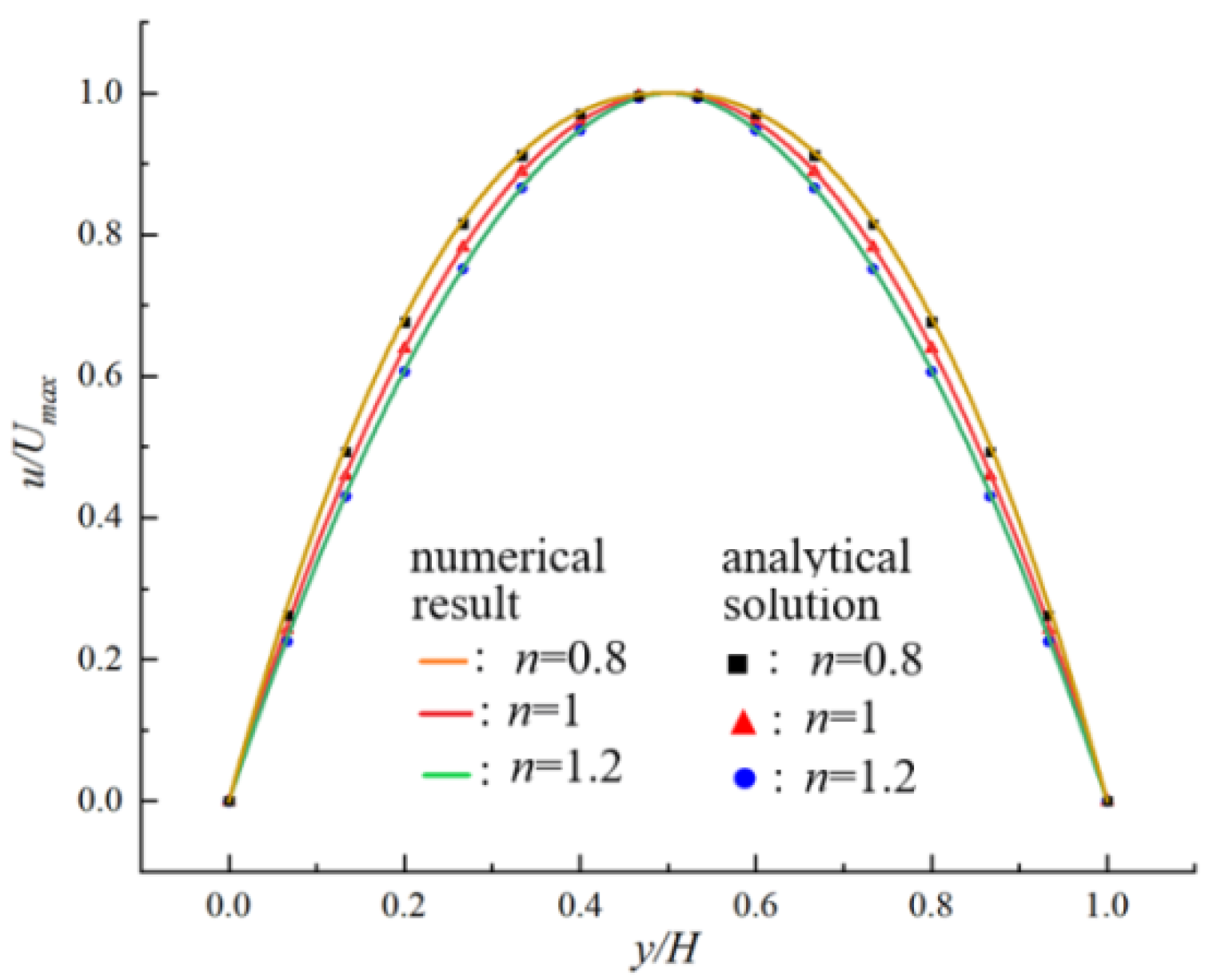
3.1. Velocity Profile for the Power-Law Fluid
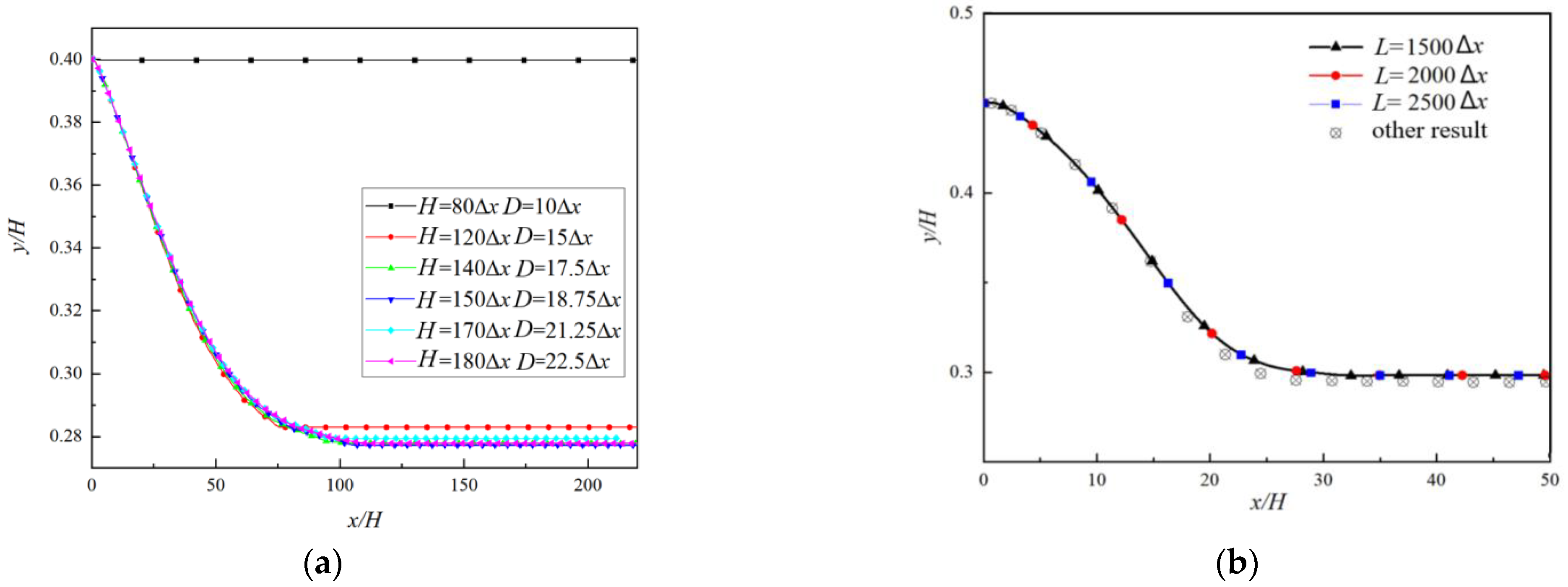
3.2. Particle Trajectories
3.3. Grid and Compute-Domain Independence
4. Results and Discussion
4.1. Effect of Fluid Properties on the Steady State of Motion of Two Particles
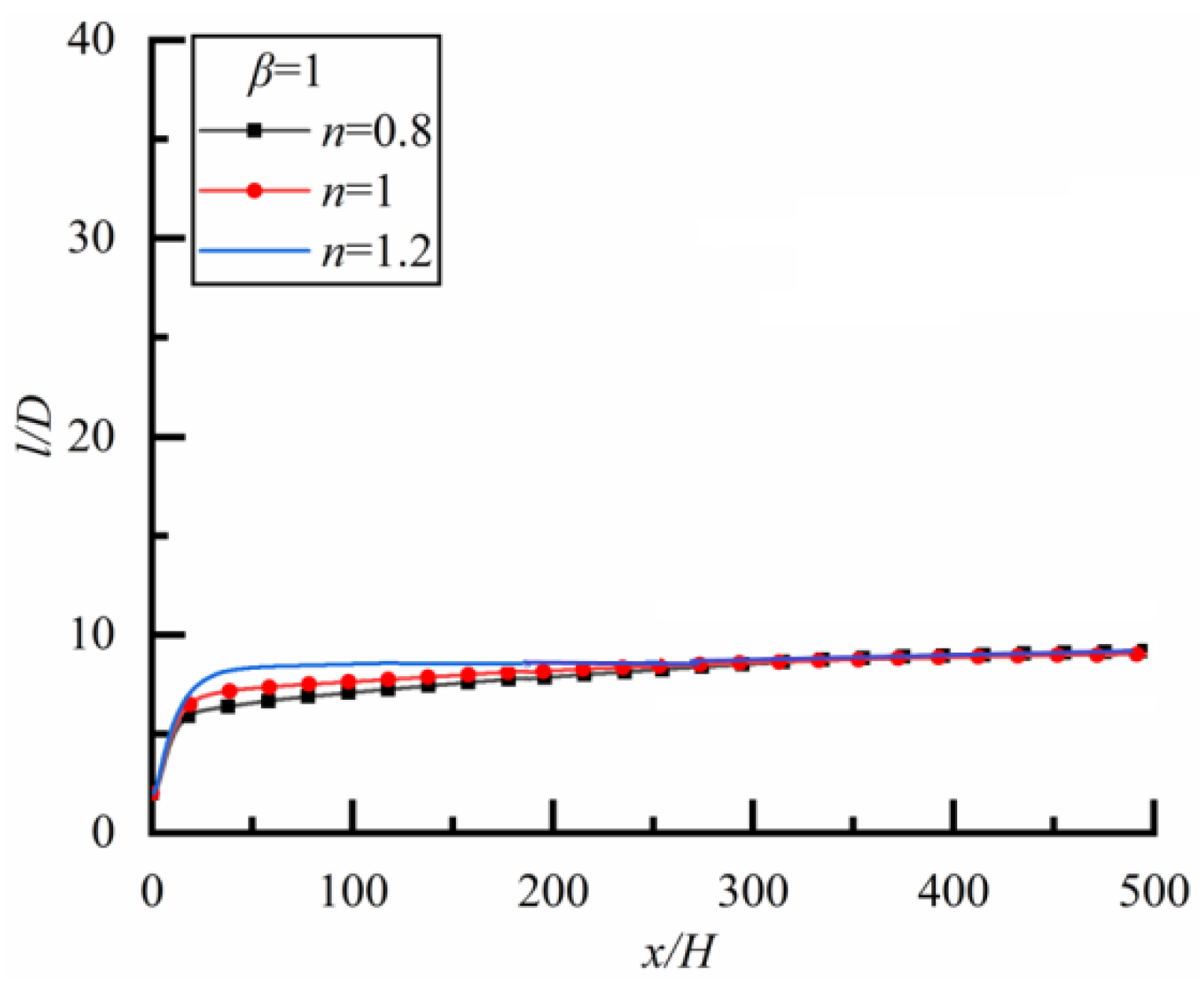
4.1.1. Two Particles of Same Diameter (β = 1)
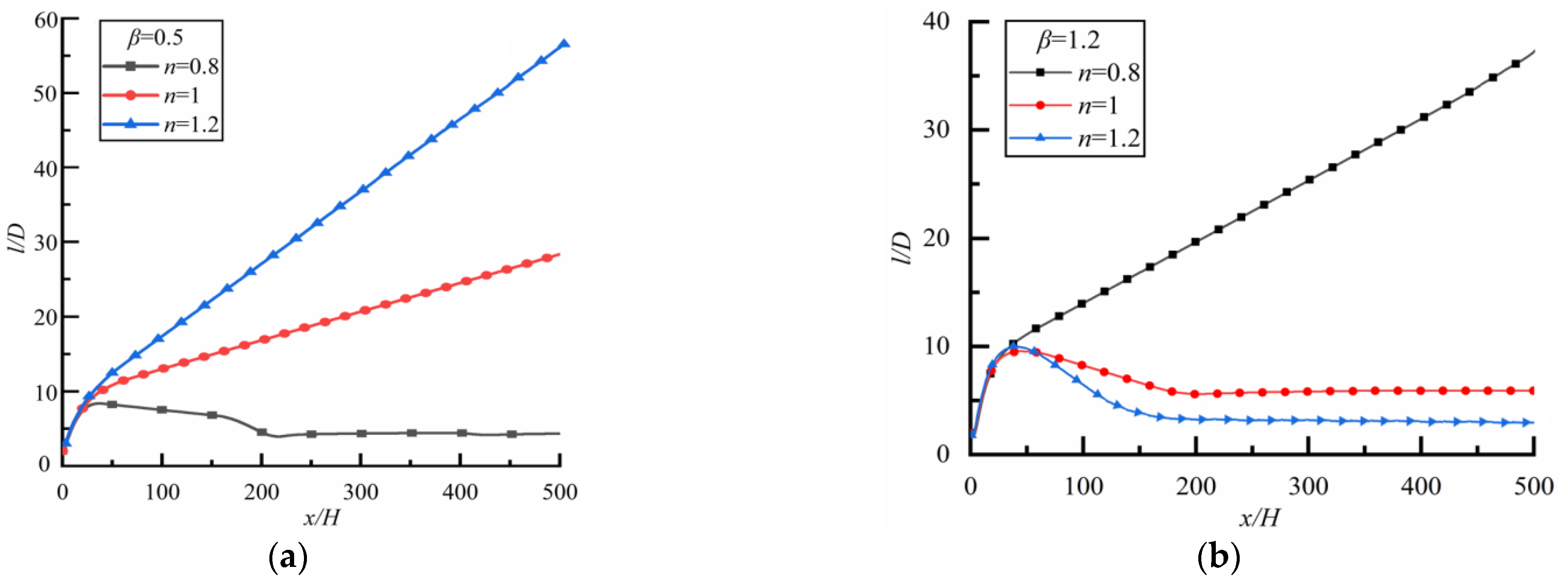
4.1.2. Two Particles with Different Sizes
4.2. Effect of Reynolds Number on the Steady State of Motion of TwoParticles
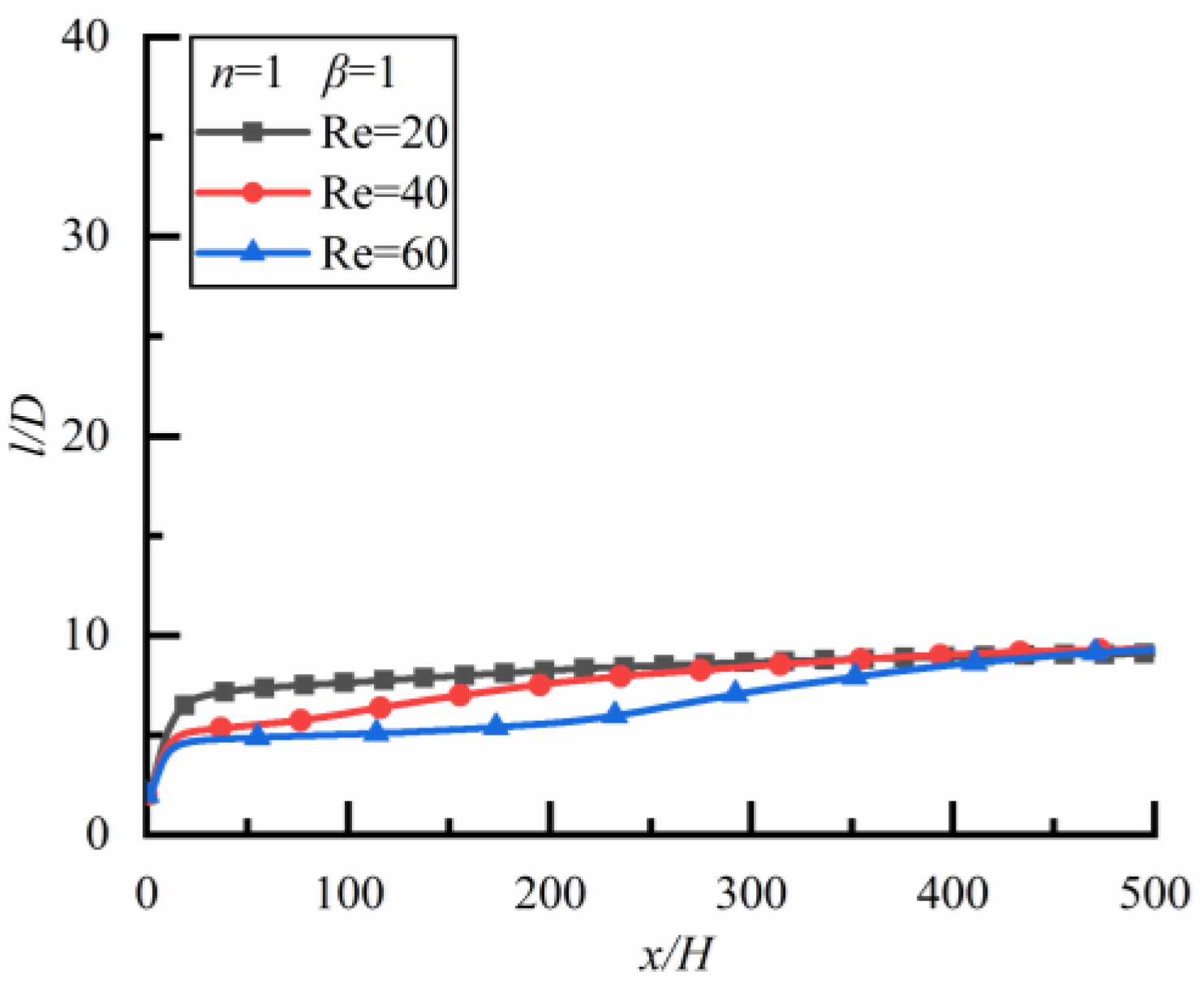
4.2.1. Two Particles of the Same Diameter
Newtonian Fluid
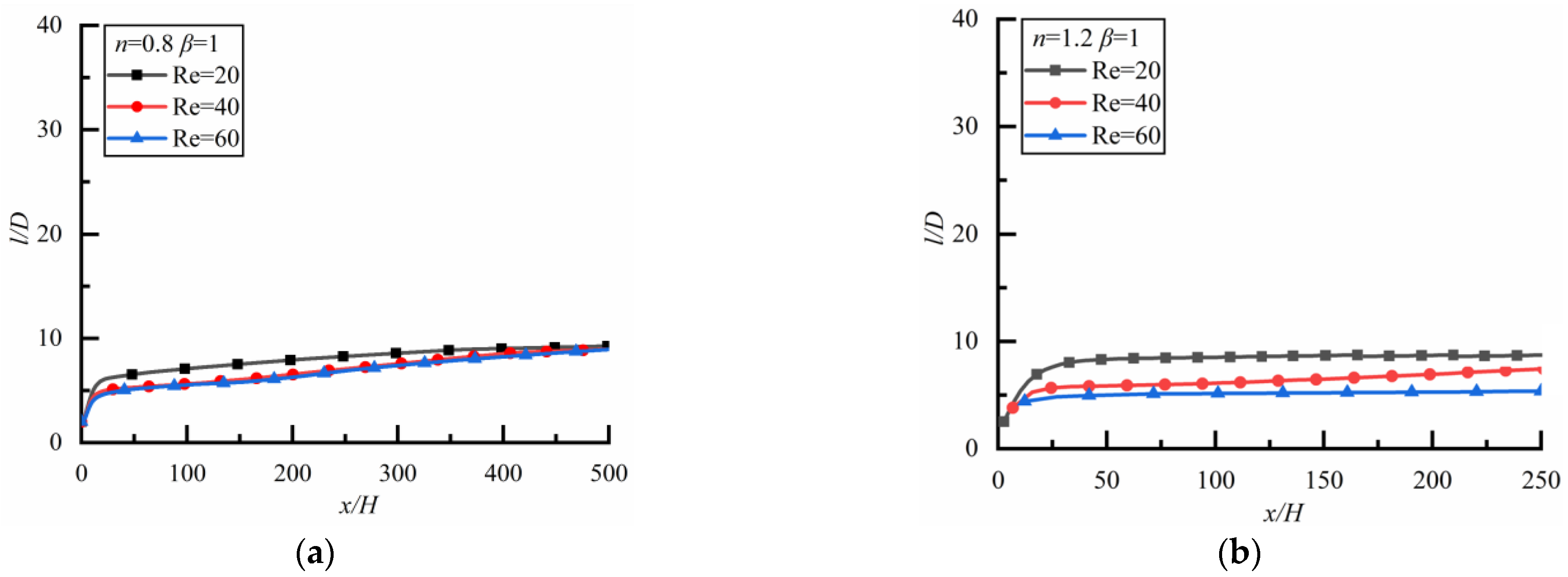
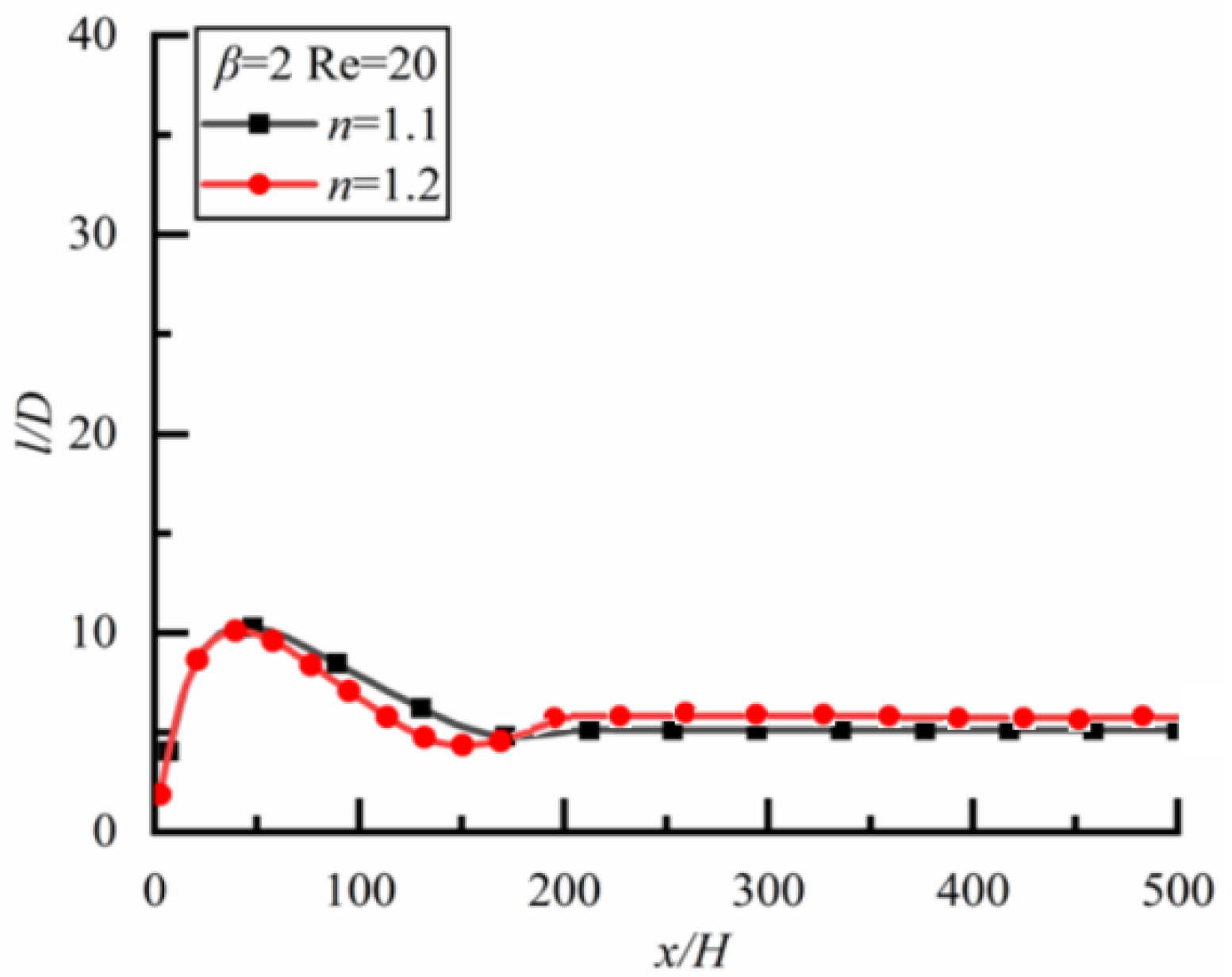
Shear-Thinning Fluid and Shear-Thickening Fluid
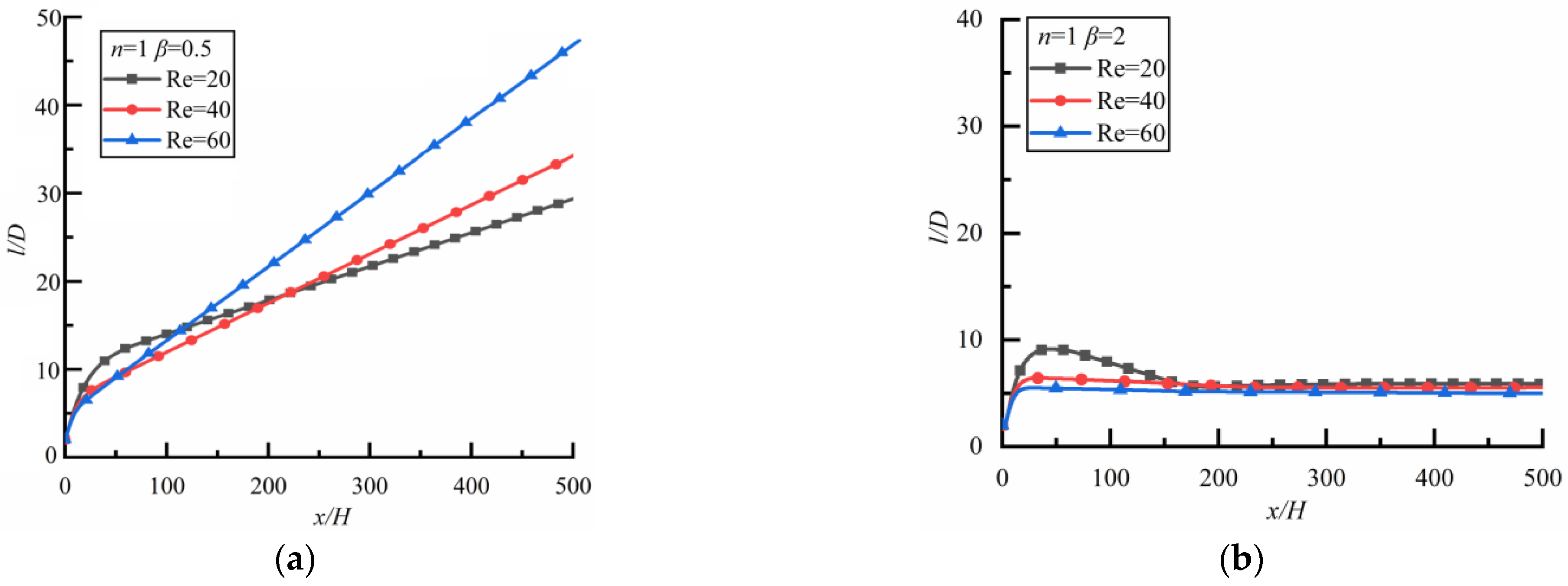
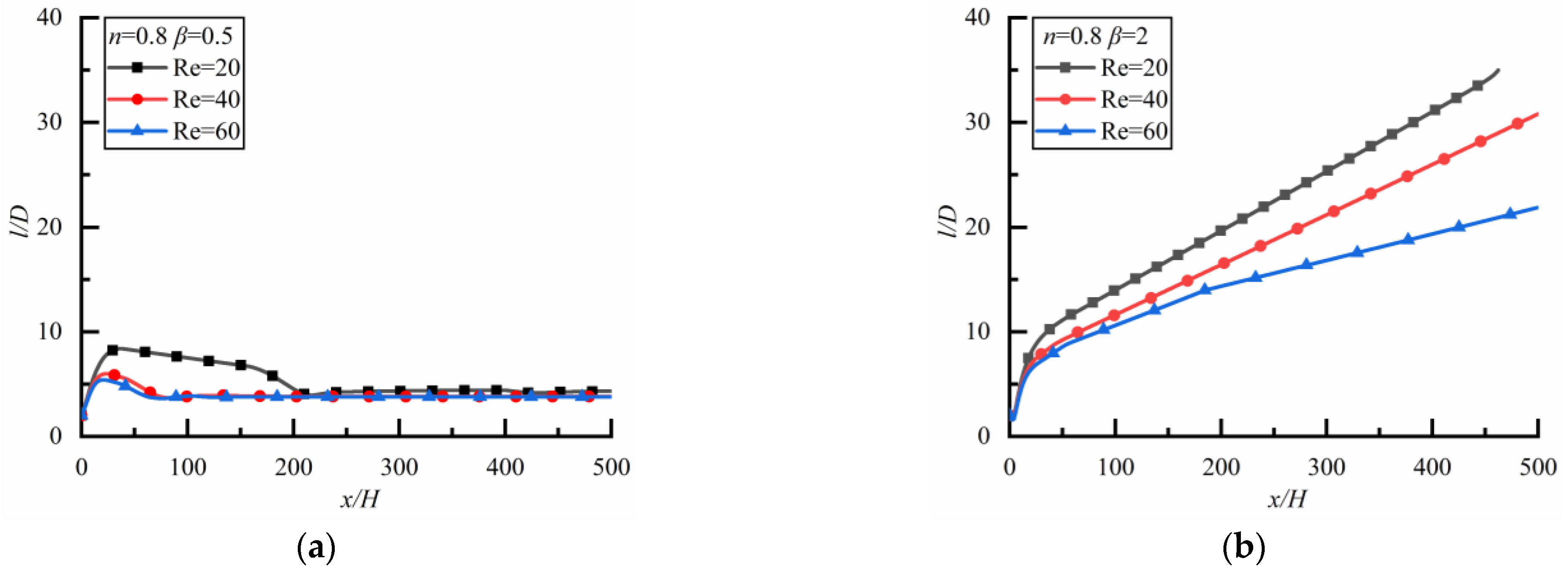
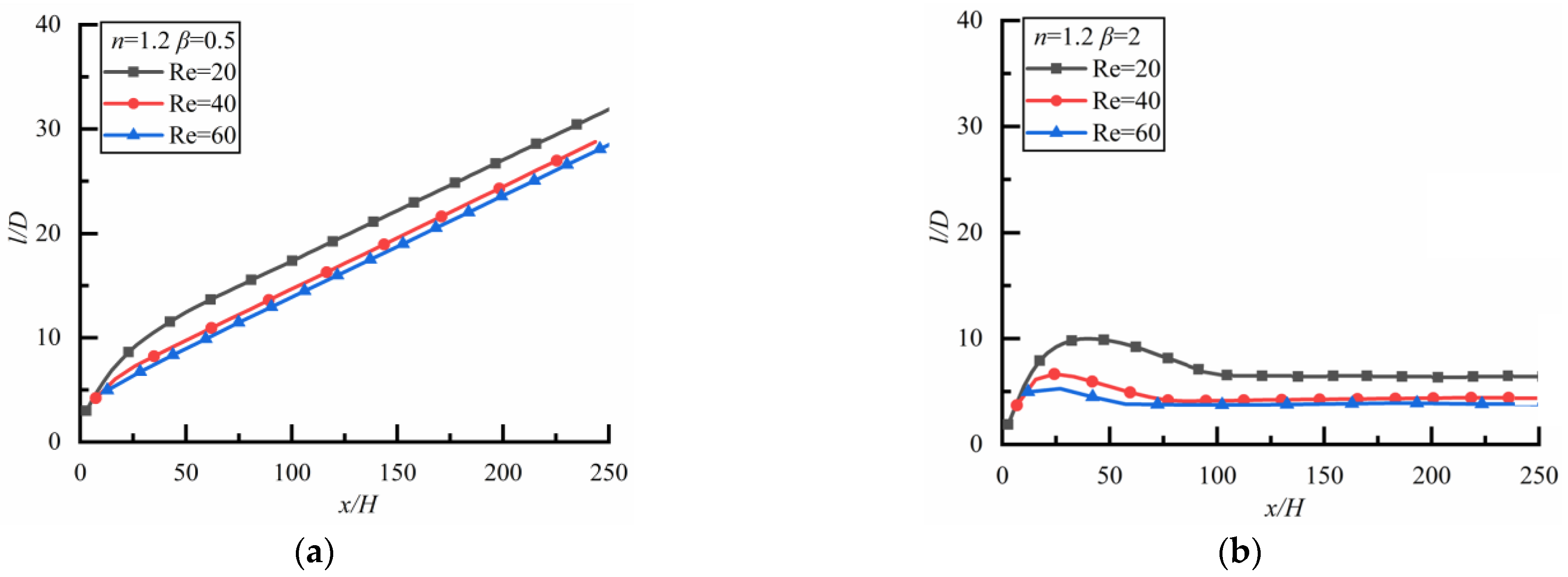
4.2.2. Two Particles with Different Sizes
Newtonian Fluid
Shear-Thinning Fluid
Shear-Thickening Fluid
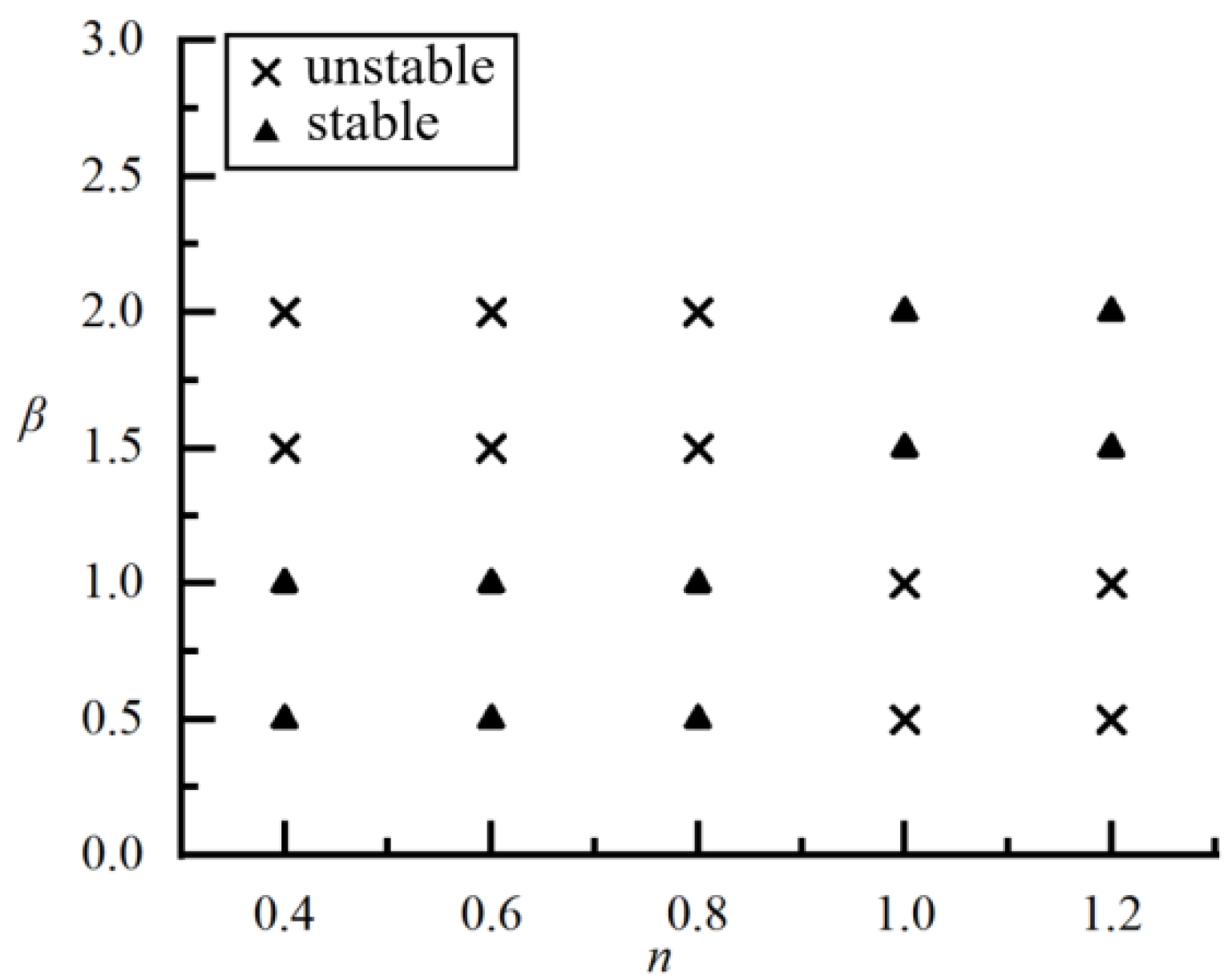
4.3. Stability Characteristics of Particle Spacing under Differentβand n
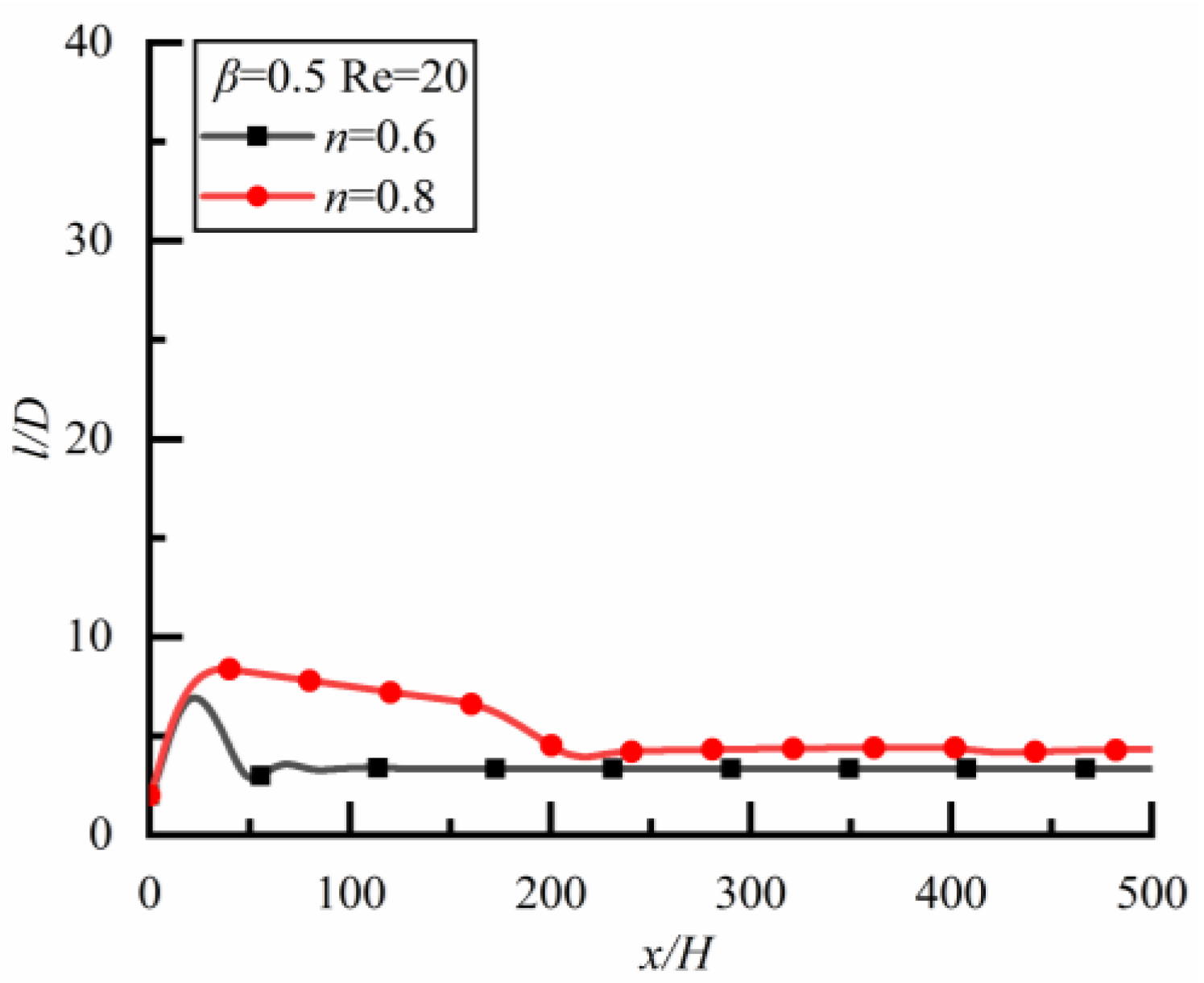
4.4. Effect of Non-Particle Spacing in Steady State
4.5. Effect of βon Particle Spacing in SteadyState
5. Conclusions
- (1)
- For two particles of the same diameter, the particle spacing increases rapidly at the initial stage, and then slowly, and the particle spacing in the steady state is independent of the power-law index of fluid. In a Newtonian fluid, the particle spacing in the steady state is independent of Re. The smaller Re is, the shorter the time for particles to reach the steady state. In shear-thinning fluid, the particle spacing increases rapidly at first and then slowly, finally approaching 10 for different Re. In shear-thickening fluid, although the particle spacing tends to be stable in the end, the values of particle spacing after stabilization are different, the smaller Re is, the larger particle spacing is.
- (2)
- For two particles of different sizes, the particle spacing does not always reach a stable state, and whether it reaches a stable state depends on the power-law index of the fluid. When the small particle is downstream, the particle spacing increases rapidly at first, then slowly and linearly in Newtonian fluid and shear-thickening fluid, but increases rapidly at first and then decreases slowly, finally approaching a constant in the shear-thinning fluid. In a Newtonian fluid, the particle spacing increases rapidly at first and then slowly and linearly, the larger Re is, the greater the growth rate is, and the larger the particle spacing is. In shear-thinning fluid, the particle spacing approaches approximately the same constant for different Re. The stronger the shear-thinning degree is, the smaller the particle spacing is. In shear-thickening fluid, particle spacing increases rapidly at first and then slowly, and cannot reach a stable state. The diameter ratio of two particles has no effect on the particle spacing in a steady state.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lee, W.; Amini, H.; Stone, H.A.; DiCarlo, D. Dynamic self-assembly and control of microfluidic particle crystals. Proc. Natl. Acad. Sci. USA 2010, 107, 22413–22418. [Google Scholar] [CrossRef] [PubMed]
- Yu, Z.; Wu, T.H.; Shao, X.; Lin, J.Z. Numerical studies of the effects of large neutrally buoyant particles on the flow in stability and transition to turbulence in pipe flow. Phys. Fluids 2013, 25, 043305. [Google Scholar] [CrossRef]
- Li, Z.; Wu, J.; Hu, G.; Hu, G. Fluid Flow in Microfluidic Chips; Science Press: Beijing, China, 2012. [Google Scholar]
- Kahkeshani, S.; Haddadi, H.; Di Carlo, D. Preferred interparticle spacings in trains of particles in inertial microchannel flows. J. Fluid Mech. 2016, 786, R3. [Google Scholar] [CrossRef]
- Humphry, K.J.; Kulkarni, P.M.; Weitz, D.A.; Morris, J.F.; Stone, H.A. Axial and lateral particle ordering infinite Reynolds number channel flows. Phys. Fluids 2010, 22, 081703. [Google Scholar] [CrossRef]
- Pan, Z.; Zhang, R.L.; Yuan, C.; Wu, H.Y. Direct measurement of microscale flow structures induced by inertialfocusing of single particle and particle trains in a confined microchannel. Phys. Fluids 2018, 30, 102005. [Google Scholar] [CrossRef]
- Gao, Y.; Magaud, P.; Lafforgue, C.; Colin, S.; Baldas, L. Inertial lateral migration and self-assembly of particles in bidisperse suspensions in microchannel flows. Microfluid. Nano Fluid. 2019, 23, 93. [Google Scholar] [CrossRef]
- Zenit, R.; Feng, J.J. Hydrodynamic interactions among bubbles, drops, and particles in non-Newtonian liquids. Annu. Rev. Fluid Mech. 2018, 50, 505–534. [Google Scholar] [CrossRef]
- Nie, D.M.; Lin, J.Z. Behavior of three circular particles in a confined power-law fluid under shear. J. Non-Newton. Fluid Mech. 2015, 221, 76–94. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J.Z.; Ku, X.K. Inertial migration of circular particles in Poiseuille flow of a power-law fluid. Phys. Fluids 2019, 31, 073306. [Google Scholar]
- Xia, Y.; Lin, J.Z.; Ku, X.K. Flow-induced rotation of circular cylinder in Poiseuille flow of power-law fluids. J. Non-Newton. Fluid Mech. 2018, 260, 120–132. [Google Scholar] [CrossRef]
- Ouyang, Z.; Lin, J.Z.; Ku, X.K. The hydrodynamic behavior of a squirmer swimming in power-law fluid. Phys. Fluids 2018, 30, 083301. [Google Scholar] [CrossRef]
- Despeyroux, A.; Ambari, A.; Richou, A.B. Wall effects on the transportation of a cylindrical particle in power-law fluids. J. Non-Newton. Fluid Mech. 2011, 166, 1173–1182. [Google Scholar] [CrossRef][Green Version]
- Chrit, F.E.; Bowie, S.; Alexeev, A. Inertial migration of spherical particles in channel flow of power law fluids. Phys. Fluids 2020, 32, 083103. [Google Scholar] [CrossRef]
- Jeffery, G.B. The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. Lond. Ser. A 1922, 102, 161–179. [Google Scholar]
- Hyväluoma, J.; Raiskinmaki, P.; Koponen, A.; Kataja, M.; Timonen, J. Lattice-Boltzmann simulation of particle suspensions in shear flow. J. Stat. Phys. 2005, 121, 149–161. [Google Scholar] [CrossRef]
- Segré, G.; Silberberg, A. Radial particle displacements in poiseuille flow of suspensions. Nature 1961, 189, 209. [Google Scholar] [CrossRef]
- Matas, J.; Glezer, V.; Guazzelli, E.; Morris, J.F. Trains of particles in finite-Reynolds-number pipe flow. Phys. Fluids 2004, 16, 4192–4195. [Google Scholar] [CrossRef]
- DiCarlo, D.; Irimia, D.; Tompkins, R.G.; Toner, M. Continuous inertial focusing, ordering, and separation of particles in microchannels. Proc. Natl. Acad. Sci. USA 2007, 104, 18892–18897. [Google Scholar] [CrossRef]
- Martel, J.M.; Toner, M. Particle focusing in curved microfluidic channels. Sci. Rep. 2013, 3, 3340. [Google Scholar] [CrossRef]
- Matas, J.; Morris, J.F.; Guazzelli, É. Lateral force on a rigid sphere in large-inertial a minar pipe flow. J. Fluid Mech. 2009, 621, 59–67. [Google Scholar] [CrossRef]
- Matas, J.; Morris, J.F.; Guazzelli, É. Inertial migration of rigid spherical particles in Poiseuille flow. J. Fluid Mech. 1999, 515, 171–195. [Google Scholar] [CrossRef]
- Hur, S.C.; Tse, H.T.; DiCarlo, D. Sheathless inertial cell ordering for extreme through put flow cytometry. Lab Chip 2010, 10, 274–280. [Google Scholar] [CrossRef] [PubMed]
- Yan, Y.; Morris, J.F.; Koplik, J. Hydrodynamic interaction of two particles in confined linear shear flow at finite Reynolds number. Phys. Fluids 2007, 19, 113305. [Google Scholar] [CrossRef]
- D’Avino, G.; Greco, F.; Maffettone, P.L. Particle migration due to viscoelasticity of the suspending liquid and its relevance in microfluidic devices. Annu. Rev. Fluid Mech. 2017, 49, 341–360. [Google Scholar] [CrossRef]
- Schaaf, C.; Stark, H. Inertial migration and axial control of deformable capsules. Soft Matter 2017, 13, 3544–3555. [Google Scholar] [CrossRef]
- Hu, X.; Lin, J.Z.; Guo, Y.; Ku, X.K. Motion and equilibrium position of elliptical and rectangular particles in a channel flow of a power-law fluid. Powder Technol. 2021, 377, 585–596. [Google Scholar] [CrossRef]
- Schaaf, C.; Rühle, F.; Stark, H. A flowing pair of particles in inertial microfluidics. Soft Matter 2019, 15, 1988–1998. [Google Scholar] [CrossRef]
- Hood, K.; Roper, M. Pair wise interactions in inertially driven one-dimensional microfluidic crystals. Phys. Rev. Fluids 2018, 3, 094201. [Google Scholar] [CrossRef]
- Chen, D.; Lin, J.Z.; Hu, X. Research on the inertial migration characteristics of bi-disperse particles in channel flow. Appl. Sci. 2021, 11, 8800. [Google Scholar] [CrossRef]
- Hu, X.; Lin, P.F.; Lin, J.Z.; Zhu, Z.C.; Yu, Z.S. On the polydisperse particle migration and formation of chains in a square channel flow of non-Newtonian fluids. J. Fluid Mech. 2022, 936, A5. [Google Scholar] [CrossRef]
- Bao, F.B.; Lin, J.Z. Burnett simulation of gas flow and heat transfer in micro Poiseuille flow. Int. J. Heat Mass Transf. 2008, 51, 4139–4144. [Google Scholar] [CrossRef]
- Nie, D.M.; Lin, J.Z. A LB-DF/FD method for particle suspensions. Commun. Comput. Phys. 2010, 7, 544–563. [Google Scholar]
- Qian, Y.H.; Dhumieres, D.; Lallemand, P. Lattice BGK models for navier-stokes equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- He, X.Y.; Shan, X.W.; Doolen, G.D. Discrete Boltzmann equation model for non ideal gases. Phys. Rev. E 1998, 57, R13–R16. [Google Scholar] [CrossRef]
- Gabbanelli, S.; Drazer, G.; Koplik, J. Lattice Boltzmann method for non-Newtonian (power-law) fluids. Phys. Rev. E 2005, 72, 046312. [Google Scholar] [CrossRef]
- Ladd, A.J.C. Numerical simulations of particulate suspensions via a discretized Boltzmann equation. Part 2. Numerical results. J. Fluid Mech. 1994, 271, 311–339. [Google Scholar] [CrossRef]
- Aidun, C.K.; Lu, Y.; Ding, E.J. Direct analysis of particulate suspensions with inertia using the discrete Boltzmannequation. J. Fluid Mech. 1998, 373, 287–311. [Google Scholar] [CrossRef]
- Glowinski, R.; Pan, T.W.; Hesla, T.I.; Joseph, D.D.; Periaux, J. A fictitious domain approach to the direct numericalsimulation of incompressible viscous flow past moving rigid bodies: Application to particulate flow. J. Comput. Phys. 2001, 169, 363–426. [Google Scholar] [CrossRef]
- Metzner, A.B.; Reed, J.C. Flow of non-Newtonian fluids-correlation of the laminar, transition, and turbulent-flow regions. AIChEJ 1955, 1, 434–440. [Google Scholar] [CrossRef]
- DiCarlo, D.; Edd, J.F.; Humphry, K.J.; Stone, H.A.; Toner, M. Particle segregation and dynamics in confined flows. Phys. Rev. Lett. 2009, 102, 094503. [Google Scholar] [CrossRef]
- Bird, R.B.; Dai, G.C.; Yarusso, B.J. The rheology and flow of visco plastic materials. Rev. Chem. Eng. 1983, 1, 1–70. [Google Scholar] [CrossRef]
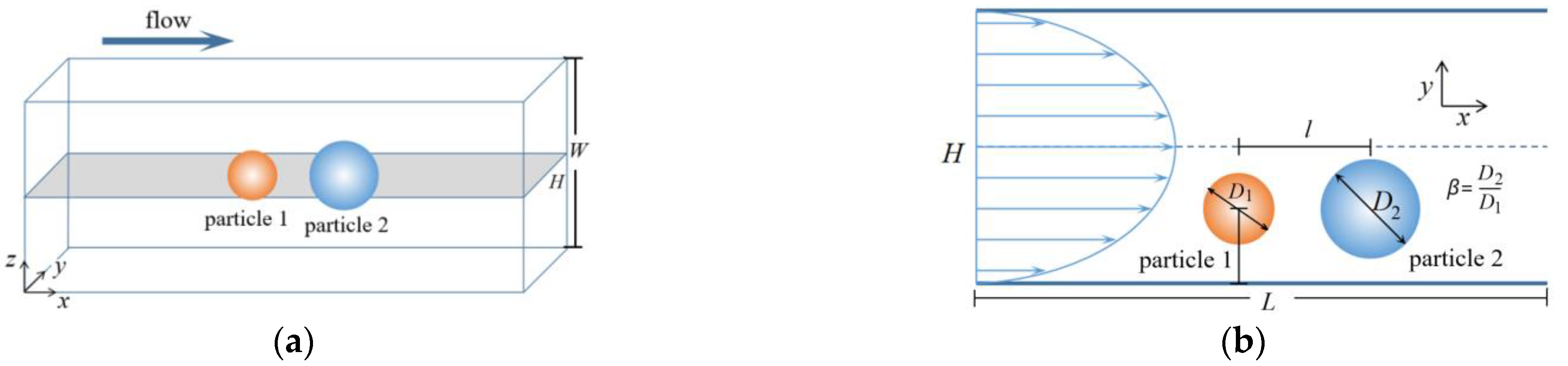


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, D.; Lin, J. Steady State of Motion of Two Particles in Poiseuille Flow of Power-Law Fluid. Polymers 2022, 14, 2368. https://doi.org/10.3390/polym14122368
Chen D, Lin J. Steady State of Motion of Two Particles in Poiseuille Flow of Power-Law Fluid. Polymers. 2022; 14(12):2368. https://doi.org/10.3390/polym14122368
Chicago/Turabian StyleChen, Dongmei, and Jianzhong Lin. 2022. "Steady State of Motion of Two Particles in Poiseuille Flow of Power-Law Fluid" Polymers 14, no. 12: 2368. https://doi.org/10.3390/polym14122368
APA StyleChen, D., & Lin, J. (2022). Steady State of Motion of Two Particles in Poiseuille Flow of Power-Law Fluid. Polymers, 14(12), 2368. https://doi.org/10.3390/polym14122368






