Fire-Shaped Nozzles to Produce a Stress Peak for Deformability Studies
Abstract
:1. Introduction
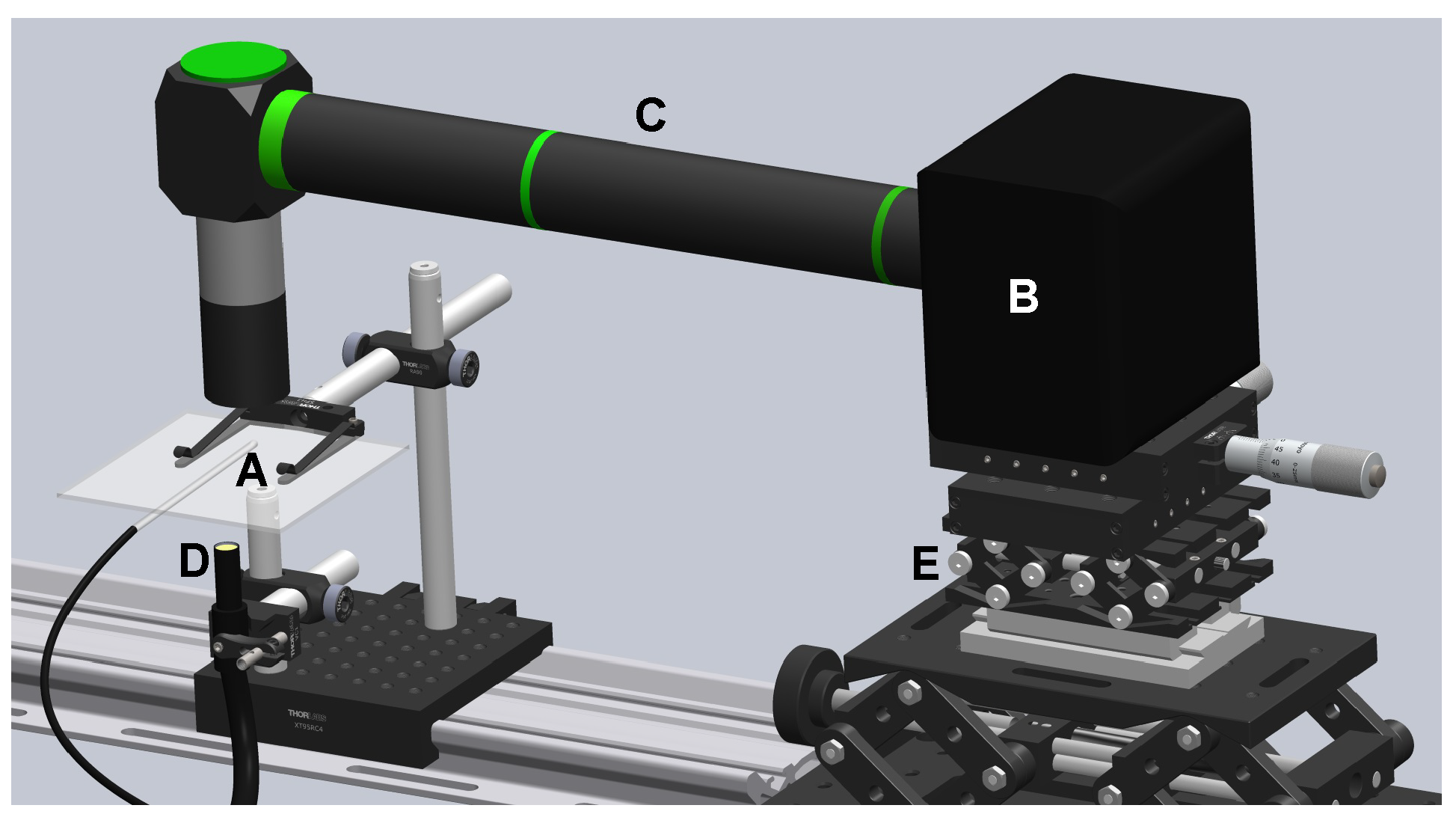
2. Materials and Methods
2.1. Deformation and Size Measurements
2.2. Fabrication and Characterization of the Nozzles
2.3. PDMS Particle Suspension Preparation
3. Results
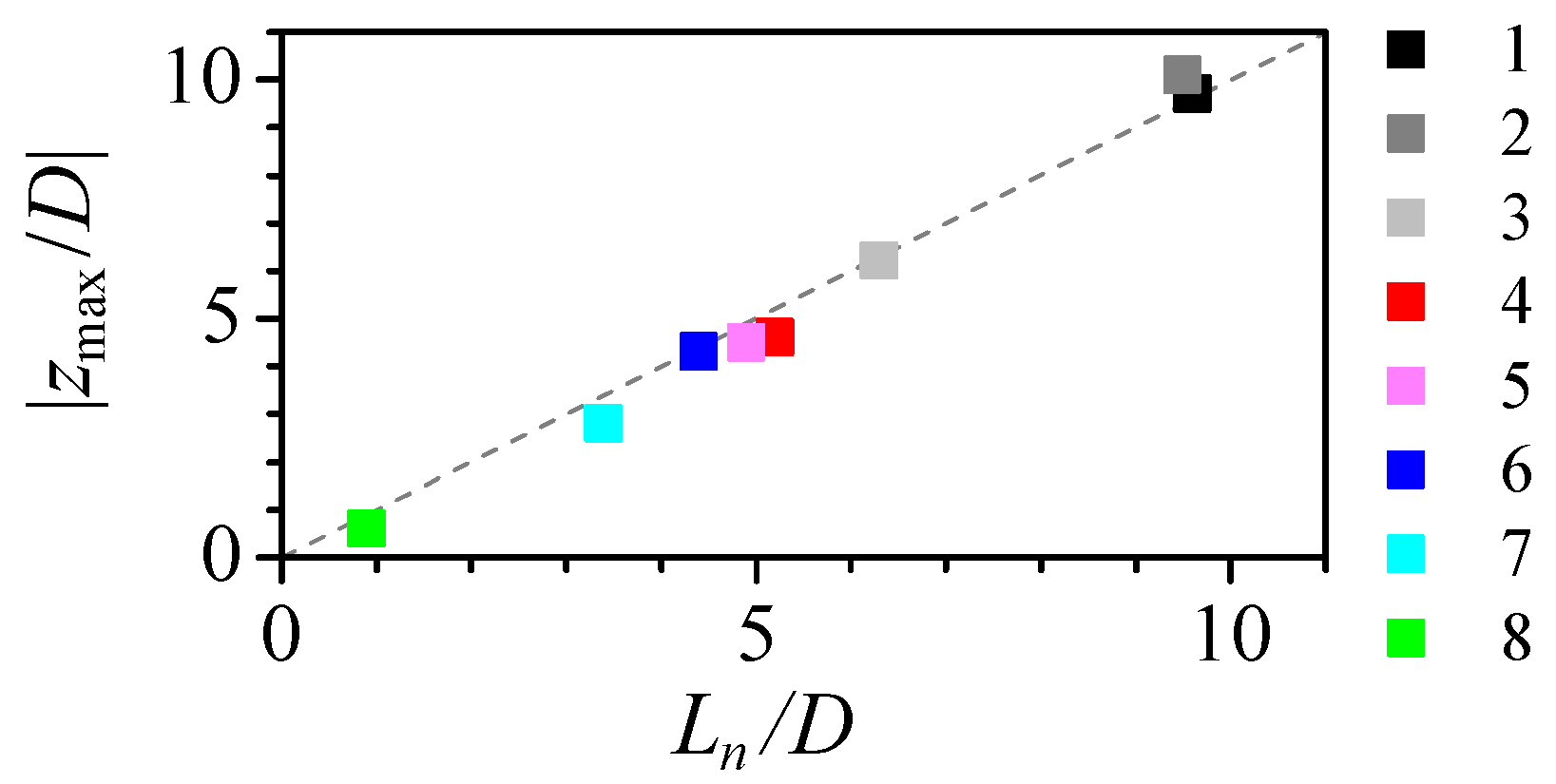
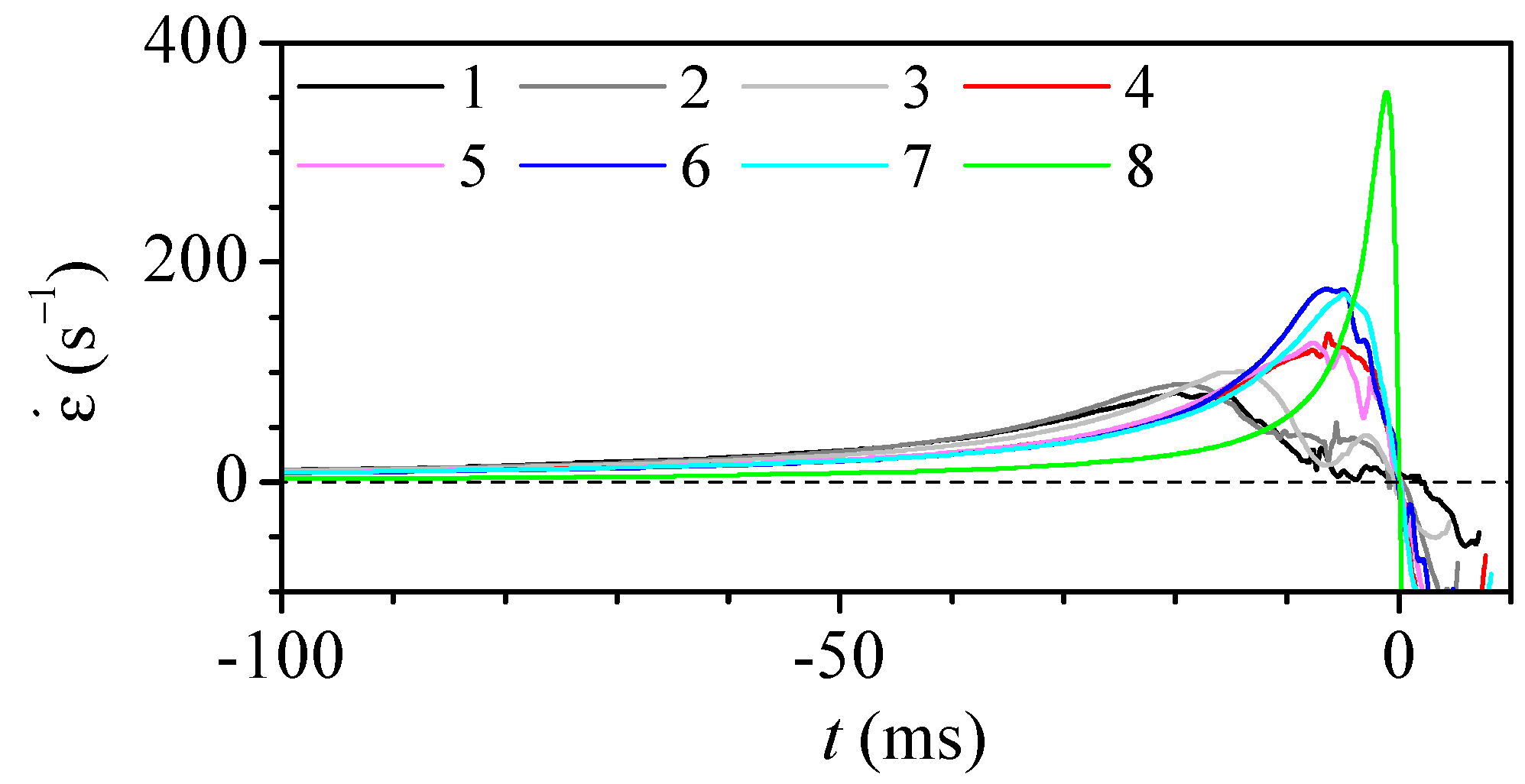
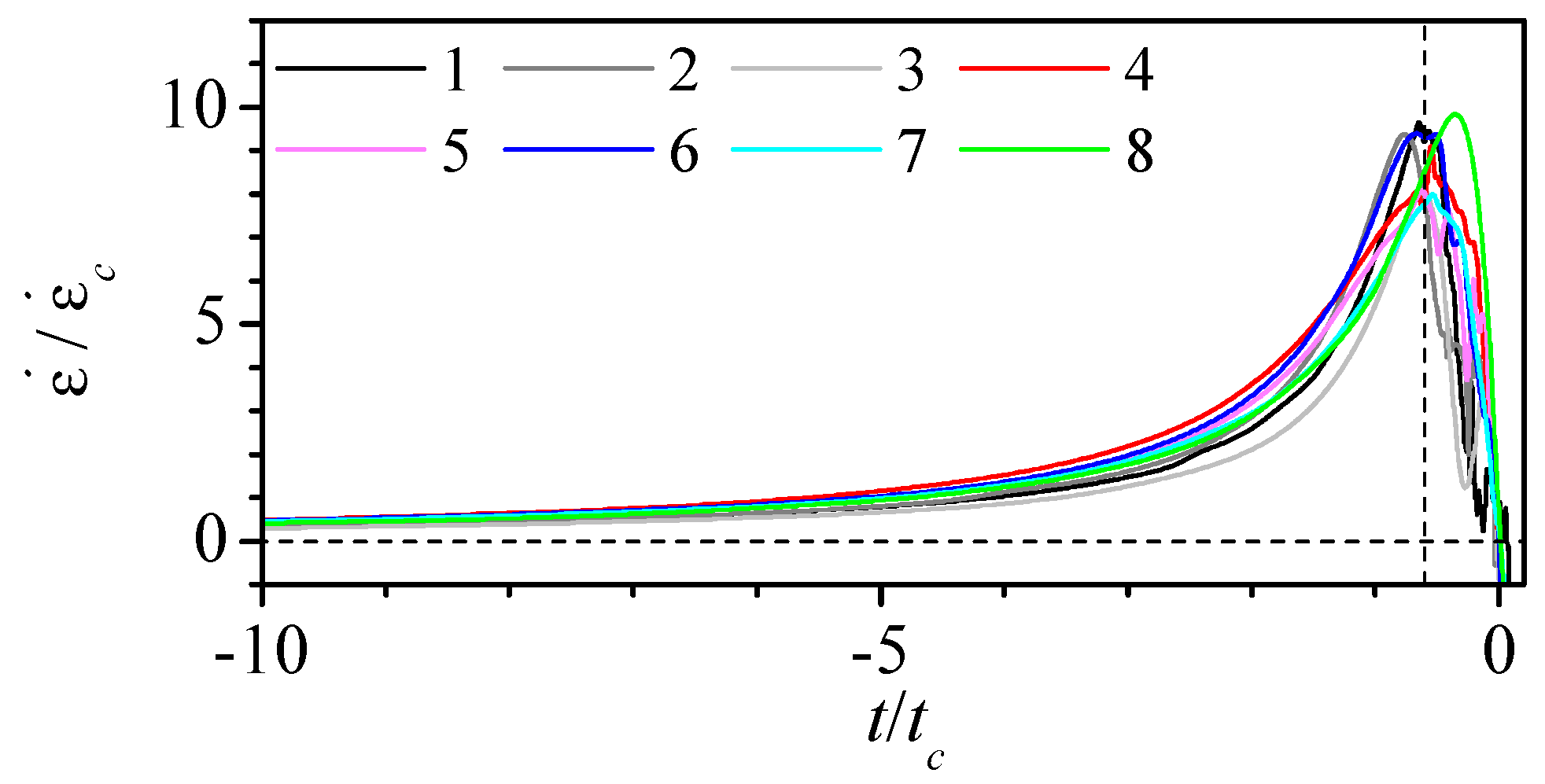
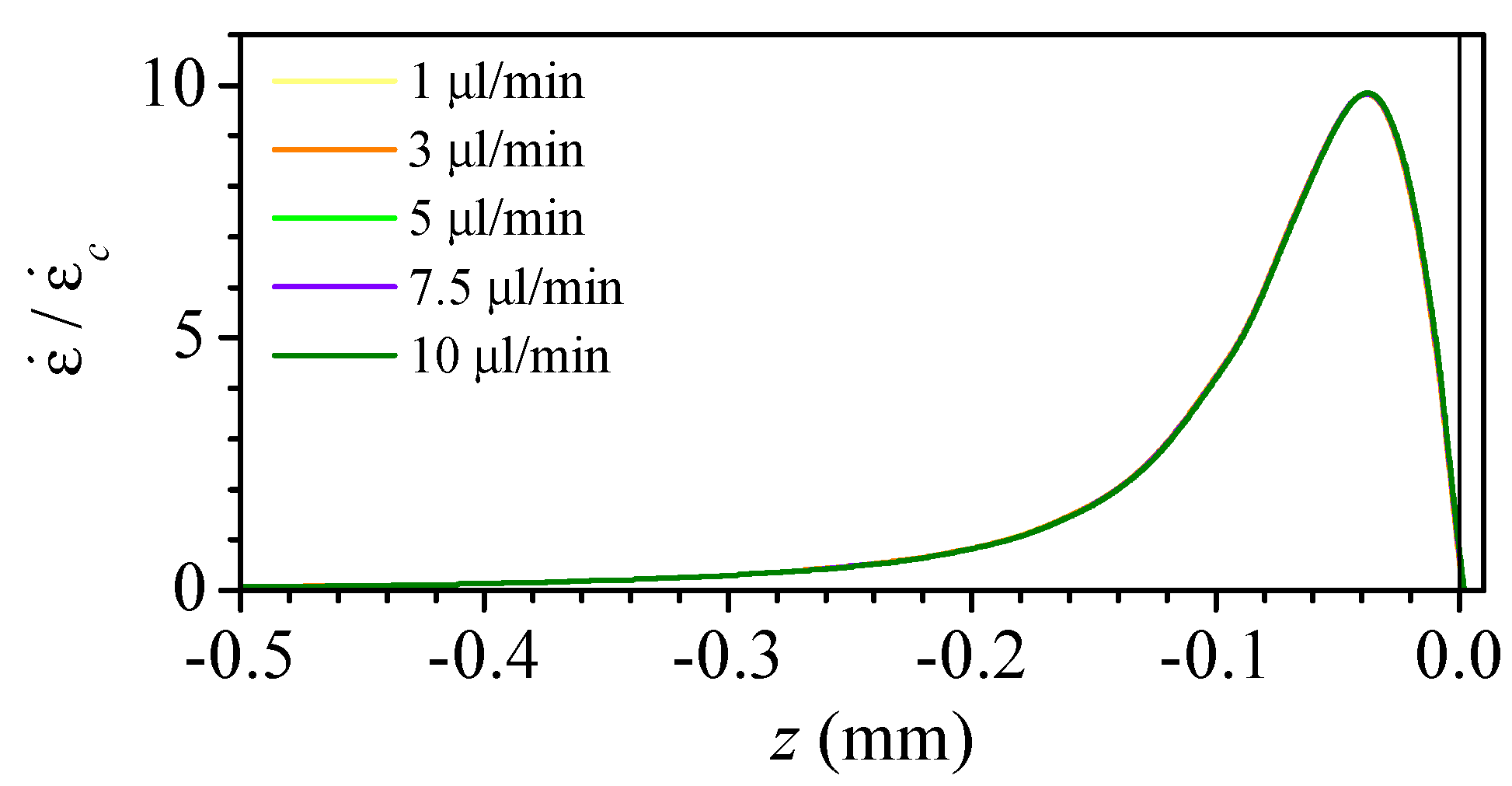
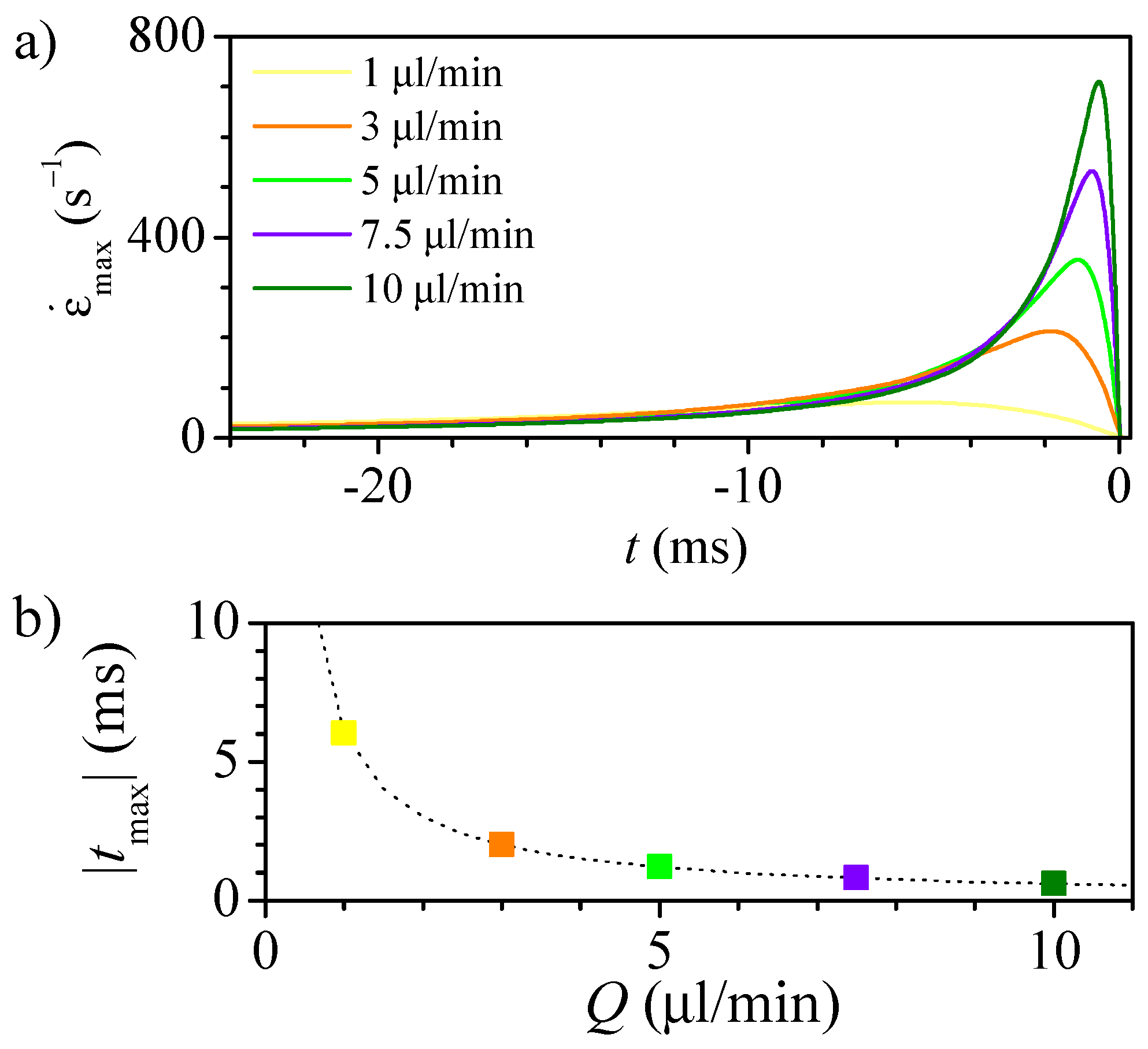
3.1. Numerical Study of the Flow
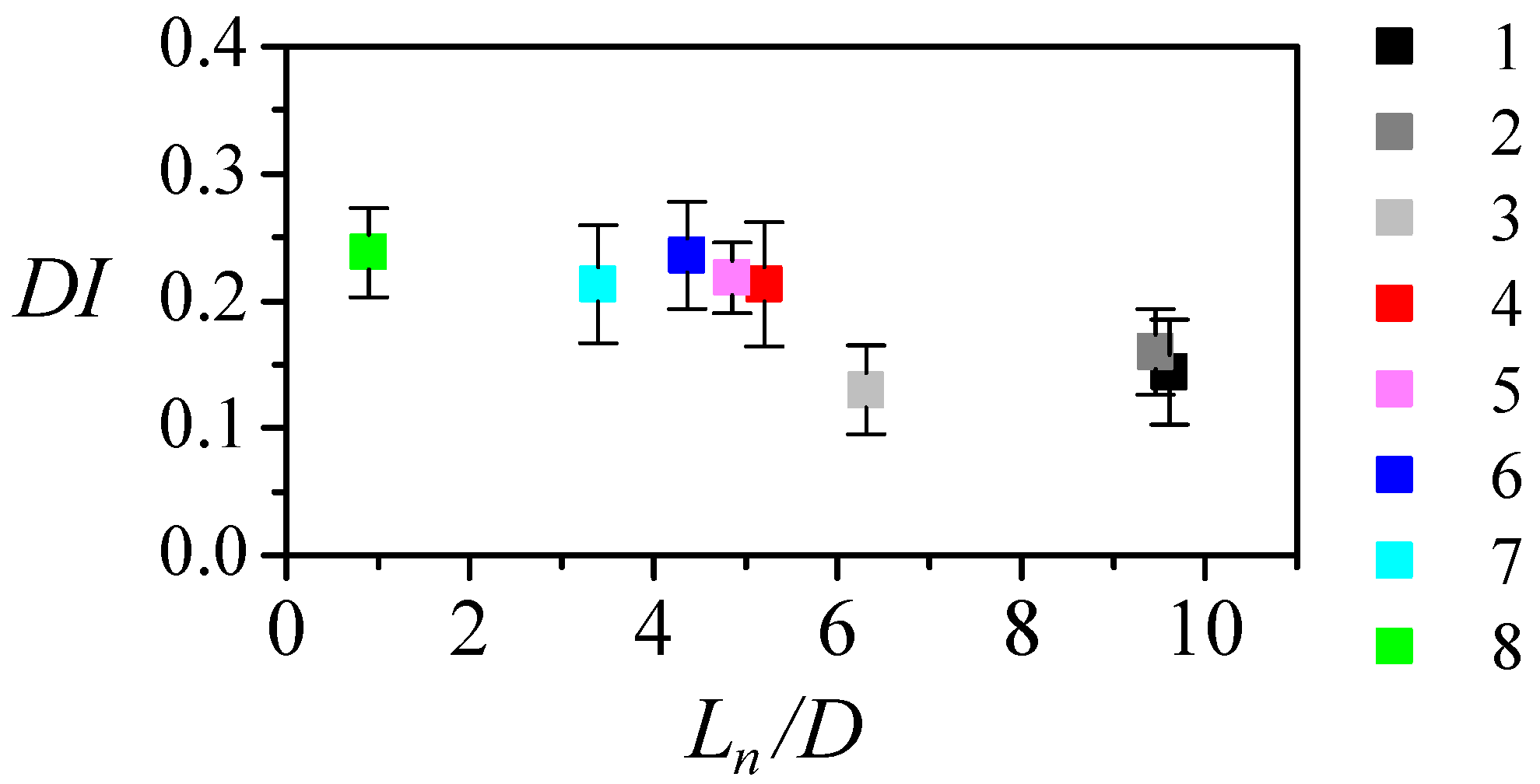
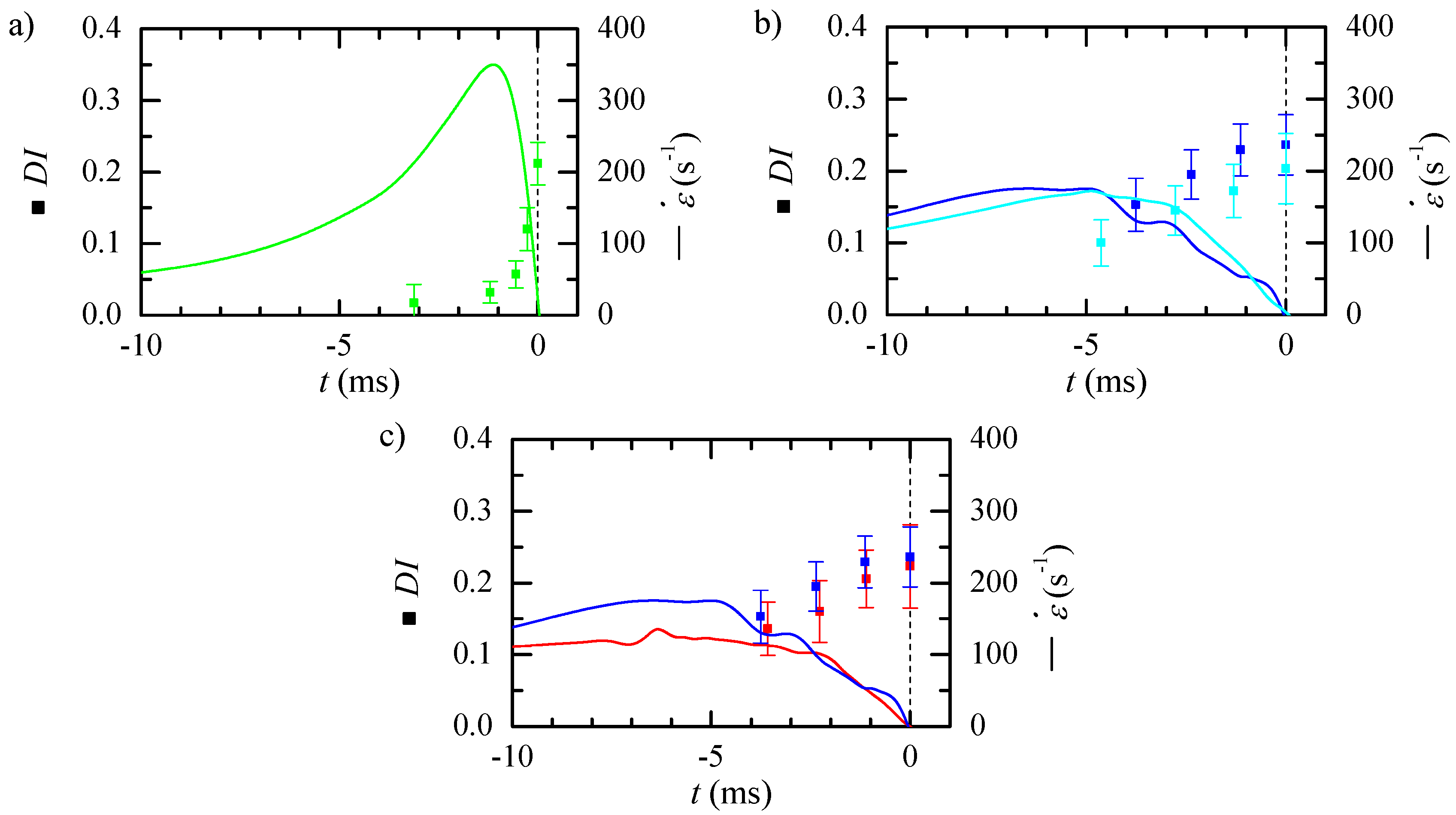
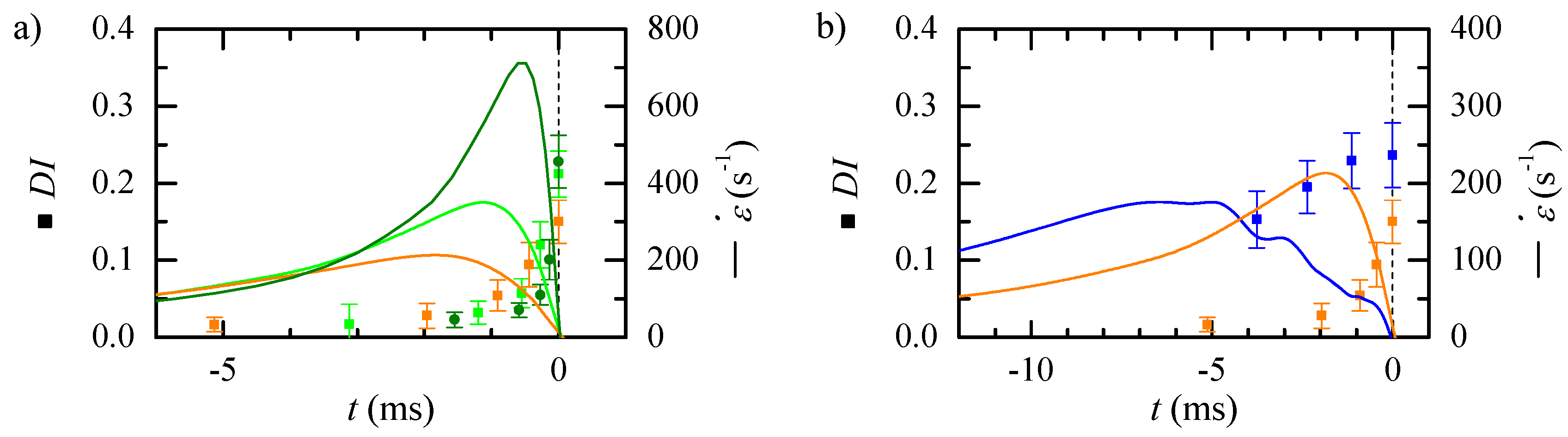
3.2. Experimental Measurement of Particle Deformation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- do Nascimento, D.F.; Avendaño, J.A.; Mehl, A.; Moura, M.J.; Carvalho, M.S.; Duncanson, W.J. Flow of tunable elastic microcapsules through constrictions. Sci. Rep. 2017, 7, 11898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goff, A.L.; Kaoui, B.; Kurzawa, G.; Haszon, B.; Salsac, A. Squeezing bio-capsules into a constriction: Deformation till break-up. Soft Matter 2017, 13, 7644. [Google Scholar] [CrossRef]
- Delcea, M.; Möhwald, H.; Skirtach, A.G. Stimuli-responsive LbL capsules and nanoshells for drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 730–747. [Google Scholar] [CrossRef] [PubMed]
- Baskurt, O.K.; Meiselman, H.J. Blood Rheology and Hemodynamics. Semin. Thromb. Hemost. 2003, 29, 435–450. [Google Scholar]
- Pinho, D.; Muñoz-Sánchez, B.N.; Anes, C.F.; Vega, E.J.; Lima, R. Flexible PDMS microparticles to mimic RBCs in blood particulate analogue fluids. Mech. Res. Commun. 2019, 100, 103399. [Google Scholar] [CrossRef] [Green Version]
- Neubauer, M.P.; Poehlmann, M.; Fery, A. Microcapsule mechanics: From stability to function. Adv. Colloid Interface Sci. 2014, 207, 65–80. [Google Scholar] [CrossRef] [PubMed]
- Danielczok, J.G.; Terriac, E.; Hertz, L.; Petkova-Kirova, P.; Lautenschläger, F.; Laschke, M.W.; Kaestner, L. Red Blood Cell Passage of Small Capillaries Is Associated with Transient Ca2+-mediated Adaptations. Front. Physiol. 2017, 8, 979. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gangotra, A.; Biviano, M.; Dagastine, R.R.; Berry, J.D.; Willmott, G.R. Use of microaspiration to study the mechanical properties of polymer gel microparticles. Soft Matter 2017, 15, 7286. [Google Scholar] [CrossRef] [PubMed]
- Trégouët, C.; Salez, T.; Monteux, C.; Reyssat, M. Microfluidic probing of the complex interfacial rheology of multilayer capsules. Soft Matter 2019, 15, 2782. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Zhu, Y.; Xu, D.; Alam, M.; Shui, L.; Chen, H. Cell elasticity measurement using a microfluidic device with real-time pressure feedback. Lab. Chip 2020, 20, 2343. [Google Scholar] [CrossRef]
- Huisjes, R.; Bogdanova, A.; van Solinge, W.W.; Schiffelers, R.M.; Kaestner, L.; van Wijk, R. Squeezing for Life – Properties of Red Blood Cell Deformability. Front. Physiol. 2018, 9, 656. [Google Scholar] [CrossRef]
- Sadek, S.H.; Rubio, M.; Lima, R.; Vega, E.J. Blood Particulate Analogue Fluids: A Review. Materials 2021, 14, 2451. [Google Scholar] [CrossRef]
- Abkarian, M.; Faivre, M.; Horton, R.; Smistrup, K.; Best-Popescu, C.A.; Stone, H.A. Cellular-scale hydrodynamics. Biomed. Mater. 2008, 3, 034011. [Google Scholar] [CrossRef] [Green Version]
- Piergiovanni, M.; Galli, V.; Holzner, G.; Stavrakis, S.; DeMello, A.; Dubini, G. Deformation of leukaemia cell lines in hyperbolic microchannels: Investigating the role of shear and extensional components. Lab Chip 2020, 20, 2539. [Google Scholar] [CrossRef]
- Otto, O.; Rosendahl, P.; Mietke, A.; Golfier, S.; Herold, C.; Klaue, D.; Girardo, S.; Pagliara, S.; Ekpenyong, A.; Jacobi, A.; et al. Real-time deformability cytometry: On-the-fly cell mechanical phenotyping. Nat. Methods 2015, 12, 199–202. [Google Scholar] [CrossRef]
- Guruprasad, P.; Mannino, R.G.; Caruso, C.; Zhang, H.; Josephson, C.D.; Roback, J.D.; Lam, W.A. Integrated automated particle tracking microfluidic enables high-throughput cell deformability cytometry for red cell disorders. Am. J. Hematol. 2019, 94, 189–199. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Chen, G.; Lin, Y.; Wang, G. A lab-on-a-chip capillary network for red blood cell hydrodynamics. Microfluid Nanofluid 2010, 9, 585–591. [Google Scholar] [CrossRef]
- Hu, S.; Lam, R. Characterization of viscoelastic properties of normal and cancerous human breast cells using a confining microchannel. Microfluid. Nanofluid. 2017, 21, 68. [Google Scholar] [CrossRef]
- Shelby, J.P.; White, J.; Ganesan, K.; Rathod, P.K.; Chiu, D.T. A microfluidic model for single-cell capillary obstruction by Plasmodium falciparuminfected erythrocytes. Proc. Natl. Acad. Sci. USA 2003, 100, 14618–14622. [Google Scholar] [CrossRef] [Green Version]
- Man, Y.; Kucukal, E.; An, R.; Watson, Q.D.; Bosch, J.; Zimmerman, P.A.; Little, J.A.; Gurkan, U.A. Microfluidic assessment of red blood cell mediated microvascular occlusion. Lab. Chip 2020, 20, 2086. [Google Scholar] [CrossRef] [PubMed]
- Man, Y.; Maji, D.; An, R.; Ahuja, S.P.; Little, J.A.; Suster, M.A.; Mohseni, P.; Gurkan, U.A. Microfluidic electrical impedance assessment of red blood cell-mediated microvascular occlusion. Lab. Chip 2021, 21, 1036. [Google Scholar] [CrossRef] [PubMed]
- Man, Y.; Kucukal, E.; An, R.; Bode, A.; Little, J.A.; Gurkan, U.A. Standardized microfluidic assessment of red blood cellmediated microcapillary occlusion: Association with clinical phenotype and hydroxyurea responsiveness in sickle cell disease. Microcirculation 2020, 28, 12662. [Google Scholar] [CrossRef] [PubMed]
- Islamzada, E.; Matthews, K.; Guo, Q.; Santoso, A.T.; Duffy, S.P.; Scott, M.D.; Ma, H. Deformability based sorting of stored red blood cells reveals donor-dependent aging curves. Lab. Chip 2019, 20, 226. [Google Scholar] [CrossRef]
- Piety, N.Z.; Stutz, J.; Yilmaz, N.; Xia, H.; Yoshida, T.; Shevkoplyas, S.S. Microfluidic capillary networks are more sensitive than ektacytometry to the decline of red blood cell deformability induced by storage. Sci. Rep. 2021, 11, 604. [Google Scholar] [CrossRef]
- Galindo-Rosales, F.J.; Oliveira, M.S.N.; Alves, M.A. Optimized cross-slot microdevices for homogeneous extension. RSC Adv. 2014, 4, 7799–7804. [Google Scholar] [CrossRef] [Green Version]
- Cha, S.; Shin, T.; Lee, S.S.; Shim, W.; Lee, G.; Lee, S.J.; Kim, Y.; Kim, J.M. Cell Stretching Measurement Utilizing Viscoelastic Particle Focusing. Anal. Chem. 2012, 84, 10471–10477. [Google Scholar] [CrossRef]
- Yaginuma, T.; Oliveira, M.; Lima, R.; Ishikawa, T.; Yamaguchi, T. Human red blood cell behaviour under homogeneous extensional flow in a hyperbolic-shaped microchannel. Biomicrofluidics 2013, 7, 054110. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, S.S.; Yim, Y.; Ahn, K.H.; Lee, S.J. Extensional flow-based assessment of red blood cell deformability using hyperbolic converging microchannel. Biomed. Microdevices 2009, 11, 1021–1027. [Google Scholar] [CrossRef] [PubMed]
- Faghih, M.M.; Sharp, M.K. Deformation of human red blood cells in extensional flow through a hyperbolic contraction. Biomech. Model. Mechanobiol. 2020, 19, 251–261. [Google Scholar] [CrossRef]
- Guerrero, J.; Chang, Y.; Fragkopoulos, A.A.; Fernández-Nieves, A. Capillary-Based Microfluidics-Coflow, Flow-Focusing, Electro-Coflow, Drops, Jets, and Instabilities. Small 2020, 16, 1904344. [Google Scholar] [CrossRef]
- Montanero, J.M.; Gañán-Calvo, A.M. Dripping, jetting and tip streaming. Rep. Prog. Phys. 2020, 83, 097001. [Google Scholar] [CrossRef] [PubMed]
- Muñoz-Sánchez, B.N.; Cabezas, M.G. Borosilicate nozzles manufactured by reproducible fire shaping. J. Mater. Process. Technol. 2018, 261, 173–183. [Google Scholar] [CrossRef]
- Muñoz-Sánchez, B.N.; Gañán-Calvo, A.M.; Cabezas, M.G. A new fire shaping approach to produce highly axisymmetric and reproducible nozzles. J. Mater. Process. Technol. 2019, 270, 241–253. [Google Scholar] [CrossRef]
- Rubio, A.; Rodríguez, S.; Cabezas, M.G. Capabilities and limitations of fire-shaping to produce glass nozzles. Materials 2020, 13, 5477. [Google Scholar] [CrossRef]
- Rubio, A.; Faustino, V.; Cabezas, M.G.; Lima, R.; Vega, E.J. Fire-shaped cylindrical glass micronozzles to measure cell deformability. J. Micromech. Microeng. 2019, 29, 105001. [Google Scholar] [CrossRef]
- López, M.; Rubio, M.; Sadek, S.; Vega, E.J. A simple emulsification technique for the production of micro-sized flexible powder of polydimethylsiloxane (PDMS). Powder Technol. 2020, 366, 610–616. [Google Scholar] [CrossRef]
- Carneiro, J.; Lima, R.; Campos, J.B.L.M.; Miranda, J.M. A microparticle blood analogue suspension matching blood rheology. Soft Matter 2021, 17, 3963. [Google Scholar] [CrossRef]

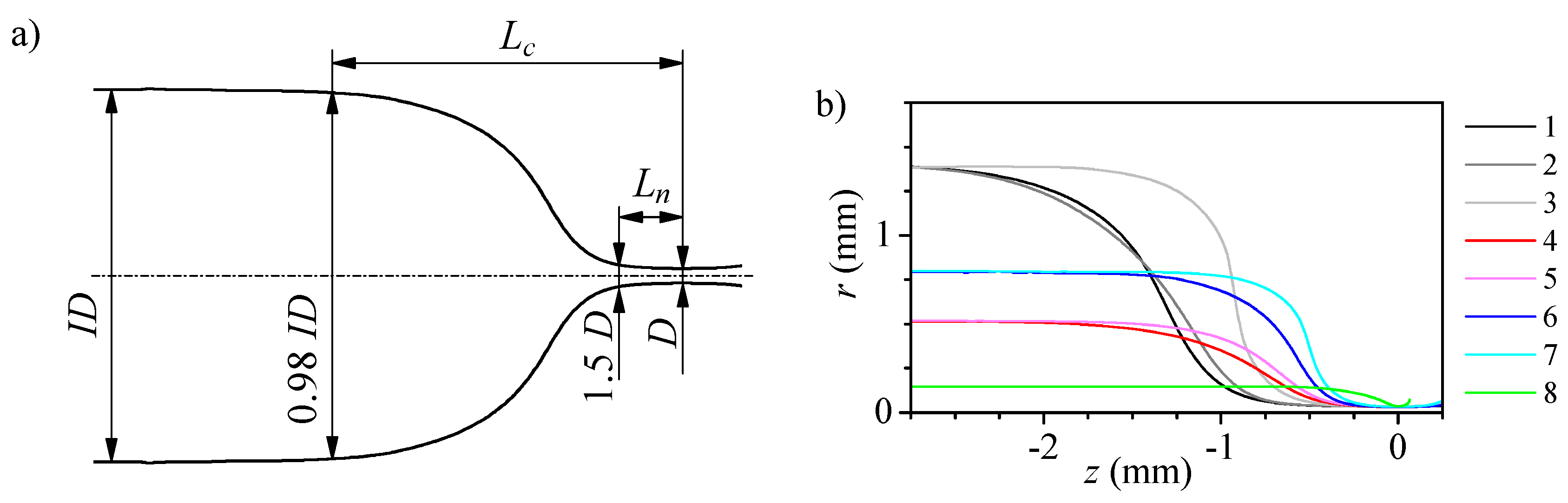
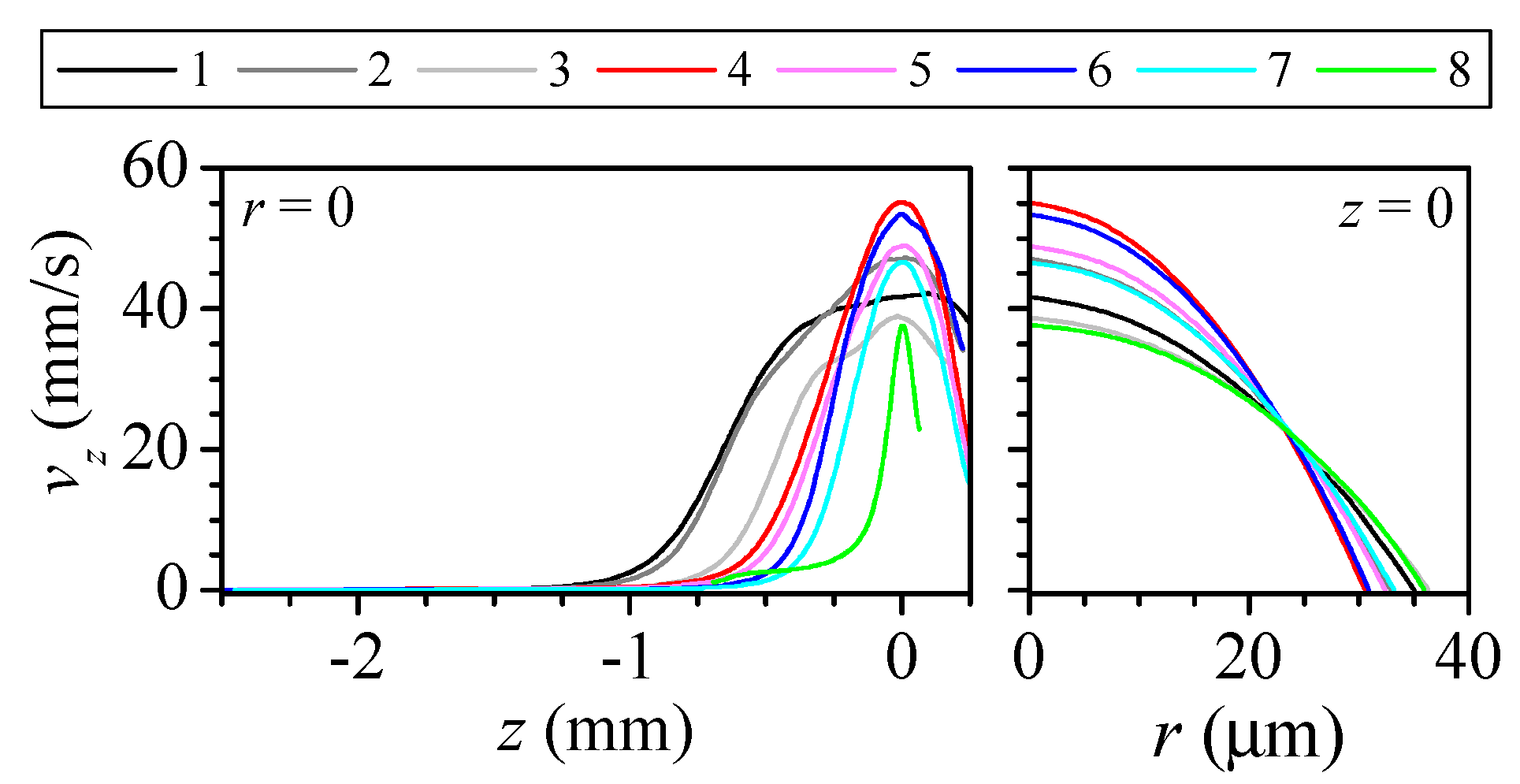
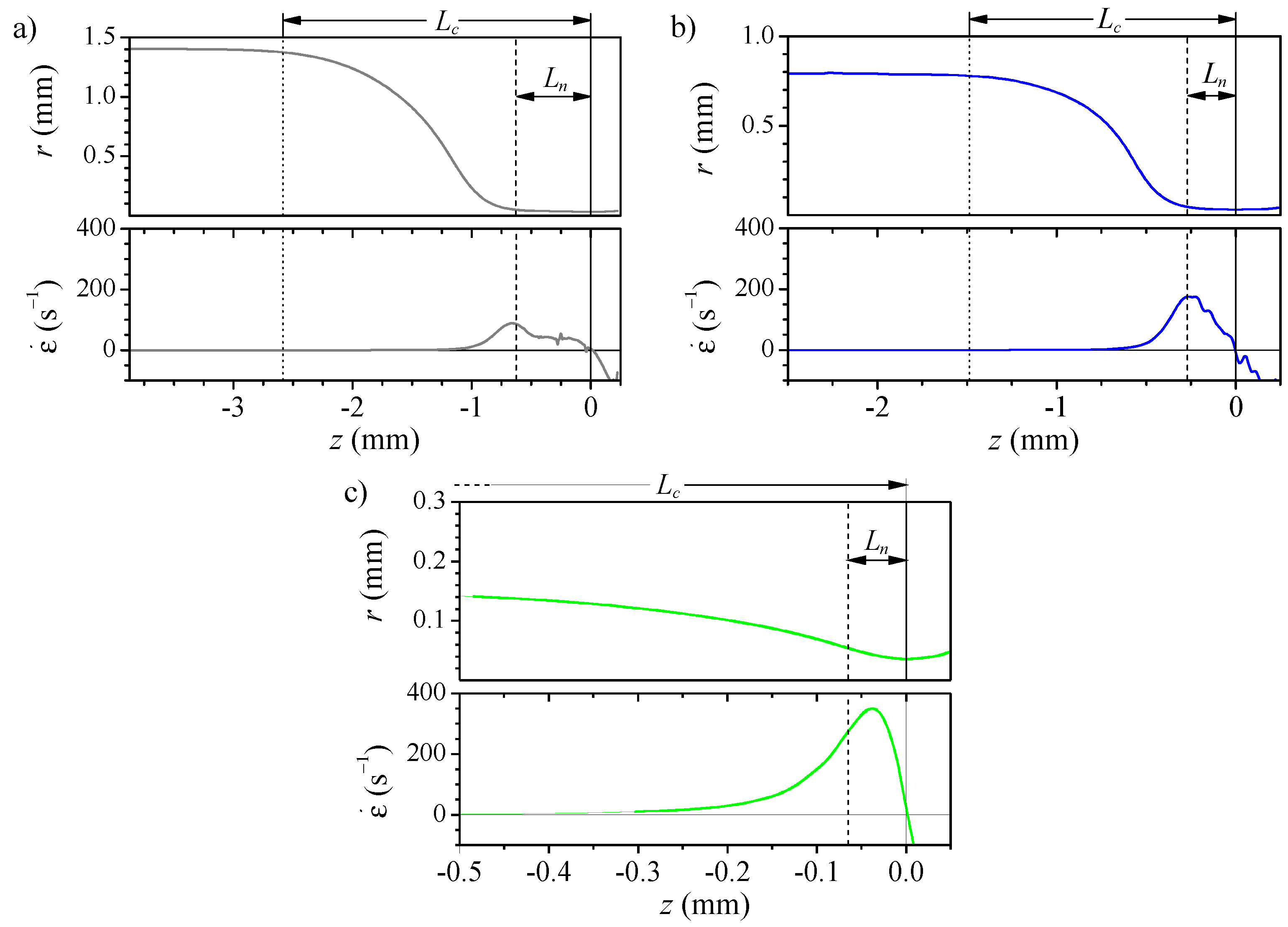

| Nozzle Geometry | Capillary Geometry | Fabrication Parameters | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Nozzle | D [m] | [mm] | [m] | OD [mm] | ID [mm] | Wall | [mm] | [mm] | [s] |
| 1 | 72 ± 2 | 2.61 | 672 | 3.7 ± 0.1 | 2.8 ± 0.1 | Thick | 3.5 | 15 | 900 |
| 2 | 65 ± 5 | 2.60 | 625 | 3.3 ± 0.1 | 2.8 ± 0.1 | Thin | 3.5 | 15 | 240 |
| 3 | 73 ± 3 | 1.61 | 475 | 3.3 ± 0.1 | 2.8 ± 0.1 | Thin | 4.5 | 15 | 600 |
| 4 | 63 ± 3 | 1.91 | 327 | 2.0 ± 0.1 | 1.0 ± 0.1 | Thick | 5.5 | 15 | 70 |
| 5 | 65 ± 1 | 1.62 | 314 | 2.0 ± 0.1 | 1.0 ± 0.1 | Thick | 6 | 15 | 120 |
| 6 | 62 ± 1 | 1.49 | 271 | 2.0 ± 0.1 | 1.6 ± 0.1 | Thin | 5.5 | 15 | 70 |
| 7 | 69 ± 7 | 1.12 | 220 | 2.0 ± 0.1 | 1.6 ± 0.1 | Thin | 6.6 | 15 | 480 |
| 8 | 72 ± 1 | 0.57 | 65 | 0.4 ± 0.04 | 0.3 ± 0.03 | Thin | 7.9 | 15 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rubio, A.; López, M.; Vega, E.J.; Cabezas, M.G. Fire-Shaped Nozzles to Produce a Stress Peak for Deformability Studies. Polymers 2022, 14, 2784. https://doi.org/10.3390/polym14142784
Rubio A, López M, Vega EJ, Cabezas MG. Fire-Shaped Nozzles to Produce a Stress Peak for Deformability Studies. Polymers. 2022; 14(14):2784. https://doi.org/10.3390/polym14142784
Chicago/Turabian StyleRubio, Alejandro, Marta López, Emilio J. Vega, and María G. Cabezas. 2022. "Fire-Shaped Nozzles to Produce a Stress Peak for Deformability Studies" Polymers 14, no. 14: 2784. https://doi.org/10.3390/polym14142784
APA StyleRubio, A., López, M., Vega, E. J., & Cabezas, M. G. (2022). Fire-Shaped Nozzles to Produce a Stress Peak for Deformability Studies. Polymers, 14(14), 2784. https://doi.org/10.3390/polym14142784







