Theory of Weakly Polydisperse Cytoskeleton Filaments
Abstract
1. Introduction
2. Materials and Methods
2.1. The Free Energy Density Functional
2.1.1. Ideal Gas Free Energy
2.1.2. Interaction Free Energy
2.2. The Distribution Functions
2.3. Free Energy in the Nematic Phase
2.3.1. Orientational Free Energy
2.3.2. Interaction Free Energy
2.3.3. Mixing Free Energy
2.4. Free Energy in the Isotropic Phase
2.5. Isotropic–Nematic Phase at Equilibrium
3. Results
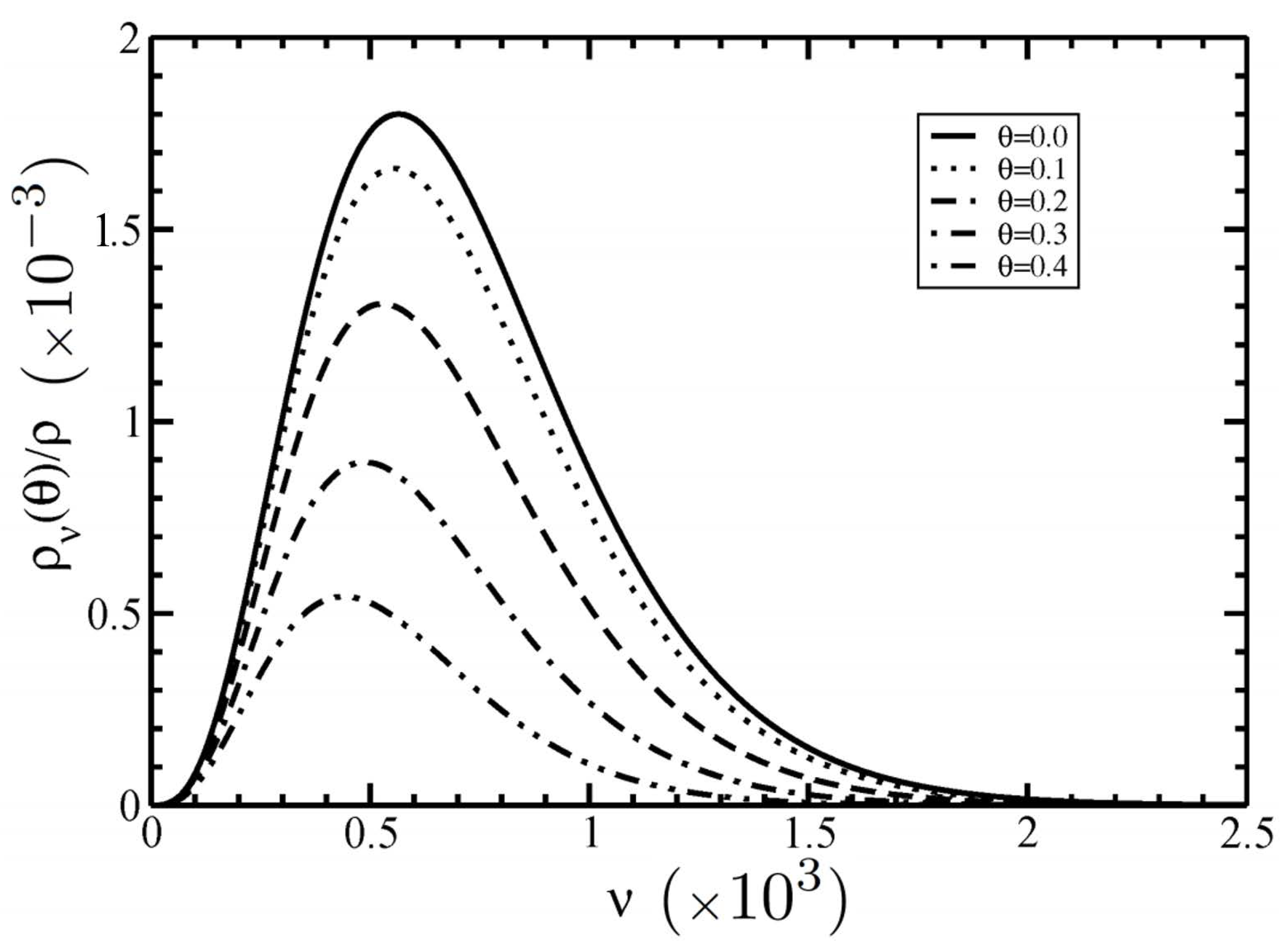
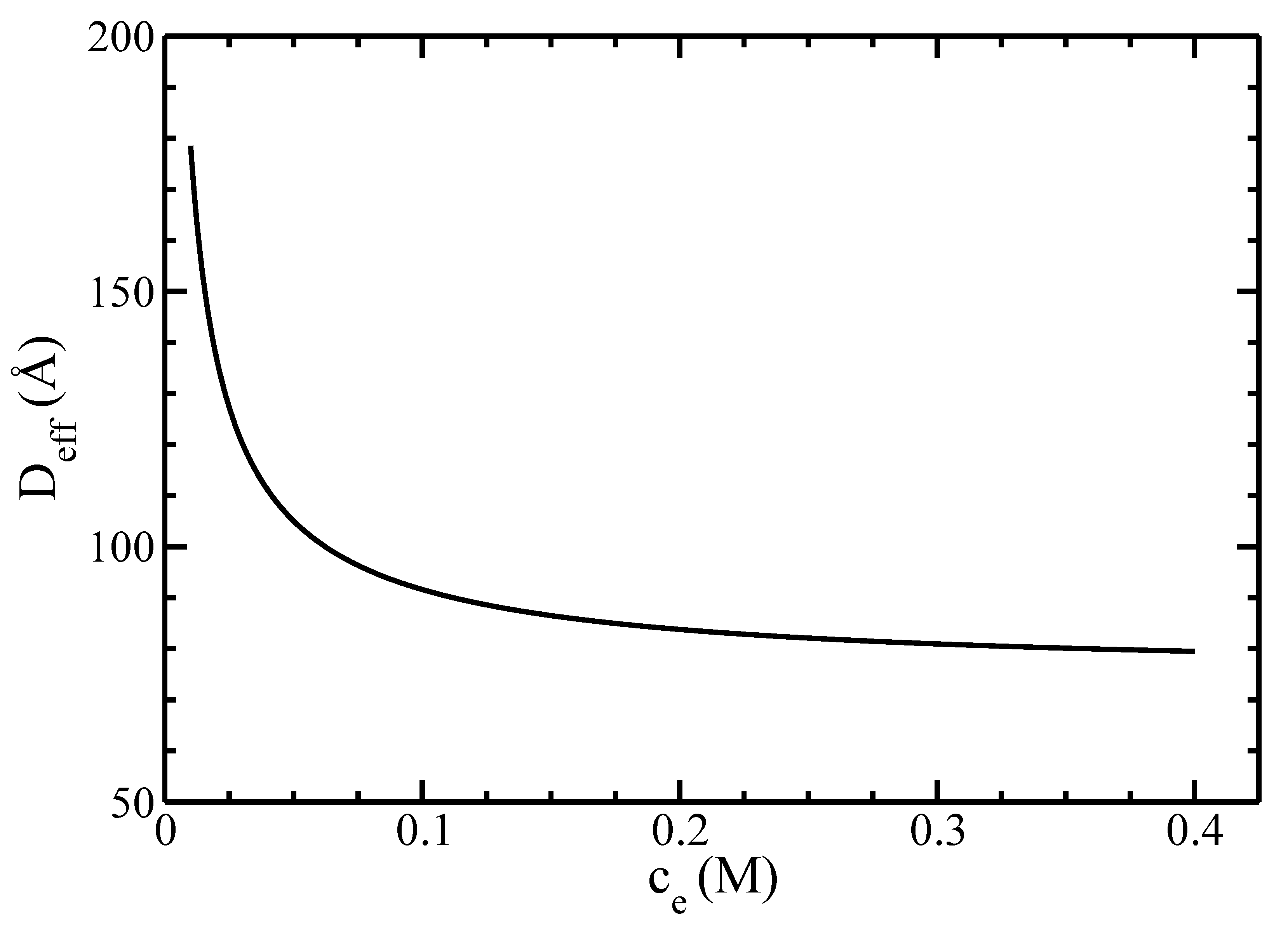
3.1. Distribution Functions
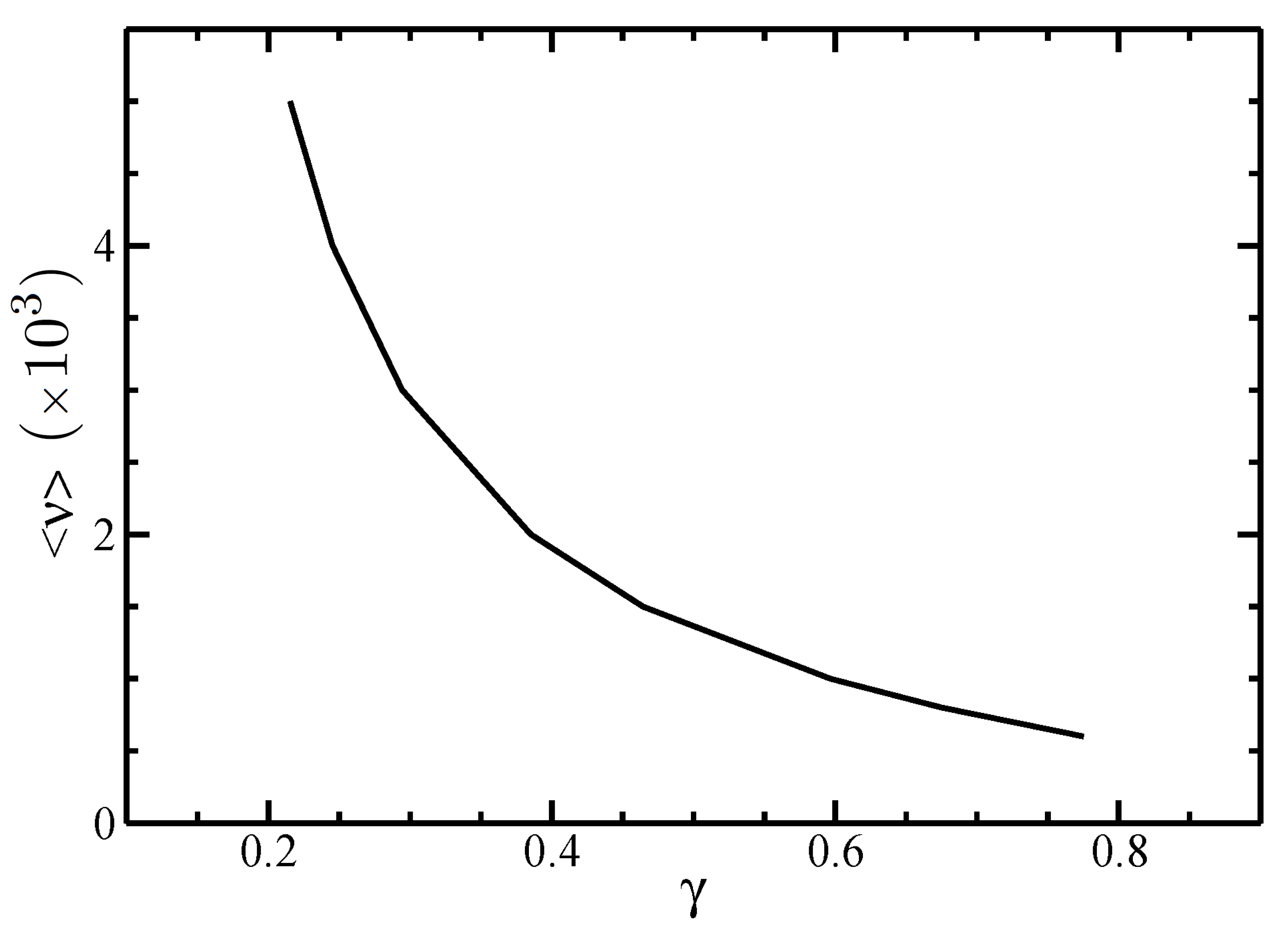
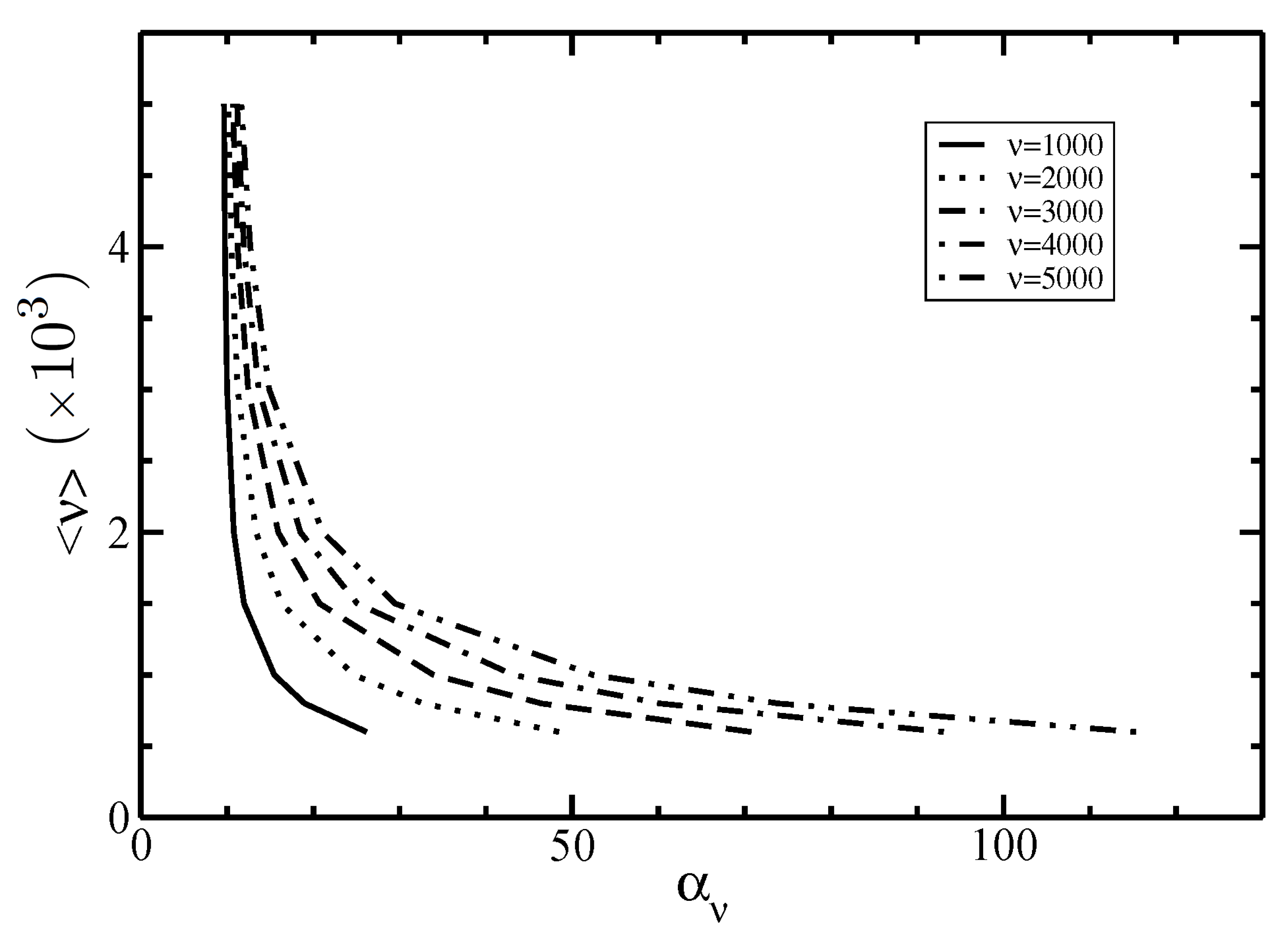
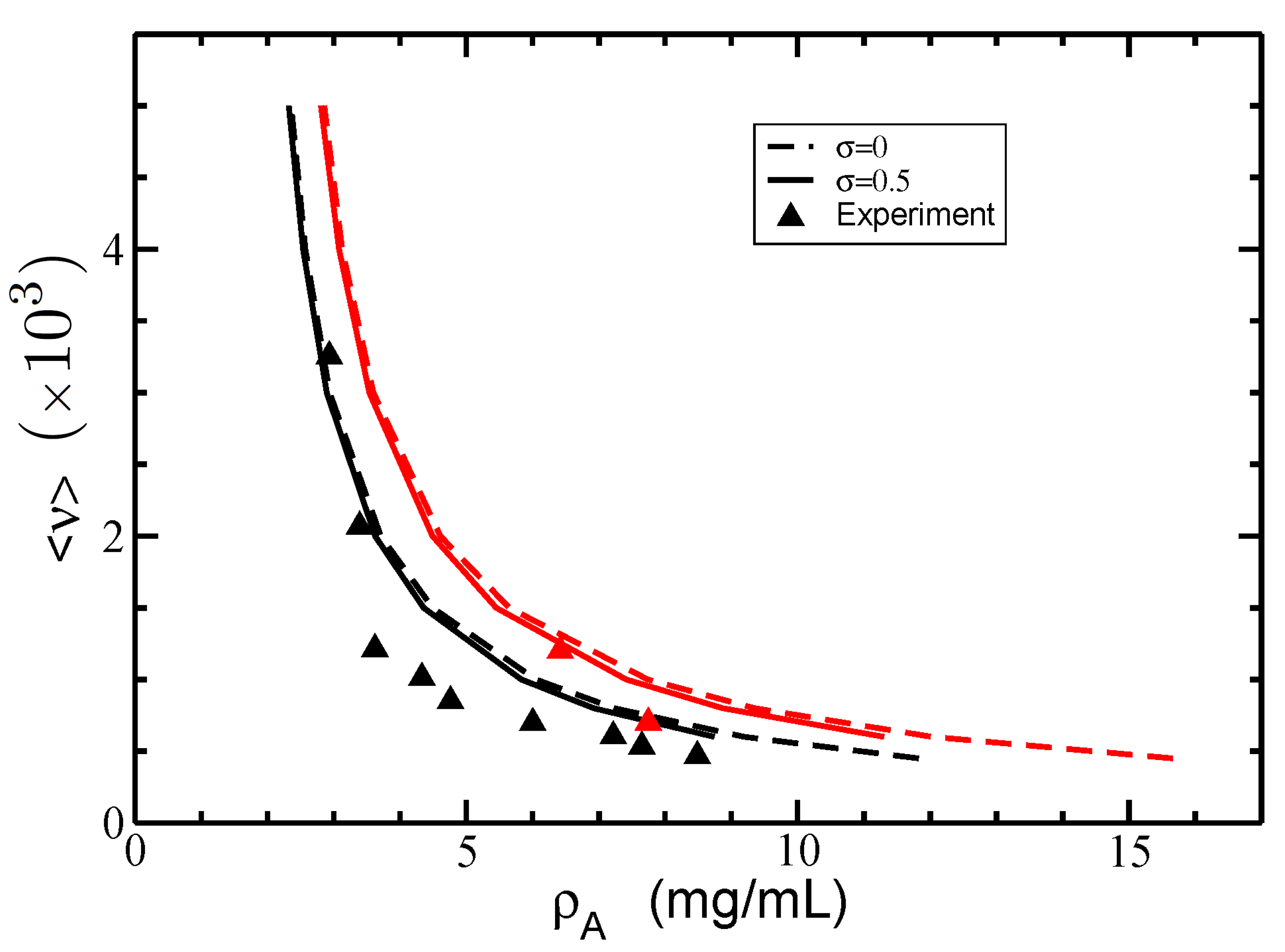
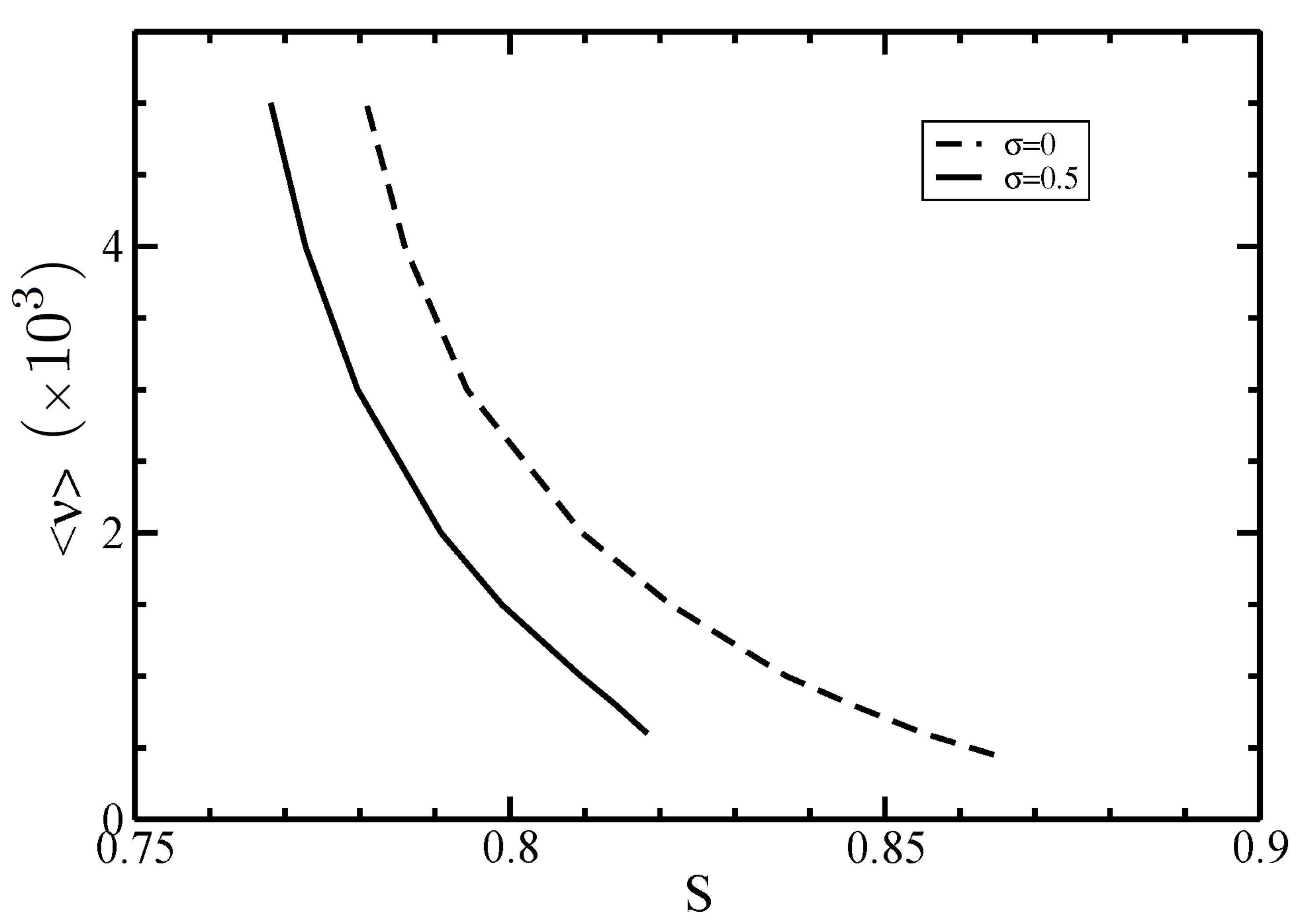
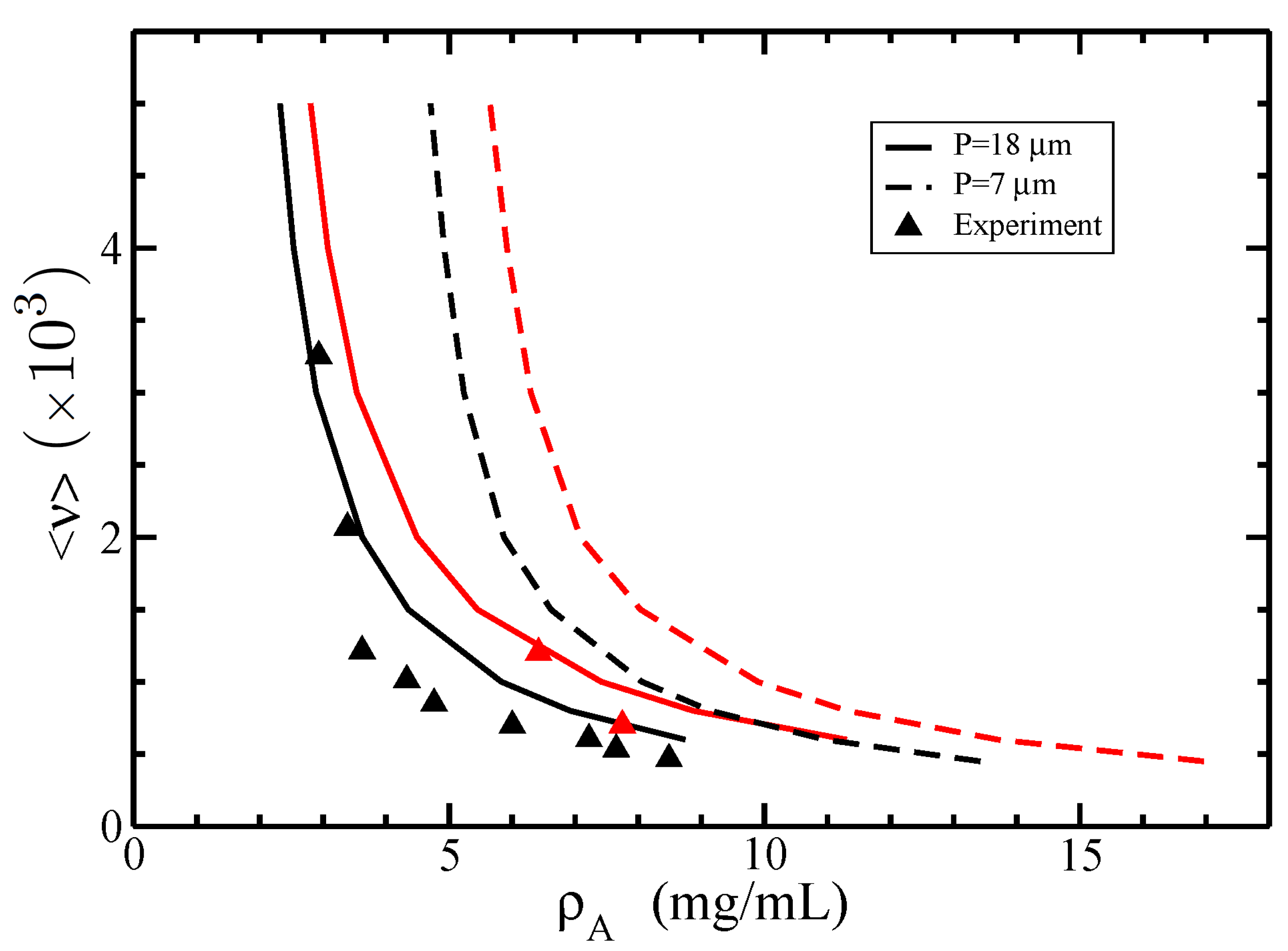
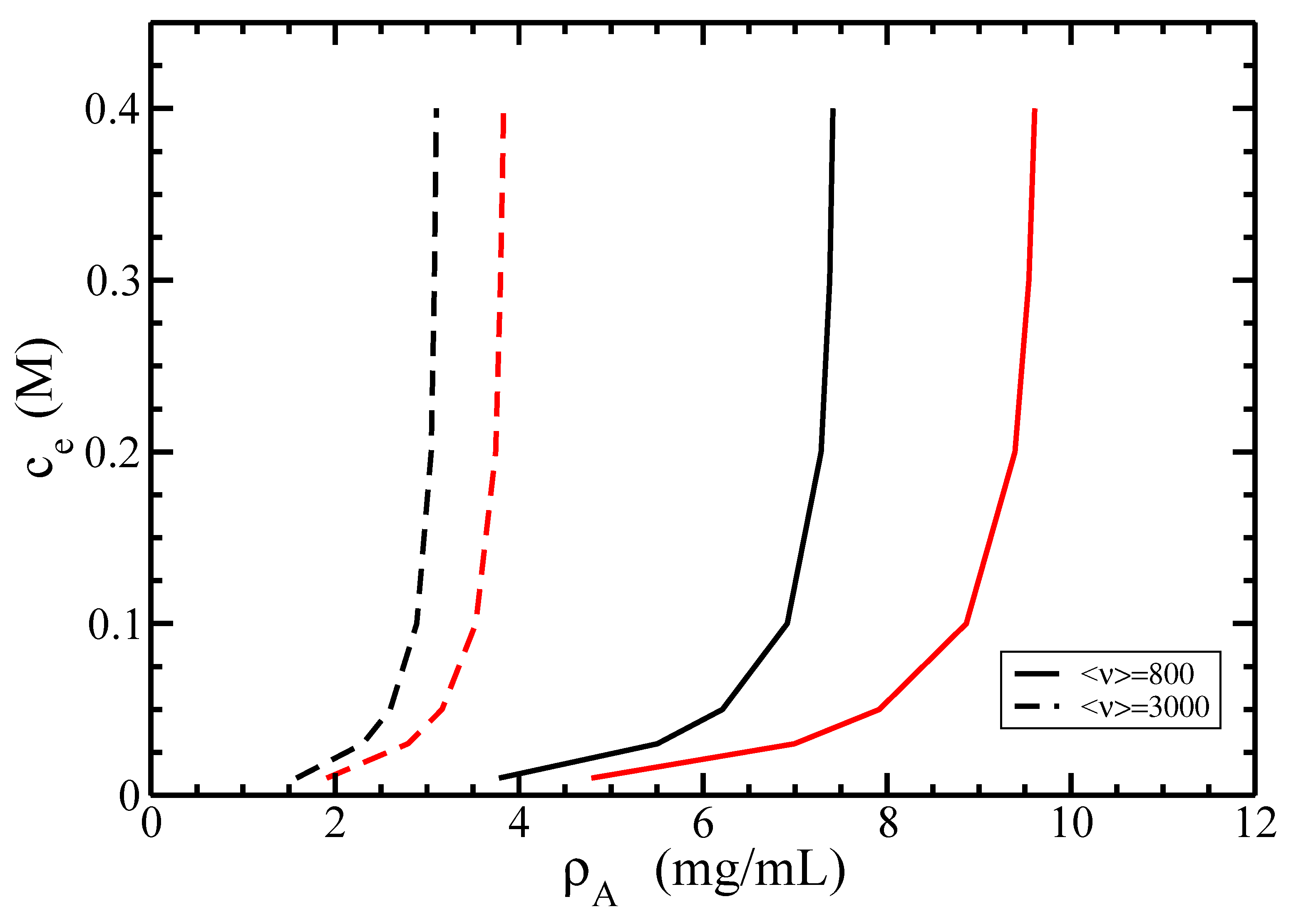
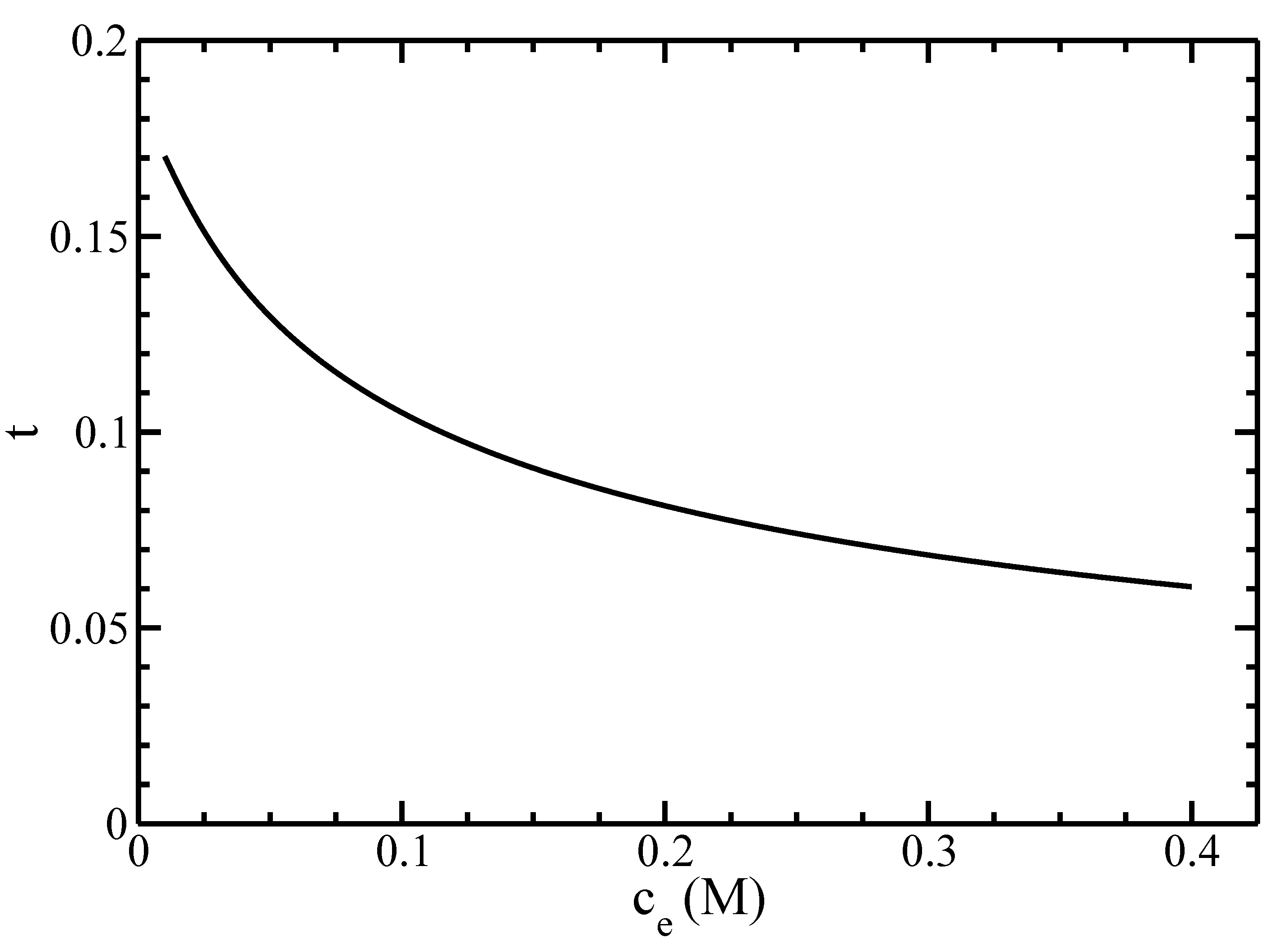
3.2. Isotropic–Nematic Phase Diagram
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Cluster Integral Bν1ν2(ω1,ω2) in Equation
Appendix B. Schulz Distribution Function in Equation
Appendix C. Orientational Energy for in Equation
Appendix D. Interaction Energy fint in Equations
Appendix E. Asymptotic Expression for fmix in the Monodisperse Limit
References
- Alberts, B.; Johnson, A.; Lewis, J.; Raff, M.; Roberts, K.; Walter, P. Molecular Biology of the Cell, 6th ed.; Garland Science: New York, NY, USA, 2002; p. 1400. [Google Scholar]
- Borukhov, I.; Bruinsma, R.; Gelbart, W.; Liu, A. Structural polymorphism of the cytoskeleton: A model of linker-assisted filament aggregation. Proc. Natl. Acad. Sci. USA 2005, 102, 3673–3678. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Yamazaki, M.; Ito, T. Osmoelastic Coupling in Biological Structures: Formation of Parallel Bundles of Actin Filaments in a Crystalline-like Structure Caused by Osmotic Stress. Biophys. J. 1989, 28, 6513–6518. [Google Scholar] [CrossRef] [PubMed]
- Suzuki, A.; Yamazaki, M.; Ito, T. Polymorphism of F-Actin Assembly. 1. A Quantitative Phase Diagram of F-Actin. Biophys. J. 1996, 35, 5238–5244. [Google Scholar] [CrossRef] [PubMed]
- Wong, G.; Tang, J.; Lin, A.; Li, Y.; Janmey, P.; Safinya, C. Hierarchical self-assembly of F-actin and cationic lipid complexes: Stacked three-layer tubule networks. Science 2000, 288, 2035–2039. [Google Scholar] [CrossRef]
- Xu, J.; Schwarz, W.H.; Kas, J.A.; Stossel, T.P.; Janmey, P.A.; Pollard, T.D. Mechanical Properties of Actin Filament Networks Depend on Preparation, Polymerization Conditions, and Storage of Actin Monomers. Biophys. J. 1998, 74, 2731–2740. [Google Scholar] [CrossRef]
- D’Este, E.; Kamin, D.; Gottfert, F.; Al-Hady, A.; Hell, S.W. STED Nanoscopy Reveals the Ubiquity of Subcortical Cytoskeleton Periodicity in Living Neurons. Cell Rep. 2015, 10, 1246–1251. [Google Scholar] [CrossRef]
- Jones, S.L.; Korobova, F.; Svitkina, T. Axon initial segment cytoskeleton comprises a multiprotein submembranous coat containing sparse actin filaments. J. Cell Biol. 2014, 205, 67–81. [Google Scholar] [CrossRef]
- Lukinavicius, G.; Reymond, L.; D’Este, E.; Masharina, A.; Gottfert, F.; Ta, H.; Guther, A.; Fournier, M.; Rizzo, S.; Waldmann, H.; et al. Fluorogenic probes for live-cell imaging of the cytoskeleton. Nat. Methods 2014, 11, 731–733. [Google Scholar] [CrossRef]
- Onsager, L. The effects of shape on the interaction of colloidal particles. Ann. N. Y. Acad. Sci. 1949, 51, 627–659. [Google Scholar] [CrossRef]
- Vroege, G.; Lekkerkerker, H. Phase transitions in lyotropic colloidal and polymer liquid crystals. Rep. Prog. Phys. 1992, 55, 1241–1309. [Google Scholar] [CrossRef]
- Stroobants, A.; Lekkerkerker, H.N.W.; Odijk, T. Effect of Electrostatic Interaction on the Liquid Crystal Phase Transition in Solutions of Rodlike Polyelectrolytes. Macromolecules 1986, 19, 2232–2238. [Google Scholar] [CrossRef]
- Odijk, T. Theory of Lyotropic Polymer Liquid Crystals. Macromolecules 1986, 19, 2313–2329. [Google Scholar] [CrossRef]
- Khokhlov, A.; Semenov, A. Liquid-crystalline ordering in the solution of long persistence chains. Physical A 1981, 108, 546–556. [Google Scholar] [CrossRef]
- Khokhlov, A.; Semenov, A. Liquid-crystalline ordering in a solution of partially flexible macromolecules. Physical A 1982, 112, 605–614. [Google Scholar] [CrossRef]
- Hentschke, R. Equation of State for Persistent-Flexible Liquid-Crystal Polymers. Comparison with Poly(Y-benzyl-L-glutamate) in Dimethylformamide. Macromolecules 1990, 23, 1192–1196. [Google Scholar] [CrossRef]
- Sluckin, T. Polydispersity in liquid crystal systems. Liq. Cryst. 1989, 6, 111–131. [Google Scholar] [CrossRef]
- Chen, Z.Y. Effect of polydispersity on the isotropic–nematic phase transition of rigid rods. Phys. Rev. E 1994, 50, 2849–2855. [Google Scholar] [CrossRef]
- Speranza, A.; Sollich, P. Simpified Onsager Theory for Isotropic-nematic phase equilibria of length polydisperse hard rods. J. Chem. Phys. 2002, 117, 5421–5436. [Google Scholar] [CrossRef]
- Wensink, H.; Vroege, G. Isotropic-nematic phase behavior of length-polydisperse hard rods. J. Chem. Phys. 2003, 119, 6868–6882. [Google Scholar] [CrossRef]
- Speranza, A.; Sollich, P. Isotropic-nematic phase equilibria in the Onsager theory of hard rods with length polydispersity. Phys. Rev. E 2003, 67, 061702. [Google Scholar] [CrossRef]
- McMullen, W.E.; Gelbart, W.M.; Ben-Shaul, A. Isotropic-nematic transition in micellized solutions. J. Chem. Phys. 1985, 82, 5616–5623. [Google Scholar] [CrossRef]
- McMullen, W.E.; Gelbart, W.M.; Ben-Shaul, A. Translational and Rotational Contributions to the Size of Micelles in Dilute Soap Solutions. J. Phys. Chem. 1984, 88, 6649–6654. [Google Scholar] [CrossRef]
- Biron, D.; Moses, E.; Borukhov, I.; Safran, S.A. Inter-filament attractions narrow the length distribution of actin filaments. Europhys. Lett. 2006, 73, 464–470. [Google Scholar] [CrossRef]
- Drogemeier, J.; Hinsen, H.; Eimer, W. Flexibility of F-Actin in Aqueous Solution: A Study on Filaments of Different Average Lengths. Macromolecules 1994, 27, 87–95. [Google Scholar] [CrossRef]
- Suzuki, A.; Maeda, T.; Ito, T. Formation of liquid crystalline phase of actin filament solutions and its dependence on filament length as studied by optical birefringence. Biophys. J. 1991, 59, 25–30. [Google Scholar] [CrossRef][Green Version]
- Brenner, S.; Parsegian, V. A physical method for deriving the electrostatic interaction between rod-like polyions at all mutual angles. Biophys. J. 1974, 14, 327–334. [Google Scholar] [CrossRef]
- van Roij, R. The isotropic and nematic liquid crystal phase of colloidal rods. Eur. J. Phys. 2005, 26, S57–S67. [Google Scholar] [CrossRef][Green Version]
- Zimm, B. Apparatus and Methods for Measurement and Interpretation of the Angular Variation of Light Scattering; Preliminary Results on Polystyrene Solutions. J. Chem. Phys. 1948, 16, 1099–1116. [Google Scholar] [CrossRef]
- Janmey, P.; Peetermans, J.; Zaner, K.; Stossel, T.; Tanaka, T. Structure and Mobility of Actin Filaments as Measured by Quasielastic Light Scattering, Viscometry, and Electron Microscopy. J. Biol. Chem. 1986, 261, 8357–8362. [Google Scholar] [CrossRef]
- Press, W.H.; Teulkolsky, S.A.; Vetterling, V.T.; Flannery, B.P. Numerical Recipes in Fortran 77: The Art of Scientific Computing, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997; Volume 1, p. 818. [Google Scholar]
- Warshavsky, V.; Marucho, M. Polar-solvation classical density-functional theory for electrolyte aqueous solutions near a wall. Phys. Rev. E 2016, 93, 042607. [Google Scholar] [CrossRef] [PubMed]
- Grosberg, A.; Khokhlov, A. Statistical Theory of Polymeric Lyotropic Liquid Crystals. Adv. Polym. Sci. 1981, 41, 55–97. [Google Scholar]
- Hunley, C.; Mohsin, M.; Marucho, M. Electrical impulse characterization along actin filaments in pathological conditions. Comput. Phys. Commun. 2022, 275, 108317. [Google Scholar] [CrossRef]
- Jin, Z.; Wu, J. Density functional theory for encapsidated polyelectrolytes: A comparison with Monte Carlo simulation. J. Chem. Phys. 2012, 137, 044905. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Yu, Y.X.; Gao, G.H. Density functional study on the structural and thermodynamic properties of aqueous DNA-electrolyte solution in the framework of cell model. J. Chem. Phys. 2008, 128, 185101. [Google Scholar] [CrossRef] [PubMed]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 5th ed.; Academic Press: Boston, MA, USA, 1994; p. 1204. [Google Scholar]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Warshavsky, V.; Marucho, M. Theory of Weakly Polydisperse Cytoskeleton Filaments. Polymers 2022, 14, 2042. https://doi.org/10.3390/polym14102042
Warshavsky V, Marucho M. Theory of Weakly Polydisperse Cytoskeleton Filaments. Polymers. 2022; 14(10):2042. https://doi.org/10.3390/polym14102042
Chicago/Turabian StyleWarshavsky, Vadim, and Marcelo Marucho. 2022. "Theory of Weakly Polydisperse Cytoskeleton Filaments" Polymers 14, no. 10: 2042. https://doi.org/10.3390/polym14102042
APA StyleWarshavsky, V., & Marucho, M. (2022). Theory of Weakly Polydisperse Cytoskeleton Filaments. Polymers, 14(10), 2042. https://doi.org/10.3390/polym14102042






