Mikto-Arm Stars as Soft-Patchy Particles: From Building Blocks to Mesoscopic Structures
Abstract
1. Introduction
2. Models and Methods
- 1.
- 2.
- The space around the stars was filled with randomly oriented PB chains; due to the random orientation and random placement of the chains and the stars, there were voids between the molecules, and the density was much lower than the one of a fully equilibrated system. The fraction of the chains added in this step varied depending on the system; it was around 1/2 of the overall mass of the matrix for the s2/PB system and 1/4 for the s8/PB system.
- 3.
- A very short NPT simulation of around 50 ps was performed to slightly orient the PB chains and make space for the insertion of more chains of the matrix. The velocity-rescale algorithm was used to maintain the temperature at 600 K and the Berendsen barostat to keep the pressure at 1 atm. The time step was 0.1 fs. Due to the chosen high temperature and incompressibility of the PB matrix, the small voids got progressively filled by the quickly rearranging PB matrix and the barostat did not lead to any abrupt deformation of the system. In multiple iterations, we inserted the given number of chains, i.e., the number which corresponds to the star weight fraction of 15%. Notice that at this stage the system still contained heterogeneities in density (i.e., small voids between randomly placed items).
- 4.
- To reduce heterogeneities in density in the blend of stars and linear chains, we run a longer run (few nanoseconds) with the same settings as in step 3 until the box size fluctuated around an average value. Note that, in principle, it is possible to insert randomly the required number of chains at once in the step 1 and 2 above (i.e., to skip the step 3), if the box size is enlarged to fit all molecules; however, such initial configuration leads to numerical instabilities, as the differences in density in different parts of the box are huge, which causes a malfunction of the barostat.
- 5.
- Once the box size fluctuated around an average value, we changed the time step to 1 fs and continue the equilibration for another 20 ns.
- 6.
- We performed a run of 40 ns using Langevin dynamics at 500 K. The random component of the Langevin thermostat helps overcome possible barriers related to the rearrangement of the system components.
- 7.
- A cooling run of 20 ns was performed to reduce the temperature from 500K to 400K.
- 8.
- We fixed the bonds with the LINCS algorithm [80] and performed the pre-production run. The temperature K was maintained by the Nose–Hoover thermostat and the pressure of 1 atm by the Parrinello–Rahman barostat. The length of the pre-production run varied with , from 155 to 185 ns.
3. Results
3.1. Properties of the Building Blocks: Intramolecular Analysis
3.2. Properties of the Macromolecular Assembly: Intermolecular Analysis
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PEO | poly(ethylene oxide) |
| PS | polystyrene |
| PB | polybutadiene |
References
- Zhang, Z.; Horsch, M.A.; Lamm, M.H.; Glotzer, S.C. Tethered Nano Building Blocks: Toward a Conceptual Framework for Nanoparticle Self-Assembly. Nano Lett. 2003, 3, 1341–1346. [Google Scholar] [CrossRef]
- Akcora, P.; Liu, H.; Kumar, S.; Moll, J.; Li, Y.; Benicewicz, B.; Schadler, L.; Acehan, D.; Panagiotopoulos, A.; Pryamitsyn, V.; et al. Anisotropic self-assembly of spherical polymer-grafted nanoparticles. Nat. Mater. 2009, 8, 354–359. [Google Scholar] [CrossRef] [PubMed]
- Pryamtisyn, V.; Ganesan, V.; Panagiotopoulos, A.Z.; Liu, H.; Kumar, S.K. Modeling the anisotropic self-assembly of spherical polymer-grafted nanoparticles. J. Chem. Phys. 2009, 131, 221102. [Google Scholar] [CrossRef]
- Koerner, H.; Drummy, L.F.; Benicewicz, B.; Li, Y.; Vaia, R.A. Nonisotropic Self-Organization of Single-Component Hairy Nanoparticle Assemblies. ACS Macro Lett. 2013, 2, 670–676. [Google Scholar] [CrossRef]
- Nie, Z.; Fava, D.; Kumacheva, E.; Zou, S.; Walker, G.; Rubinstein, M. Self-assembly of metal-polymer analogues of amphiphilic triblock copolymers. Nat. Mater. 2007, 6, 609–614. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Grason, G.M.; Santangelo, C.D. Mesophases of soft-sphere aggregates. Soft Matter 2009, 5, 3629–3638. [Google Scholar] [CrossRef]
- Kietzke, T.; Neher, D.; Landfester, K.; Montenegro, R.; Güntner, R.; Scherf, U. Novel approaches to polymer blends based on polymer nanoparticles. Nat. Mater. 2003, 2, 408–412. [Google Scholar] [CrossRef]
- Abbas, S.; Lodge, T.P. Superlattice Formation in a Binary Mixture of Block Copolymer Micelles. Phys. Rev. Lett. 2006, 97, 097803. [Google Scholar] [CrossRef]
- Gröschel, A.H.; Schacher, F.H.; Schmalz, H.; Borisov, O.V.; Zhulina, E.B.; Walther, A.; Müller, A.H. Precise hierarchical self-assembly of multicompartment micelles. Nat. Commun. 2012, 3, 710. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Bluemle, M.J.; Bates, F.S. Discovery of a Frank-Kasper sigma phase in sphere-forming block copolymer melts. Science 2010, 330, 349–353. [Google Scholar] [CrossRef]
- Walther, A.; Müller, A.H.E. Janus Particles: Synthesis, Self-Assembly, Physical Properties, and Applications. Chem. Rev. 2013, 113, 5194–5261. [Google Scholar] [CrossRef]
- Liang, F.; Zhang, C.; Yang, Z. Rational Design and Synthesis of Janus Composites. Adv. Mater. 2014, 26, 6944–6949. [Google Scholar] [CrossRef]
- Deng, R.; Liu, S.; Liang, F.; Wang, K.; Zhu, J.; Yang, Z. Polymeric Janus Particles with Hierarchical Structures. Macromolecules 2014, 47, 3701–3707. [Google Scholar] [CrossRef]
- Higuchi, T.; Tajima, A.; Motoyoshi, K.; Yabu, H.; Shimomura, M. Frustrated Phases of Block Copolymers in Nanoparticles. Angew. Chem. Int. Ed. 2008, 47, 8044–8046. [Google Scholar] [CrossRef]
- Higuchi, T.; Tajima, A.; Yabu, H.; Shimomura, M. Spontaneous formation of polymer nanoparticles with inner micro-phase separation structures. Soft Matter 2008, 4, 1302–1305. [Google Scholar] [CrossRef]
- Casagrande, C.; Fabre, P.; Raphaël, E.; Veyssié, M. “Janus Beads”: Realization and Behaviour at Water/Oil Interfaces. EPL (Europhys. Lett.) 1989, 9, 251–255. [Google Scholar] [CrossRef]
- de Gennes, P.G. Soft Matter (Nobel Lecture). Angew. Chem. Int. Ed. Engl. 1992, 31, 842–845. [Google Scholar] [CrossRef]
- Glotzer, S.C.; Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 2007, 6, 557–562. [Google Scholar] [CrossRef]
- Zhang, Z.; Glotzer, S.C. Self-Assembly of Patchy Particles. Nano Lett. 2004, 4, 1407–1413. [Google Scholar] [CrossRef]
- Liddell, C.; Summers, C.; Gokhale, A. Stereological estimation of the morphology distribution of ZnS clusters for photonic crystal applications. Mater. Charact. 2003, 50, 69–79. [Google Scholar] [CrossRef]
- Gangwal, S.; Pawar, A.; Kretzschmar, I.; Velev, O.D. Programmed assembly of metallodielectric patchy particles in external AC electric fields. Soft Matter 2010, 6, 1413–1418. [Google Scholar] [CrossRef]
- Coluzza, I.; van Oostrum, P.D.; Capone, B.; Reimhult, E.; Dellago, C. Sequence controlled self-knotting colloidal patchy polymers. Phys. Rev. Lett. 2013, 110, 075501. [Google Scholar] [CrossRef]
- Champion, J.A.; Katare, Y.K.; Mitragotri, S. Making polymeric micro-and nanoparticles of complex shapes. Proc. Natl. Acad. Sci. USA 2007, 104, 11901–11904. [Google Scholar] [CrossRef]
- Langer, R.; Tirrell, D.A. Designing materials for biology and medicine. Nature 2004, 428, 487–492. [Google Scholar] [CrossRef]
- Grätzel, M. Photoelectrochemical cells. Nature 2001, 414, 338–344. [Google Scholar] [CrossRef]
- Pawar, A.B.; Kretzschmar, I. Multifunctional patchy particles by glancing angle deposition. Langmuir 2009, 25, 9057–9063. [Google Scholar] [CrossRef]
- Yake, A.M.; Snyder, C.E.; Velegol, D. Site-specific functionalization on individual colloids: Size control, stability, and multilayers. Langmuir 2007, 23, 9069–9075. [Google Scholar] [CrossRef]
- Cho, Y.S.; Yi, G.R.; Lim, J.M.; Kim, S.H.; Manoharan, V.N.; Pine, D.J.; Yang, S.M. Self-organization of bidisperse colloids in water droplets. J. Am. Chem. Soc. 2005, 127, 15968–15975. [Google Scholar] [CrossRef]
- Snyder, C.E.; Yake, A.M.; Feick, J.D.; Velegol, D. Nanoscale functionalization and site-specific assembly of colloids by particle lithography. Langmuir 2005, 21, 4813–4815. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, D.; Möhwald, H. Decoration of microspheres with gold nanodots—Giving colloidal spheres valences. Angew. Chem. 2005, 117, 7945–7948. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, D.; Möhwald, H. Patterning microsphere surfaces by templating colloidal crystals. Nano Lett. 2005, 5, 143–146. [Google Scholar] [CrossRef] [PubMed]
- Manoharan, V.N.; Elsesser, M.T.; Pine, D.J. Dense packing and symmetry in small clusters of microspheres. Science 2003, 301, 483–487. [Google Scholar] [CrossRef]
- Pawar, A.B.; Kretzschmar, I. Patchy particles by glancing angle deposition. Langmuir 2008, 24, 355–358. [Google Scholar] [CrossRef]
- Pawar, A.B.; Kretzschmar, I. Fabrication, assembly, and application of patchy particles. Macromol. Rapid Commun. 2010, 31, 150–168. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Y.; Breed, D.R.; Manoharan, V.N.; Feng, L.; Hollingsworth, A.D.; Weck, M.; Pine, D.J. Colloids with valence and specific directional bonding. Nature 2012, 491, 51–55. [Google Scholar] [CrossRef]
- Ito, T.; Okazaki, S. Pushing the limits of lithography. Nature 2000, 406, 1027–1031. [Google Scholar] [CrossRef]
- Glotzer, S.C.; Solomon, M.J.; Kotov, N.A. Self-assembly: From nanoscale to microscale colloids. AIChE J. 2004, 50, 2978–2985. [Google Scholar] [CrossRef]
- Zhou, Y.; Ma, X.; Zhang, L.; Lin, J. Directed assembly of functionalized nanoparticles with amphiphilic diblock copolymers. Phys. Chem. Chem. Phys. 2017, 19, 18757–18766. [Google Scholar] [CrossRef]
- Bianchi, E.; Capone, B.; Coluzza, I.; Rovigatti, L.; van Oostrum, P.D.J. Limiting the valence: Advancements and new perspectives on patchy colloids, soft functionalized nanoparticles and biomolecules. Phys. Chem. Chem. Phys. 2017, 19, 19847–19868. [Google Scholar] [CrossRef]
- Kim, A.; Yao, L.; Kalutantirige, F.; Zhou, S.; Chen, Q. Patchy Nanoparticle Synthesis and Self-Assembly. In Self-Assembly of Nanostructures and Patchy Nanoparticles; Mehraeen, S., Ed.; IntechOpen: Rijeka, Croatia, 2020; Chapter 4. [Google Scholar]
- Rozynek, Z.; Józefczak, A. Patchy colloidosomes—An emerging class of structures. Eur. Phys. J. Spec. Top. 2016, 225, 741–756. [Google Scholar] [CrossRef]
- Kern, N.; Frenkel, D. Fluid–fluid coexistence in colloidal systems with short-ranged strongly directional attraction. J. Chem. Phys. 2003, 118, 9882–9889. [Google Scholar] [CrossRef]
- Zhang, Z.; Keys, A.S.; Chen, T.; Glotzer, S.C. Self-assembly of patchy particles into diamond structures through molecular mimicry. Langmuir 2005, 21, 11547–11551. [Google Scholar] [CrossRef]
- Bianchi, E.; Largo, J.; Tartaglia, P.; Zaccarelli, E.; Sciortino, F. Phase diagram of patchy colloids: Towards empty liquids. Phys. Rev. Lett. 2006, 97, 168301. [Google Scholar] [CrossRef]
- Noya, E.G.; Vega, C.; Doye, J.P.; Louis, A.A. The stability of a crystal with diamond structure for patchy particles with tetrahedral symmetry. J. Chem. Phys. 2010, 132, 234511. [Google Scholar] [CrossRef]
- Bianchi, E.; Kahl, G.; Likos, C.N. Inverse patchy colloids: From microscopic description to mesoscopic coarse-graining. Soft Matter 2011, 7, 8313–8323. [Google Scholar] [CrossRef]
- Rocklin, D.Z.; Zhou, S.; Sun, K.; Mao, X. Transformable topological mechanical metamaterials. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef]
- Sun, K.; Souslov, A.; Mao, X.; Lubensky, T. Surface phonons, elastic response, and conformal invariance in twisted kagome lattices. Proc. Natl. Acad. Sci. USA 2012, 109, 12369–12374. [Google Scholar] [CrossRef]
- Kraft, D.J.; Hilhorst, J.; Heinen, M.A.; Hoogenraad, M.J.; Luigjes, B.; Kegel, W.K. Patchy polymer colloids with tunable anisotropy dimensions. J. Phys. Chem. B 2011, 115, 7175–7181. [Google Scholar] [CrossRef] [PubMed]
- van Oostrum, P.L.; Hejazifar, M.; Niedermayer, C.; Reimhult, E. Simple method for the synthesis of inverse patchy colloids. J. Phys. Condens. Matter 2015, 27, 234105. [Google Scholar] [CrossRef]
- Rovigatti, L.; Russo, J.; Romano, F. How to simulate patchy particles. Eur. Phys. J. E 2018, 41, 59. [Google Scholar] [CrossRef]
- Li, Z.W.; Sun, Z.Y.; Lu, Z.Y. Simulation Models of Soft Janus and Patchy Particles. In Self-Assembling Systems; John Wiley & Sons, Ltd.: Chichester, UK, 2016; Chapter 5; pp. 109–133. [Google Scholar]
- Sciortino, F.; Giacometti, A.; Pastore, G. Phase diagram of janus particles. Phys. Rev. Lett. 2009, 103, 237801. [Google Scholar] [CrossRef] [PubMed]
- Giacometti, A.; Lado, F.; Largo, J.; Pastore, G.; Sciortino, F. Phase diagram and structural properties of a simple model for one-patch particles. J. Chem. Phys. 2009, 131, 174114. [Google Scholar] [CrossRef]
- Sciortino, F.; Giacometti, A.; Pastore, G. A numerical study of one-patch colloidal particles: From square-well to Janus. Phys. Chem. Chem. Phys. 2010, 12, 11869–11877. [Google Scholar] [CrossRef] [PubMed]
- Yan, L.T.; Popp, N.; Ghosh, S.K.; Boker, A. Self-assembly of Janus nanoparticles in diblock copolymers. ACS Nano 2010, 4, 913–920. [Google Scholar] [CrossRef]
- Nguyen, T.D.; Phillips, C.L.; Anderson, J.A.; Glotzer, S.C. Rigid body constraints realized in massively-parallel molecular dynamics on graphics processing units. Comput. Phys. Commun. 2011, 182, 2307–2313. [Google Scholar] [CrossRef]
- Capone, B.; Coluzza, I.; LoVerso, F.; Likos, C.N.; Blaak, R. Telechelic star polymers as self-assembling units from the molecular to the macroscopic scale. Phys. Rev. Lett. 2012, 109, 238301. [Google Scholar] [CrossRef] [PubMed]
- Capone, B.; Coluzza, I.; Blaak, R.; Verso, F.L.; Likos, C.N. Hierarchical self-assembly of telechelic star polymers: From soft patchy particles to gels and diamond crystals. New J. Phys. 2013, 15, 095002. [Google Scholar] [CrossRef]
- Bianchi, E.; Capone, B.; Kahl, G.; Likos, C.N. Soft-patchy nanoparticles: Modeling and self-organization. Faraday Discuss. 2015, 181, 123–138. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Moghimi, E.; Chubak, I.; Founta, D.; Ntetsikas, K.; Polymeropoulos, G.; Hadjichristidis, N.; Likos, C.N.; Vlassopoulos, D. The influence of arm composition on the self-assembly of low-functionality telechelic star polymers in dilute solutions. Colloid Polym. Sci. 2021, 299, 497–507. [Google Scholar] [CrossRef]
- Jaramillo-Cano, D.; Camargo, M.; Likos, C.N.; Gârlea, I.C. Dynamical Properties of Concentrated Suspensions of Block Copolymer Stars in Shear Flow. Macromolecules 2020, 53, 10015–10027. [Google Scholar] [CrossRef] [PubMed]
- Gârlea, I.C.; Jaramillo-Cano, D.; Likos, C.N. Self-organization of gel networks formed by block copolymer stars. Soft Matter 2019, 15, 3527–3540. [Google Scholar] [CrossRef] [PubMed]
- Jaramillo-Cano, D.; Formanek, M.; Likos, C.N.; Camargo, M. Star block-copolymers in shear flow. J. Phys. Chem. B 2018, 122, 4149–4158. [Google Scholar] [CrossRef] [PubMed]
- Gârlea, I.C.; Bianchi, E.; Capone, B.; Rovigatti, L.; Likos, C.N. Hierarchical self-organization of soft patchy nanoparticles into morphologically diverse aggregates. Curr. Opin. Colloid Interface Sci. 2017, 30, 1–7. [Google Scholar] [CrossRef]
- Bianchi, E.; van Oostrum, P.D.; Likos, C.N.; Kahl, G. Inverse patchy colloids: Synthesis, modeling and self-organization. Curr. Opin. Colloid Interface Sci. 2017, 30, 8–15. [Google Scholar] [CrossRef]
- Bačová, P.; Glynos, E.; Anastasiadis, S.H.; Harmandaris, V. Nanostructuring Single-Molecule Polymeric Nanoparticles via Macromolecular Architecture. ACS Nano 2019, 13, 2439–2449. [Google Scholar] [CrossRef]
- Bačová, P.; Glynos, E.; Anastasiadis, S.H.; Harmandaris, V. Spatio-temporal heterogeneities in nanosegregated single-molecule polymeric nanoparticles. Soft Matter 2020, 16, 4584–4590. [Google Scholar] [CrossRef]
- Bačová, P.; Foskinis, R.; Glynos, E.; Rissanou, A.N.; Anastasiadis, S.H.; Harmandaris, V. Effect of macromolecular architecture on the self-assembly behavior of copolymers in a selective polymer host. Soft Matter 2018, 14, 9562–9570. [Google Scholar] [CrossRef]
- Bačová, P.; Glynos, E.; Anastasiadis, S.H.; Harmandaris, V. How does the number of arms affect the properties of mikto-arm stars in a selective oligomeric matrix? Insights from atomistic simulations. ACS Omega 2021, 6, 1138–1148. [Google Scholar] [CrossRef]
- Bicerano, J. Glass Transition. In Encyclopedia of Polymer Science and Technology; American Cancer Society: Atlanta, GA, USA, 2001. [Google Scholar]
- Glynos, E.; Papoutsakis, L.; Pan, W.; Giannelis, E.P.; Nega, A.D.; Mygiakis, E.; Sakellariou, G.; Anastasiadis, S.H. Nanostructured Polymer Particles as Additives for High Conductivity, High Modulus Solid Polymer Electrolytes. Macromolecules 2017, 50, 4699–4706. [Google Scholar] [CrossRef]
- Han, C.D.; Chun, S.B.; Hahn, S.F.; Harper, S.Q.; Savickas, P.J.; Meunier, D.M.; Li, L.; Yalcin, T. Phase Behavior of Polystyrene/Polybutadiene and Polystyrene/Hydrogenated Polybutadiene Mixtures: Effect of the Microstructure of Polybutadiene. Macromolecules 1998, 31, 394–402. [Google Scholar] [CrossRef]
- Voutsas, E.C.; Pappa, G.D.; Boukouvalas, C.J.; Magoulas, K.; Tassios, D.P. Miscibility in Binary Polymer Blends: Correlation and Prediction. Ind. Eng. Chem. Res. 2004, 43, 1312–1321. [Google Scholar] [CrossRef]
- Roe, R.J.; Zin, W.C. Determination of the Polymer-Polymer Interaction Parameter for the Polystyrene-Polybutadiene Pair. Macromolecules 1980, 13, 1221–1228. [Google Scholar] [CrossRef]
- Gkolfi, E.; Bačová, P.; Harmandaris, V. Size and Shape Characteristics of Polystyrene and Poly(ethylene oxide) Star Polymer Melts Studied by Atomistic Simulations. Macromol. Theory Simul. 2021, 30, 2000067. [Google Scholar] [CrossRef]
- Bačová, P.; Gkolfi, E.; Hawke, L.G.D.; Harmandaris, V. Dynamical heterogeneities in non-entangled polystyrene and poly(ethylene oxide) star melts. Phys. Fluids 2020, 32, 127117. [Google Scholar] [CrossRef]
- Chen, H.L.; Wu, J.C.; Lin, T.L.; Lin, J.S. Crystallization Kinetics in Microphase-Separated Poly(ethylene oxide)-block-poly(1,4-butadiene). Macromolecules 2001, 34, 6936–6944. [Google Scholar] [CrossRef]
- Yilmaz, E.; Yilmaz, O.; Caner, H. Miscibility studies on polystyrene/poly(ethylene oxide) and polybutadiene-graft-polystyrene/poly(ethylene oxide) blends by dilute solution viscometry. Eur. Polym. J. 1996, 32, 927–933. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.C.; Fraaije, J.G.E.M. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Lingenheil, M.; Denschlag, R.; Reichold, R.; Tavan, P. The “Hot-Solvent/Cold-Solute” Problem Revisited. J. Chem. Theory Comput. 2008, 4, 1293–1306. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Humphrey, W.; Dalke, A.; Schulten, K. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 1. United-Atom Description of n-Alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Wick, C.D.; Martin, M.G.; Siepmann, J.I. Transferable Potentials for Phase Equilibria. 4. United-Atom Description of Linear and Branched Alkenes and Alkylbenzenes. J. Phys. Chem. B 2000, 104, 8008–8016. [Google Scholar] [CrossRef]
- Fischer, J.; Paschek, D.; Geiger, A.; Sadowski, G. Modeling of Aqueous Poly(oxyethylene) Solutions: 1. Atomistic Simulations. J. Phys. Chem. B 2008, 112, 2388–2398. [Google Scholar] [CrossRef]
- Kalyuzhnyi, O.; Ilnytskyi, J.M.; Holovatch, Y.; von Ferber, C. Universal shape characteristics for the mesoscopic star-shaped polymer via dissipative particle dynamics simulations. J. Phys. Condens. Matter 2018, 30, 215101. [Google Scholar] [CrossRef] [PubMed]
- Chancellor, A.J.; Seymour, B.T.; Zhao, B. Characterizing Polymer-Grafted Nanoparticles: From Basic Defining Parameters to Behavior in Solvents and Self-Assembled Structures. Anal. Chem. 2019, 91, 6391–6402. [Google Scholar] [CrossRef] [PubMed]
- Rovigatti, L.; Capone, B.; Likos, C.N. Soft self-assembled nanoparticles with temperature-dependent properties. Nanoscale 2016, 8, 3288–3295. [Google Scholar] [CrossRef] [PubMed]
- Asai, M.; Cacciuto, A.; Kumar, S.K. Quantitative analogy between polymer-grafted nanoparticles and patchy particles. Soft Matter 2015, 11, 793–797. [Google Scholar] [CrossRef]
- Bozorgui, B.; Meng, D.; Kumar, S.K.; Chakravarty, C.; Cacciuto, A. Fluctuation-Driven Anisotropic Assembly in Nanoscale Systems. Nano Lett. 2013, 13, 2732–2737. [Google Scholar] [CrossRef] [PubMed]
- Eisenhaber, F.; Lijnzaad, P.; Argos, P.; Sander, C.; Scharf, M. The double cubic lattice method: Efficient approaches to numerical integration of surface area and volume and to dot surface contouring of molecular assemblies. J. Comput. Chem. 1995, 16, 273–284. [Google Scholar] [CrossRef]
- Li, D.; Sheng, X.; Zhao, B. Environmentally Responsive “Hairy” Nanoparticles: Mixed Homopolymer Brushes on Silica Nanoparticles Synthesized by Living Radical Polymerization Techniques. J. Am. Chem. Soc. 2005, 127, 6248–6256. [Google Scholar] [CrossRef] [PubMed]
- Shibuya, Y.; Nguyen, H.V.T.; Johnson, J.A. Mikto-Brush-Arm Star Polymers via Cross-Linking of Dissimilar Bottlebrushes: Synthesis and Solution Morphologies. ACS Macro Lett. 2017, 6, 963–968. [Google Scholar] [CrossRef]
- Johnson, K.J.; Glynos, E.; Sakellariou, G.; Green, P. Dynamics of Star-Shaped Polystyrene Molecules: From Arm Retraction to Cooperativity. Macromolecules 2016, 49, 5669–5676. [Google Scholar] [CrossRef]
- Asai, M.; Zhao, D.; Kumar, S.K. Accurate estimation of the polymer coverage of hairy nanoparticles. Soft Matter 2018, 14, 7906–7915. [Google Scholar] [CrossRef] [PubMed]
- Eslami, H.; Khanjari, N.; Müller-Plathe, F. Self-Assembly Mechanisms of Triblock Janus Particles. J. Chem. Theory Comput. 2019, 15, 1345–1354. [Google Scholar] [CrossRef] [PubMed]
- Mahynski, N.A.; Rovigatti, L.; Likos, C.N.; Panagiotopoulos, A.Z. Bottom-Up Colloidal Crystal Assembly with a Twist. ACS Nano 2016, 10, 5459–5467. [Google Scholar] [CrossRef] [PubMed]
- Chen, Q.; Bae, S.; Granick, S. Directed self-assembly of a colloidal kagome lattice. Nature 2011, 469, 381–384. [Google Scholar] [CrossRef]

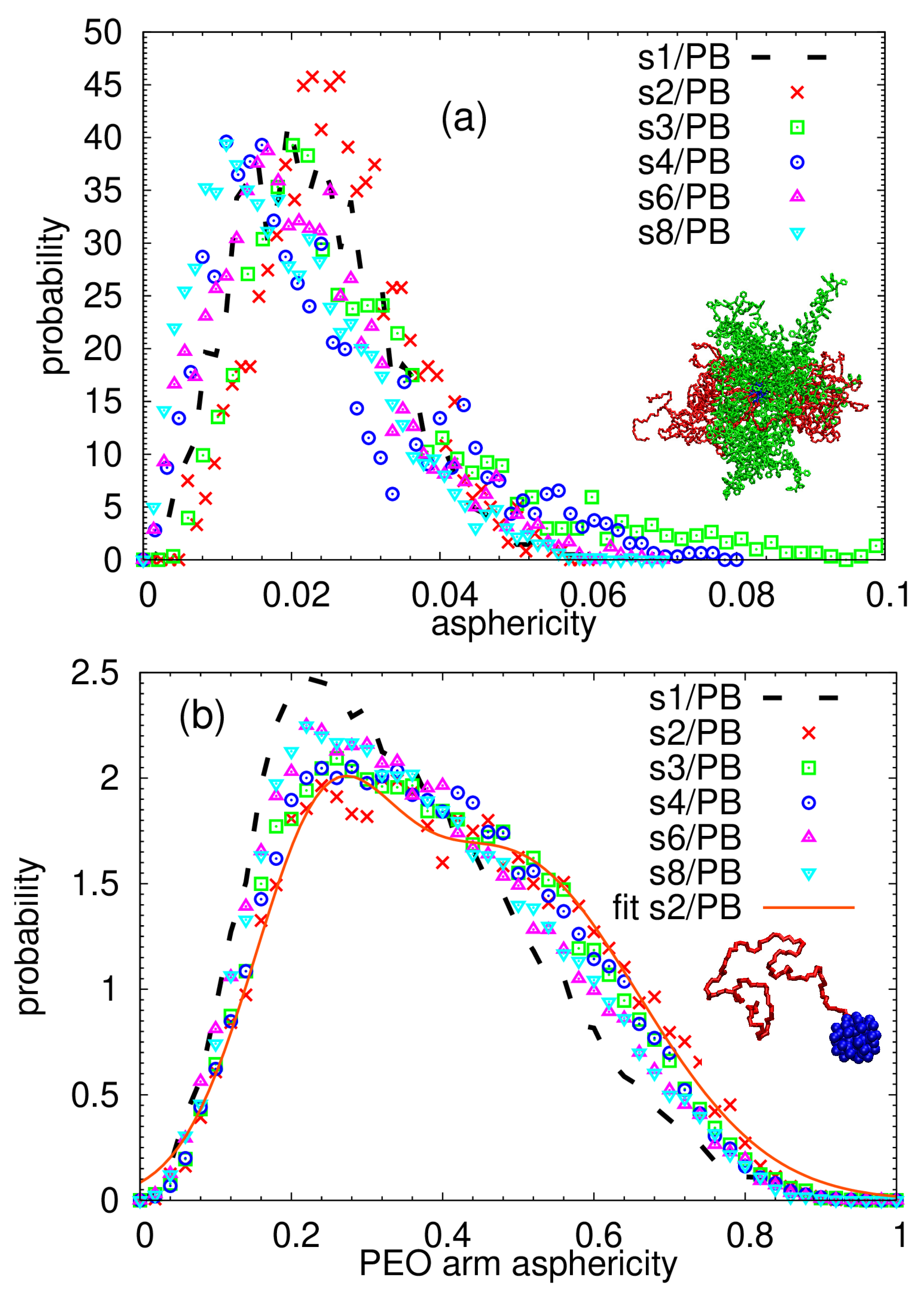
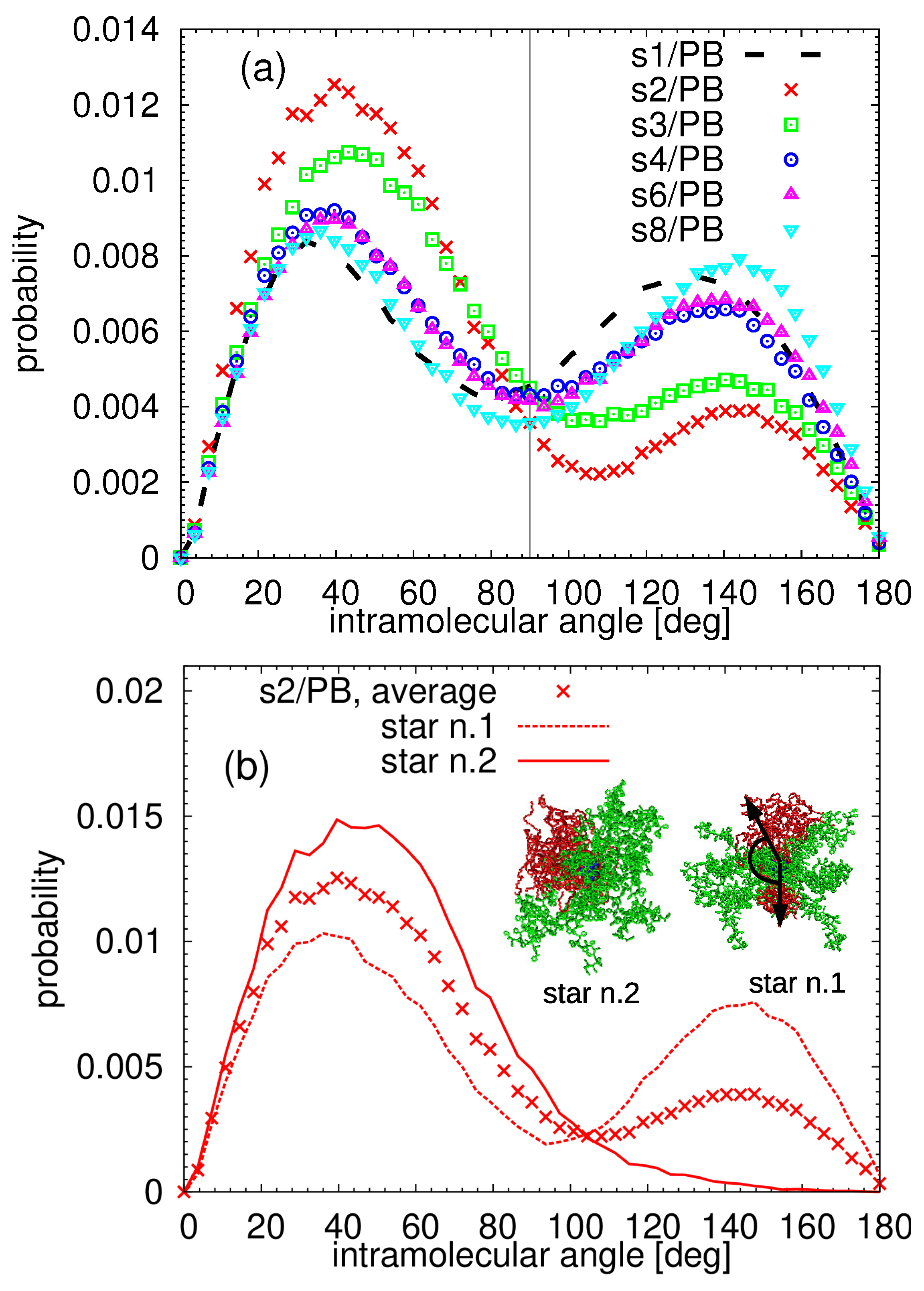
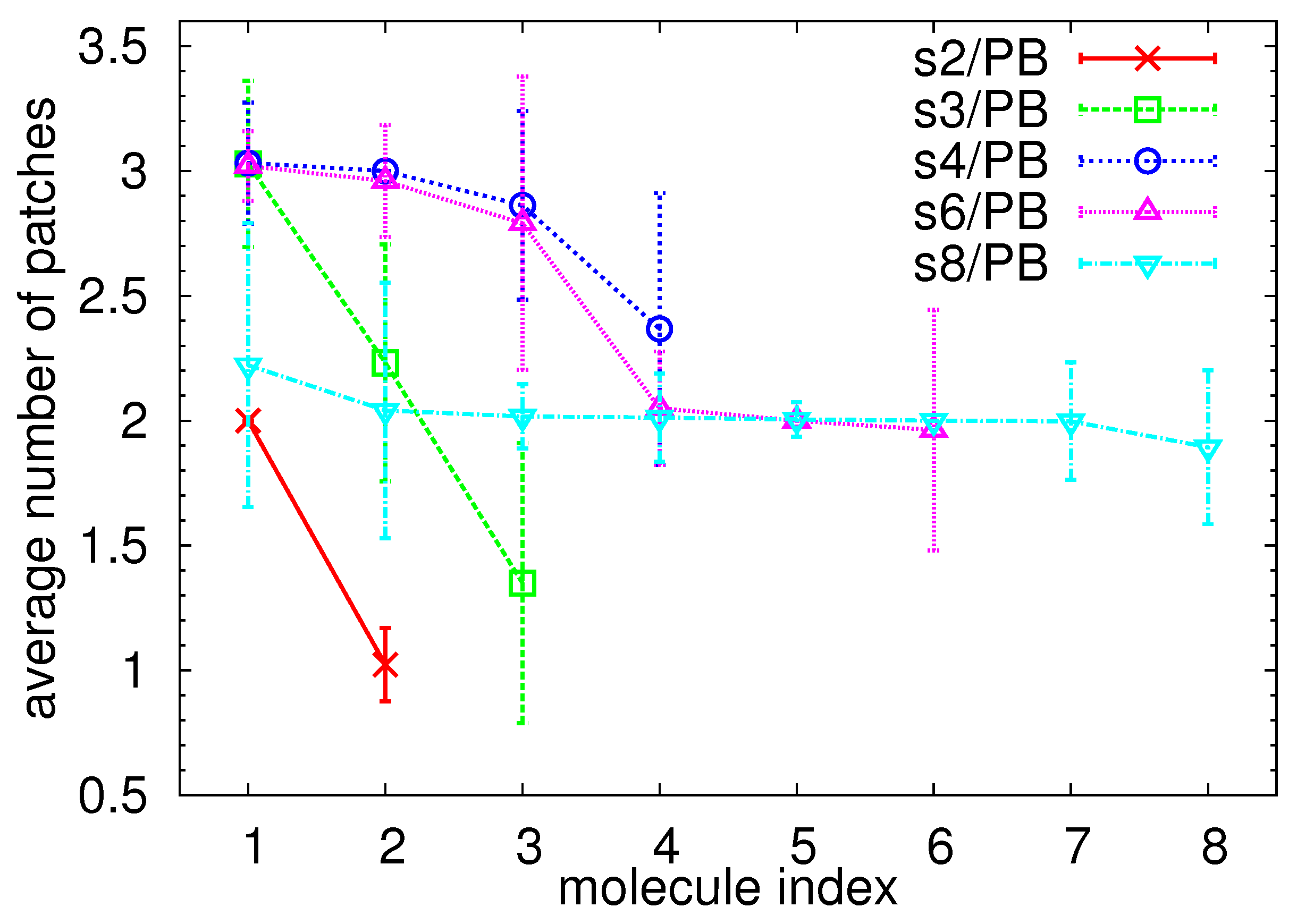

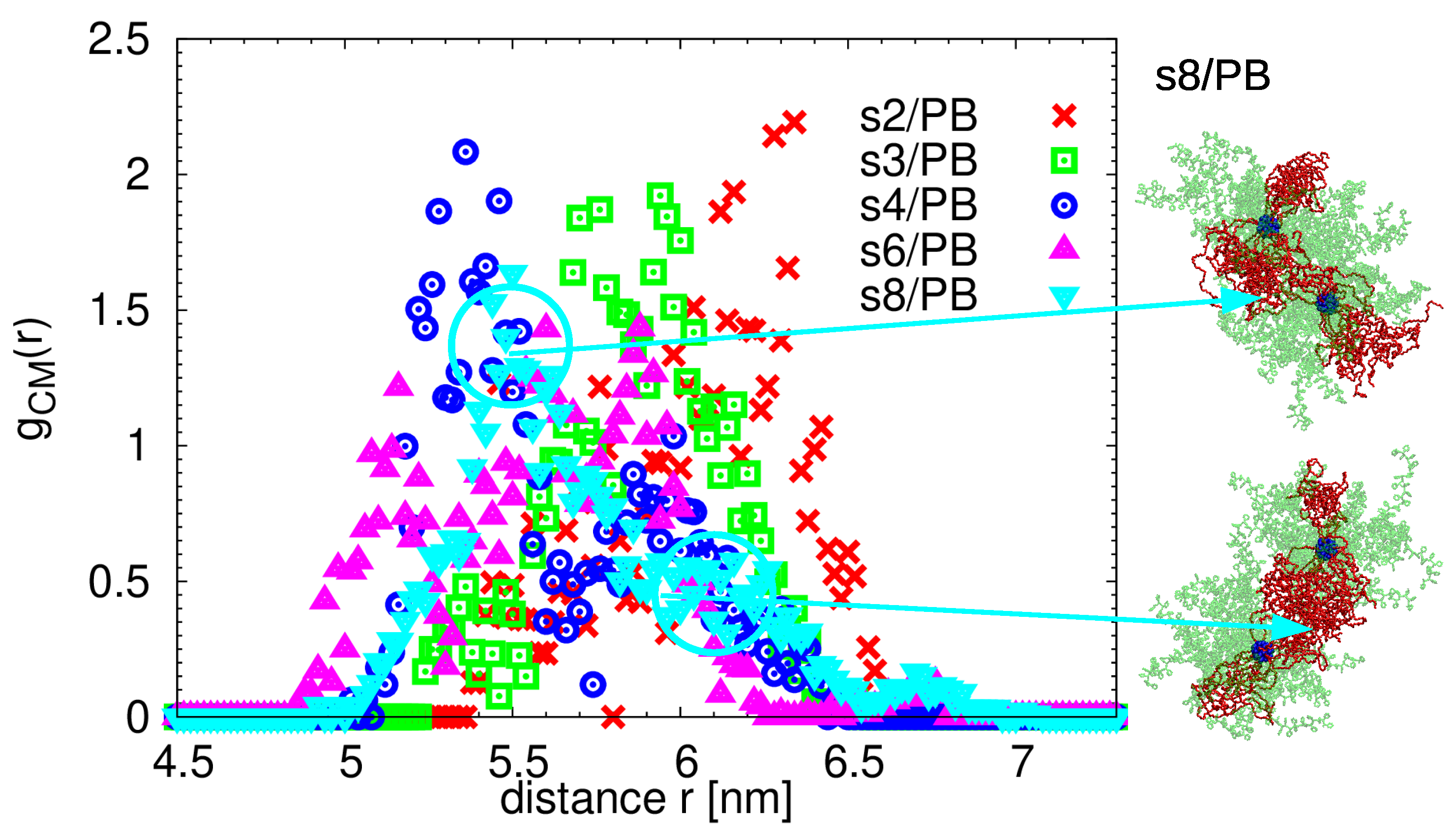
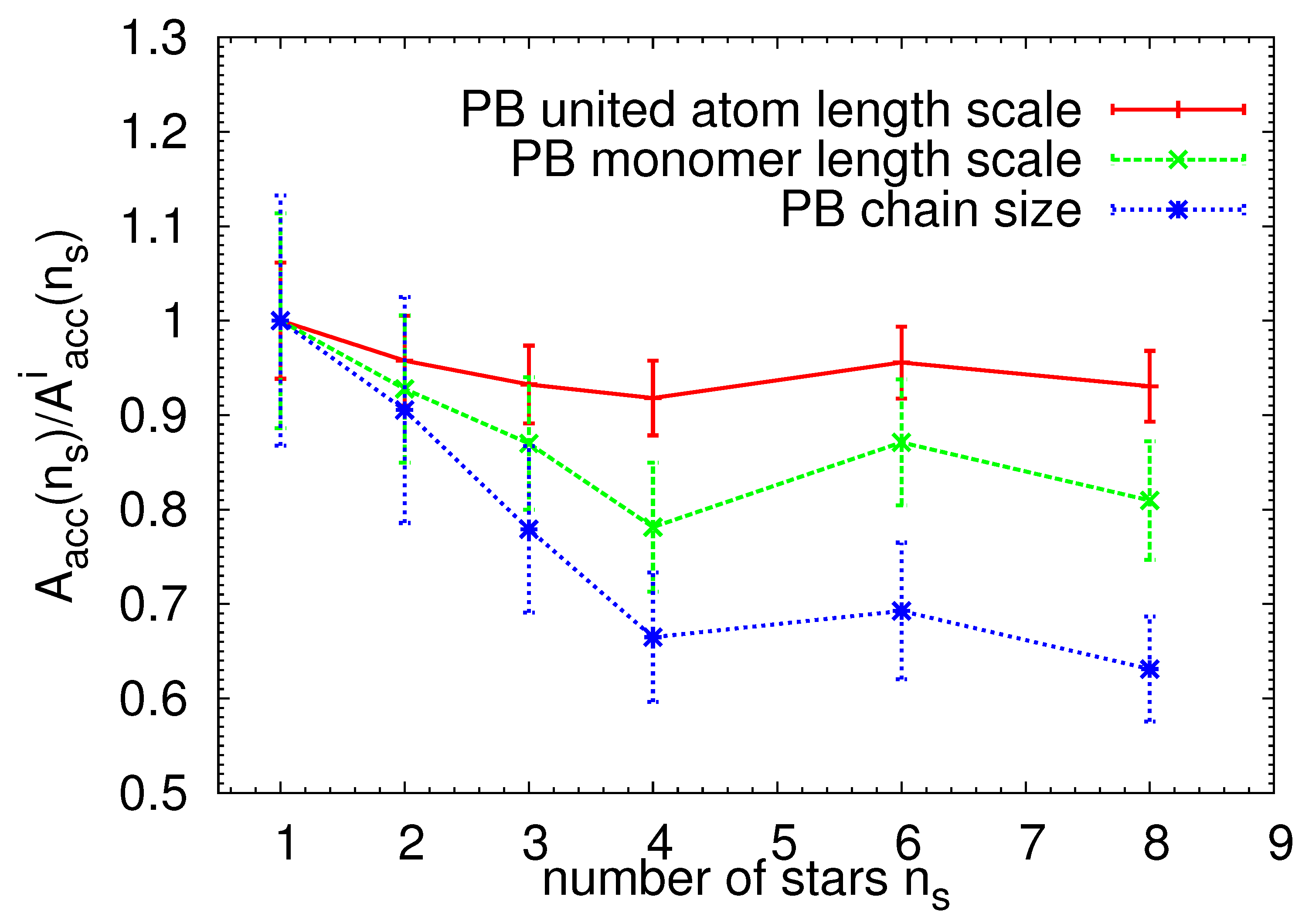
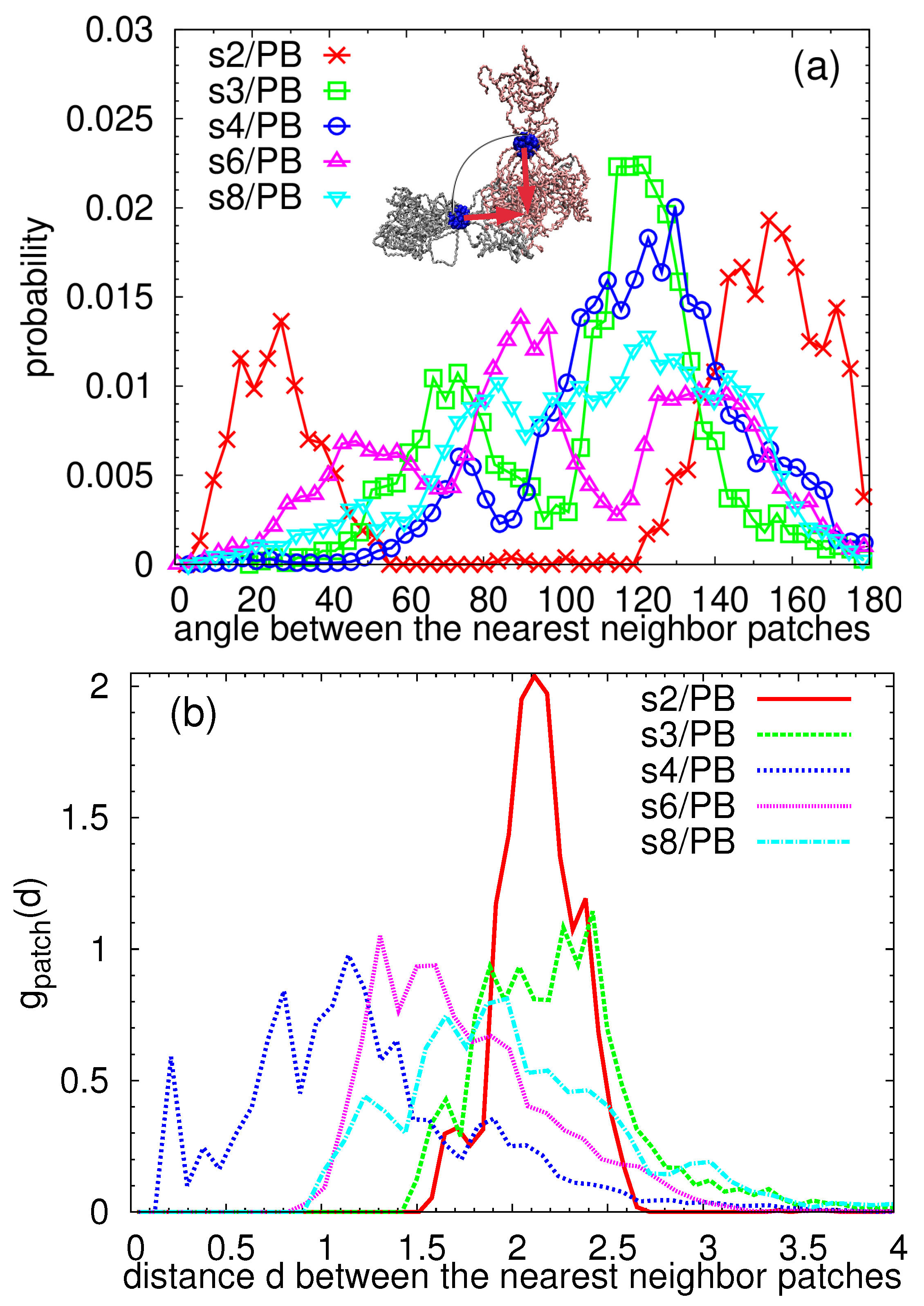

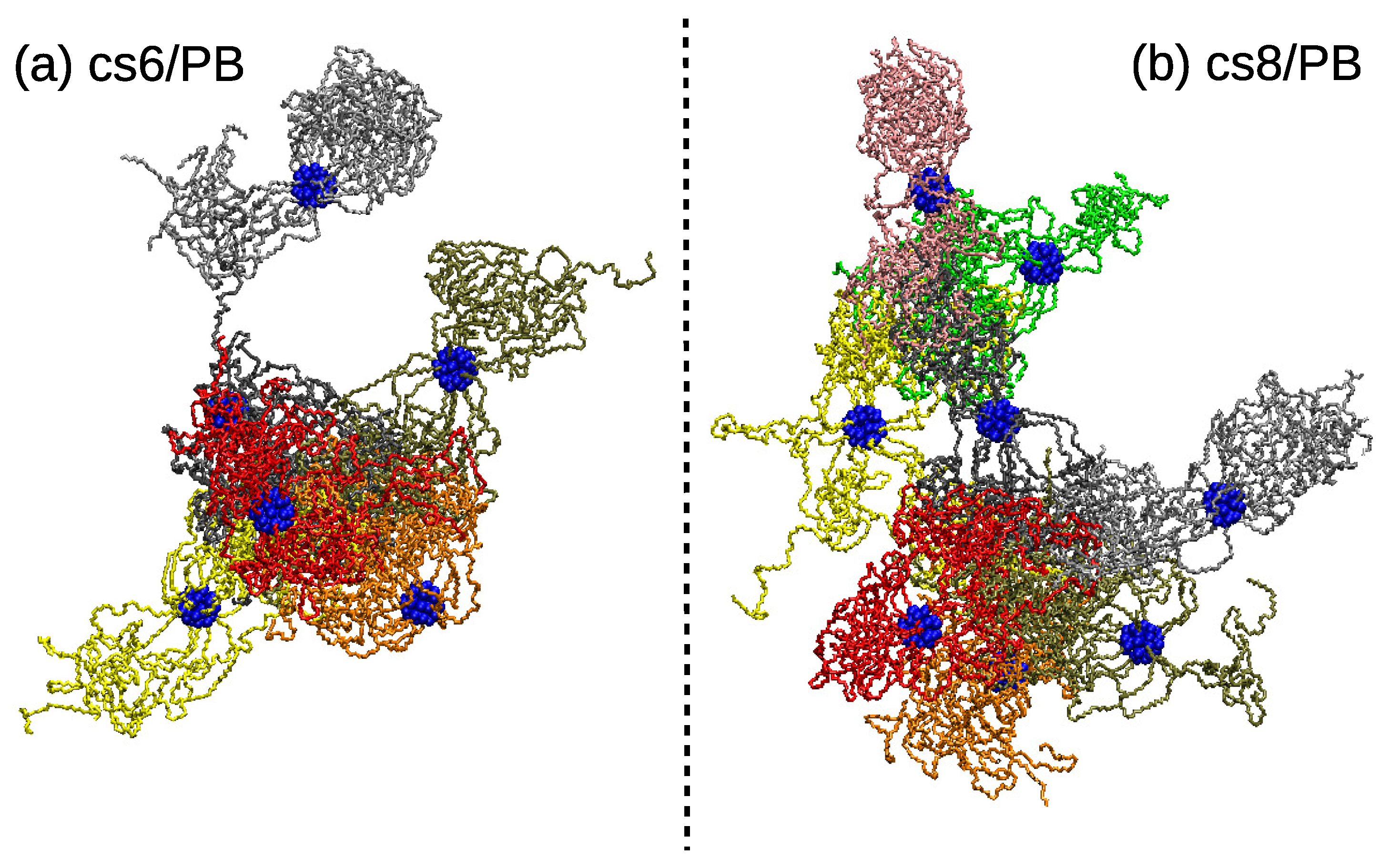
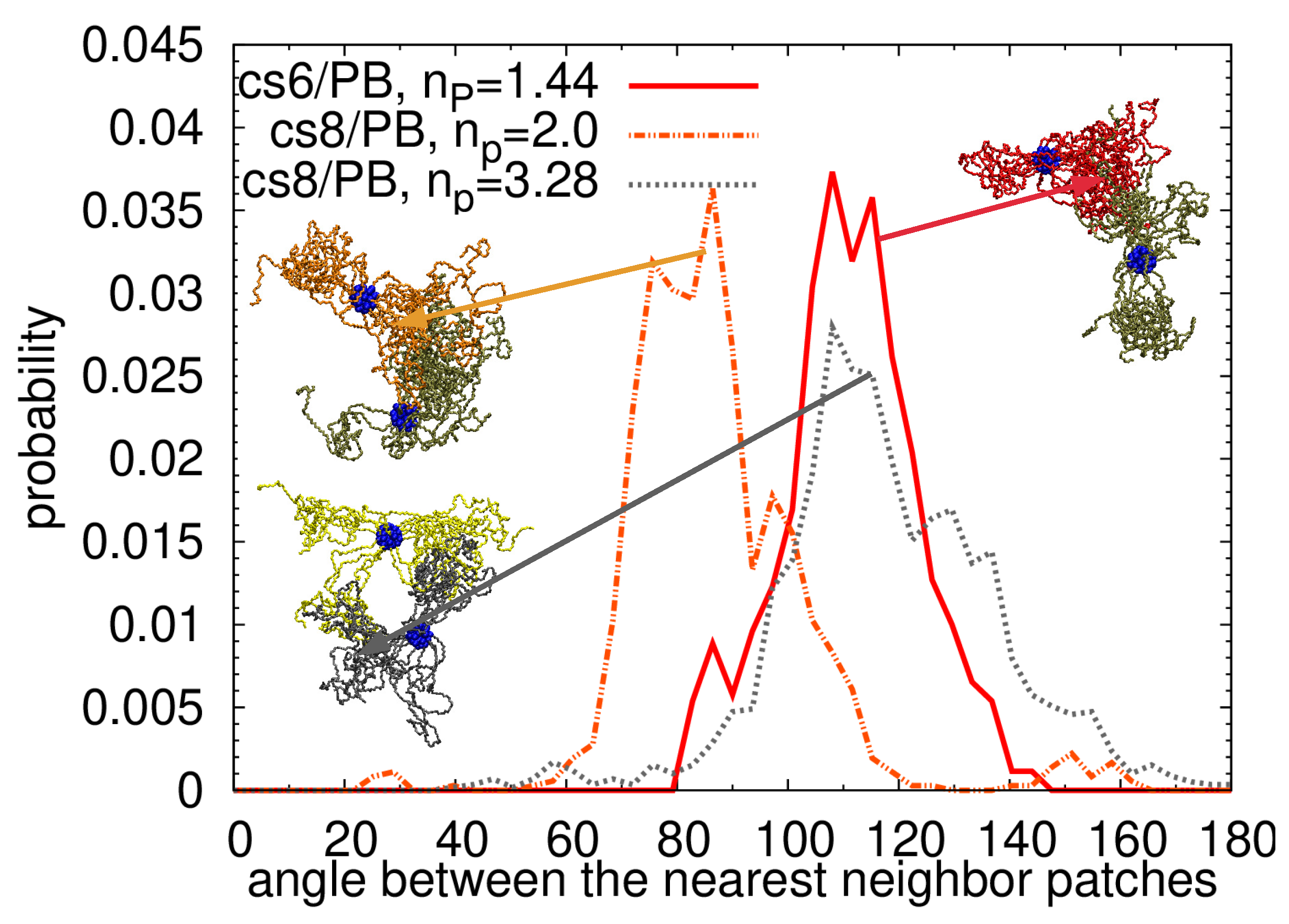
| System | [nm] | Arms | [nm] | [nm] |
|---|---|---|---|---|
| 1s/PB | 3.32 ± 0.06 | PEO | 3.97 ± 0.80 | 2.75 ± 0.11 |
| PS | 4.48 ± 1.51 | 3.50 ± 0.08 | ||
| 2s/PB | 3.37 ± 0.04 | PEO | 3.81 ± 0.67 | 2.52 ± 0.07 |
| PS | 4.98 ± 0.64 | 3.50 ± 0.06 | ||
| 3s/PB | 3.40 ± 0.04 | PEO | 3.78 ± 0.70 | 2.68 ± 0.07 |
| PS | 4.55 ± 0.48 | 3.50 ± 0.05 | ||
| 4s/PB | 3.43 ± 0.03 | PEO | 4.10 ± 0.53 | 3.00 ± 0.07 |
| PS | 4.39 ± 0.42 | 3.56 ± 0.04 | ||
| 6s/PB | 3.38 ± 0.03 | PEO | 4.07 ± 0.28 | 2.91 ± 0.04 |
| PS | 4.43 ± 0.25 | 3.52 ± 0.03 | ||
| 8s/PB | 3.42 ± 0.03 | PEO | 3.86 ± 0.32 | 2.98 ± 0.03 |
| PS | 5.03 ± 0.29 | 3.56 ± 0.03 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bačová, P.; Mintis, D.G.; Gkolfi, E.; Harmandaris, V. Mikto-Arm Stars as Soft-Patchy Particles: From Building Blocks to Mesoscopic Structures. Polymers 2021, 13, 1114. https://doi.org/10.3390/polym13071114
Bačová P, Mintis DG, Gkolfi E, Harmandaris V. Mikto-Arm Stars as Soft-Patchy Particles: From Building Blocks to Mesoscopic Structures. Polymers. 2021; 13(7):1114. https://doi.org/10.3390/polym13071114
Chicago/Turabian StyleBačová, Petra, Dimitris G. Mintis, Eirini Gkolfi, and Vagelis Harmandaris. 2021. "Mikto-Arm Stars as Soft-Patchy Particles: From Building Blocks to Mesoscopic Structures" Polymers 13, no. 7: 1114. https://doi.org/10.3390/polym13071114
APA StyleBačová, P., Mintis, D. G., Gkolfi, E., & Harmandaris, V. (2021). Mikto-Arm Stars as Soft-Patchy Particles: From Building Blocks to Mesoscopic Structures. Polymers, 13(7), 1114. https://doi.org/10.3390/polym13071114








