Creep Response of Carbon-Fiber-Reinforced Composite Using Homogenization Method
Abstract
1. Introduction
2. Homogenized Model of Carbon Fiber Composite
2.1. Macroscopic Equations
2.2. Evaluation of the Homogenized Coefficients
- If one starts from local equations, it is possible to determine the strain and stress field. By using the averages, the homogenized coefficients can be evaluated;
- One can use the variational formulation and find the function which allows computation of the homogenized coefficients.
2.3. Evaluation of Homogenized Coefficients for FRP
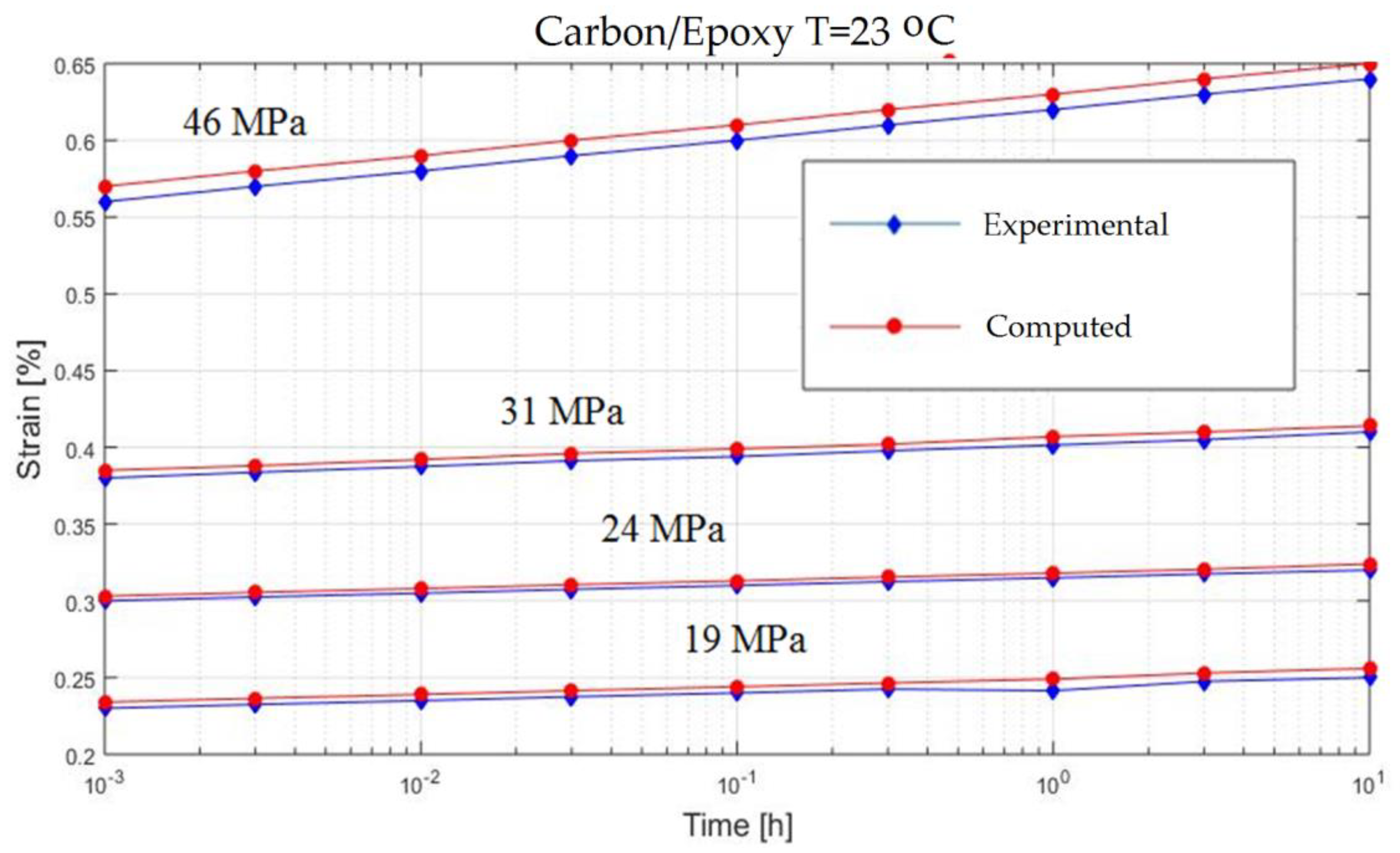
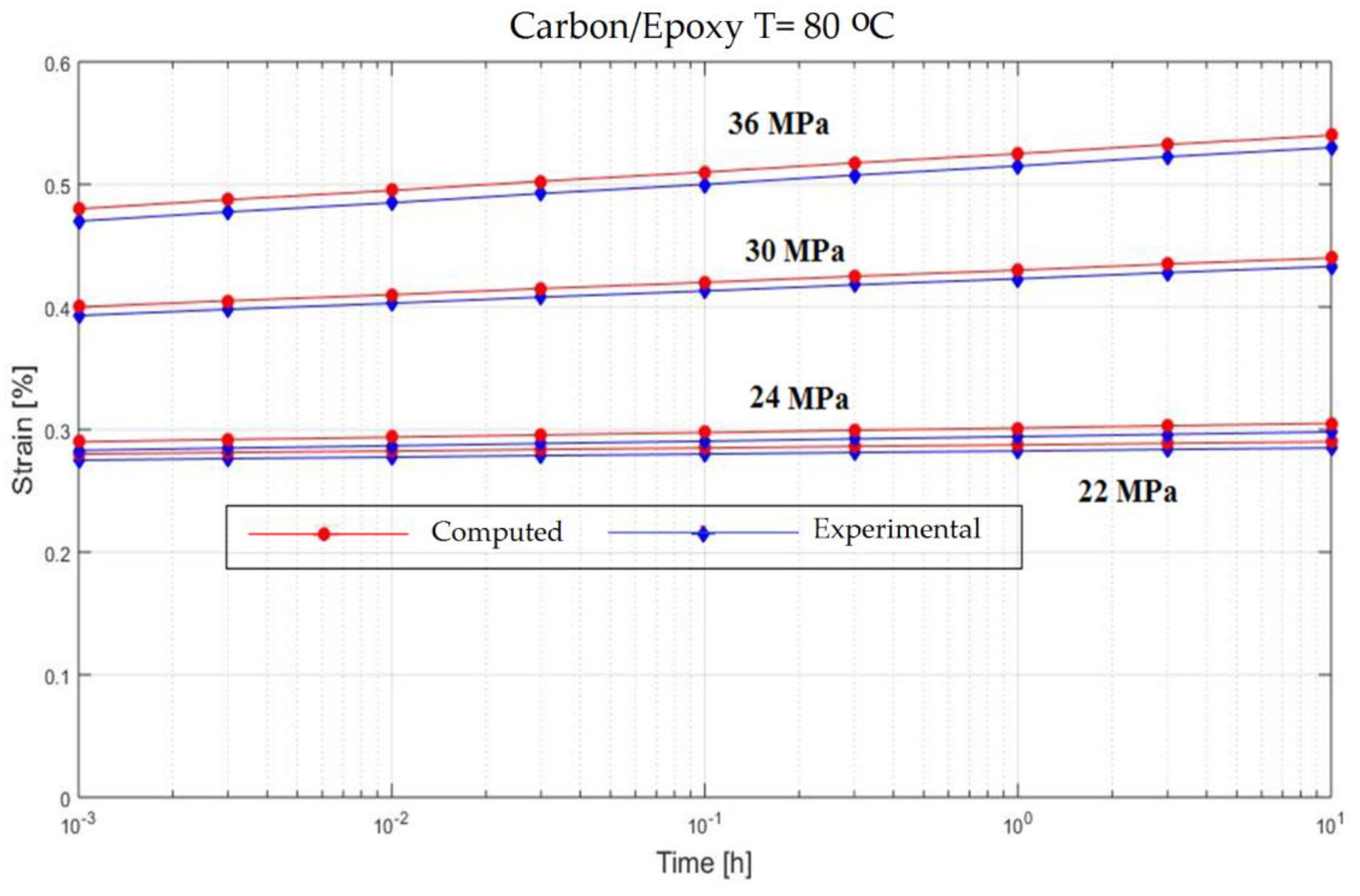
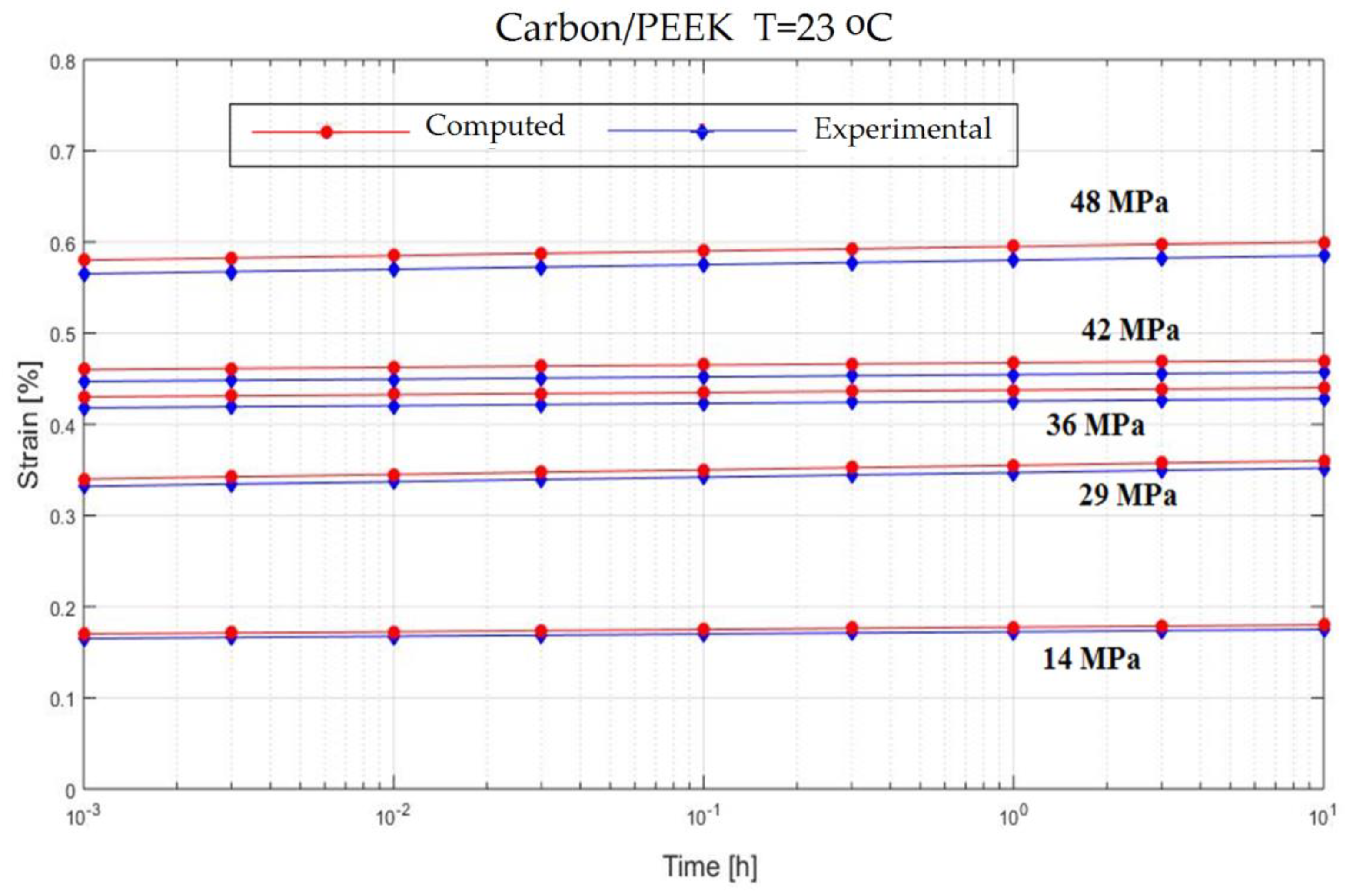
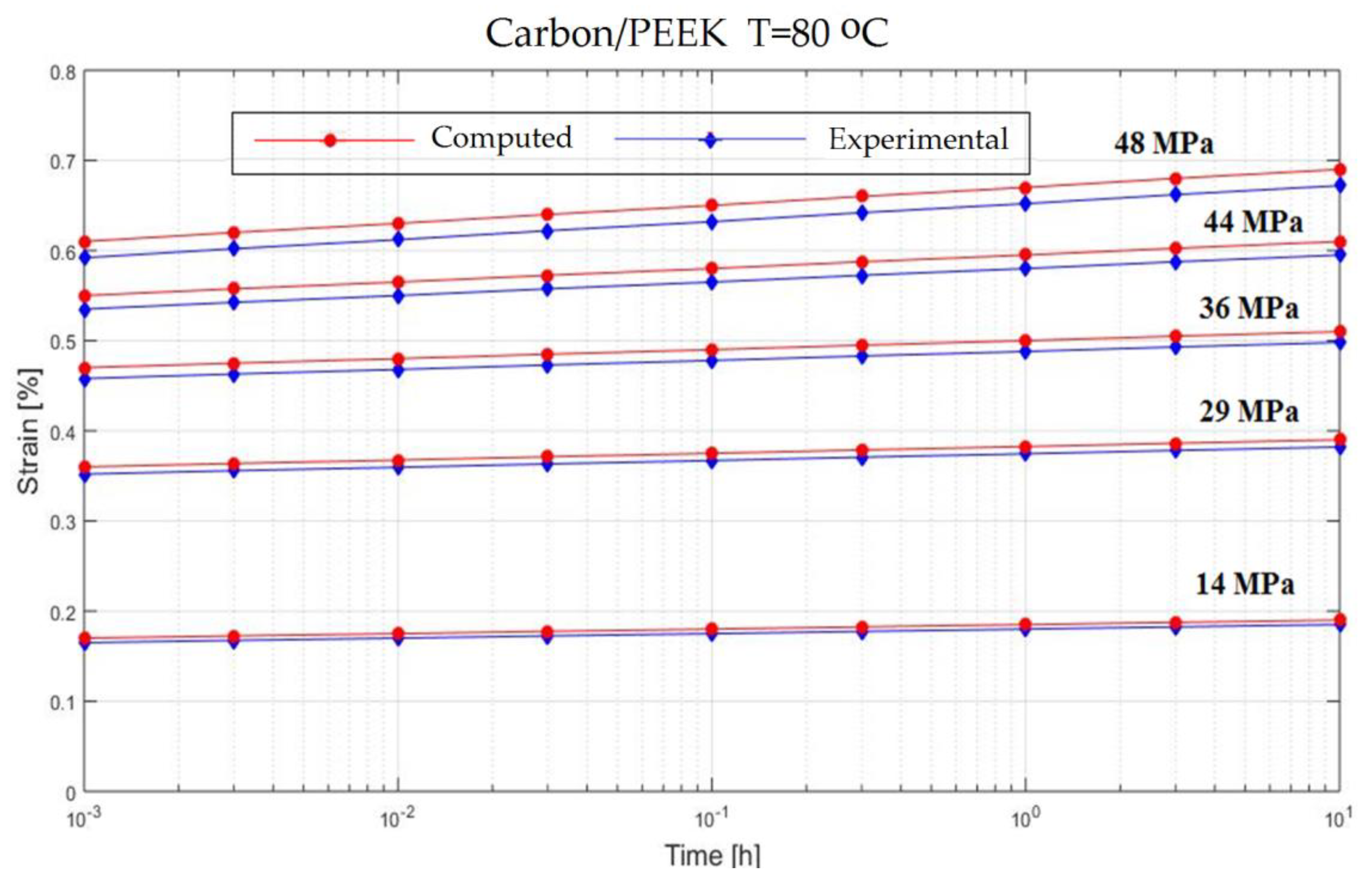
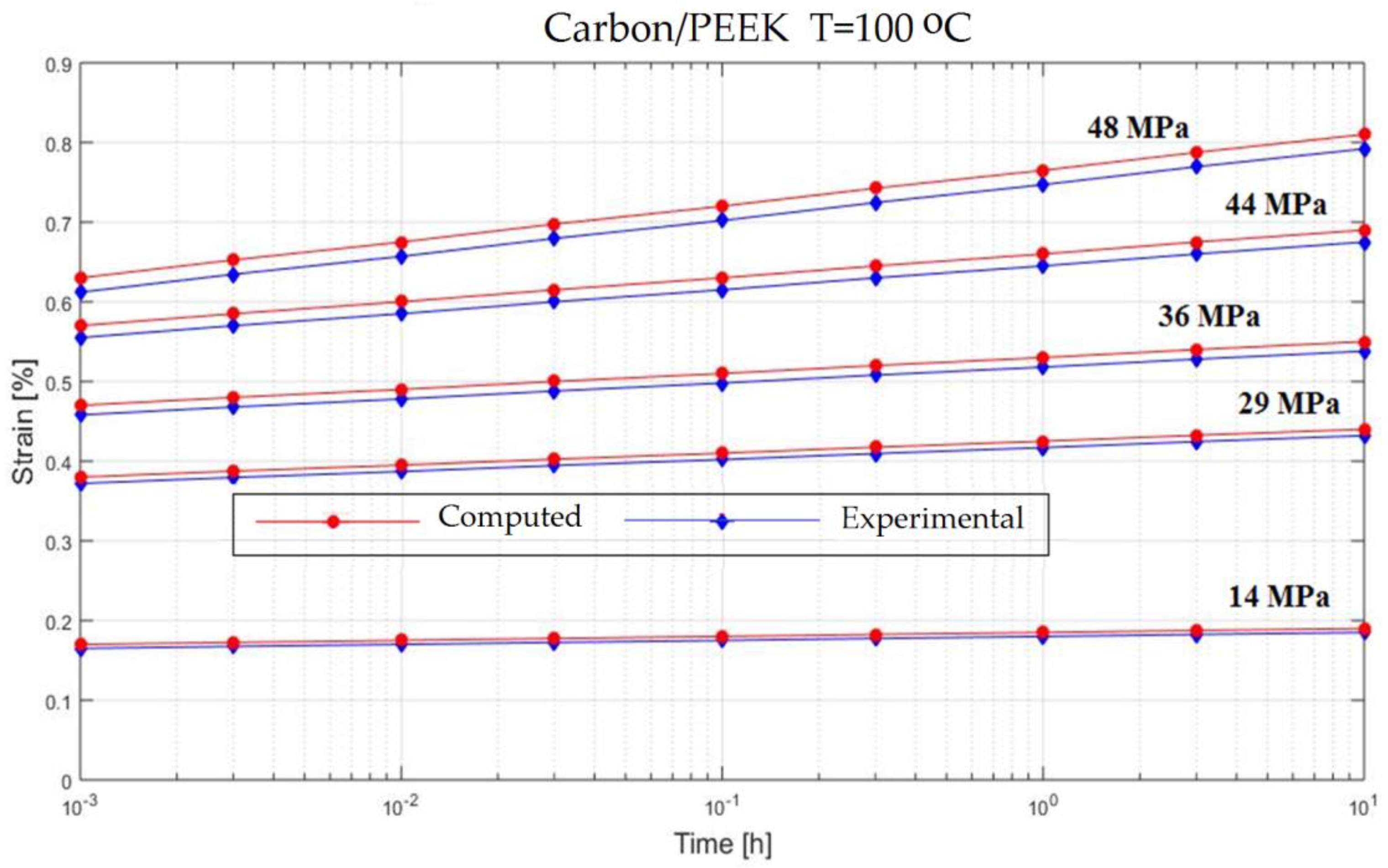
3. Experimental Creep Response of Fiber Reinforced Composite
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Cristescu, N.D.; Craciun, E.-M.; Soós, E. Mechanics of Elastic Composites; Chapman and Hall/CRC: Boca Raton, FL, USA, 2003. [Google Scholar]
- Zaoui, A. Homogenization Techniques for Composite Media; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1987; Volume 272, Chapter 4. [Google Scholar]
- Garajeu, M. Contribution à L’étude du Comportement Non Lineaire de Milieu Poreaux Avec ou Sans Renfort. Ph.D. Thesis, Aix-Marseille University, Marseille, France, 1995. [Google Scholar]
- Brauner, C.; Herrmann, A.S.; Niemeier, P.M.; Schubert, K. Analysis of the non-linear load and temperature-dependent creep behaviour of thermoplastic composite materials. J. Thermoplast. Compos. Mater. 2016, 30, 302–317. [Google Scholar] [CrossRef]
- Fett, T. Review on Creep-Behavior of Simple Structures. Res. Mech. 1988, 24, 359–375. [Google Scholar]
- Sá, M.F.; Gomes, A.; Correia, J.; Silvestre, N. Creep behavior of pultruded GFRP elements—Part 1: Literature review and experimental study. Compos. Struct. 2011, 93, 2450–2459. [Google Scholar] [CrossRef]
- Brinson, H.F.; Morris, D.H.; Yeow, Y.I. A New Method for the Accelerated Characterization of Composite Materials. In Proceeding of the Sixth International Conference on Experimental Stress Analysis, Munich, Germany, 18–22 September 1978. [Google Scholar]
- Jinsheng, X.; Hongli, W.; Xiaohong, Y.; Long, H.; Chang Sheng, Z. Application of TTSP to non-linear deformation in composite propellant. Emerg. Mater. Res. 2018, 7, 19–24. [Google Scholar] [CrossRef]
- Nakano, T. Applicability condition of time–temperature superposition principle (TTSP) to a multi-phase system. Mech. Time-Depend. Mater. 2012, 17, 439–447. [Google Scholar] [CrossRef]
- Achereiner, F.; Engelsing, K.; Bastian, M. Accelerated Measurement of the Long-Term Creep Behaviour of Plastics. Superconductivity 2017, 247, 389–402. [Google Scholar]
- Schaffer, B.G.; Adams, D.F. Nonlinear Viscoelastic Behavior of a Composite Material Using a Finite Element Micromechanical Analysis; Department Report UWME-DR-001-101-1; Department of Mechanical Engineering; University of Wyoming: Laramie, WY, USA, 1980. [Google Scholar]
- Schapery, R. Nonlinear viscoelastic solids. Int. J. Solids Struct. 2000, 37, 359–366. [Google Scholar] [CrossRef]
- Violette, M.G.; Schapery, R. Time-Dependent Compressive Strength of Unidirectional Viscoelastic Composite Materials. Mech. Time-Depend. Mater. 2002, 6, 133–145. [Google Scholar] [CrossRef]
- Mohan, R.; Adams, D.F. Nonlinear creep-recovery response of a polymer matrix and its composites. Exp. Mech. 1985, 25, 262–271. [Google Scholar] [CrossRef]
- Findley, W.N.; Adams, C.H.; Worley, W.J. The Effect of Temperature on the Creep of Two Laminated Plastics as Interpreted by the Hyperbolic Sine Law and Activation Energy Theory. In Proceedings of the American Society for Testing and Materials, Conshohocken, PA, USA, 1 January 1948; Volume 48, pp. 1217–1239. [Google Scholar]
- Findley, W.N.; Khosla, G. Application of the Superposition Principle and Theories of Mechanical Equation of State, Strain, and Time Hardening to Creep of Plastics under Changing Loads. J. Appl. Phys. 1955, 26, 821. [Google Scholar] [CrossRef]
- Dillard, D.A.; Brinson, H.F. A Nonlinear Viscoelastic Characterization of Graphite Epoxy Composites. In Proceedings of the 1982 Joint Conference on Experimental Mechanics, Oahu, HI, USA, 23–28 May 1982. [Google Scholar]
- Dillard, D.A.; Morris, D.H.; Brinson, H.F. Creep and Creep Rupture of Laminated Hraphite/Epoxy Composites. Ph.D. Thesis, Virginia Polytechnic Institute and State University, Blacksburg, VA, USA, 30 September 1980. [Google Scholar]
- Walrath, D.E. Viscoelastic response of a unidirectional composite containing two viscoelastic constituents. Exp. Mech. 1991, 31, 111–117. [Google Scholar] [CrossRef]
- Hashin, Z. On Elastic Behavior of Fibre Reinforced Materials of Arbitrary Transverse Phase Geometry. J. Mech. Phys. Solids 1965, 13, 119–134. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. On some variational principles in anisotropic and nonhomogeneous elasticity. J. Mech. Phys. Solids 1962, 10, 335–342. [Google Scholar] [CrossRef]
- Hashin, Z.; Shtrikman, S. A Variational Approach to the Theory of the Elastic Behavior of Multiphase Materials. J. Mech. Phyds. Solids 1963, 11, 127–140. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Weng, G.J. Effective Elastic Moduli of Ribbon-Reinforced Composites. J. Appl. Mech. 1990, 57, 158–167. [Google Scholar] [CrossRef]
- Hill, R. Theory of Mechanical Properties of Fiber-strengthened Materials: I Elastic Behavior. J. Mech. Phys. Solids 1964, 12, 199–212. [Google Scholar] [CrossRef]
- Hill, R. Theory of Mechanical Properties of Fiber-strengthened Materials: II Inelastic Behavior. J. Mech. Phys. Solids 1964, 12, 213–218. [Google Scholar] [CrossRef]
- Hill, R. Theory of Mechanical Properties of Fiber-strengthened Materials: III Self-Consistent Model. J. Mech. Phys. Solids 1965, 13, 189–198. [Google Scholar] [CrossRef]
- Weng, Y.M.; Wang, G.J. The Influence of Inclusion Shape on the Overall Viscoelastic Behavior of Compoisites. J. Appl. Mech. 1992, 59, 510–518. [Google Scholar] [CrossRef]
- Mori, T.; Tanaka, K. Average Stress in the Matrix and Average Elastic Energy of Materials with Misfitting Inclusions. Acta Metal. 1973, 21, 571–574. [Google Scholar] [CrossRef]
- Aboudi, J. Micromechanical characterization of the non-linear viscoelastic behavior of resin matrix composites. Compos. Sci. Technol. 1990, 38, 371–386. [Google Scholar] [CrossRef]
- Aboudi, J. Mechanics of Composite Materials—A Unified Micromechanical Approach; Elsevier: Amsterdam, The Netherlands, 1991. [Google Scholar]
- Katouzian, M.; Vlase, S. Creep Response of Neat and Carbon-Fiber-Reinforced PEEK and Epoxy Determined Using a Micromechanical Model. Symmetry 2020, 12, 1680. [Google Scholar] [CrossRef]
- Abbas, I.A.; Marin, M. Analytical solution of thermoelastic interaction in a half-space by pulsed laser heating. Phys. E Low-Dimensional Syst. Nanostruct. 2017, 87, 254–260. [Google Scholar] [CrossRef]
- Vlase, S.; Teodorescu-Draghicescu, H.; Motoc, D.L. Behavior of Multiphase Fiber-Reinforced Polymers under Short Time Cyclic Loading. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 419–423. [Google Scholar]
- Teodorescu-Draghicescu, H.; Stanciu, A.; Vlase, S.; Scutaru, L.; Calin, M.R.; Serbina, L. Finite Element Method Analysis of Some Fibre-Reinforced Composite Laminates. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 782–785. [Google Scholar]
- Stanciu, A.; Teodorescu-Drǎghicescu, H.; Vlase, S.; Scutaru, M.L.; Cǎlin, M.R. Mechanical behavior of CSM450 and RT800 laminates subjected to four-point bend tests. Optoelectron. Adv. Mater. Rapid Commun. 2012, 6, 495–497. [Google Scholar]
- Niculiţă, C.; Vlase, S.; Bencze, A.; Mihălcică, M.; Calin, M.R.; Serbina, L. Optimum stacking in a multi-ply laminate used for the skin of adaptive wings. Optoelectron. Adv. Mater. Rapid Commun. 2011, 5, 1233–1236. [Google Scholar]
- Katouzian, M.; Vlase, S.; Calin, M.R. Experimental procedures to determine the viscoelastic parameters of laminated composites. J. Optoelectron. Adv. Mater. 2011, 13, 1185–1188. [Google Scholar]
- Teodorescu-Draghicescu, H.; Vlase, S.; Stanciu, M.D.; Curtu, I.; Mihalcica, M. Advanced Pultruded Glass Fibers-Reinforced Isophtalic Polyester Resin. Mater. Plast. 2015, 52, 62–64. [Google Scholar]
- Teodorescu-Draghicescu, H.; Vlase, S.; Scutaru, L.; Serbina, L.; Calin, M.R. Hysteresis effect in a three-phase polymer matrix composite subjected to static cyclic loadings. Optoelectron. Adv. Mater Rapid Commun. 2011, 5, 273–277. [Google Scholar]
- Jain, A. Micro and mesomechanics of fibre reinforced composites using mean field homogenization formulations: A review. Mater. Today Commun. 2019, 21, 100552. [Google Scholar] [CrossRef]
- Lee, H.; Choi, C.W.; Jin, J.W. Homogenization-based multiscale analysis for equivalent mechanical properties of nonwoven carbon-fiber fabric composites. J. Mech. Sci. Technol. 2019, 33, 4761–4770. [Google Scholar] [CrossRef]
- Koley, S.; Mohite, P.M.; Upadhyay, C.S. Boundary layer effect at the edge of fibrous composites using homogenization theory. Compos. Part B Eng. 2019, 173, 106815. [Google Scholar] [CrossRef]
- Xin, H.H.; Mosallam, A.; Liu, Y.Q. Mechanical characterization of a unidirectional pultruded composite lamina using micromechanics and numerical homogenization. Construction and Building Materials 2019, 216, 101–118. [Google Scholar] [CrossRef]
- Chao, Y.; Zheng, K.G.; Ning, F.D. Mean-field homogenization of elasto-viscoplastic composites based on a new mapping-tangent linearization approach. Sci. China-Technol. Sci. 2019, 62, 736–746. [Google Scholar] [CrossRef]
- Sokołowski, D.; Kamiński, M. Computational Homogenization of Anisotropic Carbon/RubberComposites with Stochastic Interface Defects. In Carbon-BasedNanofillers and Their Rubber Nanocomposites; Elsevier: Amsterdam, The Netherlands, 2019; Chapter 11; pp. 323–353. [Google Scholar]
- Dellepiani, M.G.; Vega, C.R.; Pina, J.C. Numerical investigation on the creep response of concrete structures by means of a multi-scale strategy. Constr. Build. Mater. 2020, 263, 119867. [Google Scholar] [CrossRef]
- Choo, J.; Semnani, S.J.; White, J.A. An anisotropic viscoplasticity model for shale based on layered microstructure homogenization. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 502–520. [Google Scholar] [CrossRef]
- Cruz-Gonzalez, O.L.; Rodriguez-Ramos, R.; Otero, J.A. On the effective behavior of viscoelastic composites in three dimensions. Int. J. Eng. Sci. 2020, 157, 103377. [Google Scholar] [CrossRef]
- Katouzian, M.; Vlase, S. Mori-Tanaka Formalism-Based Method Used to Estimate the Viscoelastic Parameters of Laminated Composites. Polymers 2020, 12, 2481. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, P.P.; Zhou, Y.X. A micromechanics-based constitutive model for linear viscoelastic particle-reinforced composites. Mech. Mater. 2020, 140, 103228. [Google Scholar] [CrossRef]
- Kotha, S.; Ozturk, D.; Ghosh, S. Parametrically homogenized constitutive models (PHCMs) from micromechanical crystal plasticity FE simulations, part I: Sensitivity analysis and parameter identification for Titanium alloys. Int. J. Plast. 2019, 120, 296–319. [Google Scholar] [CrossRef]
- Gallican, V.; Brenner, R. Homogenization estimates for the effective response of fractional viscoelastic particulate composites. Contin. Mech. Thermodyn. 2019, 31, 823–840. [Google Scholar] [CrossRef]
- Bobyleva, T.; Shamaev, A. Various ways to build effective characteristics for a pipe made of a layered composite material. In Proceedings of the 22nd International Scientific Conference on Construction-The Formation of Living Environment (FORM), Tashkent, Uzbekistan, 18–21 April 2019; Volume 97, p. 02027. [Google Scholar] [CrossRef]
- Marin, M.; Vlase, S.; Paun, M. Considerations on double porosity structure for micropolar bodies. AIP Adv. 2015, 5, 037113. [Google Scholar] [CrossRef]
- Xiao, B.; Huang, Q.; Chen, H.; Chen, X.; Long, G. A fractal model for capillary flow through a single tortuous capillary with roughened surfaces in fibrous porous media. Fractals 2021, 29, 2150017. [Google Scholar] [CrossRef]
- Liang, M.; Fu, C.; Xiao, B.; Luo, L.; Wang, Z. A fractal study for the effective electrolyte diffusion through charged porous media. Int. J. Heat Mass Transfer. 2019, 137, 365–371. [Google Scholar] [CrossRef]
- Sanchez-Palencia, E. Homogenization method for the study of composite media. In Asymptotic Analysis II Lecture Notes in Mathematics; Verhulst, F., Ed.; Springer: Berlin/Heidelberg, Germany, 1983; Volume 985. [Google Scholar] [CrossRef]
- Sanchez-Palencia, E. Non-homogeneous media and vibration theory. In Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 1980. [Google Scholar] [CrossRef]
- Xu, W.; Nobutada, O. A Homogenization Theory for Time-Dependent Deformation of Composites with Periodic Internal Structures. JSME Int. J. Ser. A Solid Mech. Mater. Eng. 1998, 41, 309–317. [Google Scholar]
- Duvaut, G. Homogénéisation des plaques à structure périodique en théorie non linéaire de Von Karman. In Journées d’Analyse Non Linéaire; Lecture Notes in Mathematics; Springer: Berlin/Heidelberg, Germany, 1977; Volume 665, pp. 56–69. [Google Scholar]
- Caillerie, D. Homogénisation d’un corps élastique renforcé par des fibres minces de grande rigidité et réparties périodiquement. Compt. Rend. Acad. Sci. Paris Ser. 1981, 292, 477–480. [Google Scholar]
- Bensoussan, A.; Lions, J.L.; Papanicolaou, G. Asymptotic Analysis for Periodic Structures; American Mathematical Soc.: North-Holland, Amsterdam, The Netherlands, 1978. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katouzian, M.; Vlase, S. Creep Response of Carbon-Fiber-Reinforced Composite Using Homogenization Method. Polymers 2021, 13, 867. https://doi.org/10.3390/polym13060867
Katouzian M, Vlase S. Creep Response of Carbon-Fiber-Reinforced Composite Using Homogenization Method. Polymers. 2021; 13(6):867. https://doi.org/10.3390/polym13060867
Chicago/Turabian StyleKatouzian, Mostafa, and Sorin Vlase. 2021. "Creep Response of Carbon-Fiber-Reinforced Composite Using Homogenization Method" Polymers 13, no. 6: 867. https://doi.org/10.3390/polym13060867
APA StyleKatouzian, M., & Vlase, S. (2021). Creep Response of Carbon-Fiber-Reinforced Composite Using Homogenization Method. Polymers, 13(6), 867. https://doi.org/10.3390/polym13060867






