Optimisation on Thermoforming of Biodegradable Poly (Lactic Acid) (PLA) by Numerical Modelling
Abstract
1. Introduction
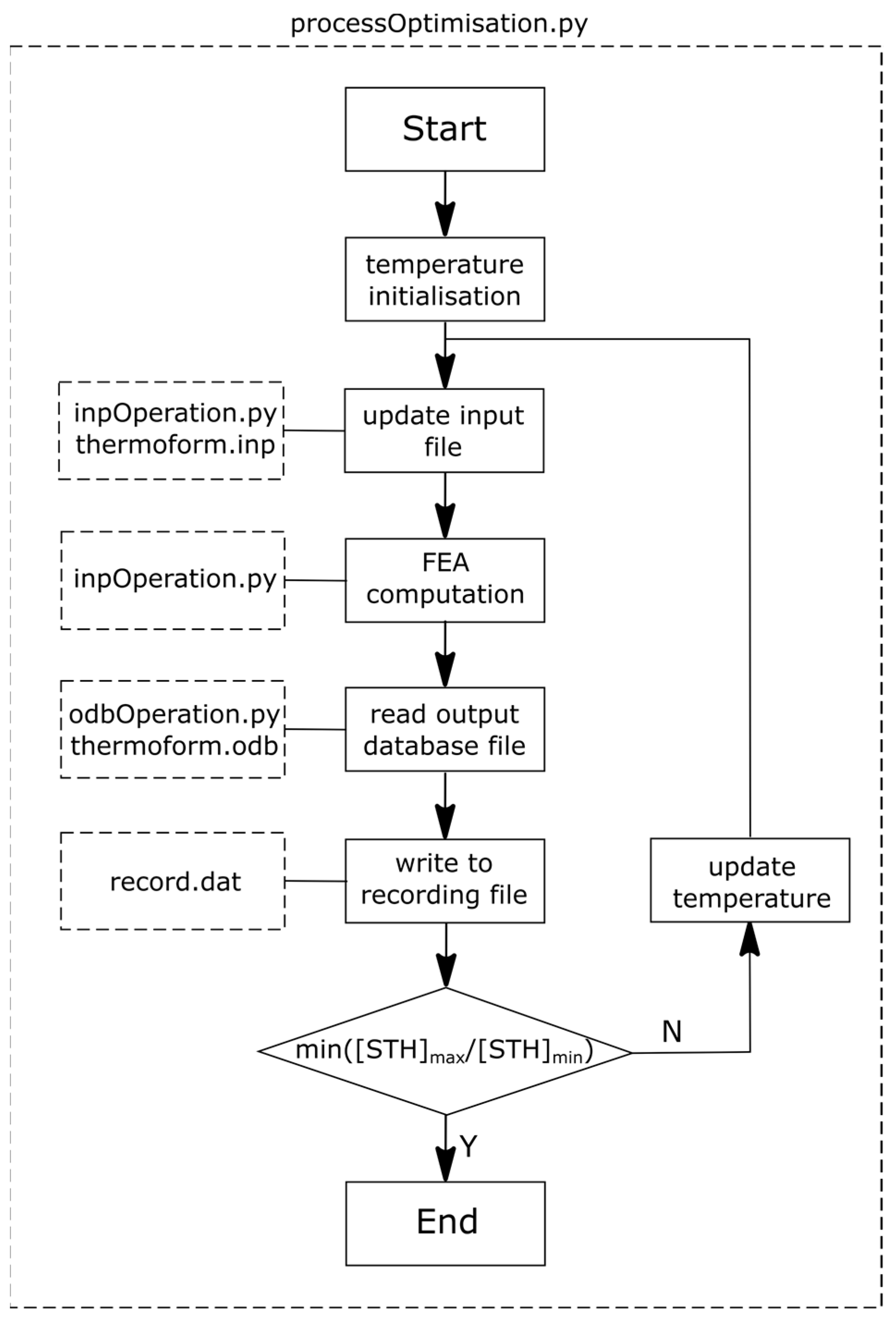
2. Materials and Methods
3. Results
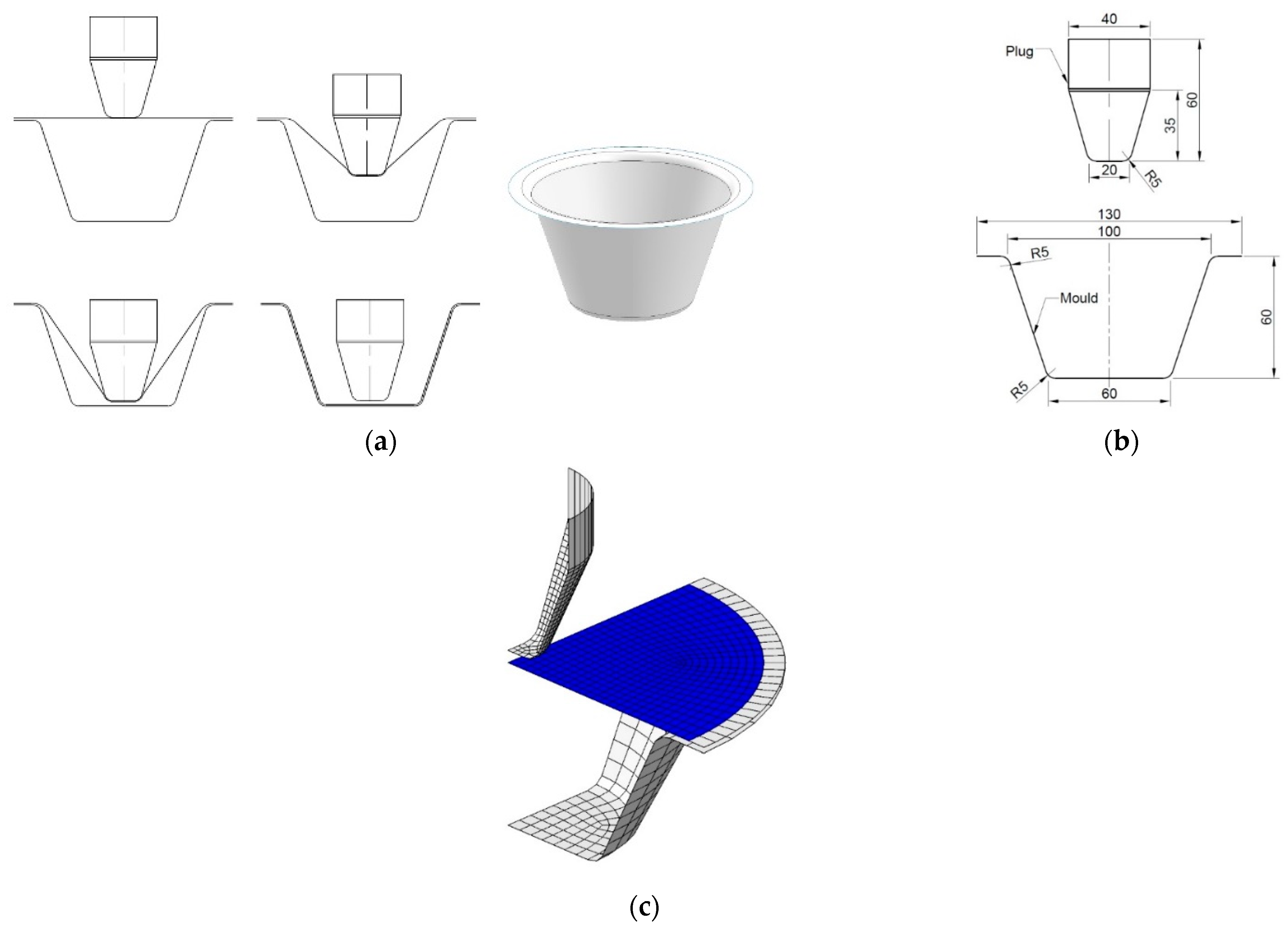
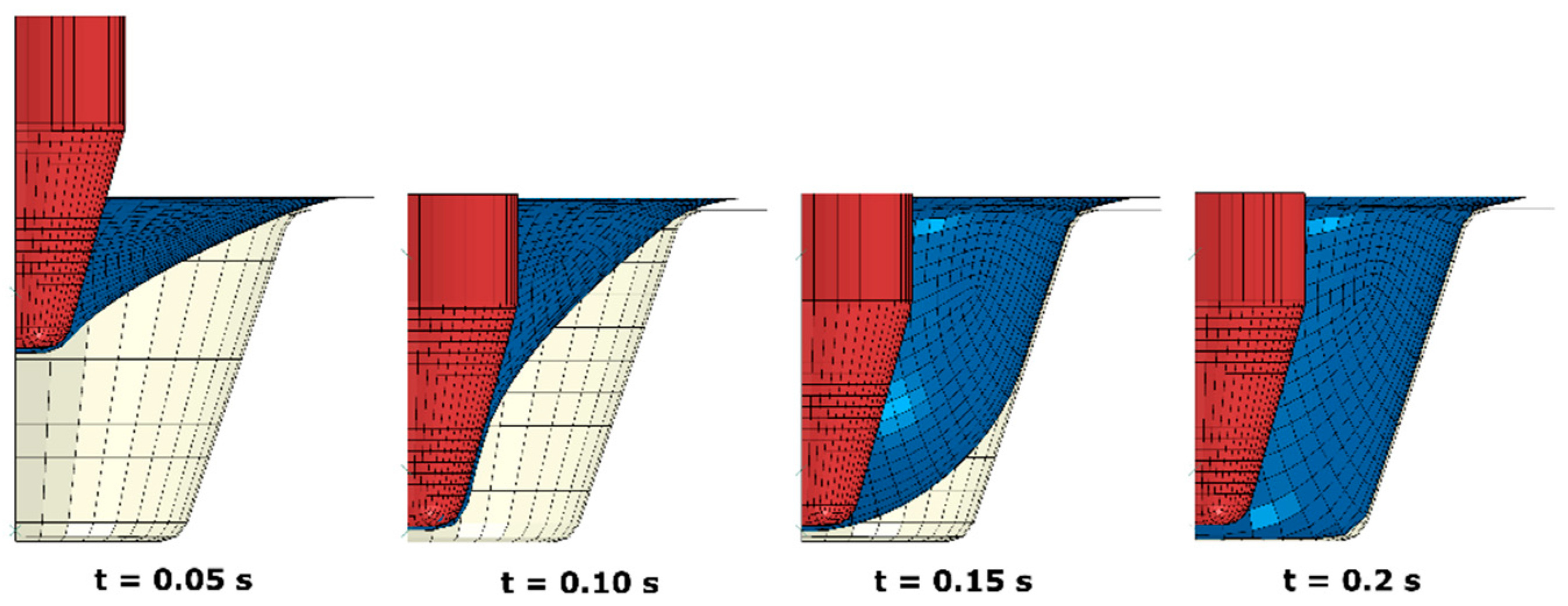
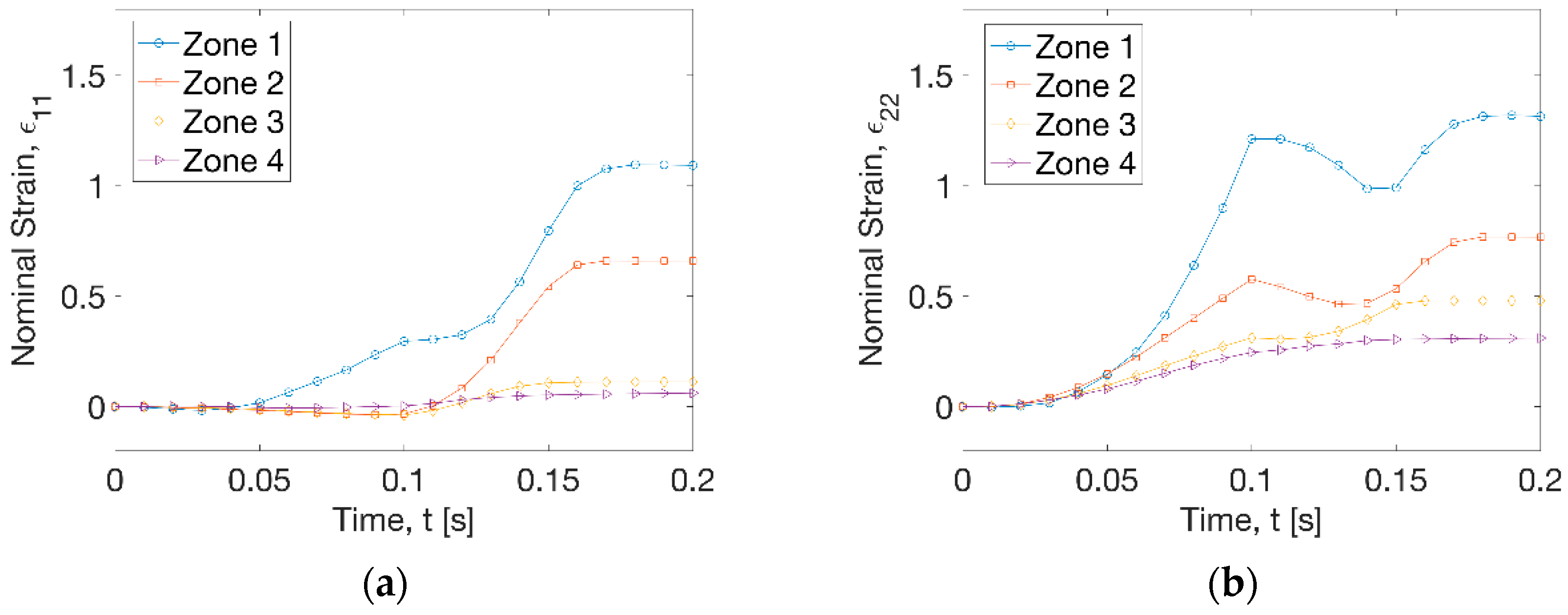
3.1. Forming Process
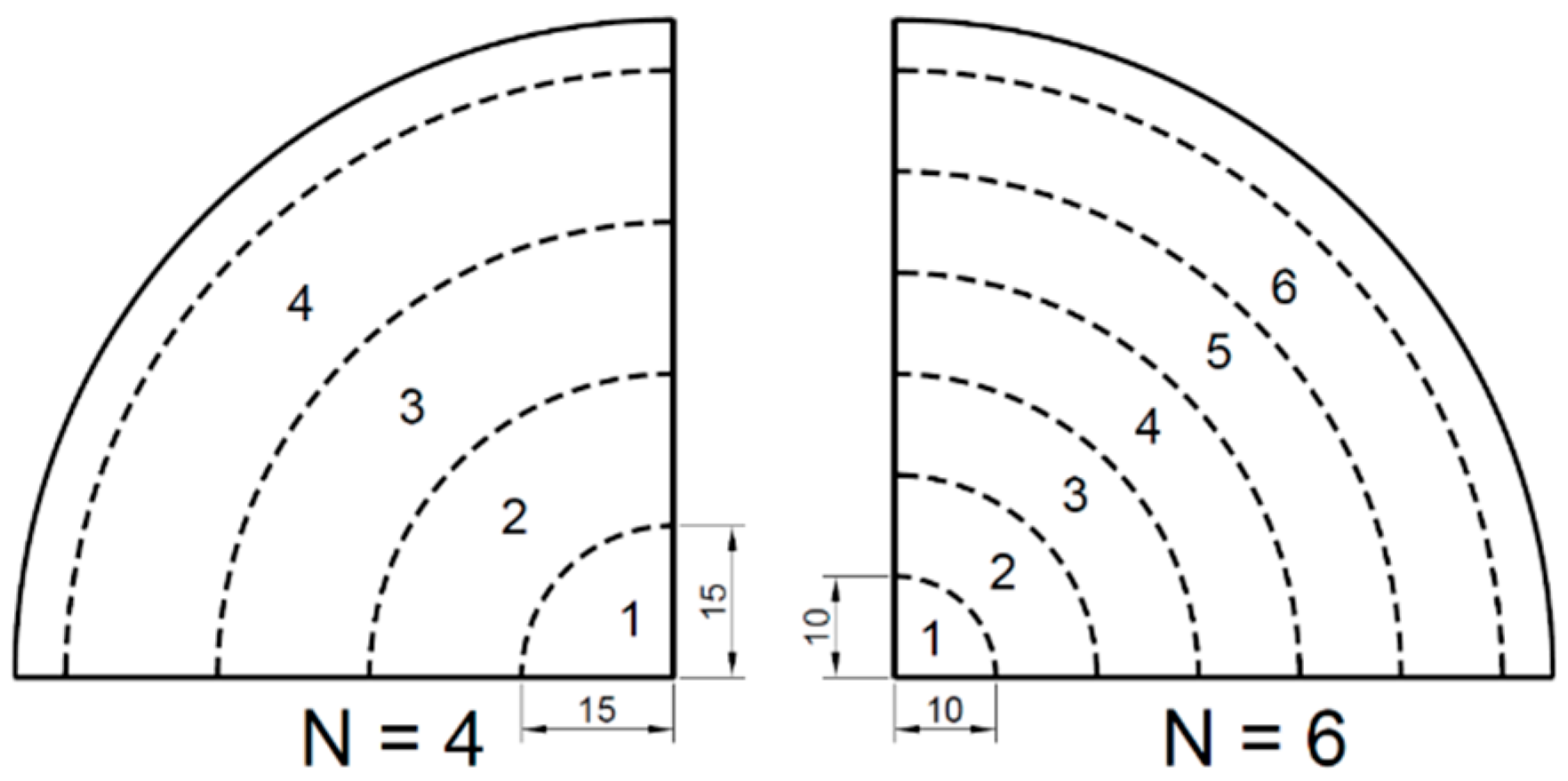
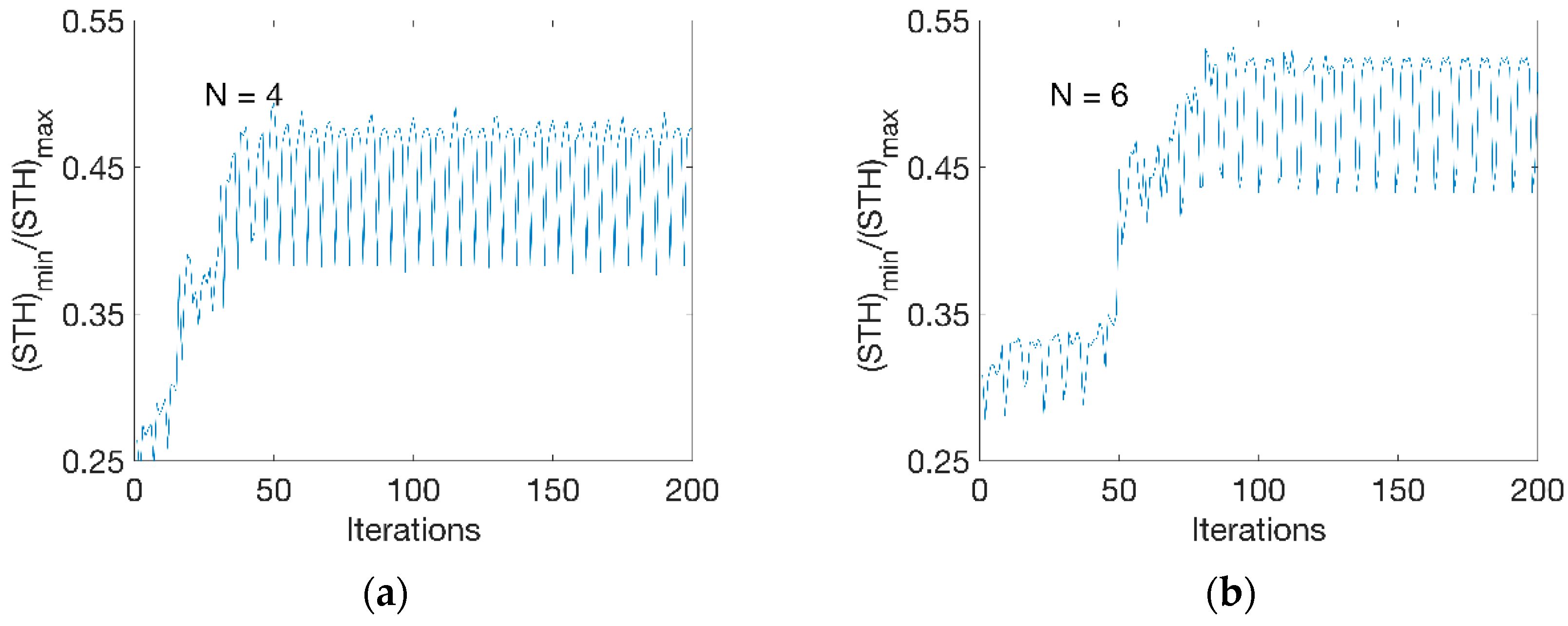
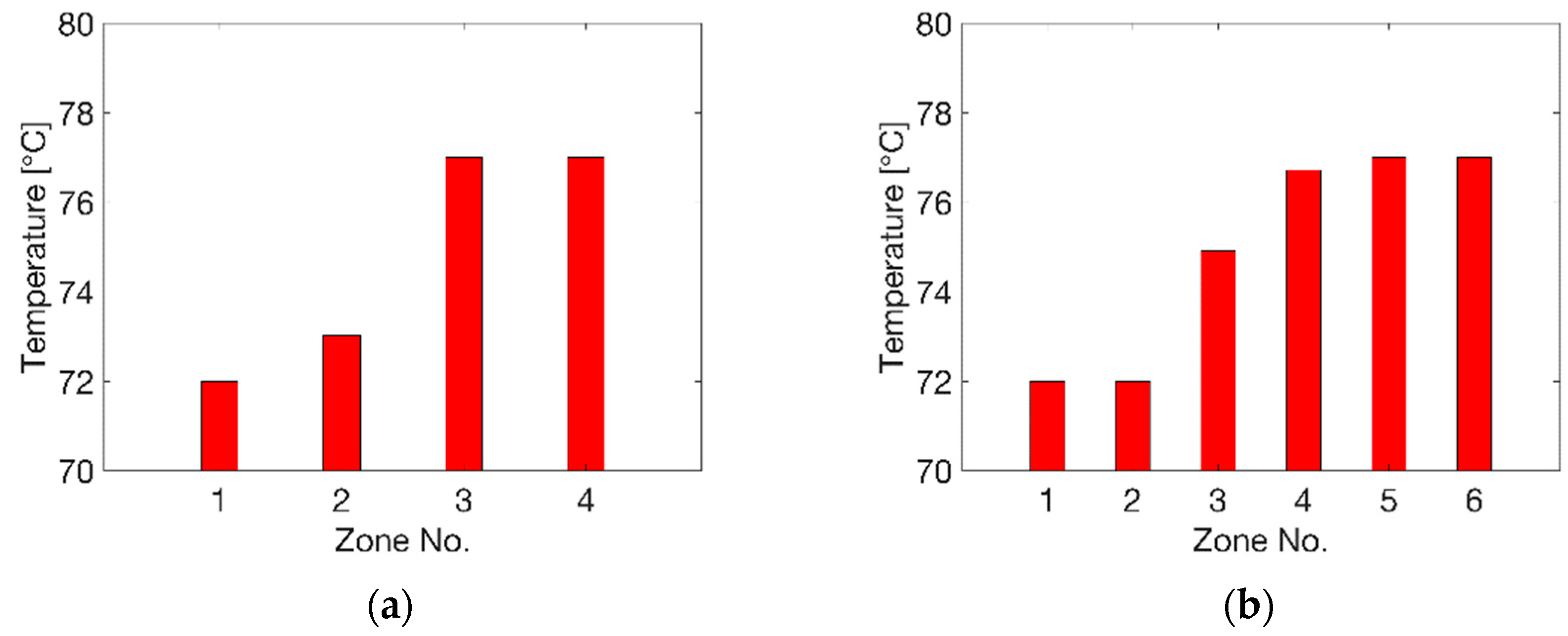
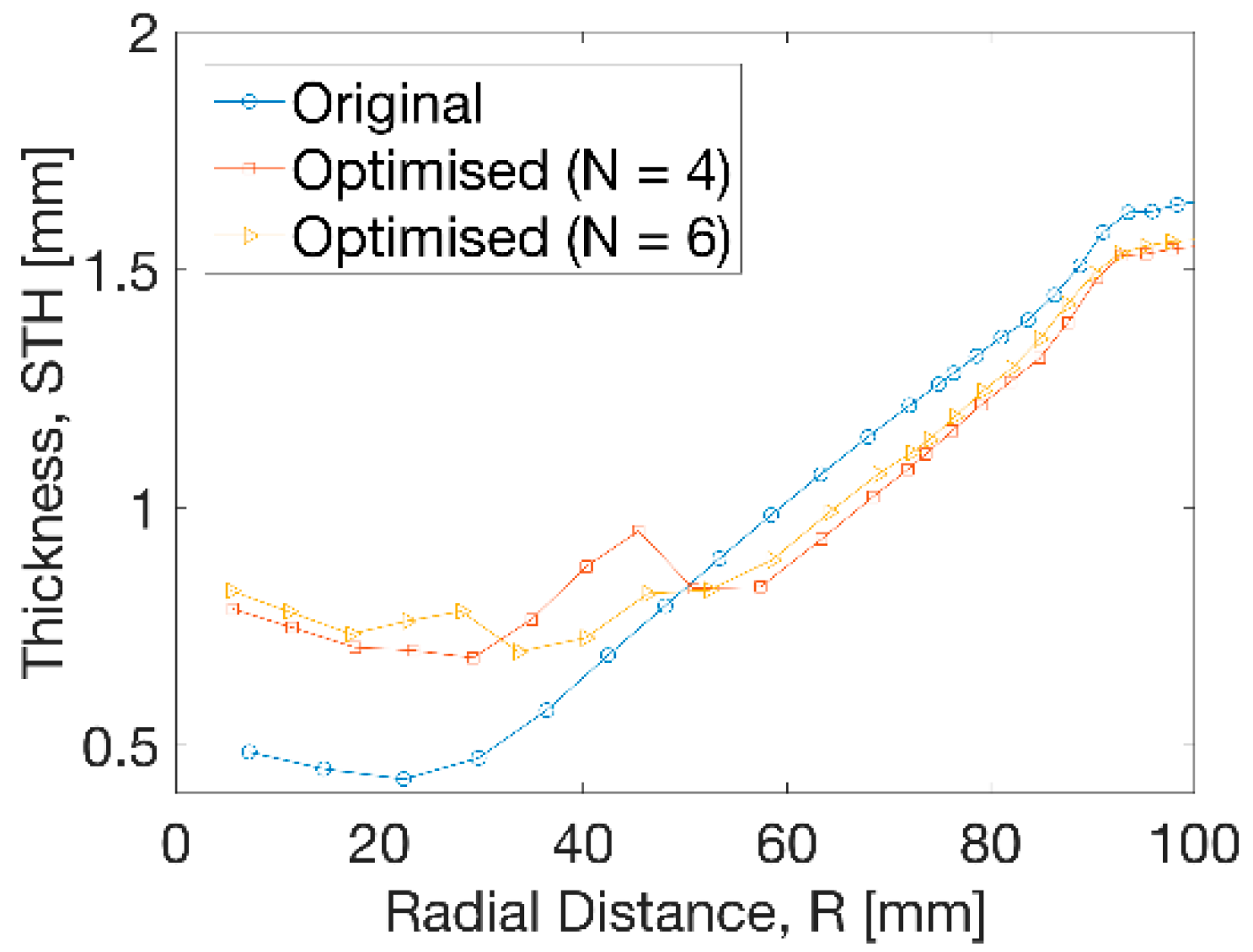
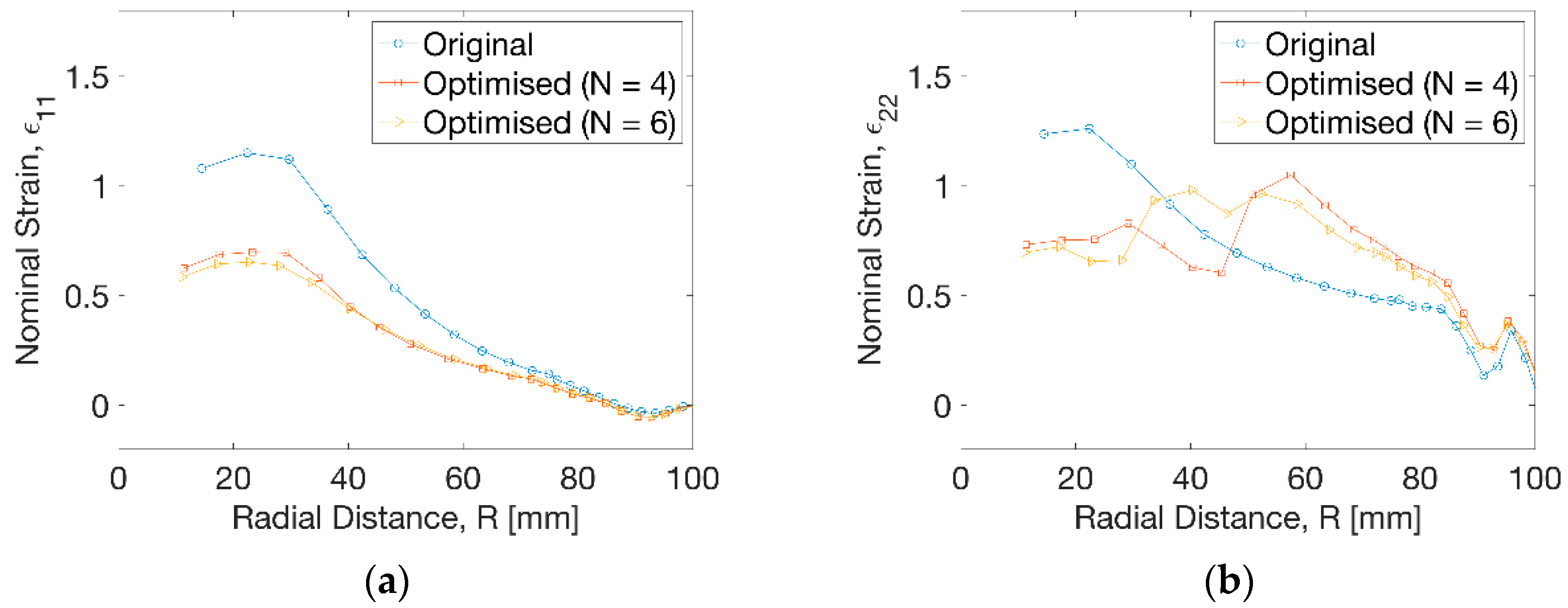
3.2. Optimisation Result
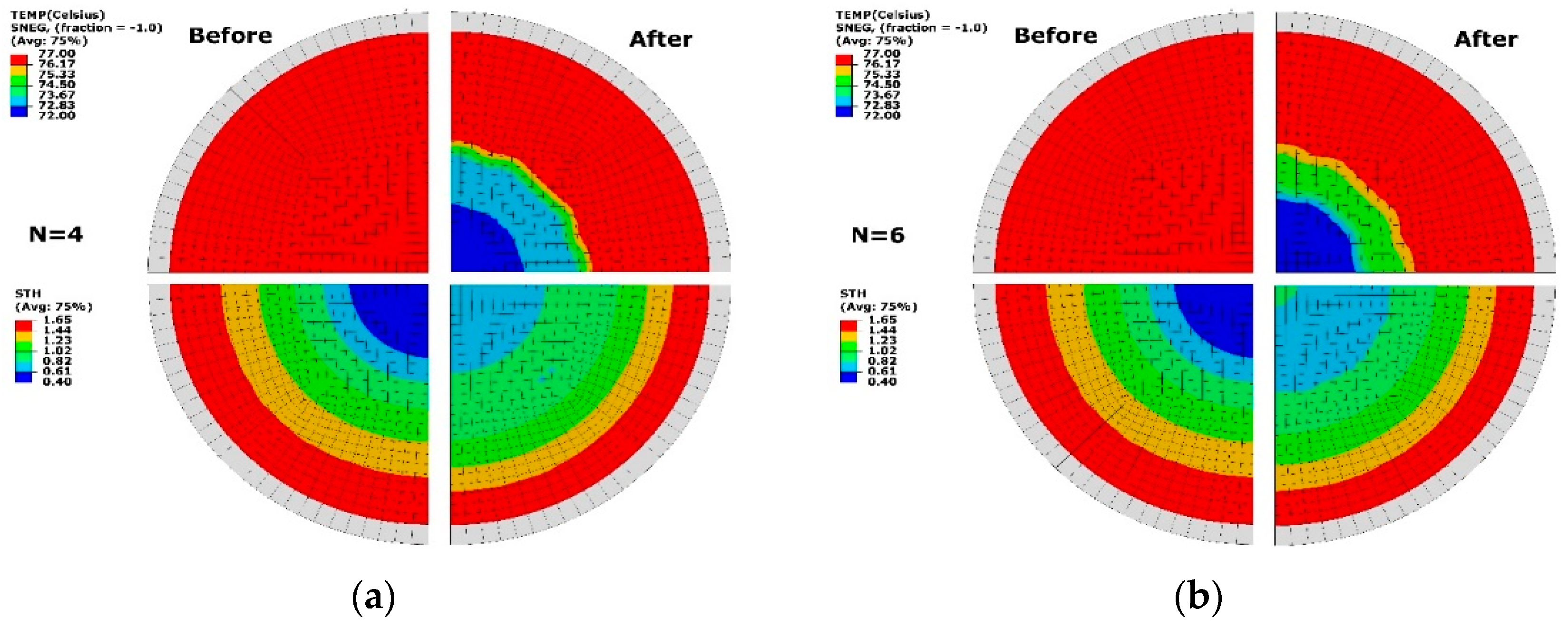
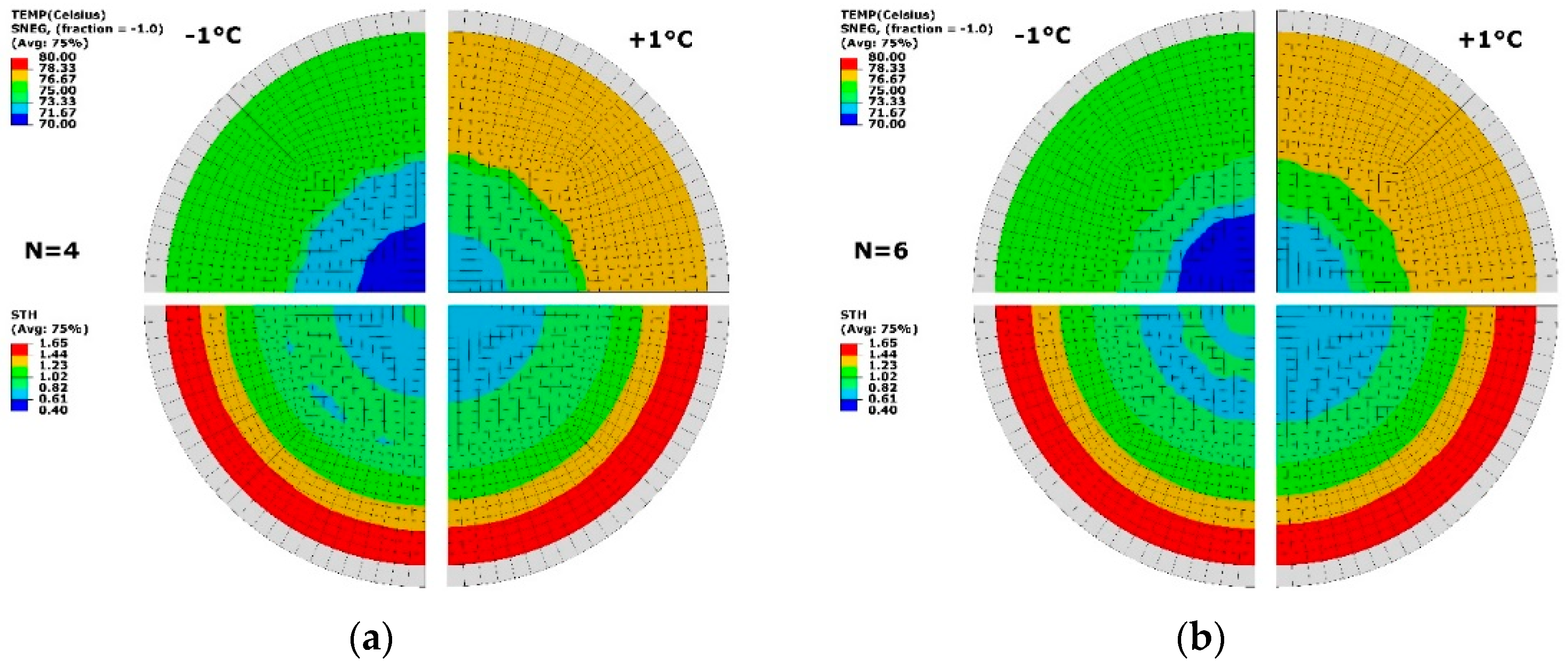
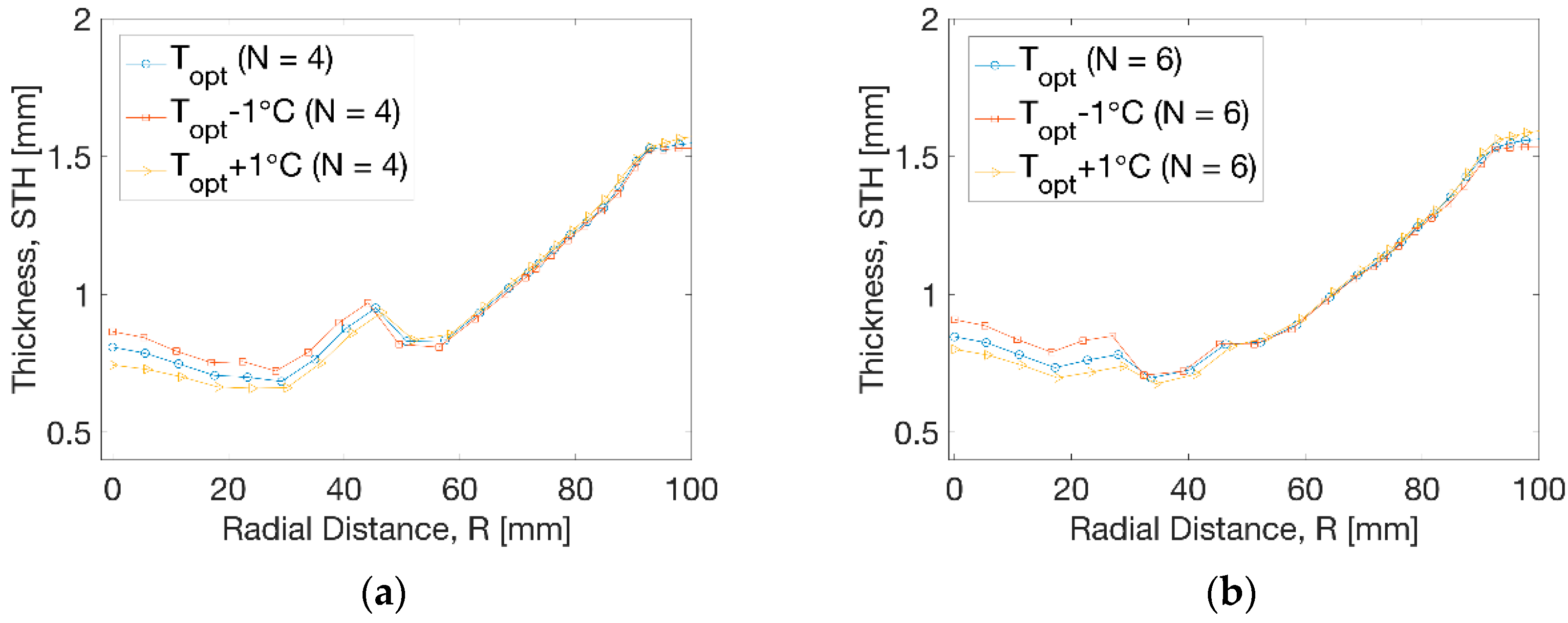
3.3. Temperature Perturbation
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Throne, J. Thermoforming. In Applied Plastics Engineering Handbook: Processing, Materials, and Applications, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2017; ISBN 9780323390408. [Google Scholar]
- Engelmann, S. Advanced Thermoforming: Methods, Machines and Materials, Applications and Automation; John Wiley & Sons: Hoboken, NJ, USA, 2012; ISBN 9781118207086. [Google Scholar]
- Peelman, N.; Ragaert, P.; De Meulenaer, B.; Adons, D.; Peeters, R.; Cardon, L.; Van Impe, F.; Devlieghere, F. Application of bioplastics for food packaging. Trends Food Sci. Technol. 2013, 32, 128–141. [Google Scholar] [CrossRef]
- Siracusa, V.; Rocculi, P.; Romani, S.; Rosa, M.D. Biodegradable polymers for food packaging: A review. Trends Food Sci. Technol. 2008, 19, 634–643. [Google Scholar] [CrossRef]
- Muller, J.; González-Martínez, C.; Chiralt, A. Combination Of Poly(lactic) acid and starch for biodegradable food packaging. Materials 2017, 10, 952. [Google Scholar] [CrossRef]
- Garlotta, D. A Literature Review of Poly(Lactic Acid). J. Polym. Environ. 2001. [Google Scholar] [CrossRef]
- Stoclet, G.; Seguela, R.; Lefebvre, J.M.; Elkoun, S.; Vanmansart, C. Strain-induced molecular ordering in polylactide upon uniaxial stretching. Macromolecules 2010, 43, 1488–1498. [Google Scholar] [CrossRef]
- Zhou, C.; Li, H.; Zhang, W.; Li, J.; Huang, S.; Meng, Y.; DeClaville Christiansen, J.; Yu, D.; Wu, Z.; Jiang, S. Direct investigations on strain-induced cold crystallization behavior and structure evolutions in amorphous poly(lactic acid) with SAXS and WAXS measurements. Polymer 2016, 90, 111–121. [Google Scholar] [CrossRef]
- Zhang, X.; Schneider, K.; Liu, G.; Chen, J.; Brüning, K.; Wang, D.; Stamm, M. Structure variation of tensile-deformed amorphous poly(l-lactic acid): Effects of deformation rate and strain. Polymer 2011. [Google Scholar] [CrossRef]
- Ou, X.; Cakmak, M. Influence of biaxial stretching mode on the crystalline texture in polylactic acid films. Polymer 2008, 49, 5344–5352. [Google Scholar] [CrossRef]
- Velazquez-Infante, J.C.; Gamez-Perez, J.; Franco-Urquiza, E.A.; Santana, O.O.; Carrasco, F.; Ll Maspoch, M. Effect of the unidirectional drawing on the thermal and mechanical properties of PLA films with different L -isomer content. J. Appl. Polym. Sci. 2013, 127, 2661–2669. [Google Scholar] [CrossRef]
- Wei, H.; Menary, G.; Buchanan, F.; Yan, S.; Nixon, J. Experimental characterisation on the behaviour of PLLA for stretch blowing moulding of bioresorbable vascular scaffolds. Int. J. Mater. Form. 2020. [Google Scholar] [CrossRef]
- Leite, W.; Campos Rubio, J.; Mata Cabrera, F.; Carrasco, A.; Hanafi, I. Vacuum Thermoforming Process: An Approach to Modeling and Optimization Using Artificial Neural Networks. Polymers 2018, 10, 143. [Google Scholar] [CrossRef]
- Harron, G.W.; Harkin-Jones, E.M.A.; Martin, P.J. Plug force monitoring for the control and optimization of the thermoforming process. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2003, 217, 181–188. [Google Scholar] [CrossRef]
- Chy, M.I.; Boulet, B. Estimation and control of temperature profile over a sheet in thermoforming process using non-equidistant temperature sensor. In Proceedings of the 2011 IEEE Industry Applications Society Annual Meeting, Orlando, FL, USA, 9–13 October 2011; pp. 1–8. [Google Scholar]
- Jebara, M.; Belhabib, S.; Boillereaux, L.; Havet, M.; Sarda, A.; Mousseau, P.; Deterre, R. Implementation of a parametric procedure allowing efficient positioning of heat sources: Application to high-temperature composites thermoforming process. Int. J. Simul. Multidiscip. Des. Optim. 2017, 8, A12. [Google Scholar] [CrossRef]
- O’Connor, C.P.J.; Menary, G.; Martin, P.J.; McConville, E. Finite element analysis of the thermoforming of Polypropylene. Int. J. Mater. Form. 2008, 1, 779–782. [Google Scholar] [CrossRef]
- Chang, Y.W.; Cheng, J.H. Numerical and experimental investigation of polycarbonate vacuum-forming process. J. Chin. Inst. Eng. 2013, 36, 831–841. [Google Scholar] [CrossRef]
- McCool, R.; Martin, P.J.; Jones, E.H. Development of a plug assisted thermofroming simulation. In Proceedings of the PPS23: The Polymer Processing Society 23rd Annual Meeting, Salvador, Brazil, 27–31 May 2007. [Google Scholar]
- Van Mieghem, B.; Desplentere, F.; Van Bael, A.; Ivens, J. Improvements in thermoforming simulation by use of 3D digital image correlation. Express Polym. Lett. 2015, 9, 119–128. [Google Scholar] [CrossRef]
- Modławski, M.; Jaruga, T. Computer simulation of thermoforming process and its verification using a rapid tooling mould. In MATEC Web of Conferences; EDP Sciences: Paris, France, 2018; Volume 02032, pp. 1–10. [Google Scholar] [CrossRef]
- Wang, C.H.; Nied, H.F. Temperature optimization for improved thickness control in thermoforming. J. Mater. Process. Manuf. Sci. 1999, 8, 113–126. [Google Scholar] [CrossRef]
- Hsiao, S.W.; Kikuchi, N. Numerical analysis and optimal design of composite thermoforming process. Comput. Methods Appl. Mech. Eng. 1999, 177, 1–34. [Google Scholar] [CrossRef]
- Soon, K.G. An Investigation of Temperature Control Issues Related to Intelligent Thermoforming; Lehigh University: Bethlehem, PA, USA, 2000. [Google Scholar]
- Szegda, D. Experimental Investigation and Computational Modelling of the Thermoforming Process of Thermoplastic Starch. Ph.D. Thesis, Brunel University, Uxbridge, UK, 2009. [Google Scholar]
- Guzman-Maldonado, E.; Hamila, N.; Naouar, N.; Moulin, G.; Boisse, P. Simulation of thermoplastic prepreg thermoforming based on a visco-hyperelastic model and a thermal homogenization. Mater. Des. 2016, 93, 431–442. [Google Scholar] [CrossRef]
- Lee, R.E.; Guo, Y.; Tamber, H.; Planeta, M.; Leung, S.N.S. Thermoforming of Polylactic Acid Foam Sheets: Crystallization Behaviors and Thermal Stability. Ind. Eng. Chem. Res. 2016, 55, 560–567. [Google Scholar] [CrossRef]
- Chapleau, N.; Huneault, M.A.; Li, H. Biaxial orientation of polylactide/thermoplastic starch blends. Int. Polym. Process. 2007, 22, 402–409. [Google Scholar] [CrossRef]
- Bergström, J.S.; Hayman, D. An Overview of Mechanical Properties and Material Modeling of Polylactide (PLA) for Medical Applications. Ann. Biomed. Eng. 2016, 44, 330–340. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, J.; Spencer, P. Modelling the Mechanical and Strain Recovery Behaviour of Partially Crystalline PLA. Polymers 2019, 11, 1342. [Google Scholar] [CrossRef] [PubMed]
- Blair, R.W.; Dunne, N.J.; Lennon, A.B.; Menary, G.H. Characterisation and constitutive modelling of biaxially stretched poly(L- lactic acid) sheet for application in coronary stents. J. Mech. Behav. Biomed. Mater. 2018, 86, 113–121. [Google Scholar] [CrossRef] [PubMed]
- Wei, H.; Yan, S.; Goel, S.; Menary, G. Characterization and modelling the mechanical behaviour of poly ( l-lactic acid ) for the manufacture of bioresorbable vascular scaffolds by stretch blow moulding. Int. J. Mater. Form. 2020, 13, 43–57. [Google Scholar] [CrossRef]
- Buckley, C.P.; Jones, D.C.; Jones, D.P. Hot-drawing of poly(ethylene terephthalate) under biaxial stress: Application of a three-dimensional glass-rubber constitutive model. Polymer 1996, 37, 2403–2414. [Google Scholar] [CrossRef]
- Buckley, C.P. Glass-rubber constitutive model for amorphous polymers near the glass transition. Polymer 1995, 36, 3301–3312. [Google Scholar] [CrossRef]
- Adams, A.M.; Buckley, C.P.; Jones, D.P. Biaxial hot drawing of poly(ethylene terephthalate): Measurements and modelling of strain-stiffening. Polymer 2000, 41, 771–786. [Google Scholar] [CrossRef]
- Løvdal, A.L.V.; Andreasen, J.W.; Mikkelsen, L.P.; Agersted, K.; Almdal, K. Mechanical properties of biaxially strained poly(l-lactide) tubes: Strain rate and temperature dependence. J. Appl. Polym. Sci. 2017, 134, 6–11. [Google Scholar] [CrossRef]
- Muminul Islam Chy, M.; Boulet, B.; Haidar, A. A Model Predictive Controller of Plastic Sheet Temperature for a Thermoforming Process. In Proceedings of the American Control Conference; Shoureshi, R.A., Ed.; IEEE: San Francisco, CA, USA, 2011; pp. 4410–4415. [Google Scholar]
- Ou, X.; Cakmak, M. Comparative study on development of structural hierarchy in constrained annealed simultaneous and sequential biaxially stretched polylactic acid films. Polymer 2010. [Google Scholar] [CrossRef]
- Razavi, M.; Wang, S.Q. Why Is Crystalline Poly(lactic acid) Brittle at Room Temperature? Macromolecules 2019, 52, 5429–5441. [Google Scholar] [CrossRef]
- Tábi, T.; Sajó, I.E.; Szabó, F.; Luyt, A.S.; Kovács, J.G. Crystalline structure of annealed polylactic acid and its relation to processing. Express Polym. Lett. 2010. [Google Scholar] [CrossRef]
- Løvdal, A.; Andreasen, J.W.; Mikkelsen, L.P.; Agersted, K.; Almdal, K. Characterization of biaxial strain of poly(l-lactide) tubes. Polym. Int. 2016, 65, 133–141. [Google Scholar] [CrossRef]
- Wang, Y.; Li, M.; Wang, K.; Shao, C.; Li, Q.; Shen, C. Unusual structural evolution of poly(lactic acid) upon annealing in the presence of an initially oriented mesophase. Soft Matter 2014, 10, 1512–1518. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, H. Optimisation on Thermoforming of Biodegradable Poly (Lactic Acid) (PLA) by Numerical Modelling. Polymers 2021, 13, 654. https://doi.org/10.3390/polym13040654
Wei H. Optimisation on Thermoforming of Biodegradable Poly (Lactic Acid) (PLA) by Numerical Modelling. Polymers. 2021; 13(4):654. https://doi.org/10.3390/polym13040654
Chicago/Turabian StyleWei, Huidong. 2021. "Optimisation on Thermoforming of Biodegradable Poly (Lactic Acid) (PLA) by Numerical Modelling" Polymers 13, no. 4: 654. https://doi.org/10.3390/polym13040654
APA StyleWei, H. (2021). Optimisation on Thermoforming of Biodegradable Poly (Lactic Acid) (PLA) by Numerical Modelling. Polymers, 13(4), 654. https://doi.org/10.3390/polym13040654





