Interface and Interphase in Polymer Nanocomposites with Bare and Core-Shell Gold Nanoparticles
Abstract
1. Introduction
2. Model and Simulation Method
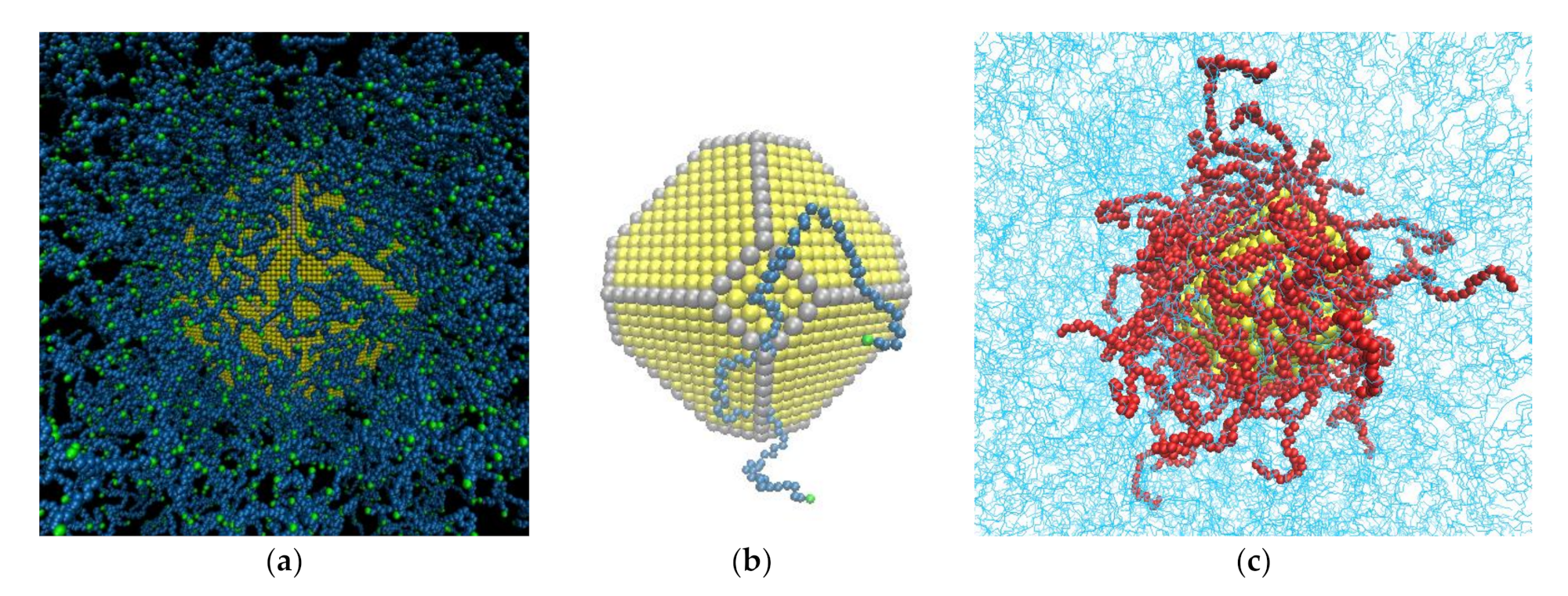
2.1. Shape of Au NPs
2.2. Generation and Equilibration of Model Systems
- (a)
- First, in order to obtain initial PE/grafted Au configurations, we added the anchors to the Au surface randomly by using a Monte Carlo algorithm in suitable positions according to the shape of the Au and taking into account the absorption sites of sulfur in the DFT calculations of alkanethiols adsorbed on Au.
- (b)
- Second, we equilibrate the hybrid system through energy minimization and long simulation runs. Energy minimization of the core/shell system was performed followed by MD simulation runs up to 10 ns in the NVT ensemble. Then, the Au nanoparticle, grafted or not, was placed at a close distance (about 0.5 nm) to several well-equilibrated polymer samples [109].
- (c)
- The final step of our “equilibration protocol” involves the execution of long MD simulations, of the order of 30 ns. Throughout this time we monitored the motion of the whole hybrid system. Our simulations run times were much higher than the relaxation times of the chains [109].
2.3. Analysis Method
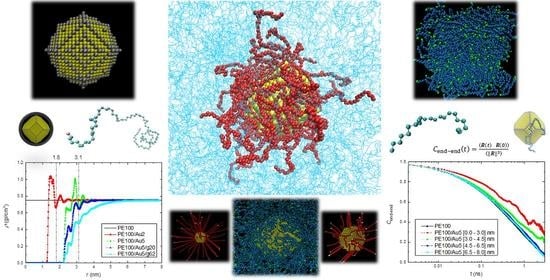
3. Results
3.1. Structural Properties
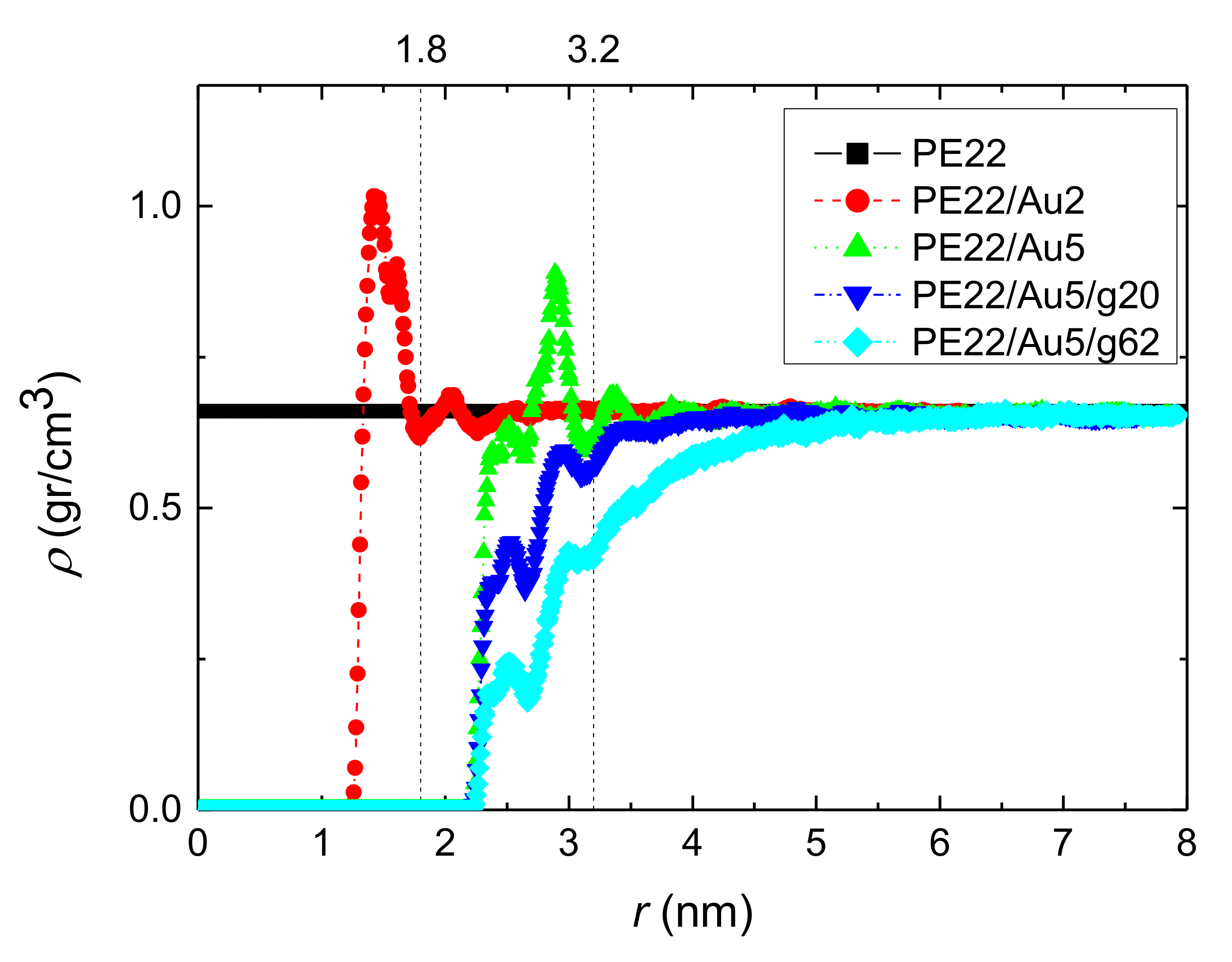
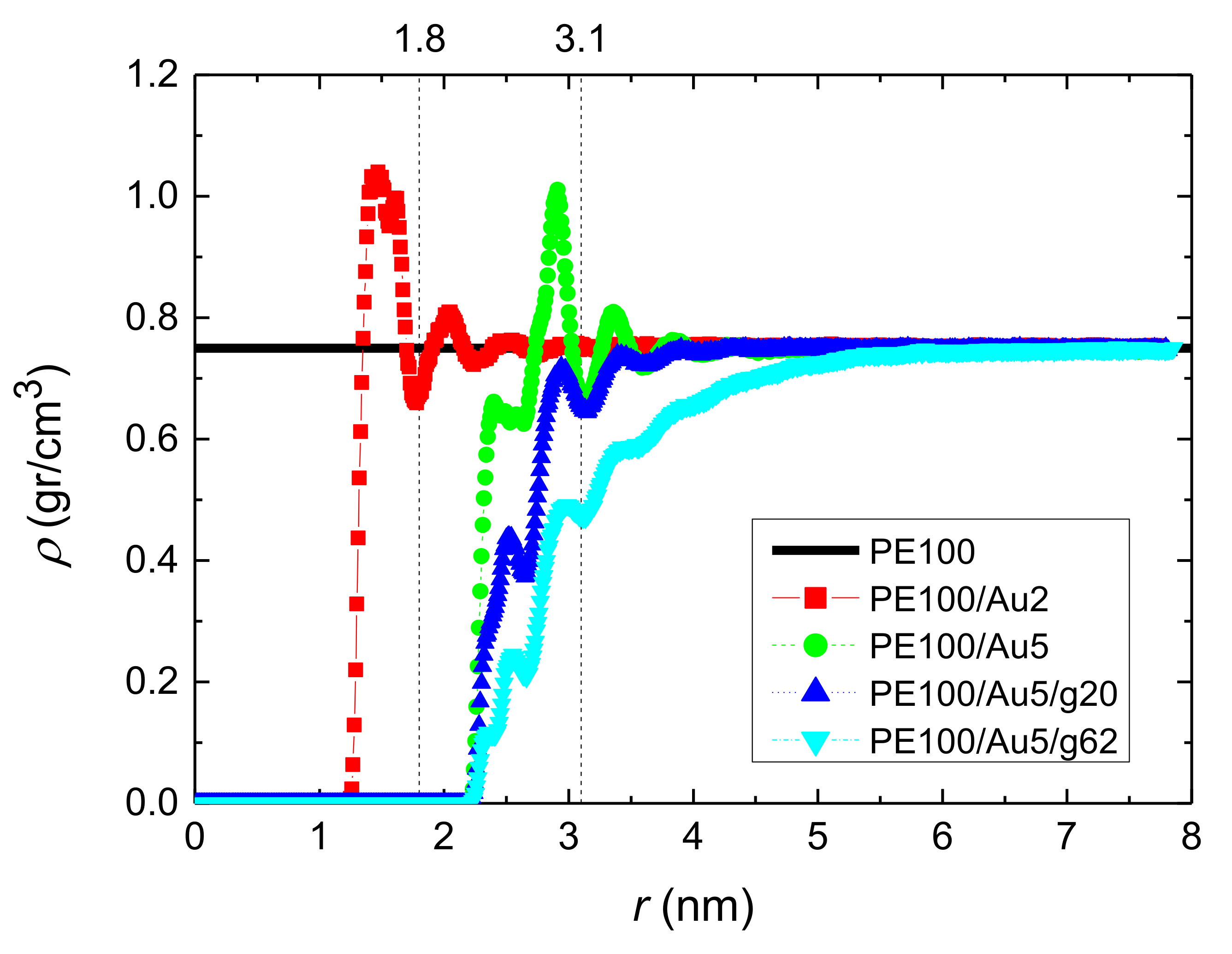
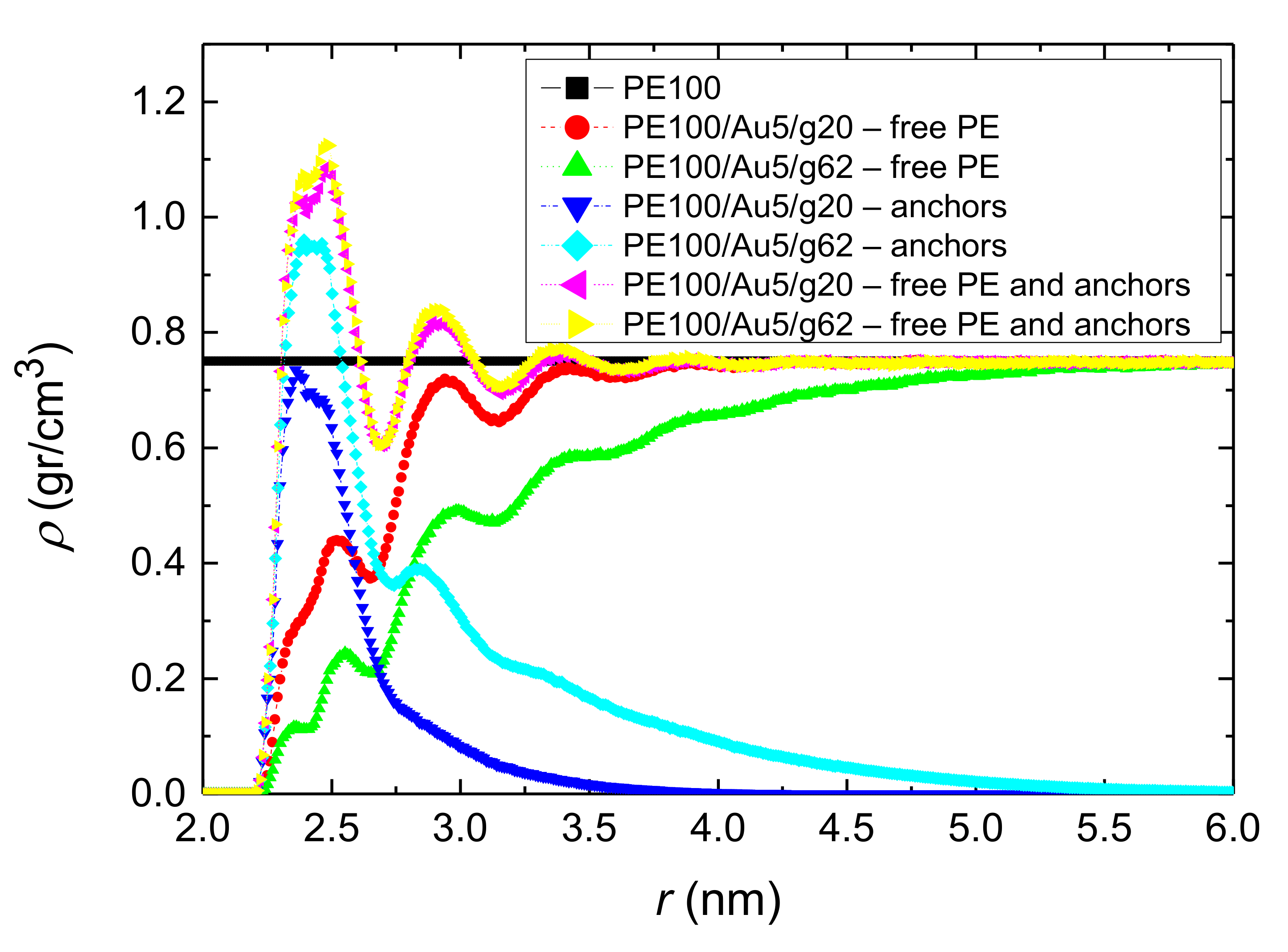
3.1.1. Density Profiles
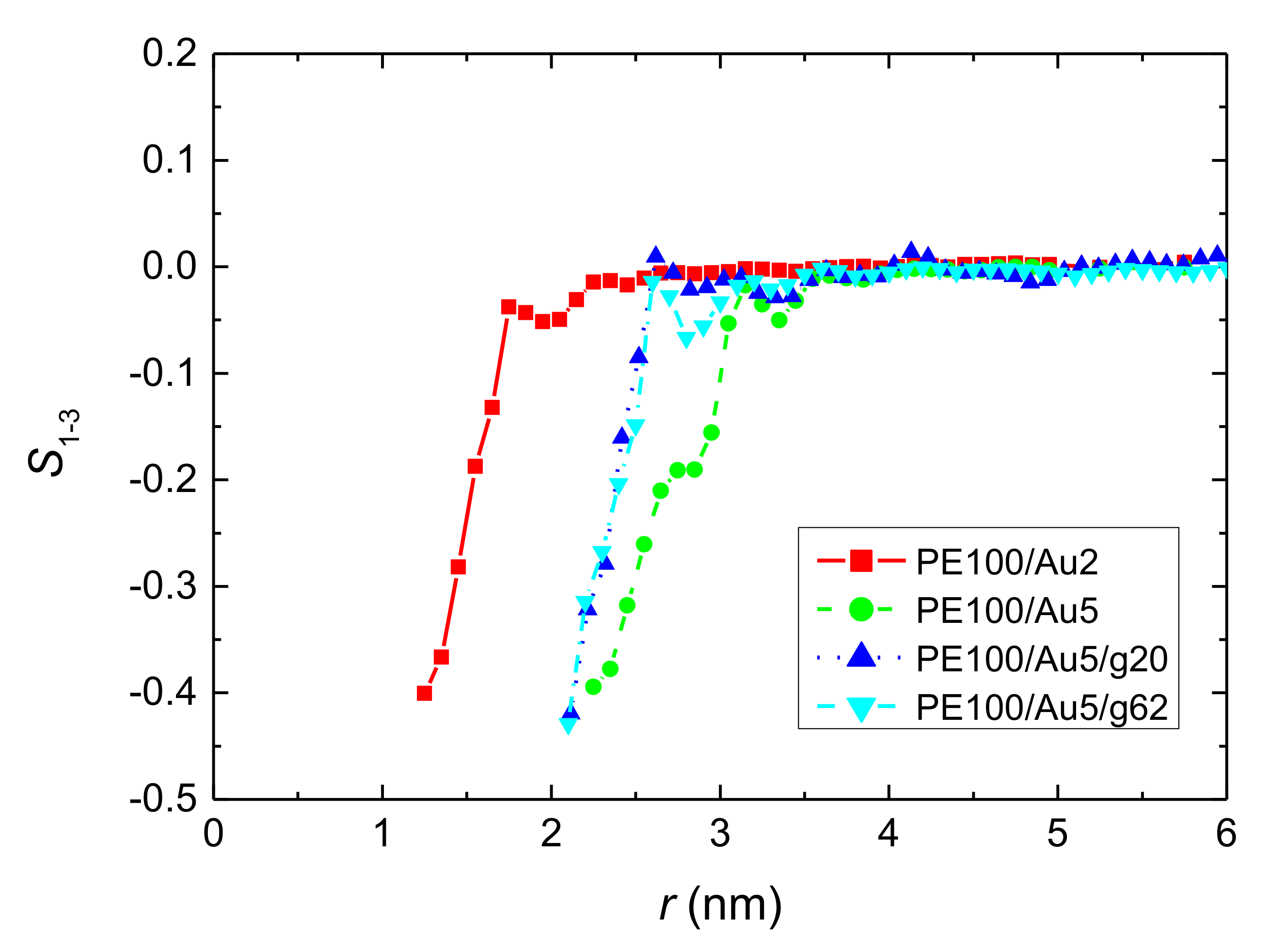
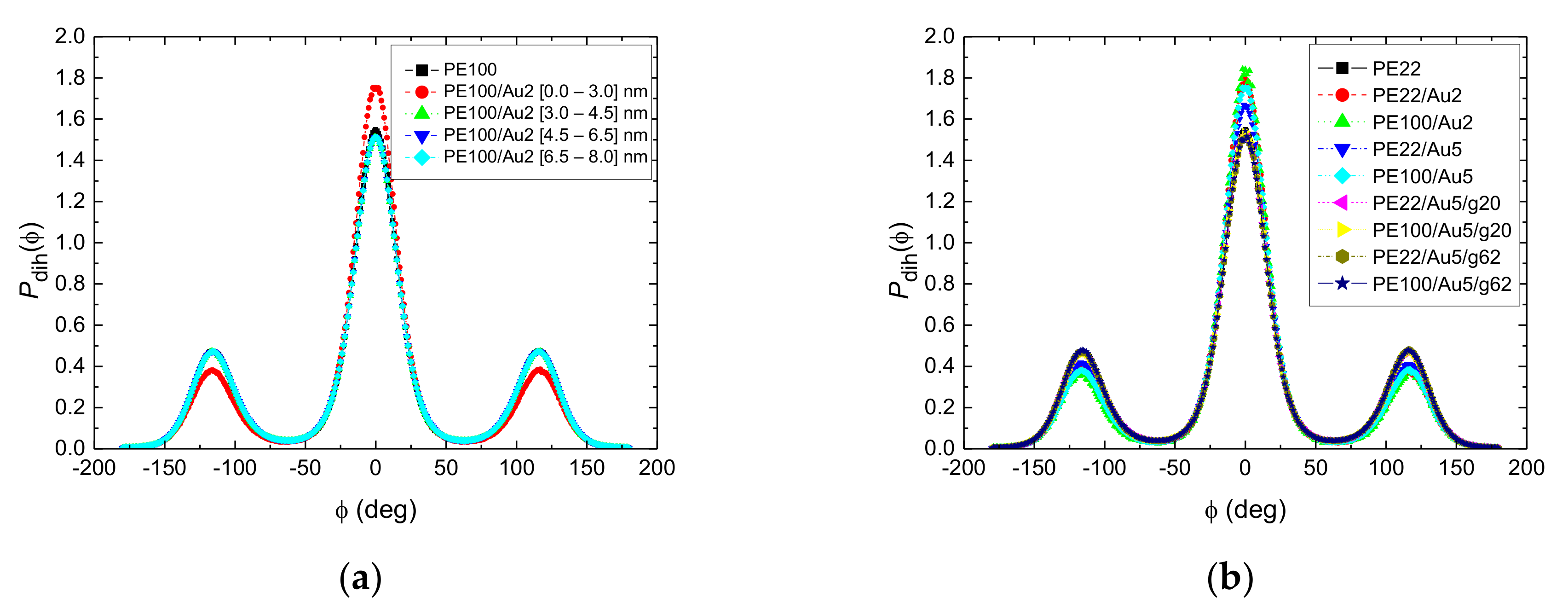
3.1.2. Structure of PE Chains
3.2. Dynamical Properties
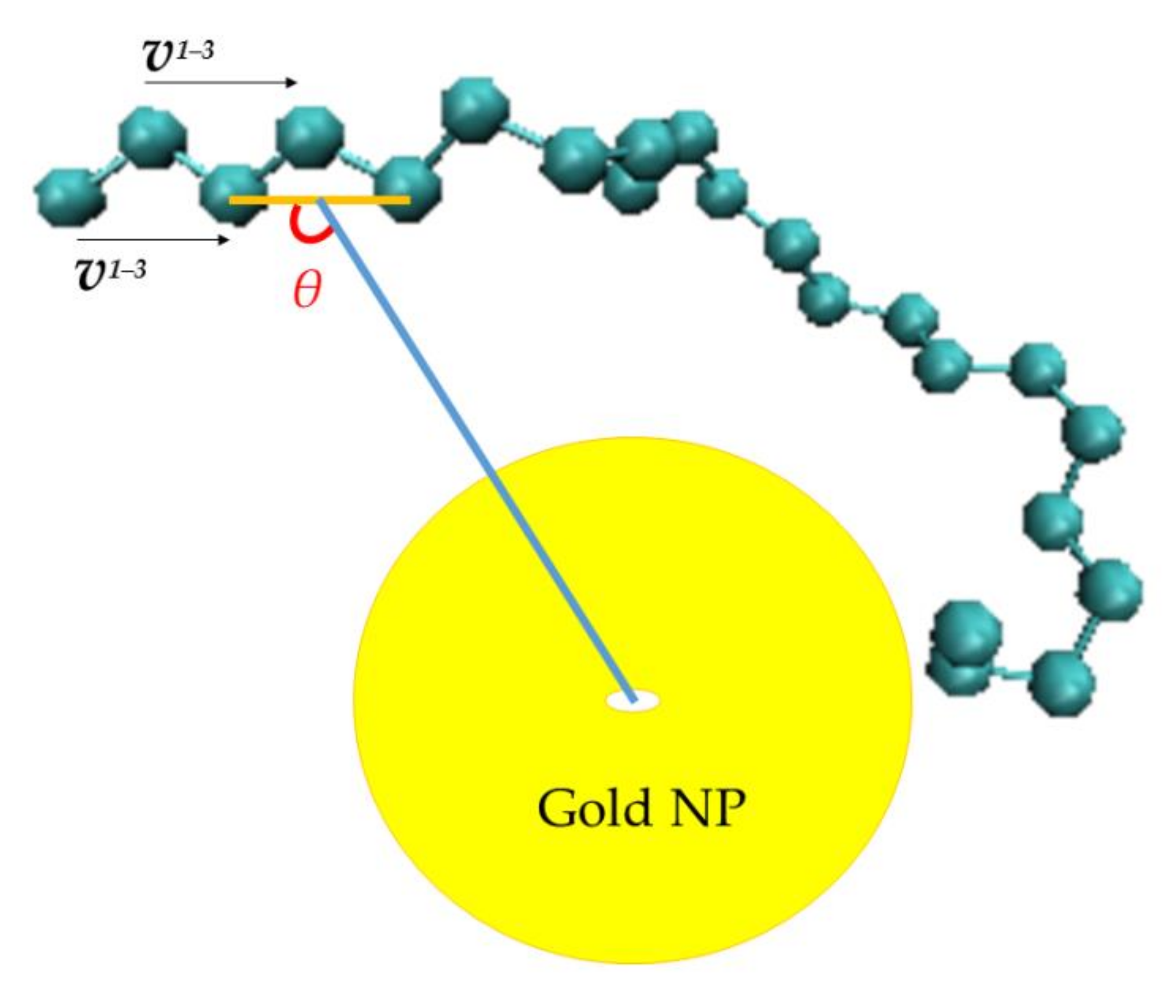
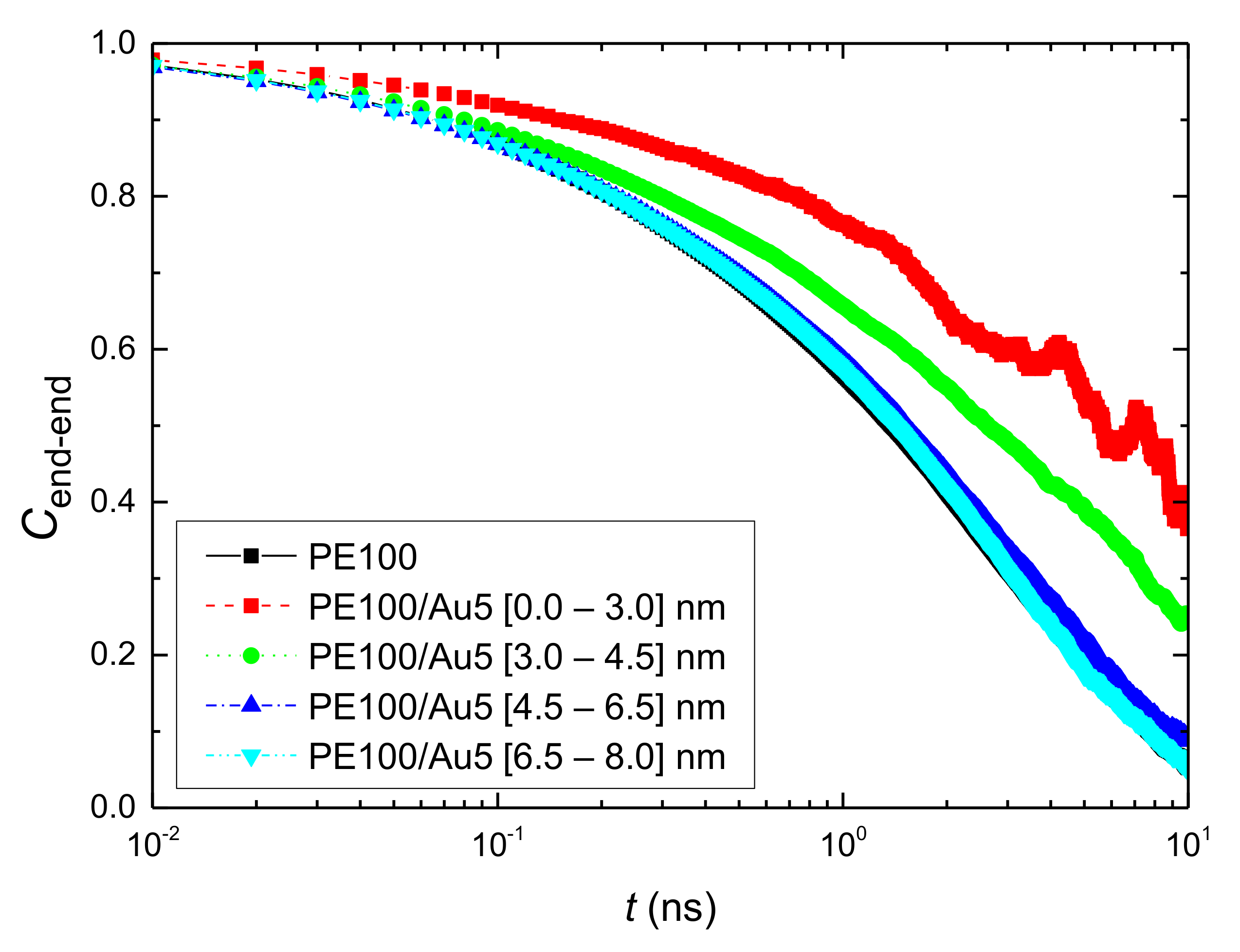
3.2.1. Orientational Dynamics
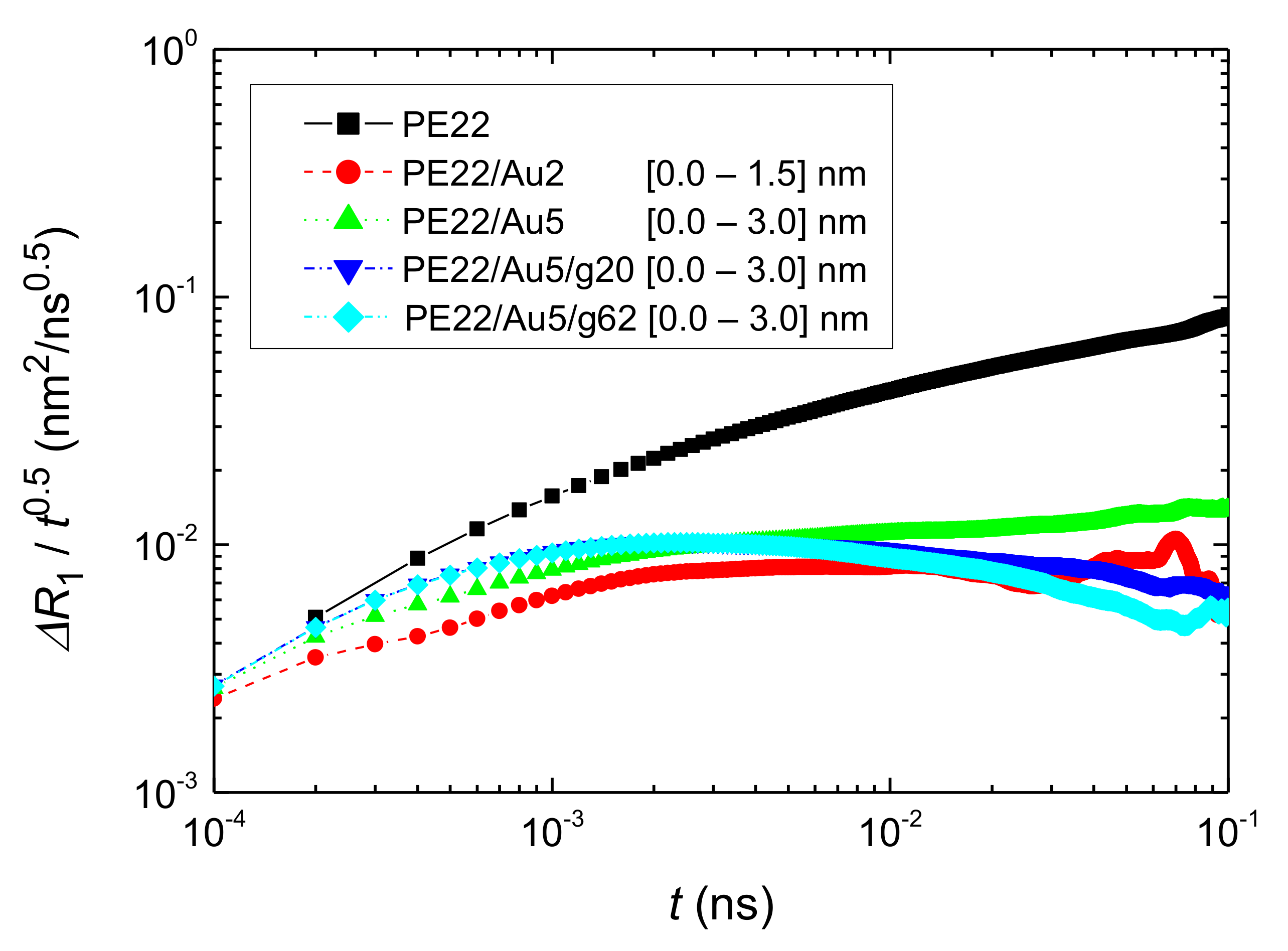
3.2.2. Translational Dynamics
4. Discussion and Conclusions
- Local structural and conformational features were analyzed at the level of both individual segments (atoms or bonds) and entire chains. Due to the intermolecular PE/Au NP (adhesive) interaction the local monomer PE mass density exhibits a maximum near the gold surface. At short distances chain segments tend to orientate almost parallel to the Au NP surface. This randomizes gradually as the chain segments move away from the interface. Furthermore, in the dihedral angle distribution at the PE/gold NP interface we observed an increase of “trans” population compared to the bulk one. This reflects the more ordered polymer chain structures.
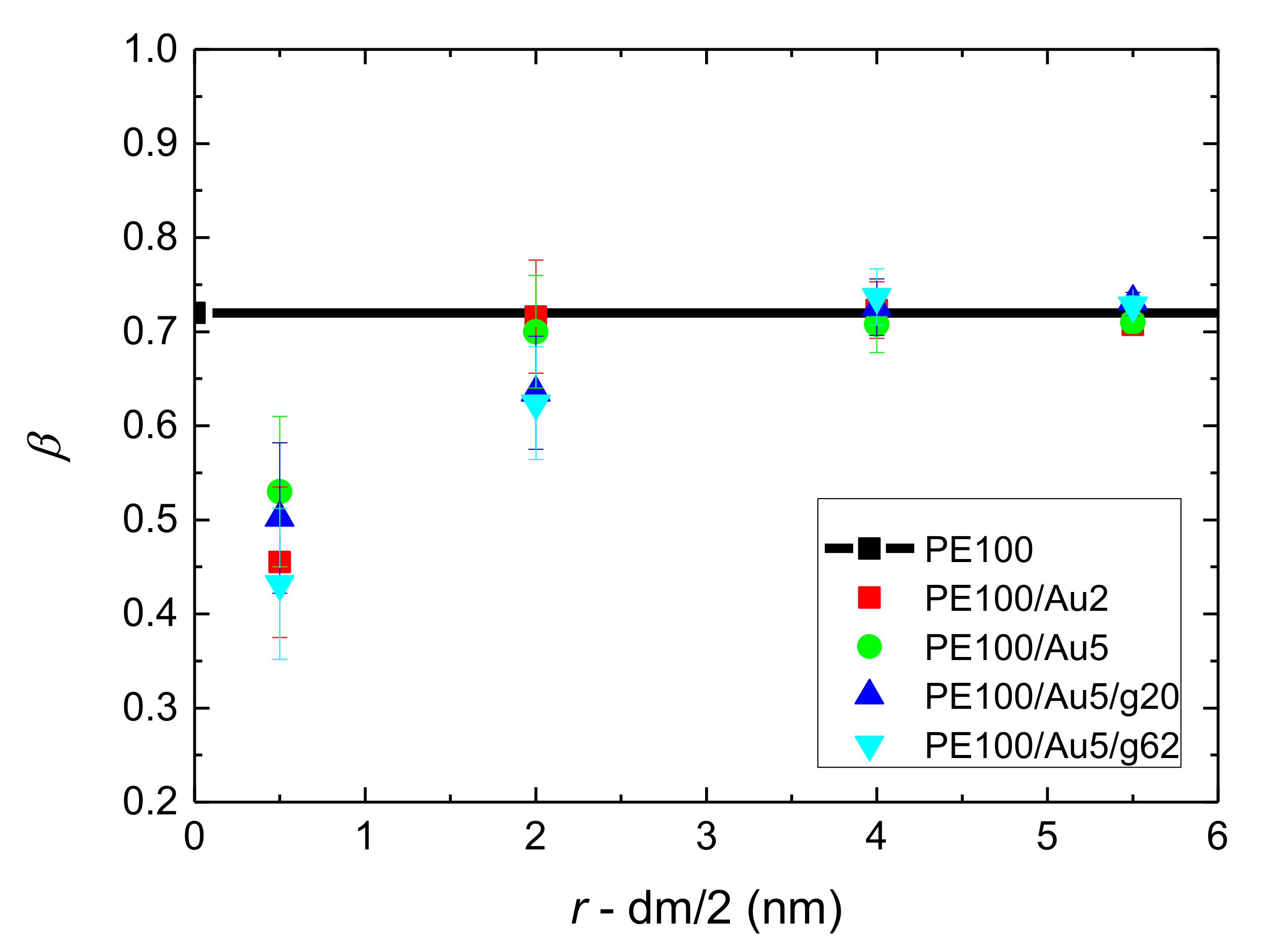
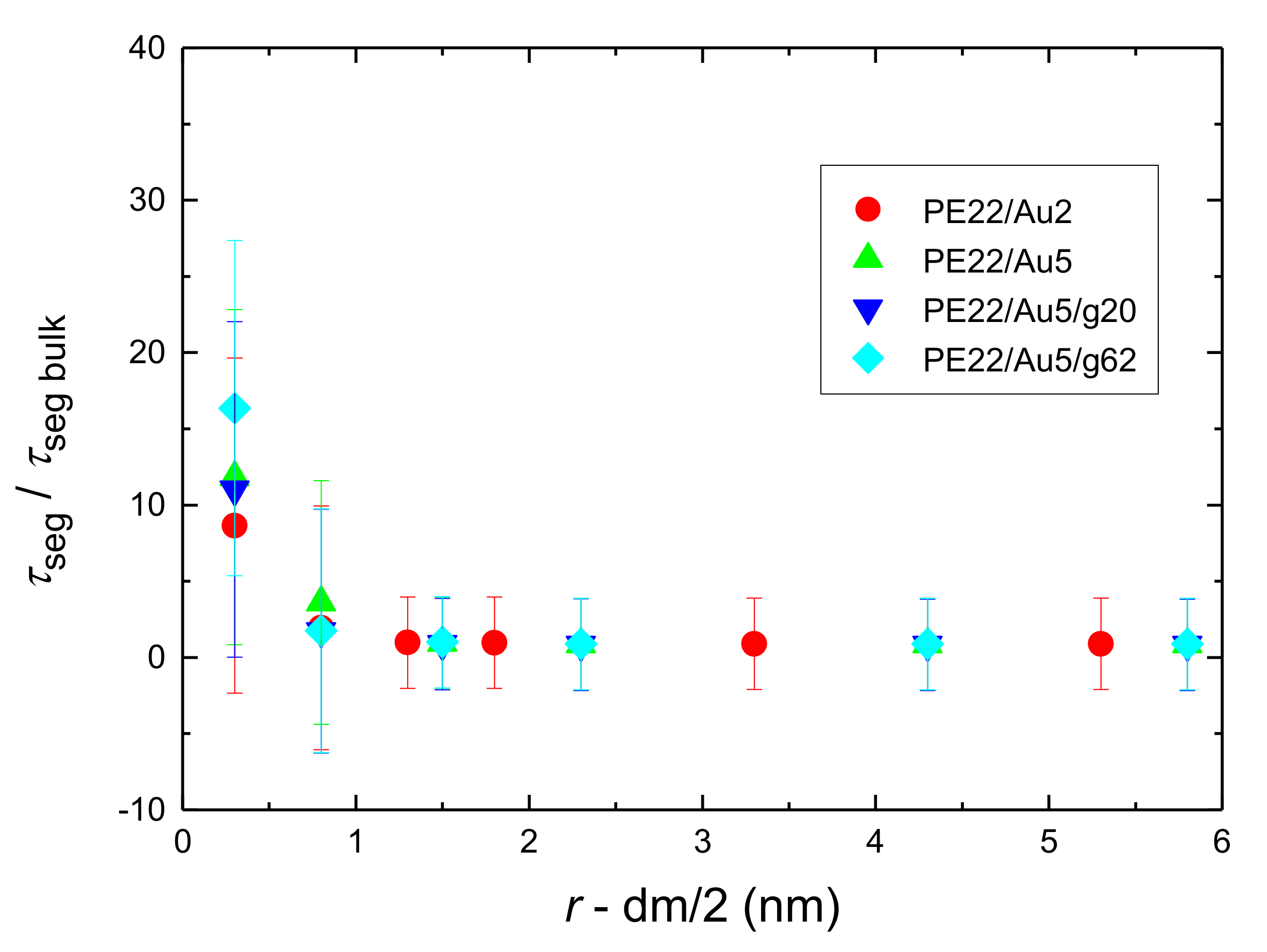
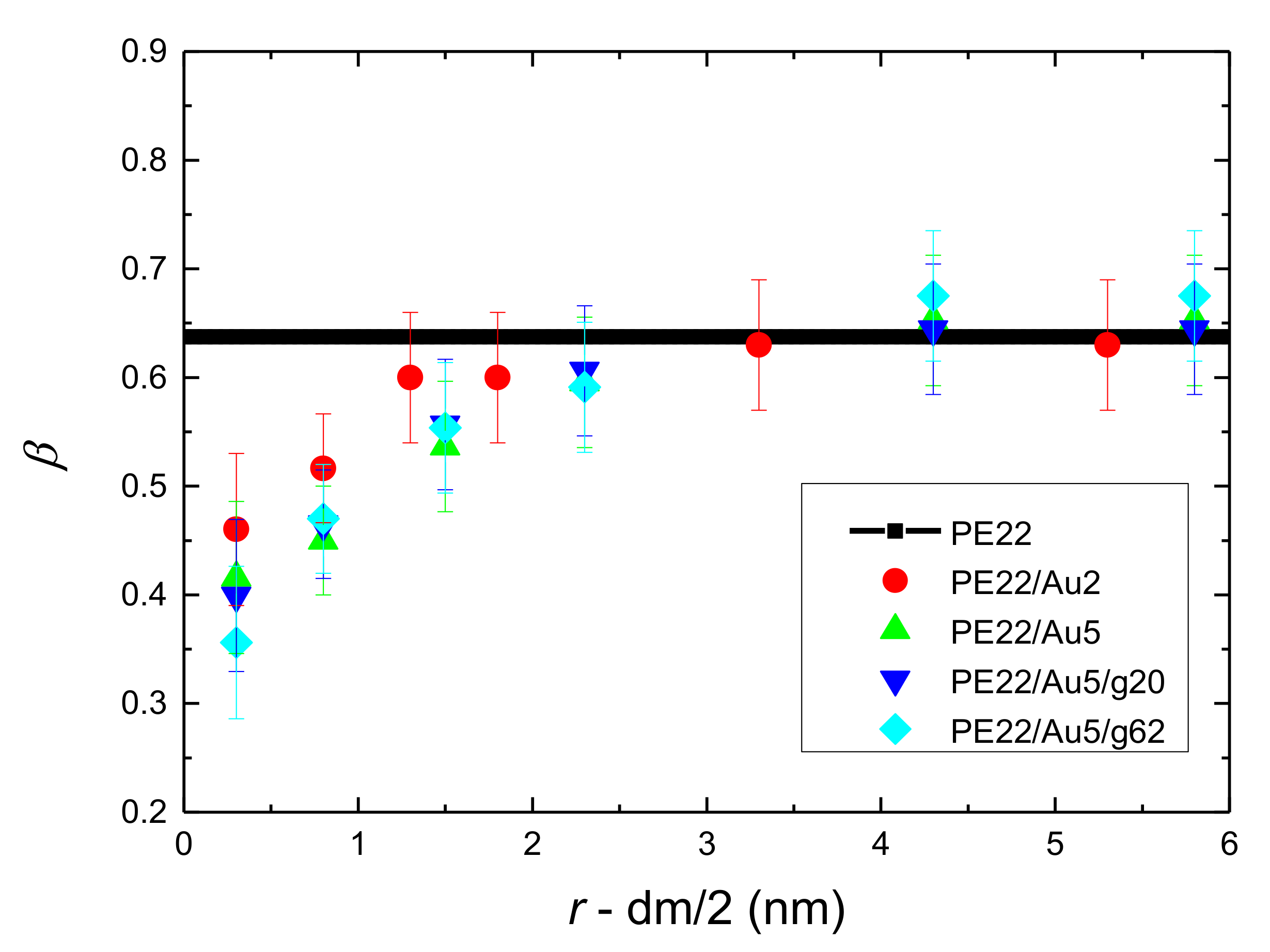
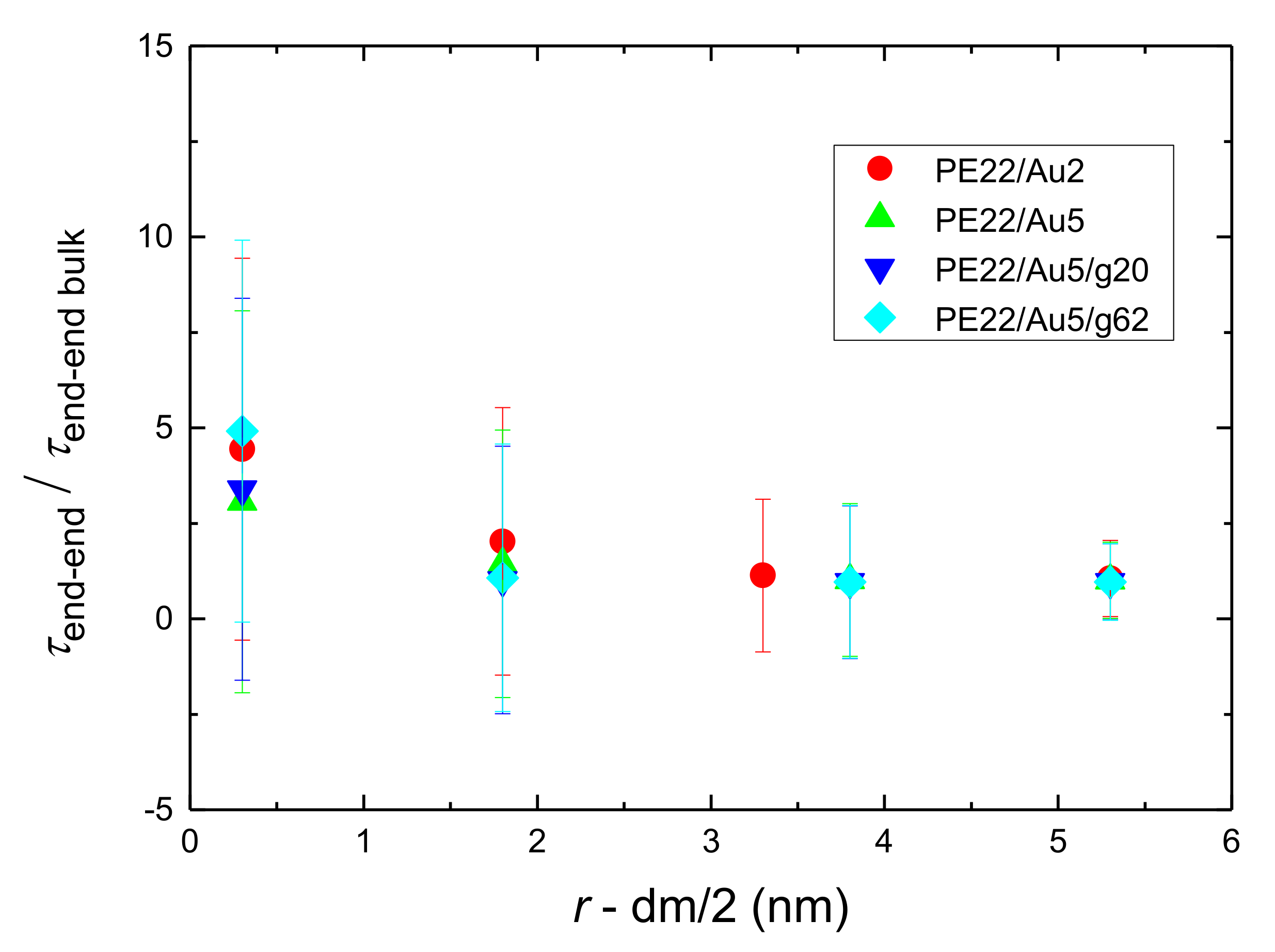
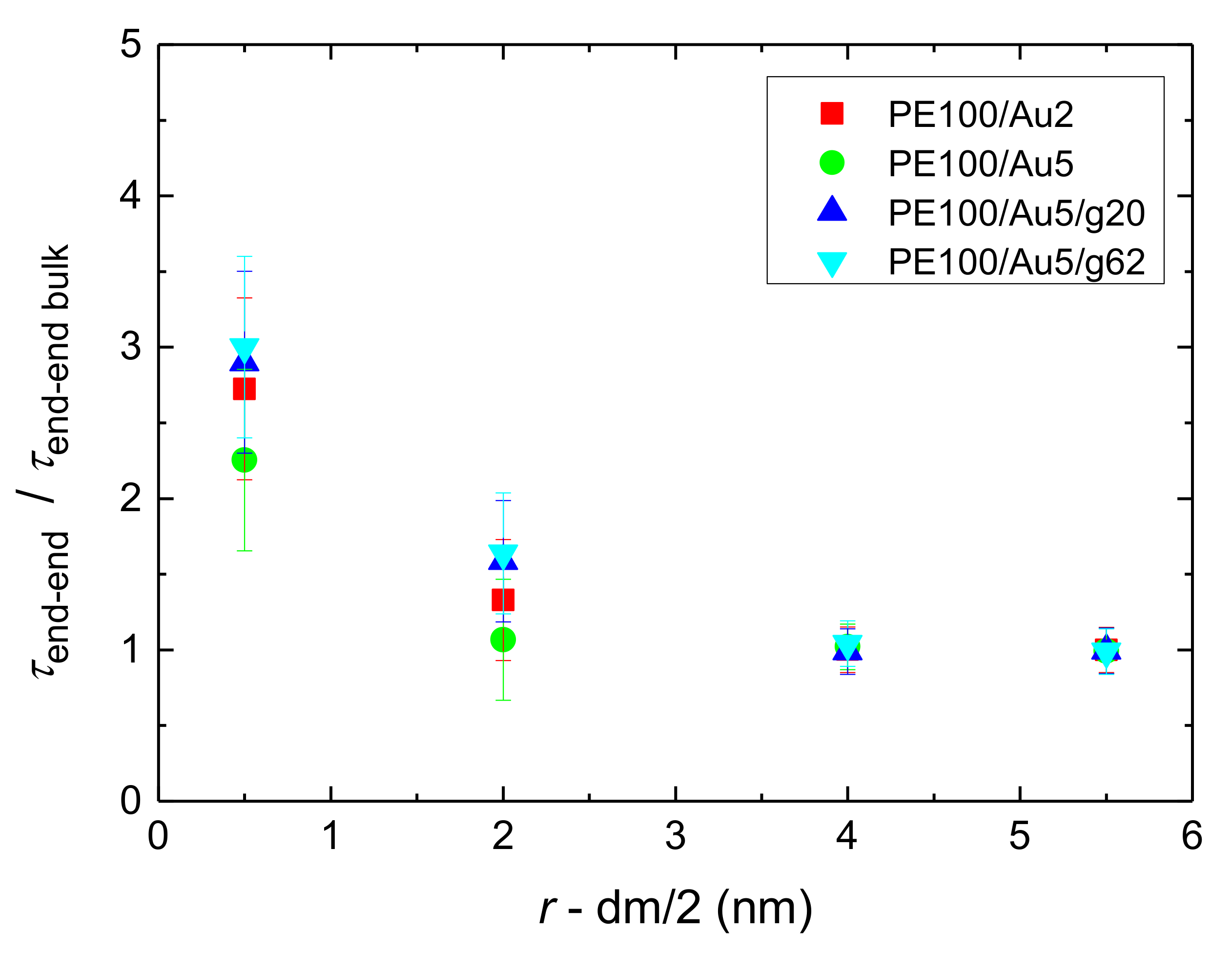
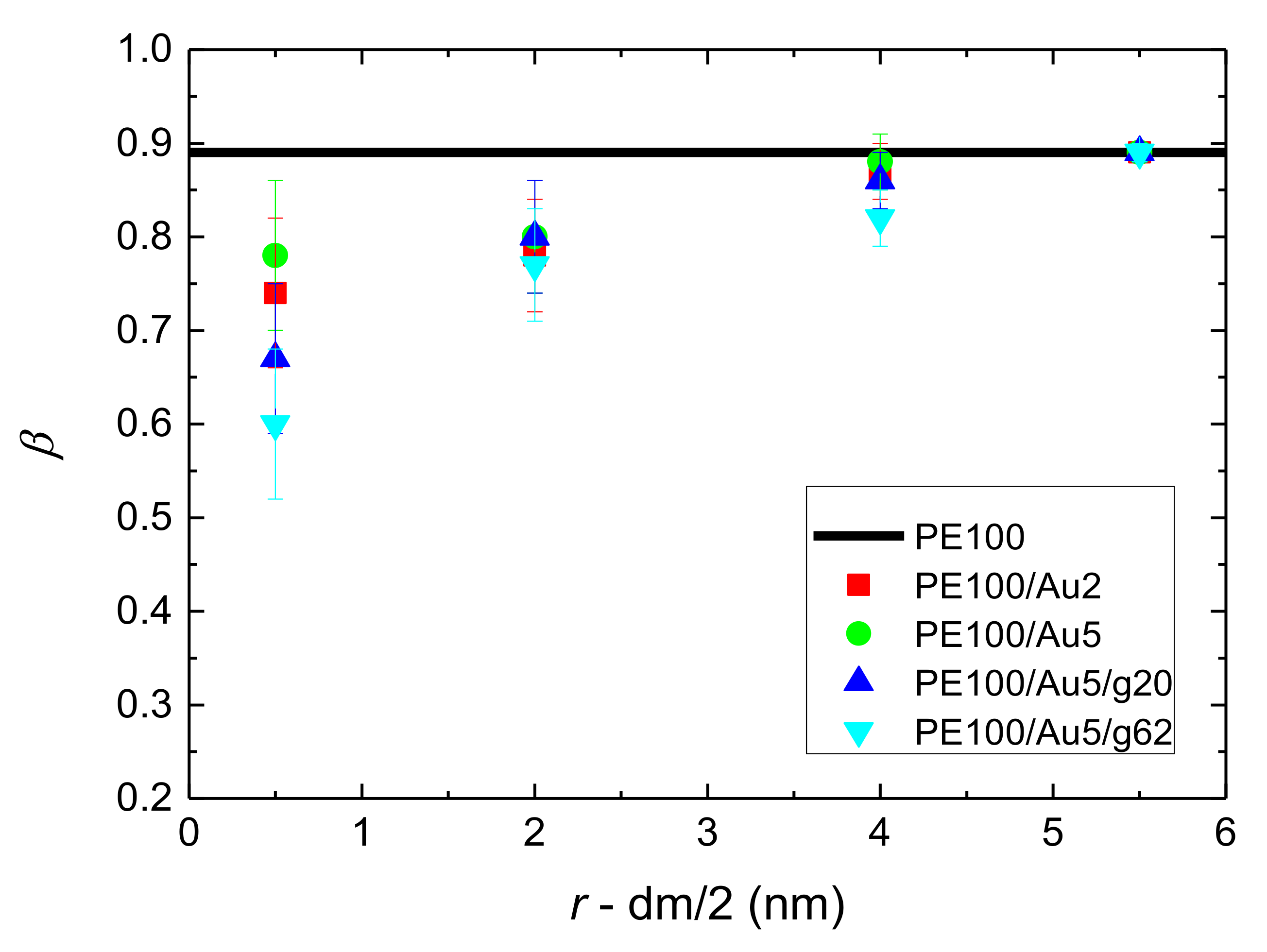
- Orientational relaxation of PE chains in the hybrid systems at the segmental and terminal level was quantified through the time autocorrelation function of a segmental vector and the end-to-end vector of PE chain respectively. In all cases the PE chains which were closer to the Au NP had much slower orientantional dynamics (segmental relaxation time, τseg, is about 10 times longer) in comparison to the bulk one. Moving away from the interface up to a specific distance, we noticed faster C1–3(t) decorrelation, while beyond this, all curves coincide. Moreover, we observed broader distribution of the polymer orientational dynamics in comparison to the bulk one (smaller β-exponent values).
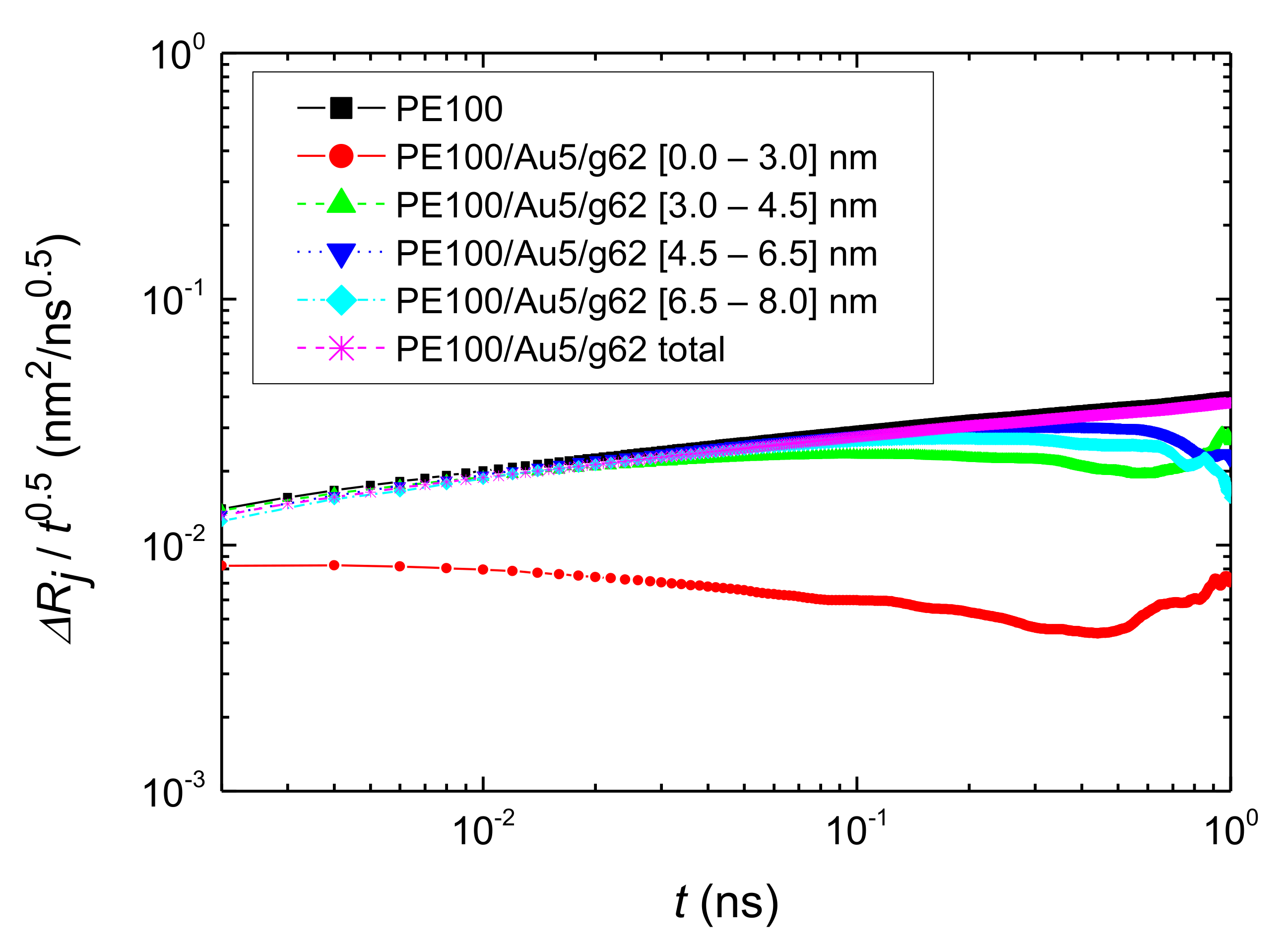
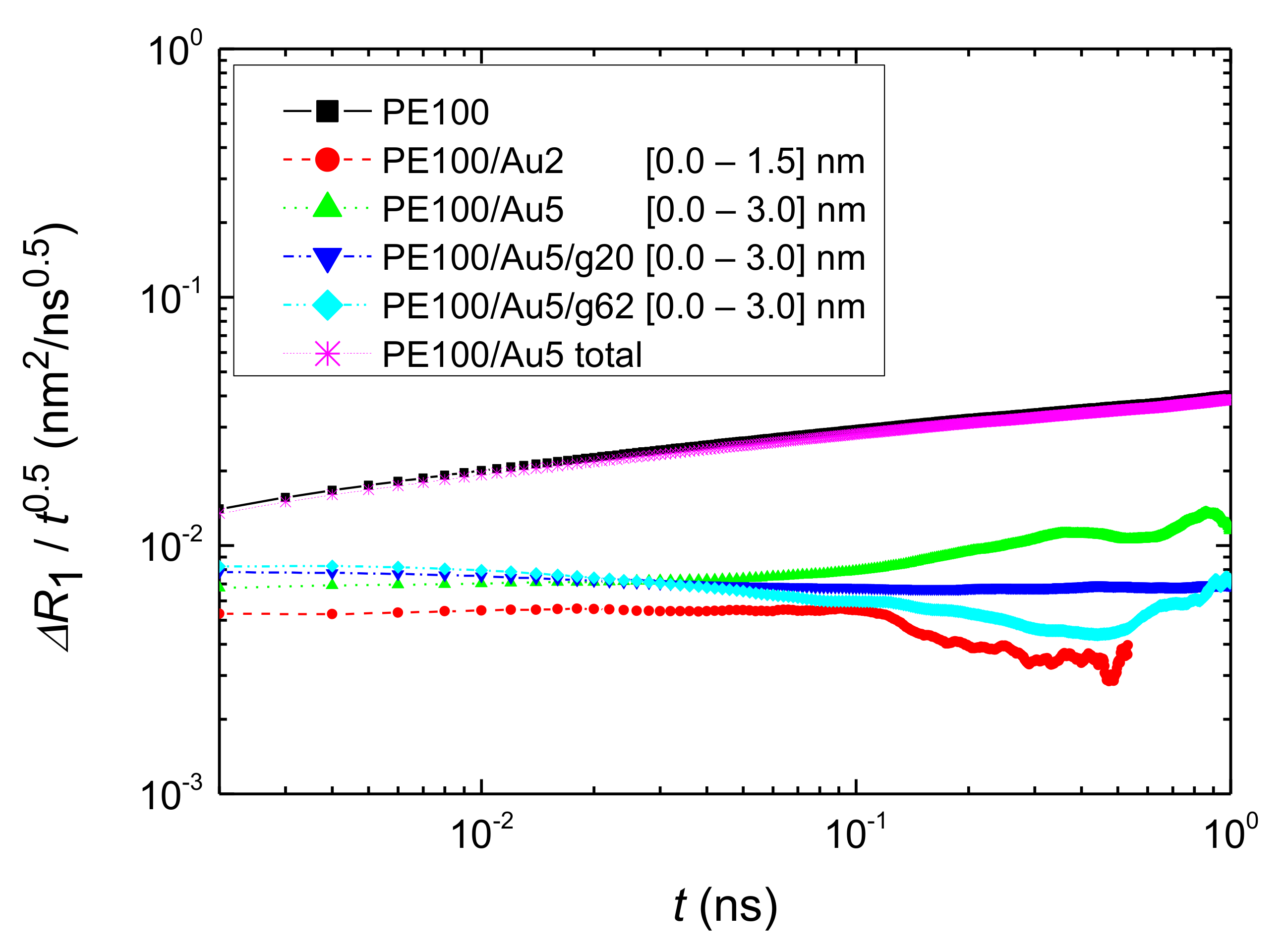
- Translational segmental and center of masses dynamics of PE chains were examined by calculating the average mean-square displacement. Due to the polymer/gold nanoparticle interfaces, for all model hybrid systems, PE chains closer to the Au NP are slower, compared to the bulk one.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Non-Bonded Interactions | ||||
|---|---|---|---|---|
| Lennard-Jones | ||||
| Atom Types | mass (g/mol) | σ (nm) | ε (kJoule/mol) | |
| CH2 | 14.027 | 0.395 | 0.3824 | |
| CH3 | 15.035 | 0.395 | 0.3824 | |
| S–CH2 | 32.066–14.027 | 0.372 | 0.7219 | |
| S–CH3 | 32.066–15.035 | 0.372 | 0.8761 | |
| Morse | ||||
| Atom Types | mass (g/mol) | D0 (kJoule/mol) | α (nm−1) | r0 (nm) |
| Au–CH2 | 196.967–14.027 | 1.6885 | 11.69 | 0.4085 |
| Au–CH3 | 196.967–15.035 | 1.6885 | 11.69 | 0.4085 |
| Bonded Interactions | |||||
|---|---|---|---|---|---|
| Bond | b (nm) | kb (kJ/mol·nm2) | |||
| CH2–CH2 | 0.154 | 100,000.00 | |||
| CH2–CH3 | 0.154 | 100,000.00 | |||
| CH3–CH2 | 0.154 | 100,000.00 | |||
| S–CH2 | 0.181 | fixed | |||
| Angle | θ° (deg) | kθ (kJ/mol * rad2) | |||
| CH2–CH2–CH2 | 114 | 519.611 | |||
| CH3–CH2–CH2 | 114 | 519.611 | |||
| CH2–CH2–CH3 | 114 | 519.611 | |||
| S–CH2–CH2 | 114 | 519.611 | |||
| Dihedral | (KJ/mol) | (KJ/mol) | (KJ/mol) | (KJ/mol) | |
| CH3–CH2–CH2–CH2 | 4.276 | −1.12968 | 13.1545 | 0.00 | |
| CH2–CH2–CH2–CH2 | 4.276 | −1.12968 | 13.1545 | 0.00 | |
| CH2–CH2–CH2–CH3 | 4.276 | −1.12968 | 13.1545 | 0.00 | |
| S–CH2–CH2–CH2 | 4.276 | −1.12968 | 13.1545 | 0.00 | |
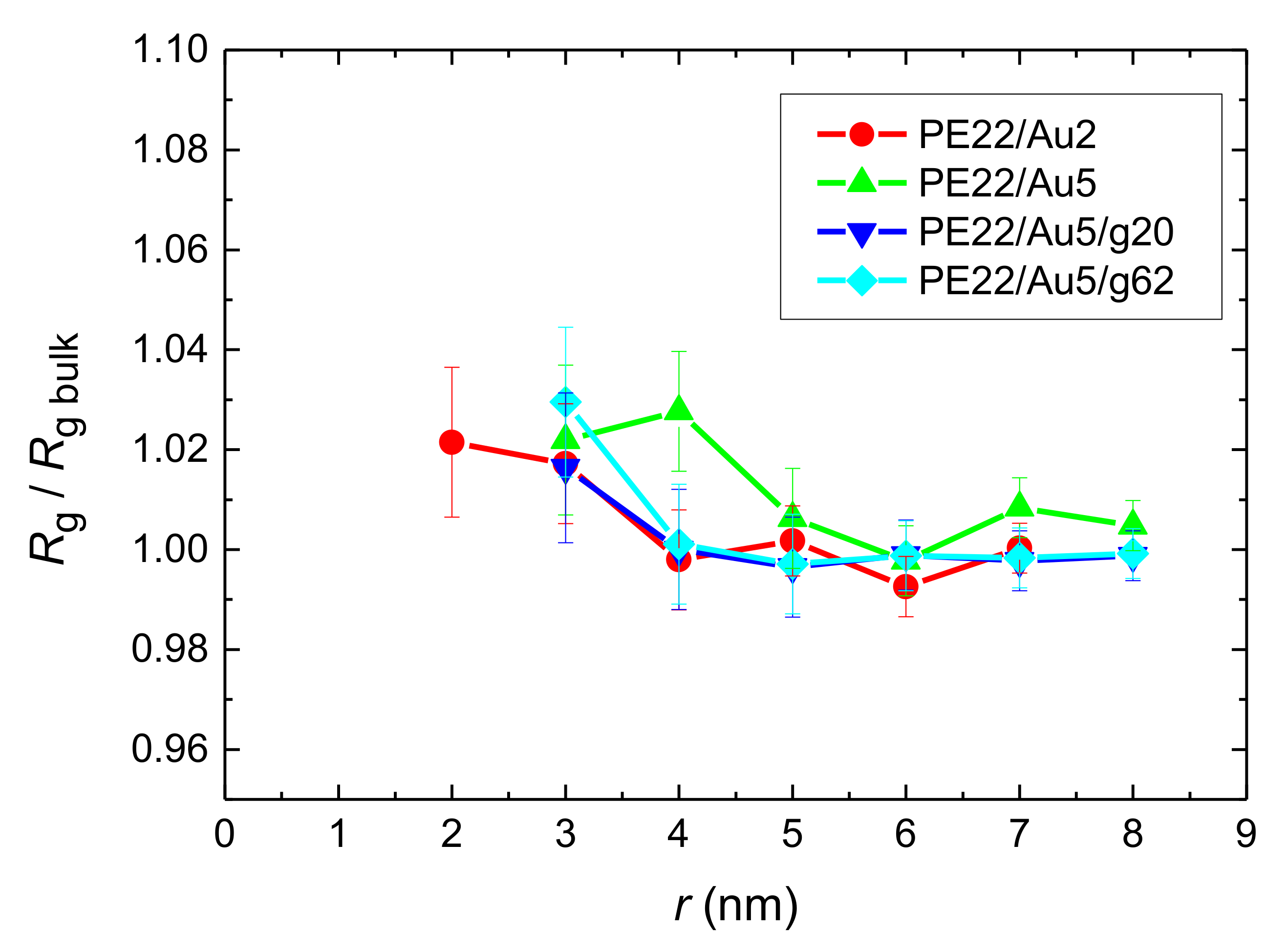
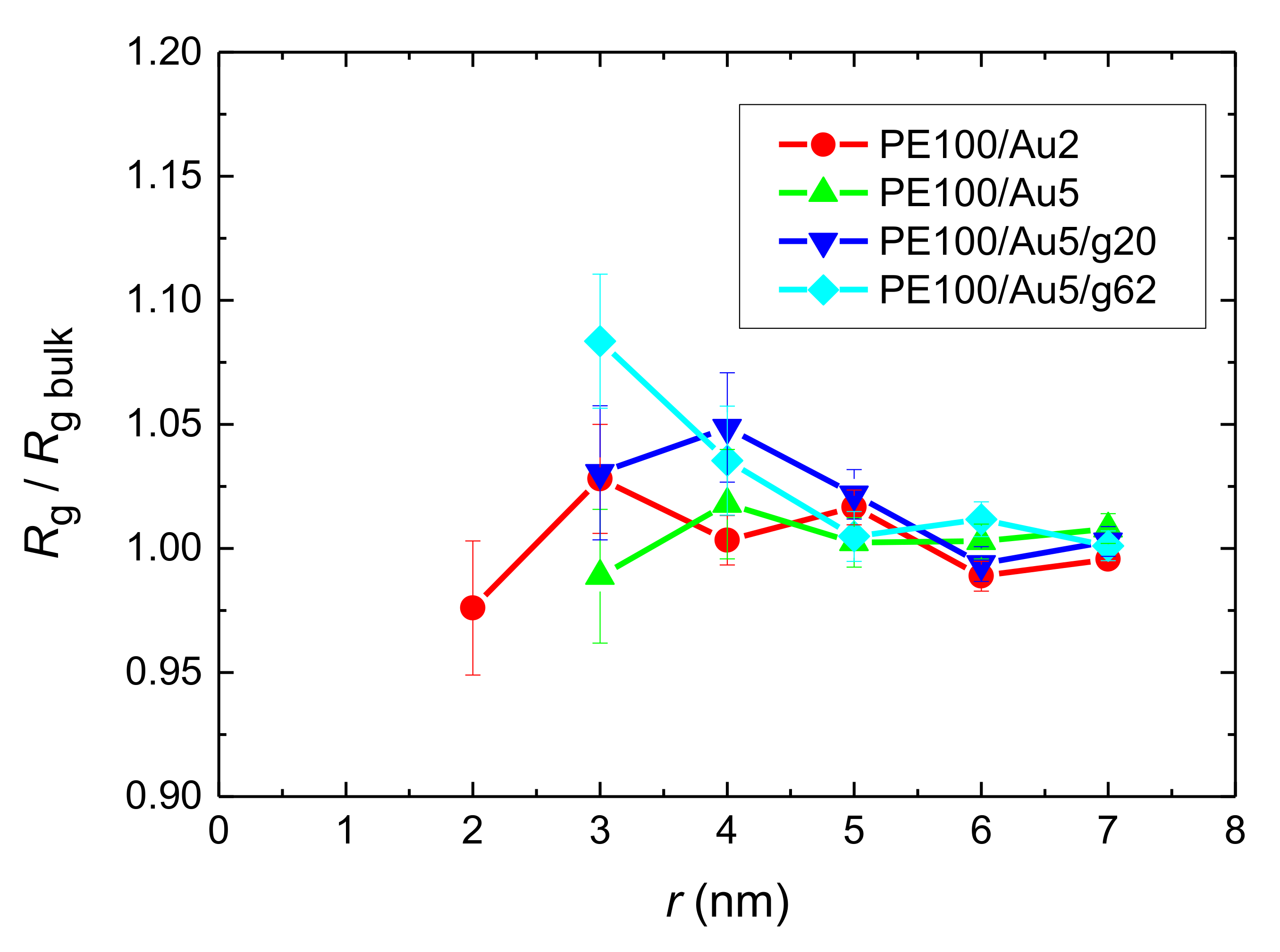
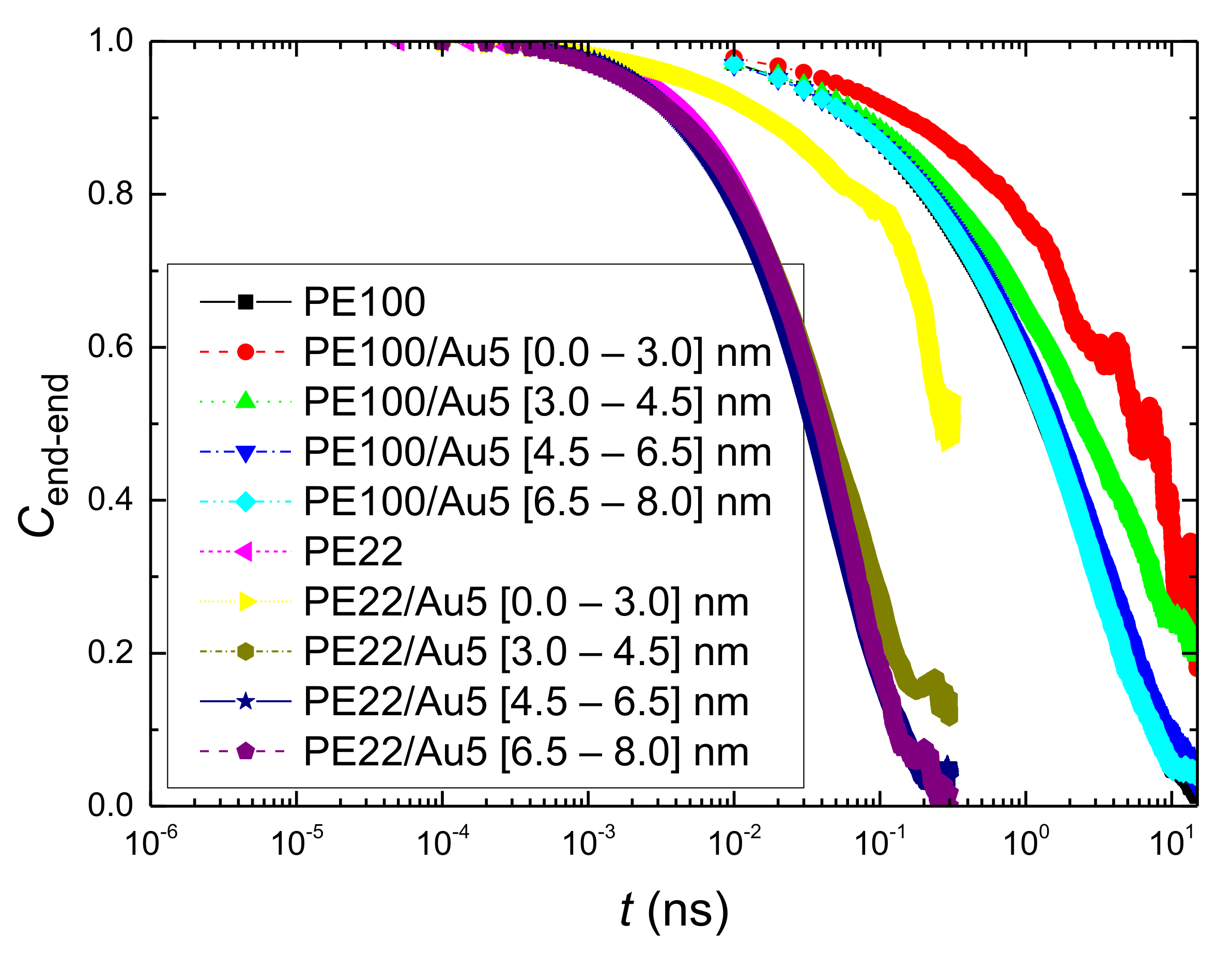
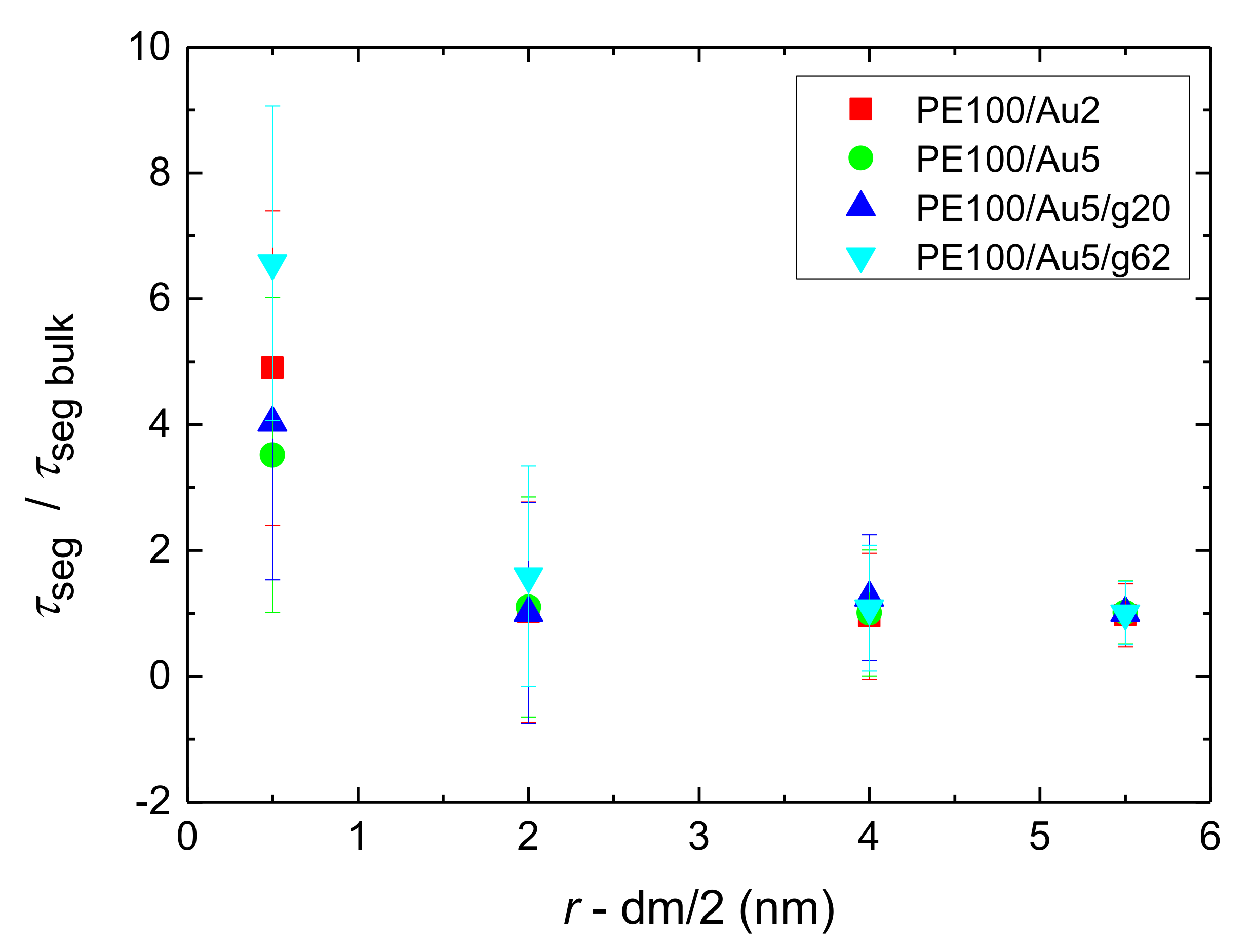

References
- Fu, S.-Y.; Sun, Z.; Huang, P.; Li, Y.-Q.; Hu, N. Some basic aspects of polymer nanocomposites: A critical review. Nano Mater. Sci. 2019, 1, 2–30. [Google Scholar] [CrossRef]
- Alonso-Redondo, E.; Belliard, L.; Rolle, K.; Graczykowski, B.; Tremel, W.; Djafari-Rouhani, B.; Fytas, G. Robustness of elastic properties in polymer nanocomposite films examined over the full volume fraction range. Sci. Rep. 2018, 8, 16986. [Google Scholar] [CrossRef] [PubMed]
- Bačová, P.; Rissanou, A.N.; Harmandaris, V.; Harmaris, V. Edge-Functionalized Graphene as a Nanofiller: Molecular Dynamics Simulation Study. Macromolecules 2015, 48, 9024–9038. [Google Scholar] [CrossRef]
- Srivastava, S.; Schaefer, J.L.; Yang, Z.; Tu, Z.; Archer, L.A. 25th Anniversary Article: Polymer-Particle Composites: Phase Stability and Applications in Electrochemical Energy Storage. Adv. Mater. 2013, 26, 201–234. [Google Scholar] [CrossRef]
- Kumar, S.K.; Krishnamoorti, R. Nanocomposites: Structure, Phase Behavior, and Properties. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 37–58. [Google Scholar] [CrossRef] [PubMed]
- Giannelis, E.P. Polymer Layered Silicate Nanocomposites. Adv. Mater. 1996, 8, 29–35. [Google Scholar] [CrossRef]
- Balazs, A.C.; Emrick, T.; Russell, T.P. Nanoparticle Polymer Composites: Where Two Small Worlds Meet. Science 2006, 314, 1107–1110. [Google Scholar] [CrossRef]
- Devi, J.M. Aggregation of thiol coated gold nanoparticles: A simulation study on the effect of polymer coverage density and solvent. Comput. Mater. Sci. 2014, 86, 174–179. [Google Scholar] [CrossRef]
- Ma, J.-Z.; Liu, Y.-H.; Bao, Y.; Liu, J.-L.; Zhang, J. Research advances in polymer emulsion based on “core–shell” structure particle design. Adv. Colloid Interface Sci. 2013, 197, 118–131. [Google Scholar] [CrossRef]
- Chrissopoulou, K.; Andrikopoulos, K.S.; Fotiadou, S.; Bollas, S.; Karageorgaki, C.; Christofilos, D.; Voyiatzis, G.A.; Anastasiadis, S.H. Crystallinity and Chain Conformation in PEO/Layered Silicate Nanocomposites. Macromolecules 2011, 44, 9710–9722. [Google Scholar] [CrossRef]
- Corbierre, M.K.; Cameron, N.S.; Sutton, M.; Laaziri, K.; Lennox, R.B. Gold Nanoparticle/Polymer Nanocomposites: Dispersion of Nanoparticles as a Function of Capping Agent Molecular Weight and Grafting Density. Langmuir 2005, 21, 6063–6072. [Google Scholar] [CrossRef]
- Kotelyanskii, M.; Theodorou, D.N. Simulation Methods for Polymers; Marcel Dekker Inc.: New York, NY, USA, 2004. [Google Scholar]
- Dhoke, S.K.; Khanna, A. Study on electrochemical behavior of Nano-ZnO modified alkyd-based waterborne coatings. J. Appl. Polym. Sci. 2009, 113, 2232–2237. [Google Scholar] [CrossRef]
- Laachachi, A.; Ruch, D.; Addiego, F.; Ferriol, M.; Cochez, M.; Cuesta, J.M.L. Effect of ZnO and organo-modified montmorillonite on thermal degradation of poly(methyl methacrylate) nanocomposites. Polym. Degrad. Stab. 2009, 94, 670–678. [Google Scholar] [CrossRef]
- Dashtizadeh, A.; Abdouss, M.; Mahdavi, H.; Khorassani, M. Acrylic coatings exhibiting improved hardness, solvent resistance and glossiness by using silica nano-composites. Appl. Surf. Sci. 2011, 257, 2118–2125. [Google Scholar] [CrossRef]
- Che, X.-C.; Jin, Y.-Z.; Lee, Y.-S. Preparation of nano-TiO2/polyurethane emulsions via in situ RAFT polymerization. Prog. Org. Coatings 2010, 69, 534–538. [Google Scholar] [CrossRef]
- Zhu, A.; Shi, Z.; Cai, A.; Zhao, F.; Liao, T. Synthesis of core–shell PMMA–SiO2 nanoparticles with suspension–dispersion–polymerization in an aqueous system and its effect on mechanical properties of PVC composites. Polym. Test. 2008, 27, 540–547. [Google Scholar] [CrossRef]
- Wen, X.-F.; Li, M.-Z.; Pi, P.-H.; Chen, J.; Yang, Z.-R. Study of the physicochemical properties of silica powder and the stability of organic–inorganic hybrid emulsion in the presence of ethanol. Colloids Surf. A Physicochem. Eng. Asp. 2008, 327, 103–110. [Google Scholar] [CrossRef]
- Kritikos, G.; Karatasos, K. Temperature dependence of dynamic and mechanical properties in poly(acrylic acid)/graphene oxide nanocomposites. Mater. Today Commun. 2017, 13, 359–366. [Google Scholar] [CrossRef]
- España-Sánchez, B.L.; Ávila-Orta, C.A.; Padilla-Vaca, F.; Neira-Velázquez, M.G.; González-Morones, P.; Rodríguez-González, J.A.; Hernández-Hernández, E.; Rangel-Serrano, A.; Barriga-C, E.D.; Yate, L.; et al. Enhanced Antibacterial Activity of Melt Processed Poly(propylene) Ag and Cu Nanocomposites by Argon Plasma Treatment. Plasma Process. Polym. 2014, 11, 353–365. [Google Scholar] [CrossRef]
- Babu, K.F.; Dhandapani, P.; Maruthamuthu, S.; Kulandainathan, M.A. One pot synthesis of polypyrrole silver nanocomposite on cotton fabrics for multifunctional property. Carbohydr. Polym. 2012, 90, 1557–1563. [Google Scholar] [CrossRef] [PubMed]
- Palza, H. Antimicrobial Polymers with Metal Nanoparticles. Int. J. Mol. Sci. 2015, 16, 2099–2116. [Google Scholar] [CrossRef] [PubMed]
- Nascimento, H.P.; Oliveira, M.D.; De Melo, C.P.; Silva, G.J.; Cordeiro, M.T.; Andrade, C.A. An impedimetric biosensor for detection of dengue serotype at picomolar concentration based on gold nanoparticles-polyaniline hybrid composites. Colloids Surfaces B Biointerfaces 2011, 86, 414–419. [Google Scholar] [CrossRef] [PubMed]
- Pérez-López, A.M.; Rubio-Ruiz, B.; Sebastian, V.; Hamilton, L.; Adam, C.; Bray, T.L.; Irusta, S.; Brennan, P.M.; Lloyd-Jones, G.C.; Sieger, D.; et al. Gold-Triggered Uncaging Chemistry in Living Systems. Angew. Chem. Int. Ed. 2017, 56, 12548–12552. [Google Scholar] [CrossRef]
- Shevach, M.; Fleischer, S.; Shapira, A.; Dvir, T. Gold Nanoparticle-Decellularized Matrix Hybrids for Cardiac Tissue Engineering. Nano Lett. 2014, 14, 5792–5796. [Google Scholar] [CrossRef]
- Ribeiro, M.; Ferraz, M.P.; Monteiro, F.J.; Fernandes, M.H.; Beppu, M.M.; Mantione, D.; Sardon, H. Antibacterial silk fibroin/nanohydroxyapatite hydrogels with silver and gold nanoparticles for bone regeneration. Nanomed. Nanotechnol. Biol. Med. 2017, 13, 231–239. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Ye, E.; Lakshminarayanan, R.; Loh, X.J. Recent Advances of Using Hybrid Nanocarriers in Remotely Controlled Therapeutic Delivery. Small 2016, 12, 4782–4806. [Google Scholar] [CrossRef] [PubMed]
- Bodelón, G.; Montes-García, V.; Fernández-López, C.; Pastoriza-Santos, I.; Pérez-Juste, J.; Liz-Marzán, L.M. Au@pNIPAM SERRS Tags for Multiplex Immunophenotyping Cellular Receptors and Imaging Tumor Cells. Small 2015, 11, 4149–4157. [Google Scholar] [CrossRef]
- Xiao, C.; Wu, Q.; Chang, A.; Peng, Y.; Xu, W.; Wu, W. Responsive Au@polymer hybrid microgels for the simultaneous modulation and monitoring of Au-catalyzed chemical reaction. J. Mater. Chem. A 2014, 2, 9514–9523. [Google Scholar] [CrossRef]
- Tang, F.; Ma, N.; Wang, X.; He, F.; Li, L. Hybrid conjugated polymer-Ag@PNIPAM fluorescent nanoparticles with metal-enhanced fluorescence. J. Mater. Chem. 2011, 21, 16943–16948. [Google Scholar] [CrossRef]
- Zhang, J.; Ma, N.; Tang, F.; Cui, Q.; He, F.; Li, L. pH- and Glucose-Responsive Core–Shell Hybrid Nanoparticles with Controllable Metal-Enhanced Fluorescence Effects. ACS Appl. Mater. Interfaces 2012, 4, 1747–1751. [Google Scholar] [CrossRef]
- Tamayo, L.; Palza, H.; Bejarano, J.; Zapata, P.A. 8—Polymer Composites with Metal Nanoparticles: Synthesis, Properties, and Applications. In Polymer Composites with Functionalized Nanoparticles; Pielichowski, K., Majka, T.M., Eds.; Elsevier: Amsterdam, The Netherlands, 2019; pp. 249–286. [Google Scholar]
- Ding, Y.; Jiang, Z.; Saha, K.; Kim, C.S.; Kim, S.T.; Landis, R.F.; Rotello, V.M. Gold Nanoparticles for Nucleic Acid Delivery. Mol. Ther. 2014, 22, 1075–1083. [Google Scholar] [CrossRef] [PubMed]
- Lai, C.-T.; Sun, W.; Palekar, R.U.; Thaxton, C.S.; Schatz, G.C. Molecular Dynamics Simulation and Experimental Studies of Gold Nanoparticle Templated HDL-like Nanoparticles for Cholesterol Metabolism Therapeutics. ACS Appl. Mater. Interfaces 2017, 9, 1247–1254. [Google Scholar] [CrossRef]
- Zhou, P.; Jia, S.; Pan, D.; Wang, L.; Gao, J.; Lu, J.; Shi, J.; Tang, Z.; Hua-Jie, L. Reversible Regulation of Catalytic Activity of Gold Nanoparticles with DNA Nanomachines. Sci. Rep. 2015, 5, srep14402. [Google Scholar] [CrossRef]
- Teranishi, T. Fabrication and electronic properties of gold nanoparticle superlattices. Comptes Rendus Chim. 2003, 6, 979–987. [Google Scholar] [CrossRef]
- Kim, Y.; Johnson, A.R.C.; Hupp, J.T. Gold Nanoparticle-Based Sensing of “Spectroscopically Silent” Heavy Metal Ions. Nano Lett. 2001, 1, 165–167. [Google Scholar] [CrossRef]
- Boisselier, E.; Astruc, D. Gold nanoparticles in nanomedicine: Preparations, imaging, diagnostics, therapies and toxicity. Chem. Soc. Rev. 2009, 38, 1759–1782. [Google Scholar] [CrossRef] [PubMed]
- Lal, S.; Link, S.; Halas, N.J. Nano-optics from sensing to waveguiding. Nat. Photon. 2007, 1, 641–648. [Google Scholar] [CrossRef]
- Lu, Y.; Yin, Y.; Li, Z.-Y.; Xia, Y. Synthesis and Self-Assembly of Au@SiO2Core−Shell Colloids. Nano Lett. 2002, 2, 785–788. [Google Scholar] [CrossRef]
- Zhang, R.-C.; Sun, D.; Zhang, R.; Lin, W.-F.; Macias-Montero, M.; Patel, J.; Askari, S.; McDonald, C.; Mariotti, D.; Maguire, P. Gold nanoparticle-polymer nanocomposites synthesized by room temperature atmospheric pressure plasma and their potential for fuel cell electrocatalytic application. Sci. Rep. 2017, 7, 46682. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Tao, P.; Liu, Y.; Xu, H.; Ye, Q.; Hu, H.; Song, C.; Chen, Z.; Shang, W.; Deng, T. Rapid Charging of Thermal Energy Storage Materials through Plasmonic Heating. Sci. Rep. 2015, 4, srep06246. [Google Scholar] [CrossRef] [PubMed]
- Edwardson, T.G.W.; Lau, K.L.; Bousmail, D.; Serpell, C.J.; Sleiman, H.F. Transfer of molecular recognition information from DNA nanostructures to gold nanoparticles. Nat. Chem. 2016, 8, 162–170. [Google Scholar] [CrossRef]
- Govorov, A.O.; Zhang, W.; Skeini, T.; Richardson, H.; Lee, J.; Kotov, N.A. Gold nanoparticle ensembles as heaters and actuators: Melting and collective plasmon resonances. Nanoscale Res. Lett. 2006, 1, 84–90. [Google Scholar] [CrossRef]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Shinde, S.K.; Kim, D.-Y.; Saratale, R.G.; Syed, A.; Ameen, F.; Kim, D.-Y. A Spectral Probe for Detection of Aluminum (III) Ions Using Surface Functionalized Gold Nanoparticles. Nanomaterials 2017, 7, 287. [Google Scholar] [CrossRef] [PubMed]
- Alsawafta, M.; Badilescu, S.; Paneri, A.; Truong, V.-V.; Packirisamy, M. Gold-Poly(methyl methacrylate) Nanocomposite Films for Plasmonic Biosensing Applications. Polymers 2011, 3, 1833–1848. [Google Scholar] [CrossRef]
- Betzer, O.; Meir, R.; Dreifuss, T.; Shamalov, K.; Motiei, M.; Shwartz, A.; Baranes, K.; Cohen, C.J.; Shraga-Heled, N.; Ofir, R.; et al. In-Vitro Optimization of Nanoparticle-Cell Labeling Protocols for In-vivo Cell Tracking Applications. Sci. Rep. 2015, 5, 15400. [Google Scholar] [CrossRef]
- Liu, M.; Li, Q.; Liang, L.; Li, J.; Wang, K.; Li, J.; Lv, M.; Chen, N.; Song, H.; Lee, J.; et al. Real-time visualization of clustering and intracellular transport of gold nanoparticles by correlative imaging. Nat. Commun. 2017, 8, 15646. [Google Scholar] [CrossRef] [PubMed]
- Park, J.H.; Lim, Y.T.; Park, O.O.; Kim, J.K.; Yu, J.-W.; Kim, Y.C. Polymer/Gold Nanoparticle Nanocomposite Light-Emitting Diodes: Enhancement of Electroluminescence Stability and Quantum Efficiency of Blue-Light-Emitting Polymers. Chem. Mater. 2004, 16, 688–692. [Google Scholar] [CrossRef]
- Gupta, R.; Rai, B. Effect of Size and Surface Charge of Gold Nanoparticles on their Skin Permeability: A Molecular Dynamics Study. Sci. Rep. 2017, 7, srep45292. [Google Scholar] [CrossRef]
- Ghosh, P.; Han, G.; De, M.; Kim, C.K.; Rotello, V.M. Gold nanoparticles in delivery applications☆. Adv. Drug Deliv. Rev. 2008, 60, 1307–1315. [Google Scholar] [CrossRef]
- Remediakis, I.N.; López, N.; Nørskov, J.K. CO oxidation on gold nanoparticles: Theoretical studies. Appl. Catal. A Gen. 2005, 291, 13–20. [Google Scholar] [CrossRef]
- Remediakis, I.N.; Lopez, N.; Nørskov, J.K. CO Oxidation on Rutile-Supported Au Nanoparticles. Angew. Chem. Int. Ed. 2005, 44, 1824–1826. [Google Scholar] [CrossRef]
- Haruta, M. 4 Catalysis and applications of gold nanoparticles. In Studies in Surface Science and Catalysis; Anpo, M., Onaka, M., Yamashita, H., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; pp. 31–38. [Google Scholar]
- Von White, G.; Mohammed, F.S.; Kitchens, C.L. Small-Angle Neutron Scattering Investigation of Gold Nanoparticle Clustering and Ligand Structure Under Antisolvent Conditions. J. Phys. Chem. C 2011, 115, 18397–18405. [Google Scholar] [CrossRef]
- Jia, H.; Grillo, I.; Titmuss, S. Small Angle Neutron Scattering Study of Polyelectrolyte Brushes Grafted to Well-Defined Gold Nanoparticle Interfaces. Langmuir 2010, 26, 7482–7488. [Google Scholar] [CrossRef]
- Jang, J.D.; Jeon, S.-W.; Yoon, Y.-J.; Bang, J.; Han, Y.S.; Kim, T.-H. Self-assembly of gold nanoparticles in a block copolymer aggregate template driven by hydrophobic interactions. Polym. Chem. 2019, 10, 6269–6277. [Google Scholar] [CrossRef]
- Coelho, S.C.; Pereira, M.D.C.; Rangel, M.; Ivanova, G. Structural characterization of functionalized gold nanoparticles for drug delivery in cancer therapy: A NMR based approach. Phys. Chem. Chem. Phys. 2015, 17, 18971–18979. [Google Scholar] [CrossRef] [PubMed]
- Zhou, B.; Shen, M.; Banyai, I.; Shi, X. Structural characterization of PEGylated polyethylenimine-entrapped gold nanoparticles: An NMR study. Analyst 2016, 141, 5390–5397. [Google Scholar] [CrossRef] [PubMed]
- Guo, C.; Yarger, J.L. Characterizing gold nanoparticles by NMR spectroscopy. Magn. Reson. Chem. 2018, 56, 1074–1082. [Google Scholar] [CrossRef] [PubMed]
- Farea, M.O.; Abdelghany, A.M.; Oraby, A.H. Optical and dielectric characteristics of polyethylene oxide/sodium alginate-modified gold nanocomposites. RSC Adv. 2020, 10, 37621–37630. [Google Scholar] [CrossRef]
- Mangal, R.; Srivastava, S.; Archer, L.A. Phase stability and dynamics of entangled polymer–nanoparticle composites. Nat. Commun. 2015, 6, 7198. [Google Scholar] [CrossRef] [PubMed]
- Mijovic, J.; Lee, H.; Kenny, J.M.; Mays, J. Dynamics in Polymer−Silicate Nanocomposites As Studied by Dielectric Relaxation Spectroscopy and Dynamic Mechanical Spectroscopy. Macromolecules 2006, 39, 2172–2182. [Google Scholar] [CrossRef]
- Papadimitriou, K.D.; Skountzos, E.N.; Gkermpoura, S.S.; Polyzos, I.; Mavrantzas, V.G.; Galiotis, C.; Tsitsilianis, C. Molecular Modeling Combined with Advanced Chemistry for the Rational Design of Efficient Graphene Dispersing Agents. ACS Macro Lett. 2015, 5, 24–29. [Google Scholar] [CrossRef]
- Monti, S.; Carravetta, V.; Ågren, H. Decoration of gold nanoparticles with cysteine in solution: Reactive molecular dynamics simulations. Nanoscale 2016, 8, 12929–12938. [Google Scholar] [CrossRef] [PubMed]
- Ndoro, T.V.M.; Voyiatzis, E.; Ghanbari, A.; Theodorou, D.N.; Boöhm, M.C.; Muüller-Plathe, F. Interface of Grafted and Ungrafted Silica Nanoparticles with a Polystyrene Matrix: Atomistic Molecular Dynamics Simulations. Macromolecules 2011, 44, 2316–2327. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J.; Banavar, J.R. Computer Simulation of Liquids. Phys. Today 1989, 42, 105–106. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Claredon: Oxford, UK, 1986. [Google Scholar]
- Karatasos, K. Self-Association and Complexation of the Anti-Cancer Drug Doxorubicin with PEGylated Hyperbranched Polyesters in an Aqueous Environment. J. Phys. Chem. B 2013, 117, 2564–2575. [Google Scholar] [CrossRef] [PubMed]
- Karatrantos, A.V.; Clarke, N.; Kröger, M. Modeling of Polymer Structure and Conformations in Polymer Nanocomposites from Atomistic to Mesoscale: A Review. Polym. Rev. 2016, 56, 385–428. [Google Scholar] [CrossRef]
- Harmandaris, V.; Angelopoulou, D.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic molecular dynamics simulation of diffusion in binary liquid n-alkane mixtures. J. Chem. Phys. 2002, 116, 7656–7665. [Google Scholar] [CrossRef]
- Milano, G.; Santangelo, G.; Ragone, F.; Cavallo, L.; Di Matteo, A. Gold Nanoparticle/Polymer Interfaces: All Atom Structures from Molecular Dynamics Simulations. J. Phys. Chem. C 2011, 115, 15154–15163. [Google Scholar] [CrossRef]
- Rissanou, A.N.; Papananou, H.; Petrakis, V.S.; Doxastakis, M.; Andrikopoulos, K.S.; Voyiatzis, G.A.; Chrissopoulou, K.; Harmandaris, V.; Anastasiadis, S.H. Structural and Conformational Properties of Poly(ethylene oxide)/Silica Nanocomposites: Effect of Confinement. Macromolecules 2017, 50, 6273–6284. [Google Scholar] [CrossRef]
- Fotiadou, S.; Karageorgaki, C.; Chrissopoulou, K.; Karatasos, K.; Tanis, I.; Tragoudaras, D.; Frick, B.; Anastasiadis, S.H. Structure and Dynamics of Hyperbranched Polymer/Layered Silicate Nanocomposites. Macromolecules 2013, 46, 2842–2855. [Google Scholar] [CrossRef]
- Voyiatzis, E.; Rahimi, M.; Müller-Plathe, F.; Böhm, M.C. How Thick Is the Polymer Interphase in Nanocomposites? Probing It by Local Stress Anisotropy and Gas Solubility. Macromolecules 2014, 47, 7878–7889. [Google Scholar] [CrossRef]
- Binder, K. Monte Carlo and Molecular Dynamics Simulations in Polymer Science; Oxford University Press: New York, NY, USA, 1995. [Google Scholar]
- Vogiatzis, G.G.; Theodorou, D.N. Structure of Polymer Layers Grafted to Nanoparticles in Silica–Polystyrene Nanocomposites. Macromolecules 2013, 46, 4670–4683. [Google Scholar] [CrossRef]
- Tsourtou, F.D.; Alexiadis, O.; Mavrantzas, V.G.; Kolonias, V.; Housos, E. Atomistic Monte Carlo and molecular dynamics simulation of the bulk phase self-assembly of semifluorinated alkanes. Chem. Eng. Sci. 2015, 121, 32–50. [Google Scholar] [CrossRef]
- Ginzburg, V.V. Polymer-Grafted Nanoparticles in Polymer Melts: Modeling Using the Combined SCFT–DFT Approach. Macromolecules 2013, 46, 9798–9805. [Google Scholar] [CrossRef]
- Posel, Z.; Posocco, P.; Lísal, M.; Fermeglia, M.; Pricl, S. Highly grafted polystyrene/polyvinylpyridine polymer gold nanoparticles in a good solvent: Effects of chain length and composition. Soft Matter 2016, 12, 3600–3611. [Google Scholar] [CrossRef]
- Lin, J.; Zhang, H.; Morovati, V.; Dargazany, R. PEGylation on mixed monolayer gold nanoparticles: Effect of grafting density, chain length, and surface curvature. J. Colloid Interface Sci. 2017, 504, 325–333. [Google Scholar] [CrossRef]
- Hagita, K.; Morita, H.; Doi, M.; Takano, H. Coarse-Grained Molecular Dynamics Simulation of Filled Polymer Nanocomposites under Uniaxial Elongation. Macromolecules 2016, 49, 1972–1983. [Google Scholar] [CrossRef]
- Patra, T.K.; Singh, J.K. Coarse-grain molecular dynamics simulations of nanoparticle-polymer melt: Dispersion vs. agglomeration. J. Chem. Phys. 2013, 138, 144901. [Google Scholar] [CrossRef] [PubMed]
- Quan, X.; Peng, C.; Dong, J.; Zhou, J. Structural properties of polymer-brush-grafted gold nanoparticles at the oil–water interface: Insights from coarse-grained simulations. Soft Matter 2016, 12, 3352–3359. [Google Scholar] [CrossRef]
- Matsuda, T.; Smith, G.D.; Winkler, R.G.; Yoon, D.Y. Stochastic Dynamics Simulations of n-Alkane Melts Confined between Solid Surfaces: Influence of Surface Properties and Comparison with Scheutjens-Fleer Theory. Macromolecules 1995, 28, 165–173. [Google Scholar] [CrossRef]
- Johnston, K.; Harmandaris, V. Hierarchical simulations of hybrid polymer—Solid materials. Soft Matter 2013, 9, 6696–6710. [Google Scholar] [CrossRef]
- Johnston, K.; Harmandaris, V. Hierarchical Multiscale Modeling of Polymer—Solid Interfaces: Atomistic to Coarse-Grained Description and Structural and Conformational Properties of Polystyrene—Gold Systems. Macromolecules 2013, 46, 5741–5750. [Google Scholar] [CrossRef]
- Priestley, R.D.; Ellison, C.J.; Broadbelt, L.J.; Torkelson, J.M. Structural Relaxation of Polymer Glasses at Surfaces, Interfaces, and In Between. Science 2005, 309, 456–459. [Google Scholar] [CrossRef] [PubMed]
- Harmandaris, V.A.; Daoulas, A.K.C.; Mavrantzas, V.G. Molecular Dynamics Simulation of a Polymer Melt/Solid Interface: Local Dynamics and Chain Mobility in a Thin Film of Polyethylene Melt Adsorbed on Graphite. Macromolecules 2005, 38, 5796–5809. [Google Scholar] [CrossRef]
- Daoulas, K.C.; Harmandaris, V.A.; Mavrantzas, V.G. Detailed Atomistic Simulation of a Polymer Melt/Solid Interface: Structure, Density, and Conformation of a Thin Film of Polyethylene Melt Adsorbed on Graphite. Macromolecules 2005, 38, 5780–5795. [Google Scholar] [CrossRef]
- Anastasiadis, S.H.; Karatasos, K.; Vlachos, G.; Manias, E.; Giannelis, E.P. Nanoscopic-Confinement Effects on Local Dynamics. Phys. Rev. Lett. 2000, 84, 915–918. [Google Scholar] [CrossRef] [PubMed]
- Johnson, K.; Harmandaris, V. Properties of short polystyrene chains confined between two gold surfaces through a combined density functional theory and classical molecular dynamics approach. Soft Matter 2012, 8, 6320–6332. [Google Scholar] [CrossRef]
- Mischler, C.; Baschnagel, J.; Dasgupta, S.; Binder, K. Structure and dynamics of thin polymer films: A case study with the bond-fluctuation model. Polymers 2002, 43, 467–476. [Google Scholar] [CrossRef]
- Aoyagi, T.; Takimoto, J.-I.; Doi, M. Molecular dynamics study of polymer melt confined between walls. J. Chem. Phys. 2001, 115, 552–559. [Google Scholar] [CrossRef]
- Rissanou, N.; Power, A.; Harmandaris, V. Structural and Dynamical Properties of Polyethylene/Graphene Nanocomposites through Molecular Dynamics Simulations. Polymers 2015, 7, 390–417. [Google Scholar] [CrossRef]
- Hore, M.J.A.; Korley, L.T.J.; Kumar, S.K. Polymer-Grafted Nanoparticles. J. Appl. Phys. 2020, 128, 030401. [Google Scholar] [CrossRef]
- Ge, T.; Grest, G.S.; Rubinstein, M. Nanorheology of Entangled Polymer Melts. Phys. Rev. Lett. 2018, 120, 057801. [Google Scholar] [CrossRef]
- Peters, B.L.; Salerno, K.M.; Agrawal, A.; Perahia, D.; Grest, G.S. Coarse-Grained Modeling of Polyethylene Melts: Effect on Dynamics. J. Chem. Theory Comput. 2017, 13, 2890–2896. [Google Scholar] [CrossRef]
- Modica, K.J.; Martin, T.B.; Jayaraman, A. Effect of Polymer Architecture on the Structure and Interactions of Polymer Grafted Particles: Theory and Simulations. Macromolecules 2017, 50, 4854–4866. [Google Scholar] [CrossRef]
- Martin, T.B.; Jayaraman, A. Using Theory and Simulations to Calculate Effective Interactions in Polymer Nanocomposites with Polymer-Grafted Nanoparticles. Macromolecules 2016, 49, 9684–9692. [Google Scholar] [CrossRef]
- Ndoro, T.V.M.; Böhm, M.C.; Müller-Plathe, F. Interface and Interphase Dynamics of Polystyrene Chains near Grafted and Ungrafted Silica Nanoparticles. Macromolecules 2011, 45, 171–179. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Theodorou, D.N. Atomistic simulations of long-chain polyethylene melts flowing past gold surfaces: Structure and wall-slip. Mol. Phys. 2020, 118, e1706775. [Google Scholar] [CrossRef]
- Jabbarzadeh, A.; Atkinson, J.; Tanner, R. Nanorheology of molecularly thin films of n-hexadecane in Couette shear flow by molecular dynamics simulation. J. NonNewtonian Fluid Mech. 1998, 77, 53–78. [Google Scholar] [CrossRef]
- Berro, H.; Fillot, N.; Vergne, P.; Tokumasu, T.; Ohara, T.; Kikugawa, G. Energy dissipation in non-isothermal molecular dynamics simulations of confined liquids under shear. J. Chem. Phys. 2011, 135, 134708. [Google Scholar] [CrossRef]
- Bright, K.; Malpass, B.W.; Packham, D.E. Adhesion of Polyethylene to Metals. Nat. Cell Biol. 1969, 223, 1360–1361. [Google Scholar] [CrossRef]
- Suresh, B.; Maruthamuthu, S.; Kannan, M.; Chandramohan, A. Mechanical and surface properties of low-density polyethylene film modified by photo-oxidation. Polym. J. 2011, 43, 398–406. [Google Scholar] [CrossRef]
- Song, H.; Li, B.; Lin, Q.-B.; Wu, H.-J.; Chen, Y. Migration of silver from nanosilver–polyethylene composite packaging into food simulants. Food Addit. Contam. Part A 2011, 28, 1–5. [Google Scholar] [CrossRef] [PubMed]
- Rissanou, A.; Harmandaris, V. Dynamics of Polymer/Graphene Interfacial Systems. Soft Matter 2014, 10, 2876–2888. [Google Scholar] [CrossRef]
- Hautman, J.; Klein, M.L. Simulation of a monolayer of alkyl thiol chains. J. Chem. Phys. 1989, 91, 4994–5001. [Google Scholar] [CrossRef]
- Barmparis, G.D.; Honkala, K.; Remediakis, I.N. Thiolate adsorption on Au(hkl) and equilibrium shape of large thiolate-covered gold nanoparticles. J. Chem. Phys. 2013, 138, 64702. [Google Scholar] [CrossRef] [PubMed]
- Barmparis, G.D.; Remediakis, I.N. Dependence on CO adsorption of the shapes of multifaceted gold nanoparticles: A density functional theory. Phys. Rev. B 2012, 86. [Google Scholar] [CrossRef]
- Rissanou, A.N.; Harmandaris, V. Structural and Dynamical Properties of Polystyrene Thin Films Supported by Multiple Graphene Layers. Macromolecules 2015, 48, 2761–2772. [Google Scholar] [CrossRef]
- Uz, M.; Bulmus, V.; Altinkaya, S.A. Effect of PEG Grafting Density and Hydrodynamic Volume on Gold Nanoparticle–Cell Interactions: An Investigation on Cell Cycle, Apoptosis, and DNA Damage. Langmuir 2016, 32, 5997–6009. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Alexiadis, O.; Harmandaris, V.; Mavrantzas, V.G.; Site, L.D. Atomistic Simulation of Alkanethiol Self-Assembled Monolayers on Different Metal Surfaces via a Quantum, First-Principles Parametrization of the Sulfur−Metal Interaction. J. Phys. Chem. C 2007, 111, 6380–6391. [Google Scholar] [CrossRef]
- Barmparis, G.D.; Lodziana, Z.; Lopez, N.; Remediakis, I.N. Nanoparticle shapes by using Wulff constructions and first-principles calculations. Beilstein J. Nanotechnol. 2015, 6, 361–368. [Google Scholar] [CrossRef] [PubMed]
- Billinge, S.J.L.; Levin, I. The Problem with Determining Atomic Structure at the Nanoscale. Science 2007, 316, 561–565. [Google Scholar] [CrossRef]
- Hadjisavvas, G.; Remediakis, I.N.; Kelires, P.C. Shape and faceting of Si nanocrystals embedded ina−SiO2: A Monte Carlo study. Phys. Rev. B 2006, 74, 165419. [Google Scholar] [CrossRef]
- Herring, C. Some Theorems on the Free Energies of Crystal Surfaces. Phys. Rev. 1951, 82, 87–93. [Google Scholar] [CrossRef]
- Vilé, G.; Baudouin, D.; Remediakis, I.N.; Copéret, C.; López, N.; Pérez-Ramírez, J. Silver Nanoparticles for Olefin Production: New Insights into the Mechanistic Description of Propyne Hydrogenation. ChemCatChem 2013, 5, 3750–3759. [Google Scholar] [CrossRef]
- Li, Q.; Rellán-Piñeiro, M.; Almora-Barrios, N.; Garcia-Ratés, M.; Remediakis, I.N.; López, N. Shape control in concave metal nanoparticles by etching. Nanoscale 2017, 9, 13089–13094. [Google Scholar] [CrossRef] [PubMed]
- Pearson, D.S.; Strate, G.V.; Von Meerwall, E.; Schilling, F.C. Viscosity and self-diffusion coefficient of linear polyethylene. Macromolecules 1987, 20, 1133–1141. [Google Scholar] [CrossRef]
- Turzi, S.S. On the Cartesian definition of orientational order parameters. J. Math. Phys. 2011, 52, 053517. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Vogiatzis, G.G.; Megariotis, G.; Tzoumanekas, C.; Theodorou, D.N. Multiscale Simulations of Graphite-Capped Polyethylene Melts: Brownian Dynamics/Kinetic Monte Carlo Compared to Atomistic Calculations and Experiment. Macromolecules 2019, 52, 7503–7523. [Google Scholar] [CrossRef]
- Gulde, M.; Rissanou, A.N.; Harmandaris, V.; Müller, M.; Schäfer, S.; Ropers, C. Dynamics and Structure of Monolayer Polymer Crystallites on Graphene. Nano Lett. 2016, 16, 6994–7000. [Google Scholar] [CrossRef]
- Flory, P.J.; Volkenstein, M. Statistical mechanics of chain molecules. Biopolymers 1969, 8, 699–700. [Google Scholar] [CrossRef]
- Williams, G.; Watts, D.C. Non-symmetrical dielectric relaxation behaviour arising from a simple empirical decay function. Trans. Faraday Soc. 1970, 66, 80–85. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic Molecular Dynamics Simulation of Polydisperse Linear Polyethylene Melts. Macromolecules 1998, 31, 7934–7943. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N.; Kröger, M.; Ramírez, J.; Öttinger, H.C.; Vlassopoulos, D. Crossover from the Rouse to the Entangled Polymer Melt Regime: Signals from Long, Detailed Atomistic Molecular Dynamics Simulations, Supported by Rheological Experiments. Macromolecules 2003, 36, 1376–1387. [Google Scholar] [CrossRef]
- Paul, W.; Smith, G.D.; Yoon, D.Y. Static and Dynamic Properties of an-C100H202Melt from Molecular Dynamics Simulations. Macromolecules 1997, 30, 7772–7780. [Google Scholar] [CrossRef]
- Smith, G.D.; Bedrov, D. Dispersing Nanoparticles in a Polymer Matrix: Are Long, Dense Polymer Tethers Really Necessary? Langmuir 2009, 25, 11239–11243. [Google Scholar] [CrossRef] [PubMed]
| Name | Au NP Diameter | Au Atoms | Free PE Chains | Au/PE w/w% | Au/PE v/v% | Grafted PE Chains | Grafted PE Mers/Chain |
|---|---|---|---|---|---|---|---|
| PE100/Au2 | 25.1 Å | 459 | 1200 | 4.9 | 0.2 | - | - |
| PE100/Au5 | 50.2 Å | 3101 | 1200 | 37.6 | 1.7 | - | - |
| PE100/Au5/g20 | 50.4 Å | 2461 | 1200 | 29.7 | 1.7 | 53 | 20 |
| PE100/Au5/g62 | 50.4 Å | 2461 | 1200 | 29.7 | 1.7 | 53 | 62 |
| PE100 | - | - | 240 | - | - | - | - |
| PE22/Au2 | 25.1 Å | 459 | 5040 | 5.8 | 0.4 | - | - |
| PE22/Au5 | 50.2 Å | 3101 | 5040 | 38.8 | 1.6 | - | - |
| PE22/Au5/g20 | 50.4 Å | 2461 | 5040 | 30.8 | 1.6 | 53 | 20 |
| PE22/Au5/g62 | 50.4 Å | 2461 | 5040 | 30.8 | 1.6 | 53 | 62 |
| PE22 | - | - | 420 | - | - | - | - |
| Property | Bare Au NPs | Grafted Au NPs |
|---|---|---|
| Density | 0.5–1.0 nm | 1.7–3.0 nm |
| Structural | 0.5–1.0 nm | 0.5–1.3 nm |
| Local (segmental) dynamics | 1.0–2.0 nm | 0.5–1.5 nm |
| Global dynamics | 3.0–4.0 nm | 1.0–2.0 nm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Power, A.J.; Remediakis, I.N.; Harmandaris, V. Interface and Interphase in Polymer Nanocomposites with Bare and Core-Shell Gold Nanoparticles. Polymers 2021, 13, 541. https://doi.org/10.3390/polym13040541
Power AJ, Remediakis IN, Harmandaris V. Interface and Interphase in Polymer Nanocomposites with Bare and Core-Shell Gold Nanoparticles. Polymers. 2021; 13(4):541. https://doi.org/10.3390/polym13040541
Chicago/Turabian StylePower, Albert J., Ioannis N. Remediakis, and Vagelis Harmandaris. 2021. "Interface and Interphase in Polymer Nanocomposites with Bare and Core-Shell Gold Nanoparticles" Polymers 13, no. 4: 541. https://doi.org/10.3390/polym13040541
APA StylePower, A. J., Remediakis, I. N., & Harmandaris, V. (2021). Interface and Interphase in Polymer Nanocomposites with Bare and Core-Shell Gold Nanoparticles. Polymers, 13(4), 541. https://doi.org/10.3390/polym13040541