An Extended Thickness-Dependent Moisture Absorption Model for Unidirectional Carbon/Epoxy Composites
Abstract
1. Introduction
2. Materials and Methods
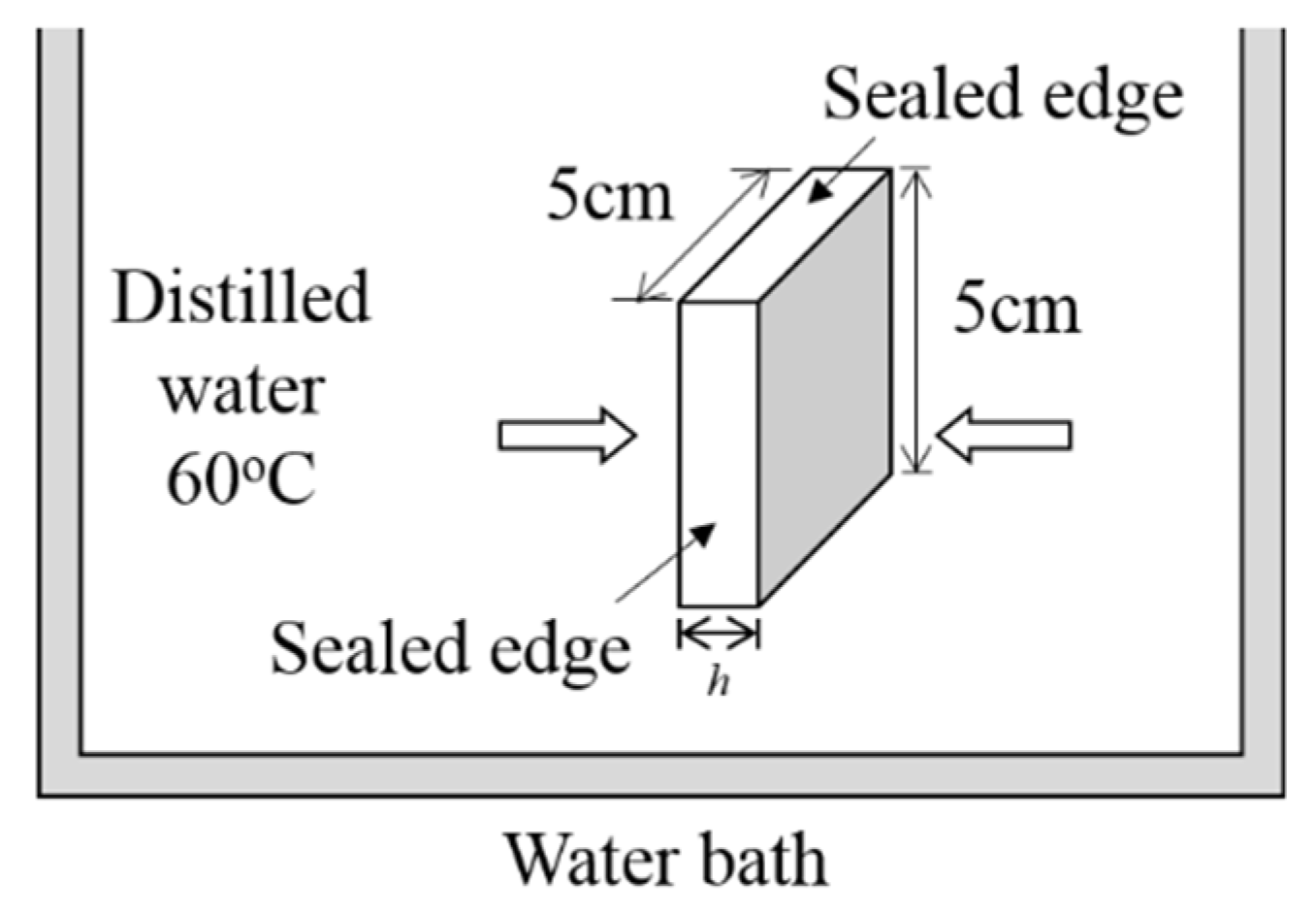
2.1. Materials and Specimens
2.2. Moisture Absorption Test
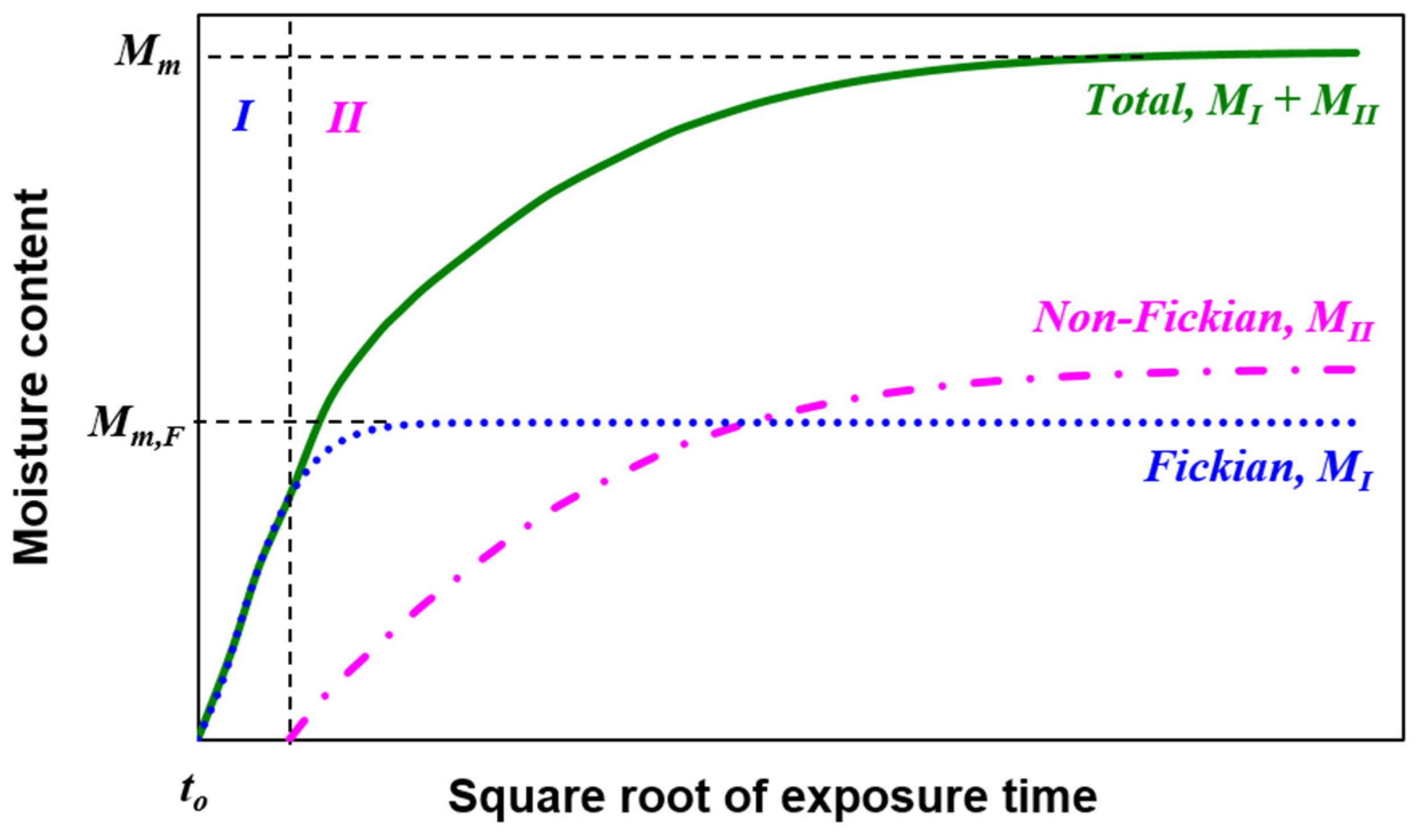
3. Thickness-Dependent Moisture Absorption Model
4. Experimental Results and Discussion
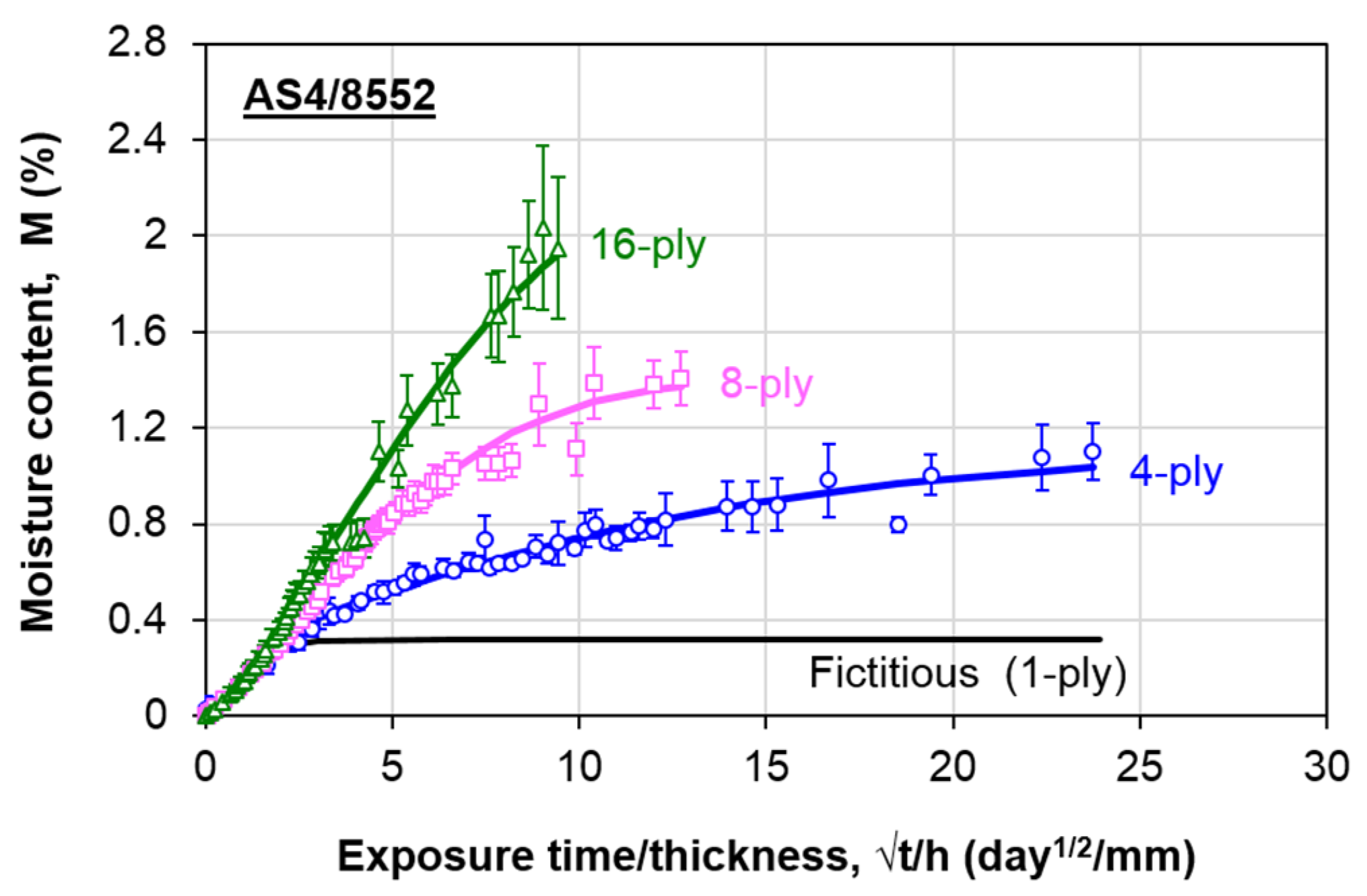
4.1. Moisture Absorption Curves
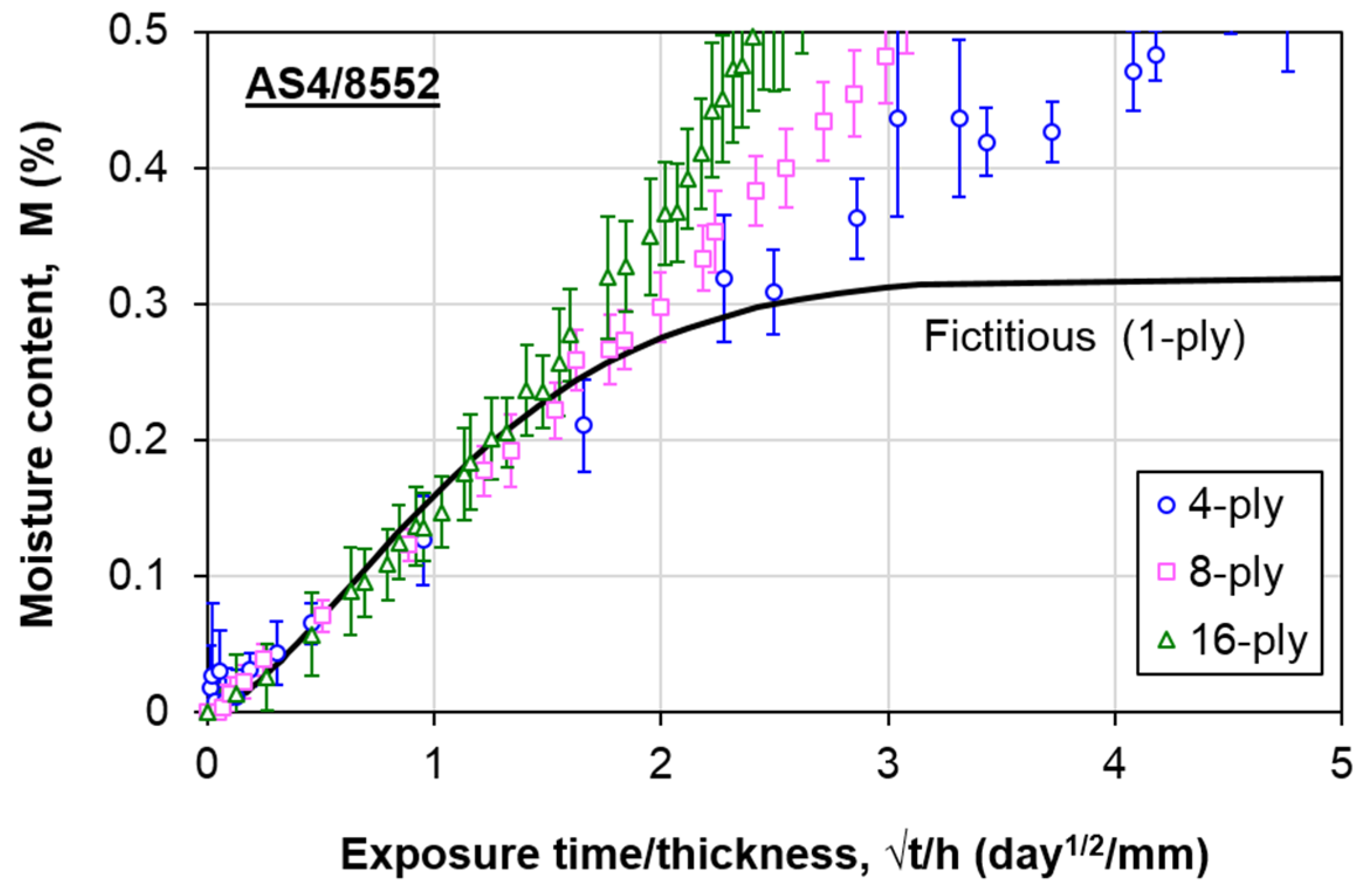
4.2. Fictitious Fickian Diffusion Curve
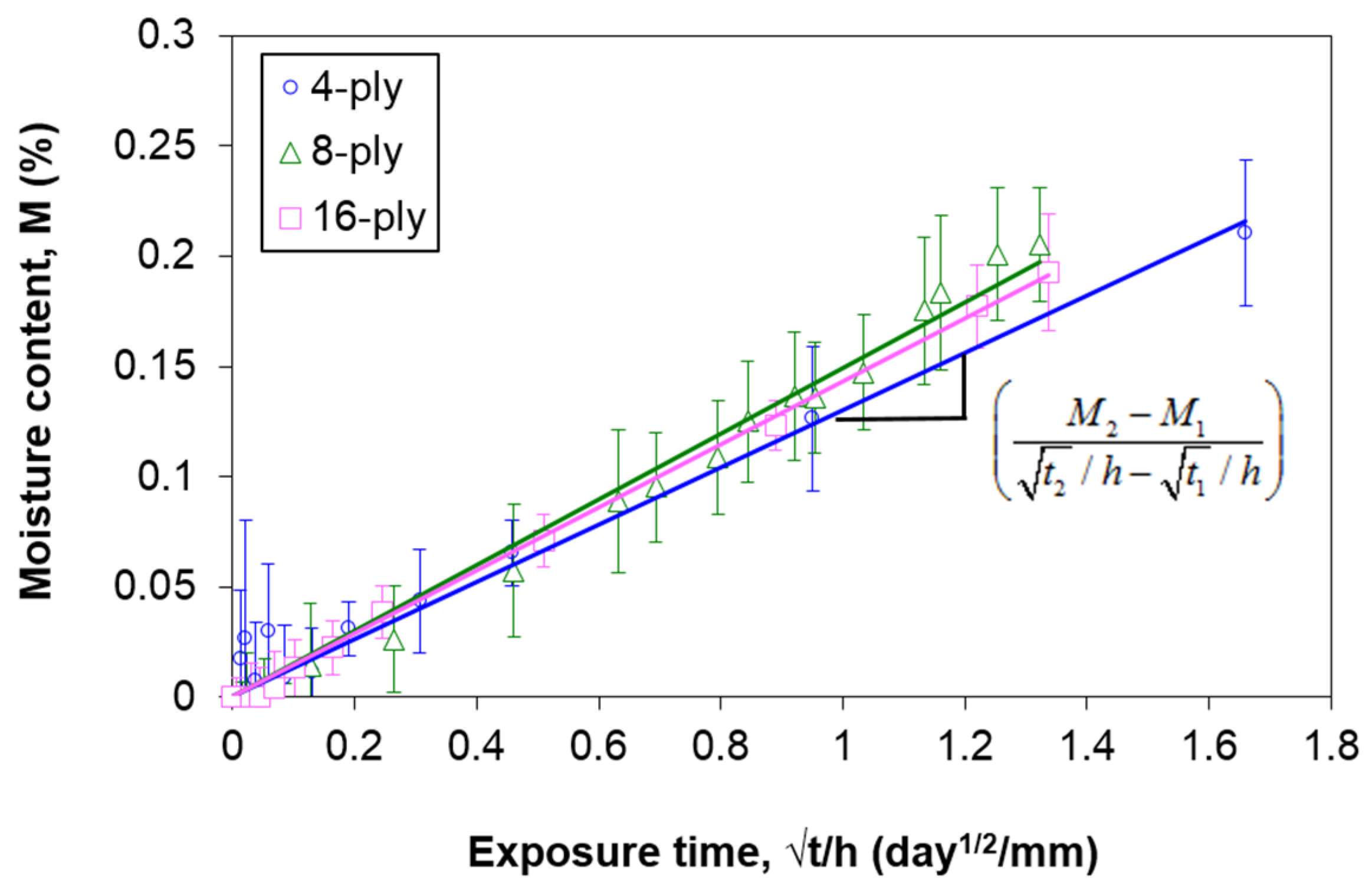
- The deviation of the reduced experimental curves in this study was estimated to be 60% of Mm,F. From there, estimate the average Mm,F for the material (Table 1). A coefficient of variation (C.V) of 8.11% signifies good repeatability of the results;
- Determine the apparent diffusivity, Dz, of the fictitious Fickian curve using Equation (2). For the composite used in this study, Dz is estimated to be 4.25 × 10−2 mm2/day;
- Plot the fictitious Fickian curve (which is the first term in Equation (1)) using Equation (3). For the AS4/8552 carbon/epoxy composite, the unit ply thickness hF = 0.15 mm.
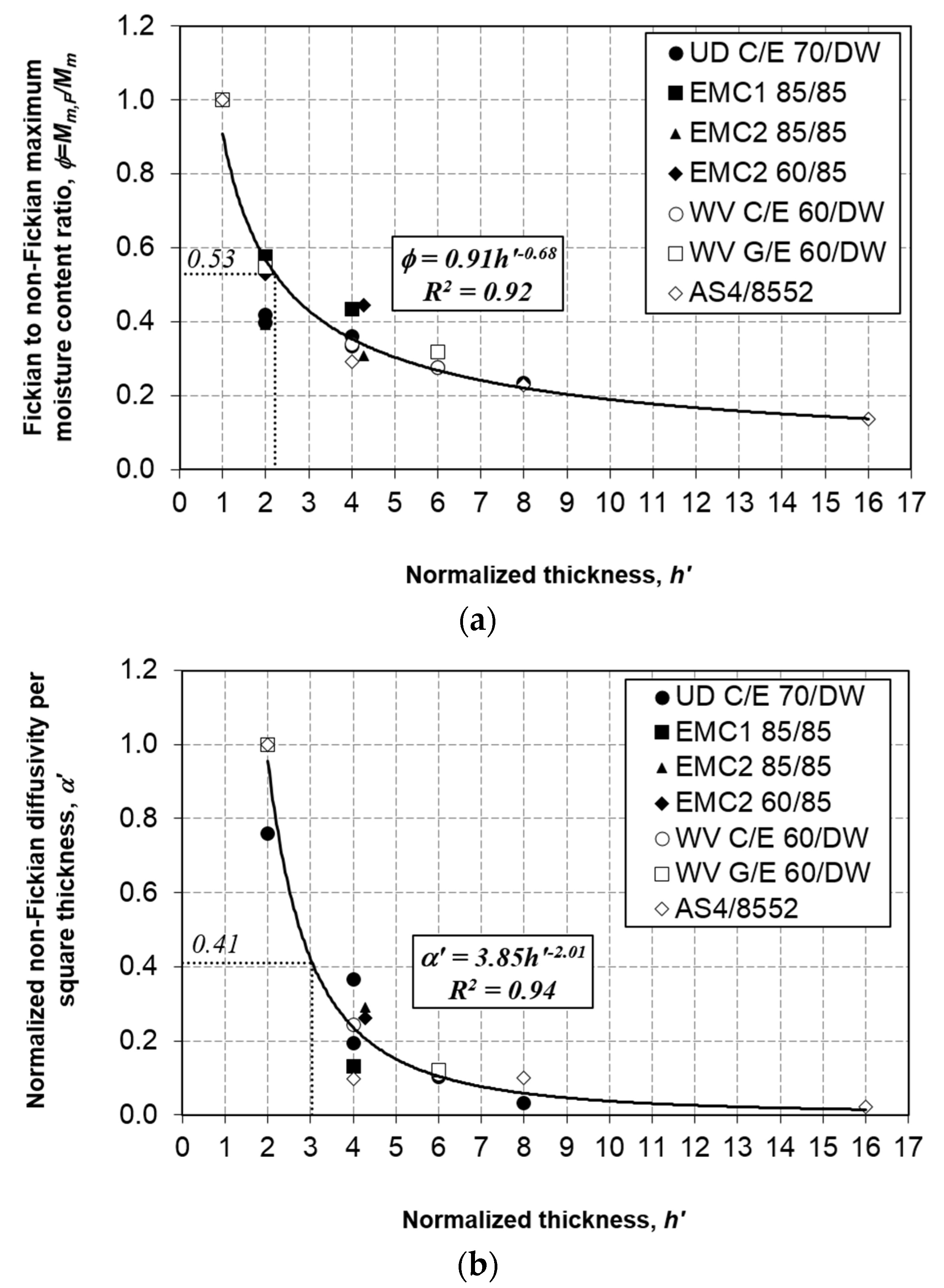
4.3. Determination of Non-Fickian Parameters
- Calculate ϕ = Mm,F/Mm for each thickness;
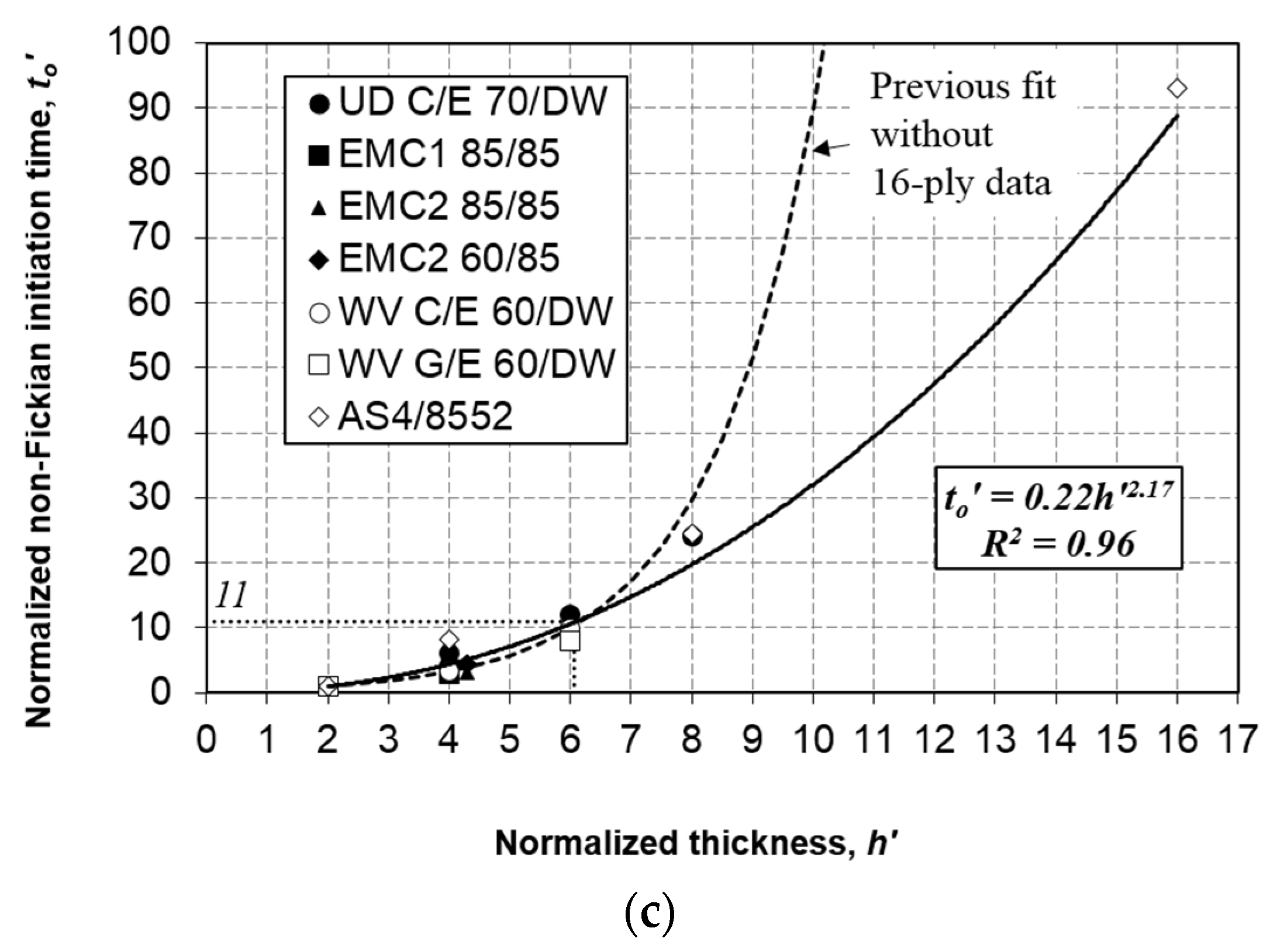
- Plot the fictitious Fickian curve, together with the experimental curves (Figure 5). Estimate the deviation point (√to/h) from the figure. From there, determine to for each thickness;
- Subtract the experimental moisture content M(t) from the analytical MI(t) (which is determined in the previous section). This step gives the experimental MII(t) term;
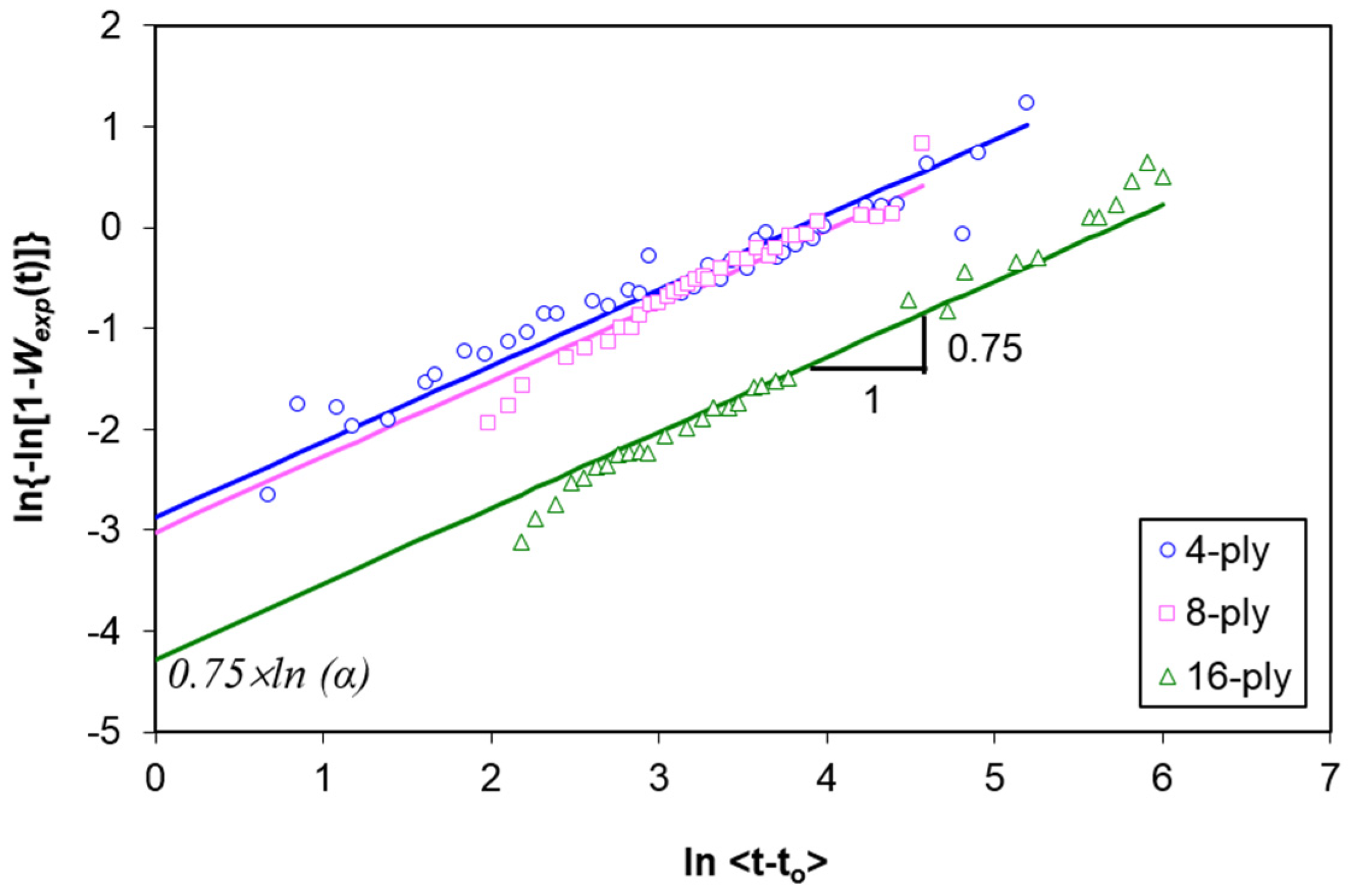
- Plot the experimental W(t) (denoted as Wexp(t)) using Equation (4) below:
- Apply logarithms of both sides twice for the analytical W(t) term:
- Plot the curve of ln[−ln[1 − Wexp(t)]] versus 0.75 × ln<t − to>, and fit the data with a straight line. From the ordinate intersection (0.75 × ln α), determine the value of α. As an example, Figure 6 labels the slope and y-intercept of the 16-ply composite.
4.4. Generalization of Non-Fickian Parameters
4.5. Characterization of the Distribution Model for Non-Fickian Parameters
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guermazi, N.; Ben Tarjem, A.; Ksouri, I.; Ayedi, H.F. On the durability of FRP composites for aircraft structures in hygrothermal conditioning. Compos. Part B Eng. 2016, 85, 294–304. [Google Scholar] [CrossRef]
- Middendorf, P.; Metzner, C. Aerospace applications of non-crimp fabric composites. In Non-Crimp Fabric Composites; Lomov, S.V., Ed.; Woodhead Publishing: Cambridge, UK, 2011; pp. 441–449e. [Google Scholar]
- Mad Asasaari, S.F.; Wong, K.J.; Tamin, M.N.; Johar, M. Moisture absorption effects on the mechanical properties of carbon/epoxy composites. Int. J. Struct. Integr. 2020, 11, 605–614. [Google Scholar] [CrossRef]
- Wong, K.J.; Gong, X.J.; Aivazzadeh, S.; Tamin, M.N. Moisture effects on patch bonded composite repairs. Key Eng. Mater. 2016, 709, 3–6. [Google Scholar] [CrossRef]
- Wong, K.J.; Israr, H.A.; Tamin, M.N. Characterisation of moisture absorption effects on the strength of composite materials. Adv. Mater. Res. 2015, 1125, 69–73. [Google Scholar] [CrossRef]
- Barbosa, A.P.C.; Fulco, A.P.P.; Guerra, E.S.; Arakaki, F.K.; Tosatto, M.; Costa, M.C.B.; Melo, J.D.D. Accelerated aging effects on carbon fiber/epoxy composites. Compos. Part B Eng. 2017, 110, 298–306. [Google Scholar] [CrossRef]
- Meng, M.; Rizvi, M.J.; Grove, S.M.; Le, H.R. Effects of hygrothermal stress on the failure of CFRP composites. Compos. Struct. 2015, 133, 1024–1035. [Google Scholar] [CrossRef]
- Johar, M.; Chong, W.W.F.; Kang, H.S.; Wong, K.J. Effects of moisture absorption on the different modes of carbon/epoxy composites delamination. Polym. Degrad. Stab. 2019, 165, 117–125. [Google Scholar] [CrossRef]
- Davidson, B.D.; Kumar, M.; Soffa, M.A. Influence of mode ratio and hygrothermal condition on the delamination toughness of a thermoplastic particulate interlayered carbon/epoxy composite. Compos. Part A Appl. Sci. Manuf. 2009, 40, 67–79. [Google Scholar] [CrossRef]
- LeBlanc, L.R.; LaPlante, G. Experimental investigation and finite element modeling of mixed-mode delamination in a moisture-exposed carbon/epoxy composite. Compos. Part A Appl. Sci. Manuf. 2016, 81, 202–213. [Google Scholar] [CrossRef]
- Zhao, Y.; Liu, W.; Seah, L.K.; Chai, G.B. Delamination growth behavior of a woven E-glass/bismaleimide composite in seawater environment. Compos. Part B Eng. 2016, 106, 332–343. [Google Scholar] [CrossRef]
- Bao, L.-R.; Yee, A.F.; Lee, C.Y.C. Moisture absorption and hygrothermal aging in a bismaleimide resin. Polymer 2001, 42, 7327–7333. [Google Scholar] [CrossRef]
- Bao, L.-R.; Yee, A.F. Moisture diffusion and hygrothermal aging in bismaleimide matrix carbon fiber composites. Part I: Uni-weave composites. Compos. Sci. Technol. 2002, 62, 2099–2110. [Google Scholar] [CrossRef]
- Bao, L.-R.; Yee, A.F. Moisture diffusion and hygrothermal aging in bismaleimide matrix carbon fiber composites. Part II: Woven and hybrid composites. Compos. Sci. Technol. 2002, 62, 2111–2119. [Google Scholar] [CrossRef]
- Karbhari, V.M.; Xian, G. Hygrothermal effects on high Vf pultruded unidirectional carbon/epoxy composites: Moisture uptake. Compos. Part B Eng. 2009, 40, 41–49. [Google Scholar] [CrossRef]
- Manfredi, L.B.; Santis, H.D.; Vázquez, A. Influence of the addition of montmorillonite to the matrix of unidirectional glass fibre/epoxy composites on their mechanical and water absorption properties. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1726–1731. [Google Scholar] [CrossRef]
- Wang, Y.; Zhu, W.; Wan, B.; Meng, Z.; Han, B. Hygrothermal ageing behavior and mechanism of carbon nanofibers modified flax fiber-reinforced epoxy laminates. Compos. Part A Appl. Sci. Manuf. 2021, 140, 106142. [Google Scholar] [CrossRef]
- Berens, A.R.; Hopfenberg, H.B. Diffusion and relaxation in glassy polymer powders: 2. Separation of diffusion and relaxation parameters. Polymer 1978, 19, 489–496. [Google Scholar] [CrossRef]
- Yian, Z.; Zhiying, W.; Keey, S.L.; Boay, C.G. Long-term viscoelastic response of E-glass/bismaleimide composite in seawater environment. Appl. Compos. Mater. 2015, 22, 693–709. [Google Scholar] [CrossRef]
- Carter, H.G.; Kibler, K.G. Langmuir-type model for anomalous moisture diffusion in composite resins. J. Compos. Mater. 1978, 12, 118–131. [Google Scholar] [CrossRef]
- LaPlante, G.; Ouriadov, A.V.; Lee-Sullivan, P.; Balcom, B.J. Anomalous moisture diffusion in an epoxy adhesive detected by magnetic resonance imaging. J. Appl. Polym. Sci. 2008, 109, 1350–1359. [Google Scholar] [CrossRef]
- Ameli, A.; Dalta, N.V.; Papini, M.; Spelt, J.K. Hygrothermal properties of highly toughened epoxy adhesives. J. Adhes. 2010, 86, 698–725. [Google Scholar] [CrossRef]
- Lee, M.H.; Peppas, N.A. Water transport in graphite/epoxy composites. J. Appl. Polym. Sci. 1993, 47, 1349–1359. [Google Scholar] [CrossRef]
- Popineau, S.; Rondeau-Mouro, C.; Sulpice-Gaillet, C.; Shanahan, M.E.R. Free/bound water absorption in an epoxy adhesive. Polymer 2005, 46, 10733–10740. [Google Scholar] [CrossRef]
- La Saponara, V. Environmental and chemical degradation of carbon/epoxy and structural adhesive for adhesive for aerospace applications: Fickian and anomalous diffusion, Arrhenius kinetics. Compos. Struct. 2011, 93, 2180–2195. [Google Scholar] [CrossRef]
- Barink, M.; Mavinkurve, A.; Janssen, J. Predicting non-Fickian moisture diffusion in EMCs for application in micro-electronic devices. Microelectron. Reliab. 2016, 62, 45–49. [Google Scholar] [CrossRef]
- Loh, W.K.; Crocombe, A.D.; Abdel Wahab, M.M.; Ashcroft, I.A. Modelling anomalous moisture uptake, swelling and thermal characteristics of a rubber toughened epoxy adhesive. Int. J. Adhes. Adhes. 2005, 25, 1–12. [Google Scholar] [CrossRef]
- Placette, M.D.; Fan, X.; Zhao, J.-H.; Edwards, D. Dual stage modeling of moisture absorption and desorption in epoxy mold compounds. Microelectron. Reliab. 2012, 52, 1401–1408. [Google Scholar] [CrossRef]
- Shirangi, M.H.; Auerspeg, J.; Koyuncu, M.; Walter, H.; Müller, W.H.; Michel, B. Characterization of dual-stage moisture diffusion, residual moisture content and hygroscopic swelling of epoxy molding compounds. In Proceedings of the 9th EuroSime2008, Freibury, Germany, 20–23 April 2008. [Google Scholar]
- Wong, K.J.; Low, K.O.; Israr, H.A.; Tamin, M.N. Thickness-dependent non-Fickian moisture absorption in epoxy molding compounds. Microelectron. Reliab. 2016, 65, 160–166. [Google Scholar] [CrossRef]
- Johar, M.; Kang, H.S.; Chong, W.W.F.; Wong, K.J. A further generalized thickness-dependent non-Fickian moisture absorption model using plain woven epoxy composites. Polym. Test. 2018, 69, 522–527. [Google Scholar] [CrossRef]
- Rajaram, A.N.; Gin Boay, C.; Srikanth, N. Effect of curing on the hygrothermal behaviour of epoxy and its carbon composite material. Compos. Commun. 2020, 22, 100507. [Google Scholar] [CrossRef]
- ASTM International. ASTM D5229. Standard Test Method for Moisture Absorption Properties and Equilibrium Conditioning of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2010. [Google Scholar]

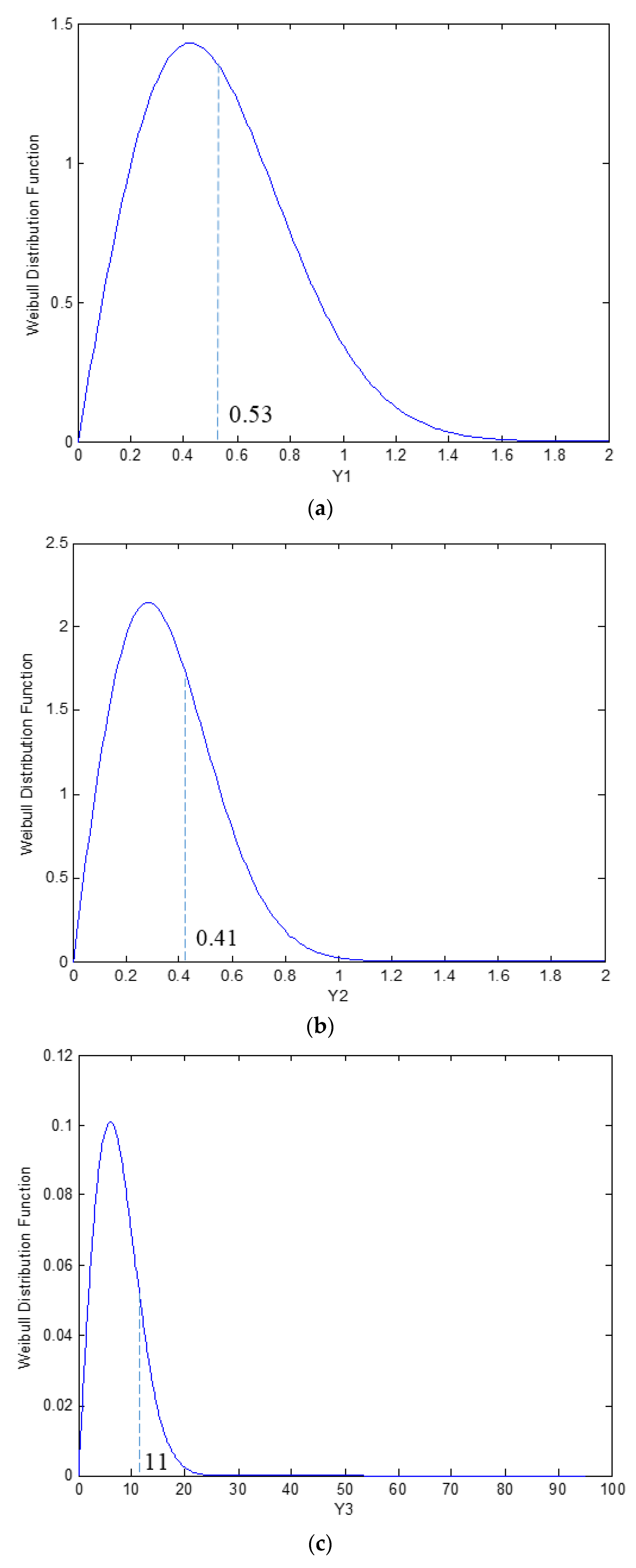

| No. of Ply | Mm,F | Slope, (M2 − M1)/(√t2/h − √t1/h) | R2 |
|---|---|---|---|
| 4 | 0.319 | 0.1356 | 0.9843 |
| 8 | 0.297 | 0.1486 | 0.9957 |
| 16 | 0.349 | 0.1646 | 0.9801 |
| Average | 0.322 | 0.1496 | |
| S.D | 0.0261 | 0.0145 | - |
| C.V (%) | 8.11 | 9.71 | - |
| h (mm) | 0.6 | 1.2 | 2.4 | |
|---|---|---|---|---|
| Parameter | ||||
| ϕ | 0.29 | 0.23 | 0.14 | |
| α (10−3 day−1) | 19.3 | 20.1 | 4.2 | |
| to (hours) | 24 | 71 | 269 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azizan, A.; Johar, M.; Karam Singh, S.S.; Abdullah, S.; Koloor, S.S.R.; Petrů, M.; Wong, K.J.; Tamin, M.N. An Extended Thickness-Dependent Moisture Absorption Model for Unidirectional Carbon/Epoxy Composites. Polymers 2021, 13, 440. https://doi.org/10.3390/polym13030440
Azizan A, Johar M, Karam Singh SS, Abdullah S, Koloor SSR, Petrů M, Wong KJ, Tamin MN. An Extended Thickness-Dependent Moisture Absorption Model for Unidirectional Carbon/Epoxy Composites. Polymers. 2021; 13(3):440. https://doi.org/10.3390/polym13030440
Chicago/Turabian StyleAzizan, Azisyahirah, Mahzan Johar, Salvinder Singh Karam Singh, Shahrum Abdullah, Seyed Saeid Rahimian Koloor, Michal Petrů, King Jye Wong, and Mohd Nasir Tamin. 2021. "An Extended Thickness-Dependent Moisture Absorption Model for Unidirectional Carbon/Epoxy Composites" Polymers 13, no. 3: 440. https://doi.org/10.3390/polym13030440
APA StyleAzizan, A., Johar, M., Karam Singh, S. S., Abdullah, S., Koloor, S. S. R., Petrů, M., Wong, K. J., & Tamin, M. N. (2021). An Extended Thickness-Dependent Moisture Absorption Model for Unidirectional Carbon/Epoxy Composites. Polymers, 13(3), 440. https://doi.org/10.3390/polym13030440











