Manufacturing and Analysis of Overmolded Hybrid Fiber Polyamide 6 Composite
Abstract
1. Introduction
2. Experimental
2.1. Materials
2.2. Manufacturing of Hybrid Overmolded Composites
2.3. Design of Experiment
2.4. Characterization
- W = pendulum weight.
- R = pendulum arm length, m.
- A = initial angle of the pendulum hammer.
- Β = final angle after impact.
- Ec = corrected energy, absorbed by breaking test specimen, J.
- ac = Charpy impact strength, kJ/m2
- h = specimen thickness, mm.
- b = specimen width, mm.
3. Results and Discussion
3.1. Testing Results
3.2. Analysis of Variance (ANOVA) and Model Fitting of the Responses
3.2.1. Flexural Strength
3.2.2. Impact Strength
+ 0.052 AC − 0.036 AD + (2.6 × 10−3) BC − 0.027 BD − 0.039 CD − 0.045 A2
+ 9.24 B2 + 9.89 C2 + 0.088 D2
3.2.3. Interlaminar Shear Strength (ILSS)
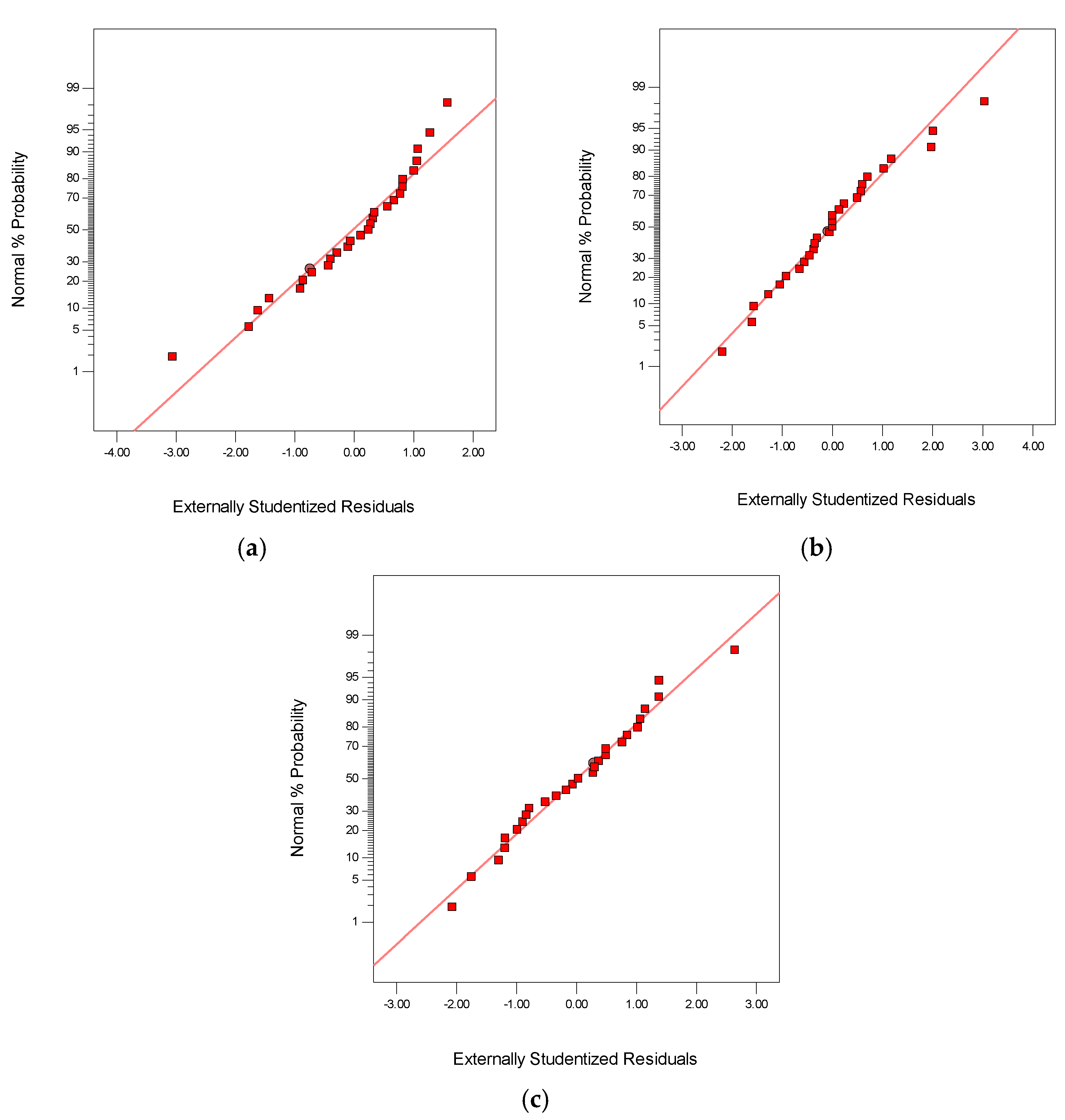
3.3. Diagnostic Plots of the Responses
3.4. Effect of Process Factors on the Responses
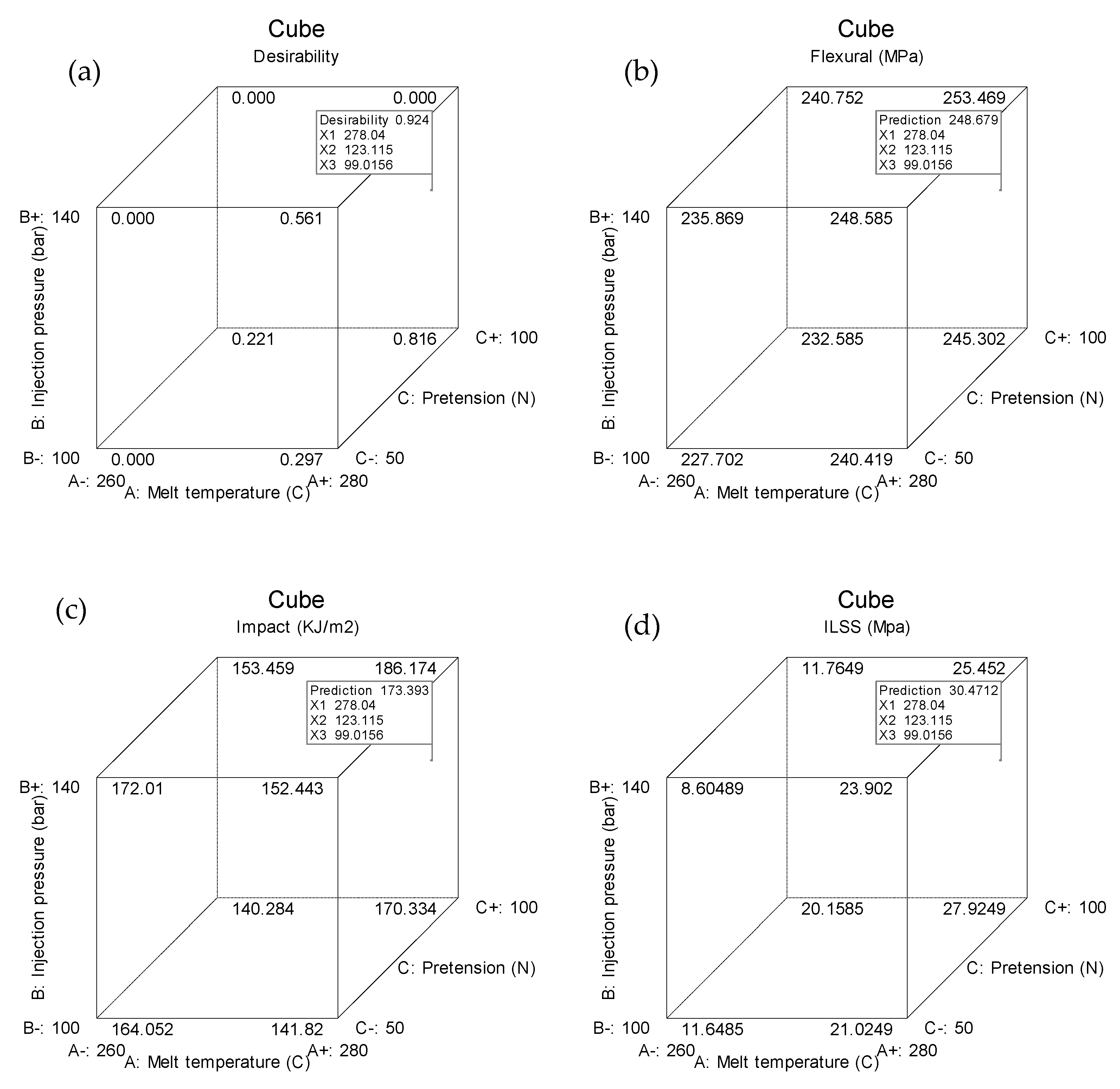
3.5. Optimization of Process Parameters
3.6. Confirmation Experiment
3.7. Microstructure of Fractured Surface
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Wan, Y.; Takahashi, J. Tensile properties and aspect ratio simulation of transversely isotropic discontinuous carbon fiber reinforced thermoplastics. Compos. Sci. Technol. 2016, 137, 167–176. [Google Scholar] [CrossRef]
- Friedrich, K.; Almajid, A.A. Manufacturing Aspects of Advanced Polymer Composites for Automotive Applications. Appl. Compos. Mater. 2013, 20, 107–128. [Google Scholar] [CrossRef]
- Jiang, B.; Fu, L.; Zhang, M.; Weng, C. Effect of thermal gradient on interfacial behavior of hybrid fiber reinforced polypropylene composites fabricated by injection overmolding technique. Polym. Compos. 2020, 41, 4064–4073. [Google Scholar] [CrossRef]
- Huang, P.W.; Peng, H.-S.; Hwang, S.-J.; Huang, C.-T. The Low Breaking Fiber Mechanism and Its Effect on the Behavior of the Melt Flow of Injection Molded Ultra-Long Glass Fiber Reinforced Polypropylene Composites. Polymers 2021, 13, 2492. [Google Scholar] [CrossRef] [PubMed]
- Gibson Ronald, F. Principles of Composite Material Mechanics, 3rd ed.; CRC Press: New York, NY, USA, 1994. [Google Scholar]
- Rosato, D.V. Plastics Processing Data Handbook, 2nd ed.; Chapman & Hall: London, UK, 1997. [Google Scholar]
- Wang, Q.; Sun, L.; Li, L.; Yang, W.; Zhang, Y.; Dai, Z.; Xiong, Z. Experimental and numerical investigations on microstructures and mechanical properties of hybrid fiber reinforced thermoplastic polymer. Polym. Test. 2018, 70, 215–225. [Google Scholar] [CrossRef]
- Sealy, C.; Egger, P. Molding the future: ENGEL takes composite approach to composites. In Reinforced Plastics; Elsevier Ltd.: Amsterdam, The Netherlands, 2016; pp. 10–13. [Google Scholar]
- Shao, Y.; Xu, F.; Liu, W.; Zhou, M.; Li, W.; Hui, D. Influence of cryogenic treatment on mechanical and interfacial properties of carbon nanotube fiber/bisphenol-F epoxy composite. Compos. Part B 2017, 125, 195–202. [Google Scholar] [CrossRef]
- Song, M.G.; Kweon, J.H.; Choi, J.H.; Byun, J.H.; Song, M.H.; Shin, S.J.; Lee, T.J. Effect of manufacturing methods on the shear strength of composite single-lap bonded joints. Compos. Struct. 2010, 92, 2194–2202. [Google Scholar] [CrossRef]
- Hassan, A.K.F.; Abdullah, O.A. New methodology for prestressing fiber composites. Univers. J. Mech. Eng. 2015, 3, 252–261. [Google Scholar] [CrossRef][Green Version]
- Mertiny, P.; Ellyin, F. Influence of the filament winding tension on physical and mechanical properties of reinforced composites. Compos. Part A 2002, 33, 1615–1622. [Google Scholar] [CrossRef]
- Torayca. T700S Data Sheet No. CFA-005; Toray Carbon Fibers: Santa Ana, CA, USA, 2018. [Google Scholar]
- Toray Industries. AMILAN PA 6 30 GF; Toray Industries: Tokyo, Japan, 2006. [Google Scholar]
- Mostafa, N.H.; Ismarrubie, Z.N.; Sapuan, S.M. Fibre prestressed polymer-matrix composites: A review. J. Compos. Mater. 2017, 51, 39–66. [Google Scholar] [CrossRef]
- Budiyantoro, C.; Rochardjo, H.S.B.; Nugroho, G. Effects of Processing Variables of Extrusion–Pultrusion Method on the Impregnation Quality of Thermoplastic Composite Filaments. Polymers 2020, 12, 2833. [Google Scholar] [CrossRef]
- Goodship, V. Practical Guide to Injection Moulding; Rapra Technology: Shropshire, UK, 2004. [Google Scholar]
- Antony, J. Design of Experiments for Engineers and Scientists; Buttonworth-Heineman: London, UK, 2014. [Google Scholar]
- Bradley, N. The Response Surface Methodology Department of Mathematical Sciences; Indiana University of South Bend: South Bend, IN, USA, 2017. [Google Scholar]
- Ryu, Y.; Sohn, J.; Sohn, J.S.; Cha, S.W. Shrinkage and Warpage Minimization of Glass-Fiber-Reinforced Polyamide 6 Parts by Microcellular Foam Injection Molding. Polymers 2020, 12, 889. [Google Scholar] [CrossRef]
- Sing, J.; Ching, Y.C.; Abdullah, L.C.; Ching, Y.K.; Razali, D.; Gan, S.N. Optimization of Mechanical Properties for Polyoxymethylene/Glass Fiber/Polytetrafluoroethylene Composites Using Response Surface Methodology. Polymers 2018, 10, 338. [Google Scholar]
- ISO. ISO 178—Determination of Flexural Properties; ISO: Berlin, Germany, 2019. [Google Scholar]
- ASTM. ASTM-D2344-Short-Beam-Strength of Polymer Matrix Composit-Materials and Their Laminates; ASTM: West Conshohocken, PA, USA, 2003. [Google Scholar]
- ISO. ISO 179—Determination of Charpy Impact Properties; ISO: Brussels, Belgium, 2013. [Google Scholar]
- Maier, A.; Schramm, N.; Kroll, L. Temperature-dependent interlaminar shear strength of unidirectional continuous fiber-reinforced thermoplastic profiles. Compos. Struct. 2021, 255, 112959. [Google Scholar] [CrossRef]
- Yaghoobi, H. An experimental investigation and optimization on the impact strength of kenaf fiber biocomposite: Application of response surface methodology. Polym. Bull. 2018, 75, 3283–3309. [Google Scholar] [CrossRef]
- Chen, W.; Nguyen, M.; Chiu, W. Optimization of the plastic injection molding process using the Taguchi method, RSM, and hybrid GA-PSO. Int. J. Adv. Manuf. Technol. 2016, 83, 1873–1886. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Cunha, A. Using Multi-objective Evolutionary Algorithms for Optimization of the Cooling System in Polymer Injection Molding. Int. Polym. Process. 2012, 27, 213–223. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Cunha, G.A. Using multiobjective evolutionary algorithms in the optimization of operating conditions of polymer injection molding. Polym. Eng. Sci. 2010, 50, 1667–1678. [Google Scholar] [CrossRef]
- Amdoun, R.; Khelifi, L.; Khelifi-slaoui, M.; Amroune, S.; Asch, M.; Gontier, E. The Desirability Optimization Methodology; a Tool to Predict Two Antagonist Responses in Biotechnological Systems: Case of Biomass Growth and Hyoscyamine Content in Elicited Datura starmonium Hairy Roots. Iran J. Biotechnol. 2018, 16, 1–19. [Google Scholar] [CrossRef]
- Wu, C.; Lui, W.; Peng, J. Optimization of Extrusion Variables and Maleic Anhydride Content on Biopolymer Blends Based on Poly(hydroxybutyrate-co-hydroxyvalerate)/Poly(vinyl acetate) with Tapioca Starch. Polymers 2018, 10, 827. [Google Scholar] [CrossRef]
- Pal, S.; Gauri, S.K. A desirability functions-based approach for simultaneous optimization of quantitative and ordinal response variables in industrial processes. Int. J. Eng. Sci. Technol. 2018, 10, 76–87. [Google Scholar] [CrossRef]
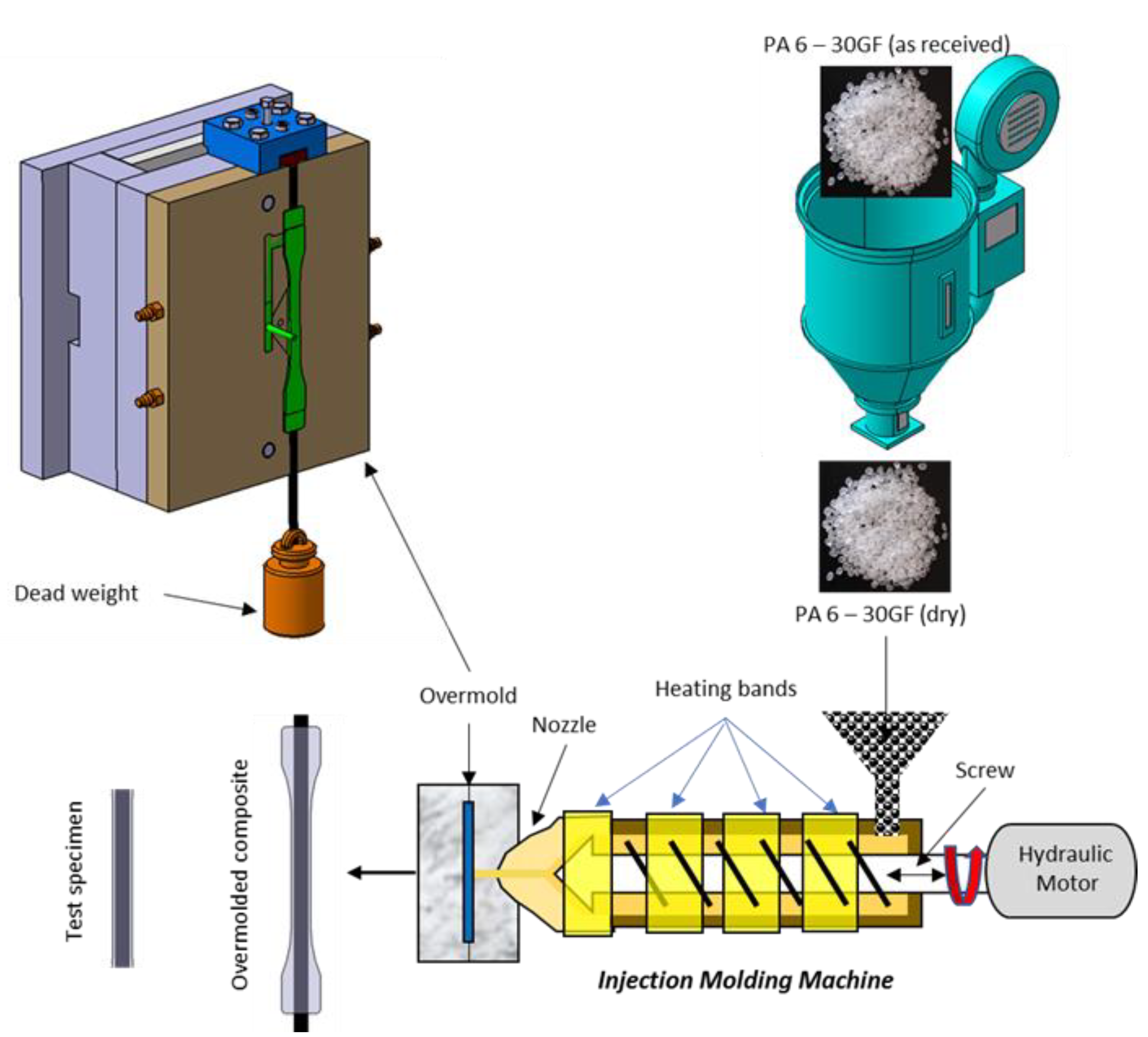



| Material | Properties | Values |
|---|---|---|
| carbon fiber (T700SC 12K) | filament diameter (µm) | 7 |
| density (g/cm3) | 1.8 | |
| tensile strength (Mpa) | 4900 | |
| Amilan PA 6-30 GF | density (g/cm3) | 1.36 |
| melting temperature (°C) | 225 | |
| flexural strength at 23 °C (Mpa) | 280 (dry) | |
| 145 (2.5% water) | ||
| flexural modulus at 23 °C (Gpa) | 9.5 (dry) | |
| 5.1 (2.5% water) | ||
| charpy impact, unnotched, at 23 °C (kJ/m2) | 80 (dry) | |
| 100 (2.5% water) | ||
| liquid nitrogen | boiling point (°C) | −196 |
| density, liquid @ BP, 1 atm (Kg/m3) | 808.5 | |
| specific gravity, liquid (water = 1) @ 20 °C, 1 atm | 0.808 |
| Parameters | Values | Unit |
|---|---|---|
| screw speed | 160 | rpm |
| charging time | 3.42 | s |
| backpressure | 50 | bar |
| hot size | 70 | mm |
| velocity transfer pressure | 35 | mm |
| injection speed | 80 | mm/s |
| filling time | 0.535 | s |
| packing pressure | 300 | kg/cm2 |
| packing time | 2 | s |
| cooling time | 15 | s |
| cooling temperature | 40 | °C |
| Factors | Coding | Actual Level | ||
|---|---|---|---|---|
| Low (−1) | Middle (0) | High (+1) | ||
| Melting temperature (°C) | A | 260 | 270 | 280 |
| Injection pressure (bar) | B | 100 | 120 | 140 |
| Fiber pretension (N) | C | 50 | 75 | 100 |
| Nitrogen immersion (min) | D | 10 | 15 | 20 |
| Run | Code | Actual | ||||||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | A | B | C | D | |
| 1 | 0 | 0 | 0 | 0 | 270 | 120 | 75 | 15 |
| 2 | 1 | 0 | −1 | 0 | 280 | 120 | 50 | 15 |
| 3 | −1 | 0 | 1 | 0 | 260 | 120 | 100 | 15 |
| 4 | 0 | 0 | 0 | 0 | 270 | 120 | 75 | 15 |
| 5 | 1 | 0 | 0 | −1 | 280 | 120 | 75 | 10 |
| 6 | 0 | 0 | 1 | −1 | 270 | 120 | 100 | 10 |
| 7 | −1 | 0 | 0 | −1 | 260 | 120 | 75 | 10 |
| 8 | 1 | 1 | 0 | 0 | 280 | 140 | 75 | 15 |
| 9 | 0 | 1 | 0 | −1 | 270 | 140 | 75 | 10 |
| 10 | 1 | −1 | 0 | 0 | 280 | 100 | 75 | 15 |
| 11 | −1 | 0 | 0 | 1 | 260 | 120 | 75 | 20 |
| 12 | 0 | −1 | 0 | −1 | 270 | 100 | 75 | 10 |
| 13 | 0 | −1 | 1 | 0 | 270 | 100 | 100 | 15 |
| 14 | 0 | 0 | 1 | 1 | 270 | 120 | 100 | 20 |
| 15 | 0 | 0 | −1 | −1 | 270 | 120 | 50 | 10 |
| 16 | 1 | 0 | 0 | 1 | 280 | 120 | 75 | 20 |
| 17 | 0 | 0 | −1 | 1 | 270 | 120 | 50 | 20 |
| 18 | −1 | −1 | 0 | 0 | 260 | 100 | 75 | 15 |
| 19 | −1 | 0 | −1 | 0 | 260 | 120 | 50 | 15 |
| 20 | 0 | 0 | 0 | 0 | 270 | 120 | 75 | 15 |
| 21 | 0 | 1 | −1 | 0 | 270 | 140 | 50 | 15 |
| 22 | 0 | 1 | 0 | 1 | 270 | 140 | 75 | 20 |
| 23 | 1 | 0 | 1 | 0 | 280 | 120 | 100 | 15 |
| 24 | −1 | 1 | 0 | 0 | 260 | 140 | 75 | 15 |
| 25 | 0 | −1 | 0 | 1 | 270 | 100 | 75 | 20 |
| 26 | 0 | −1 | −1 | 0 | 270 | 100 | 50 | 15 |
| 27 | 0 | 1 | 1 | 0 | 270 | 140 | 100 | 15 |
| Run | Parameters | ||||||
|---|---|---|---|---|---|---|---|
| A | B | C | D | Flexural Strength (Mpa) | Impact Strength (kJ/m2) | ILSS (Mpa) | |
| 1 | 270 | 120 | 75 | 15 | 245.4 | 153.271 | 32.6 |
| 2 | 280 | 120 | 50 | 15 | 238 | 144.569 | 24.53 |
| 3 | 260 | 120 | 100 | 15 | 241.2 | 137.285 | 19.36 |
| 4 | 270 | 120 | 75 | 15 | 247.5 | 153.271 | 29.9 |
| 5 | 280 | 120 | 75 | 10 | 252.8 | 151.469 | 30 |
| 6 | 270 | 120 | 100 | 10 | 249.2 | 166.974 | 28.85 |
| 7 | 260 | 120 | 75 | 10 | 245.6 | 151.621 | 20.97 |
| 8 | 280 | 140 | 75 | 15 | 250 | 155.148 | 26.8607 |
| 9 | 270 | 140 | 75 | 10 | 246.8 | 166.879 | 24 |
| 10 | 280 | 100 | 75 | 15 | 238.6 | 151.469 | 24.86 |
| 11 | 260 | 120 | 75 | 20 | 235.2 | 158.979 | 26.8 |
| 12 | 270 | 100 | 75 | 10 | 233.2 | 148.862 | 29.9 |
| 13 | 270 | 100 | 100 | 15 | 235 | 155.225 | 30.2 |
| 14 | 270 | 120 | 100 | 20 | 241.2 | 157.775 | 24.48 |
| 15 | 270 | 120 | 50 | 10 | 239 | 153.271 | 24.83 |
| 16 | 280 | 120 | 75 | 20 | 237.8 | 151.545 | 19.86 |
| 17 | 270 | 120 | 50 | 20 | 237.4 | 162.506 | 29.8 |
| 18 | 260 | 100 | 75 | 15 | 207.2 | 147.942 | 20.32 |
| 19 | 260 | 120 | 50 | 15 | 221.5 | 166.974 | 21.63 |
| 20 | 270 | 120 | 75 | 15 | 230 | 153.271 | 28.4 |
| 21 | 270 | 140 | 50 | 15 | 233.4 | 173.393 | 21.28 |
| 22 | 270 | 140 | 75 | 20 | 242 | 162.28 | 21 |
| 23 | 280 | 120 | 100 | 15 | 234.2 | 167.162 | 20.65 |
| 24 | 260 | 140 | 75 | 15 | 224.4 | 148.957 | 16.4 |
| 25 | 270 | 100 | 75 | 20 | 231.4 | 155.072 | 29.6 |
| 26 | 270 | 100 | 50 | 15 | 233.2 | 171.479 | 22.72 |
| 27 | 270 | 140 | 100 | 15 | 231 | 162.356 | 23.41 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Note |
|---|---|---|---|---|---|---|
| Model | 900.98 | 4 | 225.24 | 3.21 | 0.0323 | significant |
| A-Melt temperature | 485.14 | 1 | 485.14 | 6.90 | 0.0154 | significant |
| B-Injection pressure | 200.08 | 1 | 200.08 | 2.85 | 0.1056 | |
| C-Fiber pretension | 71.54 | 1 | 71.54 | 1.02 | 0.3239 | |
| D-Nitrogen immersion | 144.21 | 1 | 144.21 | 2.05 | 0.1660 | |
| Residual | 1545.90 | 22 | 70.27 | |||
| Lack of Fit | 1363.30 | 20 | 68.16 | 0.75 | 0.7155 | not significant |
| Pure Error | 182.61 | 2 | 91.30 | |||
| Cor Total | 2446.88 | 26 | ||||
| Adeq Precision | 5.79 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Note |
|---|---|---|---|---|---|---|
| Model | 1558.28 | 14 | 111.31 | 3.82 | 0.0127 | significant |
| A-Melt temperature | 7.69 | 1 | 7.69 | 0.26 | 0.6168 | |
| B-Injection pressure | 126.52 | 1 | 126.52 | 4.34 | 0.0592 | |
| C-Fiber pretension | 53.83 | 1 | 53.83 | 1.85 | 0.1991 | |
| D-Nitrogen immersion | 6.87 | 1 | 6.87 | 0.24 | 0.6359 | |
| AB | 1.78 | 1 | 1.78 | 0.061 | 0.8092 | |
| AC | 683.34 | 1 | 683.34 | 23.45 | 0.0004 | significant |
| AD | 13.25 | 1 | 13.25 | 0.45 | 0.5128 | |
| BC | 6.80 | 1 | 6.80 | 0.23 | 0.6376 | |
| BD | 29.21 | 1 | 29.21 | 1.00 | 0.3364 | |
| CD | 84.96 | 1 | 84.96 | 2.92 | 0.1134 | |
| A2 | 110.17 | 1 | 110.17 | 3.78 | 0.0756 | |
| B2 | 72.92 | 1 | 72.92 | 2.50 | 0.1396 | |
| C2 | 204.11 | 1 | 204.11 | 7.01 | 0.0213 | significant |
| D2 | 26.27 | 1 | 26.27 | 0.90 | 0.3611 | |
| Residual | 349.61 | 12 | 29.13 | |||
| Lack of Fit | 349.61 | 10 | 34.96 | |||
| Pure Error | 0.000 | 2 | 0.000 | |||
| Cor Total | 1907.90 | 26 | ||||
| Adeq Precision | 7.55 |
| Source | Sum of Squares | df | Mean Square | F-Value | p-Value Prob > F | Note |
|---|---|---|---|---|---|---|
| Model | 383.63 | 14 | 27.40 | 3.61 | 0.0159 | significant |
| A-Melt temperature | 37.74 | 1 | 37.74 | 4.97 | 0.0456 | significant |
| B-Injection pressure | 50.63 | 1 | 50.63 | 6.67 | 0.0240 | significant |
| C-Fiber pretension | 0.39 | 1 | 0.39 | 0.051 | 0.8247 | |
| D-Nitrogen immersion | 4.10 | 1 | 4.10 | 0.54 | 0.4767 | |
| AB | 8.76 | 1 | 8.76 | 1.15 | 0.3037 | |
| AC | 0.65 | 1 | 0.65 | 0.085 | 0.7751 | |
| AD | 63.76 | 1 | 63.76 | 8.40 | 0.0134 | significant |
| BC | 7.16 | 1 | 7.16 | 0.94 | 0.3507 | |
| BD | 1.82 | 1 | 1.82 | 0.24 | 0.6329 | |
| CD | 21.81 | 1 | 21.81 | 2.87 | 0.1158 | |
| A2 | 154.53 | 1 | 154.53 | 20.36 | 0.0007 | significant |
| B2 | 51.06 | 1 | 51.06 | 6.73 | 0.0235 | significant |
| C2 | 46.27 | 1 | 46.27 | 6.10 | 0.0295 | significant |
| D2 | 2.27 | 1 | 2.27 | 0.30 | 0.5949 | |
| Residual | 91.08 | 12 | 7.59 | |||
| Lack of Fit | 82.02 | 10 | 8.20 | 1.81 | 0.4078 | not significant |
| Pure Error | 9.06 | 2 | 4.53 | |||
| Cor Total | 474.70 | 26 | ||||
| Adeq Precision | 6.867 |
| Entry | Predicted Flexural Strength | Confirmation Flexular Strength | Predicted Impact Strength | Confirmation Impact Strength | Predicted ILSS | Confirmation ILSS |
|---|---|---|---|---|---|---|
| (Mpa) | (Mpa) | (kJ/m2) | (kJ/m2) | (Mpa) | (Mpa) | |
| 1 | 248.67 | 249 | 173.4 | 171.4 | 30.47 | 30.26 |
| 2 | 246 | 169.5 | 29.99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rochardjo, H.S.B.; Budiyantoro, C. Manufacturing and Analysis of Overmolded Hybrid Fiber Polyamide 6 Composite. Polymers 2021, 13, 3820. https://doi.org/10.3390/polym13213820
Rochardjo HSB, Budiyantoro C. Manufacturing and Analysis of Overmolded Hybrid Fiber Polyamide 6 Composite. Polymers. 2021; 13(21):3820. https://doi.org/10.3390/polym13213820
Chicago/Turabian StyleRochardjo, Heru S. B., and Cahyo Budiyantoro. 2021. "Manufacturing and Analysis of Overmolded Hybrid Fiber Polyamide 6 Composite" Polymers 13, no. 21: 3820. https://doi.org/10.3390/polym13213820
APA StyleRochardjo, H. S. B., & Budiyantoro, C. (2021). Manufacturing and Analysis of Overmolded Hybrid Fiber Polyamide 6 Composite. Polymers, 13(21), 3820. https://doi.org/10.3390/polym13213820






