Sandwich Structures Reflecting Thermal Radiation Produced by the Human Body
Abstract
:1. Introduction
2. Materials and Methods
2.1. Composition of Sandwiches
2.2. Geometrical Characteristics of Layers
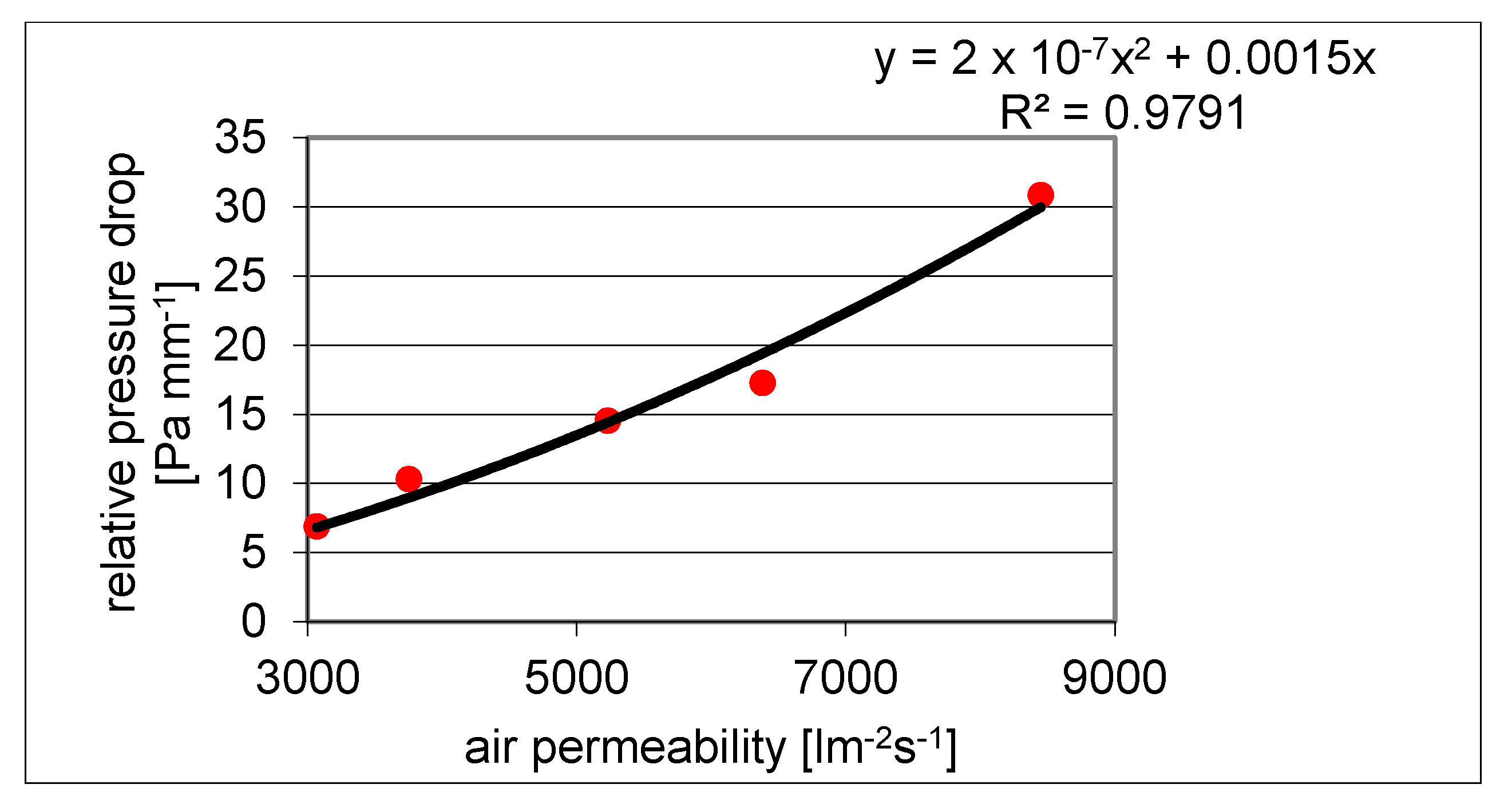
2.3. Air Permeability
2.4. Measurement of Thermal Properties
2.5. Measurement of the Degree of Thermal Insulation
2.6. Measurement of Reflectance, Transmittance, and Calculation of Absorbance
3. Results and Discussion
3.1. Geometry and Air Permeability
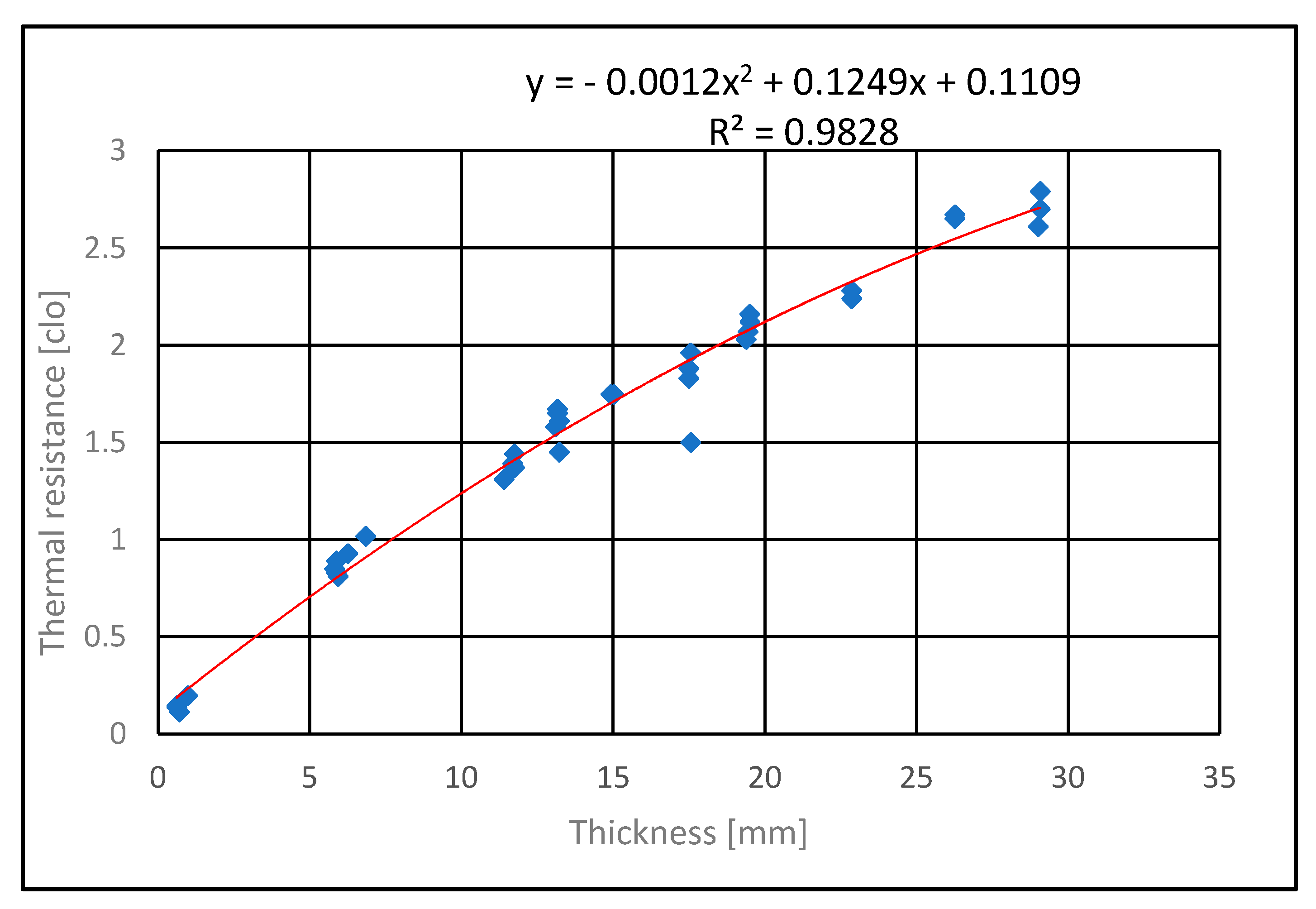
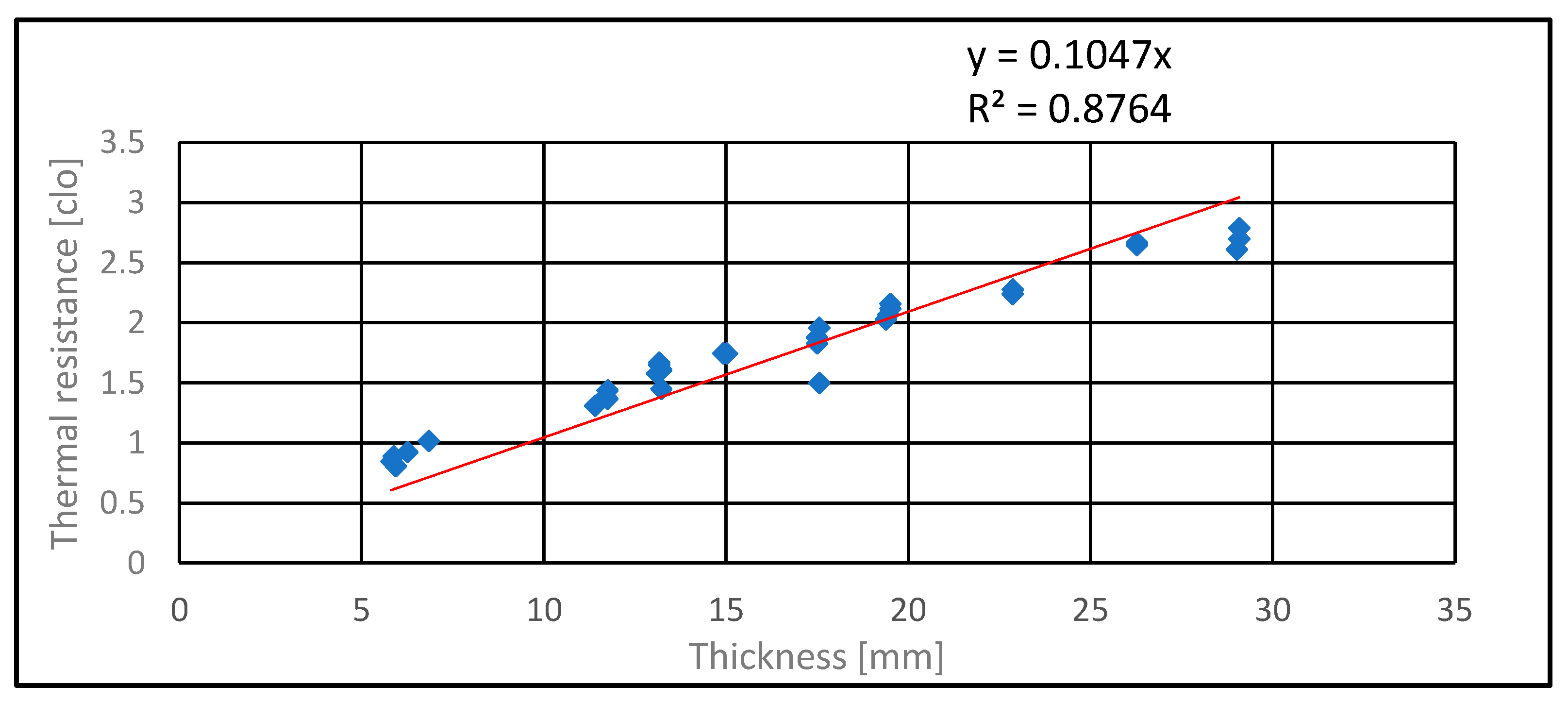
3.2. Thermal Characteristics
3.3. Degree of Resistance against Radiation
3.4. Infrared Radiation
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Srinivasan, A.V.; Mc Farland, D.M. Smart Structures; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Ramlow, H.; Andrade, K.L.; Immich, A.P.S. Smart textiles: An overview of recent progress on chromic textiles. J. Text. Inst. 2021, 112, 152–171. [Google Scholar] [CrossRef]
- Sun, M.; Lv, J.; Xu, H.; Zhang, L.; Zhong, Y.; Chen, Z.; Sui, X.; Wang, B.; Feng, X.; Mao, Z. Smart cotton fabric screen-printed with viologen polymer: Photochromic, thermochromic and ammonia sensing. Cellulose 2020, 27, 2939–2952. [Google Scholar] [CrossRef]
- Abdelrahman, M.; Nassar, S.H.; Mashaly, H.; Mahmoud, S.; Maamoun, D.; El-Sakhawy, M.; Khattab, T.A.; Kamel, S. Studies of polylactic acid and metal oxide nanoparticles-based composites for multifunctional textile prints. Coatings 2020, 10, 58. [Google Scholar] [CrossRef] [Green Version]
- Aldalbahi, A.; El-Naggar, M.E.; El-Newehy, M.H.; Rahaman, M.; Hatshan, M.R.; Khattab, T.A. Effects of technical textiles and synthetic nanofibers on environmental pollution. Polymers 2021, 13, 155. [Google Scholar] [CrossRef]
- Dong, S.; Xu, J. Research progress and prospect of Far infrared (FIR) textiles. Prog. Text. Sci. Technol. 2005, 2, 10–12. [Google Scholar]
- Zhang, X. Research and development of far infrared fiber and fabric. Tex. Res. 1994, 15, 42–45. [Google Scholar]
- Wang, J.; Tian, W. Development and Application of Healthy Textiles; China Textile & Apparel Press: Beijing, China, 2005; pp. 115–118. [Google Scholar]
- Hardy, J.D.; DuBois, E.F. Regulation the heat loss the from the human body. Proc. Natl. Acad. Sci. USA 1937, 23, 624. [Google Scholar] [CrossRef] [Green Version]
- Nouri, N. Radiative Conductivity Analysis of Low-Density Fibrous Materials, Theses and Dissertations—Mechanical Engi-neering. Master’s Thesis, University of Kentucky, Lexington, KY, USA, 2015. [Google Scholar]
- Olsen, B.W. Thermal comfort. Tech. Rev. Bruel Kjaer 1982, 2. [Google Scholar]
- Parsons, K.C. Human Thermal Environments, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Hardy, J.D. The radiation of heat from the human body III. J. Clin. Investig. 1934, 13, 615–620. [Google Scholar] [CrossRef]
- Hardy, J.D. The radiation of heat from the human body IV. J. Clin. Investig. 1934, 13, 817–831. [Google Scholar] [CrossRef]
- Hardy, J.D. The radiation of heat from the human body I. J. Clin. Investig. 1934, 13, 593–604. [Google Scholar] [CrossRef] [Green Version]
- Herman, I.P. Physics of the Human Body; Springer International Publishing: Cham, Switzerland, 2016. [Google Scholar]
- Pakdel, E.; Naebe, M.; Sun, L.; Wang, X. Advanced Functional Fibrous Materials for Enhanced Thermoregulating Performance. ACS Appl. Mater. Interfaces 2019, 11, 13039–13057. [Google Scholar] [CrossRef] [PubMed]
- Mehnert, P.; Malchaire, J.; Kampmann, B.; Piette, A.; Griefahn, B.; Gebhardt, H. Prediction of the average skin temperature in warm and hot environments. Eur J. Appl. Physiol. 2000, 82, 52–60. [Google Scholar] [CrossRef] [PubMed]
- Mairiaux, P.; Malchaire, J.; Candas, V. Prediction of mean skin temperature in warm environments. Eur. J. App. Physiol. 1987, 56, 686–692. [Google Scholar] [CrossRef]
- Wang, F.; Kuklane, K.; Gao, C.; Holmér, I. Development and validity of a universal empirical equation to predict skin surface temperature on thermal manikins. J. Therm. Biol. 2010, 35, 197–203. [Google Scholar] [CrossRef]
- Kimura, T.; Takahashi, K.; Suzuki, Y.; Konishi, Y.; Ota, Y.; Mori, C.; Ikenaga, T.; Takanami, T.; Saito, R.; Ichiishi, E.; et al. The effect of high strength static magnetic fields and ionizing radiation on gene expression and DNA damage in Caenorhabditis elegans. Bioelectromagnetic 2008, 29, 605–614. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.S.; Lin, M.Y.; Leung, T.K.; Liao, C.H.; Huang, T.T.; Huang, H.S.; Pan, H.C. Properties and biological effects of high performance ceramic powder emitting far-infrared irradiation. Instrum. Today 2007, 6, 60–66. [Google Scholar]
- Cai, L.; Song, A.Y.; Wu, P.; Hsu, P.-C.; Peng, Y.; Chen, J.; Liu, C.; Catrysse, P.B.; Liu, Y.; Yang, A.; et al. Warming up human body by nanoporous metallized polyethylene textile. Nat. Commun. 2017, 8, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Hsu, P.C. Radiative human body cooling by nanoporous polyethylene textile. Science 2017, 353, 1019–1023. [Google Scholar] [CrossRef] [Green Version]
- Hsu, P.-C.; Liu, C.; Song, A.Y.; Zhang, Z.; Peng, Y.; Xie, J.; Liu, K.; Wu, C.-L.; Catrysse, P.B.; Cai, L.; et al. A dual-mode textile for human body radiative heating and cooling. Sci. Adv. 2017, 3, e1700895. [Google Scholar] [CrossRef] [Green Version]
- Militký, J.; Křemenáová, D.; Venkataraman, M.; Večerník, J. Exceptional electromagnetic shielding properties of lightweight and porous multifunctional layers. ACS Appl. Electron. Mater. 2020, 2, 1138–1144. [Google Scholar] [CrossRef]
- Xiao, X.; Zeng, X.; Bandara, P.; Long, A. Experimental study of dynamic air permeability for woven fabrics. Text. Res. J. 2012, 82, 920–930. [Google Scholar] [CrossRef]
- Ergun, S.; Orning, A.A. Fluid flow through randomly packed columns and fluidized beds. Ind. Eng. Chem. 1949, 41, 1179–1184. [Google Scholar] [CrossRef]
- Křemenáková, D.; Militký, J.; Novosad, A.; Venkataraman, M.; Večerník, J. Textile layers enabling back reflection of human body thermal radiation. In Proceedings of the 47th Textile Research Symposium, Liberec, Czech Republic, 17–19 June 2019. [Google Scholar]

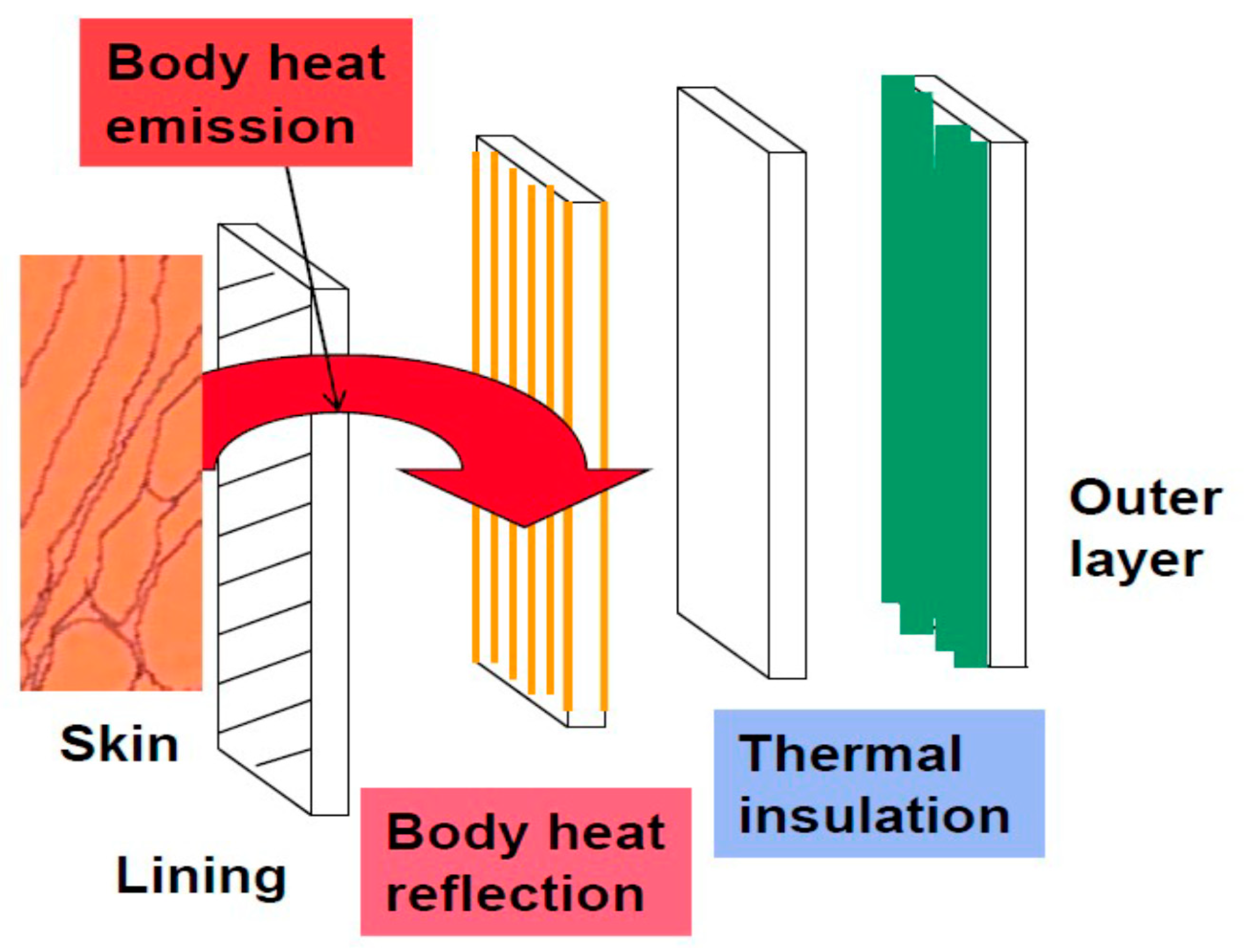
| Figure | Material | Composition | Function | Areal Weight Nominal (g∙m−2) |
|---|---|---|---|---|
 | TK U3 | Polyester canvas, Ripstop | Outer layer | 74 |
 | FT 200 | Polyester nonwoven, acrylic binder | Insulation layer | 200 |
 | VTM | Milife copper-coated polyester nonwoven | Active layer | 30 |
 | PL 07 | Polyester knitted, filet | Lining | 67 |
| Layer | Thickness (mm) | Areal Weight Real (g∙m−2) | Density (kg∙m−3) | Volume Portion (-) | Volume Porosity (-) |
|---|---|---|---|---|---|
| TK U3 | 0.117 | 75.22 | 642.91 | 0.473 | 0.527 |
| VTM | 0.102 | 35.600 | 349.020 | 0.257 | 0.743 |
| PL 07 | 0.2435 | 68.160 | 279.918 | 0.206 | 0.794 |
| FT 200 | 13.750 | 209.80 | 15.26 | 0.011 | 0.989 |
| Layer | Air Permeability (mm/s) | LL (mm/s) | UL (mm/s) |
|---|---|---|---|
| TK U3 | 71.3 | 70.2 | 72.3 |
| VTM | 1174 | 1083 | 1265 |
| FT 200 | 5229 | 5172 | 5286 |
| PL 07 | 7860 | 7707.4 | 8012.6 |
| Sandwich Type | Air Permeability (mm/s) | LL (mm/s) | UL (mm/s) |
|---|---|---|---|
| PL 07/FT 200 | 3842 | 3774 | 3910 |
| FT 200/PL 07 | 3780 | 3653 | 3907 |
| PL 07/VTM | 1124 | 1063 | 1185 |
| PL 07/FT 200/VTM | 992 | 936 | 1048 |
| PL 07/FT200/VTM/TKU3 | 152 | 150 | 153 |
| Layer | Thermal Conductivity λ (W m−1 K−1) | Thermal Resistance Rc (m2 K W−1) | Thermal Resistance (clo) | ||||
|---|---|---|---|---|---|---|---|
| Mean | LL | UL | Mean | LL | UL | ||
| FT 200 | 0.0565 | 0.0559 | 0.0572 | 0.245 | 0.241 | 0.250 | 1.58 |
| Material | Thickness (mm) | Thermal Conductivity λ (W m−1 K−1) | Thermal Resistance Rc (m2 K W−1) | Thermal Resistance (clo) | ||||
|---|---|---|---|---|---|---|---|---|
| Mean | LL | UL | Mean | LL | UL | |||
| VTM 6 layers | 0.612 | 0.0363 | 0.0351 | 0.0375 | 0.0168 | 0.0167 | 0.0169 | 0.1458 |
| PL07 4 layers | 0.974 | 0.0429 | 0.0424 | 0.0435 | 0.0226 | 0.0222 | 0.0229 | 0.1963 |
| TKU3 6 layers | 0.704 | 0.0535 | 0.0518 | 0.0552 | 0.0132 | 0.0131 | 0.0132 | 0.1144 |
| TKU3/FT200/VTM/PL07 | 15.017 | 0.0552 | 0.0541 | 0.0564 | 0.2706 | 0.2645 | 0.2767 | 1.75 |
| Layer Type | Index Ir (-) | LL (-) | UL (-) |
|---|---|---|---|
| TKU3 | 0.32 | 0.31 | 0.33 |
| FT200 | 0.52 | 0.49 | 0.56 |
| PL07 | 0.16 | 0.15 | 0.18 |
| Sample Type | Thickness (mm) | Index Ir (-) | LL (-) | UL (-) |
|---|---|---|---|---|
| PL07 + FT200 + TKU3 | 13.473 | 0.87/0.92 * | - | - |
| PL07 + VTM + TKU3 | 0.476 | 0.36/0.45 * | - | - |
| PL07 + VTM + FT200 + TKU3 | 13.576 | 0.95/0.78 | 0.92/0.77 | 0.97/0.79 |
| TKU3 2Al + FT200 + TKU3 | 13.364 | 0.83/0.84 | 0.80/0.83 | 0.85/0.86 |
| Layer | Reflectance (%) | Transmittance (%) | Absorbance (%) | ||||
|---|---|---|---|---|---|---|---|
| Mean | LL (%) | UL (%) | Mean | LL (%) | UL (%) | ||
| VTM | 81.78 | 80.95 | 82.61 | 15.27 | 12.14 | 18.39 | 2.5 |
| PL07 | 6.14 | 5.88 | 6.41 | 34.54 | 33.64 | 35.43 | 59.32 |
| TKU3 | 8.95 | 8.90 | 9.00 | 9.92 | 9.57 | 10.27 | 81.13 |
| FT200 | 3.81 | 2.64 | 4.98 | 2.12 | 1.55 | 2.68 | 94.07 |
| Sandwich Type | Reflectance (%) | ||
|---|---|---|---|
| Mean | LL | UL | |
| PL07 + FT200 + TKU3 | 9.790 | 9.374 | 10.207 |
| PL07 + VTM + FT200 + TKU3 | 21.167 | - | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Militký, J.; Křemenáková, D.; Venkataraman, M.; Večerník, J.; Martínková, L.; Marek, J. Sandwich Structures Reflecting Thermal Radiation Produced by the Human Body. Polymers 2021, 13, 3309. https://doi.org/10.3390/polym13193309
Militký J, Křemenáková D, Venkataraman M, Večerník J, Martínková L, Marek J. Sandwich Structures Reflecting Thermal Radiation Produced by the Human Body. Polymers. 2021; 13(19):3309. https://doi.org/10.3390/polym13193309
Chicago/Turabian StyleMilitký, Jiří, Dana Křemenáková, Mohanapriya Venkataraman, Josef Večerník, Lenka Martínková, and Jan Marek. 2021. "Sandwich Structures Reflecting Thermal Radiation Produced by the Human Body" Polymers 13, no. 19: 3309. https://doi.org/10.3390/polym13193309
APA StyleMilitký, J., Křemenáková, D., Venkataraman, M., Večerník, J., Martínková, L., & Marek, J. (2021). Sandwich Structures Reflecting Thermal Radiation Produced by the Human Body. Polymers, 13(19), 3309. https://doi.org/10.3390/polym13193309









