Experimental Characterization and Modeling Multifunctional Properties of Epoxy/Graphene Oxide Nanocomposites
Abstract
:1. Introduction
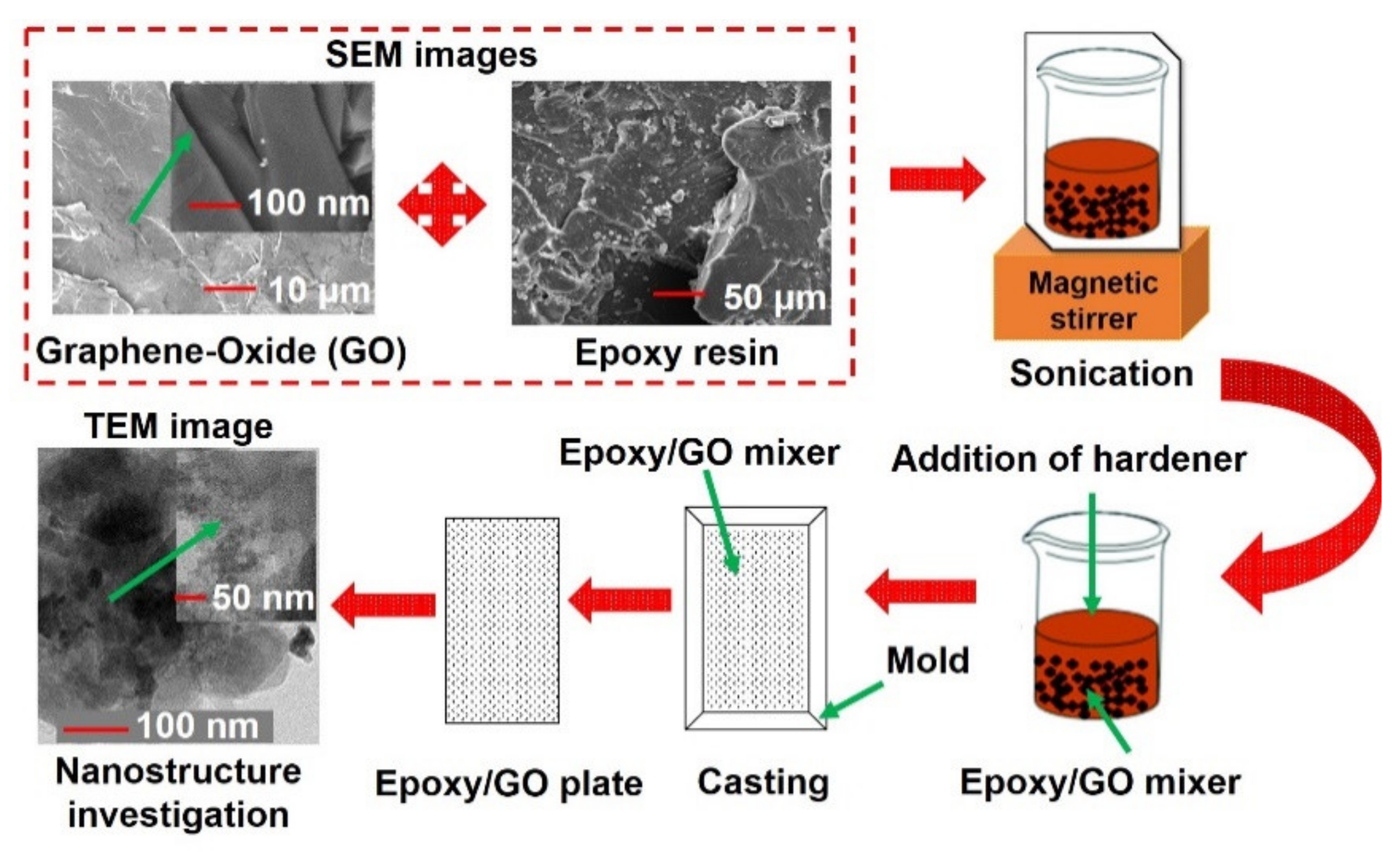
2. Materials’ and Sample Fabrication
3. Experimental Procedures
3.1. Thermo-Mechanical Experiments
3.1.1. Tensile Testing
3.1.2. Frequency–Temperature-Dependent Viscoelastic Properties
3.1.3. Thermal Conductivity (TC) Measurements
3.2. Thermal Characterization
3.2.1. Differential Scanning Calorimetry (DSC)
3.2.2. Thermogravimetric Analysis (TGA)
3.3. Electromagnetic Interference (EMI) Shielding
4. Theoretical Modeling
4.1. Young’s Modulus
4.2. Frequency–Temperature-Dependent Viscoelastic Modeling
4.2.1. Effect of Frequency on Storage Modulus and Glass Transition Temperature
4.2.2. Effect of Volume Fraction on the Storage Modulus
4.2.3. Effects of Temperature and Frequency on Storage and Loss Moduli
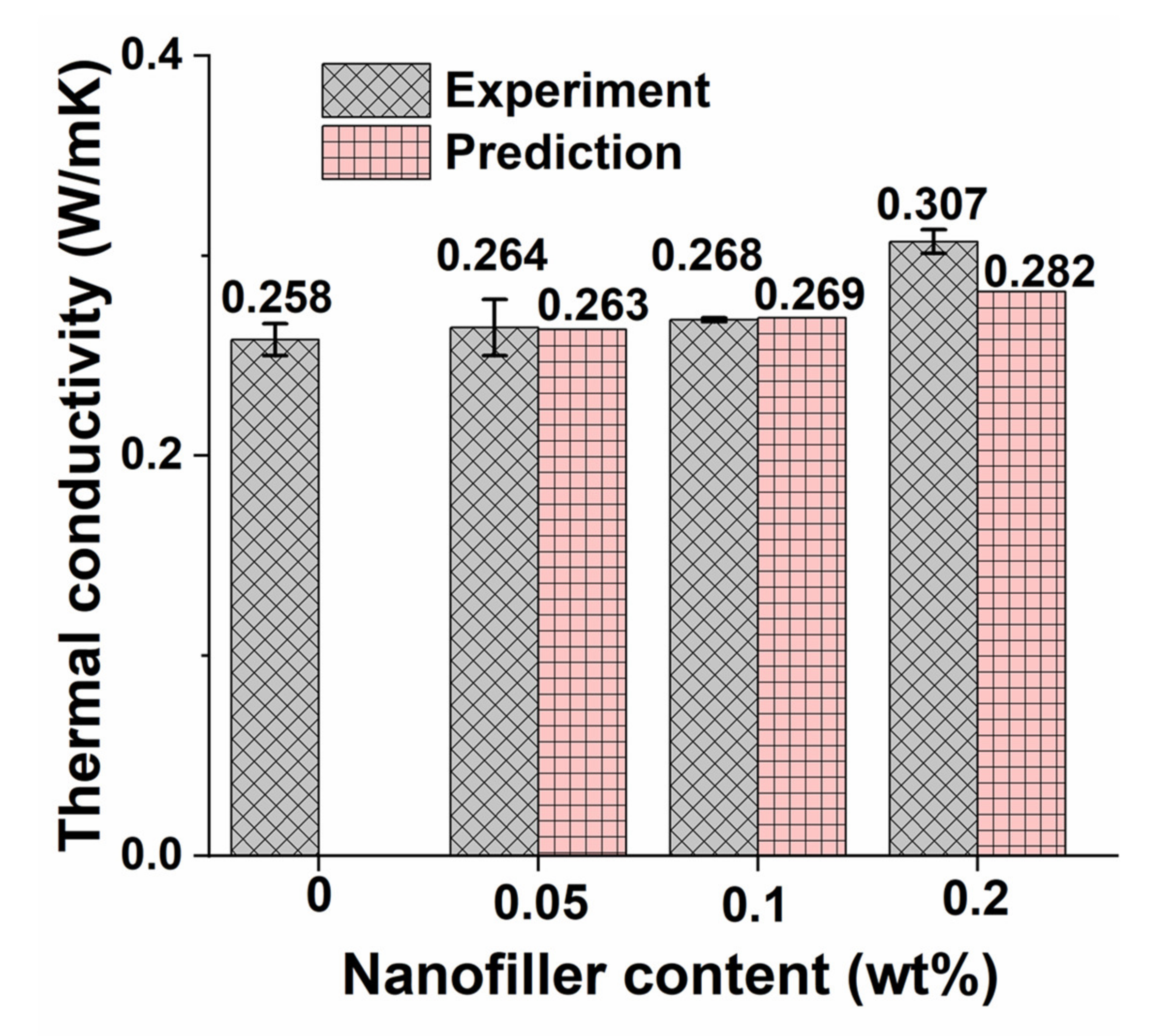
4.3. Thermal Conductivity Modeling
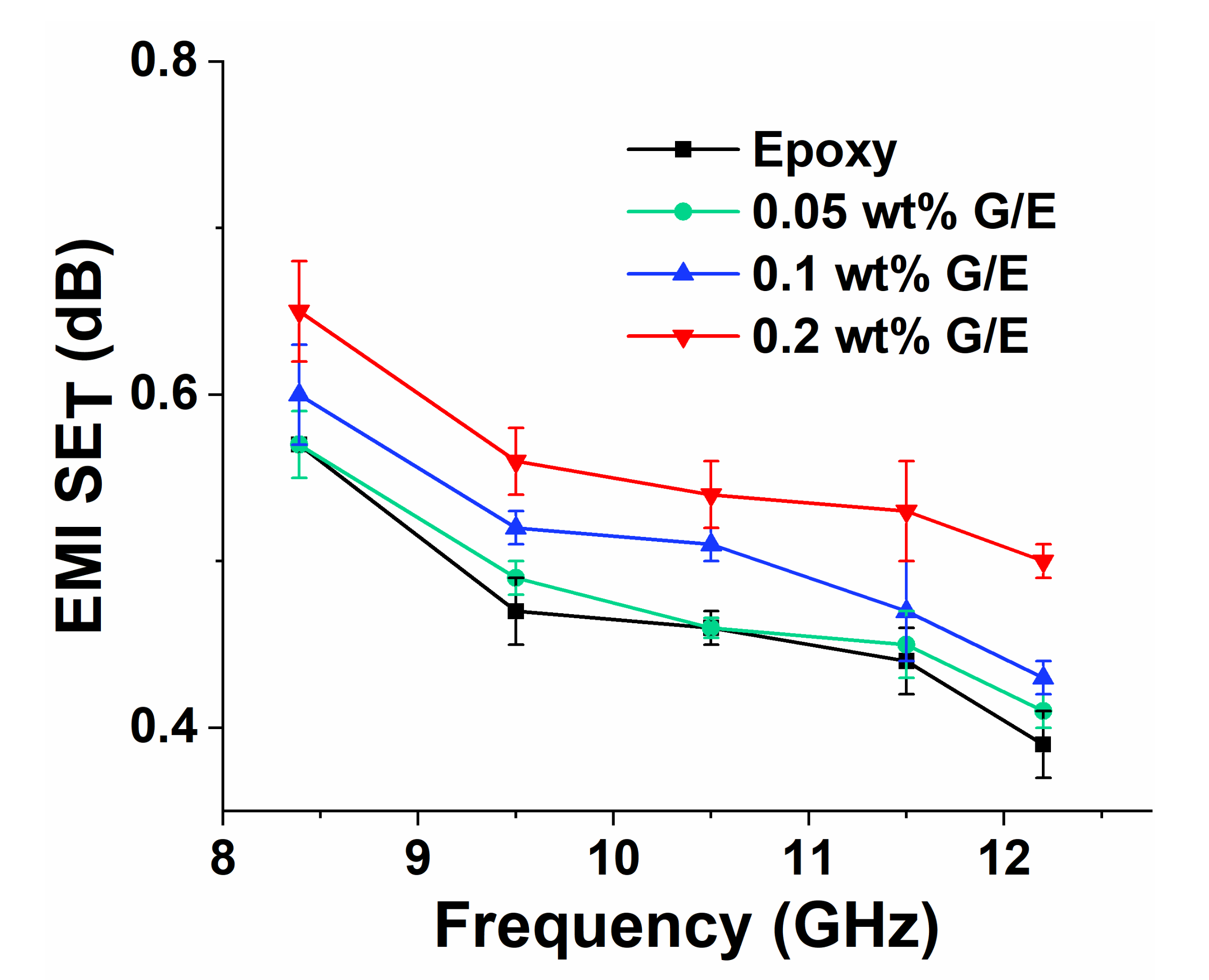
4.4. EMI Shielding Modeling
5. Results and Discussions
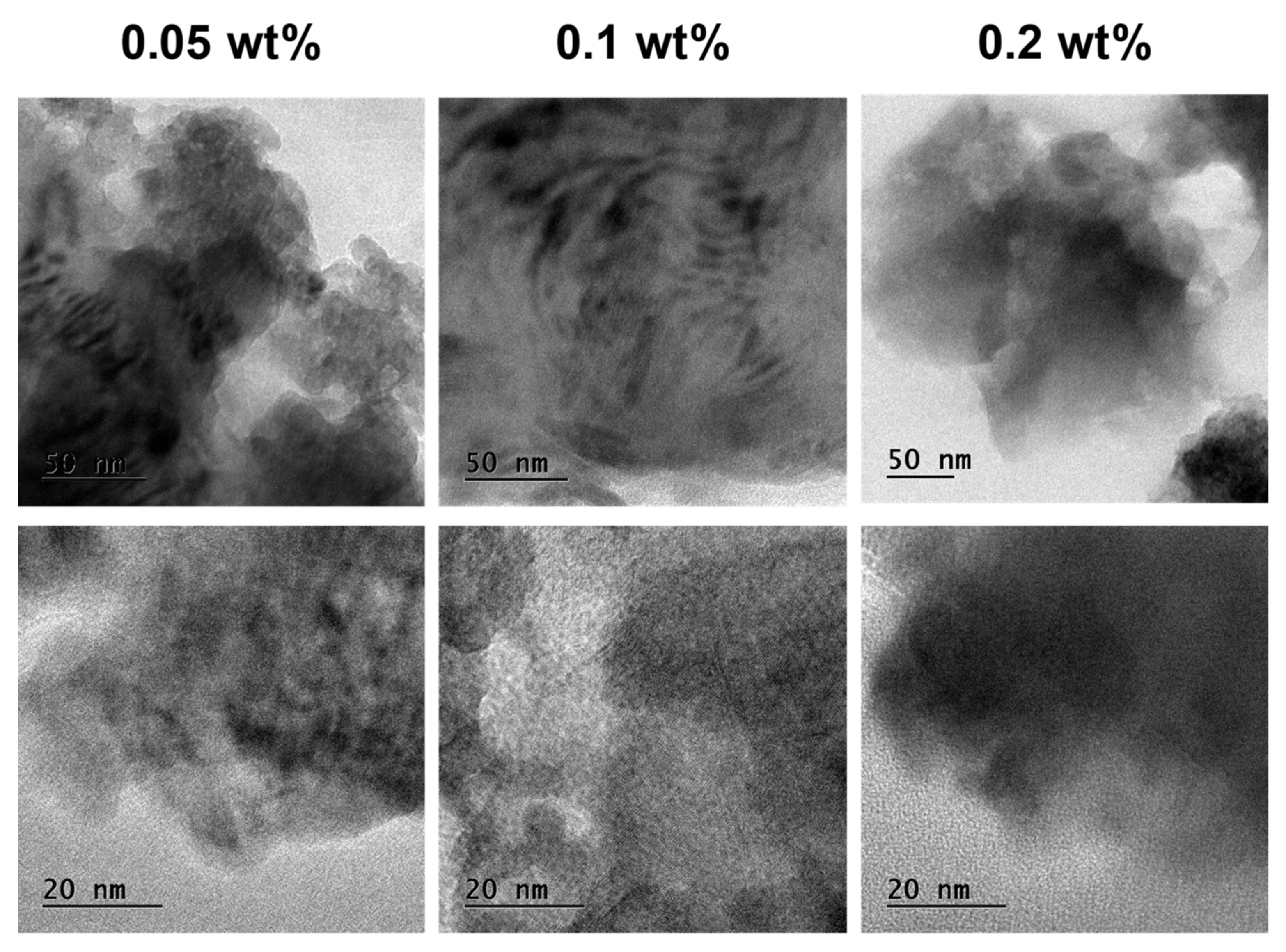
5.1. Transmission Electron Microscopy (TEM) Studies
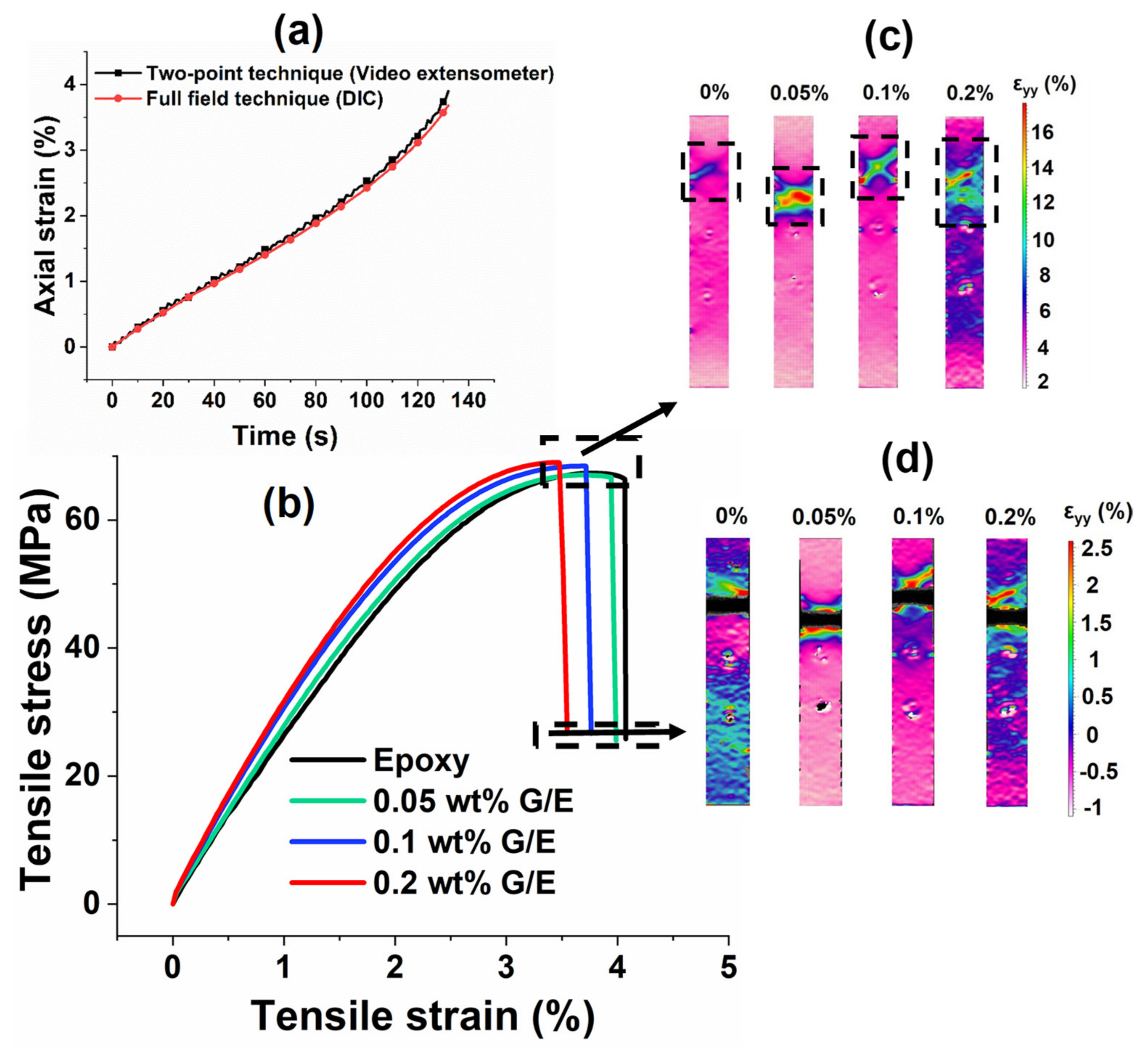
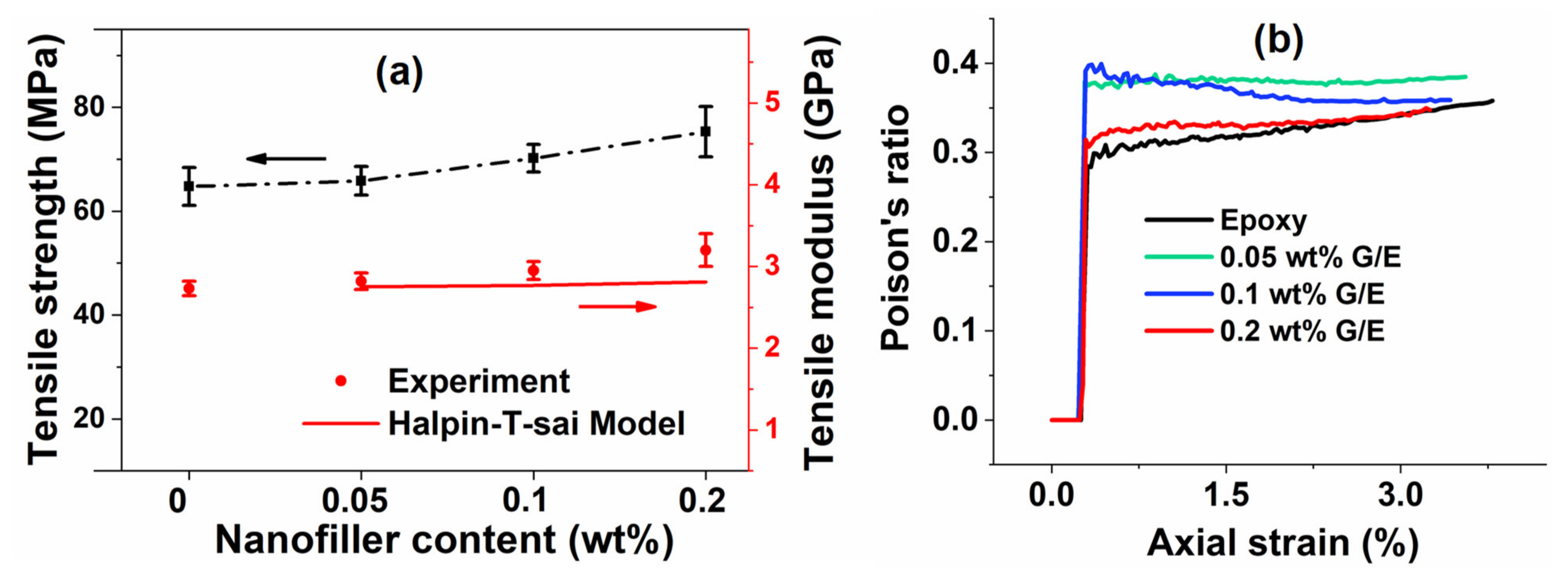
5.2. Tensile Test Results
5.3. Frequency–Temperature-Dependent Viscoelastic Properties
5.3.1. Storage and Loss Moduli
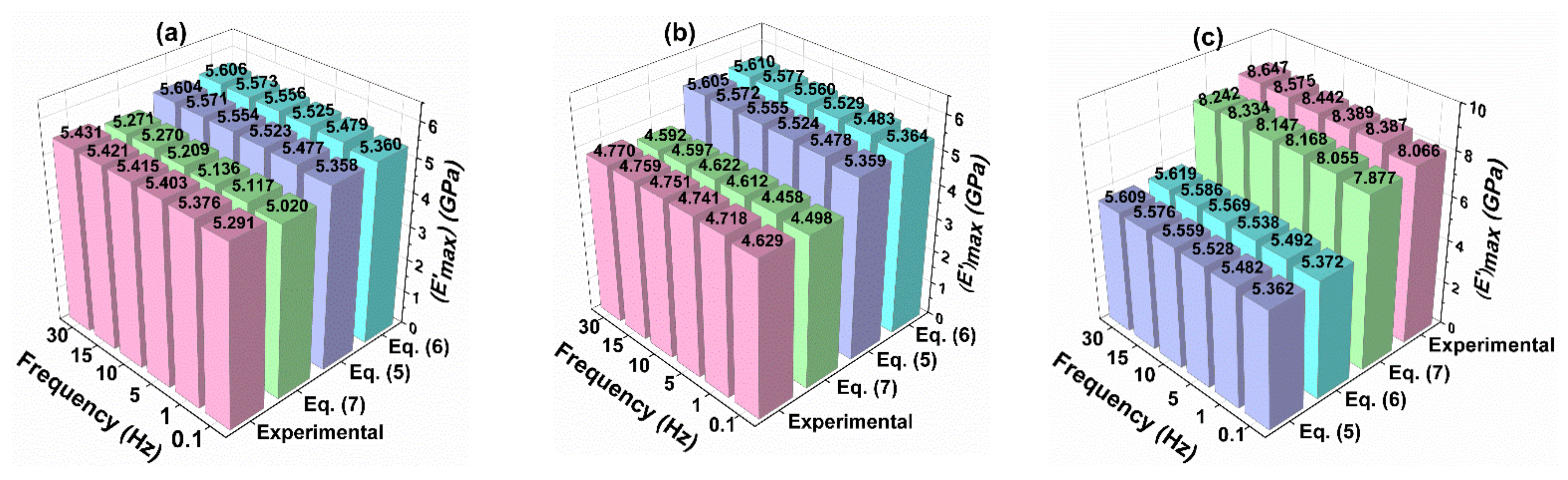
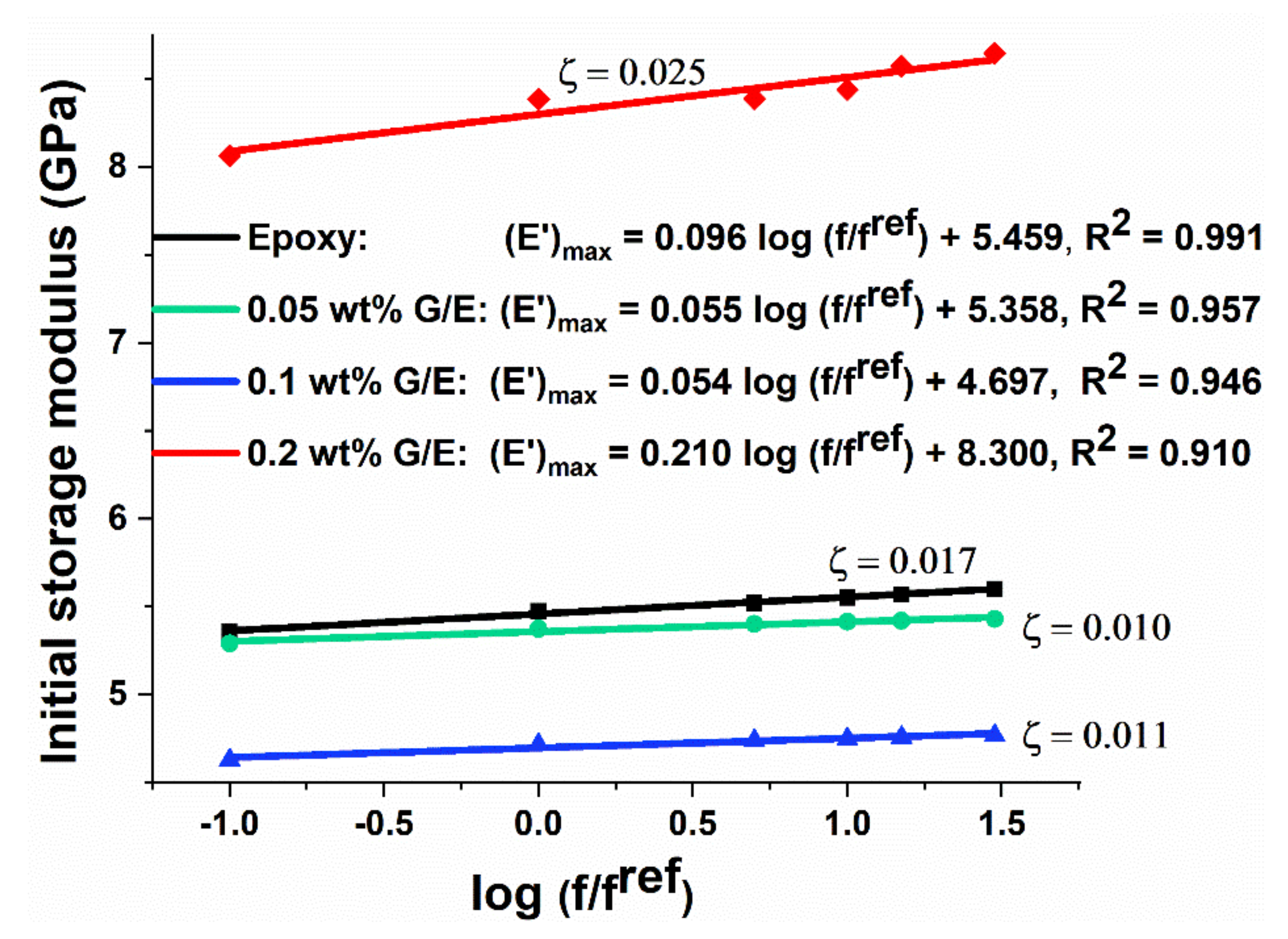
5.3.2. Effect of Frequency on Storage Modulus (E′)
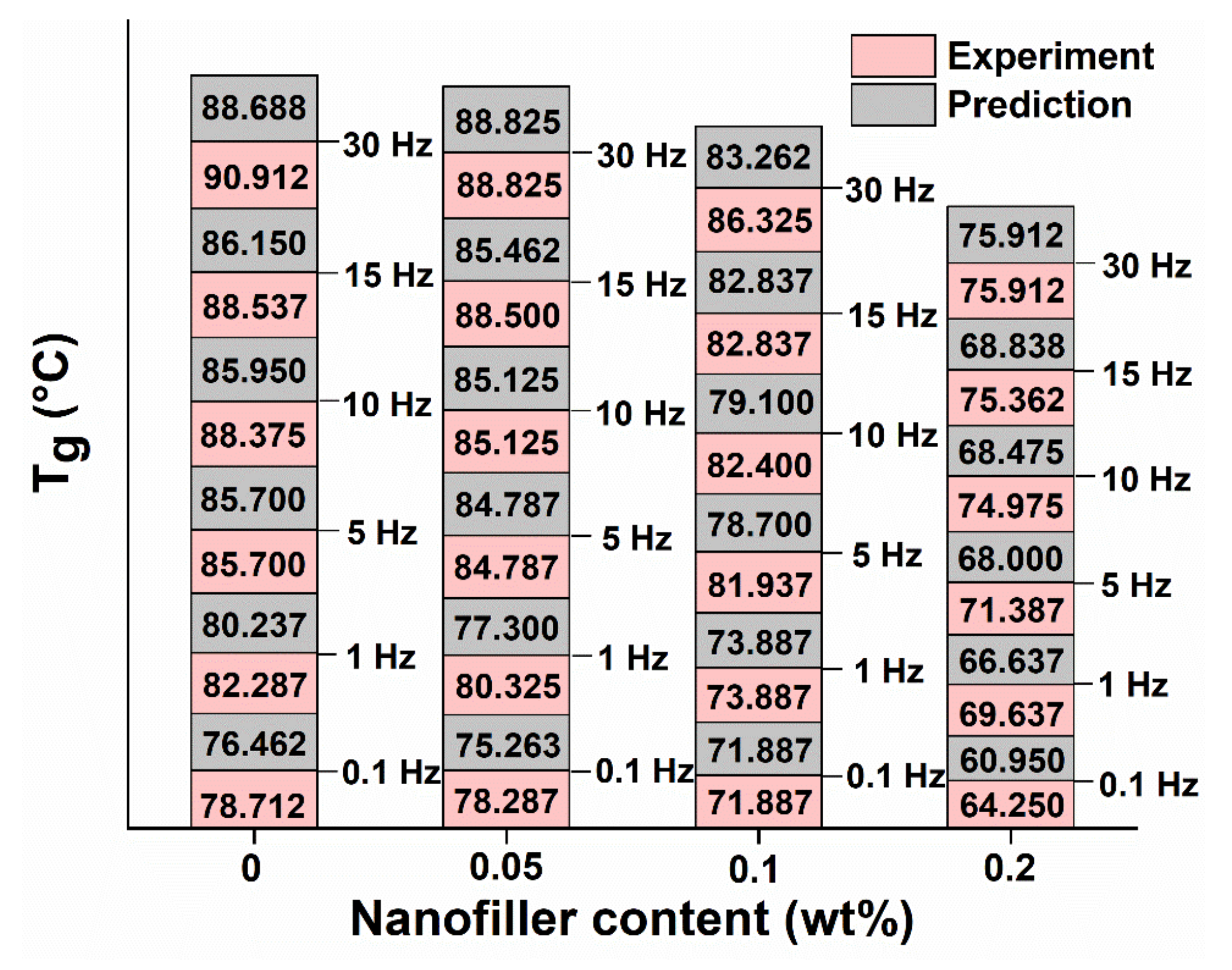
5.3.3. Experimental and Predicted Tg (tan δ)max
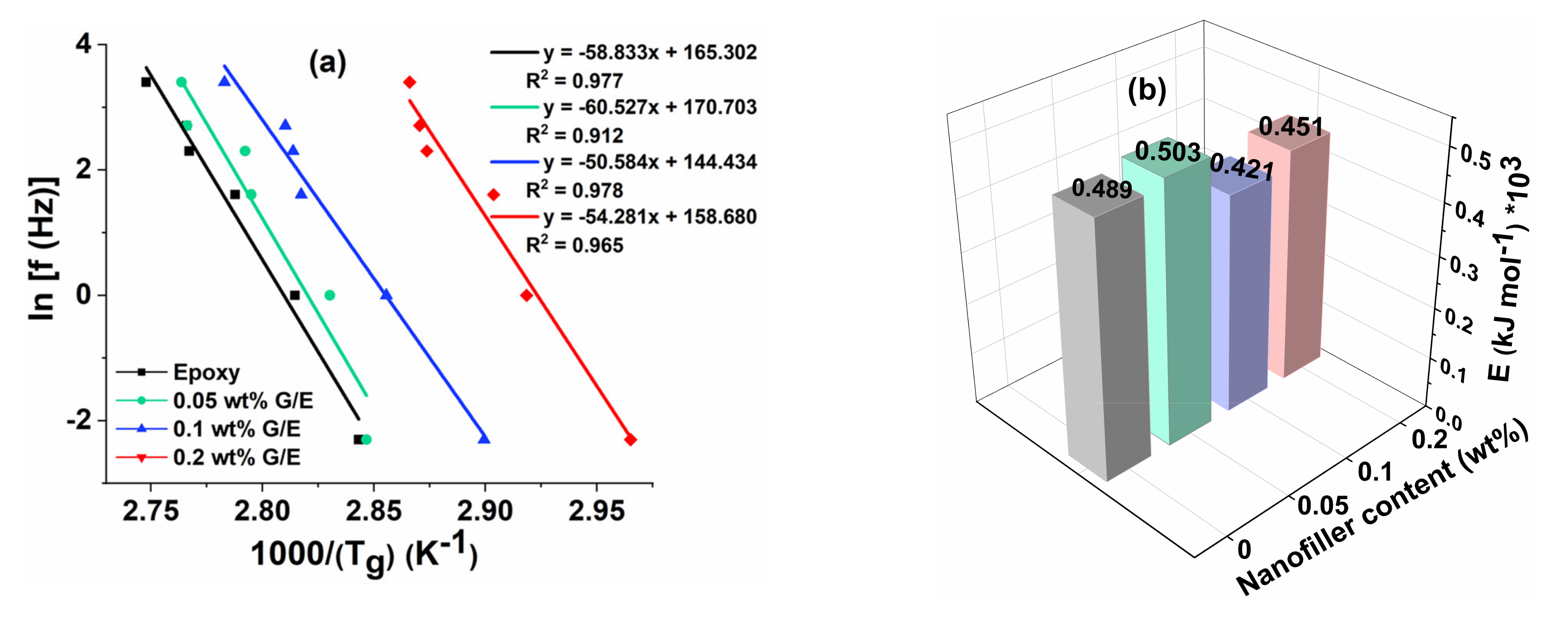
5.3.4. Effect of Frequency on Tg (tan δ)max
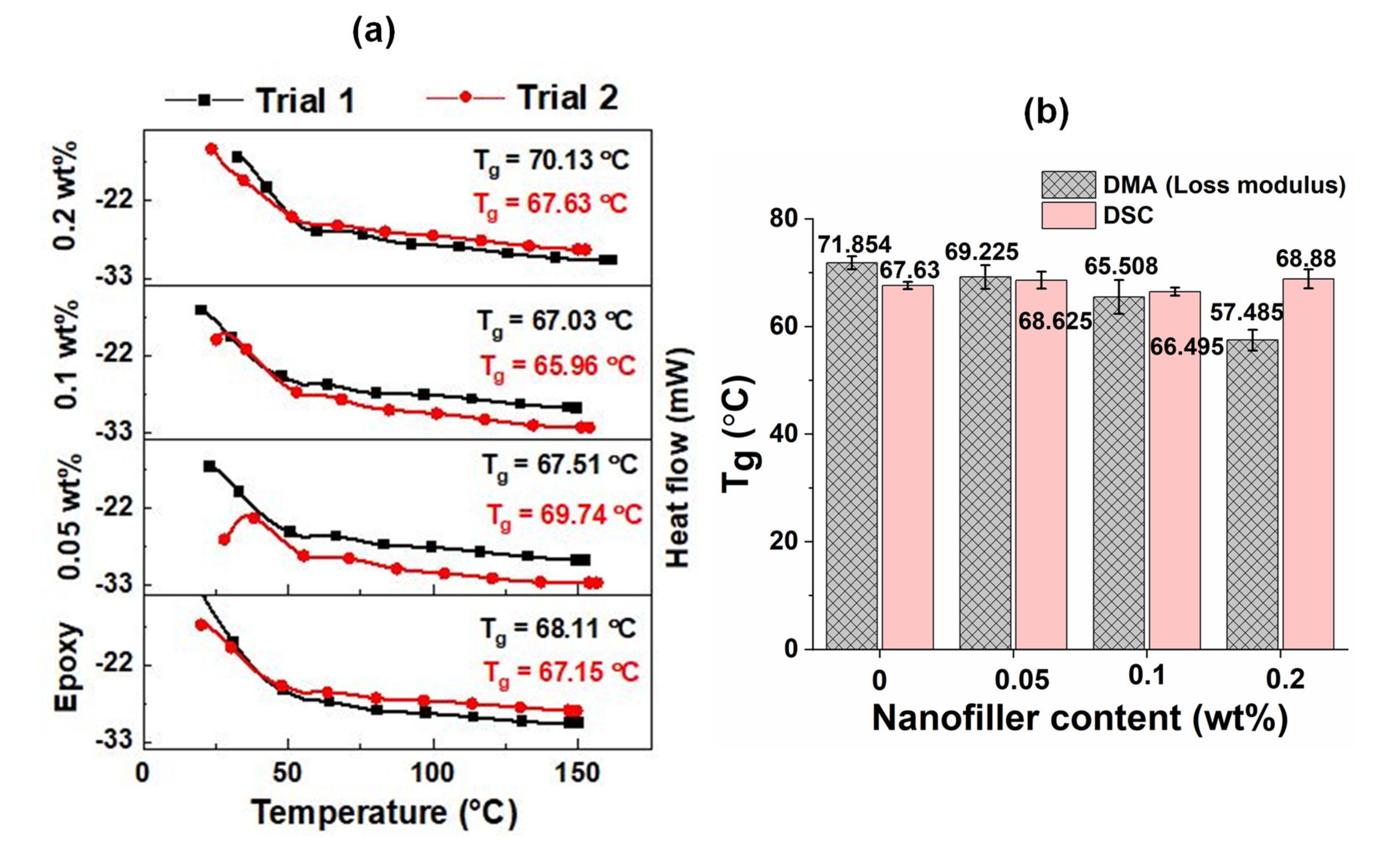
5.4. Comparison of Tg Using DSC and DMA
5.5. Thermogravimetric Analysis
5.6. Thermal Conductivity
5.7. EMI Shielding Effectiveness Measurement
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wei, L.; Chen, X.; Hong, K.; Yuan, Z.; Wang, L.; Wang, H.; Qiao, Z.; Wang, X.; Li, Z.; Wang, Z. Enhancement in mechanical properties of epoxy nanocomposites by Styrene-ethylene-butadiene-styrene grafted graphene oxide. Compos. Interfaces 2018, 26, 141–156. [Google Scholar] [CrossRef]
- Gao, J.; Yu, J.; Wu, X.; Rao, B.; Song, L.; He, Z.; Lu, S. Enhanced thermal properties for epoxy composites with a three-dimensional graphene oxide filler. Fibers Polym. 2015, 16, 2617–2626. [Google Scholar] [CrossRef]
- Yang, X.; Fan, S.; Li, Y.; Guo, Y.; Li, Y.; Ruan, K.; Zhang, S.; Zhang, J.; Kong, J.; Gu, J. Synchronously improved electromagnetic interference shielding and thermal conductivity for epoxy nanocomposites by constructing 3D copper nanowires/thermally annealed graphene aerogel framework. Compos. Part A Appl. Sci. Manuf. 2020, 128, 105670. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, W.; Li, Y.; Zhao, D.; Yin, H. Hybrid fillers of hexagonal and cubic boron nitride in epoxy composites for thermal management applications. RSC Adv. 2019, 9, 7388–7399. [Google Scholar] [CrossRef] [Green Version]
- Chen, J.; Liu, B.; Yan, L. Nanoscale thermal transport in epoxy matrix composite materials reinforced with carbon nanotubes and graphene nanoplatelets. J. Nanoparticle Res. 2019, 21, 256. [Google Scholar] [CrossRef]
- Bortz, D.R.; Heras, E.G.; Martin-Gullon, I. Impressive Fatigue Life and Fracture Toughness Improvements in Graphene Ox-ide/Epoxy Composites. Macromolecules 2011, 45, 238–245. [Google Scholar] [CrossRef]
- Murugan, P.; Naresh, K.; Shankar, K.; Velmurugan, R.; Balaganesan, G. High velocity impact damage investigation of car-bon/epoxy/clay nanocomposites using 3D Computed Tomography. Mater. Today Proc. 2018, 5, 16946–16955. [Google Scholar] [CrossRef]
- Dermani, A.K.; Kowsari, E.; Ramezanzadeh, B.; Amini, R. Screening the effect of graphene oxide nanosheets functionalization with ionic liquid on the mechanical properties of an epoxy coating. Prog. Org. Coat. 2018, 122, 255–262. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, J.; Wang, L.; Li, J.; Feng, T.; Fan, J.; Chen, L.; Gu, J. Superior wave-absorbing performances of silicone rubber composites via introducing covalently bonded SnO2@MWCNT absorbent with encapsulation structure. Compos. Commun. 2020, 22, 100486. [Google Scholar] [CrossRef]
- Yang, S.; Chalivendra, V. Theoretical modeling and experimental validation of electro-shear behavior of carbon nanotubes embedded epoxy nanocomposite. Int. J. Mech. Sci. 2020, 177, 105594. [Google Scholar] [CrossRef]
- Yang, S.; Shin, H.; Cho, M. Contribution of oxygen functional groups in graphene to the mechanical and interfacial behaviour of nanocomposites: Molecular dynamics and micromechanics study. Int. J. Mech. Sci. 2021, 189, 105972. [Google Scholar] [CrossRef]
- Hussein, A.; Kim, B. Micromechanics based FEM study on the mechanical properties and damage of epoxy reinforced with graphene based nanoplatelets. Compos. Struct. 2019, 215, 266–277. [Google Scholar] [CrossRef]
- Han, Z.; Fina, A. Thermal conductivity of carbon nanotubes and their polymer nanocomposites: A review. Prog. Polym. Sci. 2011, 36, 914–944. [Google Scholar] [CrossRef] [Green Version]
- Silva, A.A.; Stein, R.; Campos, D.; Indrusiak, T.; Soares, B.G.; Barra, G.M.O. Conducting Materials Based on Epoxy/Graphene Nano-platelet Composites with Microwave Absorbing Properties: Effect of the Processing Conditions and Ionic Liquid. Front. Mater. 2019, 6, 1–9. [Google Scholar] [CrossRef]
- Yue, L.; Pircheraghi, G.; Monemian, S.A.; Manas-Zloczower, I. Epoxy composites with carbon nanotubes and graphene nano-platelets—Dispersion and synergy effects. Carbon 2014, 78, 268–278. [Google Scholar] [CrossRef]
- Martin-Gallego, M.; Bernal, M.M.; Hernandez, M.; Verdejo, R.; Lopez-Manchado, M.A. Comparison of filler percolation and me-chanical properties in graphene and carbon nanotubes filled epoxy nanocomposites. Eur. Polym. J. 2013, 49, 1347–1353. [Google Scholar] [CrossRef] [Green Version]
- Rafiee, M.; Rafiee, J.; Wang, Z.; Song, H.; Yu, Z.-Z.; Koratkar, N. Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content. ACS Nano 2009, 3, 3884–3890. [Google Scholar] [CrossRef] [PubMed]
- Zhou, G.; Yao, H.; Zhou, Y.; Wang, W.; Peng, M. Self-assembled complexes of graphene oxide and oxidized vapor-grown carbon fibers for simultaneously enhancing the strength and toughness of epoxy and multi-scale carbon fiber/epoxy composites. Carbon 2018, 137, 6–18. [Google Scholar] [CrossRef]
- Abdin, Z.; Alim, M.A.; Saidur, R.; Islam, M.R.; Rashmi, W.; Mekhilef, S.; Wadi, A. Solar energy harvesting with the application of nano-technology. Renew. Sustain. Energy Rev. 2013, 26, 837–852. [Google Scholar] [CrossRef]
- Sun, W.; Hu, R.; Liu, H.; Zeng, M.; Yang, L.; Wang, H.; Zhu, M. Embedding nano-silicon in graphene nanosheets by plasma assisted milling for high capacity anode materials in lithium ion batteries. J. Power Sources 2014, 268, 610–618. [Google Scholar] [CrossRef]
- Gómez-Navarro, C.; Burghard, M.; Kern, K. Elastic Properties of Chemically Derived Single Graphene Sheets. Nano Lett. 2008, 8, 2045–2049. [Google Scholar] [CrossRef] [Green Version]
- Qi, B.; Yuan, Z.; Lu, S.; Liu, K.; Li, S.; Yang, L.; Yu, J. Mechanical and thermal properties of epoxy composites containing graphene oxide and liquid crystalline epoxy. Fibers Polym. 2014, 15, 326–333. [Google Scholar] [CrossRef]
- Olowojoba, G.B.; Kopsidas, S.; Eslava, S.; Gutierrez, E.S.; Kinloch, A.J.; Mattevi, C.; Rocha, V.G.; Taylor, A. A facile way to produce epoxy nanocomposites having excellent thermal conductivity with low contents of reduced graphene oxide. J. Mater. Sci. 2017, 52, 7323–7344. [Google Scholar] [CrossRef] [Green Version]
- Liu, Q.; Zhou, X.; Fan, X.; Zhu, C.; Yao, X.; Liu, Z. Mechanical and Thermal Properties of Epoxy Resin Nanocomposites Reinforced with Graphene Oxide. Polym. Technol. Eng. 2012, 51, 251–256. [Google Scholar] [CrossRef]
- Ma, J.; Meng, Q.; Zaman, I.; Zhu, S.; Michelmore, A.; Kawashima, N.; Wang, C.-H.; Kuan, H. Development of polymer composites using modified, high-structural integrity graphene platelets. Compos. Sci. Technol. 2014, 91, 82–90. [Google Scholar] [CrossRef]
- Moriche, R.; Prolongo, S.; Sánchez, M.; Jiménez-Suárez, A.; Chamizo, F.; Ureña, A. Thermal conductivity and lap shear strength of GNP/epoxy nanocomposites adhesives. Int. J. Adhes. Adhes. 2016, 68, 407–410. [Google Scholar] [CrossRef]
- Monteserín, C.; Blanco, M.; Aranzabe, E.; Aranzabe, A.; Laza, J.M.; Larrañaga-Varga, A.; Vilas, J.L. Effects of Graphene Oxide and Chem-ically-Reduced Graphene Oxide on the Dynamic Mechanical Properties of Epoxy Amine Composites. Polymers 2017, 9, 449. [Google Scholar] [CrossRef] [PubMed]
- Tang, J.; Zhou, H.; Liang, Y.; Shi, X.; Yang, X.; Zhang, J. Properties of Graphene Oxide/Epoxy Resin Composites. J. Nanomater. 2014, 2014, 1–5. [Google Scholar] [CrossRef]
- Yu, Z.; Wang, Z.; Li, H.; Teng, J.; Xu, L. Shape Memory Epoxy Polymer (SMEP) Composite Mechanical Properties Enhanced by Introducing Graphene Oxide (GO) into the Matrix. Materials 2019, 12, 1107. [Google Scholar] [CrossRef] [Green Version]
- Krishnakumar, B.; Sanka, R.S.; Binder, W.H.; Park, C.; Jung, J.; Parthasarthy, V.; Rana, S.; Yun, G.J. Catalyst free self-healable vitri-mer/graphene oxide nanocomposites. Compos. Part B Eng. 2020, 184, 107647. [Google Scholar] [CrossRef]
- Xia, T.; Zeng, D.; Li, Z.; Young, R.J.; Vallés, C.; Kinloch, I.A. Electrically conductive GNP/epoxy composites for out-of-autoclave thermoset curing through Joule heating. Compos. Sci. Technol. 2018, 164, 304–312. [Google Scholar] [CrossRef]
- Song, P.; Qiu, H.; Wang, L.; Liu, X.; Zhang, Y.; Zhang, J.; Kong, J.; Gu, J. Honeycomb structural rGO-MXene/epoxy nanocomposites for supe-rior electromagnetic interference shielding performance. Sustain. Mater. Technol. 2020, 24, e00153. [Google Scholar]
- Wang, L.; Ma, Z.; Zhang, Y.; Chen, L.; Cao, D.; Gu, J. Polymer-based EMI shielding composites with 3D conductive networks: A mini-review. SusMat 2021. [Google Scholar] [CrossRef]
- Song, P.; Liu, B.; Liang, C.; Ruan, K.; Qiu, H.; Ma, Z.; Guo, Y.; Gu, J. Lightweight, Flexible Cellulose-Derived Carbon Aerogel@Reduced Graphene Oxide/PDMS Composites with Outstanding EMI Shielding Performances and Excellent Thermal Conductivities. Nano Micro Lett. 2021, 13, 1–17. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Shi, X.; Zhang, J.; Zhang, Y.; Gu, J. Lightweight and robust rGO/sugarcane derived hybrid carbon foams with out-standing EMI shielding performance. J. Mater. Sci. Technol. 2020, 52, 119–126. [Google Scholar] [CrossRef]
- Li, Y.; Tang, J.; Huang, L.; Wang, Y.; Liu, J.; Ge, X.; Tjong, S.C.; Li, R.K.Y.; Belfiore, L.A. Facile preparation, Characterization and perfor-mance of noncovalently functionalized graphene/epoxy nanocomposites with poly(sodium 4-styrenesulfonate). Composites Part A 2015, 68, 1–9. [Google Scholar] [CrossRef]
- Wang, X.; Xing, W.; Zhang, P.; Song, L.; Yang, H.; Hu, Y. Covalent functionalization of graphene with organosilane and its use as a reinforcement in epoxy composites. Compos. Sci. Technol. 2012, 72, 737–743. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Fang, C.; Liu, N.; Liu, D. Surface modification and thermal performance of a graphene oxide/novolac epoxy composite. RSC Adv. 2018, 8, 20505–20516. [Google Scholar] [CrossRef] [Green Version]
- Jarosinski, L.; Rybak, A.; Gaska, K.; Kmita, G.; Porebska, R.; Kapusta, C. Enhanced thermal conductivity of graphene nanoplatelets epoxy composites. Mater. Sci. 2017, 35, 382–389. [Google Scholar] [CrossRef] [Green Version]
- Umer, R.; Li, Y.; Dong, Y.; Haroosh, H.J.; Liao, K. The effect of graphene oxide (GO) nanoparticles on the processing of epoxy/glass fiber composites using resin infusion. Int. J. Adv. Manuf. Technol. 2015, 81, 2183–2192. [Google Scholar] [CrossRef] [Green Version]
- Naresh, K.; Shankar, K.; Rao, B.S.; Velmurugan, R. Effect of high strain rate on glass/carbon/hybrid fiber reinforced epoxy lami-nated composites. Compos. Part B Eng. 2016, 100, 125–135. [Google Scholar] [CrossRef]
- Naresh, K.; Shankar, K.; Velmurugan, R. Digital image processing and thermo-mechanical response of pristine epoxy and dif-ferent laminate orientations of fiber reinforced polymer composites for vibration isolation applications. Int. J. Polym. Anal. 2018, 23, 684–709. [Google Scholar] [CrossRef]
- Naresh, K.; Shankar, K.; Velmurugan, R.; Gupta, N. High strain rate studies for different laminate configurations of bi-directional glass/epoxy and carbon/epoxy composites using DIC. Structures 2020, 27, 2451–2465. [Google Scholar] [CrossRef]
- Khan, K.A.; Abu Al-Rub, R.K. Modeling Time and Frequency Domain Viscoelastic Behavior of Architectured Foams. J. Eng. Mech. 2018, 144, 1–15. [Google Scholar] [CrossRef]
- Richeton, J.; Schlatter, G.; Vecchio, K.; Remond, Y.; Ahzi, S. A unified model for stiffness modulus of amorphous polymers across transition temperatures and strain rates. Polymer 2005, 46, 8194–8201. [Google Scholar] [CrossRef]
- Goertzen, W.; Kessler, M. Dynamic mechanical analysis of carbon/epoxy composites for structural pipeline repair. Compos. Part B Eng. 2007, 38, 1–9. [Google Scholar] [CrossRef]
- Devi, L.U.; Bhagawan, S.; Thomas, S. Dynamic mechanical analysis of pineapple leaf/glass hybrid fiber reinforced polyester composites. Polym. Compos. 2009, 31, 956–965. [Google Scholar] [CrossRef]
- Costa, C.S.M.F.; Fonseca, A.C.; Serra, A.C.; Coelho, J.F.J. Dynamic Mechanical Thermal Analysis of Polymer Composites Reinforced with Natural Fibers. Polym. Rev. 2016, 56, 362–383. [Google Scholar] [CrossRef]
- Vasudevan, A.; Senthil Kumaran, S.; Naresh, K.; Velmurugan, R. Experimental and analytical investigation of ther-mo-mechanical responses of pure epoxy and carbon/Kevlar/S-glass/E-glass/epoxy interply hybrid laminated composites for aerospace applications. Int. J. Polym. Anal. 2018, 23, 591–605. [Google Scholar] [CrossRef]
- Guth, E. Theory of Filler Reinforcement. J. Appl. Phys. 1945, 16, 20–25. [Google Scholar] [CrossRef]
- Feng, J.; Guo, Z. Temperature-frequency-dependent mechanical properties model of epoxy resin and its composites. Compos. Part B Eng. 2016, 85, 161–169. [Google Scholar] [CrossRef]
- Feng, J.; Guo, Z. Effects of temperature and frequency on dynamic mechanical properties of glass/epoxy composites. J. Mater. Sci. 2016, 51, 2747–2758. [Google Scholar] [CrossRef]
- Naresh, K.; Khan, K.A.; Umer, R.; Vasudevan, A. Temperature-Frequency–Dependent Viscoelastic Properties of Neat Epoxy and Fiber Reinforced Polymer Composites: Experimental Characterization and Theoretical Predictions. Polymers 2020, 12, 1700. [Google Scholar] [CrossRef] [PubMed]
- Mahanta, N.K.; Abramson, A.R. Thermal conductivity of graphene and graphene oxide nanoplatelets. In Proceedings of the 13th InterSociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems, San Diego, CA, USA, 30 May–1 June 2012; pp. 1–6. [Google Scholar]
- Ping, L.; Song, P.; Qiu, H.; Huangfu, Y.; Lu, Y.; Wang, L.; Kong, J.; Gu, J. Superior electromagnetic interference shielding perfor-mances of epoxy composites by introducing highly aligned reduced graphene oxide films. Compos. Part A 2019, 124, 105512. [Google Scholar]
- Sun, Y.; Luo, S.; Sun, H.; Zeng, W.; Ling, C.; Chen, D.; Chan, V.; Liao, K. Engineering closed-cell structure in lightweight and flexible carbon foam composite for high-efficient electromagnetic interference shielding. Carbon 2018, 136, 299–308. [Google Scholar] [CrossRef]
- Chung, D.D.L. Materials for electromagnetic interference shielding. Mater. Chem. Phys. 2020, 255, 123587. [Google Scholar] [CrossRef]
- Ud Din, I.; Naresh, K.; Umer, R.; Khan, K.A.; Drzal, L.T.; Haq, M.; Cantwell, W.J. Processing and out-of-plane properties of compo-sites with embedded graphene paper for EMI shielding applications. Compos. Part A 2020, 134, 105901. [Google Scholar] [CrossRef]
- Zhao, H.; Ding, J.; Yu, H. Variation of mechanical and thermal properties in sustainable graphene oxide/epoxy compo-sites. Sci. Rep. 2018, 8, 16560. [Google Scholar] [CrossRef] [PubMed]
- Tang, L.C.; Wan, Y.J.; Yan, D.; Pei, Y.B.; Zhao, L.; Li, Y.B.; Wu, L.B.; Jiang, J.X.; Lai, G.Q. The effect of graphene dispersion on the mechani-cal properties of graphene/epoxy composites. Carbon 2013, 60, 16–27. [Google Scholar] [CrossRef]
- Shi, Z.; Li, X.-F.; Bai, H.; Xu, W.-W.; Yang, S.-Y.; Lu, Y.; Han, J.; Wang, C.-P.; Liu, X.-J.; Li, W.-B. Influence of microstructural features on thermal expansion coefficient in graphene/epoxy composites. Heliyon 2016, 2, e00094. [Google Scholar] [CrossRef] [Green Version]
- Vimalanathan, P.; Venkateshwaran, N.; Srinivasan, S.P.; Santhanam, V.; Rajesh, M. Impact of surface adaptation and Acacia nilot-ica biofiller on static and dynamic properties of sisal fiber composite. Int. J. Polym. Anal. 2017, 23, 99–112. [Google Scholar] [CrossRef]
- Stark, W.; Jaunich, M.; McHugh, J. Carbon-fibre epoxy prepreg (CFC) curing in an autoclave analogue process controlled by Dynamic Mechanical Analysis (DMA). Polym. Test. 2013, 32, 1487–1494. [Google Scholar] [CrossRef]
- Stark, W. Investigation of the curing behaviour of carbon fibre epoxy prepreg by Dynamic Mechanical Analysis DMA. Polym. Test. 2013, 32, 231–239. [Google Scholar] [CrossRef]
- Visakh, P.M.; Nazarenko, O.B. Thermal Degradation of Polymer Blends, Composites and Nanocomposites. In Thermal Degradation of Polymer Blends, Composites and Nanocomposites; Visakh, P., Arao, Y., Eds.; Engineering Materials; Springer: Cham, Switzerland, 2015; pp. 1–16. [Google Scholar]
- Al-Zahrany, A.A. Nano-reinforced Epoxy Resin Composites with Reduced Graphene Oxide. Ph.D. Thesis, Department of Materials Science and Engineering, University of Sheffield, Sheffield, UK, 2019. [Google Scholar]
- Zhang, X.; He, Q.; Gu, H.; Wei, S.; Guo, Z. Polyaniline stabilized barium titanate nanoparticles reinforced epoxy nanocomposites with high dielectric permittivity and reduced flammability. J. Mater. Chem. C 2013, 1, 2886–2899. [Google Scholar] [CrossRef]
- Wan, Y.-J.; Gong, L.-X.; Tang, L.-C.; Wu, L.-B.; Jiang, J.-X. Mechanical properties of epoxy composites filled with silane-functionalized graphene oxide. Compos. Part A Appl. Sci. Manuf. 2014, 64, 79–89. [Google Scholar] [CrossRef]
- Ilangovan, S.; Kumaran, S.S.; Vasudevan, A.; Naresh, K. Effect of silica nanoparticles on mechanical and thermal properties of neat epoxy and filament wounded E-glass/epoxy and basalt/epoxy composite tubes. Mater. Res. Express 2019, 6, 0850e2. [Google Scholar] [CrossRef]
- Li, A.; Zhang, C.; Zhang, Y.-F. Thermal Conductivity of Graphene-Polymer Composites: Mechanisms, Properties, and Applications. Polymers 2017, 9, 437. [Google Scholar] [CrossRef] [Green Version]
- Balandin, A. Thermal properties of graphene and nanostructured carbon materials. Nat. Mater. 2011, 10, 569–581. [Google Scholar] [CrossRef] [Green Version]
- Pu, H.H.; Rhim, S.H.; Hirschmugl, C.J.; Gajdardziska-Josifovska, M.; Weinert, M.; Chen, J.H. Anisotropic thermal conductivity of semiconducting graphene monoxide. Appl. Phys. Lett. 2013, 102, 569–581. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, J.; Gu, J. Random copolymer membrane coated PBO fibers with significantly improved interfacial adhesion for PBO fibers/cyanate ester composites. Chin. J. Aeronaut. 2021, 34, 659–668. [Google Scholar] [CrossRef]
- Wang, L.; Song, P.; Lin, C.-T.; Kong, J.; Gu, J. 3D Shapeable, Superior Electrically Conductive Cellulose Nanofibers/Ti3C2Tx MXene Aerogels/Epoxy Nanocomposites for Promising EMI Shielding. Research 2020, 2020, 4093732. [Google Scholar] [CrossRef] [PubMed]


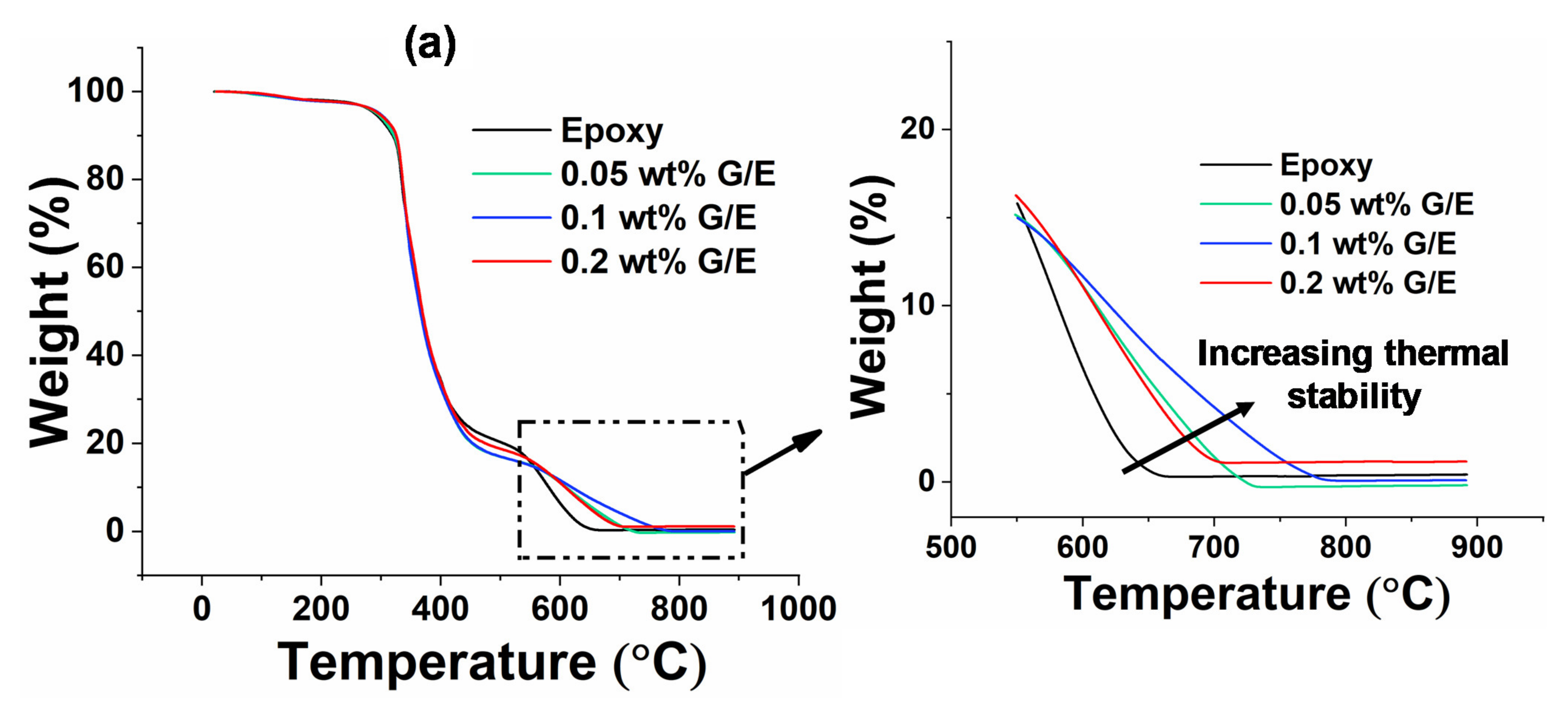
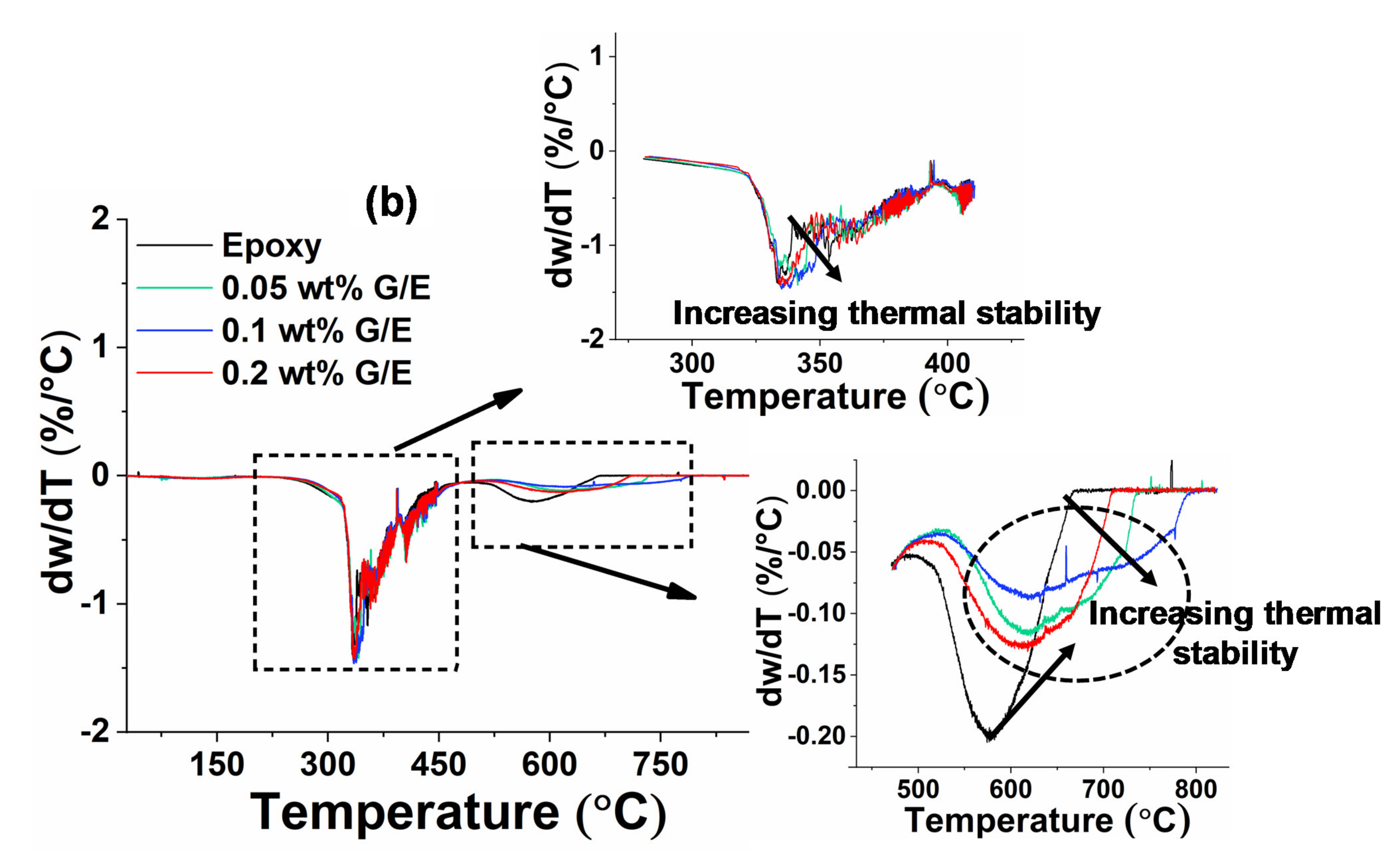
| Samples | Weight Loss Temperature (°C) | Heat-Resistance Index (THRI) (°C) | Derivative of TGA Peak Temperature (°C) | ||
|---|---|---|---|---|---|
| T5 | T30 | Tm1 | Tm2 | ||
| Epoxy | 290.13 | 343.41 | 157.83 | 333.86 | 574.24 |
| 0.05 wt% GO/epoxy | 293.46 | 344.01 | 158.66 | 341.33 | 621.27 |
| 0.1 wt% GO/epoxy | 297.95 | 343.38 | 159.35 | 335.12 | 631.66 |
| 0.2 wt% GO/epoxy | 296.33 | 344.75 | 159.44 | 336.33 | 617.90 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naresh, K.; Khan, K.A.; Umer, R. Experimental Characterization and Modeling Multifunctional Properties of Epoxy/Graphene Oxide Nanocomposites. Polymers 2021, 13, 2831. https://doi.org/10.3390/polym13162831
Naresh K, Khan KA, Umer R. Experimental Characterization and Modeling Multifunctional Properties of Epoxy/Graphene Oxide Nanocomposites. Polymers. 2021; 13(16):2831. https://doi.org/10.3390/polym13162831
Chicago/Turabian StyleNaresh, Kakur, Kamran A. Khan, and Rehan Umer. 2021. "Experimental Characterization and Modeling Multifunctional Properties of Epoxy/Graphene Oxide Nanocomposites" Polymers 13, no. 16: 2831. https://doi.org/10.3390/polym13162831
APA StyleNaresh, K., Khan, K. A., & Umer, R. (2021). Experimental Characterization and Modeling Multifunctional Properties of Epoxy/Graphene Oxide Nanocomposites. Polymers, 13(16), 2831. https://doi.org/10.3390/polym13162831