Debonding Failure Analysis of Reinforced Concrete Beams Strengthened with CFRP Plates
Abstract
:1. Introduction
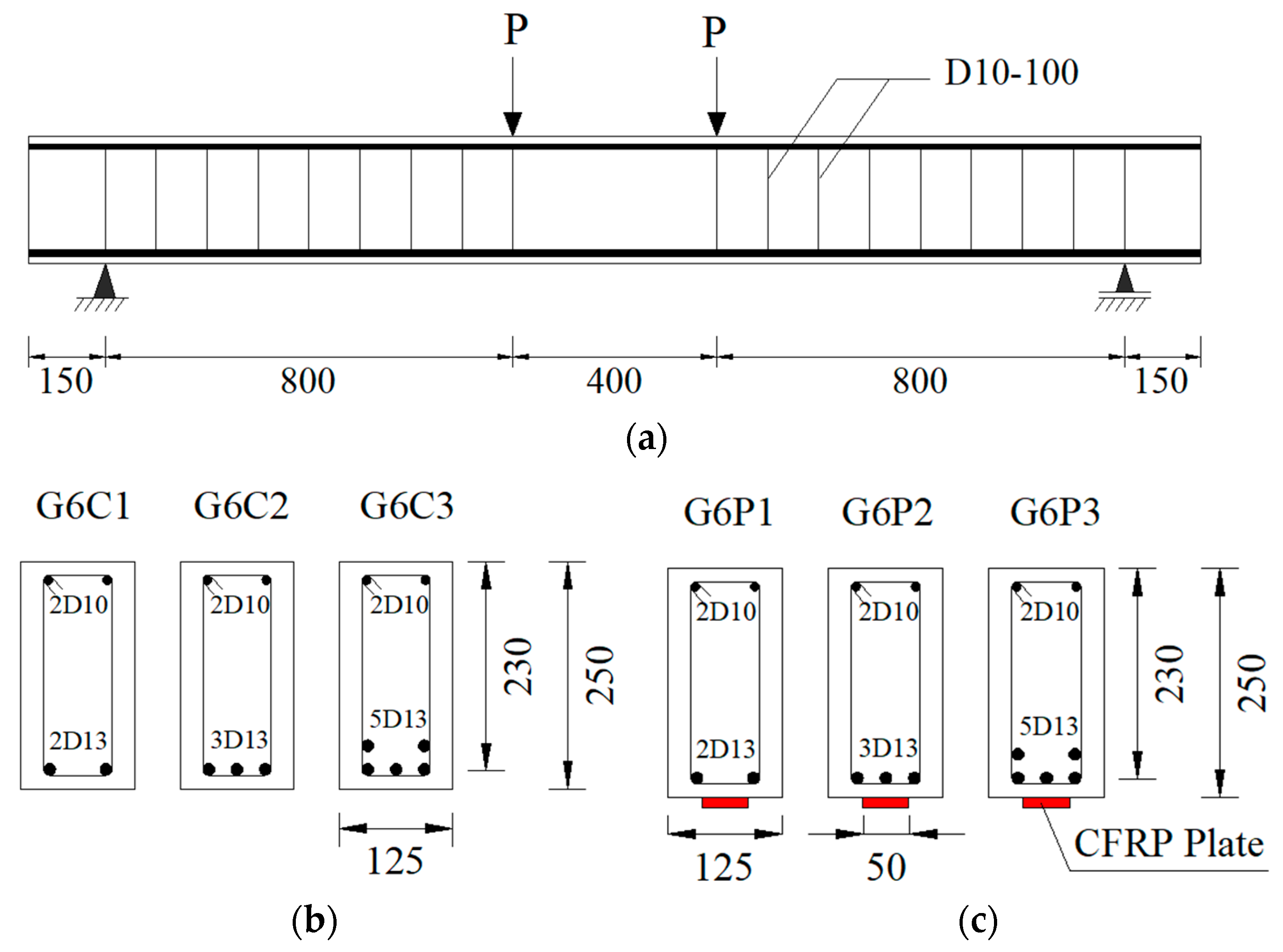
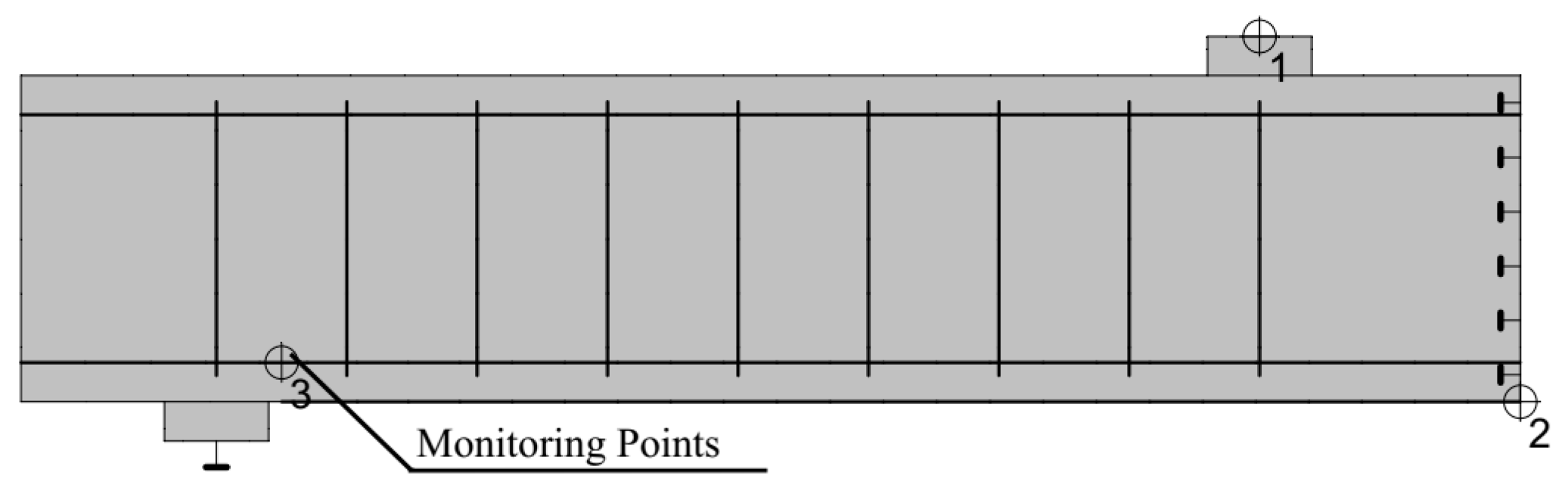
2. Experimental Study
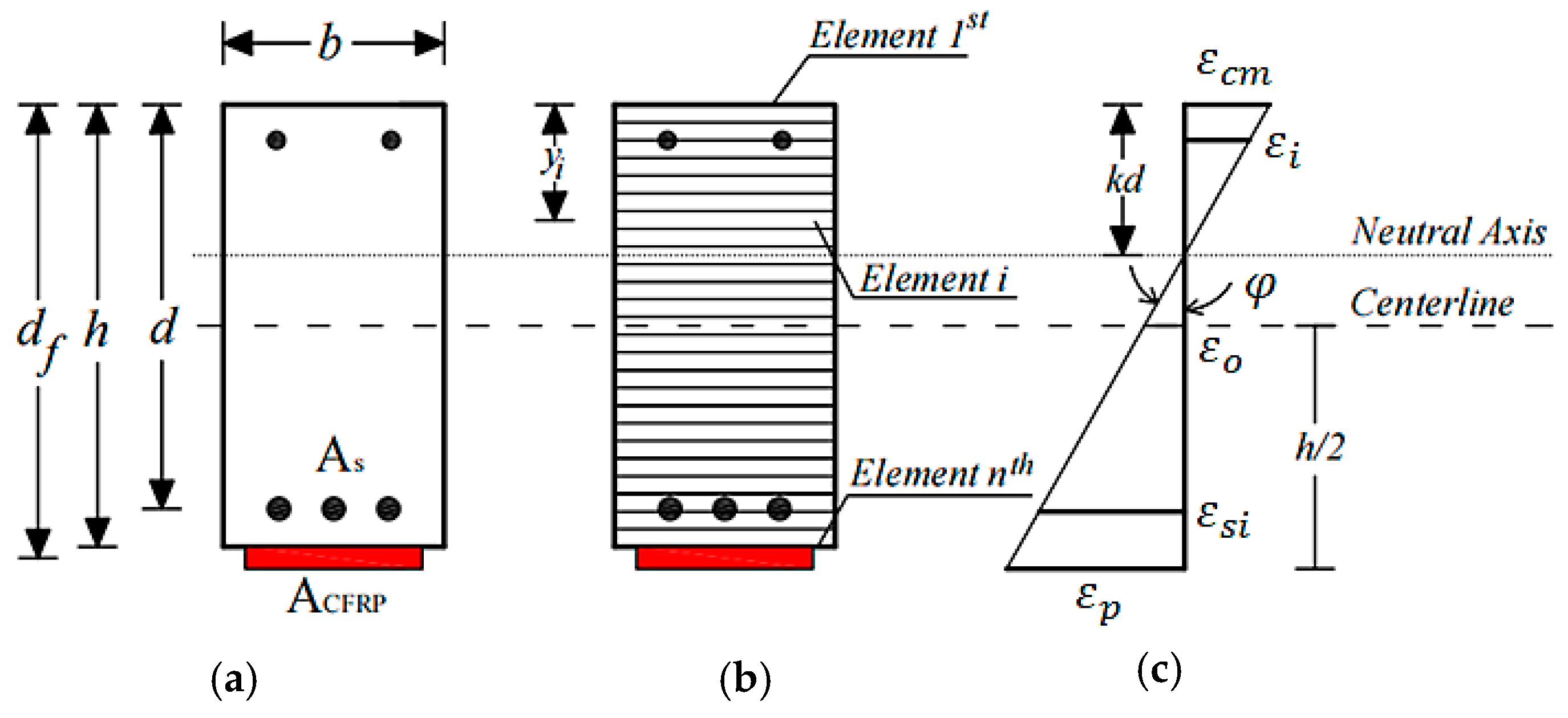
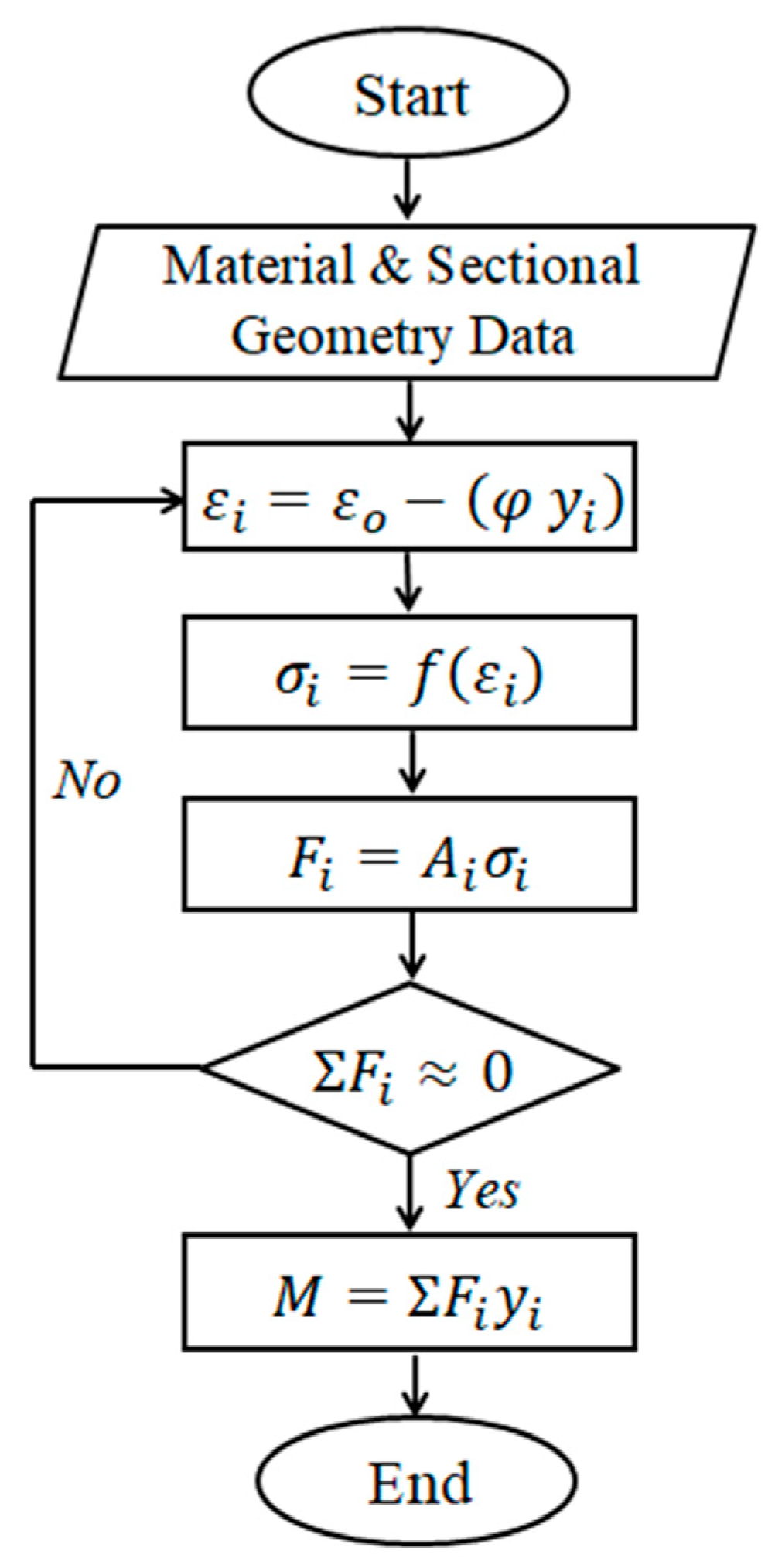
3. Fiber Element Method
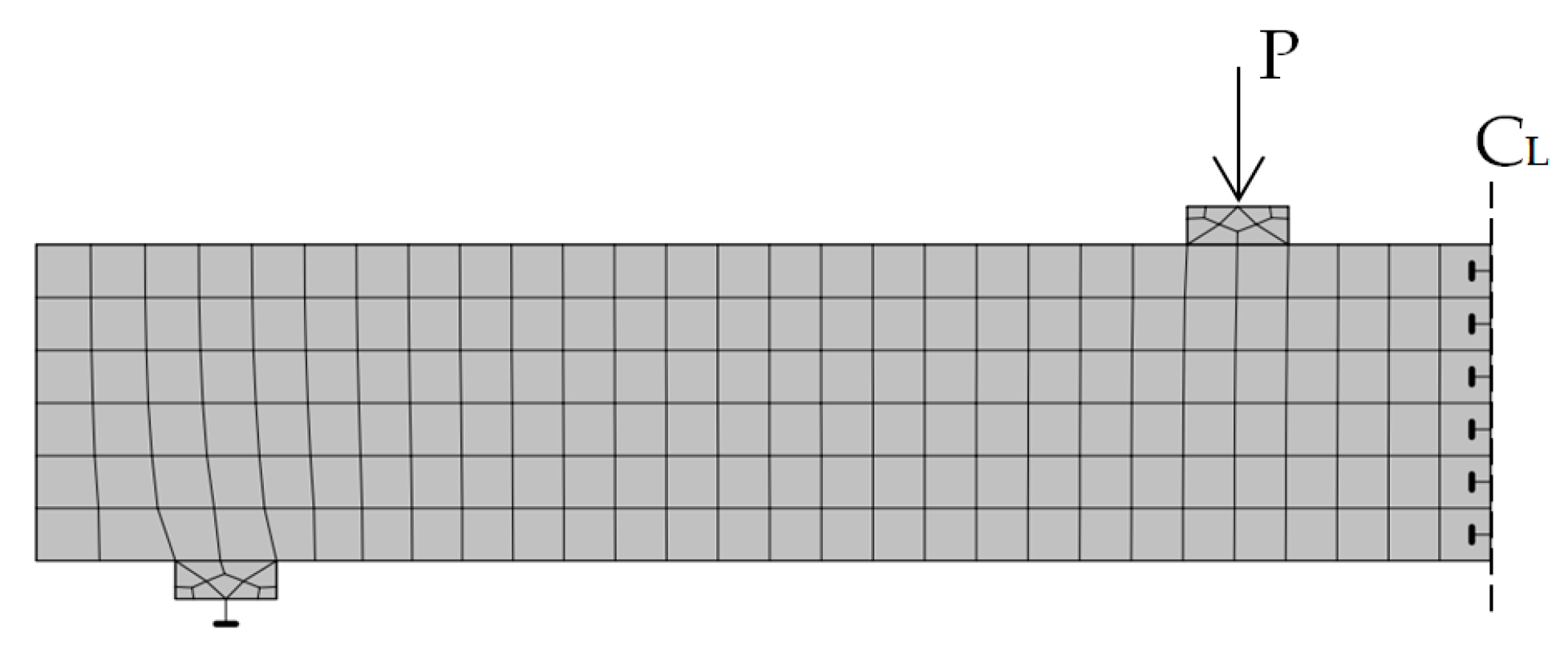
4. Finite Element Method
5. Results and Discussion
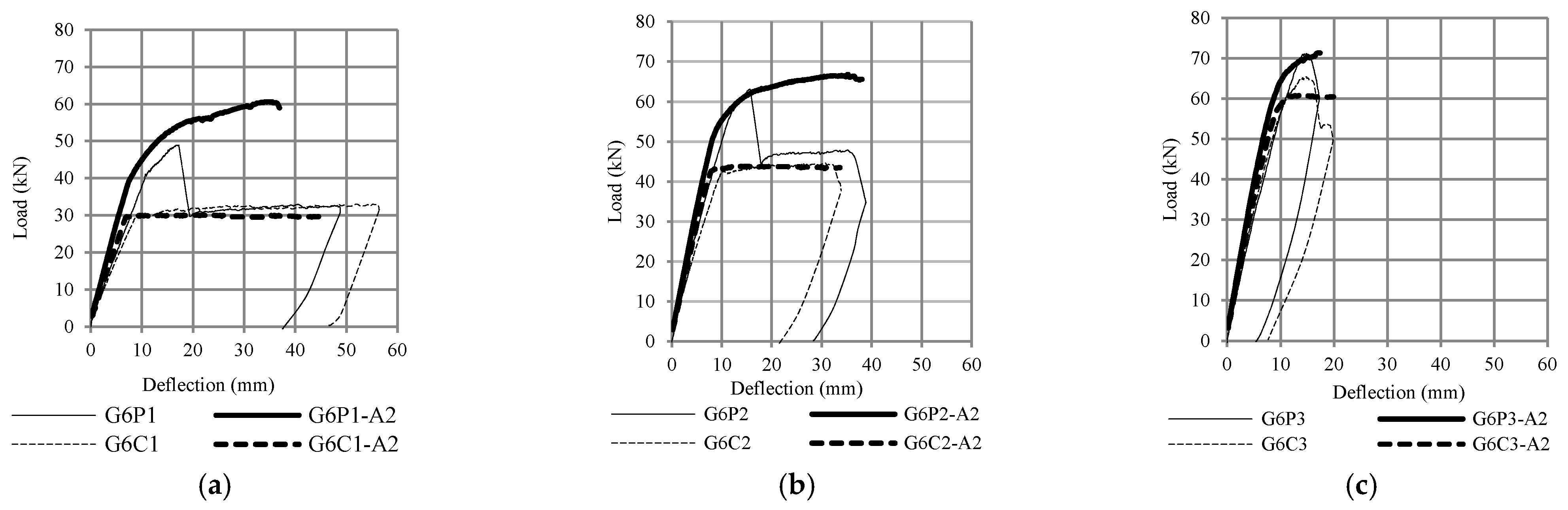
5.1. Experimental Results
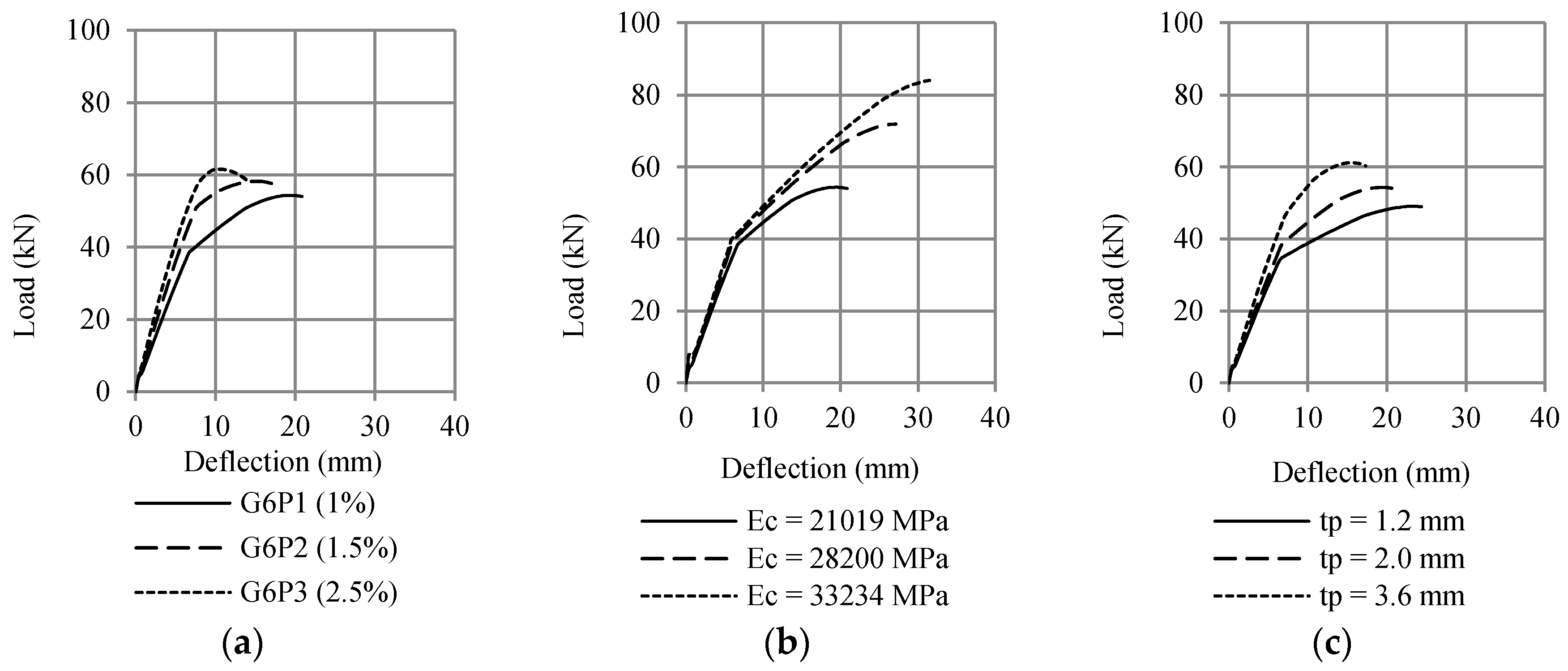
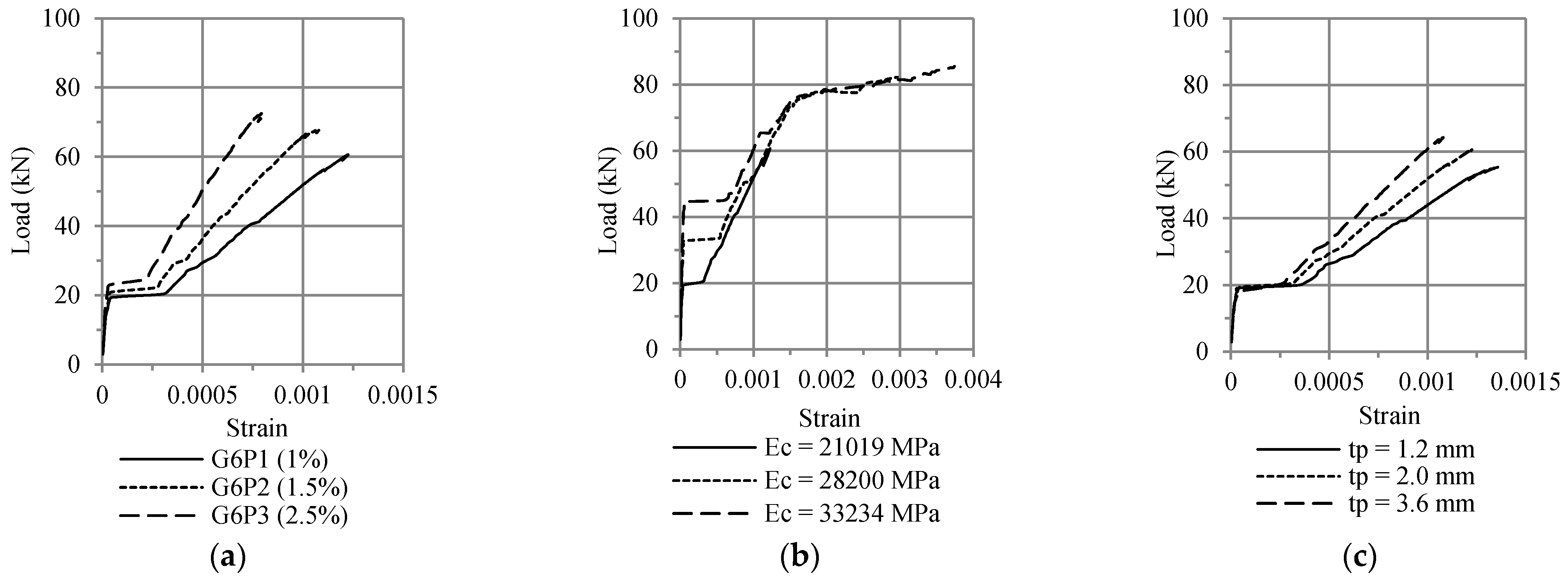
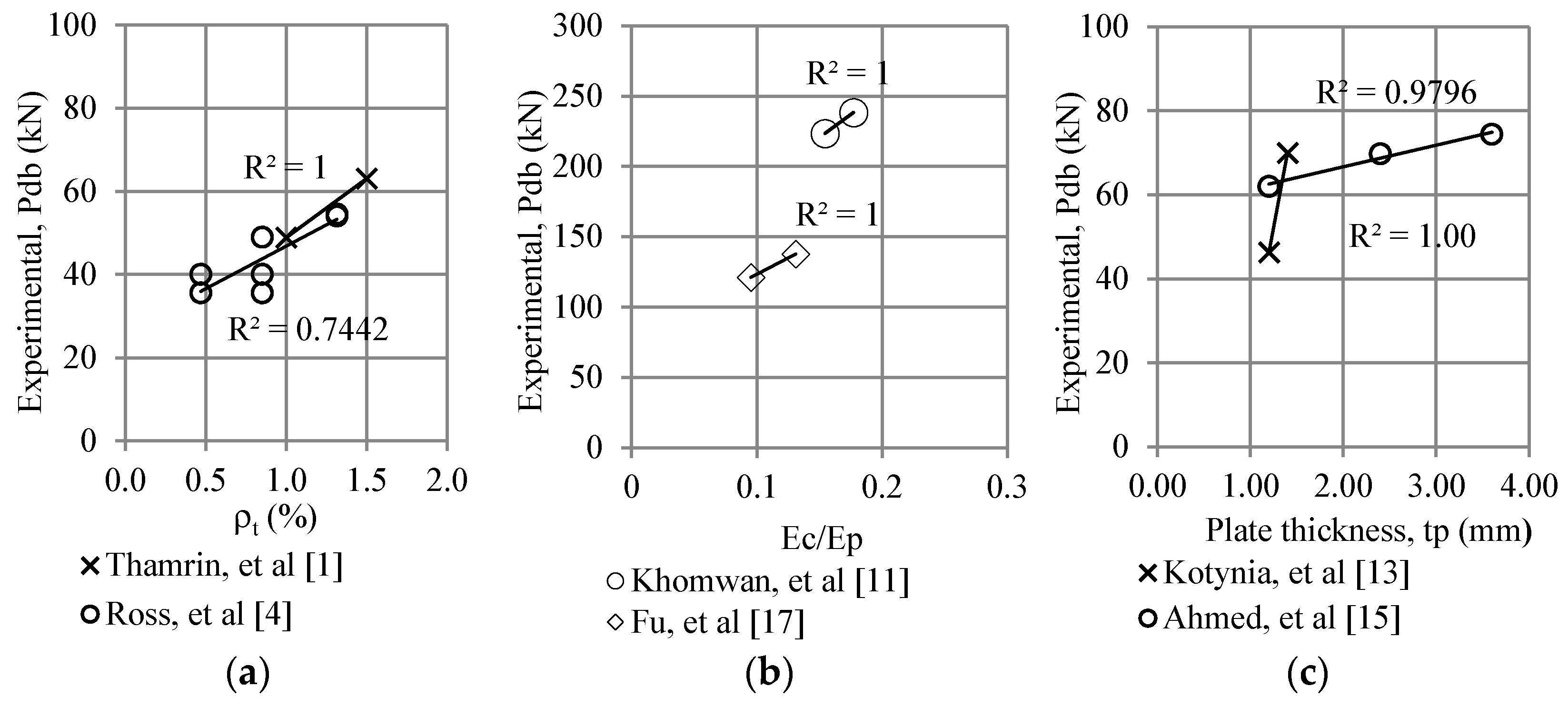
5.2. Parametric Study
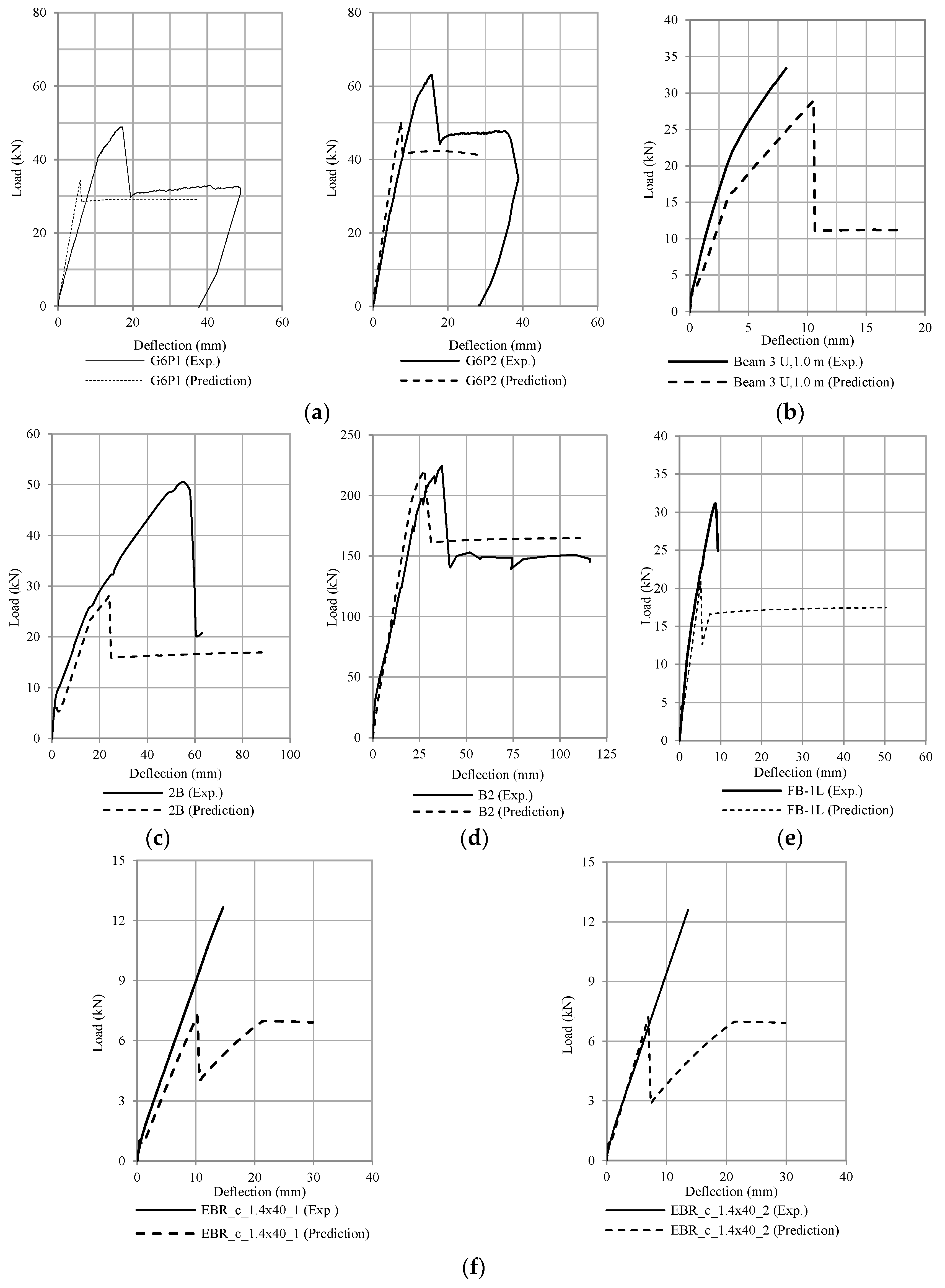
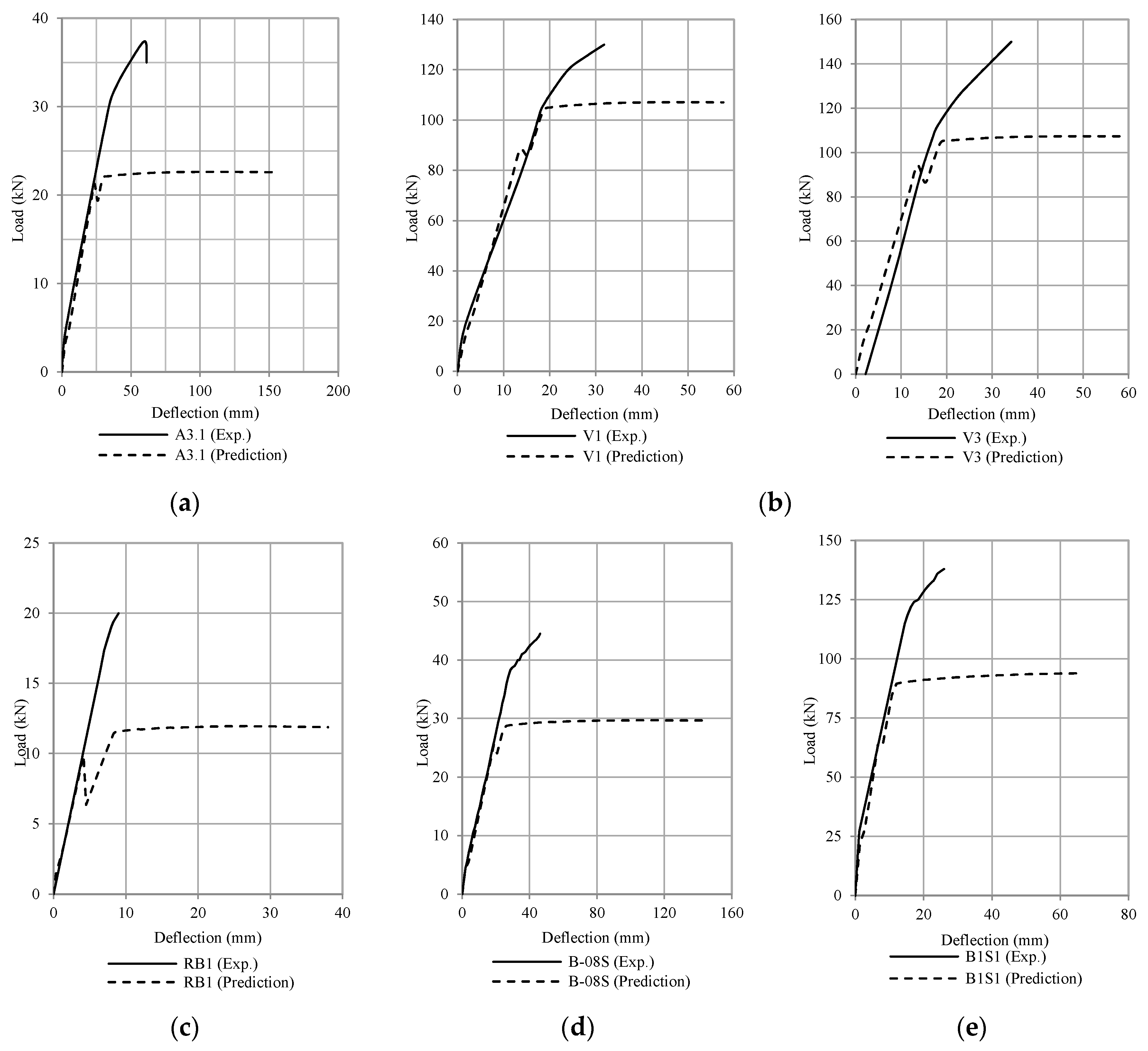
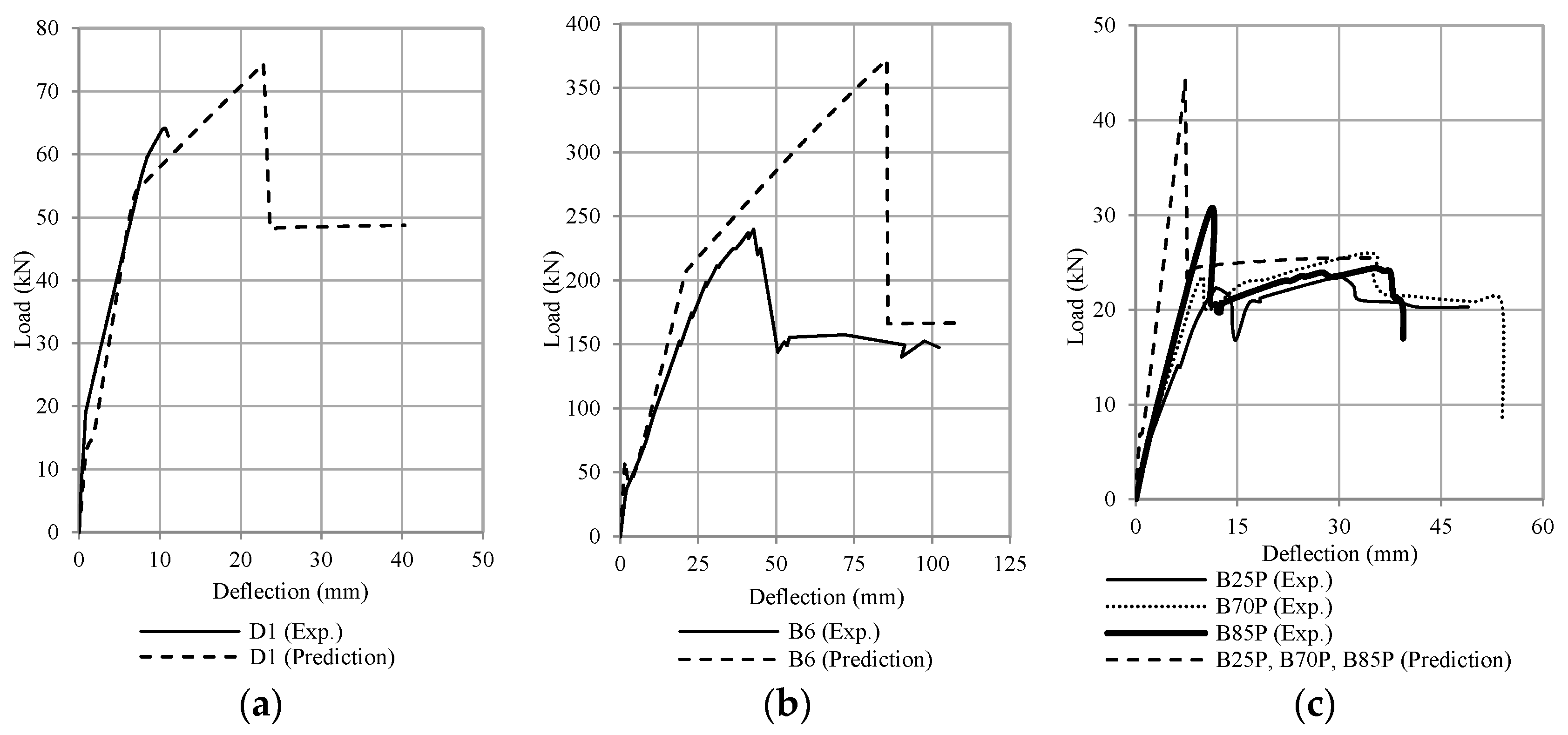
5.3. Debonding Failure Analysis
5.4. Implementation of the Proposed Model on the RCCSA Software
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Thamrin, R.; Zaidir; Zakiyyah, A. Effect of reinforcement ratio on flexural behavior of reinforced concrete beams strengthened with CFRP plates. IOP Conf. Ser. Earth Environ. Sci. 2021, 708, 012015. [Google Scholar] [CrossRef]
- Garden, H.N.; Hollaway, L.C. An experimental study of the influence of plate end anchorage of carbon fibre composite plates used to strengthen reinforced concrete beams. Compos. Struct. 1998, 42, 175–188. [Google Scholar] [CrossRef]
- Spadea, G.; Bencardino, F.; Swamy, R.N. Structural Behavior of Composite RC Beams with Externally Bonded CFRP. J. Compos. Constr. 1998, 2, 132–137. [Google Scholar] [CrossRef]
- Ross, C.A.; Jerome, D.M.; Tedesco, J.W.; Hughes, M.L. Strengthening of reinforced concrete beams with externally bonded composite laminates. Struct. J. 1999, 96, 212–220. [Google Scholar]
- Shehata, I.A.E.M.; Cerqueira, E.C.; Pinto, C.T.M. Strengthening of RC beams in flexure and shear using. In Proceedings of the 5th International Conference on Fibre-Reinforced Plastics for Reinforced Concrete Structures, Cambridge, UK, 16–18 July 2001; Volume 1, pp. 97–106. [Google Scholar]
- Nguyen, D.M.; Chan, T.K.; Cheong, H.K. Brittle Failure and Bond Development Length of CFRP-Concrete Beams. J. Compos. Constr. 2001, 5, 12–17. [Google Scholar] [CrossRef]
- Fanning, P.J.; Kelly, O. Ultimate Response of RC Beams Strengthened with CFRP Plates. J. Compos. Constr. 2001, 5, 122–127. [Google Scholar] [CrossRef]
- Brena, S.F.; Bramblett, R.M.; Wood, S.L.; Kreger, M.E. Increasing Flexural Capacity of Reinforced Concrete Beams Using Carbon Fiber-Reinforced Polymer Composites. ACI Struct. J. 2003, 100, 36–46. [Google Scholar] [CrossRef]
- Breña, S.F.; Macri, B.M. Effect of Carbon-Fiber-Reinforced Polymer Laminate Configuration on the Behavior of Strengthened Reinforced Concrete Beams. J. Compos. Constr. 2004, 8, 229–240. [Google Scholar] [CrossRef]
- Pimanmas, A.; Pornpongsaroj, P. Peeling behaviour of reinforced concrete beams strengthened with CFRP plates under various end restraint conditions. Mag. Concr. Res. 2004, 56, 73–81. [Google Scholar] [CrossRef]
- Khomwan, N.; Foster, S.J.; Smith, S.T. Debonding Failure in CFRP Flexurally Strengthened Reinforced Concrete Beams; The University of New South Wales: Sydney, Australia, 2005; ISBN 85841-407-4. [Google Scholar]
- Benjeddou, O.; Ben Ouezdou, M.; Bedday, A. Damaged RC beams repaired by bonding of CFRP laminates. Constr. Build. Mater. 2007, 21, 1301–1310. [Google Scholar] [CrossRef]
- Kotynia, R.; Baky, H.A.; Neale, K.W.; Ebead, U.A. Flexural Strengthening of RC Beams with Externally Bonded CFRP Systems: Test Results and 3D Nonlinear FE Analysis. J. Compos. Constr. 2008, 12, 190–201. [Google Scholar] [CrossRef]
- Al-Tamimi, A.K.; Hawileh, R.; Abdalla, J.; Rasheed, H.A. Effects of Ratio of CFRP Plate Length to Shear Span and End Anchorage on Flexural Behavior of SCC RC Beams. J. Compos. Constr. 2011, 15, 908–919. [Google Scholar] [CrossRef]
- Ahmed, E.; Sobuz, H.R.; Sutan, N.M. Flexural performance of CFRP strengthened RC beams with different degrees of strengthening schemes. Int. J. Phys. Sci. 2011, 6, 2229–2238. [Google Scholar] [CrossRef]
- Bilotta, A.; Ceroni, F.; Nigro, E.; Pecce, M. Efficiency of CFRP NSM strips and EBR plates for flexural strengthening of RC beams and loading pattern influence. Compos. Struct. 2015, 124, 163–175. [Google Scholar] [CrossRef]
- Fu, B.; Chen, G.M.; Teng, J.G. Mitigation of intermediate crack debonding in FRP-plated RC beams using FRP U-jackets. Compos. Struct. 2017, 176, 883–897. [Google Scholar] [CrossRef]
- Wu, Z.; Wu, Y.; Fahmy, M.F. Structures Strengthened with Bonded Composites; Woodhead Publishing: Cambridge, MA, USA, 2020; ISBN 978-0-12-821089-5. [Google Scholar]
- Mansour, W.N. Analysis of RC Continuous Beams Strengthened in Flexure with FRP Using FEM. Available online: https://www.researchgate.net/profile/Walid-Mansour/publication (accessed on 18 May 2020).
- Motavalli, M.; Czaderski, C.; Pfyl-Lang, K. Prestressed CFRP for Strengthening of Reinforced Concrete Structures: Recent Developments at Empa, Switzerland. J. Compos. Constr. 2011, 15, 194–205. [Google Scholar] [CrossRef]
- Oehlers, D.J. Reinforced Concrete Beams with Plates Glued to their Soffits. J. Struct. Eng. 1992, 118, 2023–2038. [Google Scholar] [CrossRef]
- Teng, J.G.; Chen, J.F. Debonding failures of RC beams strengthened with externally bonded FRP reinforcement: Behaviour and modelling. In Proceedings of the First Asia-Pacific Conference on FRP in Structures (APFIS 2007), Hong Kong, China, 12–14 December 2007; pp. 12–14. [Google Scholar]
- Thamrin, R.; Sari, R.P. Flexural Capacity of Strengthened Reinforced Concrete Beams with Web Bonded Steel Plates. Procedia Eng. 2017, 171, 1129–1136. [Google Scholar] [CrossRef]
- Thamrin, R. Effect of Strengthening Method and Anchorage Length on Flexural Capacity of RC Beams with Steel Plates. J. Eng. Sci. Technol. 2018, 13, 3781–3794. [Google Scholar]
- Thamrin, R. Analytical Prediction on Flexural Response of RC Beams Strengthened with Steel Plates. In Proceedings of the MATEC Web of Conferences: International Symposium on Civil and Environmental Engineering (ISCEE), Wuhan, China, 20–21 December 2016; EDP Sciences: Les Ulis, France, 2017; Volume 103, p. 2012. [Google Scholar]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef] [Green Version]
- Cervenka, V.; Jendele, L.; Cervenka, J. ATENA Program Documentation-Part 1: Theory. Available online: https://www.cervenka.cz/products/atena/documentation (accessed on 11 March 2020).






| Literature | Empirical Equations for Debonding Moment | |
|---|---|---|
| Oehlers [21] | Equation (6) | |
| Teng & Chen [22] | Equation (7) | |
| Specimen | fc’ | ft | Ec | bw | h | a | ρt | tp | Ep | Oehlers [21] | Teng&Chen [22] | Proposed Model | Pexp |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (MPa) | (MPa) | (GPa) | (mm) | (mm) | (mm) | (mm) | (GPa) | (kN) | (kN) | (kN) | (kN) | ||
| Thamrin et al. [1] | |||||||||||||
| G6P1 | 20 | 2.0 | 21 | 125 | 250 | 800 | 0.009 | 1.90 | 139 | 22.77 | 21.27 | 32.71 | 48.90 |
| G6P2 | 20 | 2.0 | 21 | 125 | 250 | 800 | 0.014 | 1.90 | 139 | 28.35 | 31.19 | 49.06 | 63.10 |
| G6P3 | 20 | 2.0 | 21 | 125 | 250 | 800 | 0.023 | 1.90 | 139 | 37.35 | 47.15 | 81.77 | 71.15 |
| Garden & Hollaway [2] | |||||||||||||
| Beam 1 U,1.0 m | 44.8 | 4.5 | 31 | 100 | 100 | 300 | 0.01 | 0.82 | 110 | 15.35 | 5.96 | 21.22 | 36.50 |
| Beam 2 U,1.0 m | 44.8 | 4.5 | 31 | 100 | 100 | 300 | 0.01 | 0.82 | 110 | 15.35 | 5.96 | 21.22 | 32.00 |
| Beam 3 U,1.0 m | 44.8 | 4.5 | 31 | 100 | 100 | 220 | 0.01 | 0.82 | 110 | 20.93 | 8.12 | 28.94 | 34.00 |
| Beam 4 U,1.0 m | 44.8 | 4.5 | 31 | 100 | 100 | 100 | 0.01 | 0.82 | 110 | 46.04 | 17.87 | 63.66 | 34.50 |
| Beam 5 U,1.0 m | 44.8 | 4.5 | 31 | 100 | 100 | 100 | 0.01 | 0.82 | 110 | 46.04 | 17.87 | 63.66 | 34.60 |
| Spadea et al. [3] | |||||||||||||
| A3.1 | 24.9 | 2.5 | 23 | 140 | 300 | 1800 | 0.011 | 1.20 | 152 | 32.22 | 18.47 | 21.14 | 37.40 |
| Ross et al. [4] | |||||||||||||
| 1B | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0047 | 0.45 | 138 | 60.01 | 7.92 | 15.19 | 40.05 |
| 1C | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0047 | 0.45 | 138 | 60.01 | 7.92 | 15.19 | 35.60 |
| 2B | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0085 | 0.45 | 138 | 80.06 | 15.10 | 27.57 | 48.95 |
| 2C | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0085 | 0.45 | 138 | 80.06 | 15.10 | 27.57 | 35.60 |
| 2D | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0085 | 0.45 | 138 | 80.06 | 15.10 | 27.57 | 40.05 |
| 3B | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0132 | 0.45 | 138 | 101.33 | 23.96 | 42.58 | 54.52 |
| 3C | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0132 | 0.45 | 138 | 101.33 | 23.96 | 42.58 | 54.07 |
| 3D | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0132 | 0.45 | 138 | 101.33 | 23.96 | 42.58 | 54.29 |
| 4B | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0187 | 0.45 | 138 | 123.76 | 34.60 | 60.68 | 53.82 |
| 4C | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0187 | 0.45 | 138 | 123.76 | 34.60 | 60.68 | 52.29 |
| 4D | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0187 | 0.45 | 138 | 123.76 | 34.60 | 60.68 | 55.63 |
| 5B | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0201 | 0.45 | 138 | 128.85 | 37.19 | 65.15 | 73.43 |
| 5C | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0201 | 0.45 | 138 | 128.85 | 37.19 | 65.15 | 73.43 |
| 5D | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0201 | 0.45 | 138 | 128.85 | 37.19 | 65.15 | 72.76 |
| 6B | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0335 | 0.45 | 138 | 171.54 | 61.32 | 108.47 | 84.55 |
| 6C | 54.8 | 5.5 | 35 | 200 | 200 | 914 | 0.0335 | 0.45 | 138 | 171.54 | 61.32 | 108.47 | 76.55 |
| Shehata et al. [5] | |||||||||||||
| V1 | 33.3 | 3.3 | 27 | 150 | 450 | 1350 | 0.010 | 1.20 | 165 | 180.83 | 95.39 | 84.87 | 140.00 |
| V3 | 34.3 | 3.4 | 28 | 150 | 450 | 1350 | 0.010 | 1.20 | 165 | 195.75 | 96.01 | 88.73 | 150.00 |
| Nguyen et al. [6] | |||||||||||||
| A950 | 26.6 | 2.7 | 24 | 120 | 150 | 440 | 0.016 | 1.20 | 181 | 15.61 | 14.34 | 25.80 | 28.10 |
| A1100 | 26.6 | 2.7 | 24 | 120 | 150 | 440 | 0.016 | 1.20 | 181 | 15.61 | 14.34 | 25.80 | 28.65 |
| A1150 | 26.6 | 2.7 | 24 | 120 | 150 | 440 | 0.016 | 1.20 | 181 | 15.61 | 14.34 | 25.80 | 29.45 |
| B1 | 37.0 | 3.7 | 29 | 120 | 150 | 440 | 0.004 | 1.20 | 181 | 12.73 | 3.53 | 10.14 | 24.60 |
| B2 | 37.0 | 3.7 | 29 | 120 | 150 | 440 | 0.044 | 1.20 | 181 | 28.95 | 41.41 | 112.69 | 65.05 |
| C5 | 20.8 | 2.1 | 21 | 120 | 150 | 440 | 0.014 | 1.20 | 181 | 16.67 | 17.41 | 15.29 | 35.50 |
| C10 | 20.8 | 2.1 | 21 | 120 | 150 | 440 | 0.015 | 1.20 | 181 | 15.74 | 16.41 | 15.86 | 34.00 |
| C20 | 20.8 | 2.1 | 21 | 120 | 150 | 440 | 0.016 | 1.20 | 181 | 14.02 | 14.47 | 17.13 | 31.50 |
| Fanning & Kelly [7] | |||||||||||||
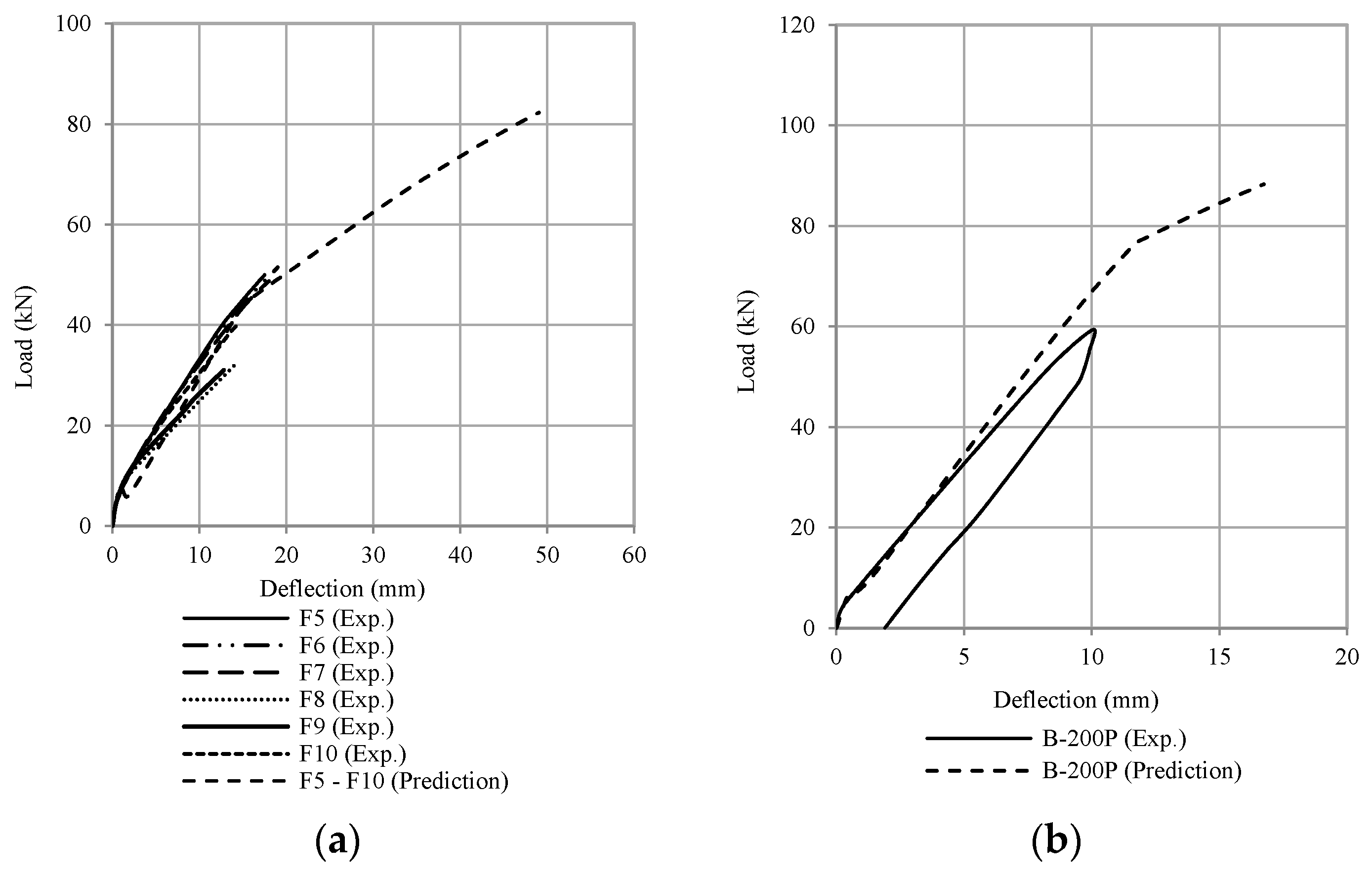
| F5 | 80 | 5.0 | 39 | 155 | 240 | 1100 | 0.011 | 1.20 | 155 | 69.59 | 25.51 | 79.64 | 50.00 |
| F6 | 80 | 5.0 | 39 | 155 | 240 | 1100 | 0.011 | 1.20 | 155 | 69.59 | 25.51 | 79.64 | 51.50 |
| F7 | 80 | 5.0 | 39 | 155 | 240 | 1100 | 0.011 | 1.20 | 155 | 69.59 | 25.51 | 79.64 | 48.75 |
| F8 | 80 | 5.0 | 39 | 155 | 240 | 1100 | 0.011 | 1.20 | 155 | 69.59 | 25.51 | 79.64 | 32.00 |
| F9 | 80 | 5.0 | 39 | 155 | 240 | 1100 | 0.011 | 1.20 | 155 | 69.59 | 25.51 | 79.64 | 31.00 |
| F10 | 80 | 5.0 | 39 | 155 | 240 | 1100 | 0.011 | 1.20 | 155 | 69.59 | 25.51 | 79.64 | 41.00 |
| Breña et al. [8] | |||||||||||||
| D1 | 37.2 | 3.7 | 29 | 203 | 406 | 1220 | 0.005 | 1.19 | 155 | 128.10 | 41.78 | 72.10 | 64.05 |
| D2 | 37.2 | 3.7 | 29 | 203 | 406 | 1220 | 0.005 | 1.19 | 155 | 128.10 | 41.78 | 72.10 | 66.95 |
| Breña et al. [9] | |||||||||||||
| A6-I | 47.7 | 4.8 | 33 | 100 | 100 | 330 | 0.008 | 1.19 | 155 | 7.98 | 5.14 | 17.44 | 34.80 |
| Pimanmas et al. [10] | |||||||||||||
| B-200P | 44 | 4.4 | 31 | 120 | 220 | 700 | 0.033 | 1.20 | 150 | 51.45 | 51.12 | 180.95 | 117.79 |
| Khomwan et al. [11] | |||||||||||||
| B2 | 37 | 3.7 | 25 | 350 | 700 | 2500 | 0.006 | 1.40 | 165 | 467.07 | 142.64 | 191.97 | 223.50 |
| B6 | 53 | 5.3 | 29 | 350 | 700 | 2500 | 0.006 | 1.40 | 165 | 574.57 | 147.06 | 315.70 | 238.50 |
| Benjeddou et al. [12] | |||||||||||||
| RB1 | 21 | 1.86 | 30 | 120 | 150 | 600 | 0.010 | 1.20 | 165 | 9.20 | 7.91 | 11.47 | 20.06 |
| Kotynia et al. [13] | |||||||||||||
| B-08 S | 32.3 | 2.8 | 27 | 150 | 300 | 1400 | 0.008 | 1.20 | 172 | 38.35 | 23.28 | 25.28 | 46.30 |
| B-08 M | 37.3 | 3.5 | 29 | 150 | 300 | 1400 | 0.008 | 1.40 | 220 | 43.51 | 21.83 | 30.97 | 70.00 |
| Al-Tamimi et al. [14] | |||||||||||||
| B85P | 54 | 5.4 | 35 | 110 | 180 | 562 | 0.009 | 1.40 | 215 | 24.21 | 16.50 | 42.59 | 30.35 |
| B25P | 54 | 5.4 | 35 | 110 | 180 | 562 | 0.009 | 1.40 | 215 | 24.21 | 16.50 | 42.59 | 25.97 |
| B70P | 54 | 5.4 | 35 | 110 | 180 | 562 | 0.009 | 1.40 | 215 | 24.21 | 16.50 | 42.59 | 23.54 |
| Ahmed et al. [15] | |||||||||||||
| FB-1L | 36 | 3.0 | 29 | 150 | 200 | 700 | 0.006 | 1.20 | 165 | 24.85 | 11.81 | 19.66 | 31.00 |
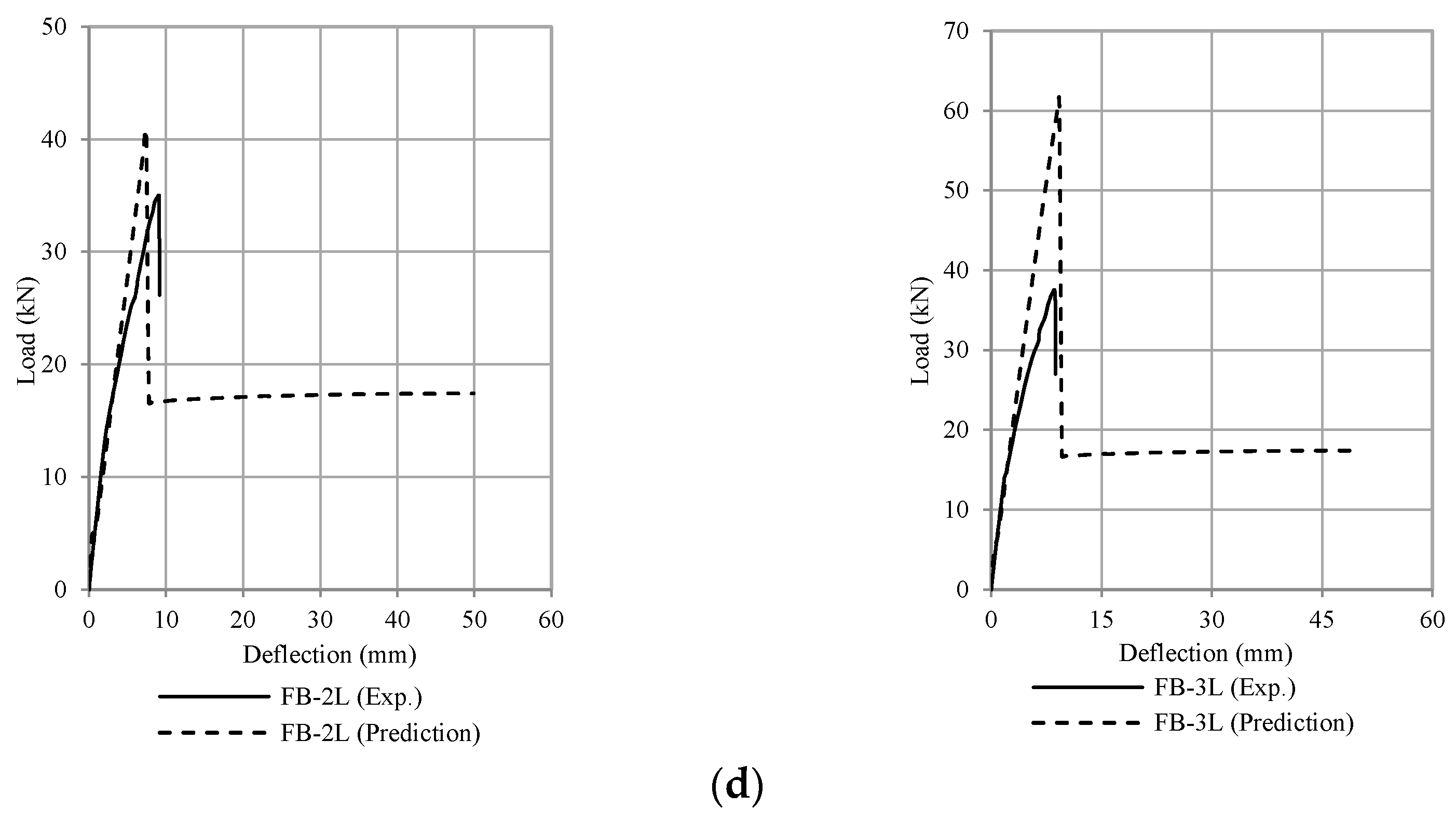
| FB-2L | 36 | 3.0 | 29 | 150 | 200 | 700 | 0.006 | 2.40 | 165 | 17.30 | 10.18 | 39.32 | 34.88 |
| FB-3L | 36 | 3.0 | 29 | 150 | 200 | 700 | 0.006 | 3.60 | 165 | 14.52 | 9.35 | 58.98 | 37.20 |
| Bilotta et al. [16] | |||||||||||||
| EBR_c_1.4x40_1 | 17.43 | 1.74 | 20 | 120 | 160 | 925 | 0.013 | 1.40 | 171 | 3.23 | 4.17 | 7.02 | 18.25 |
| EBR_c_1.4x40_2 | 17.43 | 1.74 | 20 | 120 | 160 | 925 | 0.013 | 1.40 | 171 | 4.42 | 4.20 | 7.02 | 17.60 |
| Fu et al. [17] | |||||||||||||
| B1S1 | 49 | 4.9 | 33 | 200 | 450 | 1300 | 0.008 | 0.67 | 251 | 286.39 | 83.90 | 61.75 | 137.70 |
| B1S2 | 25.9 | 2.6 | 24 | 200 | 450 | 1300 | 0.005 | 0.67 | 251 | 149.99 | 50.20 | 15.82 | 121.20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thamrin, R.; Zaidir, Z.; Desharma, S. Debonding Failure Analysis of Reinforced Concrete Beams Strengthened with CFRP Plates. Polymers 2021, 13, 2738. https://doi.org/10.3390/polym13162738
Thamrin R, Zaidir Z, Desharma S. Debonding Failure Analysis of Reinforced Concrete Beams Strengthened with CFRP Plates. Polymers. 2021; 13(16):2738. https://doi.org/10.3390/polym13162738
Chicago/Turabian StyleThamrin, Rendy, Zaidir Zaidir, and Silvy Desharma. 2021. "Debonding Failure Analysis of Reinforced Concrete Beams Strengthened with CFRP Plates" Polymers 13, no. 16: 2738. https://doi.org/10.3390/polym13162738
APA StyleThamrin, R., Zaidir, Z., & Desharma, S. (2021). Debonding Failure Analysis of Reinforced Concrete Beams Strengthened with CFRP Plates. Polymers, 13(16), 2738. https://doi.org/10.3390/polym13162738







