Field-Theoretic Simulations for Block Copolymer Melts Using the Partial Saddle-Point Approximation
Abstract
:1. Introduction
2. Field-Theoretic Simulations
2.1. Particle-Based Model
2.2. Field-Based Model
2.3. System of Noninteracting Polymers
2.4. Numerical Method
2.5. Partial Saddle-Point Approximation
2.6. Anderson Mixing
2.7. Langevin Dynamics
2.8. Effective Interaction Parameter
3. Applications
3.1. Diblock Copolymer Melts
3.2. Ternary Diblock–Homopolymer Blends
4. Discussion and Future Outlook
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hamley, I.W. The Physics of Block Copolymers; Oxford University Press: Oxford, UK, 1998. [Google Scholar]
- Bates, C.M.; Bates, F.S. 50th Anniversary Perspective: Block Polymers–Pure Potential. Macromolecules 2017, 50, 3–22. [Google Scholar] [CrossRef]
- Glaser, J.; Qin, J.; Medapuram, P.; Müller, M.; Morse, D.C. Test of a scaling hypothesis for the structure factor of disordered diblock copolymer melts. Soft Matter 2012, 8, 11310–11317. [Google Scholar] [CrossRef] [Green Version]
- Glaser, J.; Medapuram, P.; Morse, D.C. Collective and Single-Chain Correlations in Disordered Melts of Symmetric Diblock Copolymers: Quantitative Comparison of Simulations and Theory. Macromolecules 2014, 47, 851–869. [Google Scholar] [CrossRef]
- Matsen, M.W. The standard Gaussian model for block copolymer melts. J. Phys. Condens. Matter 2002, 14, R21–R47. [Google Scholar] [CrossRef]
- Qin, J.; Morse, D.C. Renormalized one-loop theory of correlations in polymer blends. J. Chem. Phys. 2009, 130, 224902. [Google Scholar] [CrossRef] [Green Version]
- Beardsley, T.M.; Matsen, M.W. Universality between experiment and simulation of a diblock copolymer melt. Phys. Rev. Lett. 2016, 117, 217801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Glaser, J.; Medapuram, P.; Beardsley, T.M.; Matsen, M.W.; Morse, D.C. Universality of Block Copolymer Melts. Phys. Rev. Lett. 2004, 113, 068302. [Google Scholar] [CrossRef] [PubMed]
- Medapuram, P.; Glaser, J.; Morse, D.C. Universal Phenomenology of Symmetric Diblock Copolymers near the Order–Disorder Transition. Macromolecules 2015, 48, 819–839. [Google Scholar] [CrossRef]
- Willis, J.D.; Beardsley, T.M.; Matsen, M.W. Calibration of a lattice model for high-molecular-weight block copolymer melts. J. Chem. Phys. 2019, 150, 204906. [Google Scholar] [CrossRef] [Green Version]
- Willis, J.D.; Beardsley, T.M.; Matsen, M.W. Simple and accurate calibration of the Flory-Huggins interaction parameter. Macromolecules 2020, 53, 9973–9982. [Google Scholar] [CrossRef]
- Ghasimakbari, T.; Morse, D.C. Order-Disorder Transitions and Free Energies in Asymmetric Diblock Copolymers. Macromolecules 2020, 53, 7399–7409. [Google Scholar] [CrossRef]
- Beardsley, T.M.; Matsen, M.W. Calibration of the Flory-Huggins interaction parameter in field-theoretic simulations. J. Chem. Phys. 2019, 150, 174902. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Ganesan, V.; Drolet, F. Field-Theoretic Computer Simulation Methods for Polymers and Complex Fluids. Macromolecules 2002, 35, 16–39. [Google Scholar] [CrossRef]
- Müller, M.; Schmid, F. Advanced Computer Simulation Approaches for Soft Matter Sciences II; Holm, C., Binder, K., Eds.; Springer: Berlin, Germany, 2005. [Google Scholar]
- Fredrickson, G.H. The Equilibrium Theory of Inhomogeneous Polymers; Oxford University Press: New York, NY, USA, 2006. [Google Scholar]
- Fredrickson, G.H. Computational field theory of polymers: Opportunities and challenges. Soft Matter 2007, 3, 1329–1334. [Google Scholar] [CrossRef] [PubMed]
- Matsen, M.W. Field theoretic approach for block polymer melts: SCFT and FTS. J. Chem. Phys. 2020, 152, 110901. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Edwards, S.F. The Statistical Mechanics of Polymers with Excluded Volume. Proc. Phys. Soc. Lond. 1975, 85, 613–624. [Google Scholar] [CrossRef]
- Helfand, E. Theory of inhomogeneous polymers: Fundamentals of the Gaussian randomwalk model. J. Chem. Phys. 1975, 63, 999–1005. [Google Scholar] [CrossRef]
- Matsen, M.W. Effect of architecture on the phase behavior of AB-type block copolymer melts. Macromolecules 2012, 45, 2161–2165. [Google Scholar] [CrossRef] [Green Version]
- Leibler, L. Theory of Microphase Separation in Block Copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Bates, F.S.; Schulz, M.F.; Khandpur, A.K.; Förster, S.; Rosedale, J.H. Fluctuations, Conformational Asymmetry and Block Copolymer Phase Behaviou. Faraday Discuss. 1994, 98, 7–18. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Helfand, E. Fluctuation effects in the theory of microphase separation in block copolymers. J. Chem. Phys. 1987, 87, 697–705. [Google Scholar] [CrossRef]
- Hamley, I.W.; Podneks, V.E. On the Landau-Brazovskii theory for block copolymer melts. Macromolecules 1997, 30, 3701–3703. [Google Scholar] [CrossRef]
- Miao, B.; Wickham, R.A. Fluctuation effects and the stability of the Fddd network phase in diblock copolymer melts. J. Chem. Phys. 2008, 128, 054902. [Google Scholar] [CrossRef]
- Takenaka, M.; Wakada, T.; Akasaka, S.; Nishitsuji, S.; Saijo, K.; Shimizu, H.; Kim, M.I.; Hasegawa, H. Orthorhombic Fddd Network in Diblock Copolymer Melts. Macromolecules 2007, 40, 4399–4402. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.-C.; Matsuda, K.; Kim, M.I.; Miyoshi, A.; Akasaka, S.; Nishitsuji, S.; Saijo, K.; Hasegawa, H.; Ito, K.; Hikima, T.; et al. Fddd Phase Boundary of Polystyrene-block-polyisoprene Diblock Copolymer Melts in the Polystyrene-Rich Region. Macromolecules 2015, 48, 2211–2216. [Google Scholar] [CrossRef]
- Grzywacz, P.; Qin, J.; Morse, D.C. Renormalization of the one-loop theory of fluctuations in polymer blends and diblock copolymer melts. Phys. Rev. E 2007, 76, 061802. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, J.; Grzywacs, P.; Morse, D.C. Renormalized one-loop theory of correlations in disordered diblock copolymers. J. Chem. Phys. 2011, 135, 084902. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Qin, J.; Morse, D.C. Fluctuations in Symmetric Diblock Copolymers: Testing Theories Old and New. Phys. Rev. Lett. 2012, 108, 238301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ganesan, V.; Fredrickson, G.H. Field-theoretic polymer simulations. Europhys. Lett. 2001, 55, 814–820. [Google Scholar] [CrossRef]
- Lennon, E.M.; Katsov, K.; Fredrickson, G.H. Free Energy Evaluation in Field-Theoretic Polymer Simulations. Phys. Rev. Lett. 2008, 101, 138302. [Google Scholar] [CrossRef]
- Delaney, K.T.; Fredrickson, G.H. Recent Developments in Fully Fluctuating Field-Theoretic Simulations of Polymer Melts and Solutions. J. Phys. Chem. B 2016, 120, 7615–7634. [Google Scholar] [CrossRef]
- Koski, J.; Chao, H.; Riggleman, R.A. Field Theoretic Simulations of Polymer Nanocomposites. J. Chem. Phys. 2013, 139, 244911. [Google Scholar] [CrossRef] [PubMed]
- Audus, D.J.; Delaney, K.T.; Ceniceros, H.D.; Fredrickson, G.H. Comparison of Pseudospectral Algorithms for Field-Theoretic Simulations of Polymers. Macromolecules 2013, 46, 8383–8391. [Google Scholar] [CrossRef]
- Reister, E.; Müller, M.; Binder, K. Spinodal decomposition in a binary polymer mixture: Dynamic self-consistent-field theory and Monte Carlo simulations. Phys. Rev. E 2001, 64, 041804. [Google Scholar] [CrossRef] [Green Version]
- Düchs, D.; Ganesan, V.; Fredrickson, G.H.; Schmid, F. Fluctuation Effects in Ternary AB + A + B Polymeric Emulsions. Macromolecules 2003, 36, 9237–9248. [Google Scholar] [CrossRef] [Green Version]
- Düchs, D.; Schmid, F. Formation and structure of the microemulsion phase in two-dimensional ternary AB + A +B polymeric emulsion. J. Chem. Phys. 2004, 121, 2798–2805. [Google Scholar] [CrossRef] [Green Version]
- Stasiak, P.; Matsen, M.W. Monte Carlo field-theoretic simulations for melts of symmetric diblock copolymer. Macromolecules 2013, 46, 8037–8045. [Google Scholar] [CrossRef]
- Anderson, D.G. Iterative Procedures for Nonlinear Integral Equations. J. Assoc. Comput. Mach. 1965, 12, 547–560. [Google Scholar] [CrossRef]
- Beardsley, T.M.; Matsen, M.W. Fluctuation Correction for the Order-Disorder Transition of Diblock Polymer Melts. J. Chem. Phys. 2021, 154, 124902. [Google Scholar] [CrossRef]
- Matsen, M.W. Self-consistent field theory for melts of low-molecular-weight diblock copolymer. Macromolecules 2012, 45, 8502–8509. [Google Scholar] [CrossRef]
- Thompson, R.B.; Rasmussen, K.O.; Lookman, T. Improved convergence in block copolymer self-consistent field theory by Anderson mixing. J. Chem. Phys. 2004, 120, 31–34. [Google Scholar] [CrossRef]
- Matsen, M.W. Fast and accurate SCFT calculations for periodic block-copolymer morphologies using the spectral method with Anderson mixing. Eur. Phys. J. E 2009, 30, 361–369. [Google Scholar] [CrossRef] [PubMed]
- Stasiak, P.; Matsen, M.W. Efficiency of pseudo-spectral algorithms with Anderson mixing for the SCFT of periodic block-copolymer phases. Eur. Phys. J. E 2011, 34, 110. [Google Scholar] [CrossRef]
- Düchs, D.; Delaney, K.T.; Fredrickson, G.H. A multi-species exchange model for fully fluctuating polymer field theory simulations. J. Chem. Phys. 2014, 36, 174103. [Google Scholar] [CrossRef] [Green Version]
- Beardsley, T.M.; Matsen, M.W. Computationally Efficient Field-Theoretic Simulations for Block Copolymer Melts. Macromolecules 2019, 52, 8840–8848. [Google Scholar] [CrossRef]
- De la Cruz, M.O.; Edwards, S.F.; Sanchez, I.C. Concentration fluctuations in polymer blend thermodynamics. J. Chem. Phys. 1988, 89, 1704–1708. [Google Scholar] [CrossRef]
- Vorselaars, B.; Stasiak, P.; Matsen, M.W. Field-theoretic simulation of block copolymers at experimentally relevant molecular weights. Macromolecules 2015, 46, 9071–9080. [Google Scholar] [CrossRef] [Green Version]
- Spencer, R.K.W.; Matsen, M.W. Fluctuation effects in blends of A+B homopolymers with AB diblock copolymer. J. Chem. Phys. 2018, 148, 204907. [Google Scholar] [CrossRef] [Green Version]
- Vorselaars, B.; Spencer, R.K.W.; Matsen, M.W. Instability of the microemulsion channel in block copolymer-homopolymer blends. Phys. Rev. Lett. 2020, 125, 117801. [Google Scholar] [CrossRef] [PubMed]
- Spencer, R.K.W.; Matsen, M.W. Coexistence of polymeric microemulsion with homopolymer-rich phases. Macromolecules 2021, 54, 1329–1337. [Google Scholar] [CrossRef]
- Bates, F.S.; Maurer, W.W.; Lipic, P.M.; Hillmyer, M.A.; Almdal, K.; Mortensen, K.; Fredrickson, G.H.; Lodge, T.P. Polymeric Bicontinuous Microemulsions. Phys. Rev. Lett. 1997, 79, 849–852. [Google Scholar] [CrossRef]
- Hillmyer, M.A.; Maurer, W.W.; Lodge, T.P.; Bates, F.S.; Almdal, K. Model bicontinuous microemulsions in ternary homopolymer block copolymer blends. J. Phys. Chem. B 1999, 103, 4814–4824. [Google Scholar] [CrossRef]
- Schwahn, D.; Mortensen, K.; Frielinghaus, H.; Almdal, K. Crossover from 3D ising to isotropic Lifshitz critical behavior in a mixture of a homopolymer blend and diblock copolymer. Phys. Rev. Lett. 1999, 82, 5056–5059. [Google Scholar] [CrossRef] [Green Version]
- Schwahn, D.; Mortensen, K.; Frielinghaus, H.; Almdal, K.; Kielhorn, L. Thermal composition fluctuations near the isotropic Lifshitz critical point in a ternary mixture of a homopolymer blend and diblock copolymer. J. Chem. Phys. 2000, 112, 5454–5472. [Google Scholar] [CrossRef] [Green Version]
- Krishnan, K.; Almdal, K.; Burghardt, W.R.; Lodge, T.P.; Bates, F.S. Shear-induced nano-macro structural transition in a polymeric bicontinuous microemulsion. Phys. Rev. Lett. 2001, 87, 098301. [Google Scholar] [CrossRef] [PubMed]
- Pipich, V.; Schwahn, D.; Willner, L. Ginzburg Number of a Homopolymer–Diblock Copolymer Mixture Covering the 3D-Ising, Isotropic Lifshitz, and Brasovskiĭ Classes of Critical Universality. Phys. Rev. Lett. 2005, 94, 117801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Habersberger, B.M.; Gillard, T.M.; Hickey, R.J.; Lodge, T.P.; Bates, F.S. Fluctuation Effects in Symmetric Diblock Copolymer–Homopolymer Ternary Mixtures near the Lamellar–Disorder Transition. ACS Macro Lett. 2014, 3, 1041–1045. [Google Scholar] [CrossRef]
- Walker, C.N.; Bryson, K.C.; Hayward, R.C.; Tew, G.N. Wide Bicontinuous Compositional Windows from Co-Networks Made with Telechelic Macromonomers. ACS Nano 2014, 8, 12376–12385. [Google Scholar] [CrossRef] [PubMed]
- Hickey, R.J.; Gillard, T.M.; Irwin, M.T.; Lodge, T.P.; Bates, F.S. Structure, viscoelasticity, and interfacial dynamics of a model polymeric bicontinuous microemulsion. Soft Matter 2016, 12, 53–66. [Google Scholar] [CrossRef]
- Hickey, R.J.; Gillard, T.M.; Irwin, M.T.; Morse, D.C.; Lodge, T.P.; Bates, F.S. Phase Behavior of Diblock Copolymer–Homopolymer Ternary Blends: Congruent First-Order Lamellar–Disorder Transition. Macromolecules 2016, 49, 7928–7944. [Google Scholar] [CrossRef]
- Zhang, B.; Xie, S.; Lodge, T.P.; Bates, F.S. Phase Behavior of Diblock Copolymer–Homopolymer Ternary Blends with a Compositionally Asymmetric Diblock Copolymer. Macromolecules 2020, 54, 460–472. [Google Scholar] [CrossRef]
- Yadav, M.; Bates, F.S.; Morse, D.C. Effects of Segment Length Asymmetry in Ternary Diblock Copolymer-Homopolymer Mixtures. Macromolecules 2019, 52, 4091–4102. [Google Scholar] [CrossRef]
- Spencer, R.K.W.; Vorselaars, B.; Matsen, M.W. Continuous thermodynamic integration in field-theoretic simulations of structured polymers. Macromol. Theory Simul. 2017, 26, 1700036. [Google Scholar] [CrossRef]
- Hajduk, D.A.; Harper, P.E.; Gruner, S.M.; Honeker, C.C.; Kim, G.; Thomas, E.L. The Gyroid: A New Equilibrium Morphology in Weakly Segregated Diblock Copolymers. Macromolecules 1994, 27, 4063–4075. [Google Scholar] [CrossRef]
- Schulz, M.F.; Bates, F.S.; Almdal, K.; Mortensen, K. Epitaxial Relationship for Hexagonal-to-Cubic Phase Transition in a Book Copolymer Mixture. Phys. Rev. Lett. 1994, 73, 86–89. [Google Scholar] [CrossRef]
- Matsen, M.W.; Schick, M. Stable and unstable phases of a diblock copolymer melt. Phys. Rev. Lett. 1994, 72, 2660–2663. [Google Scholar] [CrossRef]
- Hamley, I.W.; Koppi, K.A.; Rosedale, J.H.; Bates, F.S.; Almdal, K.; Mortensen, K. Hexagonal Mesophases between Lamellae and Cylinders in a Diblock Copolymer Melt. Macromolecules 1993, 26, 5959–5970. [Google Scholar] [CrossRef]
- Hajduk, D.A.; Takenouchi, H.; Hillmyer, M.A.; Bates, F.S.; Vigild, M.E.; Almdal, K. Stability of the Perforated Layer (PL) Phase in Diblock Copolymer Melts. Macromolecules 1997, 30, 3788–3795. [Google Scholar] [CrossRef]
- Vigild, M.E.; Almdal, K.; Mortensen, K.; Hamley, I.W.; Fairclough, J.P.A.; Ryan, A.J. Transformations to and from the Gyroid Phase in a Diblock Copolymer. Macromolecules 1998, 31, 5702–5716. [Google Scholar] [CrossRef]
- Cheng, X.; Lin, L.; Weinan, E.; Zhang, P.; Shi, A.-C. Nucleation of Ordered Phases in Block Copolymers. Phys. Rev. Lett. 2010, 104, 148301. [Google Scholar] [CrossRef] [Green Version]
- Tyler, C.T.; Morse, D.C. Orthorhombic Fddd Network in Triblock and Diblock Copolymer Melts. Phys. Rev. Lett. 2005, 94, 208302. [Google Scholar] [CrossRef]
- Müller, M.; Schick, M. Bulk and interfacial thermodynamics of a symmetric, ternary homopolymer–copolymer mixture: A Monte Carlo study. J. Chem. Phys. 1996, 105, 8885–8901. [Google Scholar] [CrossRef]
- Müller, M.; Binder, K. An algorithm for the semi-grand-canonical simulation of asymmetric polymer mixtures. Comput. Phys. Commun. 1994, 84, 173–185. [Google Scholar] [CrossRef]
- Matsen, M.W. Soft Matter: Polymer Melts and Mixtures; Gompper, G., Schick, M., Eds.; Wiley-VCH: Weinheim, Germany, 2006. [Google Scholar]
- Riggleman, R.A.; Kumar, R.; Fredrickson, G.H. Investigation of the interfacial tension of complex coacervates using field-theoretic simulations. J. Chem. Phys. 2010, 136, 024903. [Google Scholar] [CrossRef]
- Broseta, D.; Fredrickson, G.H. Phase equilibria in copolymer/homopolymer ternary blends: Molecular weight effect. J. Chem. Phys. 1990, 93, 2927–2938. [Google Scholar] [CrossRef]
- Spencer, R.K.W.; Matsen, M.W. Critical Point of Symmetric Binary Homopolymer Blends. Macromolecules 2016, 49, 6116–6125. [Google Scholar] [CrossRef]
- Spencer, R.K.W.; Matsen, M.W. Correction to Critical Point of Symmetric Binary Homopolymer Blends. Macromolecules 2018, 51, 4747–4748. [Google Scholar] [CrossRef]
- Xie, S.; Meyer, D.J.; Wang, E.; Bates, F.S.; Lodge, T.P. Structure and Properties of Bicontinuous Microemulsions from Salt-Doped Ternary Polymer Blends. Macromolecules 2019, 52, 9693–9702. [Google Scholar] [CrossRef]
- Delaney, K.T.; Fredrickson, G.H. Polymer field-theory simulations on graphics processing units. Comput. Phys. Commun. 2013, 184, 2102–2110. [Google Scholar] [CrossRef] [Green Version]
- Cheong, G.K.; Chawla, A.; Morse, D.C.; Dorfman, K.D. Open-source code for self-consistent field theory calculations of block polymer phase behavior on graphics processing units. Eur. Phys. J. E 2020, 43, 15. [Google Scholar] [CrossRef] [Green Version]
- Ceniceros, H.D.; Fredrickson, G.H. Numerical Solution of Polymer Self-Consistent Field Theory. Multiscale Model. Simul. 2004, 2, 452–474. [Google Scholar] [CrossRef] [Green Version]
- Spencer, R.K.W.; Matsen, M.W. Field-theoretic simulations of bottlebrush copolymers. J. Chem. Phys. 2018, 149, 184901. [Google Scholar] [CrossRef]
- Liu, Y.X.; Delaney, K.T.; Fredrickson, G.H. Field-Theoretic Simulations of Fluctuation-Stabilized Aperiodic “Bricks-and-Mortar” Mesophase in Miktoarm Star Block Copolymer/Homopolymer Blends. Macromolecules 2017, 50, 6263–6272. [Google Scholar] [CrossRef]
- Koski, J.P.; Riggleman, R.A. Field-theoretic simulations of block copolymer nanocomposites in a constant interfacial tension ensemble. J. Chem. Phys. 2017, 146, 164903. [Google Scholar] [CrossRef] [PubMed]
- Riggleman, R.A.; Fredrickson, G.H. Field-theoretic simulations in the Gibbs ensemble. J. Chem. Phys. 2010, 132, 024104. [Google Scholar] [CrossRef] [PubMed]
- Alexander-Katz, A.; Fredrickson, G.H. Diblock Copolymer Thin Films: A Field-Theoretic Simulation Study. Macromolecules 2007, 40, 4075–4087. [Google Scholar] [CrossRef]
- Panagiotou, E.; Delaney, K.T.; Fredrickson, G.H. Theoretical prediction of an isotropic to nematic phase transition in bottlebrush homopolymer melts. J. Chem. Phys. 2019, 151, 094901. [Google Scholar] [CrossRef] [PubMed]
- Sides, S.W.; Kim, B.J.; Kramer, E.J.; Fredrickson, G.H. Hybrid Particle-Field Simulations of Polymer Nanocomposites. Phys. Rev. Lett. 2006, 96, 250601. [Google Scholar] [CrossRef] [PubMed]
- Matsen, M.W.; Thompson, R.B. Particle Distributions in a Block Copolymer Nanocomposite. Macromolecules 2008, 41, 1853–1860. [Google Scholar] [CrossRef] [Green Version]
- Chao, H.; Hagberg, B.A.; Riggleman, R.A. The distribution of homogeneously grafted nanoparticles in polymer thin films and blends. Soft Matter 2014, 10, 8083–8094. [Google Scholar] [CrossRef]
- Alexander-Katz, A.; Fredrickson, G.H. Field-theoretic simulations of confined polymer solutions. J. Chem. Phys. 2003, 118, 9030–9038. [Google Scholar] [CrossRef]
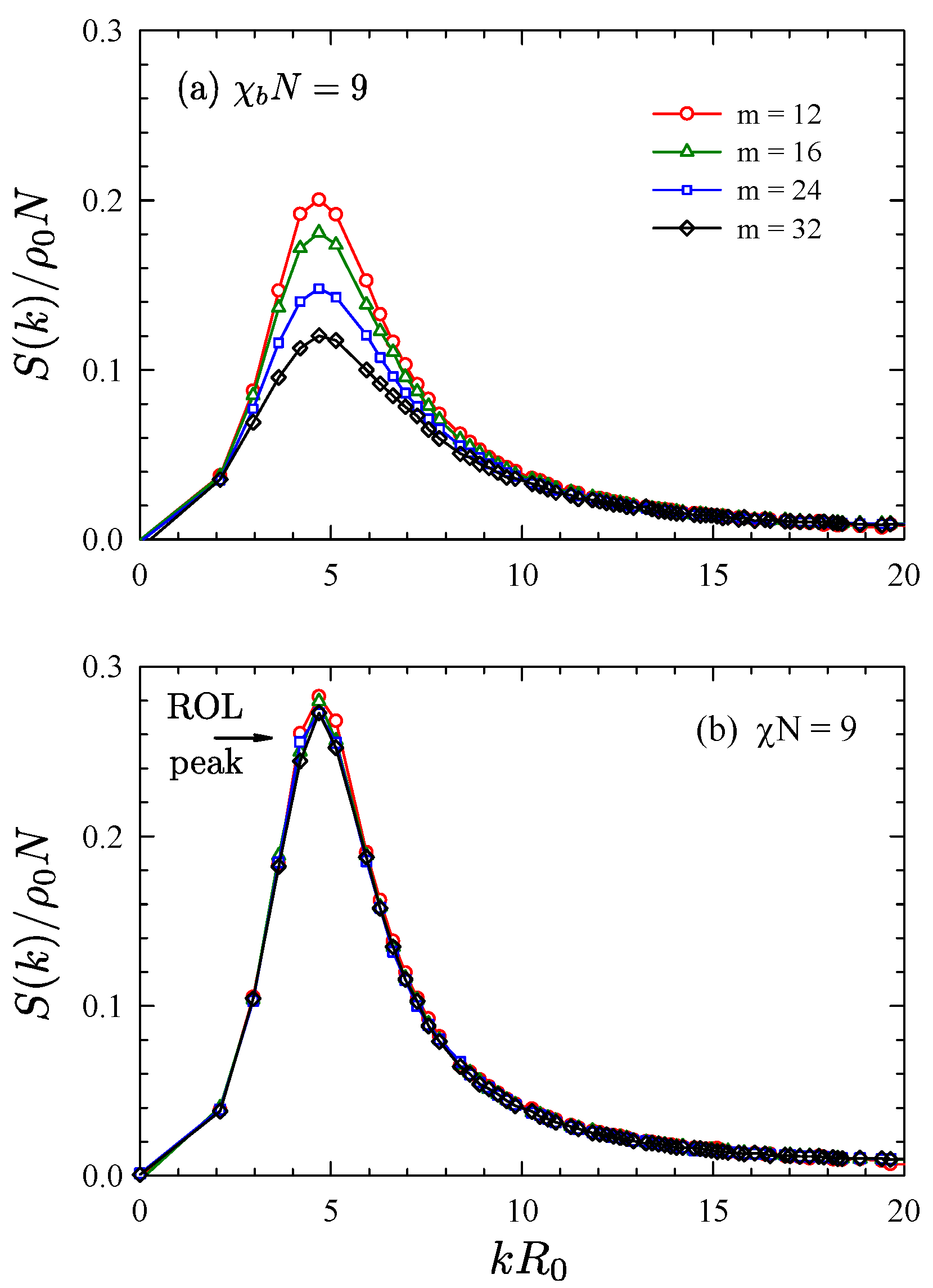
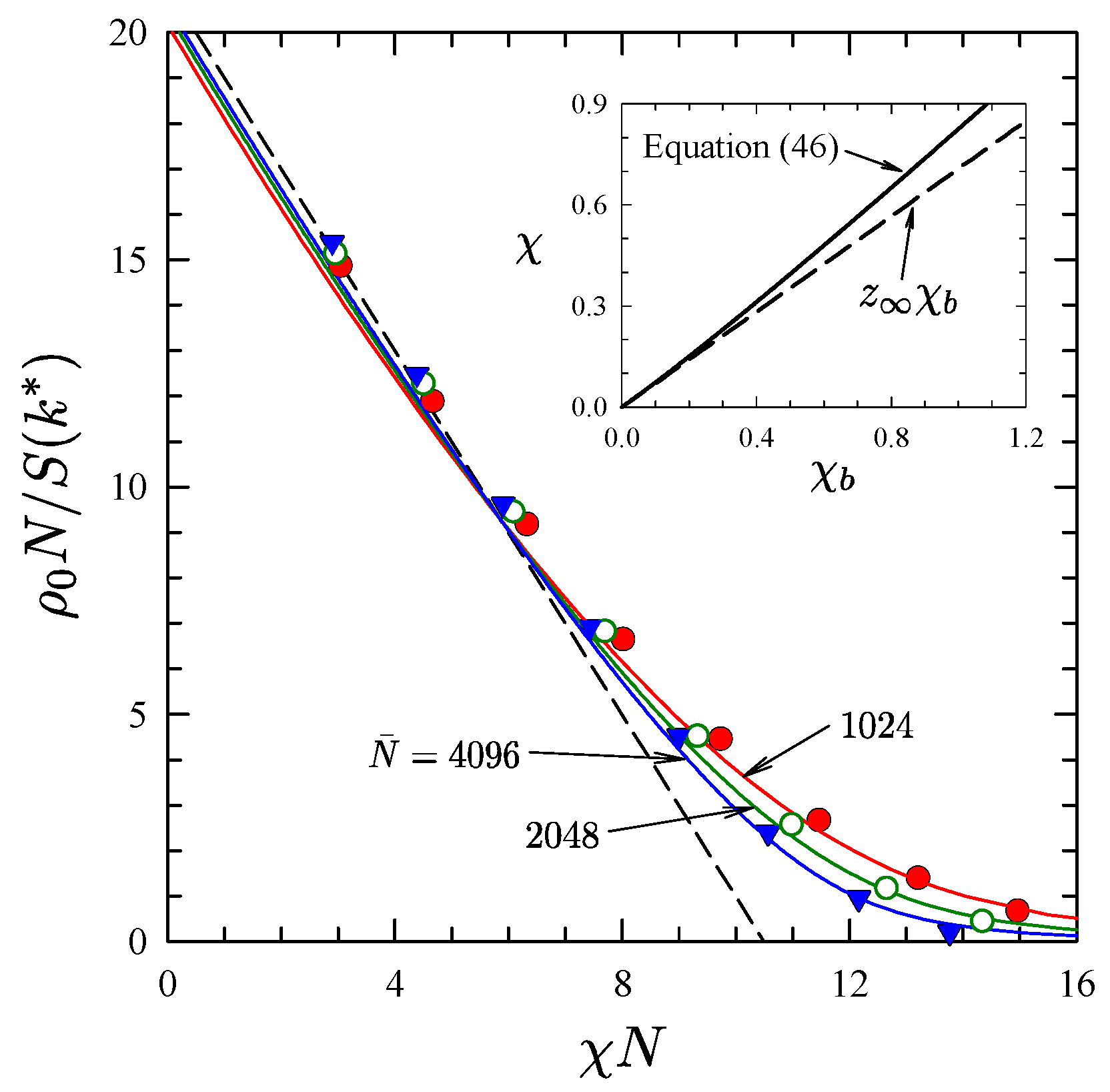

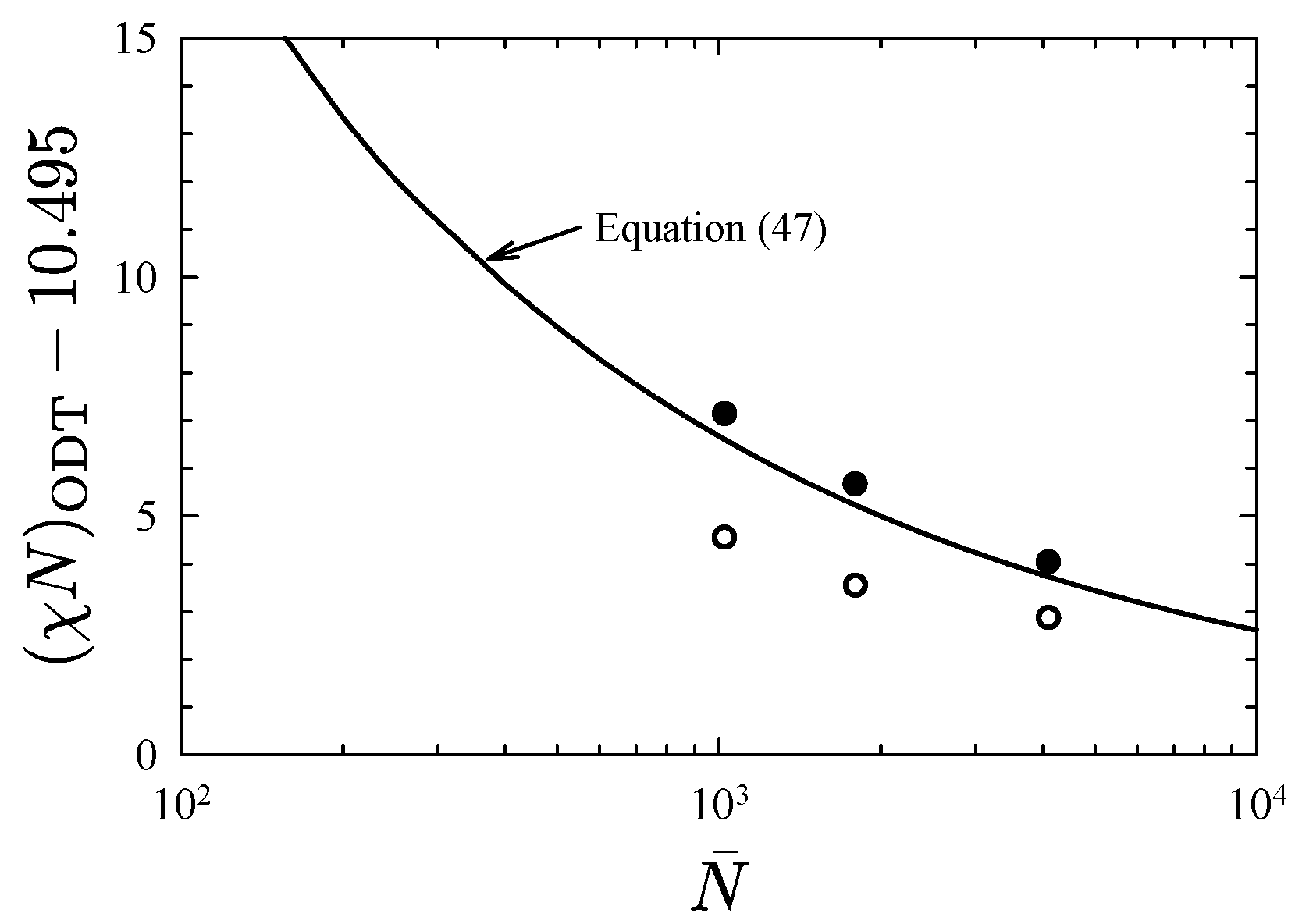
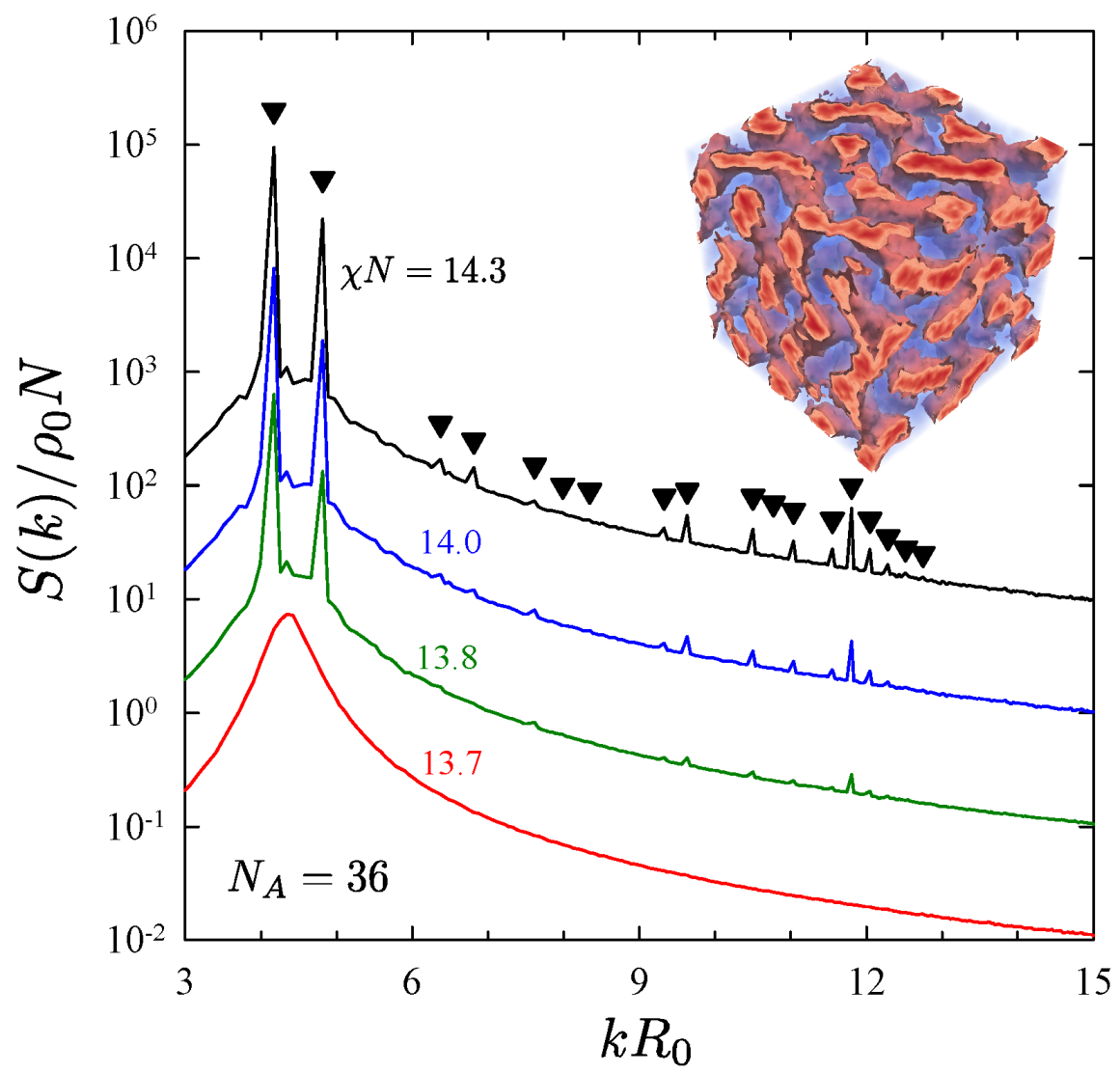


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsen, M.W.; Beardsley, T.M. Field-Theoretic Simulations for Block Copolymer Melts Using the Partial Saddle-Point Approximation. Polymers 2021, 13, 2437. https://doi.org/10.3390/polym13152437
Matsen MW, Beardsley TM. Field-Theoretic Simulations for Block Copolymer Melts Using the Partial Saddle-Point Approximation. Polymers. 2021; 13(15):2437. https://doi.org/10.3390/polym13152437
Chicago/Turabian StyleMatsen, Mark W., and Thomas M. Beardsley. 2021. "Field-Theoretic Simulations for Block Copolymer Melts Using the Partial Saddle-Point Approximation" Polymers 13, no. 15: 2437. https://doi.org/10.3390/polym13152437
APA StyleMatsen, M. W., & Beardsley, T. M. (2021). Field-Theoretic Simulations for Block Copolymer Melts Using the Partial Saddle-Point Approximation. Polymers, 13(15), 2437. https://doi.org/10.3390/polym13152437





