Stress Distribution and Fracture Toughness of Underground Reinforced Plastic Pipe Composite
Abstract
:1. Introduction
The Novelty and Objectives of the Present Study
- Measure the stress intensity factor of the cracked cylinder using the extended finite element model.
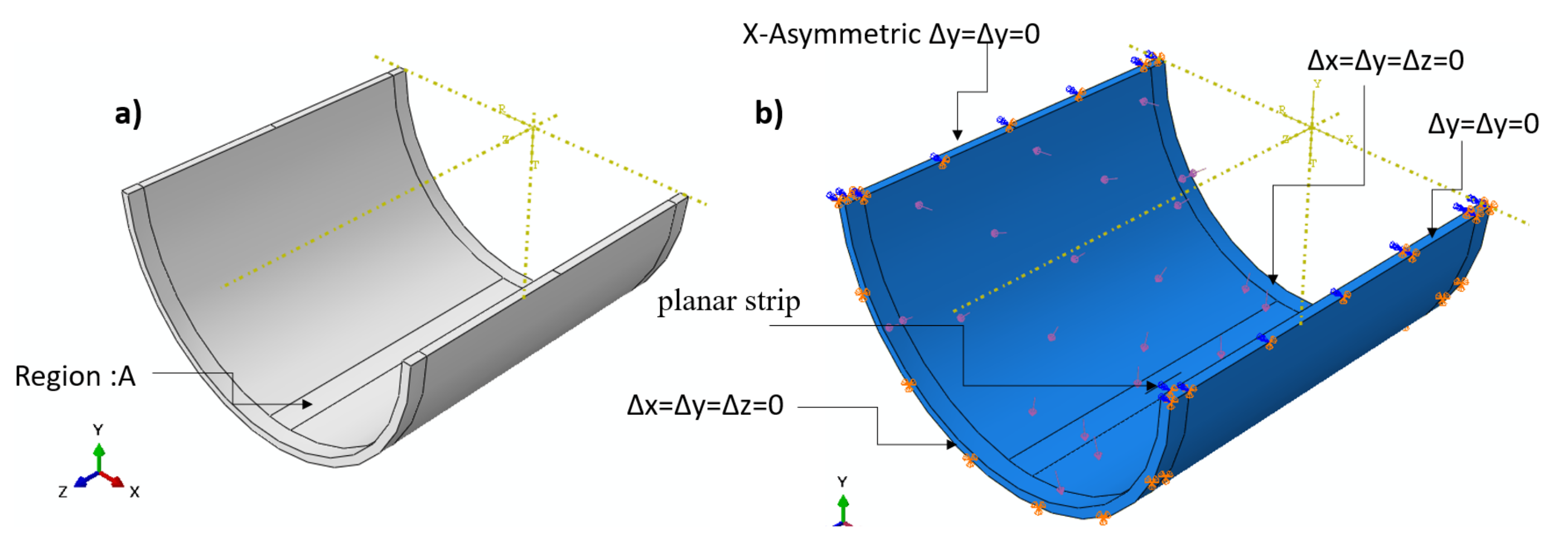
2. Mathematical Model
3. Extended Finite Element Model (XFEM)
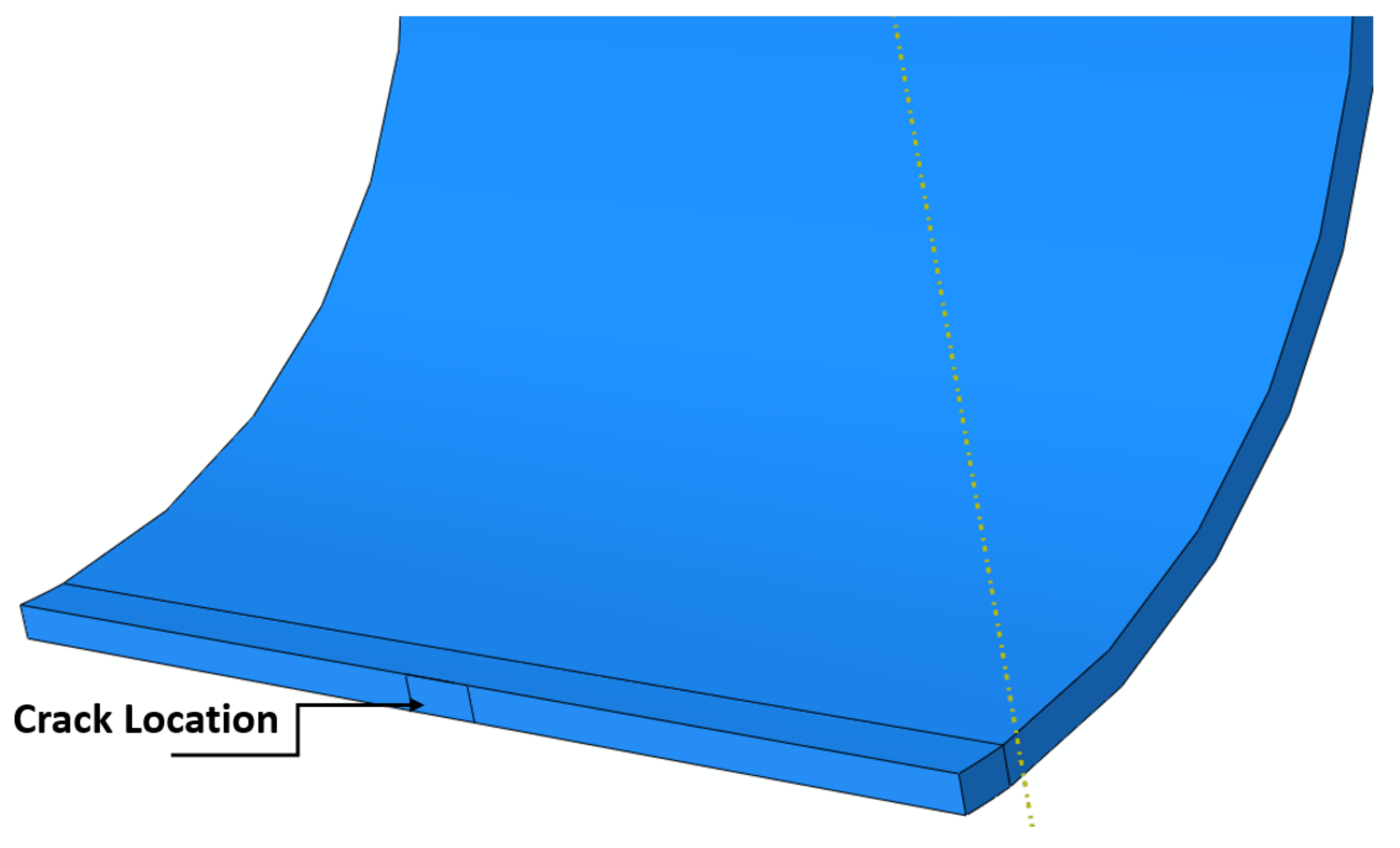
4. Experimental Work
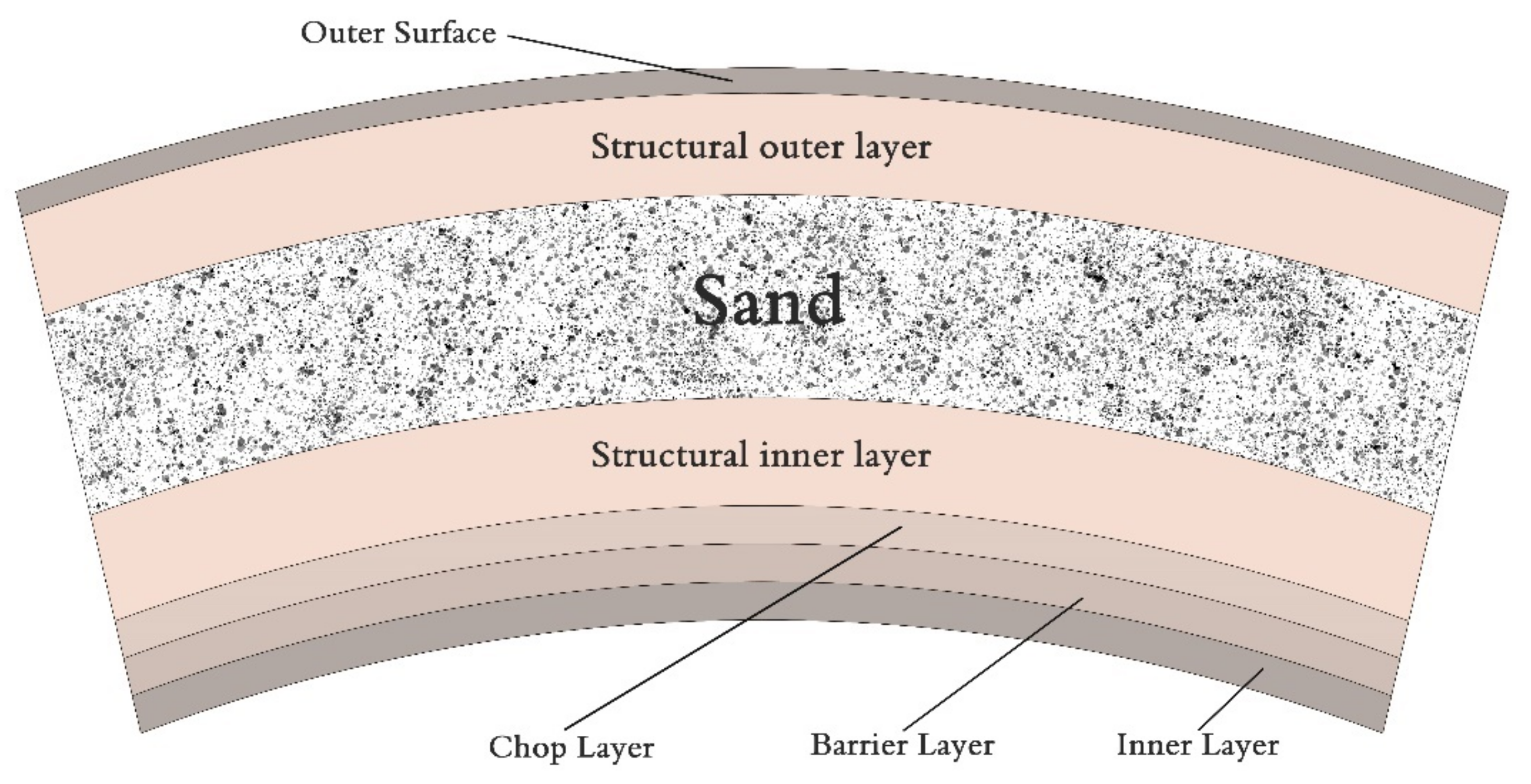
4.1. Material Description
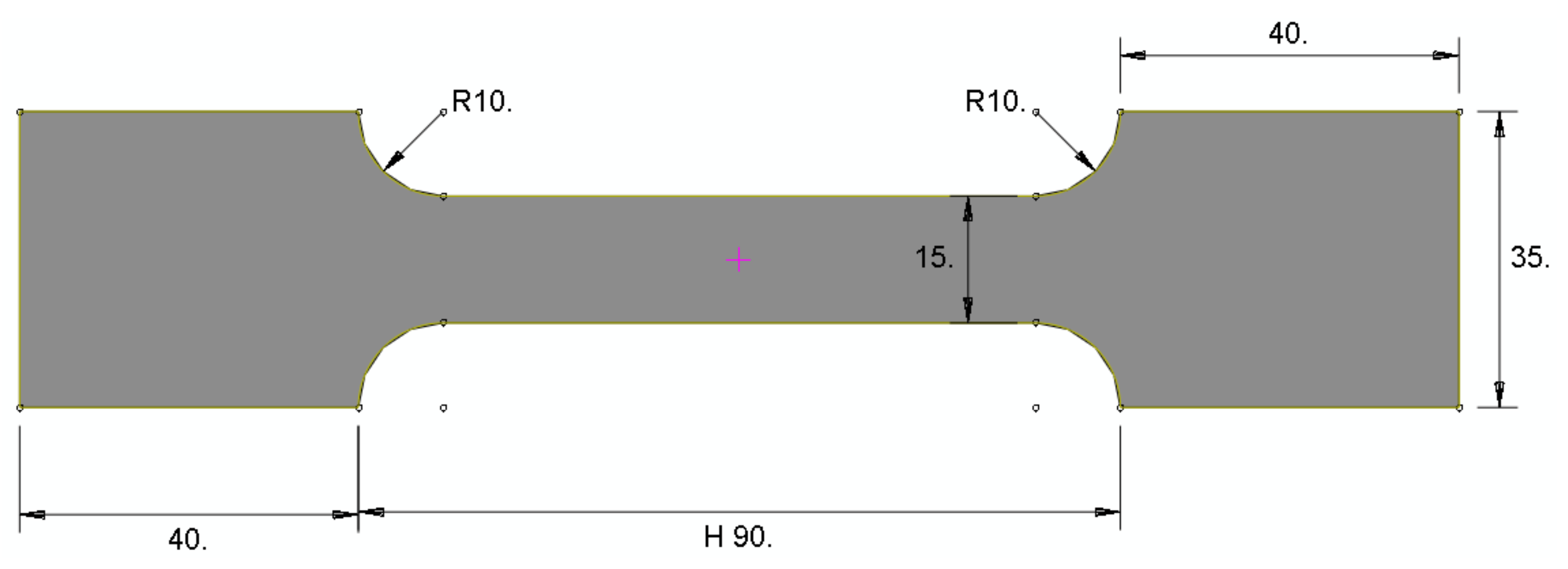
4.2. Tension Test
4.3. Fracture Toughness Test
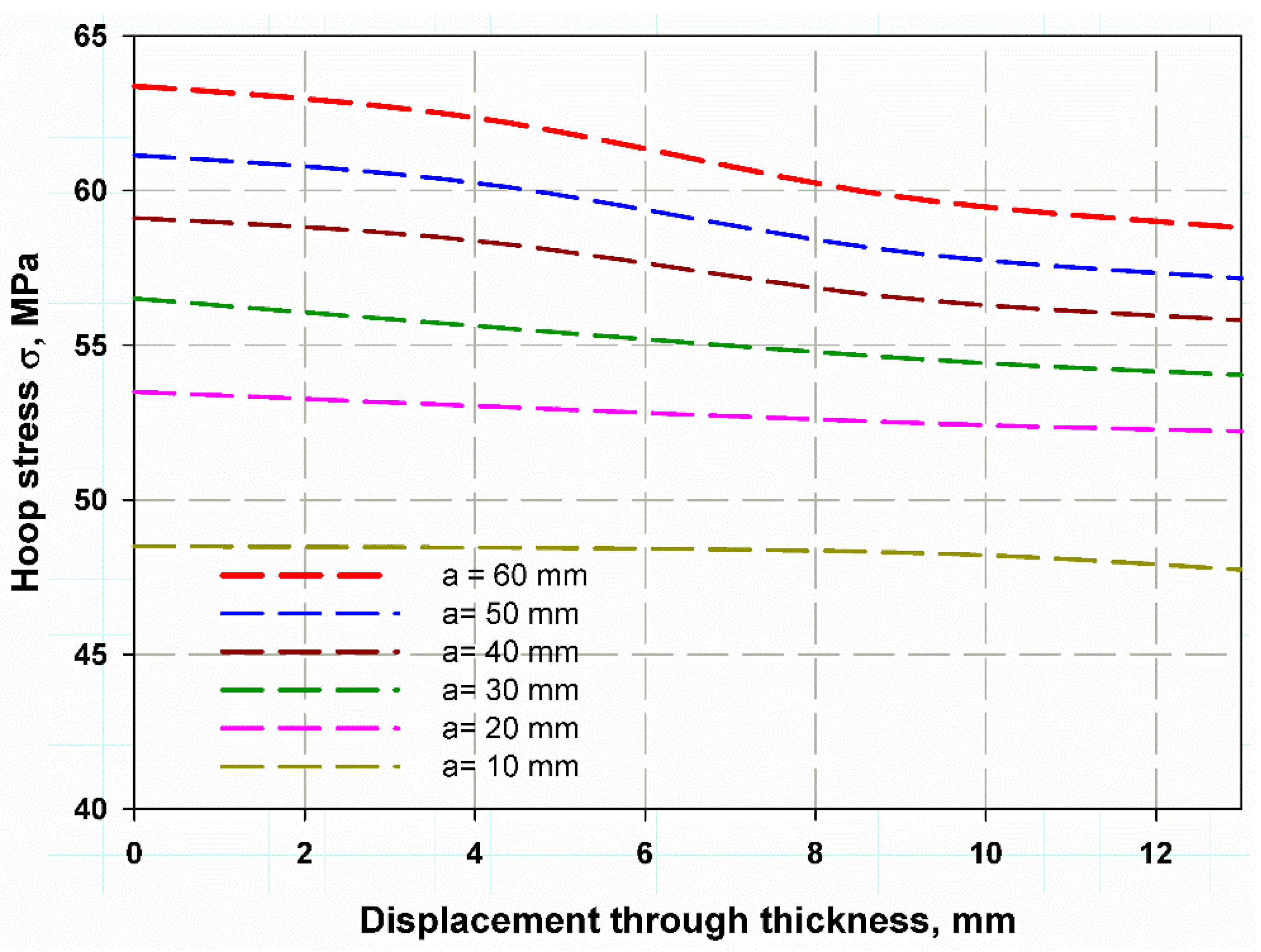
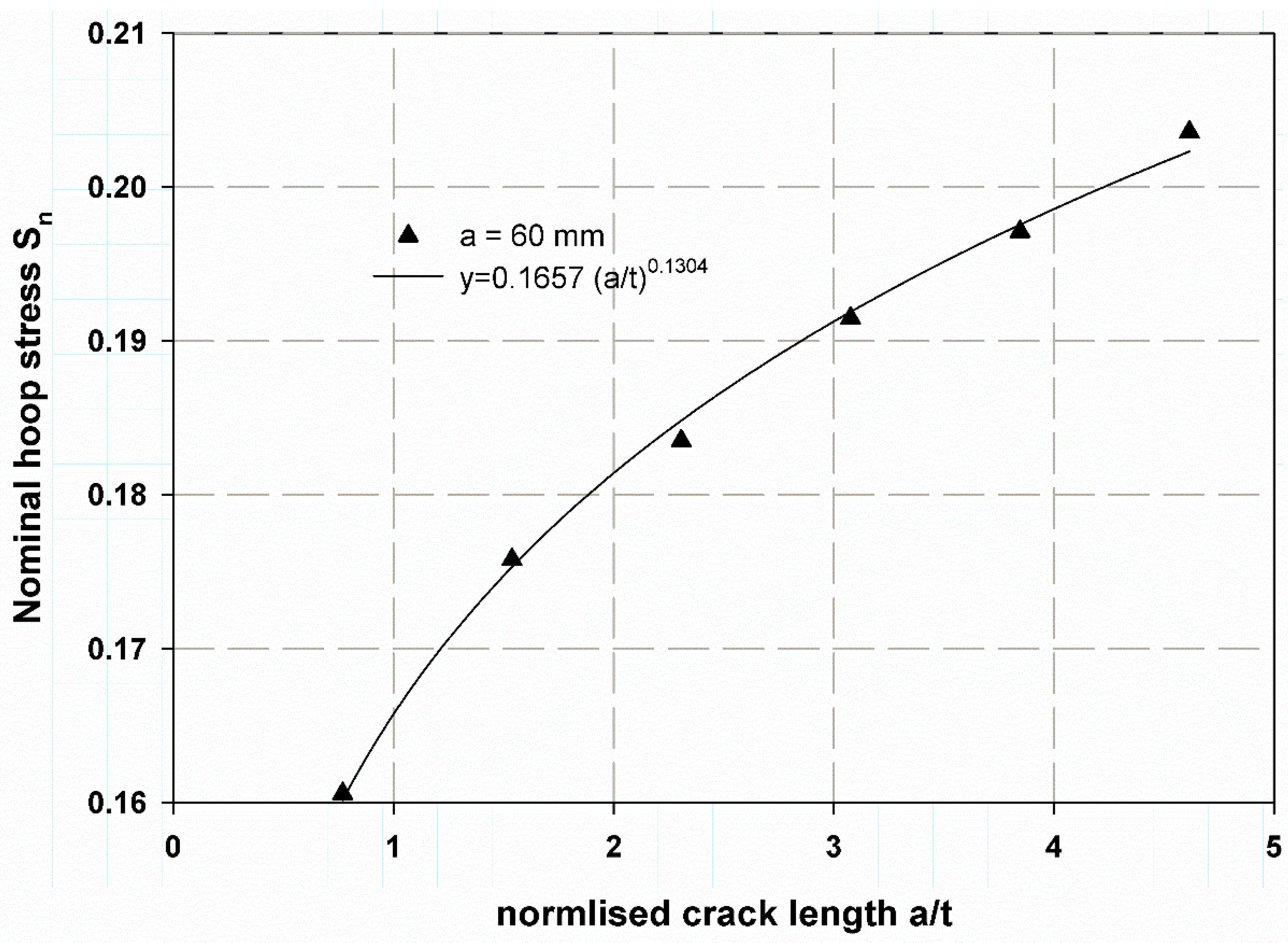
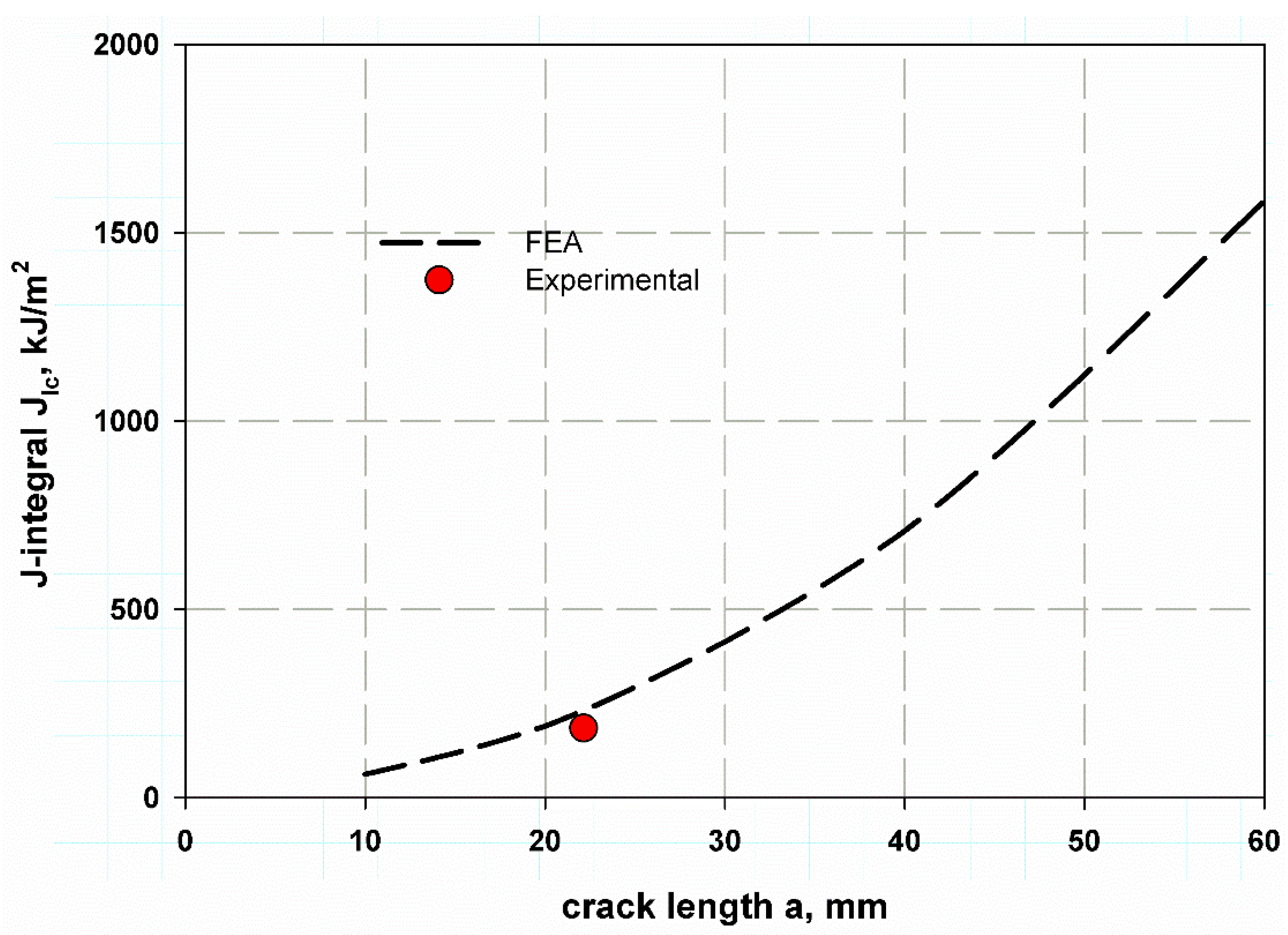
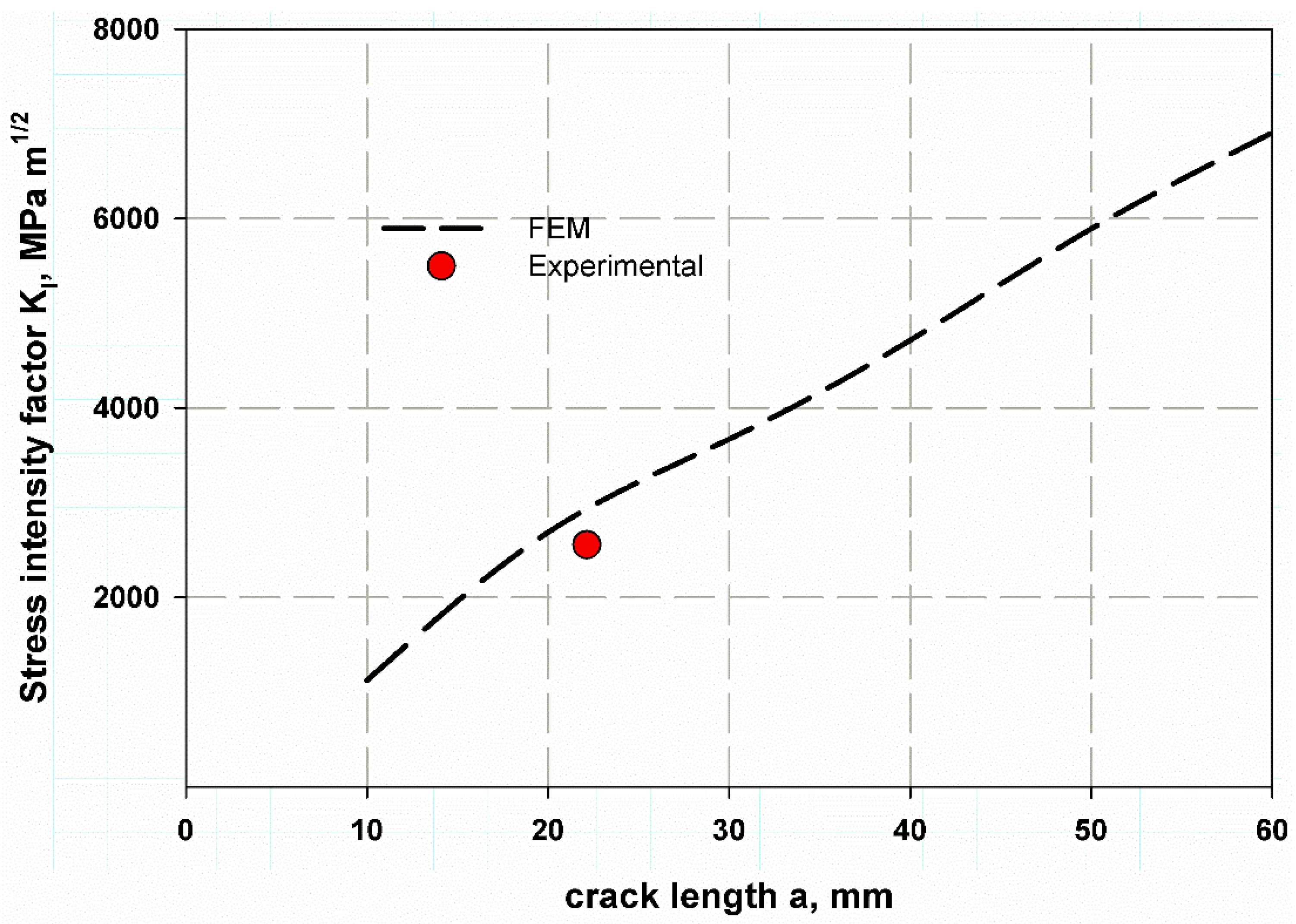
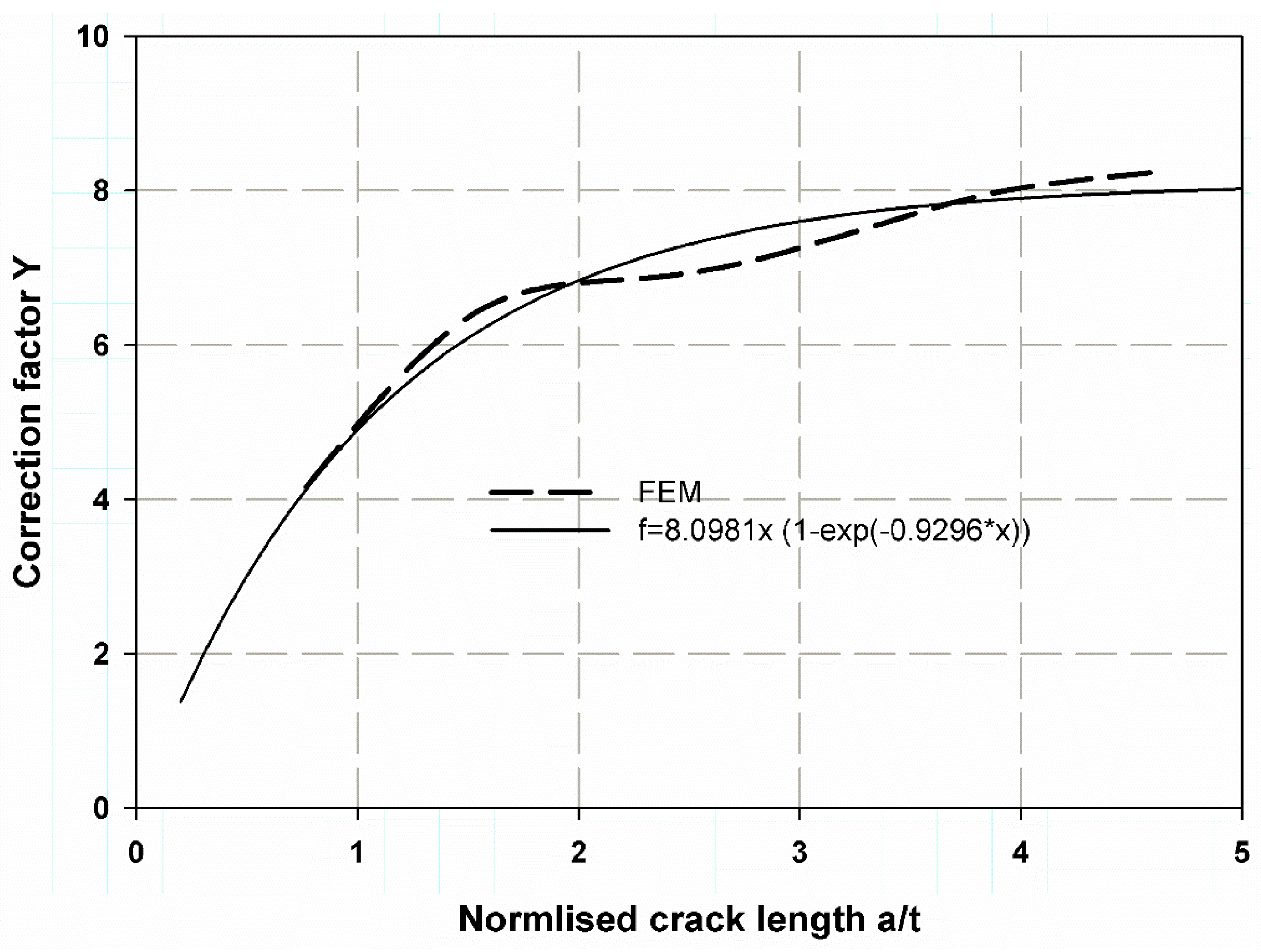
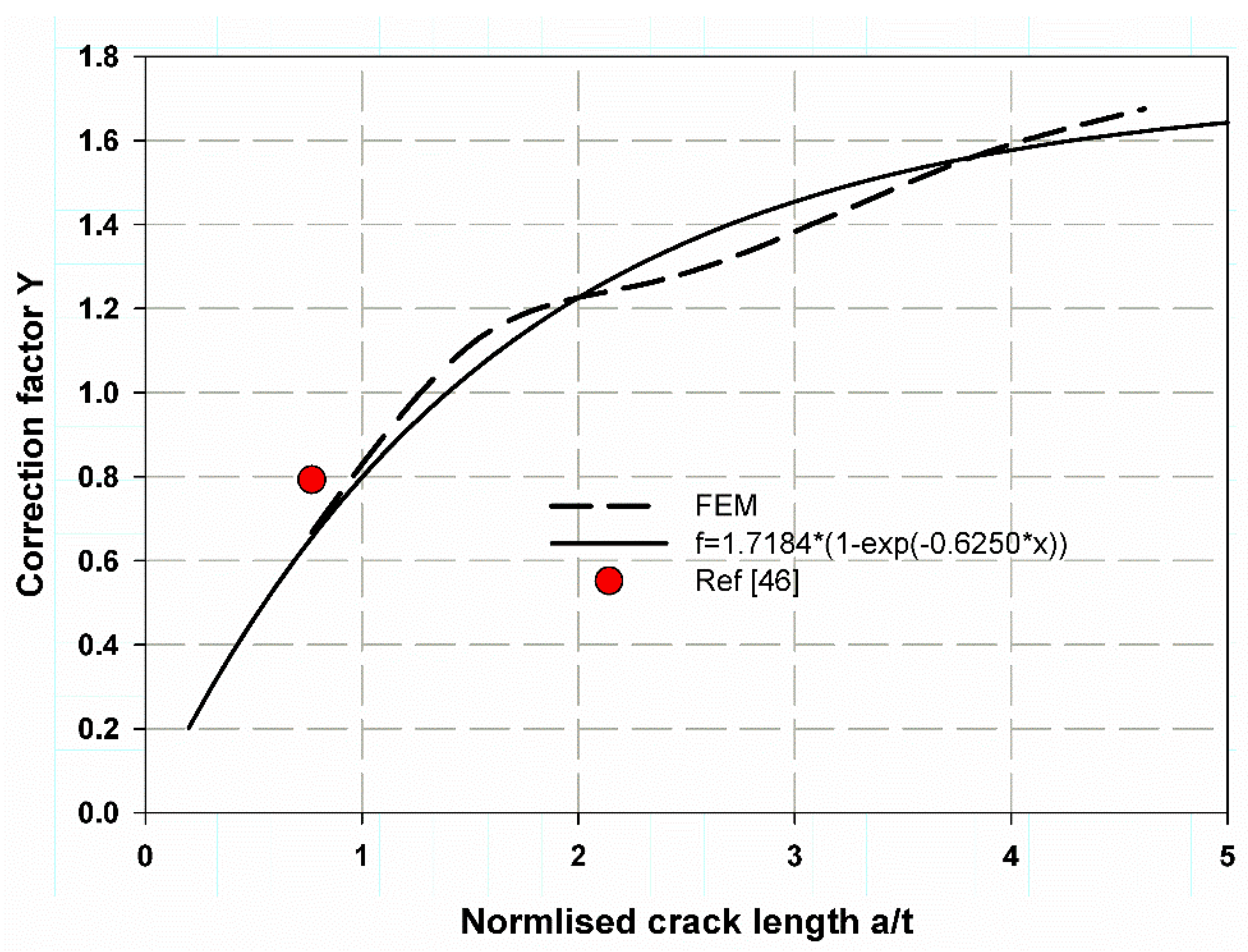
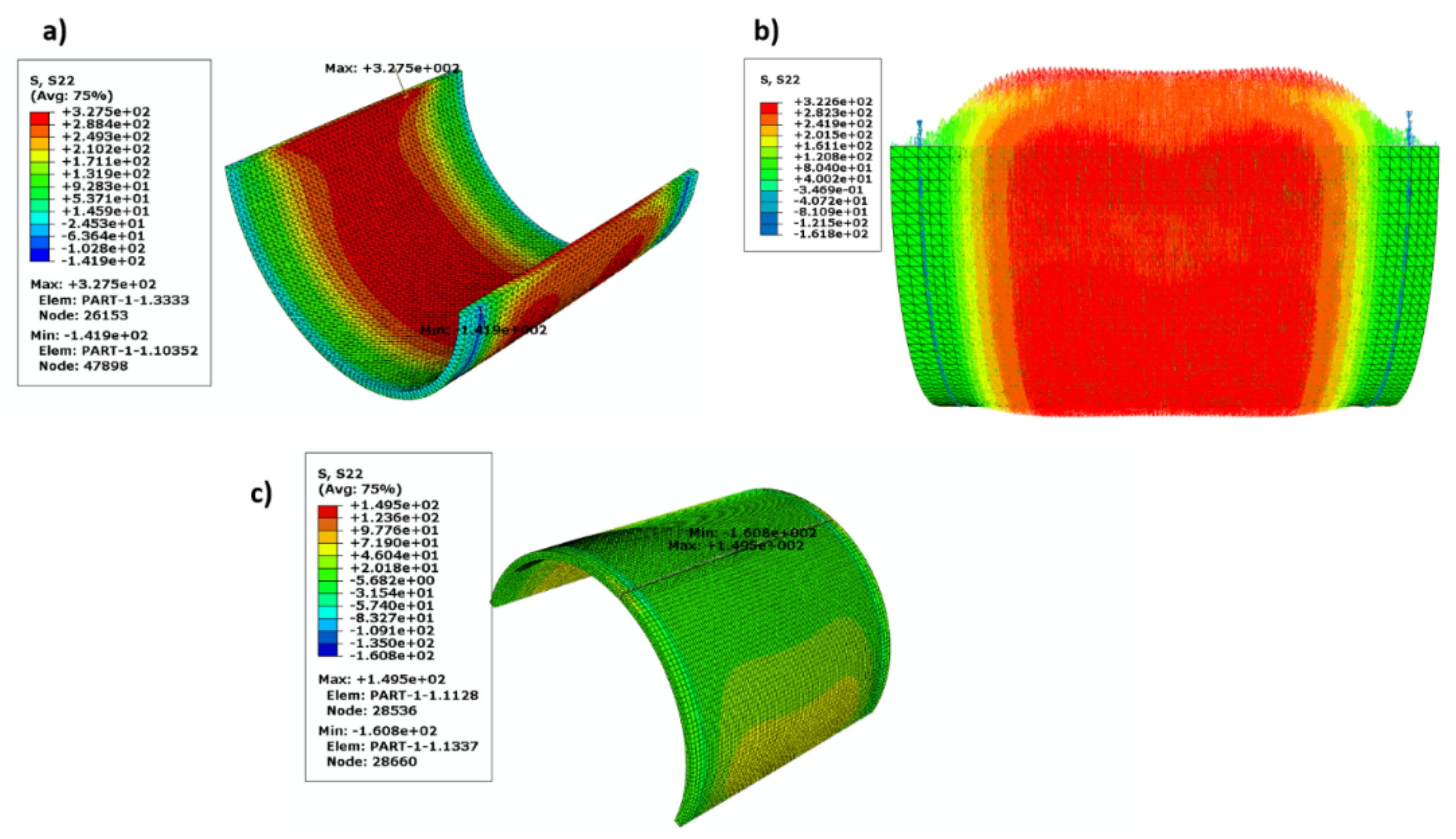
5. Results and Discussion
Mathematical Model Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Critical surface release energy | |
| Critical J-integral | |
| Mode I stress intensity factor | |
| Critical fracture toughness | |
| Internal pressure | |
| Nominal hoop stress= | |
| 5% secant load | |
| Hoop stress | |
| Longitudinal stress | |
| E1, E2 | Young’s modulus in 1 and 2 direction or X, Y |
| G12, G13, G23 | Shear modulus in 1, 2, and 3 direction |
| R | Cylinder radius |
| ν12 | Poisson’s ratio |
| Constants obtained by the well-fitted curve | |
| Shape factor | |
| Equivalent correction factor | |
| Crack length | |
| Constants form well-fitted curve | |
| Cylinder diameter | |
| Correction factor for cracked cylinder | |
| Correction factor for compact tension test specimen | |
| Cylinder thickness | |
| Compact tension test specimen dimension | |
| Equivalent Young’s modulus |
References
- Feng, C.-W. Prediction of Long-Term Creep Behavior of Epoxy Adhesives for Structural Applications. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2005. [Google Scholar]
- Abdellah, M.Y.; Hassan, M.K.; Alsoufi, M.S. Fracture and Mechanical Characteristics Degradation of Glass Fiber Reinforced Petroleum epoxy Pipes. J. Manuf. Sci. Prod. 2016, 16, 33–40. [Google Scholar] [CrossRef]
- Goertzen, W.; Kessler, M. Creep behavior of carbon fiber/epoxy matrix composites. Mater. Sci. Eng. A 2006, 421, 217–225. [Google Scholar] [CrossRef]
- Seleem, A.-E.H.A. Failure and Corrosion Analysis of Composite Glass Fiber Reinforced Pipe Lines. Ph.D. Thesis, South Valley University, Qena, Egypt, 2015. [Google Scholar]
- Farshad, M.; Necola, A. Strain corrosion of glass fibre-reinforced plastics pipes. Polym. Test. 2004, 23, 517–521. [Google Scholar] [CrossRef]
- Farshad, M.; Necola, A. Effect of aqueous environment on the long-term behavior of glass fiber-reinforced plastic pipes. Polym. Test. 2004, 23, 163–167. [Google Scholar] [CrossRef]
- Nishizaki, I.; Meiarashi, S. Long-Term Deterioration of GFRP in Water and Moist Environment. J. Compos. Constr. 2002, 6, 21–27. [Google Scholar] [CrossRef]
- Miao, Y.; Chen, H.; Cui, G.; Qi, Y. Preparation of new conductive organic coating for the fiber reinforced polymer composite oil pipe. Surf. Coat. Technol. 2021, 412, 127017. [Google Scholar] [CrossRef]
- Firouzsalari, S.E.; Dizhur, D.; Jayaraman, K.; Ingham, J.M. Bending behaviour of flax fabric-reinforced epoxy pipes. Compos. Part A Appl. Sci. Manuf. 2021, 140, 106179. [Google Scholar] [CrossRef]
- Dong, C. Flexural behaviour of carbon and glass reinforced hybrid composite pipes. Compos. Part C Open Access 2021, 4, 100090. [Google Scholar] [CrossRef]
- Xia, H.; Shi, C.; Wang, J.; Bao, X.; Li, H.; Fu, G. Effects of Thickness and Winding Angle of Reinforcement Laminates on Burst Pressure Capacity of Thermoplastic Composite Pipes. J. Offshore Mech. Arct. Eng. 2021, 143, 051802. [Google Scholar] [CrossRef]
- Xia, H.; Shi, C.; Wang, J.; Bao, X.; Li, H.; Fu, G. Effects of thickness and winding angle of the laminate on internal pressure capacity of thermoplastic composite pipes. J. Offshore Mech. Arct. Eng 2020, 4, 051802. [Google Scholar] [CrossRef]
- Rafiee, R.; Abbasi, F. Numerical and Experimental Analyses of the Hoop Tensile Strength of Filament-Wound Composite Tubes. Mech. Compos. Mater. 2020, 56, 423–436. [Google Scholar] [CrossRef]
- Abdellah, M.; Hassan, M.; Mohamed, A.; Khalil, K. A Novel and Highly Effective Natural Vibration Modal Analysis to Predict Nominal Strength of Open Hole Glass Fiber Reinforced Polymer Composites Structure. Polymers 2021, 13, 1251. [Google Scholar] [CrossRef] [PubMed]
- Stoia, D.I.; Marsavina, L.; Linul, E. Mode I Fracture Toughness of Polyamide and Alumide Samples obtained by Selective Laser Sintering Additive Process. Polymers 2020, 12, 640. [Google Scholar] [CrossRef] [Green Version]
- Antunes, M.B.; Almeida, J.H.S.; Amico, S.C. Curing and seawater aging effects on mechanical and physical properties of glass/epoxy filament wound cylinders. Compos. Commun. 2020, 22, 100517. [Google Scholar] [CrossRef]
- Günöz, A.; Kepir, Y.; Memduh, K. The investigation of hardness and density properties of GFRP composite pipes under seawater conditions. Turk. J. Eng. 2020, 6, 34–39. [Google Scholar]
- Shi, H.; An, Z.; Gao, R. Simulation of Mechanical Behavior and Structural Analysis of Glass Fiber Reinforced Mortar Pipes. Rev. Română Mater. 2020, 50, 198–204. [Google Scholar]
- Nouri, M.; Ashenai-Ghasemi, F.; Rahimi-Sherbaf, G.; Kashyzadeh, K.R. Experimental and Numerical Study of the Static Performance of a Hoop-Wrapped CNG Composite Cylinder Considering Its Variable Wall Thickness and Polymer Liner. Mech. Compos. Mater. 2020, 56, 339–352. [Google Scholar] [CrossRef]
- Sülü, İ.Y.; Temiz, Ş. Mechanical behavior of pressurized composite pipes made of various materials. Mater. Test. 2020, 62, 389–394. [Google Scholar] [CrossRef]
- Sharma, P.; Bera, T.; Semwal, K.; Badhe, R.M.; Sharma, A.; Ramakumar, S.; Neogi, S. Theoretical analysis of design of filament wound type 3 composite cylinder for the storage of compressed hydrogen gas. Int. J. Hydrogen Energy 2020, 45, 25386–25397. [Google Scholar] [CrossRef]
- Atalay, O.; Toktas, I. Notch (stress concentration) factor estimation of a cylinder under internal pressure using different approaches. Mater. Test. 2021, 63, 430–435. [Google Scholar] [CrossRef]
- Rafiee, R.; Rashedi, H.; Rezaee, S. Theoretical study of failure in composite pressure vessels subjected to low-velocity impact and internal pressure. Front. Struct. Civ. Eng. 2020, 14, 1349–1358. [Google Scholar] [CrossRef]
- Alderson, K.; Evans, K. Failure mechanisms during the transverse loading of filament-wound pipes under static and low velocity impact conditions. Composites 1992, 23, 167–173. [Google Scholar] [CrossRef]
- Guades, E.; Aravinthan, T.; Manalo, A.; Islam, M. Experimental investigation on the behaviour of square FRP composite tubes under repeated axial impact. Compos. Struct. 2013, 97, 211–221. [Google Scholar] [CrossRef] [Green Version]
- Gemi, L.; Kara, M.; Avci, A. Low velocity impact response of prestressed functionally graded hybrid pipes. Compos. Part B Eng. 2016, 106, 154–163. [Google Scholar] [CrossRef]
- Velosa, J.; Nunes, J.P.; Antunes, P.; Silva, J.; Marques, A. Development of a new generation of filament wound composite pressure cylinders. Compos. Sci. Technol. 2009, 69, 1348–1353. [Google Scholar] [CrossRef] [Green Version]
- Almeida, J.H.S., Jr.; Ribeiro, M.L.; Tita, V.; Amico, S.C. Damage and failure in carbon/epoxy filament wound composite tubes under external pressure: Experimental and numerical approaches. Mater. Des. 2016, 96, 431–438. [Google Scholar] [CrossRef]
- Huang, Z.; Qian, X.; Su, Z.; Pham, D.C.; Sridhar, N. Experimental investigation and damage simulation of large-scaled filament wound composite pipes. Compos. Part B Eng. 2020, 184, 107639. [Google Scholar] [CrossRef]
- Ahmad, M.G.; Hoa, S. Flexural stiffness of thick walled composite tubes. Compos. Struct. 2016, 149, 125–133. [Google Scholar] [CrossRef]
- Srinivasan, T.; Suresh, G.; Ramu, P.; Vignesh, R.; Harshan, A.V.; Vignesh, K. Effect of hygrothermal ageing on the compressive behavior of glass fiber reinforced IPN composite pipes. Mater. Today Proc. 2021, 45, 1354–1359. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, R.; Ruanab, K.; Maab, T.; Guoab, Y.; Guab, J. Improvement of thermal conductivities and simulation model for glass fabrics reinforced epoxy laminated composites via introducing hetero-structured BNN-30@BNNS fillers. J. Mater. Sci. Technol. 2021, 82, 239–249. [Google Scholar] [CrossRef]
- Zubail, A.; Traidia, A.; Masulli, M.; Vatopoulos, K.; Villette, T.; Taie, I. Carbon and energy footprint of nonmetallic composite pipes in onshore oil and gas flowlines. J. Clean. Prod. 2021, 305, 127150. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, J.; Tang, Y.; Kong, J.; Liu, T.; Gu, J. Polymer matrix wave-transparent composites: A review. J. Mater. Sci. Technol. 2021, 75, 225–251. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, J.; Tang, Y.; Xu, J.; Ma, H.; Kong, J.; Gu, J. Optimization of PBO fibers/cyanate ester wave-transparent laminated composites via incorporation of a fluoride-containing linear interfacial compatibilizer. Compos. Sci. Technol. 2021, 210, 108838. [Google Scholar] [CrossRef]
- Tang, L.; Zhang, J.; Gu, J. Random copolymer membrane coated PBO fibers with significantly improved interfacial adhesion for PBO fibers/cyanate ester composites. Chin. J. Aeronaut. 2021, 34, 659–668. [Google Scholar] [CrossRef]
- Tang, L.; Dang, J.; He, M.; Li, J.; Kong, J.; Tang, Y.; Gu, J. Preparation and properties of cyanate-based wave-transparent laminated composites reinforced by dopamine/POSS functionalized Kevlar cloth. Compos. Sci. Technol. 2019, 169, 120–126. [Google Scholar] [CrossRef]
- Hearn, E.J. Mechanics of Materials 2: The Mechanics of Elastic and Plastic Deformation of Solids and Structural Materials; Elsevier: Woburn, MA, USA, 1997. [Google Scholar]
- Newman, J., Jr.; Raju, I. Stress-intensity factors for internal surface cracks in cylindrical pressure vessels. J. Press. Vessel. Technol. 1980, 102, 342–346. [Google Scholar] [CrossRef]
- Hearn, E. Simple stress and strain. In Mechanics of Materials 1, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 1997; pp. 1–26. [Google Scholar] [CrossRef]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Melenk, J.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef] [Green Version]
- Datta, D. Introduction to eXtended Finite Element (XFEM) Method. arXiv 2013, arXiv:1308.5208. [Google Scholar]
- Abdellah, M.Y.; Alsoufi, M.S.; Hassan, M.K.; Ghulman, H.A.; Mohamed, A.F. Rozszerzona Analiza Numeryczna Metoda Elementów Skonczonych Efektu Skali W Epoksydowym Kompozycie Z Karbem Wzmocnionym Włóknem Szklanym [Extended Finite Element Numerical Analysis of Scale Effect in Notched Glass Fiber Reinforced Epoxy Composite]. Arch. Mech. Eng. 2015, 62, 217–236. [Google Scholar] [CrossRef] [Green Version]
- Faria, H. Failure Analysis of GRP Pipes Under Compressive Ring Loads. Master’s Thesis, Universidade do Porto, Porto, Portugal, 2005. [Google Scholar]
- Mohammed, Y.; Hassan, M.K.; Hashem, A. Analytical model to predict multiaxial laminate fracture toughness from 0° ply fracture toughness. Polym. Eng. Sci. 2013, 54, 234–238. [Google Scholar] [CrossRef]
- ASTM International. ASTM D3039/D3039M-17. Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials; ASTM International: West Conshohocken, PA, USA, 2017. [Google Scholar]
- ASTM International. D5045-14. Standard Test Methods for Plane-Strain Fracture Toughness and Strain Energy Release Rate of Plastic Materials; Book of Standards; ASTM International: West Conshohocken, PA, USA, 2014; Volume 99, pp. 1–9. [Google Scholar]
- Bažant, Z.P.; Planas, J. Fracture and Size Effect in Concrete and Other Quasibrittle Materials. In Fracture and Size Effect in Concrete and Other Quasibrittle Materials; Informa UK Limited: London, UK, 2019; Volume 16. [Google Scholar]
- Yang, L.; Yang, Y.; Zheng, H. A phase field numerical manifold method for crack propagation in quasi-brittle materials. Eng. Fract. Mech. 2021, 241, 107427. [Google Scholar] [CrossRef]
- Hassan, M.K.; Abdellah, M.Y.; Azabi, S.K.; Marzouk, W. Fracture Toughness of a Novel GLARE Composite Material. Int. J. Eng. Technol. 2015, 15, 36–41. [Google Scholar]
- Hassan, M.K. Characterization of Face Sheet/Core Debonding Strength in Sandwiched Medium Density Fiberboard. Mater. Sci. Appl. 2017, 8, 673–684. [Google Scholar] [CrossRef] [Green Version]
- Khashaba, U. In-plane shear properties of cross-ply composite laminates with different off-axis angles. Compos. Struct. 2004, 65, 167–177. [Google Scholar] [CrossRef]
- D’Antino, T.; Poggi, C. Stress Redistribution in Glass Fibers of G-FRCM Composites. Key Eng. Mater. 2019, 817, 520–527. [Google Scholar] [CrossRef]
- ASTM International. ASTM E399—90(1997). Standard Test Method for Plane-Strain Fracture Toughness of Metallic Materials; ASTM Standards; ASTM International: West Conshohocken, PA, USA, 2005. [Google Scholar]
- Pinho, S.; Robinson, P.; Iannucci, L. Fracture toughness of the tensile and compressive fibre failure modes in laminated composites. Compos. Sci. Technol. 2006, 66, 2069–2079. [Google Scholar] [CrossRef] [Green Version]
- Paris, P.C.; Sih, G.C. Stress Analysis of Cracks. In Fracture Toughness Testing and Its Applications; ASTM International: West Conshohocken, PA, USA, 2009; p. 30. [Google Scholar]
- Khashaba, U. Tensile and flexural properties of randomly oriented gfrp composites. In Proceedings of 1st International Conference on Mechanical Engineering Advanced Technology for Industrial Production; Assiut University: Assiut, Egypt, 1994; Volume 1, pp. 131–143. [Google Scholar]
- Anderson, T.; McHenry, H.; Dawes, M. Elastic-plastic fracture toughness tests with single-edge notched bend specimens. In Elastic-Plastic Fracture Test Methods: The User’s Experience; ASTM International: West Conshohocken, PA, USA, 2008; p. 210. [Google Scholar]
- Soutis, C.; Curtis, P.T.; Fleck, N.A. Compressive failure of notched carbon fibre composites. Proc. R. Soc. A Math. Phys. Sci. 1993, 440, 241–256. [Google Scholar]
- Raju, I.S.; Newman, J., Jr. Stress-intensity factors for internal and external surface cracks in cylindrical vessels. J. Press. Vessel. Technol. 1982, 104, 293–298. [Google Scholar] [CrossRef]


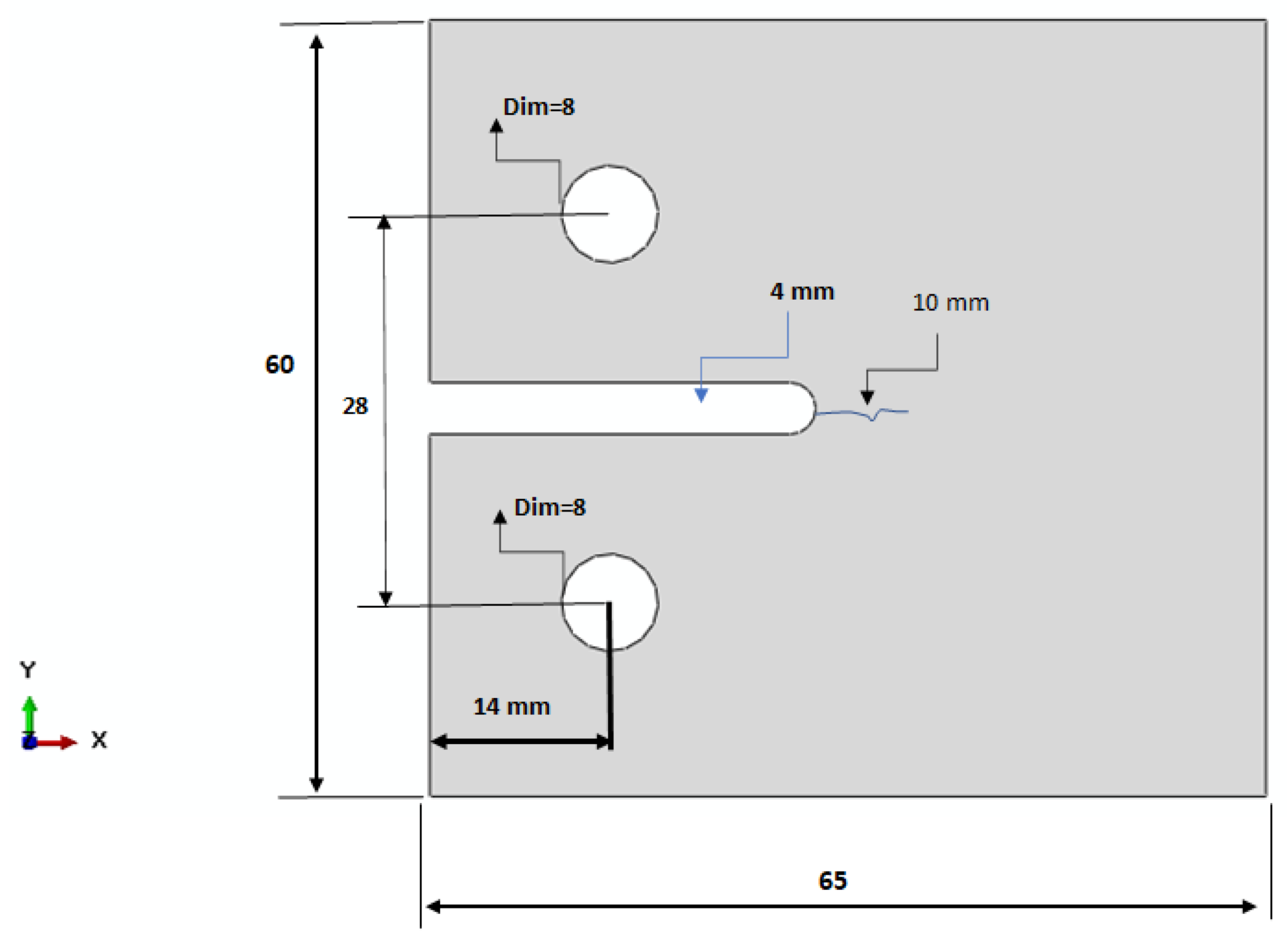
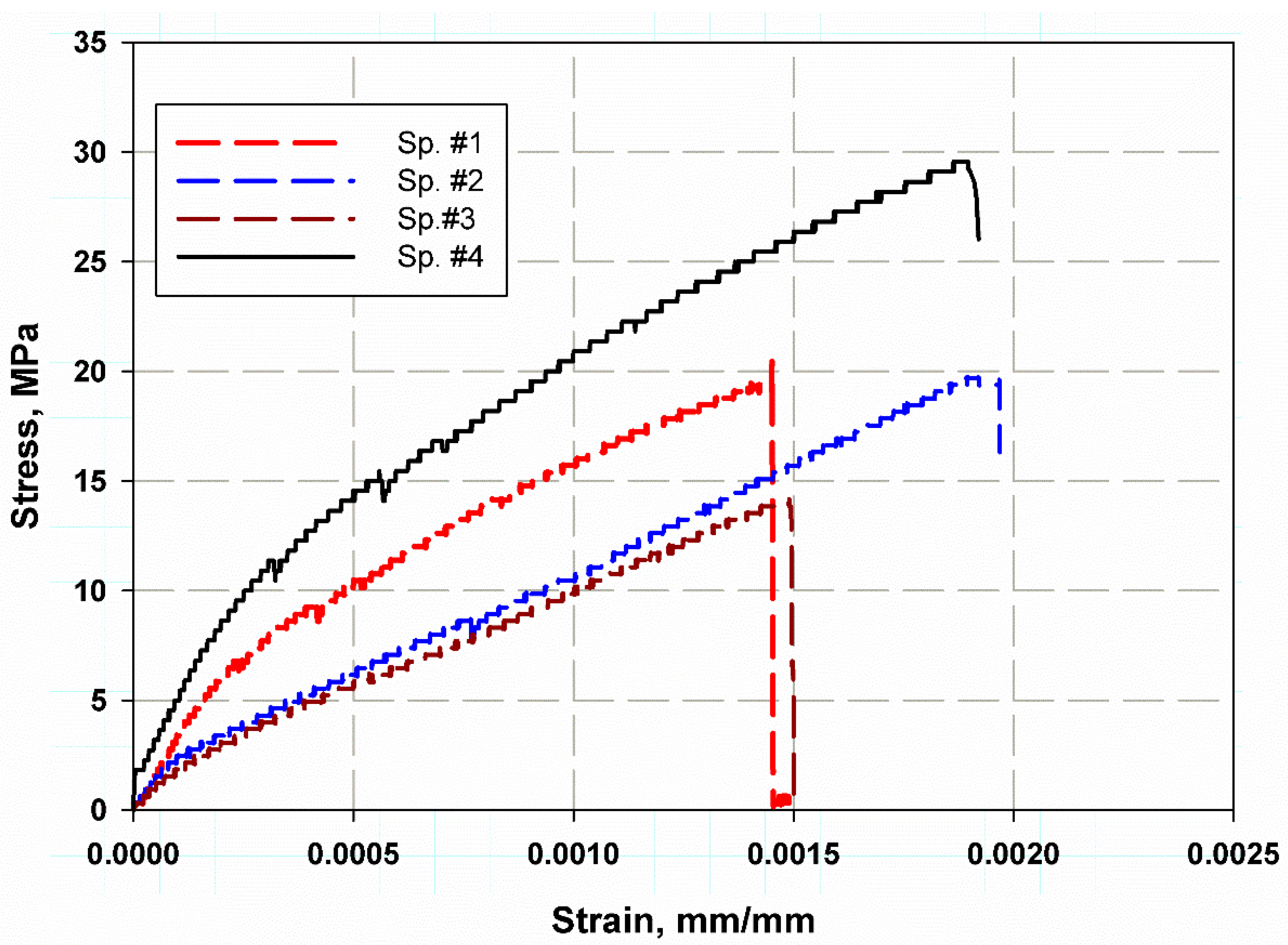
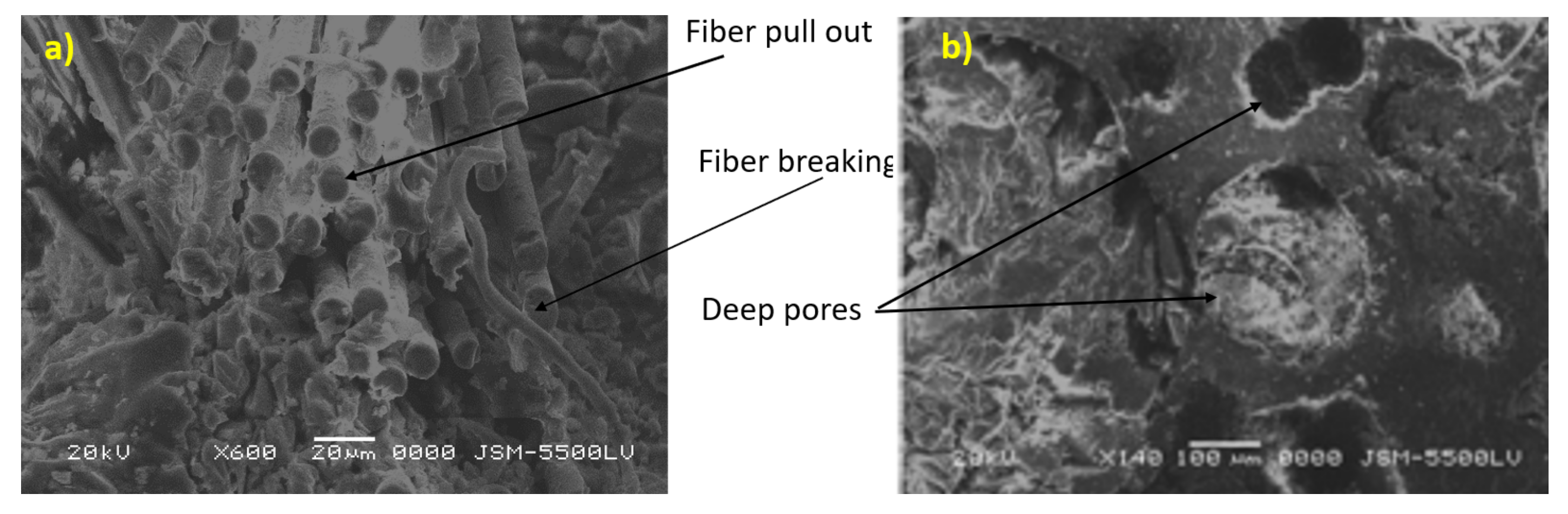
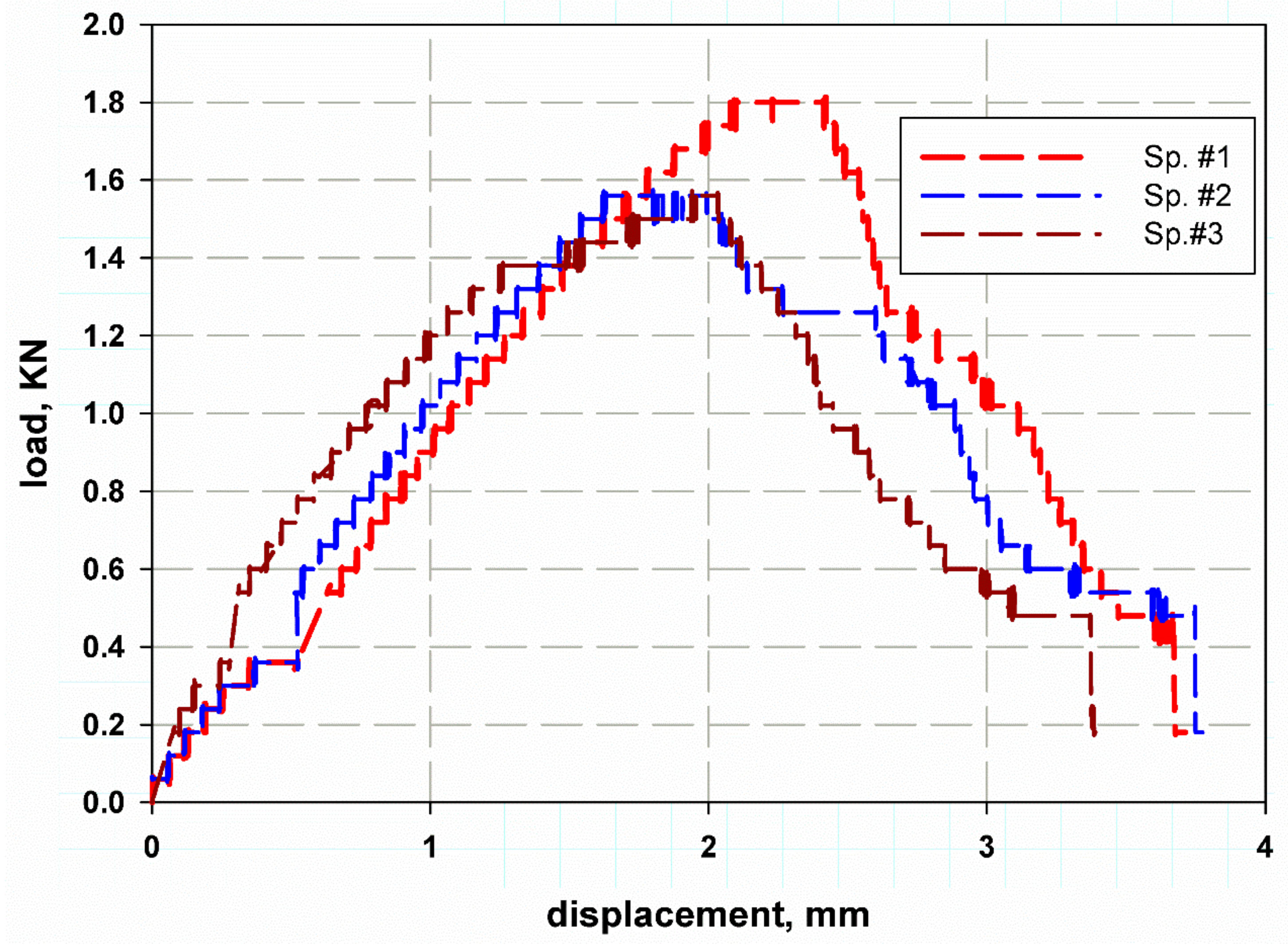

| Constituents | Average % | Viscosity/cp.25 °C | Thermal Deformation Temperature/°C | Tensile Strength/MPa | Specific Density (g/cm3) |
|---|---|---|---|---|---|
| Thermosetting unsaturated polyester (Matrix) | 30.2% | 400 | 70 | 65 | 1.12 |
| Roving | 11.8 | - | - | 3100–3400 | 2.5 |
| Matt | 13.5 | - | - | ||
| Sand | 44.5 | - | - | - | 2.66 |
| Properties | E1 (GPa) | E2 (GPa) | ν12 | G12 (GPa) | G13 (GPa) | G23 (GPa) |
|---|---|---|---|---|---|---|
| Value | 100 | 9 | 0.3 | 3.2 | 3.2 | 4 |
| a/t | Y (Nonlinear) | Ref. [61] | % Error | Y (Linear) |
|---|---|---|---|---|
| 0.2 | 0.2019 | 0.197 | 2.43 | 1.3739 |
| 0.4 | 0.3801 | 0.31 | 18.44 | 2.5147 |
| 0.6 | 0.5374 | 0.458 | 14.77 | 3.462 |
| 0.8 | 0.6761 | 0.702 | −3.83 | 4.2486 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdellah, M.Y.; Alfattani, R.; Alnaser, I.A.; Abdel-Jaber, G.T. Stress Distribution and Fracture Toughness of Underground Reinforced Plastic Pipe Composite. Polymers 2021, 13, 2194. https://doi.org/10.3390/polym13132194
Abdellah MY, Alfattani R, Alnaser IA, Abdel-Jaber GT. Stress Distribution and Fracture Toughness of Underground Reinforced Plastic Pipe Composite. Polymers. 2021; 13(13):2194. https://doi.org/10.3390/polym13132194
Chicago/Turabian StyleAbdellah, Mohammed Y., Rami Alfattani, Ibrahim A. Alnaser, and G. T. Abdel-Jaber. 2021. "Stress Distribution and Fracture Toughness of Underground Reinforced Plastic Pipe Composite" Polymers 13, no. 13: 2194. https://doi.org/10.3390/polym13132194
APA StyleAbdellah, M. Y., Alfattani, R., Alnaser, I. A., & Abdel-Jaber, G. T. (2021). Stress Distribution and Fracture Toughness of Underground Reinforced Plastic Pipe Composite. Polymers, 13(13), 2194. https://doi.org/10.3390/polym13132194






