Elucidating the Aromatic Properties of Covalent Organic Frameworks Surface for Enhanced Polar Solvent Adsorption
Abstract
1. Introduction
2. Computational Methods
2.1. QM Calculations
2.2. Atomic Models and MD Simulation
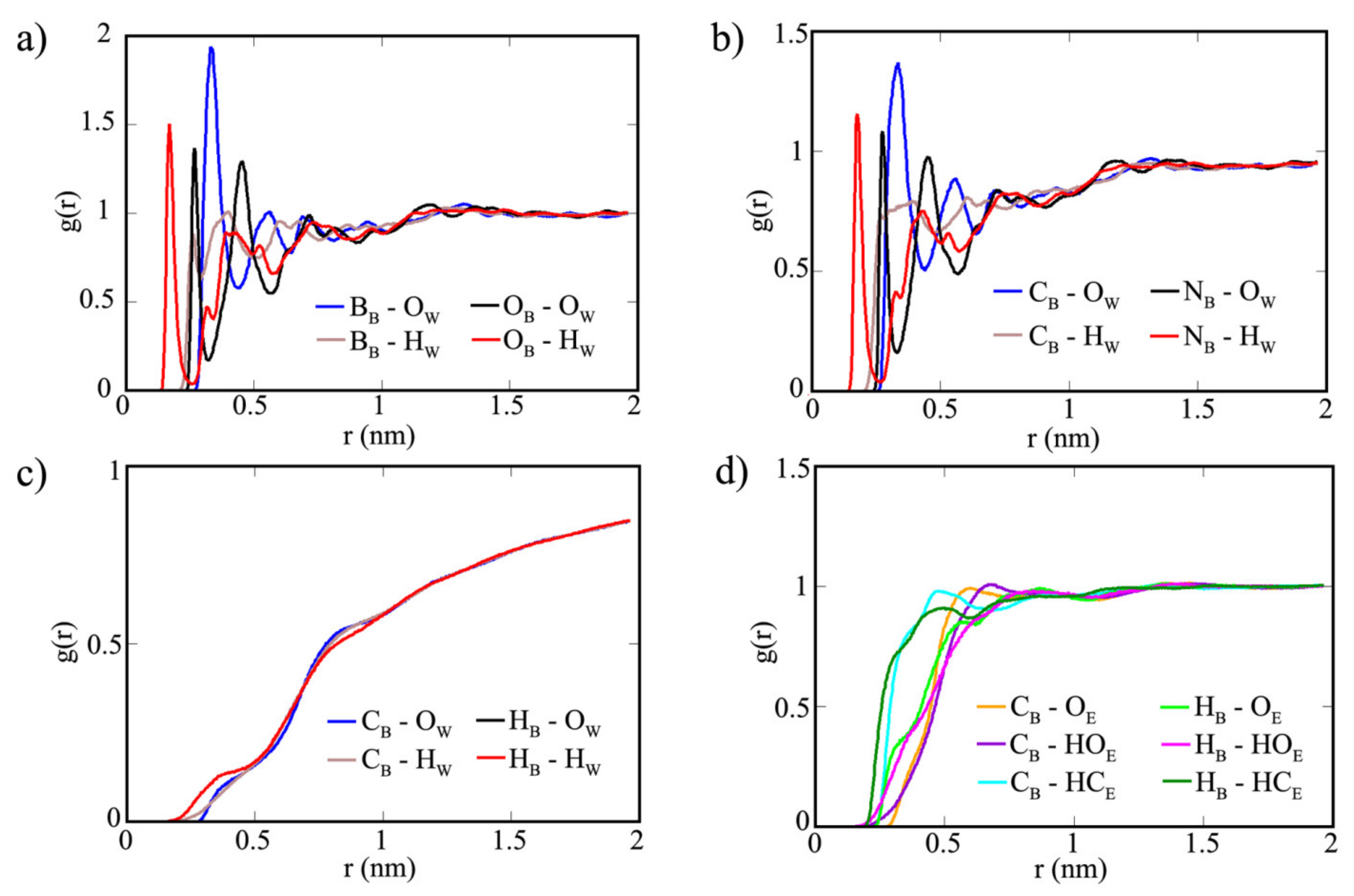
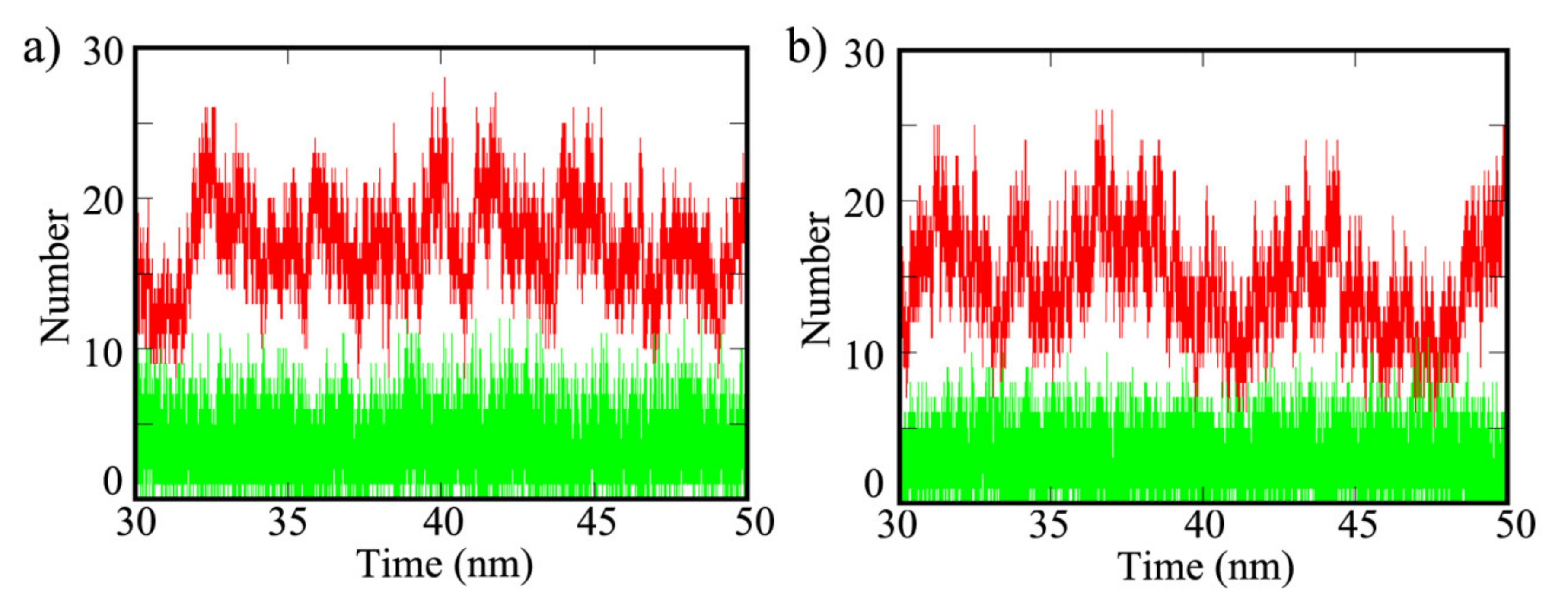
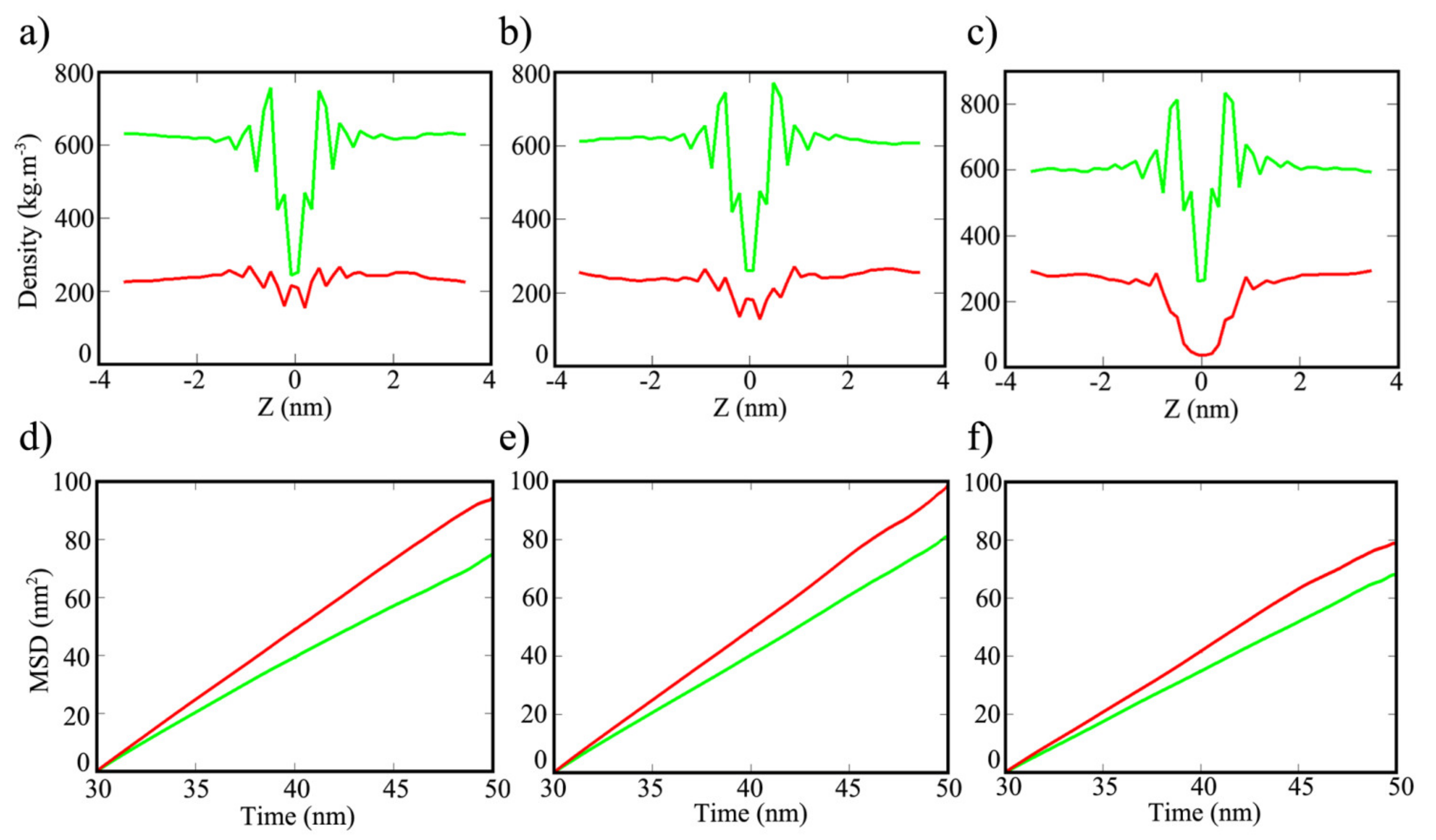
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Shi, K.J.; Yuan, D.W.; Wang, C.X.; Shu, C.H.; Li, D.Y.; Shi, Z.L.; Wu, X.Y.; Liu, P.N. Ullmann Reaction of Aryl Chlorides on Various Surfaces and the Application in Stepwise Growth of 2D Covalent Organic Frameworks. Org. Lett. 2016, 18, 1282–1285. [Google Scholar] [CrossRef]
- El-Kaderi, H.M.; Hunt, J.R.; Mendoza-Cortés, J.L.; Côté, A.P.; Taylor, R.E.; O’Keeffe, M.; Yaghi, O.M. Designed Synthesis of 3D Covalent Organic Frameworks. Science 2007, 316, 268–272. [Google Scholar] [CrossRef]
- Ding, S.-Y.; Wang, W. Covalent organic frameworks (COFs): From design to applications. Chem. Soc. Rev. 2013, 42, 548–568. [Google Scholar] [CrossRef] [PubMed]
- Han, S.S.; Furukawa, H.; Yaghi, O.M.; Goddard, I.W.A. Covalent Organic Frameworks as Exceptional Hydrogen Storage Materials. J. Am. Chem. Soc. 2008, 130, 11580–11581. [Google Scholar] [CrossRef] [PubMed]
- Mendoza-Cortés, J.L.; Han, S.S.; Furukawa, H.; Yaghi, O.M.; Goddard , W.A., III. Adsorption mechanism and uptake of methane in covalent organic frameworks: Theory and experiment. J. Phys. Chem. A 2010, 114, 10824–10833. [Google Scholar] [CrossRef]
- Yuan, S.; Li, X.; Zhu, J.; Zhang, G.; Van Puyvelde, P.; Van Der Bruggen, B. Covalent organic frameworks for membrane separation. Chem. Soc. Rev. 2019, 48, 2665–2681. [Google Scholar] [CrossRef] [PubMed]
- Dey, K.; Pal, M.; Rout, K.C.; Kunjattu, H.S.; Das, A.; Mukherjee, R.; Kharul, U.K.; Banerjee, R. Selective molecular separation by interfacially crystallized covalent organic framework thin films. J. Am. Chem. Soc. 2017, 139, 13083–13091. [Google Scholar] [CrossRef]
- Nagai, A.; Guo, Z.; Feng, X.; Jin, S.; Chen, X.; Ding, X.; Jiang, D. Pore surface engineering in covalent organic frameworks. Nat. Commun. 2011, 2, 536. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Wu, Q.; Guo, X.; Zhang, M.; Chen, B.; Wei, G.; Li, X.; Li, X.; Li, S.; Ma, L. Laminated self-standing covalent organic framework membrane with uniformly distributed subnanopores for ionic and molecular sieving. Nat. Commun. 2020, 11, 1–9. [Google Scholar] [CrossRef]
- Wang, W.; Deng, S.; Ren, L.; Li, D.; Wang, W.; Vakili, M.; Wang, B.; Huang, J.; Wang, Y.; Yu, G. Stable Covalent Organic Frameworks as Efficient Adsorbents for High and Selective Removal of an Aryl-Organophosphorus Flame Retardant from Water. ACS Appl. Mater. Interfaces 2018, 10, 30265–30272. [Google Scholar] [CrossRef]
- Kuehl, V.A.; Yin, J.; Duong, P.H.H.; Mastorovich, B.; Newell, B.S.; Li-Oakey, K.D.; Parkinson, B.A.; Hoberg, J.O. A Highly Ordered Nanoporous, Two-Dimensional Covalent Organic Framework with Modifiable Pores, and Its Application in Water Purification and Ion Sieving. J. Am. Chem. Soc. 2018, 140, 18200–18207. [Google Scholar] [CrossRef] [PubMed]
- Côté, A.P.; Benin, A.I.; Ockwig, N.W.; O’Keeffe, M.; Matzger, A.J.; Yaghi, O.M. Porous, Crystalline, Covalent Organic Frameworks. Science 2005, 310, 1166–1170. [Google Scholar] [CrossRef] [PubMed]
- Kuhn, P.; Antonietti, M.; Thomas, A. Porous, Covalent Triazine-Based Frameworks Prepared by Ionothermal Synthesis. Angew. Chem. Int. Ed. 2008, 47, 3450–3453. [Google Scholar] [CrossRef]
- Zhang, K.; He, Z.; Gupta, K.M.; Jiang, J. Computational design of 2D functional covalent–organic framework membranes for water desalination. Environ. Sci. Water Res. Technol. 2017, 3, 735–743. [Google Scholar] [CrossRef]
- Zheng, Y.-Z.; Zhou, Y.; Liang, Q.; Chen, D.-F.; Guo, R.; Lai, R.-C. Hydrogen-bonding Interactions between Apigenin and Ethanol/Water: A Theoretical Study. Sci. Rep. 2016, 6, 34647. [Google Scholar] [CrossRef]
- Fang, Q.; Chen, B.; Lin, Y.; Guan, Y. Aromatic and Hydrophobic Surfaces of Wood-derived Biochar Enhance Perchlorate Adsorption via Hydrogen Bonding to Oxygen-containing Organic Groups. Environ. Sci. Technol. 2014, 48, 279–288. [Google Scholar] [CrossRef]
- Liu, F.; Yang, J.; Xu, Z.; Yang, X. Selective surface adsorption and pore trapping for ethanol-water mixtures near single-layer polyporous graphynes. Appl. Surf. Sci. 2016, 387, 1080–1087. [Google Scholar] [CrossRef]
- Frisch, A.; Hratchian, H.P.; Dennington, R.D., II; Keith, T.A.; Millam, J.; Nielsen, B.; Holder, A.J.; Hiscocks, J. GaussView Version 5.0.8; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09 Program; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Huang, W.; Xie, W.; Huang, H.; Zhang, H.; Liu, H. Designing Organic Semiconductors with Ultrasmall Reorganization Energies: Insights from Molecular Symmetry, Aromaticity and Energy Gap. J. Phys. Chem. Lett. 2020, 11, 4548–4553. [Google Scholar] [CrossRef]
- Djouambi, N.; Bougheloum, C.; Messalhi, A.; Bououdina, M.; Banerjee, A.; Chakraborty, S.; Ahuja, R. New Concept on Photocatalytic Degradation of Thiophene Derivatives: Experimental and DFT Studies. J. Phys. Chem. C 2018, 122, 15646–15651. [Google Scholar] [CrossRef]
- Hussain, S.; Hussain, R.; Mehboob, M.Y.; Chatha, S.A.S.; Hussain, A.I.; Umar, A.; Khan, M.U.; Ahmed, M.; Adnan, M.; Ayub, K. Adsorption of Phosgene Gas on Pristine and Copper-Decorated B12N12 Nanocages: A Comparative DFT Study. ACS Omega 2020, 5, 7641–7650. [Google Scholar] [CrossRef]
- Bachrach, S.M. DFT study of the ExBox• aromatic hydrocarbon host–guest complex. J. Phys. Chem. A 2013, 117, 8484–8491. [Google Scholar] [CrossRef] [PubMed]
- Majerz, I.; Dziembowska, T. Aromaticity and Through-Space Interaction between Aromatic Rings in [2.2]Paracyclophanes. J. Phys. Chem. A 2016, 120, 8138–8147. [Google Scholar] [CrossRef] [PubMed]
- Seitz, A.E.; Eckhardt, M.; Erlebach, A.; Peresypkina, E.V.; Sierka, M.; Scheer, M. Pnictogen–Silicon Analogues of Benzene. J. Am. Chem. Soc. 2016, 138, 10433–10436. [Google Scholar] [CrossRef] [PubMed]
- Mucsi, Z.; Viskolcz, B.; Csizmadia, I.G. A Quantitative Scale for the Degree of Aromaticity and Antiaromaticity: A Comparison of Theoretical and Experimental Enthalpies of Hydrogenation. J. Phys. Chem. A 2007, 111, 1123–1132. [Google Scholar] [CrossRef] [PubMed]
- Monaco, G.; Zanasi, R. Analysis of the Nucleus-Independent Chemical Shifts of [10]Cyclophenacene: Is It an Aromatic or Antiaromatic Molecule? J. Phys. Chem. Lett. 2017, 8, 4673–4678. [Google Scholar] [CrossRef]
- Glendening, E.D.; Reed, A.E.; Carpenter, J.E.; Weinhold, F. NBO Version 3.1. There is no Corresp. Rec. Ref. Sch. 1998. [Google Scholar]
- Zou, X.; Ren, H.; Zhu, G. Topology-directed design of porous organic frameworks and their advanced applications. Chem. Commun. 2013, 49, 3925–3936. [Google Scholar] [CrossRef] [PubMed]
- Suk, M.E.; Aluru, N.R. Molecular and continuum hydrodynamics in graphene nanopores. RSC Adv. 2013, 3, 9365–9372. [Google Scholar] [CrossRef]
- Suk, M.E.; Aluru, N.R. Ion transport in sub-5-nm graphene nanopores. J. Chem. Phys. 2014, 140, 084707. [Google Scholar] [CrossRef]
- Rappé, A.K.; Casewit, C.J.; Colwell, K.S.; Goddard, W.A., III; Skiff, W.M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114, 10024–10035. [Google Scholar] [CrossRef]
- Damm, W.; Frontera, A.; Tirado–Rives, J.; Jorgensen, W.L. OPLS all-atom force field for carbohydrates. J. Comput. Chem. 1997, 18, 1955–1970. [Google Scholar] [CrossRef]
- Berendsen, H.J.C.; Grigera, J.R.; Straatsma, T.P. The missing term in effective pair potentials. J. Phys. Chem. 1987, 91, 6269–6271. [Google Scholar] [CrossRef]
- Fang, C.; Wu, H.; Lee, S.-Y.; Mahajan, R.L.; Qiao, R. The ionized graphene oxide membranes for water-ethanol separation. Carbon 2018, 136, 262–269. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, D.; Yang, Q.; Zhong, C.; Mi, J. Comparative study of separation performance of COFs and MOFs for CH4/CO2/H2 mixtures. Ind. Eng. Chem. Res. 2010, 49, 2902–2906. [Google Scholar] [CrossRef]
- Abraham, M.J.; Murtola, T.; Schulz, R.; Páll, S.; Smith, J.C.; Hess, B.; Lindahl, E. GROMACS: High performance molecular simulations through multi-level parallelism from laptops to supercomputers. SoftwareX 2015, 1–2, 19–25. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, G.; Chen, L.; Wang, Y.; Wang, X.; Zeng, S. Interaction of Graphene and its Oxide with Lipid Membrane: A Molecular Dynamics Simulation Study. J. Phys. Chem. C 2016, 120, 6225–6231. [Google Scholar] [CrossRef]
- Rogge, S.; Vanduyfhuys, L.; Ghysels, A.; Waroquier, M.; Verstraelen, T.; Maurin, G.; Van Speybroeck, V. A Comparison of Barostats for the Mechanical Characterization of Metal–Organic Frameworks. J. Chem. Theory Comput. 2015, 11, 5583–5597. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.-T.; Kim, J.; Cho, H.-Y.; Kim, S.; Ahn, W.-S. Facile synthesis of covalent organic frameworks COF-1 and COF-5 by sonochemical method. RSC Adv. 2012, 2, 10179–10181. [Google Scholar] [CrossRef]
- Charistos, N.D.; Papadopoulos, A.G.; Sigalas, M.P. Interpretation of Electron Delocalization in Benzene, Cyclobutadiene, and Borazine Based on Visualization of Individual Molecular Orbital Contributions to the Induced Magnetic Field. J. Phys. Chem. A 2014, 118, 1113–1122. [Google Scholar] [CrossRef]
- Von Schleyer, P.R.; Jiao, H. What is aromaticity? Pure Appl. Chem. 1996, 68, 209–218. [Google Scholar] [CrossRef]
- Chen, Z.; Wannere, C.S.; Corminboeuf, C.; Puchta, A.R.; Schleyer, P.V.R. Nucleus-Independent Chemical Shifts (NICS) as an Aromaticity Criterion. Chem. Rev. 2005, 105, 3842–3888. [Google Scholar] [CrossRef] [PubMed]
- Cooper, D.L.; Wright, S.C.; Gerratt, J.; Hyams, P.A.; Raimondi, M. The electronic structure of heteroaromatic molecules. Part 3. A comparison of benzene, borazine, and boroxine. J. Chem. Soc. Perkin Trans. 1989, 719–724. [Google Scholar] [CrossRef]
- Kalemos, A. The nature of the chemical bond in borazine (B3 N3 H6), boroxine (B3 O3 H3), carborazine (B2 N2 C2 H6), and related species. Int. J. Quantum Chem. 2018, 118, e25650. [Google Scholar] [CrossRef]
- Kumari, P.; Shobhna; Kaur, S.; Kashyap, H.K. Influence of Hydration on the Structure of Reline Deep Eutectic Solvent: A Molecular Dynamics Study. ACS Omega 2018, 3, 15246–15255. [Google Scholar] [CrossRef]
- Tang, H.; Zhao, Y.; Shan, S.; Yang, X.; Liu, D.; Cui, F.; Xing, B. Wrinkle- and Edge-Adsorption of Aromatic Compounds on Graphene Oxide as Revealed by Atomic Force Microscopy, Molecular Dynamics Simulation, and Density Functional Theory. Environ. Sci. Technol. 2018, 52, 7689–7697. [Google Scholar] [CrossRef]
- Sun, W.; Zeng, Q.; Yu, A. Calculation of Noncontact Forces between Silica Nanospheres. Langmuir 2013, 29, 2175–2184. [Google Scholar] [CrossRef] [PubMed]
- Dixit, S.; Crain, J.S.; Poon, W.C.K.; Finney, J.L.; Soper, A.K. Molecular segregation observed in a concentrated alcohol–water solution. Nat. Cell Biol. 2002, 416, 829–832. [Google Scholar] [CrossRef] [PubMed]
- Bussamra, B.C.; Sietaram, D.; Verheijen, P.; Mussatto, S.I.; da Costa, A.C.; van der Wielen, L.; Ottens, M. A critical assessment of the Flory-Huggins (FH) theory to predict aqueous two-phase behaviour. Sep. Purif. Technol. 2021, 255, 117636. [Google Scholar] [CrossRef]
- Lu, H.; Du, S. A phenomenological thermodynamic model for the chemo-responsive shape memory effect in polymers based on Flory–Huggins solution theory. Polym. Chem. 2014, 5, 1155–1162. [Google Scholar] [CrossRef]
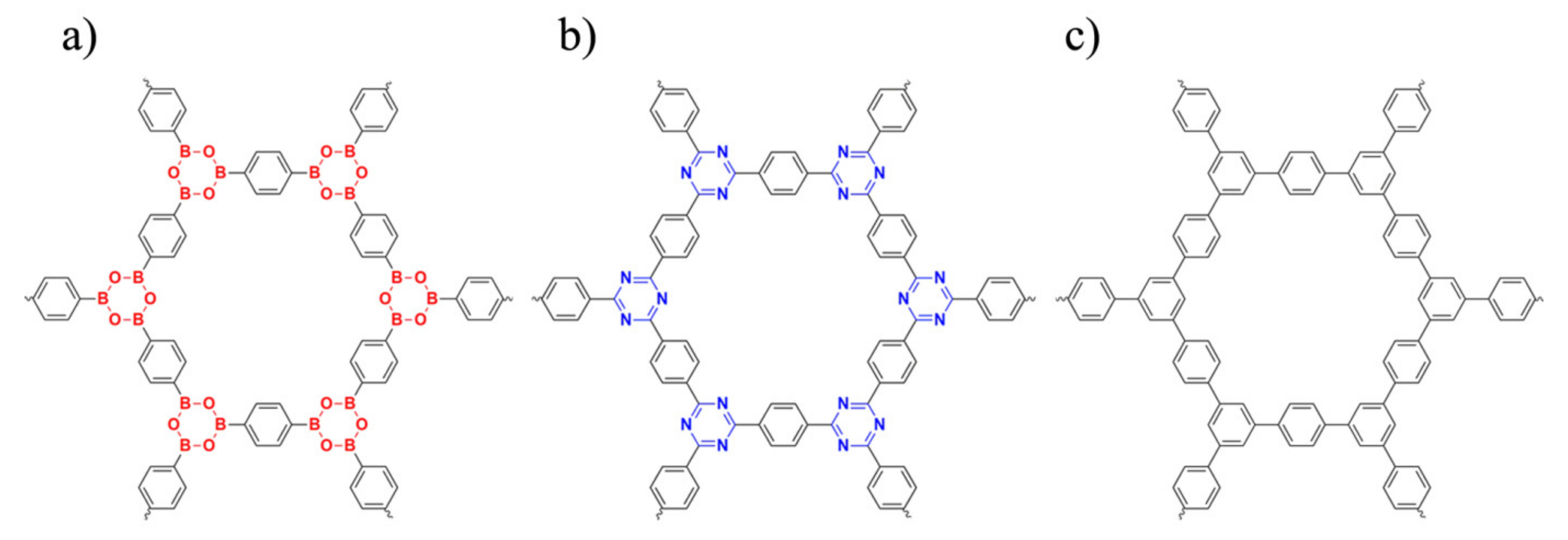
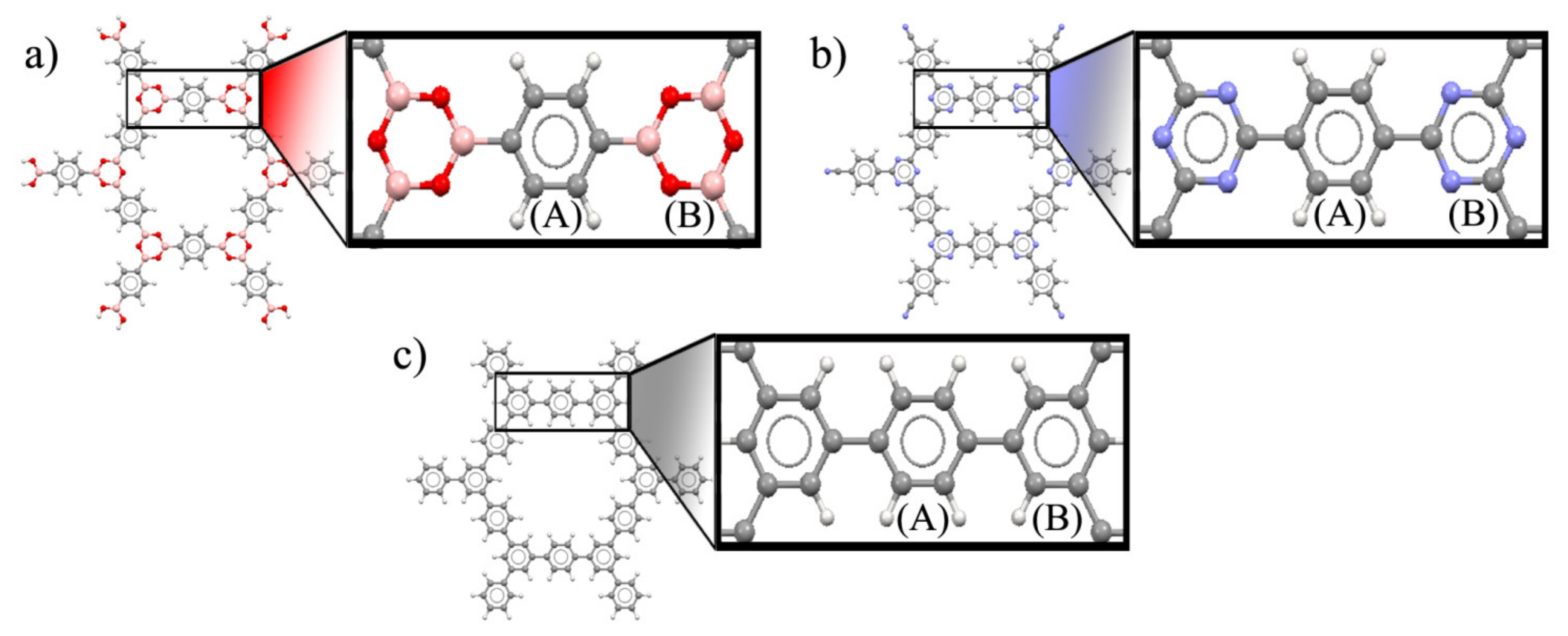
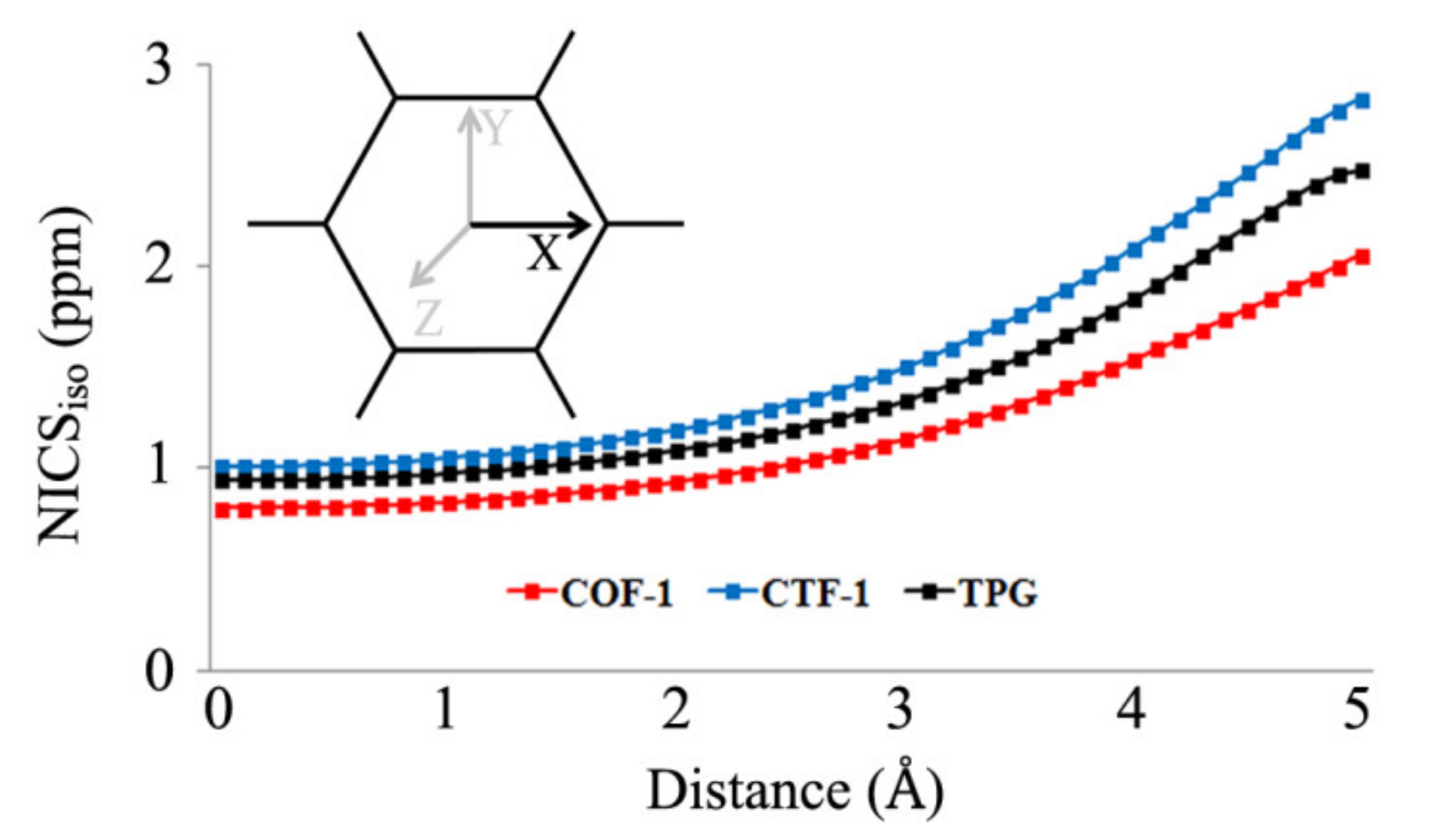
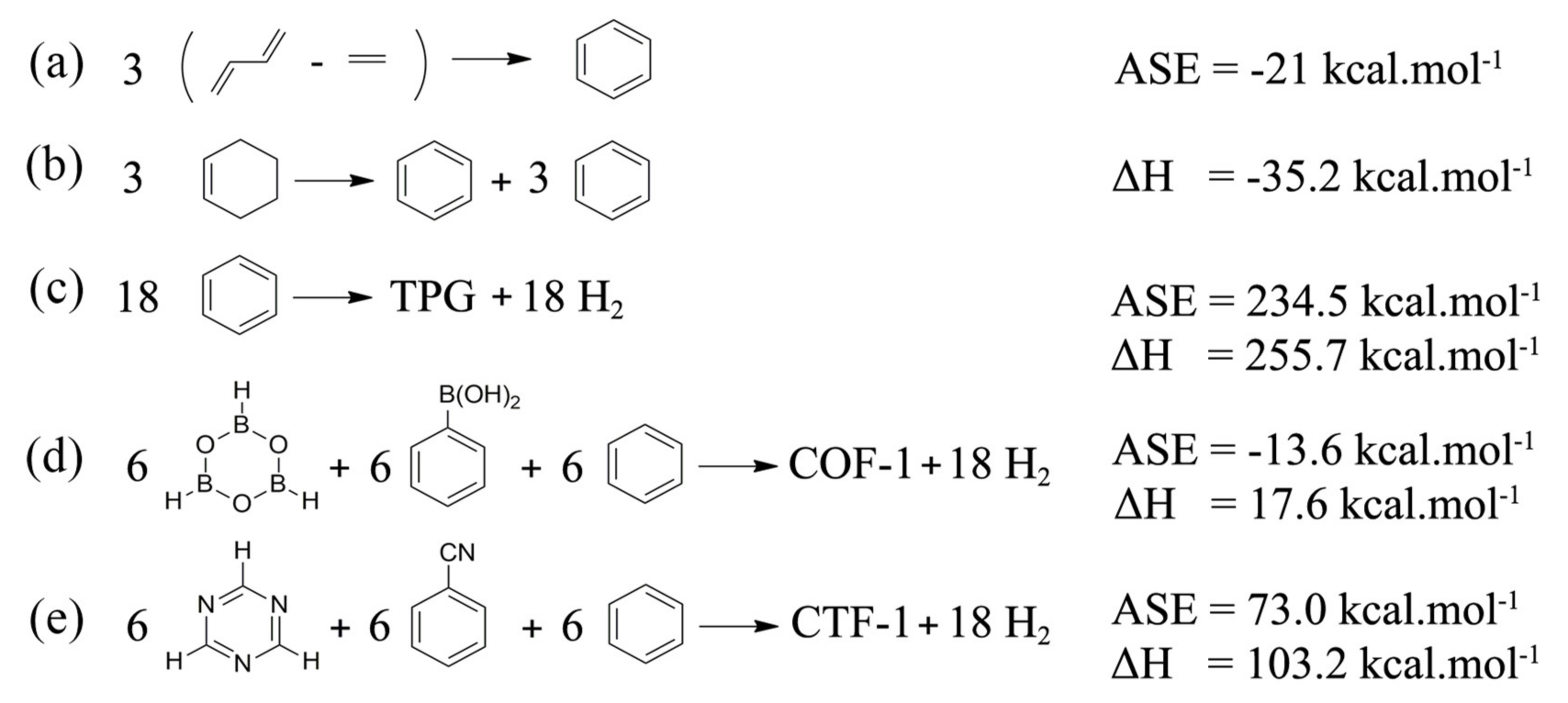

| Properties | COF-1 | CTF-1 | TPG |
|---|---|---|---|
| NICSzz(pore) 1 | 3.9 | 4.6 | 4.3 |
| NICSzz(A) | −10.5 [−28.4] | −7.2 [−25.3] | −5.3 [−23.7] |
| NICSzz(B) | 30.5 [5.2] | 12.2 [−13.6] | −0.8 [−20.9] |
| NICSzz(tot) | −19.2 | −203.4 | −304.2 |
| HOMA | 0.989 | 0.994 | 0.990 |
| HOMO (eV) | −8.70 | −9.49 | −7.34 |
| LUMO (eV) | 2.00 | 0.33 | 1.81 |
| EHL (eV) | 6.70 | 9.16 | 5.53 |
| η (eV) | 3.35 | 4.57 | 2.75 |
| S (eV) | 0.29 | 0.21 | 0.36 |
| Properties | COF-1 | CTF-1 | TPG |
|---|---|---|---|
| Donor → acceptor | σB-O → LP*B | Π *C=N → π*C=C | πC=C → π*C=C |
| Eij (kcal.mol−1) | 285.4 | 177.6 | 44.1 |
| Occupancy of σB-O | 1.821 | - | - |
| Occupancy of LP*B | 0.371 | - | - |
| Occupancy of π*C=N | - | 0.347 | - |
| Occupancy of π*C=C | - | 0.349 | - |
| Occupancy of πC=C | - | - | 1.640 |
| Occupancy of π*C=C | - | - | 0.355 |
| Solvent | COF-1 | CTF-1 | TPG | |
|---|---|---|---|---|
| Ethanol (kJ.mol−1) | vdw | −985.0 | −906.5 | −1165.1 |
| Es | −381.1 | −302.1 | −26.3 | |
| Water (kJ.mol−1) | vdw | −37.7 | −29.7 | −59.6 |
| Es | −915.4 | −640.2 | −7.4 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Borzehandani, M.Y.; Abdulmalek, E.; Abdul Rahman, M.B.; Latif, M.A.M. Elucidating the Aromatic Properties of Covalent Organic Frameworks Surface for Enhanced Polar Solvent Adsorption. Polymers 2021, 13, 1861. https://doi.org/10.3390/polym13111861
Borzehandani MY, Abdulmalek E, Abdul Rahman MB, Latif MAM. Elucidating the Aromatic Properties of Covalent Organic Frameworks Surface for Enhanced Polar Solvent Adsorption. Polymers. 2021; 13(11):1861. https://doi.org/10.3390/polym13111861
Chicago/Turabian StyleBorzehandani, Mostafa Yousefzadeh, Emilia Abdulmalek, Mohd Basyaruddin Abdul Rahman, and Muhammad Alif Mohammad Latif. 2021. "Elucidating the Aromatic Properties of Covalent Organic Frameworks Surface for Enhanced Polar Solvent Adsorption" Polymers 13, no. 11: 1861. https://doi.org/10.3390/polym13111861
APA StyleBorzehandani, M. Y., Abdulmalek, E., Abdul Rahman, M. B., & Latif, M. A. M. (2021). Elucidating the Aromatic Properties of Covalent Organic Frameworks Surface for Enhanced Polar Solvent Adsorption. Polymers, 13(11), 1861. https://doi.org/10.3390/polym13111861








