Swelling and Diffusion in Polymerized Ionic Liquids-Based Hydrogels
Abstract
:1. Introduction
2. Materials and Methods
2.1. Chemicals
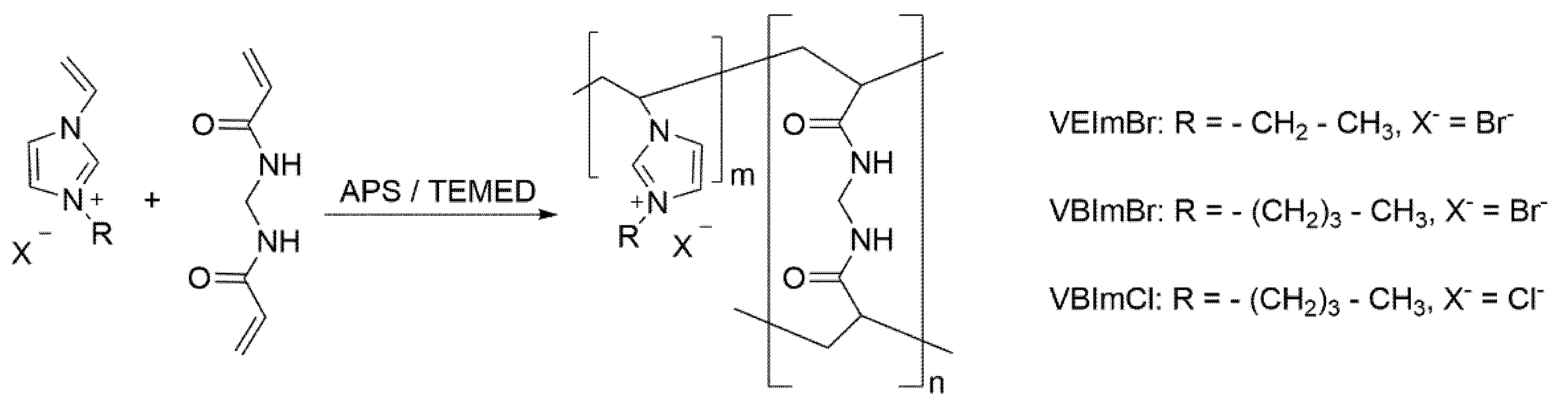
2.2. Synthesis of Polymerizable Monomers
2.3. General Procedure for Hydrogel Synthesis
2.4. Gravimetric Swelling Experiments
2.5. Calculations from Gravimetric Swelling Experiments
2.6. Diffusion Coefficients from Interval Sorption Experiments
2.7. Diffusion Weighted Magnetic Resonance Imaging (DW-MRI)
3. Results
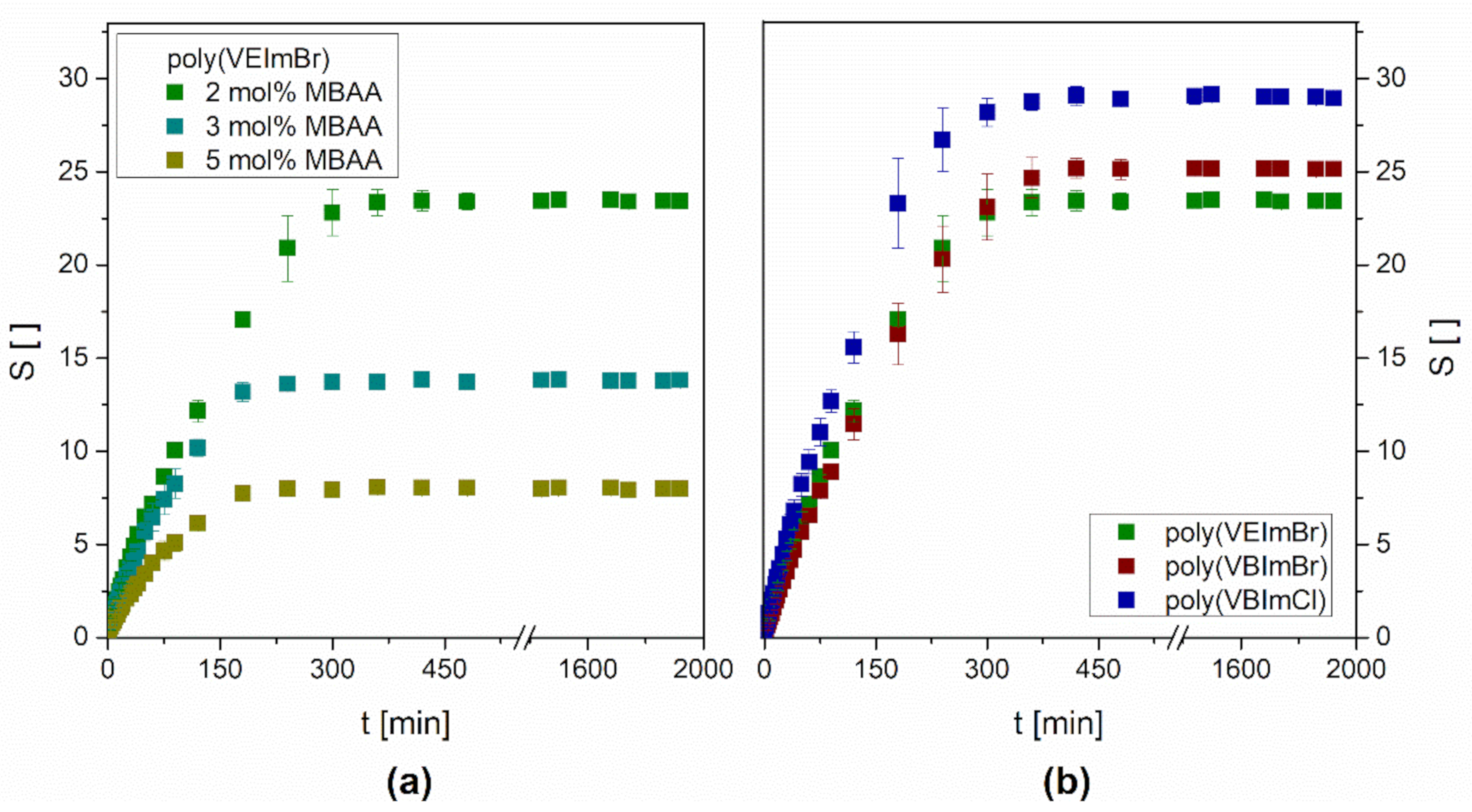
3.1. Gravimetric Swelling Experiments
3.2. Diffusion Coefficients from Gravimetric Swelling Experiments
3.3. Sorption Curves
3.4. Water Diffusion Coefficients from Gravimetric Sorption Experiments
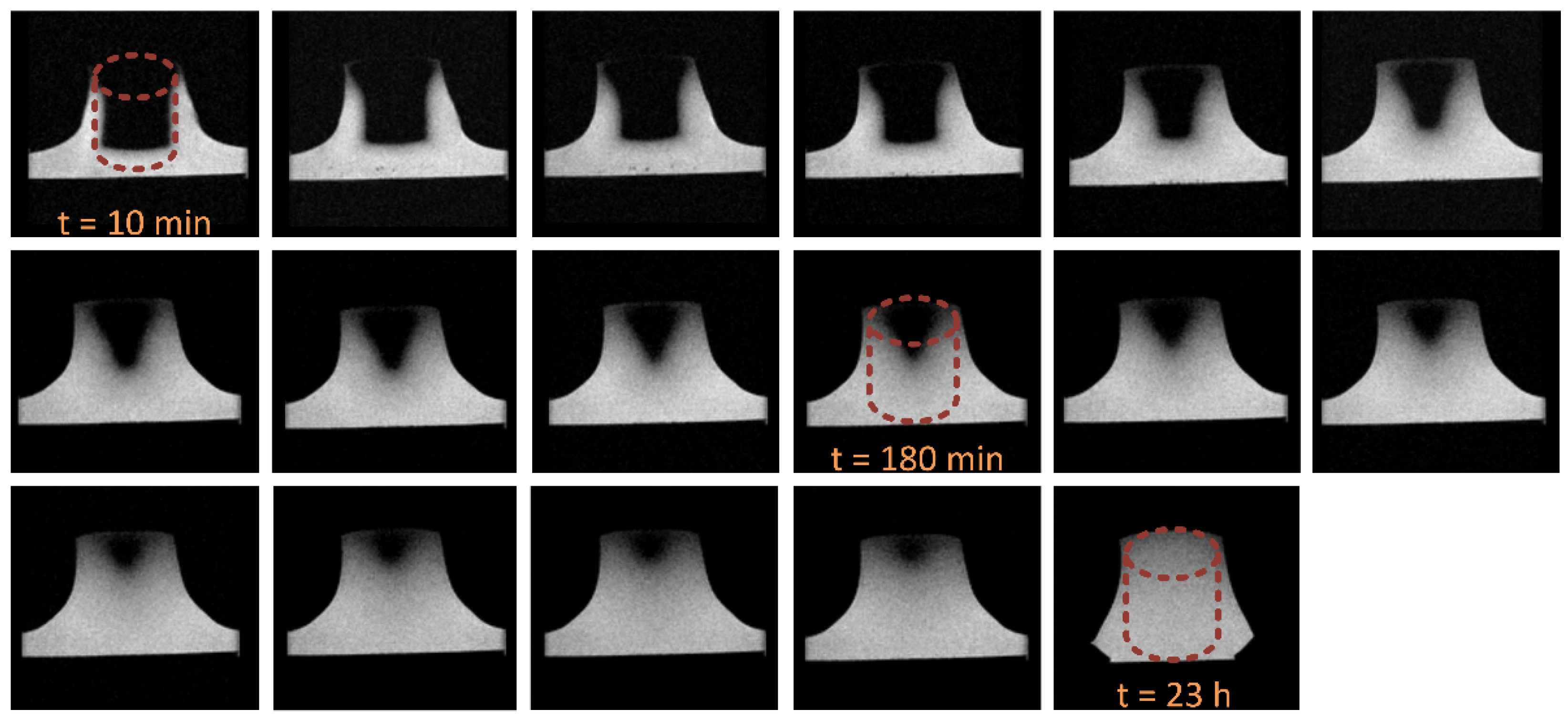
3.5. DW-MRI Measurements
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Claus, J.; Sommer, F.O.; Kragl, U. Ionic Liquids in Biotechnology and Beyond. Solid State Ion. 2018, 314, 119–128. [Google Scholar] [CrossRef]
- Gupta, P.; Vermani, K.; Garg, S. Hydrogels: From Controlled Release to pH-Responsive Drug Delivery. Drug Discov. Today 2002, 7, 569–579. [Google Scholar] [CrossRef]
- Lin, C.-C.; Anseth, K.S. PEG Hydrogels for the Controlled Release of Biomolecules in Regenerative Medicine. Pharm. Res. 2009, 26, 631–643. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lin, C.-C.; Metters, A.T. Hydrogels in Controlled Release Formulations: Network Design and Mathematical Modeling. Adv. Drug Deliv. Rev. 2006, 58, 1379–1408. [Google Scholar] [CrossRef]
- Behl, G.; Iqbal, J.; O’Reilly, N.; McLoughlin, P.; Fitzhenry, L. Synthesis and Characterization of Poly(2-hydroxyethylmethacrylate) Contact Lenses Containing Chitosan Nanoparticles as an Ocular Delivery System for Dexamethasone Sodium Phosphate. Pharm. Res. 2016, 33, 1638–1648. [Google Scholar] [CrossRef]
- De Queiroz, A.A.B.; Debieux, P.; Amaro, J.; Ferretti, M.; Cohen, M. Hydrogel Implant is as Effective as Osteochondral Autologous Transplantation for Treating Focal Cartilage Knee Injury in 24 Months. Knee Surg. Sports Traumatol. Arthrosc. 2018, 26, 2934–2941. [Google Scholar] [CrossRef]
- Claus, J.; Eickner, T.; Grabow, N.; Kragl, U.; Oschatz, S. Ion Exchange Controlled Drug Release from Polymerized Ionic Liquids. Macromol. Biosci. 2020, 20. [Google Scholar] [CrossRef]
- Colter, J.; Wirostko, B.; Coats, B. Finite Element Design Optimization of a Hyaluronic Acid-Based Hydrogel Drug Delivery Device for Improved Retention. Ann. Biomed. Eng. 2018, 46, 211–221. [Google Scholar] [CrossRef]
- Kamaly, N.; Yameen, B.; Wu, J.; Farokhzad, O.C. Degradable Controlled-Release Polymers and Polymeric Nanoparticles: Mechanisms of Controlling Drug Release. Chem. Rev. 2016, 116, 2602–2663. [Google Scholar] [CrossRef] [Green Version]
- Mehrali, M.; Thakur, A.; Pennisi, C.P.; Talebian, S.; Arpanaei, A.; Nikkhah, M.; Dolatshahi-Pirouz, A. Nanoreinforced Hydrogels for Tissue Engineering: Biomaterials that are Compatible with Load-Bearing and Electroactive Tissues. Adv. Mater. 2017, 29. [Google Scholar] [CrossRef]
- Kumar, A.; Han, S.S. PVA-Based Hydrogels for Tissue Engineering: A Review. Int. J. Polym. Mater. 2016, 66, 159–182. [Google Scholar] [CrossRef]
- Großeheilmann, J.; Bandomir, J.; Kragl, U. Preparation of Poly(ionic liquid)s-Supported Recyclable Organocatalysts for the Asymmetric Nitroaldol (Henry) Reaction. Chem. A Eur. J. 2015, 21, 18957–18960. [Google Scholar] [CrossRef]
- Grollmisch, A.; Kragl, U.; Großeheilmann, J. Enzyme Immobilization in Polymerized Ionic Liquids-based Hydrogels for Active and Reusable Biocatalysts. SynOpen 2018, 2, 0192–0199. [Google Scholar] [CrossRef] [Green Version]
- Kosto, K.B.; Deen, W.M. Hindered Convection of Macromolecules in Hydrogels. Biophys. J. 2005, 88, 277–286. [Google Scholar] [CrossRef] [Green Version]
- Peppas, N.A.; Huang, Y.; Torres-Lugo, M.; Ward, J.H.; Zhang, J. Physicochemical Foundations and Structural Design of Hydrogels in Medicine and Biology. Annu. Rev. Biomed. Eng. 2000, 2, 9–29. [Google Scholar] [CrossRef] [Green Version]
- Peppas, N. Hydrogels in Pharmaceutical Formulations. Eur. J. Pharm. Biopharm. 2000, 50, 27–46. [Google Scholar] [CrossRef]
- Peppas, A.N.; Keys, K.B.; Torres-Lugo, M.; Lowman, A.M. Poly(ethylene glycol)-Containing Hydrogels in Drug Delivery. J. Control. Release 1999, 62, 81–87. [Google Scholar] [CrossRef]
- Snorradóttir, B.S.; Jónsdóttir, F.; Sigurdsson, S.T.; Thorsteinsson, F.; Másson, M. Numerical Modelling and Experimental Investigation of Drug Release from Layered Silicone Matrix Systems. Eur. J. Pharm. Sci. 2013, 49, 671–678. [Google Scholar] [CrossRef]
- Seidlitz, A.; Nagel, S.; Semmling, B.; Grabow, N.; Martin, H.; Senz, V.; Harder, C.; Sternberg, K.; Schmitz, K.-P.; Kroemer, H.K.; et al. Examination of Drug Release and Distribution from Drug-Eluting Stents with a Vessel-Simulating Flow-Through Cell. Eur. J. Pharm. Biopharm. 2011, 78, 36–48. [Google Scholar] [CrossRef]
- Beumers, P.; Masuch, K.; Pauls, C.; Bardow, A. Diffusionskoeffizienten in Hydrogelen Mittels 1D-Ramanspektroskopie. Chem. Ing. Tech. 2012, 84, 1289–1290. [Google Scholar] [CrossRef]
- París, R.; Barrales-Rienda, J.M.; Quijada-Garrido, I. Dynamic Swelling of Hydrogels Based on Random Terpolymers of N-isopropylacrylamide, Methacrylic Acid and Poly(ethylene glycol) Macromonomer. Polymer 2009, 50, 2065–2074. [Google Scholar] [CrossRef]
- Knörgen, M.; Arndt, K.-F.; Richter, S.; Kuckling, D.; Schneider, H. Investigation of Swelling and Diffusion in Polymers by 1H NMR Imaging: LCP Networks and Hydrogels. J. Mol. Struct. 2000, 554, 69–79. [Google Scholar] [CrossRef]
- Recillas, M.; Silva, L.L.; Peniche, C.; Goycoolea, F.M.; Rinaudo, M.; Argüelles-Monal, W.M. Thermoresponsive Behavior of Chitosan-g-N-Isopropylacrylamide Copolymer Solutions. Biomacromolecules 2009, 10, 1633–1641. [Google Scholar] [CrossRef]
- Kulinowski, P.; Dorożyński, P.; Jachowicz, R.; Węglarz, W.P. An Integrated System for Dissolution Studies and Magnetic Resonance Imaging of Controlled Release, Polymer-Based Dosage Forms—A Tool for Quantitative Assessment of Hydrogel Formation Processes. J. Pharm. Biomed. Anal. 2008, 48, 685–693. [Google Scholar] [CrossRef]
- Pinaud, J.; Vignolle, J.; Gnanou, Y.; Taton, D. Poly(N-heterocyclic-carbene)s and Their CO2Adducts as Recyclable Polymer-Supported Organocatalysts for Benzoin Condensation and Transesterification Reactions. Macromolecules 2011, 44, 1900–1908. [Google Scholar] [CrossRef]
- Marcilla, R.; Blazquez, J.A.; Rodriguez, J.; Pomposo, J.A.; Mecerreyes, D. Tuning the Solubility of Polymerized Ionic Liquids by Simple Anion-Exchange Reactions. J. Polym. Sci. Part A Polym. Chem. 2003, 42, 208–212. [Google Scholar] [CrossRef]
- Hu, B.; Wu, T.; Ding, K.; Zhou, X.; Jiang, T.; Han, B. Seeding Growth of Pd/Au Bimetallic Nanoparticles on Highly Cross-Linked Polymer Microspheres with Ionic Liquid and Solvent-Free Hydrogenation. J. Phys. Chem. C 2010, 114, 3396–3400. [Google Scholar] [CrossRef]
- Green, M.D.; La Cruz, D.S.-D.; Ye, Y.; Layman, J.M.; Elabd, Y.A.; Winey, K.I.; Long, T.E. Alkyl-Substituted N-Vinylimidazolium Polymerized Ionic Liquids: Thermal Properties and Ionic Conductivities. Macromol. Chem. Phys. 2011, 212, 2522–2528. [Google Scholar] [CrossRef]
- Bandomir, J.; Schulz, A.; Taguchi, S.; Schmitt, L.; Ohno, H.; Sternberg, K.; Schmitz, K.-P.; Kragl, U. Synthesis and Characterization of Polymerized Ionic Liquids: Mechanical and Thermal Properties of a Novel Type of Hydrogels. Macromol. Chem. Phys. 2014, 215, 716–724. [Google Scholar] [CrossRef]
- Karadağ, E.; Üzüm, Ö.B.; Saraydin, D. Water Uptake in Chemically Crosslinked Poly(acrylamide-co-crotonic acid) Hydrogels. Mater. Des. 2005, 26, 265–270. [Google Scholar] [CrossRef]
- Bajpai, S.; Johnson, S. Superabsorbent Hydrogels for Removal of Divalent Toxic Ions. Part I: Synthesis and Swelling Characterization. React. Funct. Polym. 2005, 62, 271–283. [Google Scholar] [CrossRef]
- George, K.A.; Wentrup-Byrne, E.; Hill, D.J.T.; Whittaker, A.K. Investigation into the Diffusion of Water into HEMA-co-MOEP Hydrogels. Biomacromolecules 2004, 5, 1194–1199. [Google Scholar] [CrossRef] [PubMed]
- Ende, M.T.; Peppas, N.A. Transport of Ionizable Drugs and Proteins in Crosslinked Poly(acrylic acid) and Poly(acry1ic acid-co-2-hydroxyethyl methacrylate) Hydrogels. Polymer Characterization. J. Appl. Polym. Sci. 1996, 59, 673–685. [Google Scholar] [CrossRef]
- Krüger, K.-M.; Sadowski, G. Fickian and Non-Fickian Sorption Kinetics of Toluene in Glassy Polystyrene. Macromolecules 2005, 38, 8408–8417. [Google Scholar] [CrossRef]
- Coulson, C.A.; Crank, J. The Mathematics of Diffusion. Math. Gaz. 1958, 42, 165. [Google Scholar] [CrossRef] [Green Version]
- Goycoolea, F.M.; Fernández-Valle, M.E.; Aranaz, I.; Heras, A. pH- and Temperature-Sensitive Chitosan Hydrogels: Swelling and MRI Studies. Macromol. Chem. Phys. 2011, 212, 887–895. [Google Scholar] [CrossRef]
- Marcus, Y. Thermodynamics of Solvation of Ions. Part 5.—Gibbs Free Energy of Hydration at 298.15 K. J. Chem. Soc. Faraday Trans. 1991, 87, 2995–2999. [Google Scholar] [CrossRef]
- Arndt, M.C.; Sadowski, G. Modeling Poly(N-isopropylacrylamide) Hydrogels in Water/Alcohol Mixtures with PC-SAFT. Macromolecules 2012, 45, 6686–6696. [Google Scholar] [CrossRef]
- Ganji, F.; Vasheghani-Farahani, S.; Vasheghani-Farahani, E. Theoretical Description of Hydrogel Swelling: A Review. Iran. Polym. J. 2010, 19, 375–398. [Google Scholar]
- Sanopoulou, M.; Petropoulos, J.H. Systematic Analysis and Model Interpretation of Micromolecular Non-Fickian Sorption Kinetics in Polymer Films. Macromolecules 2001, 34, 1400–1410. [Google Scholar] [CrossRef]
- Hill, D.J.; Whittaker, A.K. Zainuddin Water Diffusion into Radiation Crosslinked PVA–PVP Network Hydrogels. Radiat. Phys. Chem. 2011, 80, 213–218. [Google Scholar] [CrossRef]
- Karadağ, E.; Saraydin, D. Swelling Studies of Super Water Retainer Acrylamide/Crotonic Acid Hydrogels Crosslinked by Trimethylolpropane Triacrylate and 1,4-Butanediol Dimethacrylate. Polym. Bull. 2002, 48, 299–307. [Google Scholar] [CrossRef]
- Zhao, Z.; Li, Z.; Xia, Q.; Bajalis, E.; Xi, H.; Lin, Y. Swelling/Deswelling Kinetics of PNIPAAm Hydrogels Synthesized by Microwave Irradiation. Chem. Eng. J. 2008, 142, 263–270. [Google Scholar] [CrossRef]
- Holz, M.; Heil, S.R.; Sacco, A. Temperature-Dependent Self-Diffusion Coefficients of Water and Six Selected Molecular Liquids for Calibration in Accurate 1H NMR PFG Measurements. Phys. Chem. Chem. Phys. 2000, 2, 4740–4742. [Google Scholar] [CrossRef]
- Hurle, R.L.; Easteal, A.J.; Woolf, L.A. Self-Diffusion in Monohydric Alcohols under Pressure. Methanol, Methan(2H)ol and Ethanol. J. Chem. Soc. Faraday Trans. 1 Phys. Chem. Condens. Phases 1985, 81, 769–779. [Google Scholar] [CrossRef]
- Crank, J. A Theoretical Investigation of the Influence of Molecular Relaxation and Internal Stress on Diffusion in Polymers. J. Polym. Sci. 1953, 11, 151–168. [Google Scholar] [CrossRef]
- Sari, D.P.; Kristanto, S.A.; Wahyudi, R.E.; Dwihapsari, Y. Brain Tumor Consistency Assessment using Digital Penetrometer and Diffusion Weighted MRI. In Proceedings of the 3rd International Conference on Instrumentation, Communications, Information Technology and Biomedical Engineering (ICICI-BME), Bandung, Indonesia, 7–8 November 2013; IEEE Computer Society: Bandung, Indonesia, 2013; pp. 302–306. [Google Scholar]
- Thoeny, H.C.; De Keyzer, F. Extracranial Applications of Diffusion-Weighted Magnetic Resonance Imaging. Eur. Radiol. 2007, 17, 1385–1393. [Google Scholar] [CrossRef]




| Component | Crosslinker Content | ||
|---|---|---|---|
| 2 mol% | 3 mol% | 5 mol% | |
| IL monomer | 0.300 g VEImBr/0.341 g VBImBr/0.276 g VBImCl | ||
| Ultrapure water | 432 µL | 312 µL | 65 µL |
| MBAA solution (2% w/w) | 232 µL | 352 µL | 599 µL |
| APS solution (10% w/w) | 30 µL | ||
| TEMED | 6 µL | ||
| Hydrogel MBAA Amount | Solvent | Experimental Equilibrium Swelling Seq, exp ( ) | Theoretical Equilibrium Swelling Seq, theo ( ) | Initial Swelling Rate (min−1) | Swelling Rate Constant ks (min−1) |
|---|---|---|---|---|---|
| Poly(VEImBr) 2 mol% | Water | 23.44 ± 0.39 | 25.13 | 0.227 | 3.60 × 10−4 |
| EtOH | 7.45 ± 1.02 | 8.14 | 0.010 | 1.58 × 10−4 | |
| THF | −0.02 a | −0.02 | n.d. * | n.d. * | |
| n-Hep | 0.01 b | 0.01 | n.d. * | n.d. * | |
| Poly(VEImBr) 3 mol% | Water | 13.80 ± 0.25 | 14.39 | 0.227 | 1.10 × 10−3 |
| Poly(VEImBr) 5 mol% | Water | 8.00 ± 0.19 | 8.25 | 0.165 | 2.42 × 10−3 |
| EtOH | 2.56 ± 0.12 | 2.79 | 0.005 | 5.81 × 10−4 | |
| THF | −0.02 a | −0.02 | n.d. * | n.d. * | |
| n-Hep | 0.01 b | 0.01 | n.d. * | n.d. * | |
| Poly(VBImBr) 2 mol% | Water | 25.16 ± 0.41 | 27.70 | 0.178 | 2.32 × 10−4 |
| EtOH | 10.61 ± 0.62 | 11.67 | 0.021 | 1.53 × 10−4 | |
| THF | −0.01 a | −0.01 | n.d. * | n.d. * | |
| Poly(VBImCl) 2 mol% | Water | 29.02 ± 0.39 | 31.15 | 0.277 | 2.86 × 10−4 |
| EtOH | 13.51 ± 0.40 | 14.62 | 0.039 | 1.80 × 10−4 | |
| THF | −0.01 a | −0.01 | n.d. * | n.d. * |
| Hydrogel | MBAA Amount | Equilibrium Termination | Equilibrium Water Contents (EWC) |
|---|---|---|---|
| Poly(VEImBr) | 2% | 420 min | 0.959 ± 0.001 |
| 3% | 360 min | 0.932 ± 0.001 | |
| 5% | 240 min | 0.889 ± 0.003 | |
| Poly(VBImBr) | 2% | 420 min | 0.962 ± 0.001 |
| Poly(VBImCl) | 2% | 420 min | 0.967 ± 0.001 |
| Solvent | Diffusion Parameter | Poly(VEImBr) 2 mol% | Poly(VEImBr) 5 mol% | Poly(VBImBr) 2 mol% | Poly(VBImCl) 2 mol% |
|---|---|---|---|---|---|
| Water | n | 0.800 | 0.668 | 0.837 | 0.830 |
| D × 1010 (m2 s−1) | 6.70 ± 0.85 | 6.95 ± 0.40 | 6.67 ± 1.15 | 7.65 ± 0.92 | |
| EtOH | N | 0.398 | 0.572 | 0.609 | 0.634 |
| D × 1010 (m2 s−1) | 0.37 ± 0.11 | 0.62 ± 0.23 | 0.61 ± 0.23 | 1.07 ± 0.09 |
| Hydrogel | MBAA Amount | Diffusion Coefficient D × 1010 (m2 s−1) at Different Water RH | ||
|---|---|---|---|---|
| 25% | 50% | 75% | ||
| Poly(VEImBr) | 2 mol% | 0.130 | 0.560 | 0.553 |
| 5 mol% | 0.110 | 0.322 | 0.262 | |
| Poly(VBImBr) | 2 mol% | 0.113 | 0.236 | 0.195 |
| Poly(VBImCl) | 2 mol% | 0.035 | 0.144 | 0.097 |
| Solvent | Method * | (Apparent) Diffusion Coefficient D/ADC × 1010 (m2 s−1) For | |||
|---|---|---|---|---|---|
| Poly(VEImBr) 2 mol% | Poly(VEImBr) 5 mol% | Poly(VBImBr) 2 mol% | Poly(VBImCl) 2 mol% | ||
| H2O | 1 | 6.70 ± 0.85 | 6.95 ± 0.40 | 6.67 ± 1.15 | 7.65 ± 0.92 |
| 2 | 0.553 | 0.262 | 0.195 | 0.097 | |
| 3 | 16.58 ± 0.59 | 15.90 ± 0.53 | 16.30 ± 0.47 | 15.80 ± 0.55 | |
| EtOH | 1 | 0.37 ± 0.11 | 0.62 ± 0.23 | 0.61 ± 0.23 | 1.07 ± 0.09 |
| 2 | 0.035 | 0.025 | 0.136 | 0.708 | |
| 3 | 6.51 ± 0.23 | 7.08 ± 0.62 | 6.65 ± 0.47 | 6.63 ± 0.25 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jastram, A.; Lindner, T.; Luebbert, C.; Sadowski, G.; Kragl, U. Swelling and Diffusion in Polymerized Ionic Liquids-Based Hydrogels. Polymers 2021, 13, 1834. https://doi.org/10.3390/polym13111834
Jastram A, Lindner T, Luebbert C, Sadowski G, Kragl U. Swelling and Diffusion in Polymerized Ionic Liquids-Based Hydrogels. Polymers. 2021; 13(11):1834. https://doi.org/10.3390/polym13111834
Chicago/Turabian StyleJastram, Ann, Tobias Lindner, Christian Luebbert, Gabriele Sadowski, and Udo Kragl. 2021. "Swelling and Diffusion in Polymerized Ionic Liquids-Based Hydrogels" Polymers 13, no. 11: 1834. https://doi.org/10.3390/polym13111834
APA StyleJastram, A., Lindner, T., Luebbert, C., Sadowski, G., & Kragl, U. (2021). Swelling and Diffusion in Polymerized Ionic Liquids-Based Hydrogels. Polymers, 13(11), 1834. https://doi.org/10.3390/polym13111834