Calorimetric and Dielectric Investigations of Epoxy-Based Nanocomposites with Halloysite Nanotubes as Nanofillers
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.2.1. Transmission Electron Microscopy (TEM)
2.2.2. Small- and Wide-Angle X-ray Scattering (SAXS and WAXS)
2.2.3. WAXS: Linear Combination of the Data for the Pure Epoxy and the Nanofiller
2.2.4. SAXS Pattern Simulations from 3D Objects
2.2.5. Differential Scanning Calorimetry (DSC)
2.2.6. Temperature Modulated DSC (TMDSC)
2.2.7. Fast Scanning Calorimetry (FSC)
2.2.8. Temperature Modulated FSC (TMFSC)
2.2.9. Broadband Dielectric Spectroscopy (BDS)
3. Results and Discussion
3.1. Epoxy Nanocomposite with Halloysite Nanotubes (Ep/HNT)
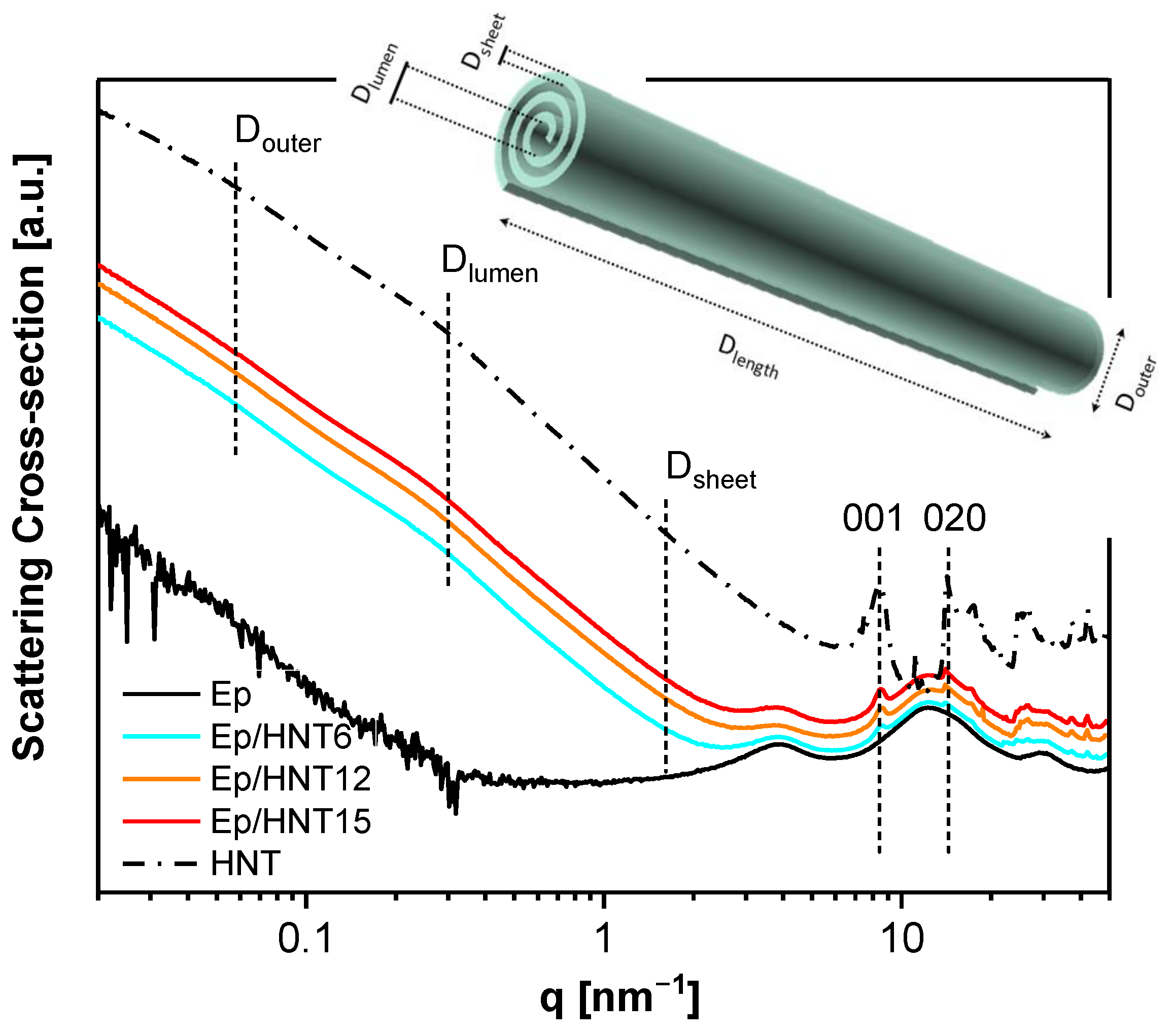
3.1.1. X-ray Scattering
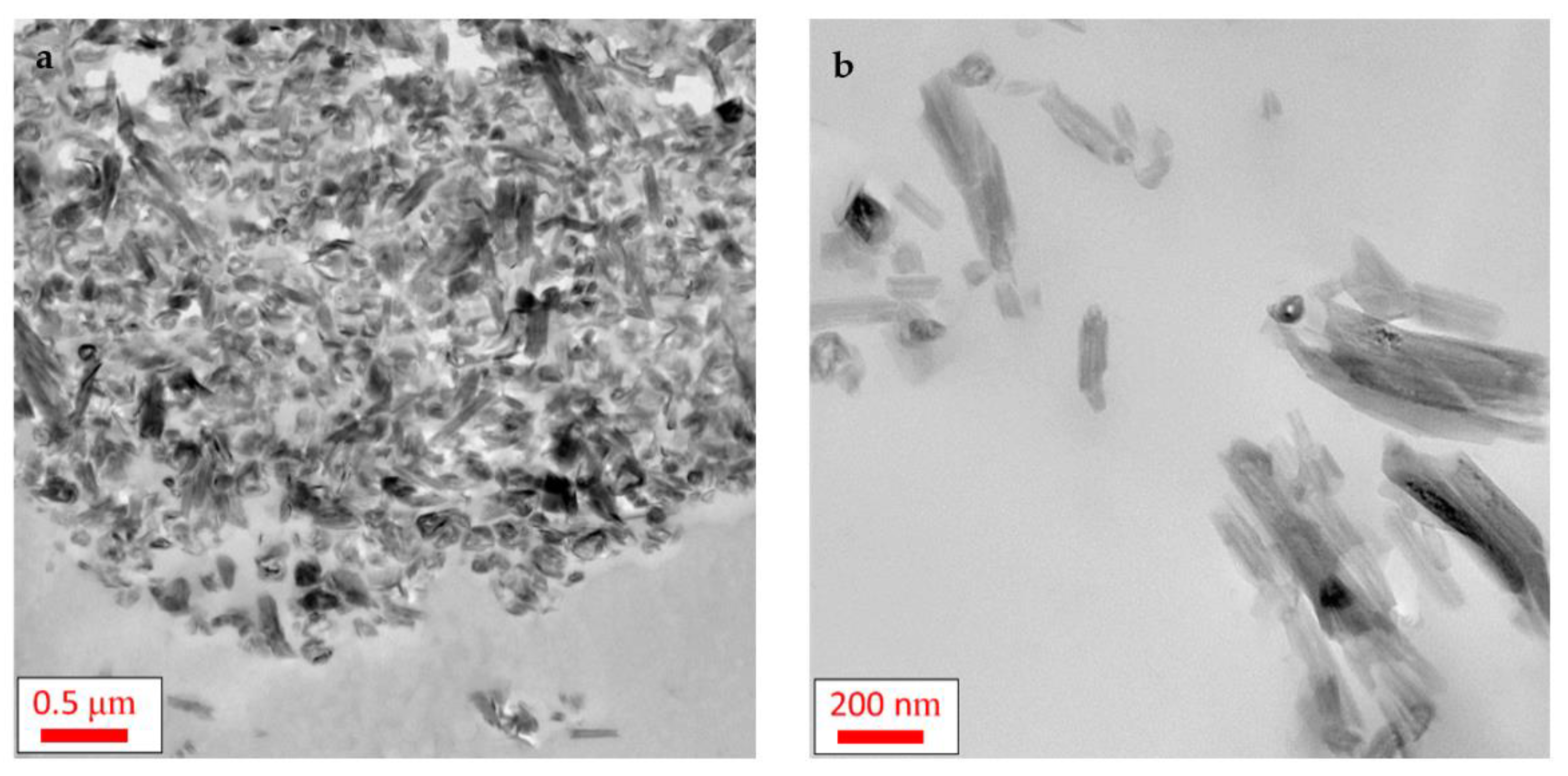
3.1.2. TEM
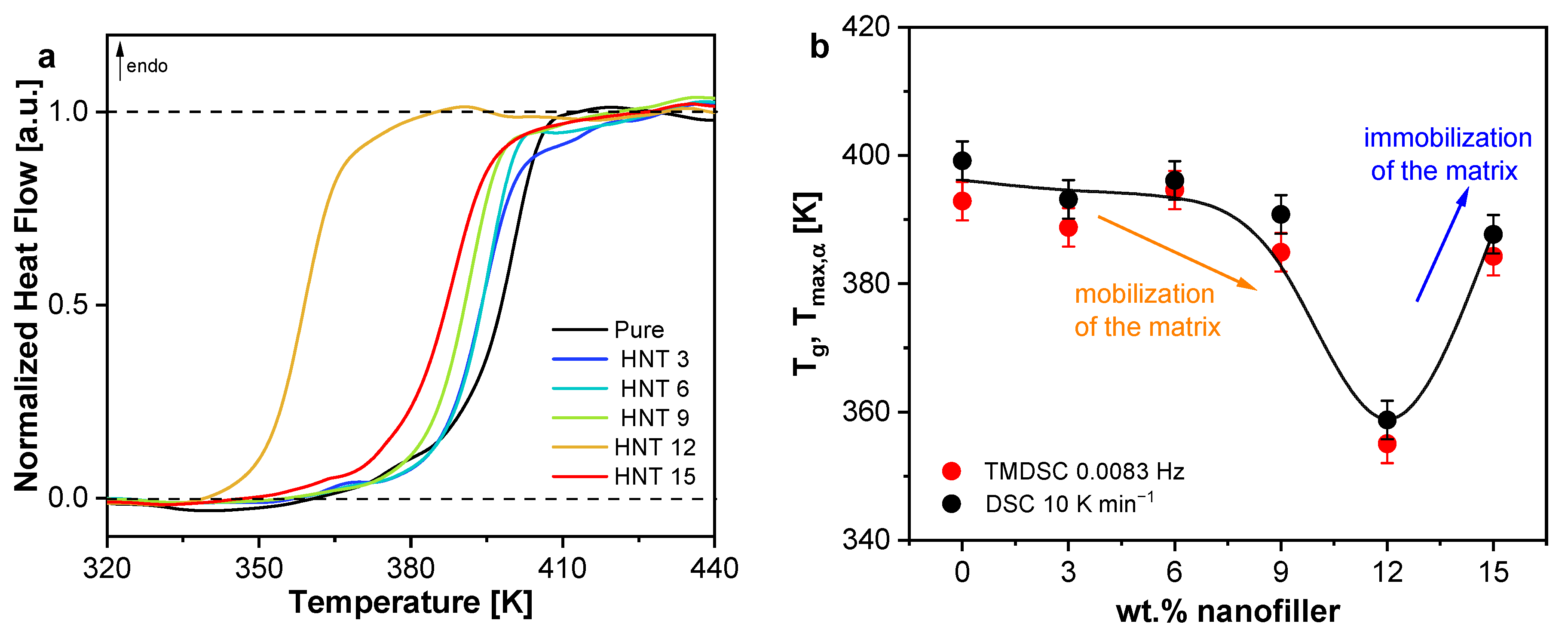
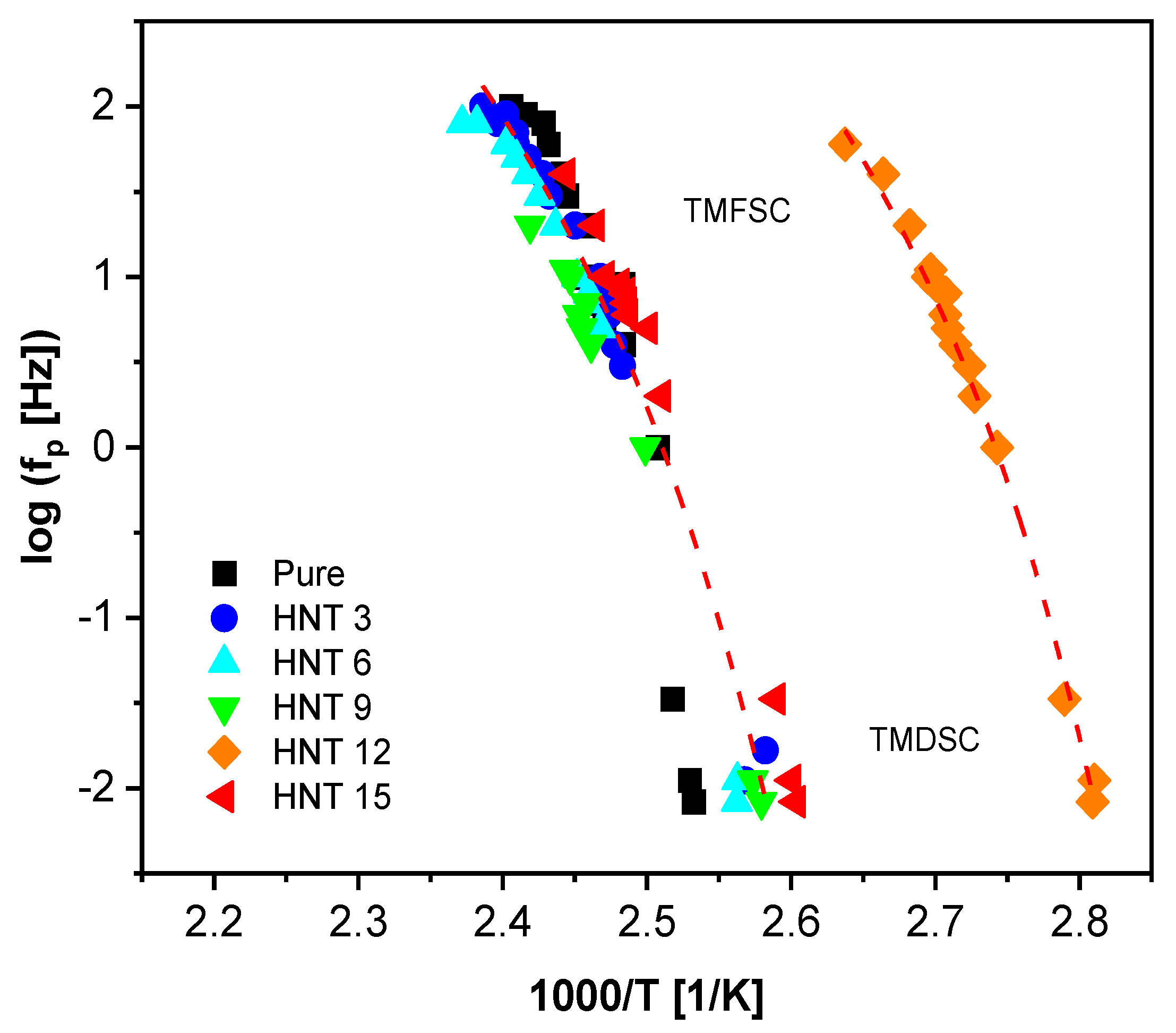
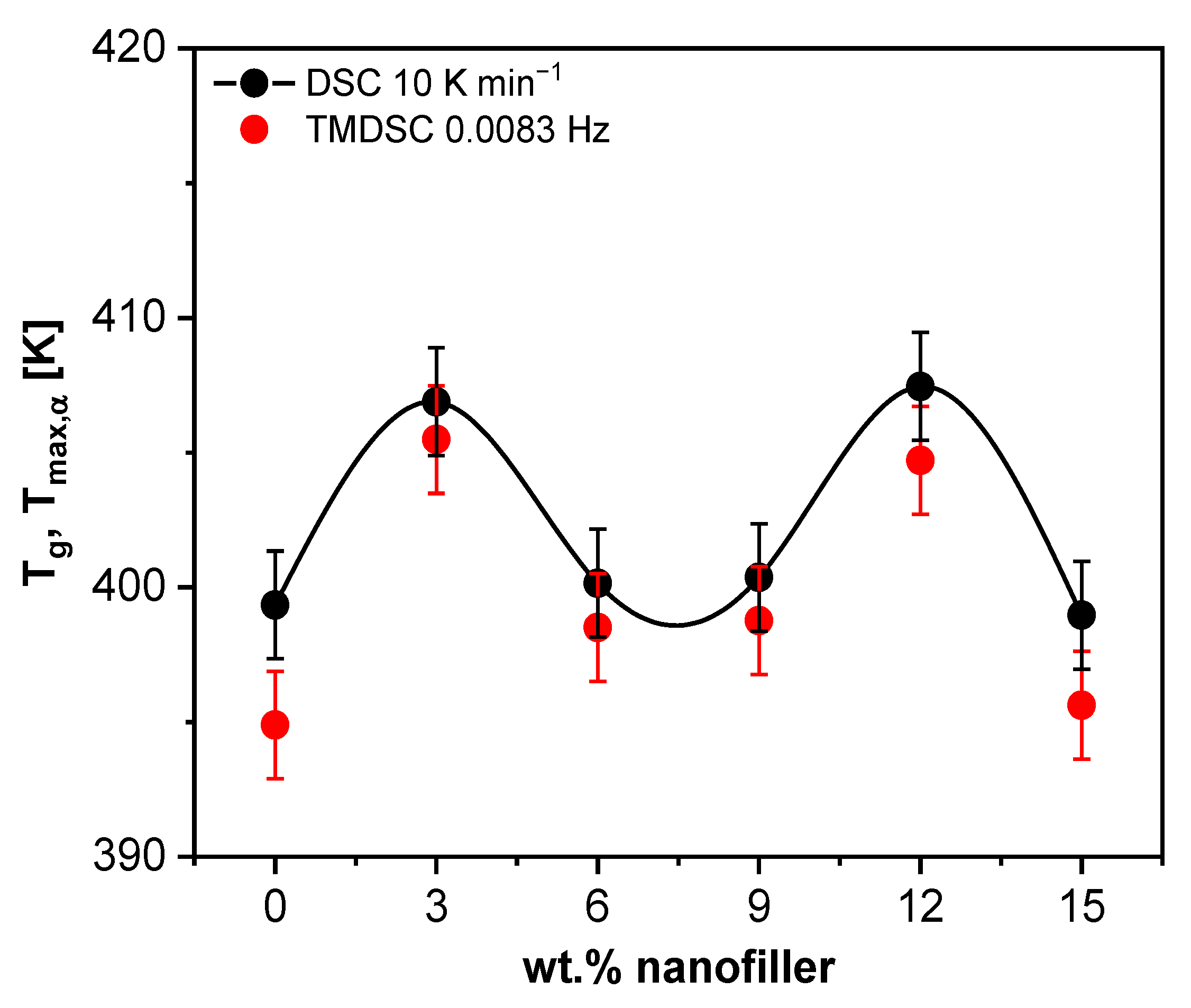
3.1.3. Calorimetry
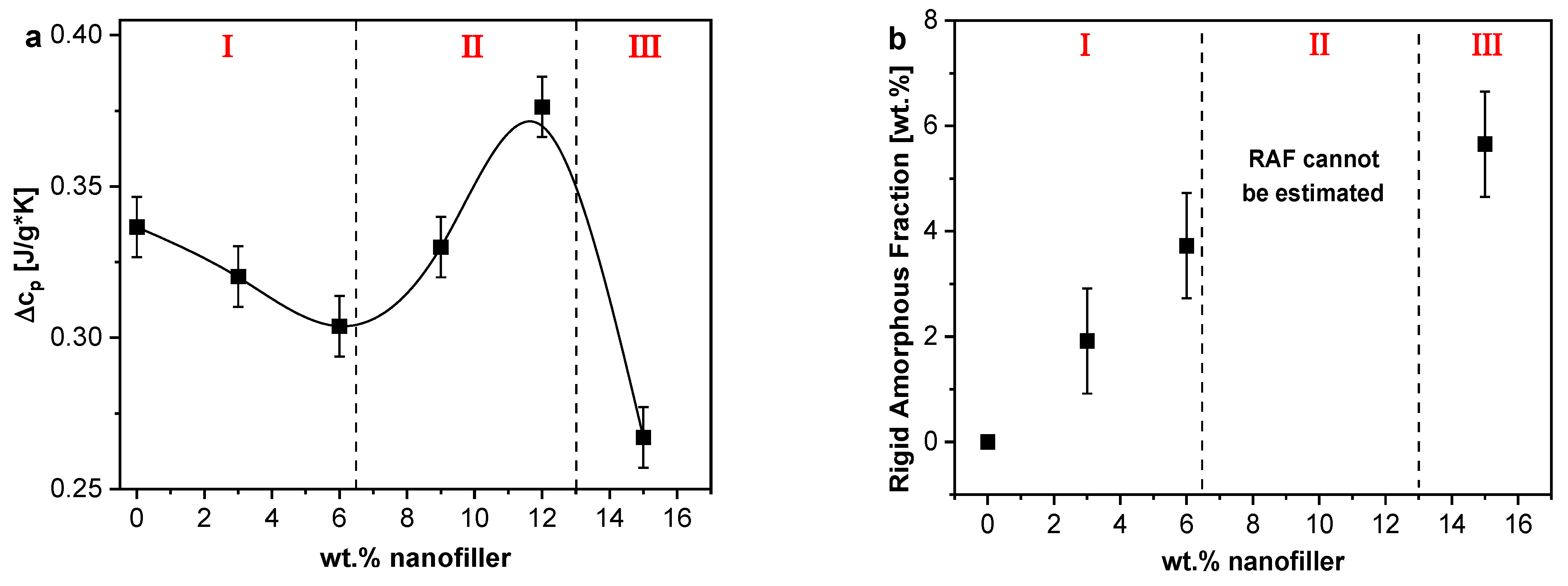
3.1.4. Specific Heat Spectroscopy
Interfacial Properties
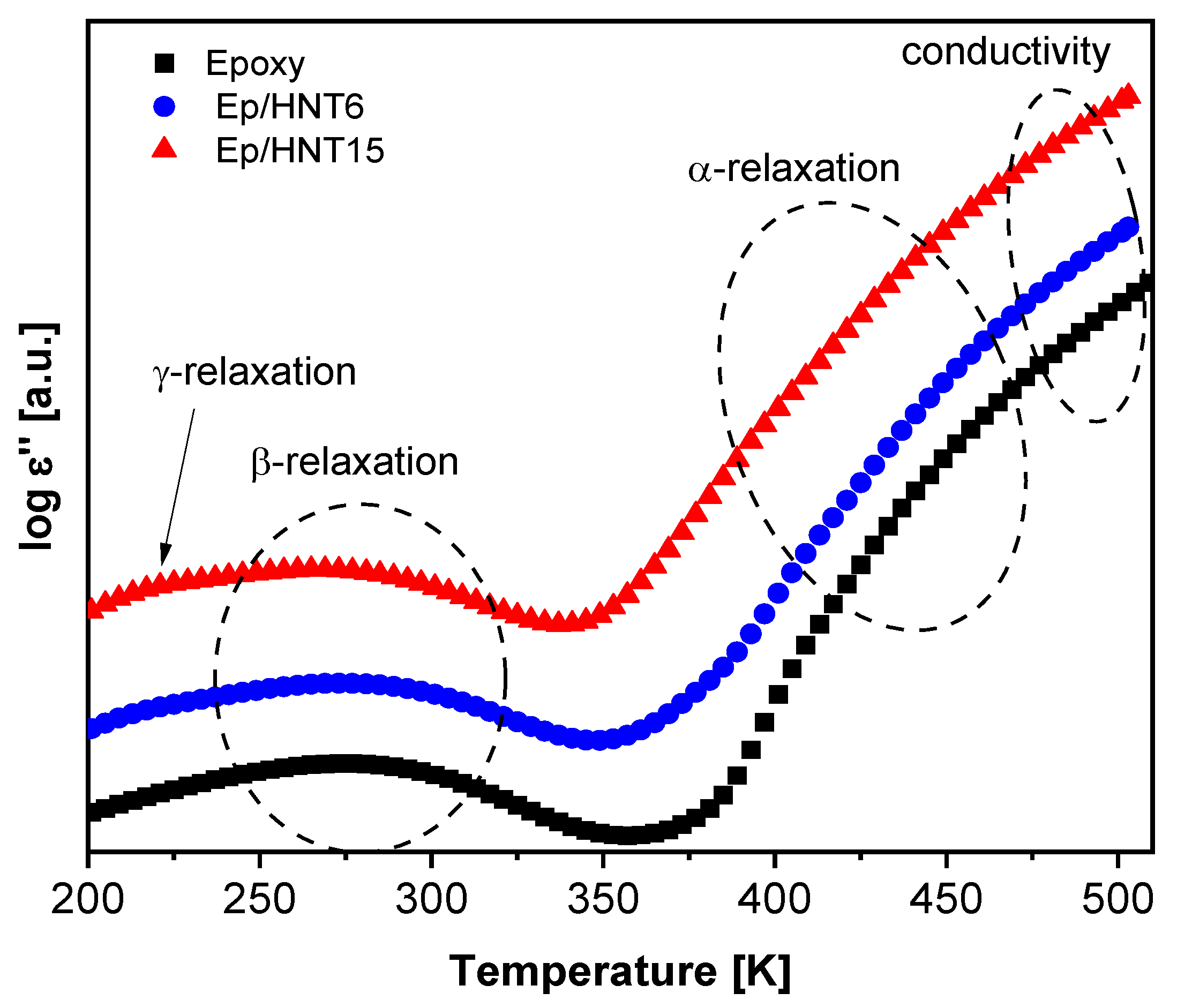
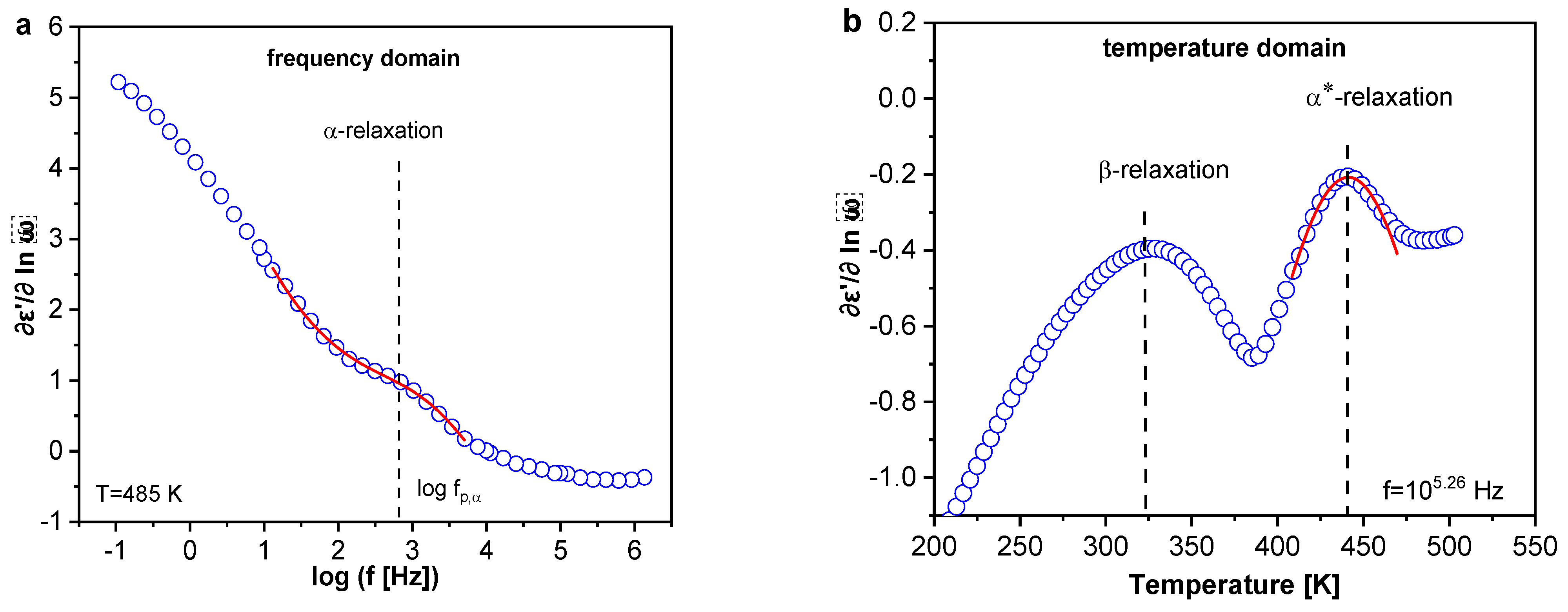
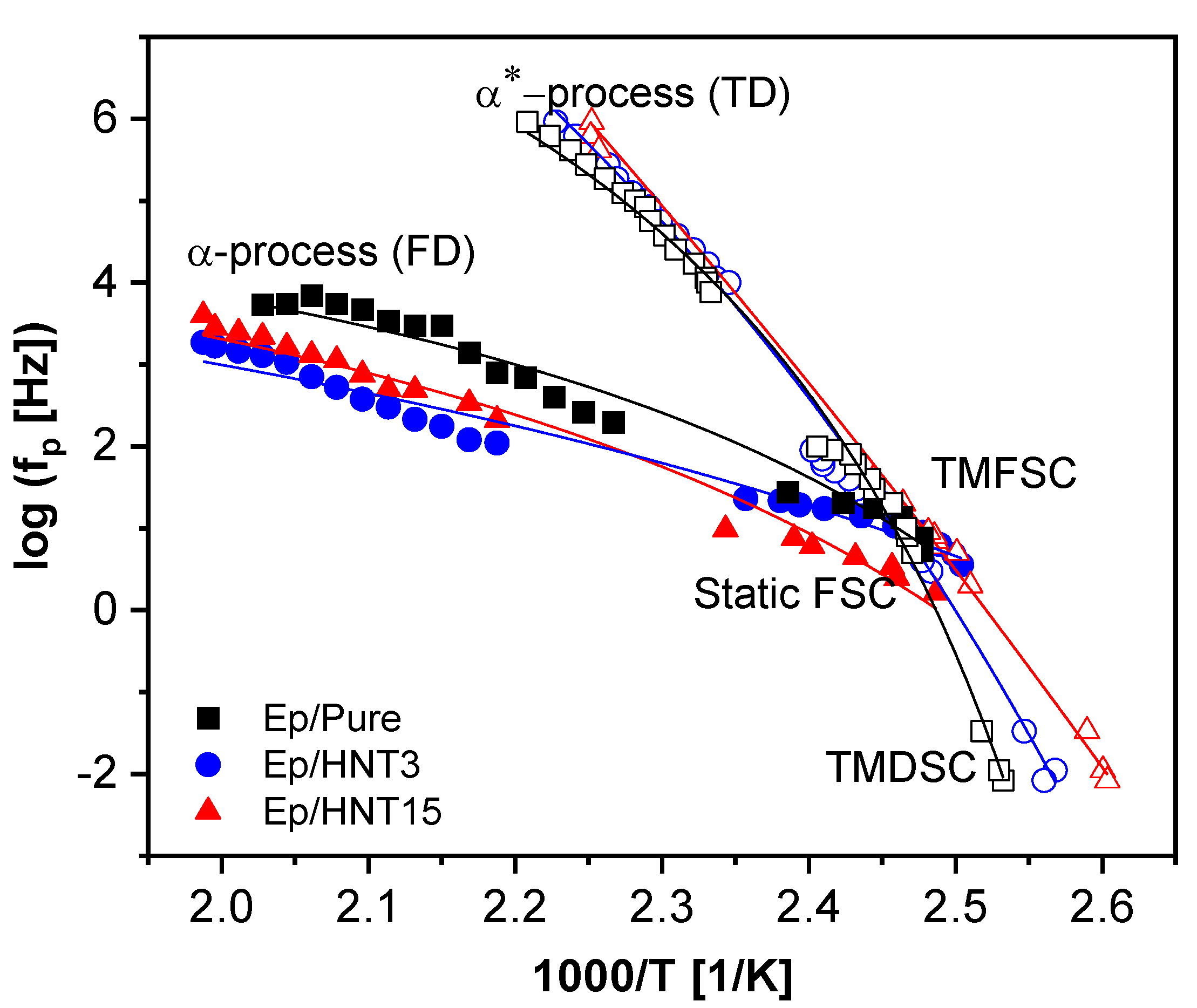
3.1.5. Broadband Dielectric Spectroscopy
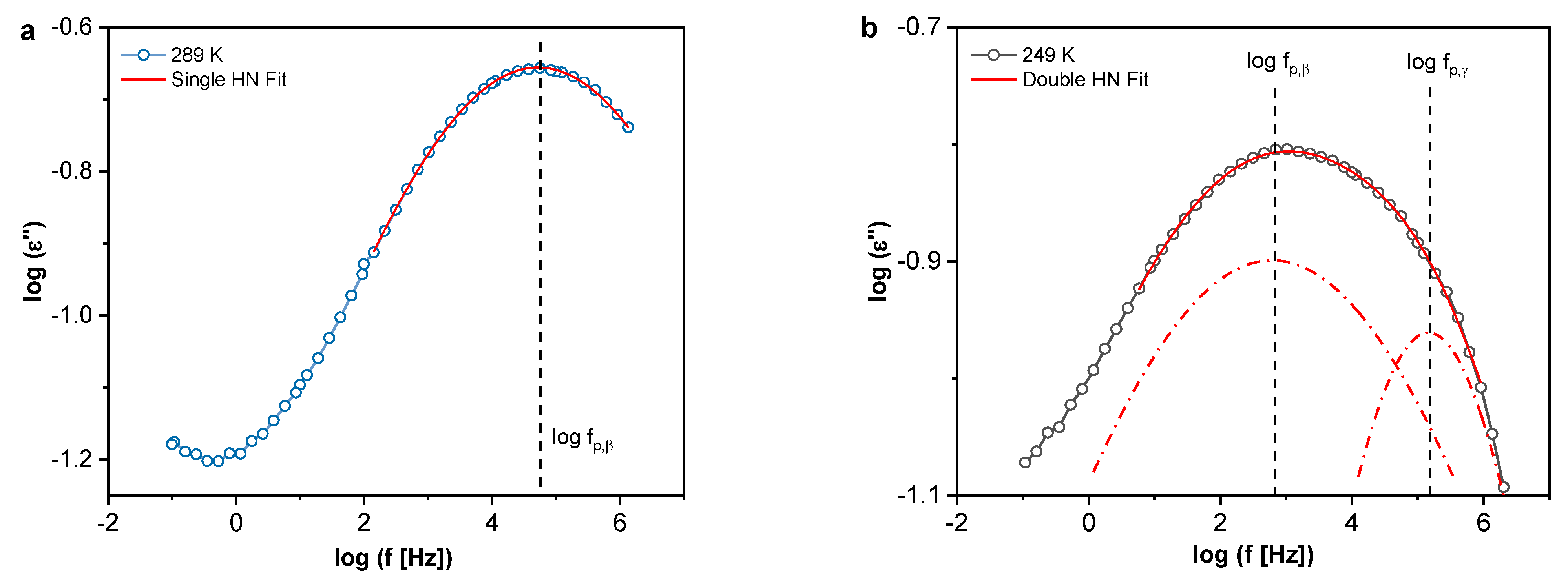
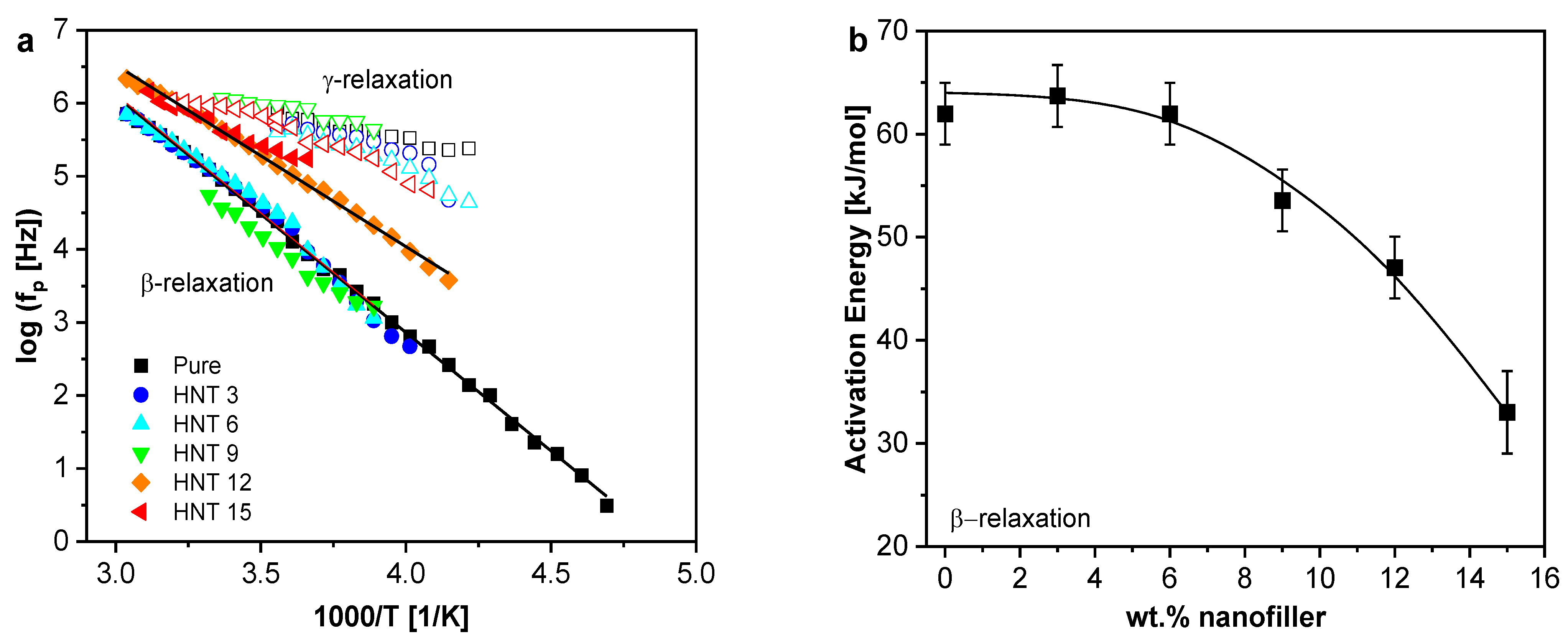
Localized Molecular Fluctuations
Segmental Dynamics
3.2. Epoxy Nanocomposite with Modified Halloysite Nanotubes (Ep/m-HNT)
3.2.1. X-ray Scattering
3.2.2. TEM
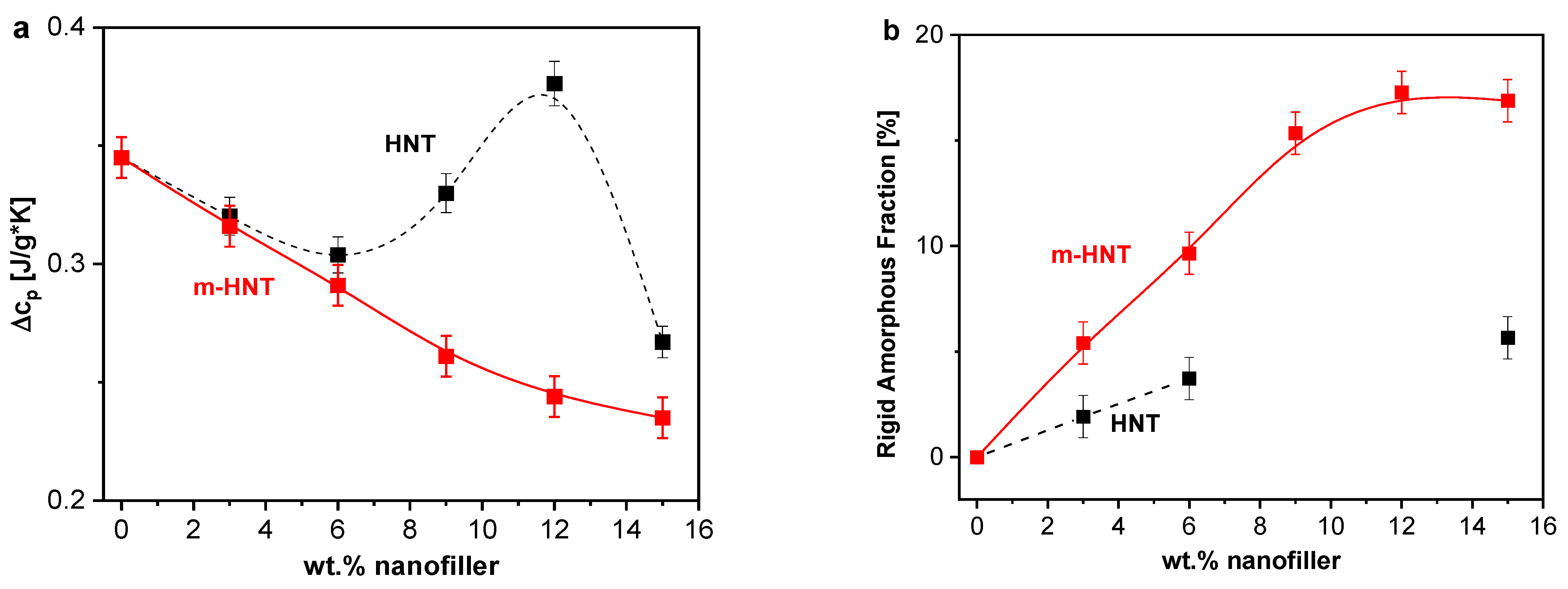
3.2.3. Calorimetry
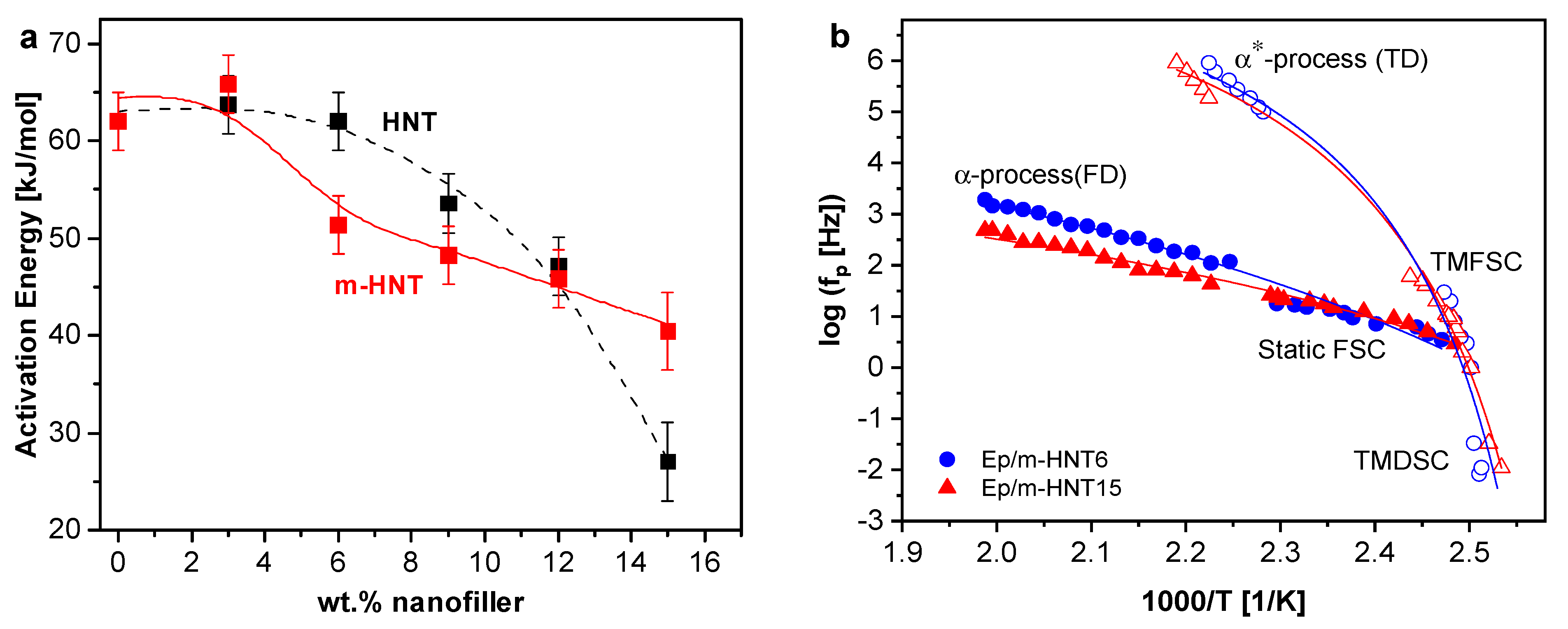
3.2.4. Specific Heat Spectroscopy
Interfacial Properties
Segmental Dynamics
3.2.5. Broadband Dielectric Spectroscopy
Localized Molecular Fluctuations
Segmental Dynamics
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Mittal, V. Polymer Nanocomposites: Synthesis, Microstructure, and Properties. In Optimization of Polymer Nanocomposite Properties; Mittal, V., Ed.; Wiley-VCH Verlag GmbH & Co. KgaA: Weinheim, Germany, 2010; p. 1. ISBN 978-3-52762-927-5. [Google Scholar]
- Dantas de Oliveira, A.; Augusto Gonçalves Beatrice, C. Polymer Nanocomposites with Different Types of Nanofiller. In Nanocomposites-Recent Evolutions; Sivasankaran, S., Ed.; IntechOpen: London, UK, 2019; p. 26. ISBN 978-1-78985-012-3. [Google Scholar]
- Müller, K.; Bugnicourt, E.; Latorre, M.; Jorda, M.; Echegoyen Sanz, Y.; Lagaron, J.M.; Miesbauer, O.; Bianchin, A.; Hankin, S.; Bölz, U.; et al. Review on the Processing and Properties of Polymer Nanocomposites and Nanocoatings and Their Applications in the Packaging, Automotive and Solar Energy Fields. Nanomaterials 2017, 7, 74. [Google Scholar] [CrossRef]
- Bailey, E.J.; Winey, K.I. Dynamics of polymer segments, polymer chains, and nanoparticles in polymer nanocomposite melts: A review. Prog. Polym. Sci. 2020, 105, 101242. [Google Scholar] [CrossRef]
- Kumar, S.K.; Benicewicz, B.C.; Vaia, R.A.; Winey, K.I. 50th Anniversary Perspective: Are Polymer Nanocomposites Practical for Applications? Macromolecules 2017, 50, 714–731. [Google Scholar] [CrossRef]
- Šupová, M.; Simha Martynková, G.; Cech Barabaszova, K. Effect of Nanofillers Dispersion in Polymer Matrices: A Review. Sci. Adv. Mater. 2010, 3, 1–25. [Google Scholar] [CrossRef]
- Deng, S.; Zhang, J.; Ye, L. Halloysite–epoxy nanocomposites with improved particle dispersion through ball mill homogenisation and chemical treatments. Compos. Sci. Technol. 2009, 69, 2497–2505. [Google Scholar] [CrossRef]
- Jana, S.C.; Jain, S. Dispersion of nanofillers in high performance polymers using reactive solvents as processing aids. Polymer 2001, 42, 6897–6905. [Google Scholar] [CrossRef]
- Zare, Y. Study of nanoparticles aggregation/agglomeration in polymer particulate nanocomposites by mechanical properties. Compos. Part A Appl. Sci. Manuf. 2016, 84, 158–164. [Google Scholar] [CrossRef]
- Dorigato, A.; Dzenis, Y.; Pegoretti, A. Filler aggregation as a reinforcement mechanism in polymer nanocomposites. Mech. Mater. 2013, 61, 79–90. [Google Scholar] [CrossRef]
- Szymoniak, P.; Qu, X.; Abbasi, M.; Pauw, B.R.; Henning, S.; Li, Z.; Wang, D.-Y.; Schick, C.; Saalwächter, K.; Schönhals, A. Spatial inhomogeneity, interfaces and complex vitrification kinetics in a network forming nanocomposite. Soft Matter 2021, 17, 2775–2790. [Google Scholar] [CrossRef] [PubMed]
- Koutsoumpis, S.; Raftopoulos, K.N.; Oguz, O.; Papadakis, C.M.; Menceloglu, Y.Z.; Pissis, P. Dynamic glass transition of the rigid amorphous fraction in polyurethane-urea/SiO2 nanocomposites. Soft Matter 2017, 13, 4580–4590. [Google Scholar] [CrossRef] [PubMed]
- Purohit, P.J.; Wang, D.-Y.; Wurm, A.; Schick, C.; Schönhals, A. Comparison of thermal and dielectric spectroscopy for nanocomposites based on polypropylene and Layered Double Hydroxide–Proof of interfaces. Eur. Polym. J. 2014, 55, 48–56. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Pissis, P. Glass transition and segmental dynamics in poly(dimethylsiloxane)/silica nanocomposites studied by various techniques. J. Non. Cryst. Solids 2007, 353, 4344–4352. [Google Scholar] [CrossRef]
- Yin, H.; Schönhals, A. Broadband Dielectric Spectroscopy on Polymer Blends. In Polymer Blends Handbook; Utracki, L.A., Wilkie, C.A., Eds.; Springer: Dordrecht, The Netherlands, 2014; pp. 1299–1356. ISBN 978-94-007-6064-6. [Google Scholar]
- Koshy, O.; Subramanian, L.; Thomas, S. Differential Scanning Calorimetry in Nanoscience and Nanotechnology. In Thermal and Rheological Measurement Techniques for Nanomaterials Characterization; Thomas, S., Thomas, R., Zachariah, A.K., Mishra, R.K., Eds.; Micro and Nano Technologies; Elsevier: Amsterdam, The Netherlands, 2017; pp. 109–122. ISBN 978-0-323-46139-9. [Google Scholar]
- Mathot, V.; Pyda, M.; Pijpers, T.; Vanden Poel, G.; van de Kerkhof, E.; van Herwaarden, S.; van Herwaarden, F.; Leenaers, A. The Flash DSC 1, a power compensation twin-type, chip-based fast scanning calorimeter (FSC): First findings on polymers. Thermochim. Acta 2011, 522, 36–45. [Google Scholar] [CrossRef]
- Schick, C. Chapter 16-Temperature modulated differential scanning calorimetry (TMDSC)–basics and applications to polymers. In Handbook of Thermal Analysis and Calorimetry. Volume 3: Applications to Polymers and Plastics; Cheng, S.Z.D., Ed.; Handbook of Thermal Analysis and Calorimetry; Elsevier Science B.V.: Amsterdam, The Netherlands, 2002; Volume 3, pp. 713–810. [Google Scholar]
- Thermal Analysis of Polymeric Materials, 1st ed.Springer-Verlag: Berlin/Heidelberg, Germany, 2005; ISBN 978-3-540-23629-0.
- Piscitelli, F.; Lavorgna, M.; Buonocore, G.G.; Verdolotti, L.; Galy, J.; Mascia, L. Plasticizing and Reinforcing Features of Siloxane Domains in Amine-Cured Epoxy/Silica Hybrids. Macromol. Mater. Eng. 2013, 298, 896–909. [Google Scholar] [CrossRef]
- Gu, H.; Ma, C.; Gu, J.; Guo, J.; Yan, X.; Huang, J.; Zhang, Q.; Guo, Z. An overview of multifunctional epoxy nanocomposites. J. Mater. Chem. C 2016, 4, 5890–5906. [Google Scholar] [CrossRef]
- Wetzel, B.; Rosso, P.; Haupert, F.; Friedrich, K. Epoxy nanocomposites–fracture and toughening mechanisms. Eng. Fract. Mech. 2006, 73, 2375–2398. [Google Scholar] [CrossRef]
- Saba, N.; Jawaid, M.; Alothman, O.Y.; Paridah, M.T.; Hassan, A. Recent advances in epoxy resin, natural fiber-reinforced epoxy composites and their applications. J. Reinf. Plast. Compos. 2016, 35, 447–470. [Google Scholar] [CrossRef]
- Yao, H.-Y.; Lin, Y.-W.; Chang, T.-H. Dielectric Properties of BaTiO3–Epoxy Nanocomposites in the Microwave Regime. Polymers 2021, 13, 1391. [Google Scholar] [CrossRef]
- Chen, C.; Justice, R.S.; Schaefer, D.W.; Baur, J.W. Highly dispersed nanosilica–epoxy resins with enhanced mechanical properties. Polymer 2008, 49, 3805–3815. [Google Scholar] [CrossRef]
- Ghasem Zadeh Khorasani, M.; Silbernagl, D.; Szymoniak, P.; Hodoroaba, V.-D.; Sturm, H. The effect of boehmite nanoparticles (γ-AlOOH) on nanomechanical and thermomechanical properties correlated to crosslinking density of epoxy. Polymer 2019, 164, 174–182. [Google Scholar] [CrossRef]
- Szymoniak, P.; Pauw, B.R.; Qu, X.; Schönhals, A. Competition of nanoparticle-induced mobilization and immobilization effects on segmental dynamics of an epoxy-based nanocomposite. Soft Matter 2020, 16, 5406–5421. [Google Scholar] [CrossRef] [PubMed]
- Szymoniak, P.; Li, Z.; Wang, D.-Y.; Schönhals, A. Dielectric and flash DSC investigations on an epoxy based nanocomposite system with MgAl layered double hydroxide as nanofiller. Thermochim. Acta 2019, 677, 151–161. [Google Scholar] [CrossRef]
- Ramirez, C.; Rico, M.; Torres, A.; Barral, L.; Lopez, J.; Montenero, B. Epoxy/POSS organic–inorganic hybrids: ATR-FTIR and DSC studies. Eur. Polym. J. 2008, 44, 3035–3045. [Google Scholar] [CrossRef]
- Han, X.; Zhang, X.; Guo, Y.; Liu, X.; Zhao, X.; Zhou, H.; Zhang, S.; Zhao, T. Synergistic Effects of Ladder and Cage Structured Phosphorus-Containing POSS with Tetrabutyl Titanate on Flame Retardancy of Vinyl Epoxy Resins. Polymers 2021, 13, 1363. [Google Scholar] [CrossRef] [PubMed]
- Shen, J.; Huang, W.; Wu, L.; Hu, Y.; Ye, M. Thermo-physical properties of epoxy nanocomposites reinforced with amino-functionalized multi-walled carbon nanotubes. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1331–1336. [Google Scholar] [CrossRef]
- Irzhak, V.I.; Dzhardimalieva, G.I.; Uflyand, I.E. Structure and properties of epoxy polymer nanocomposites reinforced with carbon nanotubes. J. Polym. Res. 2019, 26, 220. [Google Scholar] [CrossRef]
- Cividanes, L.S.; Simonetti, E.A.N.; Moraes, M.B.; Fernandes, F.W.; Thim, G.P. Influence of carbon nanotubes on epoxy resin cure reaction using different techniques: A comprehensive review. Polym. Eng. Sci. 2014, 54, 2461–2469. [Google Scholar] [CrossRef]
- Yuan, P.; Tan, D.; Annabi-Bergaya, F. Properties and applications of halloysite nanotubes: Recent research advances and future prospects. Appl. Clay Sci. 2015, 112–113, 75–93. [Google Scholar] [CrossRef]
- Du, M.; Guo, B.; Jia, D. Thermal stability and flame retardant effects of halloysite nanotubes on poly(propylene). Eur. Polym. J. 2006, 42, 1362–1369. [Google Scholar] [CrossRef]
- Li, Z.; Liu, L.; Jiménez González, A.; Wang, D.-Y. Bioinspired polydopamine-induced assembly of ultrafine Fe(OH)3 nanoparticles on halloysite toward highly efficient fire retardancy of epoxy resin via an action of interfacial catalysis. Polym. Chem. 2017, 8, 3926–3936. [Google Scholar] [CrossRef]
- Ye, Y.; Chen, H.; Wu, J.; Ye, L. High impact strength epoxy nanocomposites with natural nanotubes. Polymer 2007, 48, 6426–6433. [Google Scholar] [CrossRef]
- Lvov, Y.; Abdullayev, E. Functional polymer–clay nanotube composites with sustained release of chemical agents. Prog. Polym. Sci. 2013, 38, 1690–1719. [Google Scholar] [CrossRef]
- Vijayan, P.P.; Hany El-Gawady, Y.M.; Al-Maadeed, M.A.S.A. Halloysite Nanotube as Multifunctional Component in Epoxy Protective Coating. Ind. Eng. Chem. Res. 2016, 55, 11186–11192. [Google Scholar] [CrossRef]
- Deng, S.; Zhang, J.; Ye, L.; Wu, J. Toughening epoxies with halloysite nanotubes. Polymer 2008, 49, 5119–5127. [Google Scholar] [CrossRef]
- Liu, M.; Guo, B.; Du, M.; Cai, X.; Jia, D. Properties of halloysite nanotube–epoxy resin hybrids and the interfacial reactions in the systems. Nanotechnology 2007, 18, 455703. [Google Scholar] [CrossRef]
- Ravichandran, G.; Rathnakar, G.; Santhosh, N.; Chennakeshava, R.; Hashmi, M.A. Enhancement of mechanical properties of epoxy/halloysite nanotube (HNT) nanocomposites. SN Appl. Sci. 2019, 1. [Google Scholar] [CrossRef]
- Akbari, V.; Jouyandeh, M.; Paran, S.M.R.; Ganjali, M.R.; Abdollahi, H.; Vahabi, H.; Ahmadi, Z.; Formela, K.; Esmaeili, A.; Mohaddespour, A.; et al. Effect of Surface Treatment of Halloysite Nanotubes (HNTs) on the Kinetics of Epoxy Resin Cure with Amines. Polymers 2020, 12, 930. [Google Scholar] [CrossRef]
- Liu, M.; Jia, Z.; Jia, D.; Zhou, C. Recent advance in research on halloysite nanotubes-polymer nanocomposite. Prog. Polym. Sci. 2014, 39, 1498–1525. [Google Scholar] [CrossRef]
- Lee, H.; Dellatore, S.M.; Miller, W.M.; Messersmith, P.B. Mussel-Inspired Surface Chemistry for Multifunctional Coatings. Science 2007, 318, 426–430. [Google Scholar] [CrossRef]
- Barclay, T.G.; Hegab, H.M.; Clarke, S.R.; Ginic-Markovic, M. Versatile Surface Modification Using Polydopamine and Related Polycatecholamines: Chemistry, Structure, and Applications. Adv. Mater. Interfaces 2017, 4, 1601192. [Google Scholar] [CrossRef]
- Du, M.; Guo, B.; Jia, D. Newly emerging applications of halloysite nanotubes: A review. Polym. Int. 2010, 59, 574–582. [Google Scholar] [CrossRef]
- Phantom Plastics Halloysite Clay Nanotubes. Available online: https://phantomplastics.com/functional-fillers/halloysite/ (accessed on 30 March 2021).
- Filik, J.; Ashton, A.W.; Chang, P.C.Y.; Chater, P.A.; Day, S.J.; Drakopoulos, M.; Gerring, M.W.; Hart, M.L.; Magdysyuk, O.V.; Michalik, S.; et al. Processing two-dimensional X-ray diffraction and small-angle scattering data in DAWN 2. J. Appl. Crystallogr. 2017, 50, 959–966. [Google Scholar] [CrossRef]
- Bressler, I.; Pauw, B.R.; Thünemann, A.F. McSAS: Software for the retrieval of model parameter distributions from scattering patterns. J. Appl. Crystallogr. 2015, 48, 962–969. [Google Scholar] [CrossRef]
- Aratsu, K.; Takeya, R.; Pauw, B.R.; Hollamby, M.J.; Kitamoto, Y.; Shimizu, N.; Takagi, H.; Haruki, R.; Adachi, S.; Yagai, S. Supramolecular copolymerization driven by integrative self-sorting of hydrogen-bonded rosettes. Nat. Commun. 2020, 11, 1623. [Google Scholar] [CrossRef] [PubMed]
- Ma, W.; Wu, H.; Higaki, Y.; Takahara, A. Halloysite Nanotubes: Green Nanomaterial for Functional Organic-Inorganic Nanohybrids. Chem. Rec. 2018, 18, 986–999. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H. Selective modification of inner surface of halloysite nanotubes: A review. Nanotechnol. Rev. 2017, 6, 573–581. [Google Scholar] [CrossRef]
- Debye, P. Zerstreuung von Röntgenstrahlen. Ann. Phys. 1915, 351, 809–823. [Google Scholar] [CrossRef]
- Hansen, S. Calculation of small-angle scattering profiles using Monte Carlo simulation. J. Appl. Crystallogr. 1990, 23, 344–346. [Google Scholar] [CrossRef]
- OpenSCAD. Available online: Openscad.org (accessed on 31 March 2021).
- Schönhals, A. Dielectric Spectroscopy on the Dynamics of Amorphous Polymeric Systems. Appl. Note Dielectr. 1998, 1, 1–17. [Google Scholar]
- Sun, P.; Liu, G.; Lv, D.; Dong, X.; Wu, J.; Wang, D. Effective activation of halloysite nanotubes by piranha solution for amine modification via silane coupling chemistry. RSC Adv. 2015, 5, 52916–52925. [Google Scholar] [CrossRef]
- Abdullayev, E.; Joshi, A.; Wei, W.; Zhao, Y.; Lvov, Y. Enlargement of Halloysite Clay Nanotube Lumen by Selective Etching of Aluminum Oxide. ACS Nano 2012, 6, 7216–7226. [Google Scholar] [CrossRef]
- Stewart, G.W. Theory of X-Ray Diffraction in Liquids. Phys. Rev. 1928, 32, 558–563. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, Z.; Moon, K.-S.; Wong, C.P. Glass transition and relaxation behavior of epoxy nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2004, 42, 3849–3858. [Google Scholar] [CrossRef]
- Maggana, C.; Pissis, P. TSDC studies of the effects of plasticizer and water on the sub-Tg relaxations of an epoxy resin system. J. Macromol. Sci. Part B 1997, 36, 749–772. [Google Scholar] [CrossRef]
- Wunderlich, B. Reversible crystallization and the rigid–amorphous phase in semicrystalline macromolecules. Prog. Polym. Sci. 2003, 28, 383–450. [Google Scholar] [CrossRef]
- Alhabill, F.N.; Ayoob, R.; Andritsch, T.; Vaughan, A.S. Influence of filler/matrix interactions on resin/hardener stoichiometry, molecular dynamics, and particle dispersion of silicon nitride/epoxy nanocomposites. J. Mater. Sci. 2018, 53, 4144–4158. [Google Scholar] [CrossRef]
- Hanzon, D.W.; Yu, K.; Yakacki, C.M. Chapter Five-Activation Mechanisms of Shape-Memory Polymers. In Shape-Memory Polymer Device Design; Safranski, D.L., Griffis, J.C., Eds.; Plastics Design Library, William Andrew Publishing: Norwich, NY, USA, 2017; pp. 139–187. ISBN 978-0-323-37797-3. [Google Scholar]
- Vogel, H. Das Temperaturabhangigkeitsgesetz der Viskositat von Flussigkeiten. Phys. Z. 1921, 22, 645–646. [Google Scholar]
- Fulcher, G.S. Analysis of Recent Measurements of the Viscosity of Glasses. J. Am. Ceram. Soc. 1925, 8, 339–355. [Google Scholar] [CrossRef]
- Tammann, G.; Hesse, W. Die Abhängigkeit der Viscosität von der Temperatur bei unterkühlten Flüssigkeiten. Z. Anorg. Allg. Chem. 1926, 156, 245–257. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane analysis of α-dispersions in some polymer systems. J. Polym. Sci. Part C Polym. Symp. 1966, 14, 99–117. [Google Scholar] [CrossRef]
- Havriliak, S.; Negami, S. A complex plane representation of dielectric and mechanical relaxation processes in some polymers. Polymer 1967, 8, 161–210. [Google Scholar] [CrossRef]
- Ochi, M.; Okazaki, M.; Shimbo, M. Mechanical relaxation mechanism of epoxide resins cured with aliphatic diamines. J. Polym. Sci. Polym. Phys. Ed. 1982, 20, 689–699. [Google Scholar] [CrossRef]
- Ochi, M.; Yoshizumi, M.; Shimbo, M. Mechanical and dielectric relaxations of epoxide resins containing the spiro-ring structure. II. Effect of the introduction of methoxy branches on low-temperature relaxations of epoxide resins. J. Polym. Sci. Part B Polym. Phys. 1987, 25, 1817–1827. [Google Scholar] [CrossRef]
- Mangion, M.B.M.; Johari, G.P. Relaxations of thermosets. III. Sub-Tg dielectric relaxations of bisphenol-A–based epoxide cured with different cross-linking agents. J. Polym. Sci. Part B Polym. Phys. 1990, 28, 71–83. [Google Scholar] [CrossRef]
- Heijboer, J. Molecular Basis of Transitions and Relaxation. In Midland Macromolecular Monographs; Meier, D.J., Ed.; Gordon and Breach Science Publishers: New York, NY, USA, 1978; ISBN 9780677112404. [Google Scholar]
- Hassan, M.K.; Tucker, S.J.; Abukmail, A.; Wiggins, J.S.; Mauritz, K.A. Polymer chain dynamics in epoxy based composites as investigated by broadband dielectric spectroscopy. Arab. J. Chem. 2016, 9, 305–315. [Google Scholar] [CrossRef]
- Patil, P.N.; Rath, S.K.; Sharma, S.K.; Sudarshan, K.; Maheshwari, P.; Patri, M.; Praveen, S.; Khandelwal, P.; Pujari, P.K. Free volumes and structural relaxations in diglycidyl ether of bisphenol-A based epoxy–polyether amine networks. Soft Matter 2013, 9, 3589–3599. [Google Scholar] [CrossRef]
- Wübbenhorst, M.; van Turnhout, J. “Conduction-free” dielectric loss de/dlnf-a powerful tool for the analysis of strong (ion) conducting dielectric materials. Dielectr. Newsl. 2000, 14, 1–8. [Google Scholar]
- Klonos, P.; Panagopoulou, A.; Bokobza, L.; Kyritsis, A.; Peoglos, V.; Pissis, P. Comparative studies on effects of silica and titania nanoparticles on crystallization and complex segmental dynamics in poly(dimethylsiloxane). Polymer 2010, 51, 5490–5499. [Google Scholar] [CrossRef]
- Fragiadakis, D.; Bokobza, L.; Pissis, P. Dynamics near the filler surface in natural rubber-silica nanocomposites. Polymer 2011, 52, 3175–3182. [Google Scholar] [CrossRef]
- Donth, E. The size of cooperatively rearranging regions at the glass transition. J. Non. Cryst. Solids 1982, 53, 325–330. [Google Scholar] [CrossRef]
- Schawe, J.E.K. Vitrification in a wide cooling rate range: The relations between cooling rate, relaxation time, transition width, and fragility. J. Chem. Phys. 2014, 141, 184905. [Google Scholar] [CrossRef] [PubMed]
- Akbari, V.; Najafi, F.; Vahabi, H.; Jouyandeh, M.; Badawi, M.; Morisset, S.; Ganjali, M.R.; Saeb, M.R. Surface chemistry of halloysite nanotubes controls the curability of low filled epoxy nanocomposites. Prog. Org. Coat. 2019, 135, 555–564. [Google Scholar] [CrossRef]
- Yang, L.; Phua, S.L.; Teo, J.K.H.; Toh, C.L.; Lau, S.K.; Ma, J.; Lu, X. A Biomimetic Approach to Enhancing Interfacial Interactions: Polydopamine-Coated Clay as Reinforcement for Epoxy Resin. ACS Appl. Mater. Interfaces 2011, 3, 3026–3032. [Google Scholar] [CrossRef] [PubMed]






Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Omar, H.; Smales, G.J.; Henning, S.; Li, Z.; Wang, D.-Y.; Schönhals, A.; Szymoniak, P. Calorimetric and Dielectric Investigations of Epoxy-Based Nanocomposites with Halloysite Nanotubes as Nanofillers. Polymers 2021, 13, 1634. https://doi.org/10.3390/polym13101634
Omar H, Smales GJ, Henning S, Li Z, Wang D-Y, Schönhals A, Szymoniak P. Calorimetric and Dielectric Investigations of Epoxy-Based Nanocomposites with Halloysite Nanotubes as Nanofillers. Polymers. 2021; 13(10):1634. https://doi.org/10.3390/polym13101634
Chicago/Turabian StyleOmar, Hassan, Glen J. Smales, Sven Henning, Zhi Li, De-Yi Wang, Andreas Schönhals, and Paulina Szymoniak. 2021. "Calorimetric and Dielectric Investigations of Epoxy-Based Nanocomposites with Halloysite Nanotubes as Nanofillers" Polymers 13, no. 10: 1634. https://doi.org/10.3390/polym13101634
APA StyleOmar, H., Smales, G. J., Henning, S., Li, Z., Wang, D.-Y., Schönhals, A., & Szymoniak, P. (2021). Calorimetric and Dielectric Investigations of Epoxy-Based Nanocomposites with Halloysite Nanotubes as Nanofillers. Polymers, 13(10), 1634. https://doi.org/10.3390/polym13101634









