Mechanical Behavior of Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites
Abstract
1. Introduction
2. Materials and Methods
2.1. Sample Preparation
2.2. Scanning Electron Microscopy
2.3. Dynamic Mechanical Thermal Analysis (DMTA)
2.4. Creep Tests
2.5. Short-Term Tensile Tests
2.6. Izod Impact Tests
3. Results and Discussion
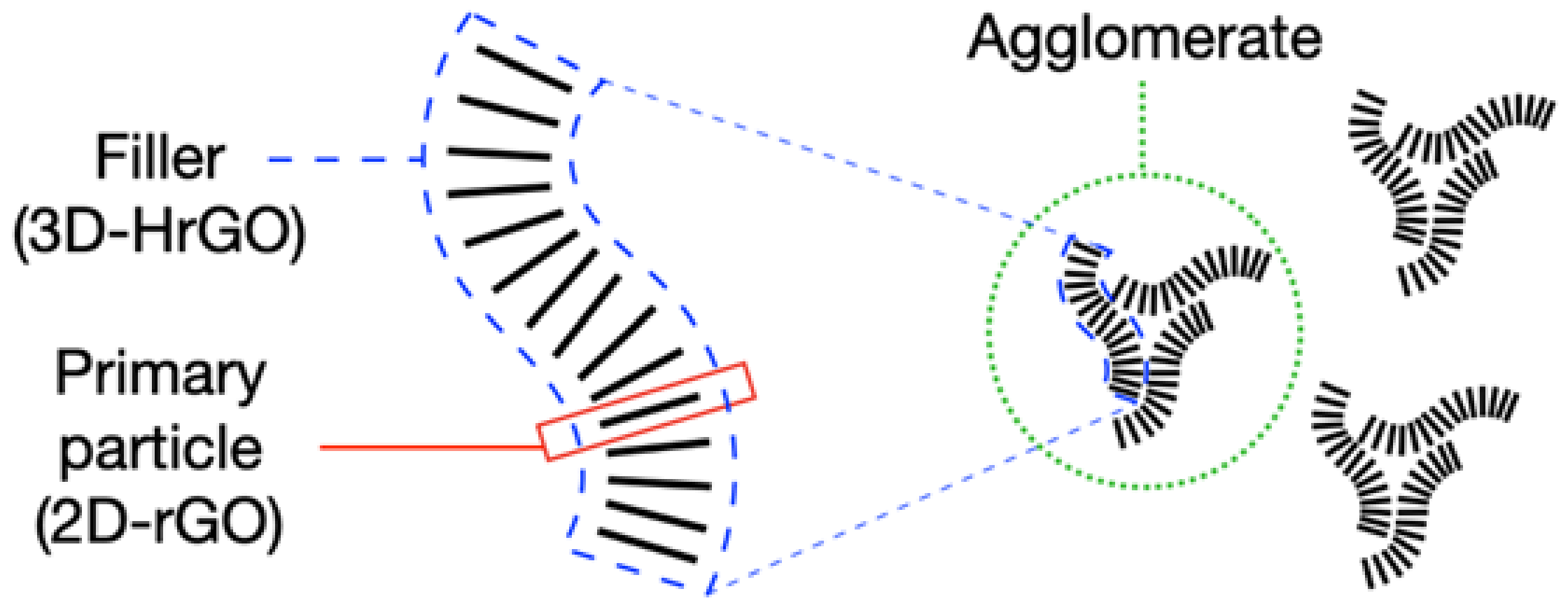
3.1. Morphology
3.2. Dynamic Mechanical Thermal Analysis (DMTA)
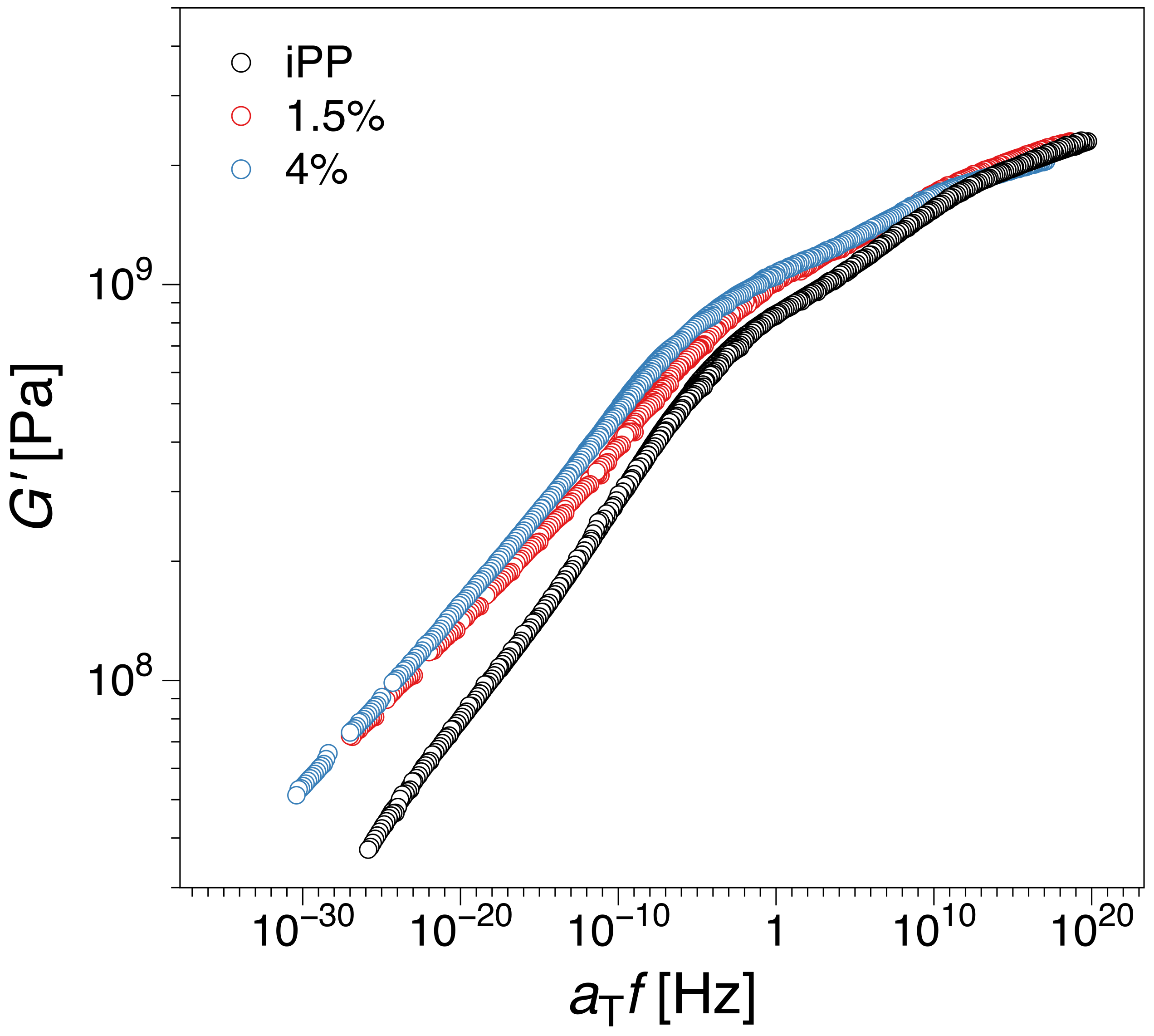
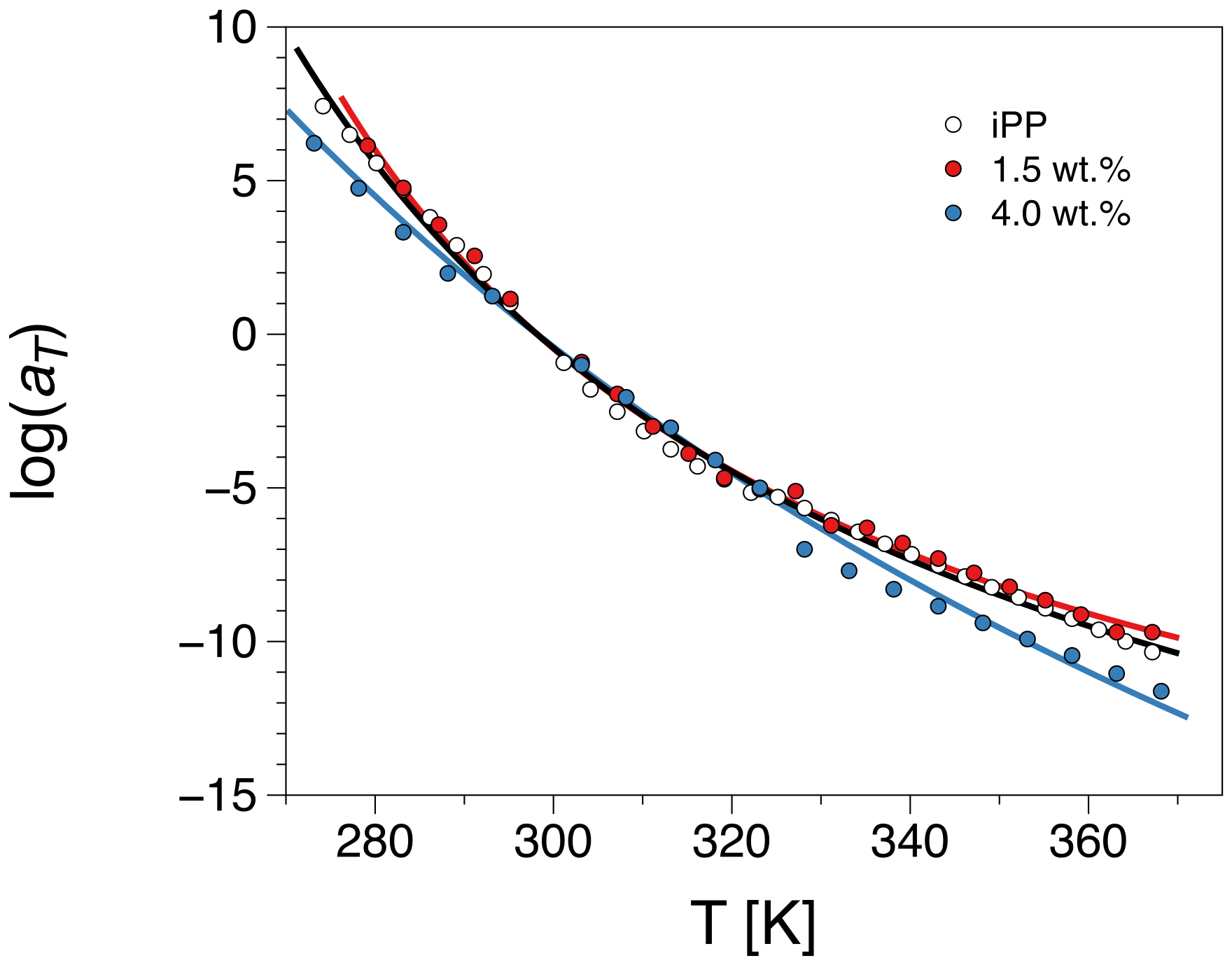
3.2.1. Construction of the Master Curve for iPP-Graphene
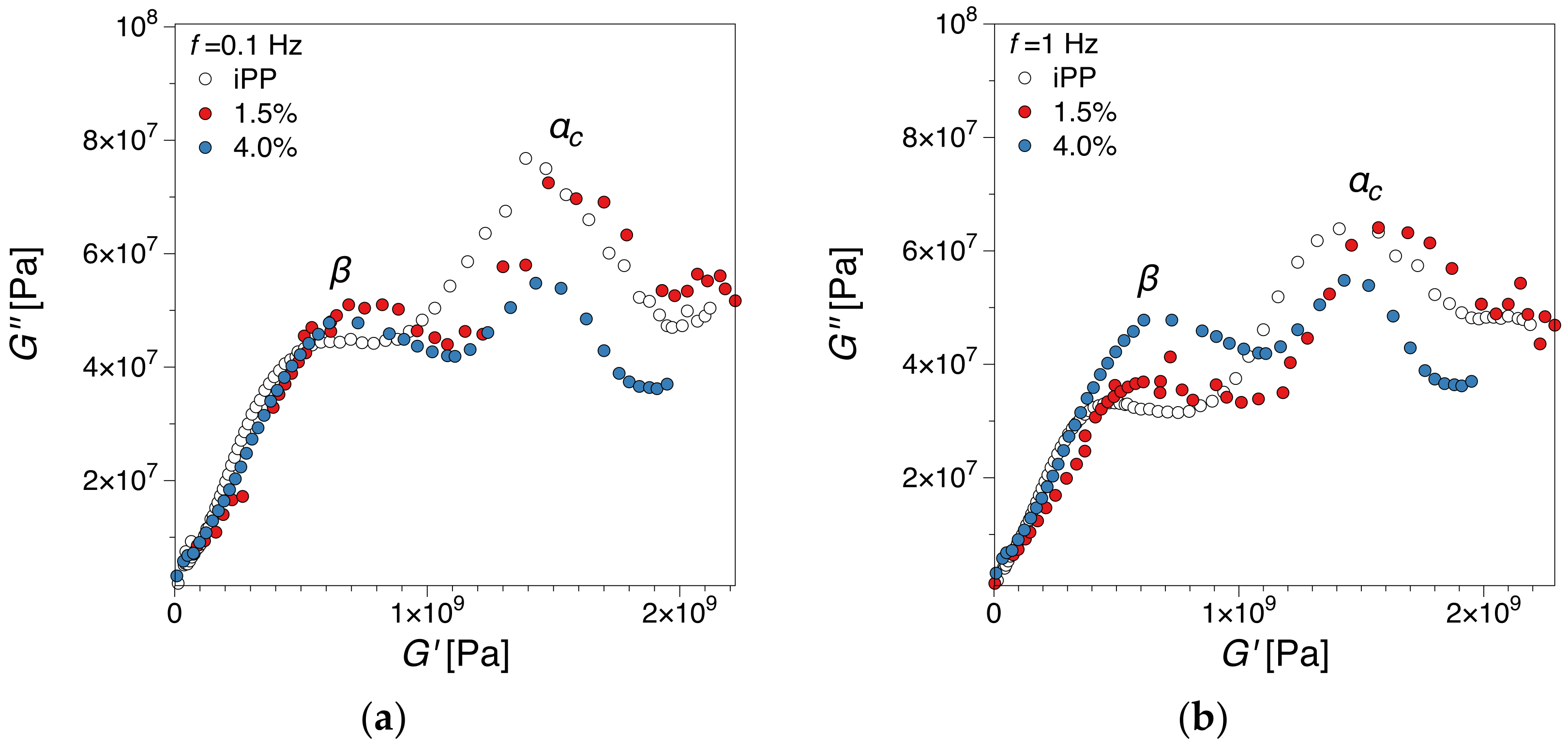
3.2.2. Cole-Cole Plots Analysis
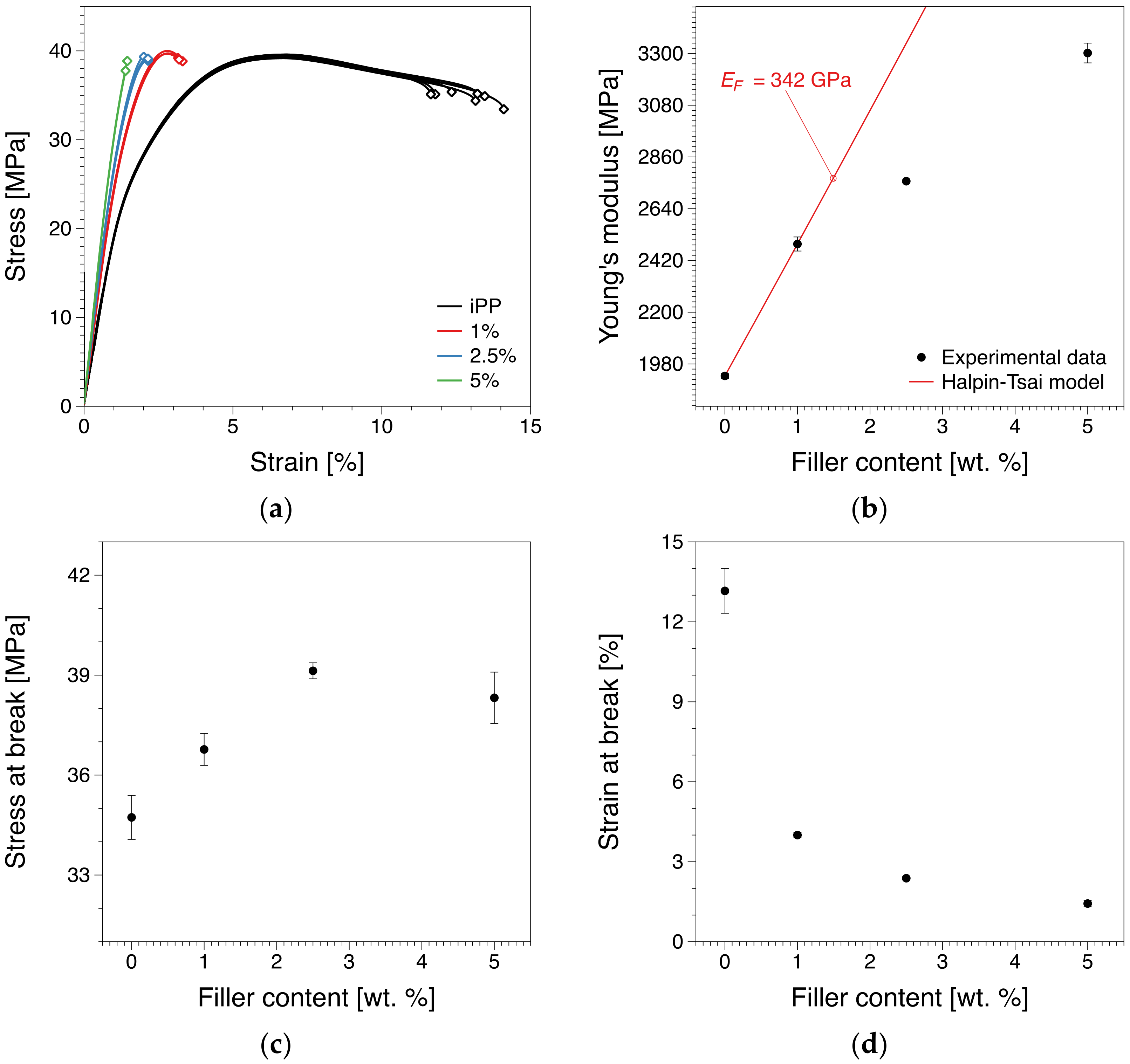
3.3. Short-Term Tensile Properties
3.4. Micromechanical Modelling
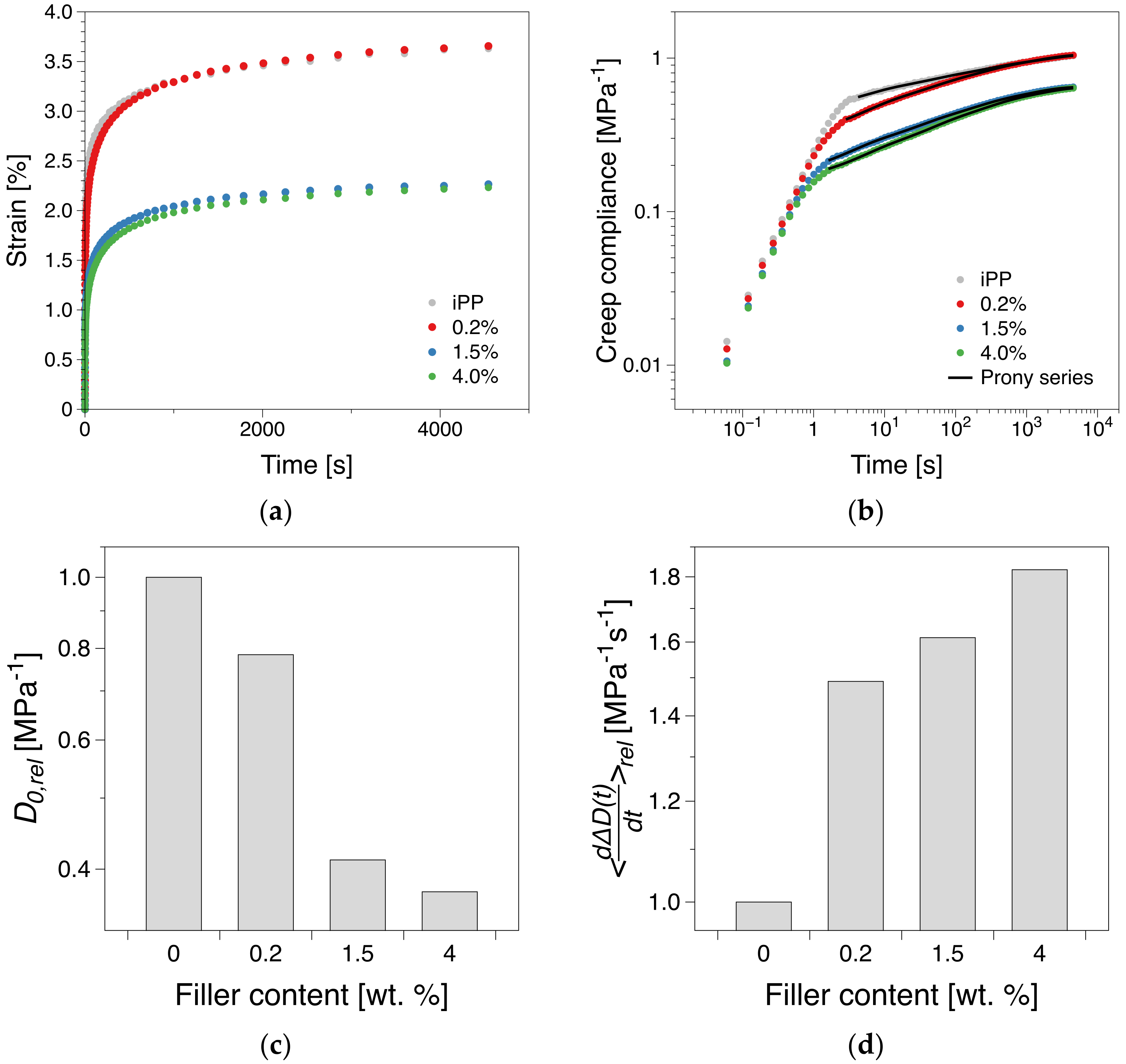
3.5. Creep
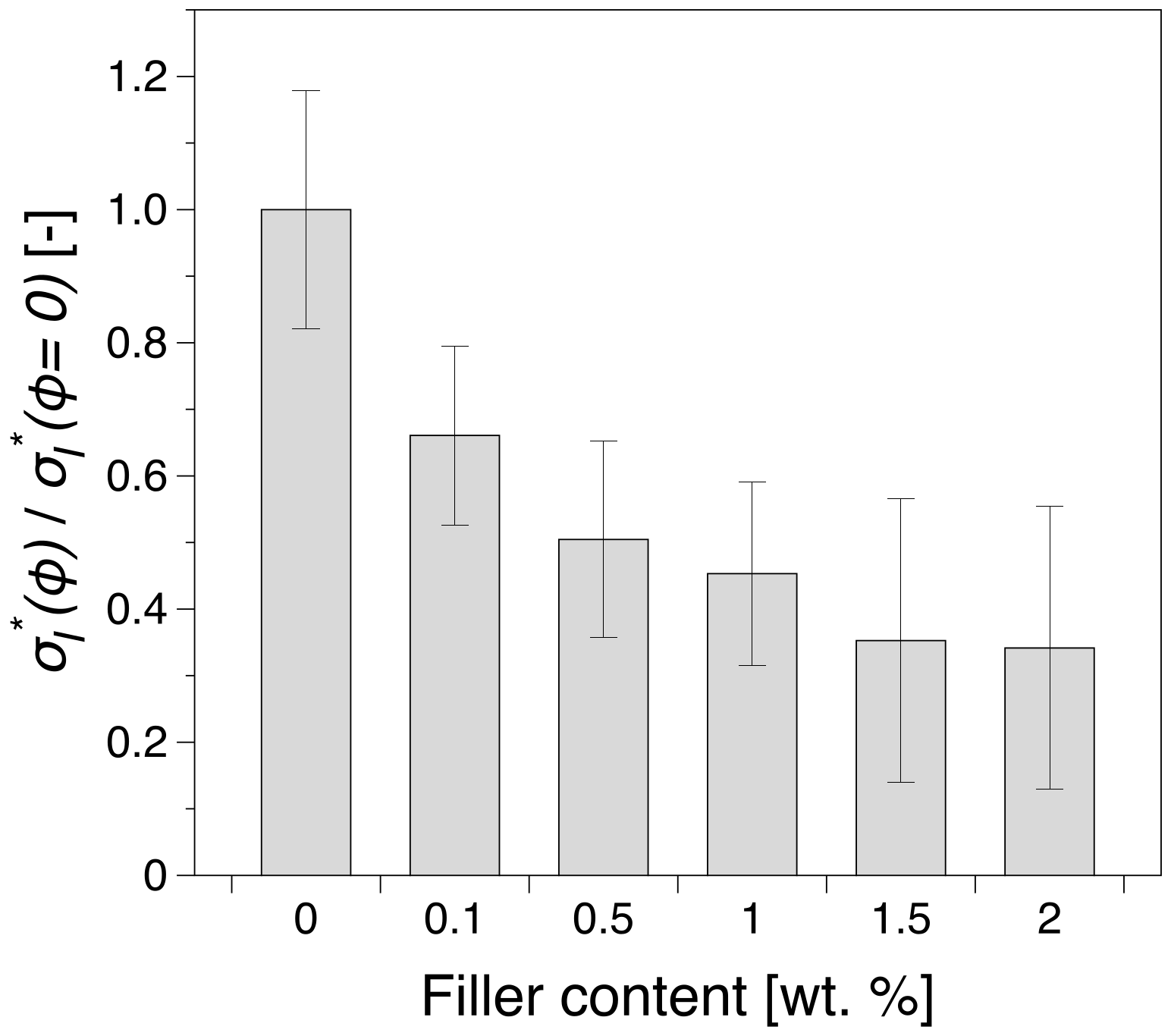
3.6. Impact Strength
4. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gkourmpis, T. Carbon-Based High Aspect Ratio Polymer Nanocomposites, Nanoscience and Computational Chemistry: Research Progress; Mercader, G.A., Haghi, A.K., Eds.; Apple Academic Press: Toronto, ON, Canada, 2014. [Google Scholar]
- Gaska, K.; Kádár, R.; Rybak, A.; Siwek, A.; Gubanski, S. Gas barrier, thermal, mechanical and rheological properties of highly aligned graphene-LDPE nanocomposites. Polymers 2017, 9, 294. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Drzal, L.T. Graphene nanoplatelet paper as a light-weight composite with excellent electrical and thermal conductivity and good gas barrier properties. Carbon 2012, 50, 1135–1145. [Google Scholar] [CrossRef]
- Kim, H.; Miura, Y.; Macosko, C.W. Graphene/polyurethane nanocomposites for improved gas barrier and electrical conductivity. Chem. Mater. 2010, 22, 3441–3450. [Google Scholar] [CrossRef]
- Röding, M.; Gaska, K.; Kádár, R.; Lorén, N. Computational screening of diffusive transport in nanoplatelet-filled composites: Use of graphene to enhance polymer barrier properties. ACS Appl. Nano Mater. 2018, 1, 160–167. [Google Scholar] [CrossRef]
- Hule, R.A.; Pochan, D.J. Polymer nanocomposites for biomedical applications. MRS Bull. 2007, 32, 354–358. [Google Scholar] [CrossRef]
- Pandit, S.; Gaska, K.; Mokkapati, V.R.S.S.; Forsberg, S.; Svensson, M.; Kádár, R.; Mijakovic, I. Antibacterial effect of boron nitride flakes with controlled orientation in polymer composites. RSC Adv. 2019, 9, 33454–33459. [Google Scholar] [CrossRef]
- Pandit, S.; Gaska, K.; Mokkapati, V.R.S.S.; Celauro, E.; Derouiche, A.; Forsberg, S.; Svensson, M.; Kádár, R.; Mijakovic, I. Precontrolled alignment of graphite nanoplatelets in polymeric composites prevents bacterial attachment. Small 2020, 16, 1904756. [Google Scholar] [CrossRef] [PubMed]
- Shahil, K.M.F.; Balandin, A.A. Graphene–multilayer graphene nanocomposites as highly efficient thermal interface materials. Nano Lett. 2012, 12, 861–867. [Google Scholar] [CrossRef]
- Rybak, A.; Jarosinski, L.; Gaska, K.; Kapusta, C. Graphene nanoplatelet-silica hybrid epoxy composites as electrical insulation with enhanced thermal conductivity. Polym. Compos. 2018, 39, E1682–E1691. [Google Scholar] [CrossRef]
- Novoselov, K.S.; Fal′ko, V.I.; Colombo, L.; Gellert, P.R.; Schwab, M.G.; Kim, K. A roadmap for graphene. Nature 2012, 490, 192. [Google Scholar] [CrossRef]
- Geim, A.K.; Novoselov, K.S. The rise of graphene. Nat. Mater. 2007, 6, 183–191. [Google Scholar] [CrossRef]
- Kim, H.; Abdala, A.A.; Macosko, C.W. Graphene/polymer nanocomposites. Macromolecules 2010, 43, 6515–6530. [Google Scholar] [CrossRef]
- Kim, H.; Macosko, C.W. Morphology and properties of polyester/exfoliated graphite nanocomposites. Macromolecules 2008, 41, 3317–3327. [Google Scholar] [CrossRef]
- Tripathi, S.N.; Rao, G.S.S.; Mathur, A.B.; Jasra, R. Polyolefin/graphene nanocomposites: A review. RSC Adv. 2017, 7, 23615–23632. [Google Scholar] [CrossRef]
- Blinzler, B.J.; Larsson, R.; Gaska, K.; Kádár, R. A Mechanics based surface image interpretation method for multifunctional nanocomposites. Nanomaterials 2019, 9, 1578. [Google Scholar] [CrossRef]
- Papageorgiou, D.G.; Kinloch, I.A.; Young, R.J. Mechanical properties of graphene and graphene-based nanocomposites. Prog. Mater. Sci. 2017, 90, 75–127. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. A new compounding method for exfoliated graphite–polypropylene nanocomposites with enhanced flexural properties and lower percolation threshold. Compos. Sci. Technol. 2007, 67, 2045–2051. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. Multifunctional polypropylene composites produced by incorporation of exfoliated graphite nanoplatelets. Carbon 2007, 45, 1446–1452. [Google Scholar] [CrossRef]
- Kovtun, A.; Treossi, E.; Mirotta, N.; Scidà, A.; Liscio, A.; Christian, M.; Valorosi, F.; Boschi, A.; Young, R.J.; Galiotis, C.; et al. Benchmarking of graphene-based materials: Real commercial products versus ideal graphene. 2D Mater. 2019, 6, 025006. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Z.; Friedrich, K.; Schlarb, A.K. Creep resistant polymer nanocomposites reinforced with multiwalled carbon nanotubes. Macromol. Rapid Commun. 2007, 28, 955–961. [Google Scholar] [CrossRef]
- Yang, X.; Wang, X.; Yang, J.; Li, J.; Wan, L. Functionalization of graphene using trimethoxysilanes and its reinforcement on polypropylene nanocomposites. Chem. Phys. Lett. 2013, 570, 125–131. [Google Scholar] [CrossRef]
- Todd, A.D.; Bielawski, C.W. Thermally reduced graphite oxide reinforced polyethylene composites: A mild synthetic approach. Polymer 2013, 54, 4427–4430. [Google Scholar] [CrossRef]
- Song, P.; Cao, Z.; Cai, Y.; Zhao, L.; Fang, Z.; Fu, S. Fabrication of exfoliated graphene-based polypropylene nanocomposites with enhanced mechanical and thermal properties. Polymer 2011, 52, 4001–4010. [Google Scholar] [CrossRef]
- Liang, J.-Z.; Du, Q.; Tsui, G.C.-P.; Tang, C.-Y. Tensile properties of graphene nano-platelets reinforced polypropylene composites. Compos. Part B Eng. 2016, 95, 166–171. [Google Scholar] [CrossRef]
- Iniestra-Galindo, M.G.; Pérez-González, J.; Marín-Santibáñez, B.M.; Balmori-Ramírez, H. Preparation at large-scale of polypropylene nanocomposites with microwaves reduced graphene oxide. Mater. Res. Express 2019, 6, 105347. [Google Scholar] [CrossRef]
- Gkourmpis, T.; Gaska, K.; Tranchida, D.; Gitsas, A.; Müller, C.; Matic, A.; Kádár, R. Melt-mixed 3D hierarchical graphene/polypropylene nanocomposites with low electrical percolation threshold. Nanomaterials 2019, 9, 1766. [Google Scholar] [CrossRef]
- Fiebig, J.; Gahleitner, M.; Paulik, C.; Wolfschwenger, J. Ageing of polypropylene: Processes and consequences. Polym. Test. 1999, 18, 257–266. [Google Scholar] [CrossRef]
- McCrum, N.G.; Buckley, C.P.; Bucknall, C.B. Principles of Polymer Engineering; Oxford University Press: Oxford, UK, 2011. [Google Scholar]
- Guedes, R.M. Creep and Fatigue in Polymer Matrix Composites, 2nd ed.; Woodhead Publishing: Sawston, UK, 2019. [Google Scholar]
- Osswald, T.A.; Menges, G. Materials Science of Polymers for Engineers, 3rd ed.; Hanser: Munich, Germany, 2012. [Google Scholar]
- Papanicolaou, G.C.; Zaoutsos, S.P. 1—Viscoelastic constitutive modeling of creep and stress relaxation in polymers and polymer matrix composites. In Creep and Fatigue in Polymer Matrix Composites; Guedes, R.M., Ed.; Woodhead Publishing: Sawston, UK, 2011; pp. 3–47. [Google Scholar] [CrossRef]
- Han, C.D. Mechanical properties of solid polymers, 2nd ed., I. M. Ward, Wiley, New York, 1983, 475 pp. J. Polym. Sci. Polym. Lett. Ed. 1985, 23, 119. [Google Scholar] [CrossRef]
- Ward, I.M.; Sweeney, J. Experimental studies of linear viscoelastic behaviour as a function of frequency and temperature: Time–temperature equivalence. In Mechanical Properties of Solid Polymers; John Wiley & Sons, Ltd.: New York, NY, USA, 2012; pp. 135–165. [Google Scholar] [CrossRef]
- Williams, M.L.; Landel, R.F.; Ferry, J.D. The temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. J. Am. Chem. Soc. 1955, 77, 3701–3707. [Google Scholar] [CrossRef]
- Faucher, J.A. Viscoelastic behavior of polyethylene and polypropylene. Trans. Soc. Rheol. 1959, 3, 81–93. [Google Scholar] [CrossRef]
- Harper, B.D.; Weitsman, Y. Characterization method for a class of thermorheologically complex materials. J. Rheol. 1985, 29, 49–66. [Google Scholar] [CrossRef]
- Miller, E. Introduction to Plastics and Composites: Mechanical Properties and Engineering Applications; Taylor & Francis: Milton Park, UK, 1995. [Google Scholar]
- Shangguan, Y.; Chen, F.; Jia, E.; Lin, Y.; Hu, J.; Zheng, Q. New insight into time-temperature correlation for polymer relaxations ranging from secondary relaxation to terminal flow: Application of a universal and developed WLF equation. Polymers 2017, 9, 567. [Google Scholar] [CrossRef] [PubMed]
- Wortmann, F.J.; Schulz, K.V. Investigations on the thermorheological simplicity of polypropylene fibres in the α-transition range. Polymer 1995, 36, 1611–1615. [Google Scholar] [CrossRef]
- Lohse, D.J. Polyolefins, Applied Polymer Science: 21st Century; Craver, C.D., Carraher, C.W., Eds.; Elsevier Science Ltd.: Oxford, UK, 2000; pp. 73–91. [Google Scholar]
- Maddah, H. Polypropylene as a promising plastic: A review. Am. J. Polym. Sci. 2016, 6, 1–11. [Google Scholar]
- Galli, P.; Vecellio, G. Technology: Driving force behind innovation and growth of polyolefins. Prog. Polym. Sci. 2001, 26, 1287–1336. [Google Scholar] [CrossRef]
- Gahleitner, M.; Resconi, L.; Doshev, P. Heterogeneous Ziegler-Natta, metallocene, and post-metallocene catalysis: Successes and challenges in industrial application. MRS Bull. 2013, 38, 229–233. [Google Scholar] [CrossRef]
- De Rosa, C.; Auriemma, F.; Vollaro, P.; Resconi, L.; Guidotti, S.; Camurati, I. Crystallization behavior of propylene−butene copolymers: The trigonal form of isotactic polypropylene and form I of isotactic poly(1-butene). Macromolecules 2011, 44, 540–549. [Google Scholar] [CrossRef]
- Doshev, P.; Lach, R.; Lohse, G.; Heuvelsland, A.; Grellmann, W.; Radusch, H.J. Fracture characteristics and deformation behavior of heterophasic ethylene–propylene copolymers as a function of the dispersed phase composition. Polymer 2005, 46, 9411–9422. [Google Scholar] [CrossRef]
- Weon, J.I.; Sue, H.J. Mechanical properties of talc- and CaCO3-reinforced high-crystallinity polypropylene composites. J. Mater. Sci. 2006, 41, 2291–2300. [Google Scholar] [CrossRef]
- Rungruang, P.; Grady, B.P.; Supaphol, P. Surface-modified calcium carbonate particles by admicellar polymerization to be used as filler for isotactic polypropylene. Colloids Surf. A Physicochem. Eng. Asp. 2006, 275, 114–125. [Google Scholar] [CrossRef]
- Avella, M.; Cosco, S.; Lorenzo, M.L.D.; Pace, E.D.; Errico, M.E.; Gentile, G. iPP based nanocomposites filled with calcium carbonate nanoparticles: Structure/properties relationships. Macromol. Symp. 2006, 234, 156–162. [Google Scholar] [CrossRef]
- Etcheverry, M.; Barbosa, S.E. Glass fiber reinforced polypropylene mechanical properties enhancement by adhesion improvement. Materials 2012, 5, 1084–1113. [Google Scholar] [CrossRef] [PubMed]
- Kalaitzidou, K.; Fukushima, H.; Drzal, L.T. Mechanical properties and morphological characterization of exfoliated graphite–polypropylene nanocomposites. Compos. Part A Appl. Sci. Manuf. 2007, 38, 1675–1682. [Google Scholar] [CrossRef]
- Krause, B.; Barbier, C.; Kunz, K.; Pötschke, P. Comparative study of singlewalled, multiwalled, and branched carbon nanotubes melt mixed in different thermoplastic matrices. Polymer 2018, 159, 75–85. [Google Scholar] [CrossRef]
- Ramanathan, T.; Abdala, A.A.; Stankovich, S.; Dikin, D.A.; Herrera-Alonso, M.; Piner, R.D.; Adamson, D.H.; Schniepp, H.C.; Chen, X.; Ruoff, R.S.; et al. Functionalized graphene sheets for polymer nanocomposites. Nat. Nanotechnol. 2008, 3, 327–331. [Google Scholar] [CrossRef]
- Ghosh, S.; Calizo, I.; Teweldebrhan, D.; Pokatilov, E.P.; Nika, D.L.; Balandin, A.A.; Bao, W.; Miao, F.; Lau, C.N. Extremely high thermal conductivity of graphene: Prospects for thermal management applications in nanoelectronic circuits. Appl. Phys. Lett. 2008, 92, 151911. [Google Scholar] [CrossRef]
- Jun, Y.S.; Um, J.G.; Jiang, G.; Yu, A. A study on the effects of graphene nano-platelets (GnPs) sheet sizes from a few to hundred microns on the thermal, mechanical, and electrical properties of polypropylene (PP)/GnPs composites. Express Polym. Lett. 2018, 12, 885–897. [Google Scholar] [CrossRef]
- Gahleitner, M.; Mileva, D.; Androsch, R.; Gloger, D.; Tranchida, D.; Sandholzer, M.; Doshev, P. Crystallinity-based product design: Utilizing the polymorphism of isotactic PP homo- and copolymers. Int. Polym. Process. 2016, 31, 618–627. [Google Scholar] [CrossRef]
- Tang, L.-C.; Wang, X.; Gong, L.-X.; Peng, K.; Zhao, L.; Chen, Q.; Wu, L.-B.; Jiang, J.-X.; Lai, G.-Q. Creep and recovery of polystyrene composites filled with graphene additives. Compos. Sci. Technol. 2014, 91, 63–70. [Google Scholar] [CrossRef]
- Ferry, J.D. Viscoelastic Properties of Polymers, 3rd ed.; Wiley: New York, NY, USA, 1980. [Google Scholar]
- Schwarzl, F.; Staverman, A.J. Time-temperature dependence of linear viscoelastic behavior. J. Appl. Phys. 1952, 23, 838–843. [Google Scholar] [CrossRef]
- Cho, K.S. Viscoelasticity of Polymers: Theory and Numerical Algorithms; Springer: Dordrecht, The Netherlands, 2016; Volume 241. [Google Scholar]
- Gitsas, A.; Floudas, G. Pressure dependence of the glass transition in atactic and isotactic polypropylene. Macromolecules 2008, 41, 9423–9429. [Google Scholar] [CrossRef]
- Saitô, N.; Okano, K.; Iwayanagi, S.; Hideshima, T. Molecular motion in solid state polymers. Solid State Phys. 1963, 14, 343–502. [Google Scholar] [CrossRef]
- Hoyos, M.; Tiemblo, P.; Gómez-Elvira, J.M. The role of microstructure, molar mass and morphology on local relaxations in isotactic polypropylene. The α relaxation. Polymer 2007, 48, 183–194. [Google Scholar] [CrossRef]
- Lezak, E.; Bartczak, Z. Plastic deformation behavior of β phase isotactic polypropylene in plane-strain compression at elevated temperatures. J. Polym. Sci. Part B Polym. Phys. 2008, 46, 92–108. [Google Scholar] [CrossRef]
- Gahleitner, M.; Grein, C.; Kheirandish, S.; Wolfschwenger, J. Nucleation of polypropylene homo- and copolymers. Int. Polym. Process. 2011, 26, 2–20. [Google Scholar] [CrossRef]
- Mileva, D.; Tranchida, D.; Gahleitner, M. Designing polymer crystallinity: An industrial perspective. Polym. Cryst. 2018, 1, e10009. [Google Scholar] [CrossRef]
- Hsu, P.; Chen, S.; Tsai, I. Mechanical properties of graphene nanosheets/polypropylene composites. AIP Conf. Proc. 2015, 1653, 020045. [Google Scholar] [CrossRef]
- Al-Saleh, M.A.; Yussuf, A.A.; Al-Enezi, S.; Kazemi, R.; Wahit, M.U.; Al-Shammari, T.; Al-Banna, A. Polypropylene/graphene nanocomposites: Effects of GNP loading and compatibilizers on the mechanical and thermal properties. Materials 2019, 12, 3924. [Google Scholar] [CrossRef]
- Kalaitzidou, K.; Fukushima, H.; Askeland, P.; Drzal, L.T. The nucleating effect of exfoliated graphite nanoplatelets and their influence on the crystal structure and electrical conductivity of polypropylene nanocomposites. J. Mater. Sci. 2008, 43, 2895–2907. [Google Scholar] [CrossRef]
- Huang, C.-L.; Lou, C.-W.; Liu, C.-F.; Huang, C.-H.; Song, X.-M.; Lin, J.-H. Polypropylene/graphene and polypropylene/carbon fiber conductive composites: Mechanical, crystallization and electromagnetic properties. Appl. Sci. 2015, 5, 1196–1210. [Google Scholar] [CrossRef]
- Xu, J.-Z.; Chen, T.; Yang, C.-L.; Li, Z.-M.; Mao, Y.-M.; Zeng, B.-Q.; Hsiao, B.S. Isothermal crystallization of poly(l-lactide) induced by graphene nanosheets and carbon nanotubes: A comparative study. Macromolecules 2010, 43, 5000–5008. [Google Scholar] [CrossRef]
- Xu, J.-Z.; Chen, C.; Wang, Y.; Tang, H.; Li, Z.-M.; Hsiao, B.S. Graphene nanosheets and shear flow induced crystallization in isotactic polypropylene nanocomposites. Macromolecules 2011, 44, 2808–2818. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H.; Chen, G. Enhanced mechanical properties of nanocomposites at low graphene content based on in situ ball milling. Polym. Compos. 2016, 37, 1190–1197. [Google Scholar] [CrossRef]
- Thostenson, E.T.; Chou, T.-W. On the elastic properties of carbon nanotube-based composites: Modelling and characterization. J. Phys. D Appl. Phys. 2003, 36, 573–582. [Google Scholar] [CrossRef]
- Rafiee, M.A.; Lu, W.; Thomas, A.V.; Zandiatashbar, A.; Rafiee, J.; Tour, J.M.; Koratkar, N.A. Graphene Nanoribbon Composites. ACS Nano 2010, 4, 7415–7420. [Google Scholar] [CrossRef] [PubMed]
- Halpin, J.C.; Thomas, R.L. Ribbon reinforcement of composites. J. Compos. Mater. 1968, 2, 488–497. [Google Scholar] [CrossRef]
- Kádár, R.; Gaska, K.; Gkourmpis, T. Nonlinear ‘oddities’ at the percolation of 3D hierarchical graphene polymer nanocomposites. Rheol. Acta 2020, 59, 333–347. [Google Scholar] [CrossRef]
- Lee, C.; Wei, X.; Kysar, J.W.; Hone, J. Measurement of the elastic properties and intrinsic strength of monolayer graphene. Science 2008, 321, 385. [Google Scholar] [CrossRef]
- Suk, J.W.; Piner, R.D.; An, J.; Ruoff, R.S. Mechanical properties of monolayer graphene oxide. ACS Nano 2010, 4, 6557–6564. [Google Scholar] [CrossRef]
- Zhang, X.; Liu, S.; Liu, H.; Zhang, J.; Yang, X. Molecular dynamics simulation of the mechanical properties of multilayer graphene oxide nanosheets. RSC Adv. 2017, 7, 55005–55011. [Google Scholar] [CrossRef]
- Soler-Crespo, R.A.; Gao, W.; Xiao, P.; Wei, X.; Paci, J.T.; Henkelman, G.; Espinosa, H.D. Engineering the mechanical properties of monolayer graphene oxide at the atomic level. J. Phys. Chem. Lett. 2016, 7, 2702–2707. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, J.; Zhao, J.; Liu, F. Mechanical properties of graphene oxides. Nanoscale 2012, 4, 5910–5916. [Google Scholar] [CrossRef] [PubMed]
- Paci, J.T.; Belytschko, T.; Schatz, G.C. Computational studies of the structure, behavior upon heating, and mechanical properties of graphite oxide. J. Phys. Chem. C 2007, 111, 18099–18111. [Google Scholar] [CrossRef]
- Gómez-Navarro, C.; Burghard, M.; Kern, K. Elastic properties of chemically derived single graphene sheets. Nano Lett. 2008, 8, 2045–2049. [Google Scholar] [CrossRef] [PubMed]


| Sample | Tg [K] [27] | ||||
|---|---|---|---|---|---|
| iPP | 273.15 | 24.6 ± 0.8 | 98 ± 4 | 33.0 ± 0.8 | 73 ± 4 |
| 1.5% | 274.67 | 21.0 ± 0.7 | 82 ± 4 | 29.4 ± 0.7 | 58 ± 4 |
| 4.0% | 274.76 | 50 ± 6 | 220 ± 30 | 56 ± 6 | 200 ± 30 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaska, K.; Manika, G.C.; Gkourmpis, T.; Tranchida, D.; Gitsas, A.; Kádár, R. Mechanical Behavior of Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites. Polymers 2020, 12, 1309. https://doi.org/10.3390/polym12061309
Gaska K, Manika GC, Gkourmpis T, Tranchida D, Gitsas A, Kádár R. Mechanical Behavior of Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites. Polymers. 2020; 12(6):1309. https://doi.org/10.3390/polym12061309
Chicago/Turabian StyleGaska, Karolina, Georgia C. Manika, Thomas Gkourmpis, Davide Tranchida, Antonis Gitsas, and Roland Kádár. 2020. "Mechanical Behavior of Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites" Polymers 12, no. 6: 1309. https://doi.org/10.3390/polym12061309
APA StyleGaska, K., Manika, G. C., Gkourmpis, T., Tranchida, D., Gitsas, A., & Kádár, R. (2020). Mechanical Behavior of Melt-Mixed 3D Hierarchical Graphene/Polypropylene Nanocomposites. Polymers, 12(6), 1309. https://doi.org/10.3390/polym12061309









