A Review on Barrier Properties of Poly(Lactic Acid)/Clay Nanocomposites
Abstract
1. Introduction
2. PLA/Layered Silicate Nanocomposites
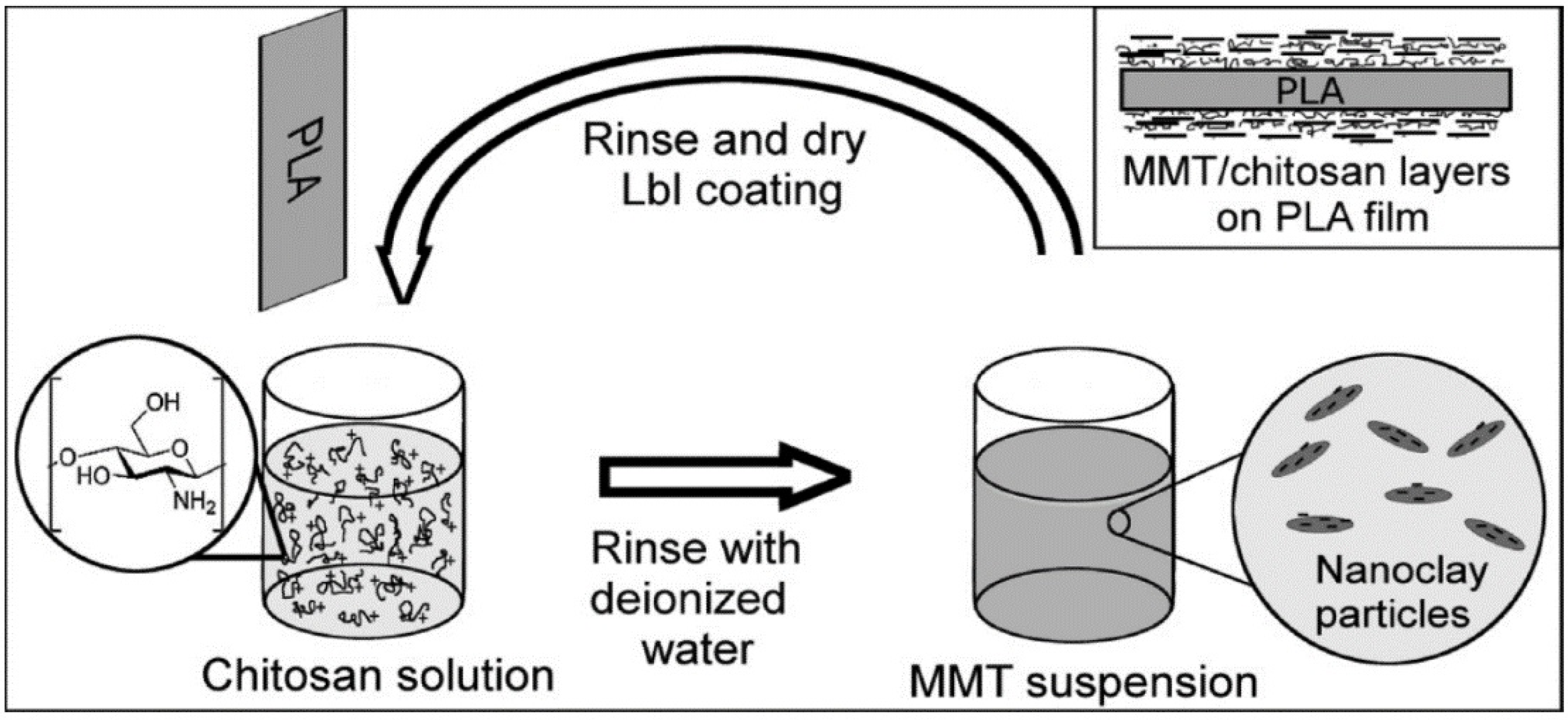
2.1. Solution Intercalation
2.2. Melt Intercalation
2.3. In Situ Polymerization
3. Barrier Performance
4. Mass Transfer in Polymers
4.1. Measurement of Mass Transport Properties
4.2. Factors Affecting Mass Transport
5. Modeling of Permeability of Polymer/Clay Nanocomposites
5.1. Periodic Arrangement of Parallel Nanoplatelets
5.2. Random Arrangement of Parallel Nanoplatelets
5.3. Platelet Arrangement at an Angle θ ≠ 90° to the Diffusion Direction
6. Model Validation for PLA/Clay Nanocomposites
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jenck, J.F.; Agterberg, F.; Droescher, M.J. Products and processes for a sustainable chemical industry: A review of achievements and prospects. Green Chem. 2004, 6, 544–556. [Google Scholar] [CrossRef]
- Kaplan, D.L. Biopolymers from Renewable Resources; Springer: Berlin, Germany, 1998. [Google Scholar]
- Mekonnen, T.; Mussone, P.; Khalil, H.; Bressler, D. Progress in bio-based plastics and plasticizing modifications. J. Mater. Chem. A 2013, 1, 13379–13398. [Google Scholar] [CrossRef]
- Kabir, E.; Kaur, R.; Lee, J.; Kim, K.-H.; Kwon, E.E. Prospects of biopolymer technology as an alternative option for non-degradable plastics and sustainable management of plastic wastes. J. Clean. Prod. 2020, 258, 120536. [Google Scholar] [CrossRef]
- Stefani, R.; Vinhal, G.L.R.R.B.; do Nascimento, D.V.; Pereira, M.C.S.; Pertuzatti, P.B.; da Silva Chaves, K. Smart Biopolymers in Food Industry. In Industrial Applications for Intelligent Polymers and Coatings; Hosseini, M., Makhlouf, A.S.H., Eds.; Springer International Publishing AG: Cham, Switzerland, 2016. [Google Scholar]
- Catalá, R.; López-Carballo, G.; Hernández-Muñoz, P.; Gavara, R. PLA and Active Packaging. In Poly(lactic acid) Science and Technology: Processing, Properties, Additives and Applications; Jiménez, A., Peltzer, M., Ruseckaite, R., Eds.; The Royal Society of Chemistry: Cambridge, UK, 2015. [Google Scholar]
- Fiori, S. Industrial uses of PLA. RSC Polym. Chem. Ser. 2015, 2015, 317–333. [Google Scholar]
- Lim, L.T.; Auras, R.; Rubino, M. Processing technologies for poly(lactic acid). Prog. Polym. Sci. 2008, 33, 820–852. [Google Scholar] [CrossRef]
- Castro-Aguirre, E.; Iñiguez-Franco, F.; Samsudin, H.; Fang, X.; Auras, R. Poly(lactic acid)—Mass production, processing, industrial applications, and end of life. Adv. Drug Deliv. Rev. 2016, 107, 333–366. [Google Scholar] [CrossRef] [PubMed]
- Farah, S.; Anderson, D.G.; Langer, R. Physical and mechanical properties of PLA, and their functions in widespread applications—A comprehensive review. Adv. Drug Deliv. Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef]
- Armentano, I.; Bitinis, N.; Fortunati, E.; Mattioli, S.; Rescignano, N.; Verdejo, R.; Lopez-Manchado, M.A.; Kenny, J.M. Multifunctional nanostructured PLA materials for packaging and tissue engineering. Prog. Polym. Sci. 2013, 38, 1720–1747. [Google Scholar] [CrossRef]
- Maharana, T.; Mohanty, B.; Negi, Y.S. Melt-solid polycondensation of lactic acid and its biodegradability. Prog. Polym. Sci. 2009, 34, 99–124. [Google Scholar] [CrossRef]
- Kang, H.; Li, Y.; Gong, M.; Guo, Y.; Guo, Z.; Fang, Q.; Li, X. An environmentally sustainable plasticizer toughened polylactide. RSC Adv. 2018, 8, 11643–11651. [Google Scholar] [CrossRef]
- Mofokeng, J.P.; Luyt, A.S.; Tábi, T.; Kovács, J. Comparison of injection moulded, natural fibre-reinforced composites with PP and PLA as matrices. J. Thermoplast. Compos. Mater. 2012, 25, 927–948. [Google Scholar] [CrossRef]
- Anderson, K.S.; Schreck, K.M.; Hillmyer, M.A. Toughening polylactide. Polym. Rev. 2008, 48, 85–108. [Google Scholar] [CrossRef]
- Garlotta, D. A Literature Review of Poly(Lactic Acid). J. Polym. Environ. 2001, 9, 63–84. [Google Scholar] [CrossRef]
- Avérous, L. Polylactic acid: Synthesis, properties and applications. In Monomer, Polymer and Composites from Renewable Resources; Belgacem, M.N., Gandini, A., Eds.; Elsevier: London, UK, 2008. [Google Scholar]
- Wee, Y.J.; Kim, J.N.; Ryu, H.W. Biotechnological production of lactic acid and its recent applications. Food Technol. Biotechnol. 2006, 44, 163–172. [Google Scholar]
- Carothers, W.H.; Borough, G.L.; Natta, F.J. Studies of polymerization and ring formation. X. The reversible polymerization of six-membered cyclic esters. J. Am. Chem. Soc. 1932, 54, 761–772. [Google Scholar] [CrossRef]
- Albertsson, A.C.; Varma, I.K. Aliphatic polyesters: Synthesis, properties and applications. Adv. Polym. Sci. 2002, 157, 1–40. [Google Scholar]
- Okada, M. Chemical syntheses of biodegradable polymers. Prog. Polym. Sci. 2002, 27, 87–133. [Google Scholar] [CrossRef]
- Madhavan Nampoothiri, K.; Nair, N.R.; John, R.P. An overview of the recent developments in polylactide (PLA) research. Bioresour. Technol. 2010, 101, 8493–8501. [Google Scholar] [CrossRef]
- Guinault, A.; Menary, G.H.; Courgneau, C.; Griffith, D.; Ducruet, V.; Miri, V.; Sollogoub, C. The effect of the stretching of PLA extruded films on their crystallinity and gas barrier properties. AIP Conf. Proc. 2011, 1353, 826–831. [Google Scholar]
- Drieskens, M.; Peeters, R.; Mullens, J.; Franco, D.; Lemstra, P.J.; Hristova-Bogaerds, D.G. Structure versus properties relationship of poly(lactic acid). I. Effect of crystallinity on barrier properties. J. Polym. Sci. Part B Polym. Phys. 2009, 47, 2247–2258. [Google Scholar] [CrossRef]
- Guinault, A.; Sollogoub, C.; Domenek, S.; Grandmontagne, A.; Ducruet, V.J. Influence of crystallinity on gas barrier and mechanical properties of PLA food packaging films. Int. J. Mater. Form. 2010, 3, 603–606. [Google Scholar] [CrossRef]
- Sonchaeng, U.; Iñiguez-Franco, F.; Auras, R.; Selke, S.; Rubino, M.; Lim, L.T. Poly(lactic acid) mass transfer properties. Prog. Polym. Sci. 2018, 86, 85–121. [Google Scholar] [CrossRef]
- Koros, W.J. Barrier Polymers and Structures. Anal. Chem. 1990, 62, 737A. [Google Scholar]
- Hedenqvist, M.S. Barrier packaging materials. In Handbook of Environmental Degradation of Materials, 3rd ed.; Kutz, M., Ed.; Elsevier Inc.: Cambridge, MA, USA, 2018. [Google Scholar]
- Majeed, K.; Jawaid, M.; Hassan, A.; Abu Bakar, A.; Abdul Khalil, H.P.S.; Salema, A.A.; Inuwa, I. Potential materials for food packaging from nanoclay/natural fibres filled hybrid composites. Mater. Des. 2013, 46, 391–410. [Google Scholar] [CrossRef]
- Bee, S.L.; Abdullah, M.A.A.; Bee, S.T.; Sin, L.T.; Rahmat, A.R. Polymer nanocomposites based on silylated-montmorillonite: A review. Prog. Polym. Sci. 2018, 85, 57–82. [Google Scholar] [CrossRef]
- Silvestre, C.; Duraccio, D.; Cimmino, S. Food packaging based on polymer nanomaterials. Prog. Polym. Sci. 2011, 36, 1766–1782. [Google Scholar] [CrossRef]
- Sinha Ray, S.; Okamoto, M. Polymer/layered silicate nanocomposites: A review from preparation to processing. Prog. Polym. Sci. 2003, 28, 1539–1641. [Google Scholar] [CrossRef]
- Nordqvist, D.; Hedenqvist, M.S. Transport Properties of Nanocomposites Based on Polymers and Layered Inorganic Fillers. In Packaging Nanotechnology; Mohanty, A.K., Misra, M., Eds.; American Scientific Publishers: Valencia, CA, USA, 2009. [Google Scholar]
- Wokadala, O.C.; Ray, S.S.; Bandyopadhyay, J.; Wesley-Smith, J.; Emmambux, N.M. Morphology, thermal properties and crystallization kinetics of ternary blends of the polylactide and starch biopolymers and nanoclay: The role of nanoclay hydrophobicity. Polymer 2015, 71, 82–92. [Google Scholar] [CrossRef]
- Hoidy, W.H.; Al-Mulla, E.A.J.; Al-Janabi, K.W. Mechanical and Thermal Properties of PLLA/PCL Modified Clay Nanocomposites. J. Polym. Environ. 2010, 18, 608–616. [Google Scholar] [CrossRef]
- Ibrahim, N.; Jollands, M.; Parthasarathy, R. Mechanical and thermal properties of melt processed PLA/organoclay nanocomposites. IOP Conf. Ser. Mater. Sci. Eng. 2017, 191, 012005. [Google Scholar] [CrossRef]
- Krishnamachari, P.; Zhang, J.; Lou, J.; Yan, J.; Uitenham, L. Biodegradable poly(Lactic Acid)/clay nanocomposites by melt intercalation: A study of morphological, thermal, and mechanical properties. Int. J. Polym. Anal. Charact. 2009, 14, 336–350. [Google Scholar] [CrossRef]
- Hasook, A.; Tanoue, S.; Iemoto, Y.; Unryu, T. Characterization and mechanical properties of poly(lactic acid)/poly(ϵ-caprolactone)/organoclay nanocomposites prepared by melt compounding. Polym. Eng. Sci. 2006, 46, 1001–1007. [Google Scholar] [CrossRef]
- Lai, S.M.; Wu, S.H.; Lin, G.G.; Don, T.M. Unusual mechanical properties of melt-blended poly(lactic acid) (PLA)/clay nanocomposites. Eur. Polym. J. 2014, 52, 193–206. [Google Scholar] [CrossRef]
- Tabatabaei, S.H.; Ajji, A. Orientation, mechanical, and optical properties of poly (lactic acid) nanoclay composite films. Polym. Eng. Sci. 2011, 51, 2151–2158. [Google Scholar] [CrossRef]
- Cele, H.M.; Ojijo, V.; Chen, H.; Kumar, S.; Land, K.; Joubert, T.; De Villiers, M.F.R.; Ray, S.S. Effect of nanoclay on optical properties of PLA/clay composite films. Polym. Test. 2014, 36, 24–31. [Google Scholar] [CrossRef]
- Stloukal, P.; Pekařová, S.; Kalendova, A.; Mattausch, H.; Laske, S.; Holzer, C.; Chitu, L.; Bodner, S.; Maier, G.; Slouf, M.; et al. Kinetics and mechanism of the biodegradation of PLA/clay nanocomposites during thermophilic phase of composting process. Waste Manag. 2015, 42, 31–40. [Google Scholar] [CrossRef]
- Castro-Aguirre, E.; Auras, R.; Selke, S.; Rubino, M.; Marsh, T. Impact of nanoclays on the biodegradation of poly(lactic acid) nanocomposites. Polymers 2018, 10, 202. [Google Scholar] [CrossRef]
- Rovera, C.; Ghaani, M.; Farris, S. Nano-inspired oxygen barrier coatings for food packaging applications: An overview. Trends Food Sci. Technol. 2020, 97, 210–220. [Google Scholar] [CrossRef]
- Choudalakis, G.; Gotsis, A.D. Permeability of polymer/clay nanocomposites: A review. Eur. Polym. J. 2009, 45, 967–984. [Google Scholar] [CrossRef]
- Kotal, M.; Bhowmick, A.K. Polymer nanocomposites from modified clays: Recent advances and challenges. Prog. Polym. Sci. 2015, 51, 127–187. [Google Scholar] [CrossRef]
- Zhu, T.T.; Zhou, C.H.; Kabwe, F.B.; Wu, Q.Q.; Li, C.S.; Zhang, J.R. Exfoliation of montmorillonite and related properties of clay/polymer nanocomposites. Appl. Clay Sci. 2019, 169, 48–66. [Google Scholar] [CrossRef]
- Tan, B.; Thomas, N.L. A review of the water barrier properties of polymer/clay and polymer/graphene nanocomposites. J. Memb. Sci. 2016, 514, 595–612. [Google Scholar] [CrossRef]
- Wolf, C.; Angellier-Coussy, H.; Gontard, N.; Doghieri, F.; Guillard, V. How the shape of fillers affects the barrier properties of polymer/non-porous particles nanocomposites: A review. J. Memb. Sci. 2018, 556, 393–418. [Google Scholar] [CrossRef]
- Kalendova, A.; Merinska, D.; Gerard, J.F.; Slouf, M. Polymer/clay nanocomposites and their gas barrier properties. Polym. Compos. 2013, 34, 1418–1424. [Google Scholar] [CrossRef]
- Cui, Y.; Kumar, S.; Rao Kona, B.; Van Houcke, D. Gas barrier properties of polymer/clay nanocomposites. RSC Adv. 2015, 5, 63669–63690. [Google Scholar] [CrossRef]
- Raquez, J.M.; Habibi, Y.; Murariu, M.; Dubois, P. Polylactide (PLA)-based nanocomposites. Prog. Polym. Sci. 2013, 38, 1504–1542. [Google Scholar] [CrossRef]
- Krikorian, V.; Pochan, D.J. Poly (l-Lactic Acid)/Layered Silicate Nanocomposite: Fabrication, Characterization, and Properties. Chem. Mater. 2003, 15, 4317–4324. [Google Scholar] [CrossRef]
- Pavlidou, S.; Papaspyrides, C.D. A review on polymer-layered silicate nanocomposites. Prog. Polym. Sci. 2008, 33, 1119–1198. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, H.; Wang, W.; Liu, T. Crystallization behavior of poly(ε-caprolactone)/layered double hydroxide nanocomposites. J. Appl. Polym. Sci. 2010, 116, 2658–2667. [Google Scholar] [CrossRef]
- Chen, G.X.; Kim, H.S.; Shim, J.H.; Yoon, J.S. Role of epoxy groups on clay surface in the improvement of morphology of poly(L-lactide)/clay composites. Macromolecules 2005, 38, 3738–3744. [Google Scholar] [CrossRef]
- Jiang, L.; Liu, B.; Zhang, J. Properties of poly(lactic acid)/poly(butylene adipate-co-terephthalate)/ nanoparticle ternary composites. Ind. Eng. Chem. Res. 2009, 48, 7594–7602. [Google Scholar] [CrossRef]
- Ozkoc, G.; Kemaloglu, S.; Quaedflieg, M. Production of poly(lactic acid)/organoclay nanocomposite scaffolds by microcompounding and polymer/particle leaching. Polym. Compos. 2010, 31, 674–683. [Google Scholar] [CrossRef]
- Hasook, A.; Muramatsu, H.; Tanoue, S.; Iemoto, Y.; Unryu, T. Preparation of nanocomposites by melt compounding polylactic acid/polyamide 12/organoclay at different screw rotating speeds using a twin screw extruder. Polym. Compos. 2008, 29, 1–8. [Google Scholar] [CrossRef]
- Katiyar, V.; Nanavati, H. In situ synthesis of high molecular weight poly(L-lactic acid) clay nanocomposites. Polym. Eng. Sci. 2011, 51, 2066–2077. [Google Scholar] [CrossRef]
- Katiyar, V.; Nanavati, H. High molecular weight poly (L-lactic acid) clay nanocomposites via solid-state polymerization. Polym. Compos. 2011, 32, 497–509. [Google Scholar] [CrossRef]
- Paul, M.A.; Delcourt, C.; Alexandre, M.; Degée, P.; Monteverde, F.; Rulmont, A.; Dubois, P. (Plasticized) polylactide/(organo-)clay nanocomposites by in situ intercalative polymerization. Macromol. Chem. Phys. 2005, 206, 484–498. [Google Scholar] [CrossRef]
- Gorrasi, G.; Tammaro, L.; Vittoria, V.; Paul, M.A.; Alexandre, M.; Dubois, P. Transport properties of water vapor in polylactide/montmorillonite nanocomposites. J. Macromol. Sci. Phys. Part B 2004, 43, 565–575. [Google Scholar] [CrossRef]
- Chang, J.H.; An, Y.U. Nanocomposites of polyurethane with various organoclays: Thermomechanical properties, morphology, and gas permeability. J. Polym. Sci. Part B Polym. Phys. 2002, 40, 670–677. [Google Scholar] [CrossRef]
- Maiti, P.; Yamada, K.; Okamoto, M.; Ueda, K.; Okamoto, K. New polylactide/layered silicate nanocomposites: Role of organoclays. Chem. Mater. 2002, 14, 4654–4661. [Google Scholar] [CrossRef]
- Ray, S.S.; Yamada, K.; Okamoto, M.; Fujimoto, Y.; Ogami, A.; Ueda, K. New polylactide/layered silicate nanocomposites. 5. Designing of materials with desired properties. Polymer 2003, 44, 6633–6646. [Google Scholar]
- Sinha Ray, S.; Yamada, K.; Okamoto, M.; Ogami, A.; Ueda, K. New polylactide/layered silicate nanocomposites. 3. High-performance biodegradable materials. Chem. Mater. 2003, 15, 1456–1465. [Google Scholar] [CrossRef]
- Sinha Ray, S.; Yamada, K.; Okamoto, M.; Ueda, K. New polylactide-layered silicate nanocomposites. 2. Concurrent improvements of material properties, biodegradability and melt rheology. Polymer 2002, 44, 857–866. [Google Scholar] [CrossRef]
- Ray, S.S.; Yamada, K.; Okamoto, M.; Ogami, A.; Ueda, K. New polylactide/layered silicate nanocomposites, 4. Structure, properties and biodegradability. Compos. Interfaces 2003, 10, 435–450. [Google Scholar] [CrossRef]
- Ray, S.S.; Yamada, K.; Ogami, A.; Okamoto, M.; Ueda, K. New polylactide/layered silicate nanocomposite: Nanoscale control over multiple properties. Macromol. Rapid Commun. 2002, 23, 943–947. [Google Scholar] [CrossRef]
- Thellen, C.; Orroth, C.; Froio, D.; Ziegler, D.; Lucciarini, J.; Farrell, R.; D’Souza, N.A.; Ratto, J.A. Influence of montmorillonite layered silicate on plasticized poly(l-lactide) blown films. Polymer 2005, 46, 11716–11727. [Google Scholar] [CrossRef]
- Lagarón, J.M.; Cabedo, L.; Cava, D.; Feijoo, J.L.; Gavara, R.; Gimenez, E. Improving packaged food quality and safety. Part 2: Nanocomposites. Food Addit. Contam. 2005, 22, 994–998. [Google Scholar] [CrossRef]
- Rhim, J.W.; Hong, S.I.; Ha, C.S. Tensile, water vapor barrier and antimicrobial properties of PLA/nanoclay composite films. LWT Food Sci. Technol. 2009, 42, 612–617. [Google Scholar] [CrossRef]
- Zenkiewicz, M.; Richert, J. Permeability of polylactide nanocomposite films for water vapour, oxygen and carbon dioxide. Polym. Test. 2008, 27, 835–840. [Google Scholar] [CrossRef]
- Zenkiewicz, M.; Richert, J.; Rózański, A. Effect of blow moulding ratio on barrier properties of polylactide nanocomposite films. Polym. Test. 2010, 29, 251–257. [Google Scholar] [CrossRef]
- Koh, H.C.; Park, J.S.; Jeong, M.A.; Hwang, H.Y.; Hong, Y.T.; Ha, S.Y.; Nam, S.Y. Preparation and gas permeation properties of biodegradable polymer/layered silicate nanocomposite membranes. Desalination 2008, 233, 201–209. [Google Scholar] [CrossRef]
- Cabedo, L.; Feijoo, J.L.; Villanueva, M.P.; Lagarón, J.M.; Giménez, E. Optimization of biodegradable nanocomposites based on aPLA/PCL blends for food packaging applications. Macromol. Symp. 2006, 233, 191–197. [Google Scholar] [CrossRef]
- Trifol, J.; Plackett, D.; Sillard, C.; Szabo, P.; Bras, J.; Daugaard, A.E. Hybrid poly(lactic acid)/nanocellulose/nanoclay composites with synergistically enhanced barrier properties and improved thermomechanical resistance. Polym. Int. 2016, 65, 988–995. [Google Scholar] [CrossRef]
- Trifol, J.; Plackett, D.; Sillard, C.; Hassager, O.; Daugaard, A.E.; Bras, J.; Szabo, P. A comparison of partially acetylated nanocellulose, nanocrystalline cellulose, and nanoclay as fillers for high-performance polylactide nanocomposites. J. Appl. Polym. Sci. 2016, 133, 43257. [Google Scholar] [CrossRef]
- Singh, S.; Gupta, R.K.; Ghosh, A.K.; Maiti, S.N.; Bhattacharya, S.N. Poly(L-lactic acid)/layered silicate nanocomposite blown film for packaging application: Thermal, mechanical and barrier properties. J. Polym. Eng. 2010, 30, 361–375. [Google Scholar] [CrossRef]
- Park, S.H.; Lee, H.S.; Choi, J.H.; Jeong, C.M.; Sung, M.H.; Park, H.J. Improvements in barrier properties of poly(lactic acid) films coated with chitosan or chitosan/clay nanocomposite. J. Appl. Polym. Sci. 2012, 125, E675–E680. [Google Scholar] [CrossRef]
- Kim, H.K.; Kim, S.J.; Lee, H.S.; Choi, J.H.; Jeong, C.M.; Sung, M.H.; Park, S.H.; Park, H.J. Mechanical and barrier properties of poly(lactic acid) films coated by nanoclay-ink composition. J. Appl. Polym. Sci. 2013, 127, 3823–3829. [Google Scholar] [CrossRef]
- Farmahini-Farahani, M.; Xiao, H.; Zhao, Y. Poly lactic acid nanocomposites containing modified nanoclay with synergistic barrier to water vapor for coated paper. J. Appl. Polym. Sci. 2014, 131, 40952. [Google Scholar] [CrossRef]
- Zheng, W.; Beeler, M.; Claus, J.; Xu, X. Poly(lactic acid)/montmorillonite blown films: Crystallization, mechanics, and permeation. J. Appl. Polym. Sci. 2017, 134, 45260. [Google Scholar] [CrossRef]
- Darie, R.N.; Pâslaru, E.; Sdrobis, A.; Pricope, G.M.; Hitruc, G.E.; Poiatǎ, A.; Baklavaridis, A.; Vasile, C. Effect of nanoclay hydrophilicity on the poly(lactic acid)/clay nanocomposites properties. Ind. Eng. Chem. Res. 2014, 53, 7877–7890. [Google Scholar] [CrossRef]
- Rhim, J.W. Effect of PLA lamination on performance characteristics of agar/κ-carrageenan/clay bio-nanocomposite film. Food Res. Int. 2013, 51, 714–722. [Google Scholar] [CrossRef]
- Jalalvandi, E.; Majid, R.A.; Ghanbari, T.; Ilbeygi, H. Effects of montmorillonite (MMT) on morphological, tensile, physical barrier properties and biodegradability of polylactic acid/starch/MMT nanocomposites. J. Thermoplast. Compos. Mater. 2015, 28, 496–509. [Google Scholar] [CrossRef]
- Othman, S.H.; Ling, H.N.; Talib, R.A.; Naim, M.N.; Risyon, N.P.; Saifullah, M. PLA/MMT and PLA/halloysite bio-nanocomposite films: Mechanical, barrier, and transparency. J. Nano Res. 2019, 59, 77–93. [Google Scholar] [CrossRef]
- Mohsen, A.H.; Ali, N.A. Mechanical, Color and Barrier, Properties of Biodegradable Nanocomposites Polylactic Acid/Nanoclay. J. Bioremediat. Biodegrad. 2018, 9, 455. [Google Scholar] [CrossRef]
- Busolo, M.A.; Fernandez, P.; Ocio, M.J.; Lagaron, J.M. Novel silver-based nanoclay as an antimicrobial in polylactic acid food packaging coatings. Food Addit. Contam. Part A Chem. Anal. Control Expo. Risk Assess. 2010, 27, 1617–1626. [Google Scholar] [CrossRef] [PubMed]
- Şengül, B.; El-abassy, R.M.A.; Materny, A.; Dilsiz, N. Poly(lactic acid)/Organo-Montmorillonite Nanocomposites: Synthesis, Structures, Permeation Properties and Applications. Polym. Sci. Ser. A 2017, 59, 891–901. [Google Scholar] [CrossRef]
- Chowdhury, S.R. Some important aspects in designing high molecular weight poly(l-lactic acid)–clay nanocomposites with desired properties. Polym. Int. 2008, 57, 1326–1332. [Google Scholar] [CrossRef]
- Jorda-Beneyto, M.; Ortuño, N.; Devis, A.; Aucejo, S.; Puerto, M.; Gutiérrez-Praena, D.; Houtman, J.; Pichardo, S.; Maisanaba, S.; Jos, A. Use of nanoclay platelets in food packaging materials: Technical and cytotoxicity approach. Food Addit. Contam. Part A Chem. Anal. Control Expo. Risk Assess. 2014, 31, 354–363. [Google Scholar] [CrossRef]
- Svagan, A.J.; Åkesson, A.; Cárdenas, M.; Bulut, S.; Knudsen, J.C.; Risbo, J.; Plackett, D. Transparent films based on PLA and montmorillonite with tunable oxygen barrier properties. Biomacromolecules 2012, 13, 397–405. [Google Scholar] [CrossRef]
- Carosio, F.; Colonna, S.; Fina, A.; Rydzek, G.; Hemmerlé, J.; Jierry, L.; Schaaf, P.; Boulmedais, F. Efficient gas and water vapor barrier properties of thin poly(lactic acid) packaging films: Functionalization with moisture resistant Nafion and clay multilayers. Chem. Mater. 2014, 26, 5459–5466. [Google Scholar] [CrossRef]
- Crank, J.; Crank, E.P.J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1979. [Google Scholar]
- Wijmans, J.G.; Baker, R.W. The solution-diffusion model: A review. J. Memb. Sci. 1995, 107, 1–21. [Google Scholar] [CrossRef]
- Crank, J. A theoretical investigation of the influence of molecular relaxation and internal stress on diffusion in polymers. J. Polym. Sci. 1953, 11, 151–168. [Google Scholar] [CrossRef]
- Crank, J.; Park, G.S. Diffusion in Polymers; Academic Press: London, UK; New York, NY, USA, 1968. [Google Scholar]
- Barrer, R.M. Diffusivities in glassy polymers for the dual mode sorption model. J. Memb. Sci. 1984, 18, 25–35. [Google Scholar] [CrossRef]
- Meares, P. Transient permeation of organic vapors through polymer membranes. J. Appl. Polym. Sci. 1965, 9, 917–932. [Google Scholar] [CrossRef]
- Hedenqvist, M.S.; Gedde, U.W. Parameters affecting the determination of transport kinetics data in highly swelling polymers above T(g). Polymer 1999, 40, 2381–2393. [Google Scholar] [CrossRef]
- Vieth, W.R. Diffusion in and Through Polymers: Principles and Applications; Hanser Publications: Cincinnati, OH, USA, 1991. [Google Scholar]
- Dhoot, S.N.; Freeman, B.D.; Stewart, M.E. Barrier Polymers. In Encyclopedia of Polymer Science and Technology; John Wiley and Sons Inc.: New York, NY, USA, 2002. [Google Scholar]
- Ziegel, K.D.; Frensdorff, H.K.; Blair, D. Measurement of Hydrogen Isotope Transport in Poly(Vinyl Fluoride) Films By Permeation-Rate Method. J. Polym. Sci. Phys. 1969, 7, 809–819. [Google Scholar] [CrossRef]
- Hedenqvist, M.; Angelstok, A.; Edsberg, L.; Larssont, P.T.; Gedde, U.W. Diffusion of small-molecule penetrants in polyethylene: Free volume and morphology. Polymer 1996, 37, 2887–2902. [Google Scholar] [CrossRef]
- Webb, J.A.; Bower, D.I.; Ward, I.M.; Cardew, P.T. The effect of drawing on the transport of gases through polyethylene. J. Polym. Sci. Part B Polym. Phys. 1993, 31, 743–757. [Google Scholar] [CrossRef]
- Paternak, R.; Schimscheimer, J.F.; Heller, J. Dynamic Approach To Diffusion and Permeation Measurements. J. Polym. Sci. Part A 2 Polym. Phys. 1970, 8, 467–479. [Google Scholar] [CrossRef]
- Hedenqvist, M.S.; Ritums, J.E.; Condé-Brana, M.; Bergman, G. Sorption and desorption of tetrachloroethylene in fluoropolymers: Effects of the chemical structure and crystallinity. J. Appl. Polym. Sci. 2003, 87, 1474–1483. [Google Scholar] [CrossRef]
- Hiltner, A.; Liu, R.Y.F.; Hu, Y.S.; Baer, E. Oxygen transport as a solid-state structure probe for polymeric materials: A review. J. Polym. Sci. Part B Polym. Phys. 2005, 43, 1047–1063. [Google Scholar] [CrossRef]
- Cohen, M.H.; Turnbull, D. Molecular transport in liquids and glasses. J. Chem. Phys. 1959, 31, 1164–1169. [Google Scholar] [CrossRef]
- Nilsson, F.; Hedenqvist, M.S.; Gedde, U.W. Small-molecule diffusion in semicrystalline polymers as revealed by experimental and simulation studies. Macromol. Symp. 2010, 298, 108–115. [Google Scholar] [CrossRef]
- Nilsson, F.; Gedde, U.W.; Hedenqvist, M.S. Penetrant diffusion in polyethylene spherulites assessed by a novel off-lattice Monte-Carlo technique. Eur. Polym. J. 2009, 45, 3409–3417. [Google Scholar] [CrossRef]
- Mogri, Z.; Paul, D.R. Gas sorption and transport in side-chain crystalline and molten poly(octadecyl acrylate). Polymer 2001, 42, 2531–2542. [Google Scholar] [CrossRef]
- Nielsen, L.E. Models for the Permeability of Filled Polymer Systems. J. Macromol. Sci. Part A Chem. 1967, 1, 929–942. [Google Scholar] [CrossRef]
- Cussler, E.L.; Hughes, S.E.; Ward, W.J.; Aris, R. Barrier membranes. J. Memb. Sci. 1988, 38, 161–174. [Google Scholar] [CrossRef]
- Brydges, W.T.; Gulati, S.T.; Baum, G. Permeability of glass ribbon-reinforced composites. J. Mater. Sci. 1975, 10, 2044–2049. [Google Scholar] [CrossRef]
- Lape, N.K.; Nuxoll, E.E.; Cussler, E.L. Polydisperse flakes in barrier films. J. Memb. Sci. 2004, 236, 29–37. [Google Scholar] [CrossRef]
- Fredrickson, G.H.; Bicerano, J. Barrier properties of oriented disk composites. J. Chem. Phys. 1999, 110, 2181–2188. [Google Scholar] [CrossRef]
- Gusev, A.A.; Lusti, H.R. Rational design of nanocomposites for barrier applications. Adv. Mater. 2001, 13, 1641–1643. [Google Scholar] [CrossRef]
- Bharadwaj, R.K. Modeling the barrier properties of polymer-layered silicate nanocomposites. Macromolecules 2001, 34, 9189–9192. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, K.; Zuo, X.; Xue, Y.; Marmorat, C.; Liu, Y.; Chang, C.C.; Rafailovich, M.H. Effects of clay platelets and natural nanotubes on mechanical properties and gas permeability of Poly (lactic acid) nanocomposites. Polymer 2016, 83, 246–259. [Google Scholar] [CrossRef]
- Picard, E.; Espuche, E.; Fulchiron, R. Effect of an organo-modified montmorillonite on PLA crystallization and gas barrier properties. Appl. Clay Sci. 2011, 53, 58–65. [Google Scholar] [CrossRef]
- Li, Y.; Ren, P.; Zhang, Q.; Shen, T.; Ci, J.; Fang, C. Properties of Poly(lactic acid )/Organo-Montmorillonite Nanocomposites Prepared by Solution Intercalation. J. Macromol. Sci. Part B Phys. 2013, 52, 1041–1055. [Google Scholar] [CrossRef]
- Bhatia, A.; Gupta, R.K.; Bhattacharya, S.N.; Choi, H.J. Analysis of Gas Permeability Characteristics of Poly( Lactic Acid )/ Poly ( Butylene Succinate ) Nanocomposites. J. Nanomater. 2012, 2012, 249094. [Google Scholar] [CrossRef]
- Tenn, N.; Follain, N.; Soulestin, J.; Crétois, R.; Bourbigot, S.; Marais, S. Effect of Nanoclay Hydration on Barrier Properties of PLA/Montmorillonite Based Nanocomposites. J. Phys. Chem. C 2013, 117, 12117–12135. [Google Scholar] [CrossRef]
- Hedenqvist, M.; Gedde, U.W. Diffusion of small-molecule penetrants in semicrystalline polymers. Prog. Polym. Sci. 1996, 21, 299–333. [Google Scholar] [CrossRef]









| Matrix | Nanoclay | Name and Formula of Organic Modifier | Penetrant | Clay Content | BIF | Ref |
|---|---|---|---|---|---|---|
| PLA | MMT | Dodecyltrimethyl ammonium, (Me)3(C12H25)N+ | O2 | 10 wt% | 2.3 | [64] |
| MMT | Hexadecyl ammonium, (C16H33)NH3+ | O2 | 10 wt% | 2.4 | ||
| Cloisite 25A | Dimethyloctyl tallow amine (Me)2(C8H17)TN+ | O2 | 10 wt% | 2.3 | ||
| PLA | Smectite | Hexadecyltributyl phosphonium (C4H9)3(C16H33)P+ | O2 | 4 wt% | 1.7 | [65] |
| PLA | MMT | Octadecyl ammonium C18H37NH3+ | O2 | 4 wt% | 1.2 | [66] |
| MMT | Octadecyltrimethyl ammonium (Me)3(C18H37)N+ | O2 | 4 wt% | 1.1 | ||
| Saponite | Hexadecyltributyl phosphonium (C4H9)3(C16H33)P+ | O2 | 4 wt% | 1.7 | ||
| Synthetic fluorine mica (SFM) | Dipolyoxyethylene alkyl (coco) methyl ammonium (CH2CH2O)xH(CH2CH2O)yH(Me) R(coco)N+ | O2 | 4 wt% | 2.8 | ||
| PLA | SFM | N-(cocoalkyl)-N,N-[bis(2-hydroxyethyl)]-N-methyl ammonium (Me)(EtOH)2R(cocoalkyl)N+ | O2 | 10 wt% | 5.5 | [67] |
| PLA | MMT | Octadecyltrimethyl ammonium (Me)3(C18H37)N+ | O2 | 7 wt% | 1.2 | [68] |
| PLA | MMT | Octadecyl ammonium C18H37NH3+ | O2 | 7 wt% | 1.5 | [69] |
| PLA | SFM | N-(cocoalkyl)-N,N-[bis(2-hydroxyethyl)]-N-methyl ammonium (Me)(EtOH)2R(cocoalkyl)N+ | O2 | 4 wt% | 2.8 | [70] |
| PLA | Cloisite 25A | Dimethyl hydrogenated tallow-2-ethylhexyl ammonium (Me)2(C8H17)(HT)N+ | O2 | 5 wt% | 1.7 | [71] |
| H2O | 5 wt% | 2.7 | ||||
| aPLA | Kaolinite | Not disclosed | O2 | 4 wt% | 1.8 | [72] |
| MMT | Not disclosed | O2 | 4 wt% | 1.1 | ||
| PLA | Cloisite 20A | Dimethyl dihydrogenated tallow quaternary ammonium (Me)2(HT)2N+ | H2O | 5 pph | 1.5 | [73] |
| Cloisite 30B | Methyltallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | H2O | 5 pph | 1.0 | ||
| Cloisite Na+ | Unmodified | H2O | 5 pph | 0.8 | ||
| PLA | Cloisite 15A | Dimethyl dihydrogenated tallow quaternary ammonium (Me)2(HT)2N+ | CO2 | 0.8 wt% | 2.0 | [76] |
| O2 | 0.8 wt% | 1.4 | ||||
| N2 | 0.8 wt% | 1.5 | ||||
| Cloisite 20A | Dimethyl dihydrogenated tallow quaternary ammonium (Me)2(HT)2N+ | CO2 | 0.8 wt% | 1.4 | ||
| O2 | 0.8 wt% | 1.1 | ||||
| N2 | 0.8 wt% | 1.5 | ||||
| Cloisite 30B | Methyl tallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | CO2 | 0.8 wt% | 2.0 | ||
| O2 | 0.8 wt% | 1.3 | ||||
| N2 | 0.8 wt% | 2.0 | ||||
| aPLA | Kaolinite | Not disclosed | O2 | 4 wt% | 1.8 | [77] |
| PLA | Cloisite 30B | Methyl tallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | O2 | 5 wt% | 1.6 | [78] |
| H2O | 5 wt% | 2.1 | ||||
| PLA | Cloisite 30B | Methyl tallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | O2 | 3 phr | 1.5 | [80] |
| PLA | Cloisite 30B | Methyl tallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | O2 | 1 wt% | 187.0 | [81] |
| H2O | 1 wt% | 1.25 | ||||
| PLA | Cloisite 30B | Methyl tallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | O2 | 2 wt% | 1.6 | [82] |
| H2O | 1 wt% | 1.2 | ||||
| PLA | Cloisite 30B | Methyl tallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | H2O | 5 wt% | 2.8 | [83] |
| PLA | Cloisite 30B | Methyl tallow-bis-2-hydroxyethyl quaternary ammonium (Me)(CH2CH2OH)2(T)N+ | O2 | 3 wt% | 1.3 | [84] |
| PLA | Cloisite 93A | Methyl dihydrogenated tallow quaternary ammonium (Me)(HT)2NH+ | O2 | 3 wt% | 2.0 | [85] |
| CO2 | 3 wt% | 3.45 | ||||
| Dellite HPS | Not disclosed | O2 | 3 wt% | 18.4 | ||
| CO2 | 3 wt% | 30.2 | ||||
| PLA | Cloisite-Na+ | Agar/κ-carrageenan | O2 | 5 wt% | 516.0 | [86] |
| PLA | MMT | unmodified | H2O | 7 wt% | 19.0 | [87] |
| PLA | MMT | Not disclosed | O2 | 3 wt% | 1.5 | [88] |
| PLA | Clay name not mentioned | Not disclosed | O2 | 4 wt% | 2.6 | [89] |
| H2O | 6 wt% | 3.1 | ||||
| PLA | Ag-based MMT | Not disclosed | H2O | 10 wt% | 1.2 | [90] |
| PLA | MMT | Dimethyldialkyl ammonium (Me)2(R)2N+ | O2 | 10 wt% | 2.0 | [91] |
| H2O | 10 wt% | 4.8 | ||||
| Aminopropyltriethoxysilane (CH3CH2O)3Si(C3H6)NH2 | O2 | 10 wt% | 1.5 | |||
| H2O | 10 wt% | 2.7 | ||||
| Distearyldimethyl ammonium (C18H37)2(Me)2N+ | O2 | 10 wt% | 1.9 | |||
| H2O | 10 wt% | 5.0 | ||||
| Hydrogenated tallow quaternary ammonium (HT)4N+ | O2 | 10 wt% | 1.7 | |||
| H2O | 10 wt% | 2.3 | ||||
| PLA | MMT (Southern clay) | Octadecyl ammonium C18H37NH3+ | O2 | 5 wt% | 1.8 | [92] |
| MMT (Nanocor) | Octadecyl ammonium C18H37NH3+ | O2 | 5 wt% | 1.3 | ||
| SFM | Octadecyl ammonium C18H37NH3+ | O2 | 5 wt% | 2.1 | ||
| PLA | MMT | Hexadecyltrimethyl ammonium (Me)3(C16H33)N+ | H2O | 4 wt% | 1.6 | [93] |
| O2 | 4 wt% | 1.7 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Singha, S.; Hedenqvist, M.S. A Review on Barrier Properties of Poly(Lactic Acid)/Clay Nanocomposites. Polymers 2020, 12, 1095. https://doi.org/10.3390/polym12051095
Singha S, Hedenqvist MS. A Review on Barrier Properties of Poly(Lactic Acid)/Clay Nanocomposites. Polymers. 2020; 12(5):1095. https://doi.org/10.3390/polym12051095
Chicago/Turabian StyleSingha, Shuvra, and Mikael S. Hedenqvist. 2020. "A Review on Barrier Properties of Poly(Lactic Acid)/Clay Nanocomposites" Polymers 12, no. 5: 1095. https://doi.org/10.3390/polym12051095
APA StyleSingha, S., & Hedenqvist, M. S. (2020). A Review on Barrier Properties of Poly(Lactic Acid)/Clay Nanocomposites. Polymers, 12(5), 1095. https://doi.org/10.3390/polym12051095






