Performance Optimization of Polymer Fibre Actuators for Soft Robotics
Abstract
1. Introduction
2. Results
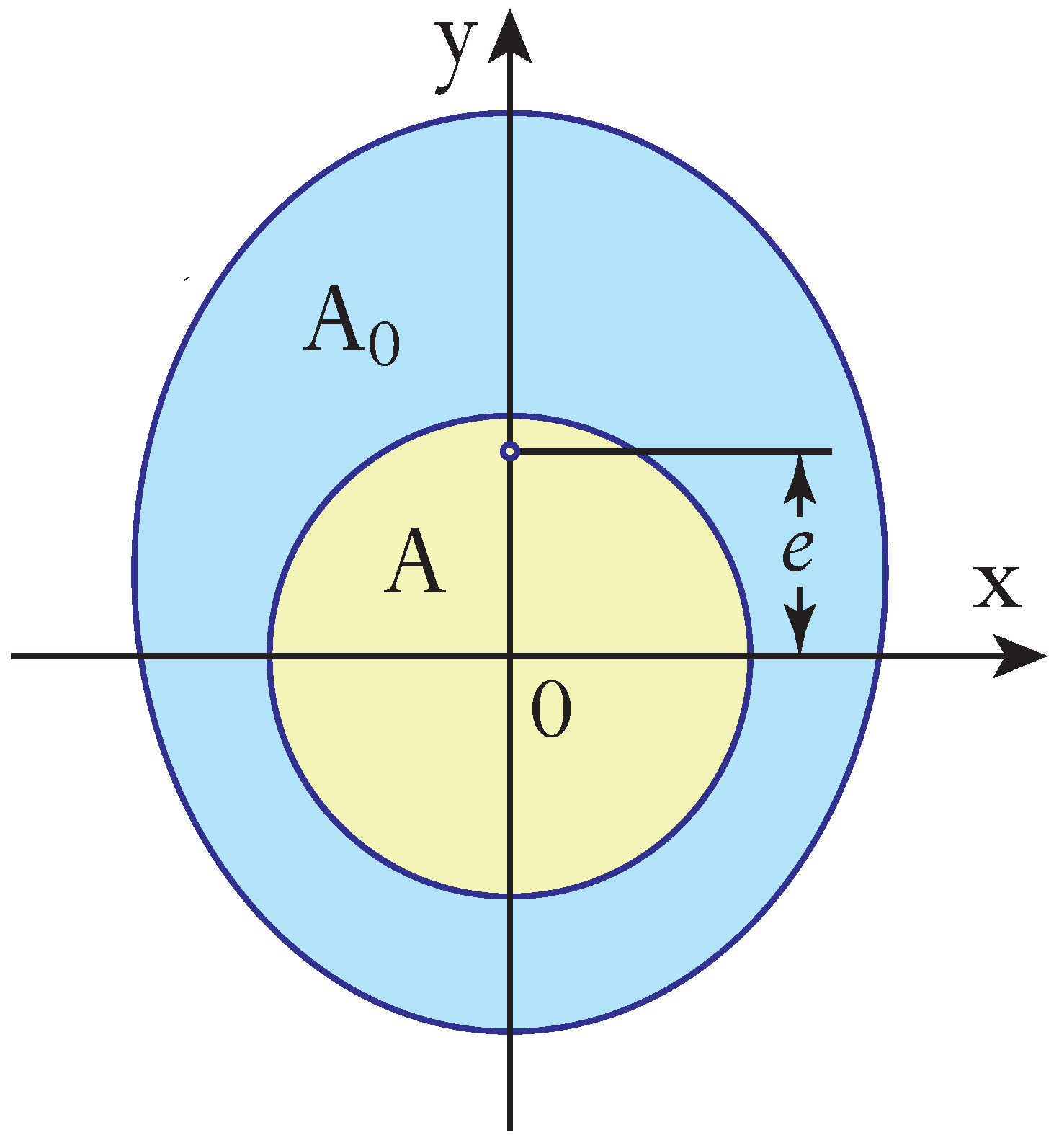
2.1. Statics of Pneumatic Actuators
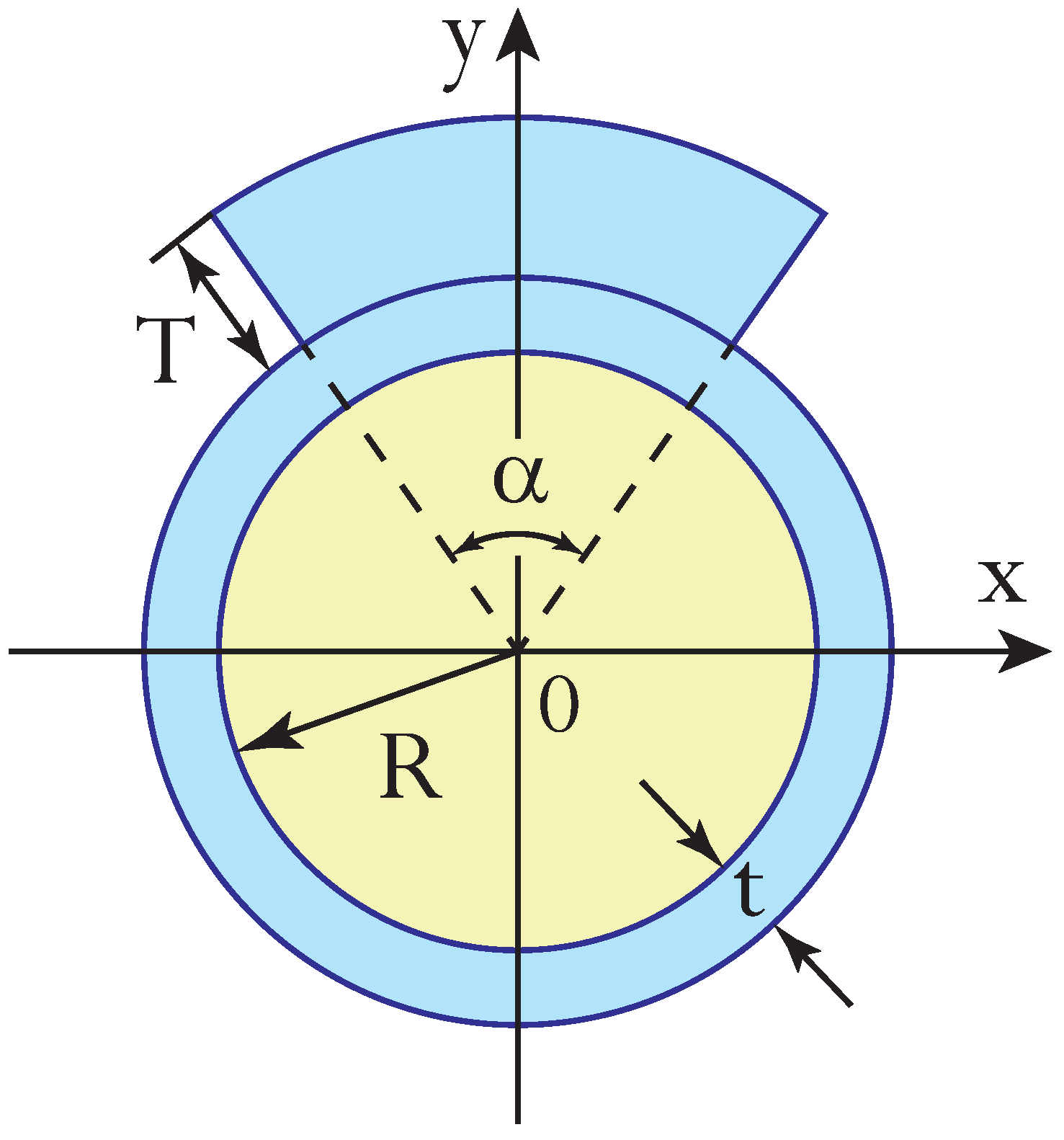
2.2. Bending of Hollow-Tube Pneumatic Actuator
3. Discussion
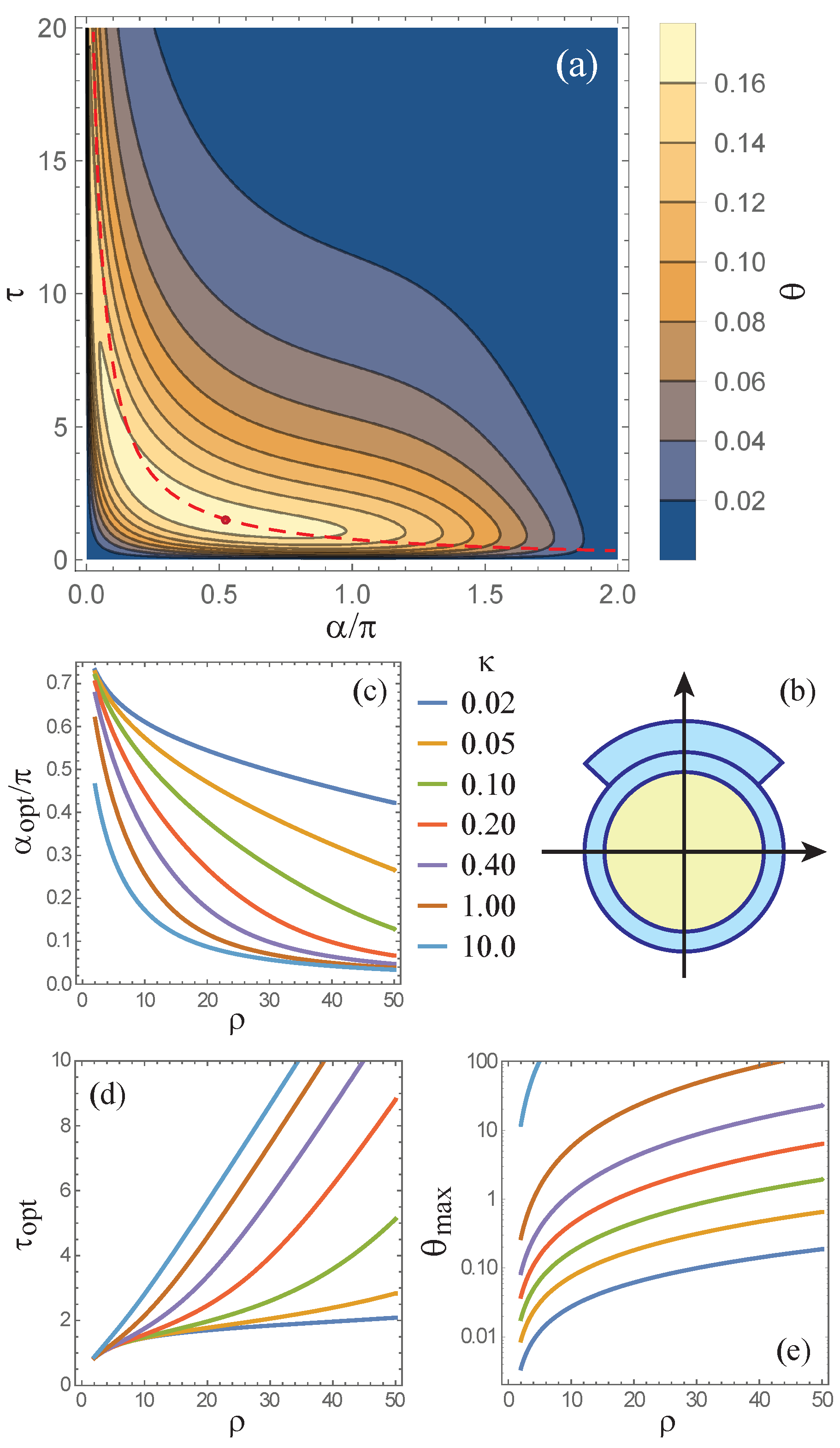
3.1. Tubes of Equal Thicknesses
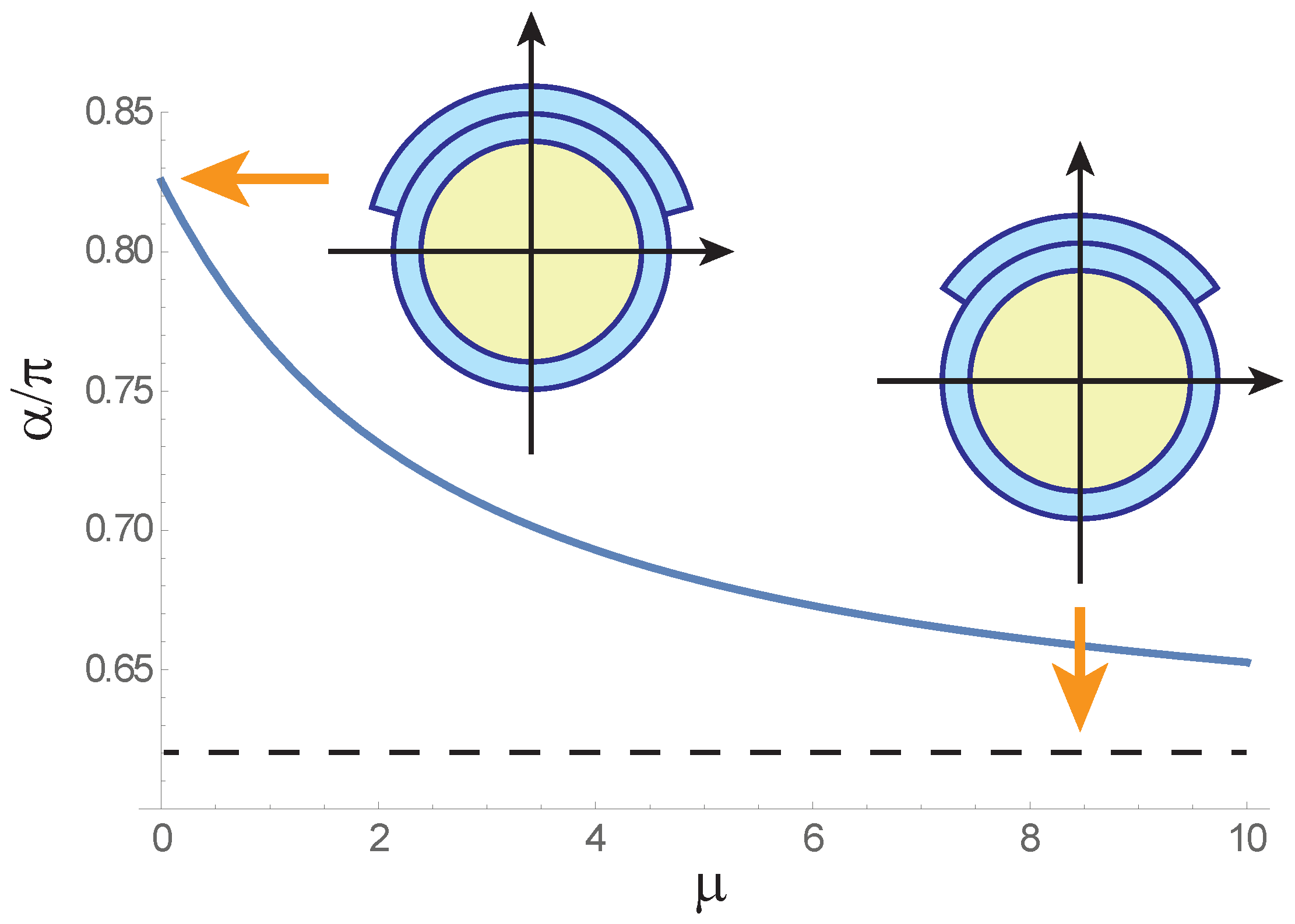
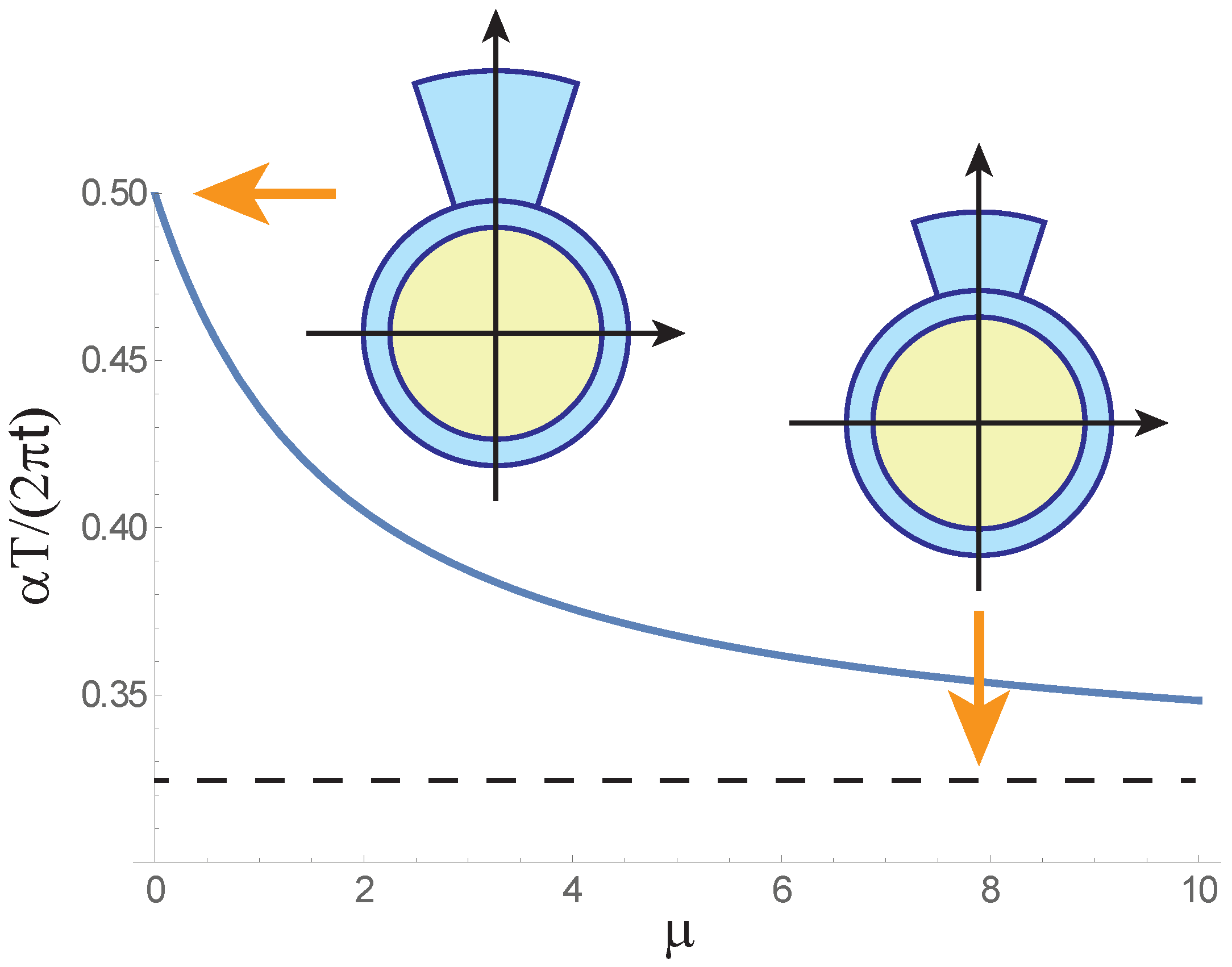
3.2. A Small Asymmetric Patch
3.3. Optimization in General Case
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| E | Young’s modulus |
| yield stress | |
| P | pressure inside the actuator |
| e | distance from the neutral axis to the centroid |
| I | area moment of inertia with respect to the neutral axis |
| area moment of inertia with respect to the centroid | |
| cross-sectional area of the polymer tube | |
| A | cross-sectional area of the pressurized volume of the polymer tube |
| L | length of the polymer tube |
| elongation of the polymer tube | |
| R | internal radius of the polymer tube |
| t | thickness of the polymer tube |
| angular width of the polymer patch | |
| T | thickness of the polymer patch |
| bending angle of the actuator |
References
- Delgado, J.M.D.; Oyedele, L.; Ajayi, A.; Akanbi, L.; Akinade, O.; Bilal, M.; Owolabi, H. Robotics and automated systems in construction: Understanding industry-specific challenges for adoption. J. Build. Eng. 2019, 26, 100868. [Google Scholar] [CrossRef]
- Ji, W.; Wang, L. Industrial robotic machining: A review. Int. J. Adv. Manufact. Technol. 2019, 103, 1239–1255. [Google Scholar] [CrossRef]
- Ogbemhe, J.; Mpofu, K.; Tlale, N.S. Achieving sustainability in manufacturing using robotic methodologies. Procedia Manufact. 2017, 8, 440–446. [Google Scholar] [CrossRef]
- Tang, Z.Q.; Heung, H.L.; Tong, K.Y.; Li, Z. Model-based online learning and adaptive control for a “human-wearable soft robot” integrated system. Int. J. Robot. Res. 2019, 1–21. [Google Scholar] [CrossRef]
- Jung, J.C.; Rodrigue, H. Film-based anisotropic balloon inflatable bending actuator. J. Mech. Sci. Technol. 2019, 33, 4469–4476. [Google Scholar] [CrossRef]
- Sangian, D.; Foroughi, J.; Farajikhah, S.; Naficy, S.; Spinks, G.M. A bladder-free, non-fluidic, conductive McKibben artificial muscle operated electro-thermally. Smart Mater. Struct. 2017, 26, 015011. [Google Scholar] [CrossRef]
- Moseley, P.; Florez, J.M.; Sonar, H.A.; Agarwal, G.; Curtin, W.; Paik, J. Modeling, design, and development of soft pneumatic actuators with finite element method. Adv. Eng. Mater. 2016, 18, 978–988. [Google Scholar] [CrossRef]
- Rus, D.; Tolley, M. Design, fabrication and control of soft robots. Nature 2015, 521, 467–475. [Google Scholar] [CrossRef] [PubMed]
- Marchese, A.D.; Katzschmann, R.K.; Rus, D. A recipe for soft fluidic elastomer robots. Soft Robot. 2015, 2, 7–25. [Google Scholar] [CrossRef] [PubMed]
- Feng, N.; Shi, Q.; Wang, H.; Gong, J.; Liu, C.; Lu, Z. A soft robotic hand: Design, analysis, sEMG control, and experiment. Int. J. Adv. Manufact. Technol. 2018, 97, 319–333. [Google Scholar] [CrossRef]
- Awad, L.N.; Bae, J.; O’Donnell, K.; De Rossi, S.M.M.; Hendron, K.; Sloot, L.H.; Kudzia, P.; Allen, S.; Holt, K.G.; Ellis, T.; et al. A soft robotic exosuit improves walking in patients after stroke. Sci. Transl. Med. 2017, 9. [Google Scholar] [CrossRef] [PubMed]
- Polygerinos, P.; Wang, Z.; Galloway, K.C.; Wood, R.J.; Walsh, C.J. Soft robotic glove for combined assistance and at-home rehabilitation. Robot. Auton. Syst. 2015, 73, 135–143. [Google Scholar] [CrossRef]
- Liang, X.; Cheong, H.; Chui, C.K.; Yeow, C.H. A fabric-based wearable soft robotic limb. J. Mech. Robot. 2019, 11, 031003. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Bao, G.; Fang, H.; Chen, L.; Wan, Y.; Xu, F.; Yang, Q.; Zhang, L. Soft robotics: Academic insights and perspectives through bibliometric analysis. Soft Robot. 2018, 5, 229–241. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Chen, Y.; Li, Y.; Chen, M.Z.; Wei, Y. Bioinspired robotic fingers based on pneumatic actuator and 3D printing of smart material. Soft Robot. 2017, 4, 147–162. [Google Scholar] [CrossRef]
- Yap, H.K.; Ng, H.Y.; Yeow, C.H. High-force soft printable pneumatics for soft robotic applications. Soft Robot. 2016, 3, 144–158. [Google Scholar] [CrossRef]
- Hwang, Y.; Paydar, O.H.; Candler, R.N. Pneumatic microfinger with balloon fins for linear motion using 3D printed molds. Sensor. Actuators B Phys. 2015, 234, 65–71. [Google Scholar] [CrossRef]
- Bauer, S.; Bauer-Gogonea, S.; Graz, I.M.; Kaltenbrunner, M.; Keplinger, C.; Schwödiauer, R. A soft future: From robots and sensor skin to energy harvesters. Adv. Mater. 2014, 26, 149–161. [Google Scholar] [CrossRef]
- Kim, S.; Laschi, C.; Trimmer, B. Soft robotics: A bioinspired evolution in robotics. Trends Biotechnol. 2013, 31, 287–294. [Google Scholar] [CrossRef]
- Shapiro, Y.; Wolf, A.; Kósa, G. Piezoelectric deflection sensor for a bi-bellows actuator. IEEE/ASME Trans. Mechatron. 2012, 18, 1226–1230. [Google Scholar] [CrossRef]
- Shapiro, Y.; Wolf, A.; Gabor, K. Bi-bellows: Pneumatic bending actuator. Sensor. Actuators A Phys. 2011, 167, 484–494. [Google Scholar] [CrossRef]
- Laschi, C.; Rossiter, J.; Iida, F.; Cianchetti, M.; Margheri, L. Soft Robotics: Trends, Applications and Challenges; Biosystems and Biorobotics; Springer: Berlin, Germany, 2016; Volume 17. [Google Scholar]
- Verl, A.; Albu-Schäffer, A.; Brock, O.; Raatz, A. Soft Robotics; Springer: Berlin, Germany, 2015. [Google Scholar]
- Pfeifer, R.; Lungarella, M.; Iida, F. The challenges ahead for bio-inspired ‘soft’ robotics. Commun. ACM 2012, 55, 76–87. [Google Scholar] [CrossRef]
- Hu, W.; Lum, G.Z.; Mastrangeli, M.; Sitti, M. Small-scale soft-bodied robot with multimodal locomotion. Nature 2018, 554, 81. [Google Scholar] [CrossRef]
- Patel, V. Future of robotics in spine surgery. Spine 2018, 43, S28. [Google Scholar] [CrossRef]
- Chen, X.Z.; Jang, B.; Ahmed, D.; Hu, C.; De Marco, C.; Hoop, M.; Mushtaq, F.; Nelson, B.J.; Pané, S. Small-scale machines driven by external power sources. Adv. Mater. 2018, 30, 1705061. [Google Scholar] [CrossRef]
- Huang, H.W.; Tibbitt, M.W.; Huang, T.Y.; Nelson, B.J. Matryoshka-inspired micro-origami capsules to enhance loading, encapsulation, and transport of drugs. Soft Robot. 2019, 6, 150–159. [Google Scholar] [CrossRef]
- Rassweiler, J.J.; Autorino, R.; Klein, J.; Mottrie, A.; Goezen, A.S.; Stolzenburg, J.U.; Rha, K.H.; Schurr, M.; Kaouk, J.; Patel, V.; et al. Future of robotic surgery in urology. BJU Int. 2017, 120, 822–841. [Google Scholar] [CrossRef]
- Hines, L.; Petersen, K.; Lum, G.Z.; Sitti, M. Soft actuators for small-scale robotics. Adv. Mater. 2017, 29, 1603483. [Google Scholar] [CrossRef]
- Diana, M.; Marescaux, J. Robotic surgery. Br. J. Surg. 2015, 102, e15–e28. [Google Scholar] [CrossRef]
- Volder, M.D.; Reynaerts, D. Pneumatic and hydraulic microactuators: A review. J. Micromech. Microeng. 2010, 20, 043001. [Google Scholar] [CrossRef]
- Zhang, M.; Li, G.; Yang, X.; Xiao, Y.; Yang, T.; Wong, T.W.; Li, T. Artificial muscle driven soft hydraulic robot: Electromechanical actuation and simplified modeling. Smart Mater. Struct. 2018, 27, 095016. [Google Scholar] [CrossRef]
- Yeo, J.C.; Yap, H.K.; Xi, W.; Wang, Z.; Yeow, C.H.; Lim, C.T. Flexible and stretchable strain sensing actuator for wearable soft robotic applications. Adv. Mater. Technol. 2016, 1, 1600018. [Google Scholar] [CrossRef]
- Agarwal, G.; Besuchet, N.; Audergon, B.; Paik, J. Stretchable materials for robust soft actuators towards assistive wearable devices. Sci. Rep. 2016, 6, 34224. [Google Scholar] [CrossRef]
- Yang, D.; Mosadegh, B.; Ainla, A.; Lee, B.; Khashai, F.; Suo, Z.; Bertoldi, K.; Whitesides, G.M. Buckling of elastomeric beams enables actuation of soft machines. Adv. Mater. 2015, 27, 6323–6327. [Google Scholar] [CrossRef]
- Tondu, B. Modelling of the McKibben artificial muscle: A review. J. Intel. Mat. Syst. Str. 2012, 23, 225–253. [Google Scholar] [CrossRef]
- Fleming, S.; Large, M.; Stefani, A. Polyurethane optical fiber sensors. In Proceedings of the Optical Sensors and Sensing Congress (ES, FTS, HISE, Sensors), OSA, San Jose, CA, USA, 25–27 June 2019; p. STh5A.1. [Google Scholar]
- Runge, A.F.J.; Stefani, A.; Lwin, R.; Fleming, S.C. Wearable polyurethane optical fiber based sensor for breathing monitoring. In Proceedings of the 26th International Conference on Optical Fiber Sensors, OSA, Lausanne, Switzerland, 24–28 September 2018; p. ThE75. [Google Scholar]
- Xue, S.; Barton, G.W.; Fleming, S.; Argyros, A. Analysis of capillary instability in metamaterials fabrication using fiber drawing technology. J. Light. Technol. 2017, 35, 2167–2174. [Google Scholar] [CrossRef]
- Fleming, S.; Stefani, A.; Hayashi, J.; Kuhlmey, B. Metamaterials fabricated by fibre drawing. In Proceedings of the 23rd Opto-Electronics and Communications Conference (OECC), Jeju Island, Korea, 2–6 July 2018; pp. 1–2. [Google Scholar]
- Argyros, A.; Tuniz, A.; Fleming, S.C.; Kuhlmey, B.T. Drawn Metamaterials. In Optofluidics, Sensors and Actuators in Microstructured Optical Fibers; Pissadakis, S., Selleri, S., Eds.; Woodhead Publishing: Sawston, UK, 2015; pp. 29–54. [Google Scholar]
- Alici, G. An effective modelling approach to estimate nonlinear bending behaviour of cantilever type conducting polymer actuators. Sensor. Actuators B Chem. 2009, 141, 284–292. [Google Scholar] [CrossRef]
- Timoshenko, S. Strength of Materials. Part 1. Elementary Theory and Problems, 3rd ed.; Krieger Pub Co.: Malabar, FL, USA, 1983; Volume 1. [Google Scholar]
- Alici, G.; Canty, T.; Mutlu, R.; Hu, W.; Sencadas, V. Modeling and experimental evaluation of bending behavior of soft pneumatic actuators made of discrete actuation chambers. Angew. Chem. Int. Ed. 2018, 5, 24–35. [Google Scholar] [CrossRef]
- Ashby, M.F.; Jones, D.R.H. Engineering Materials 1. An Introduction to Their Properties and Applications, 2nd ed.; Butterworth Heinemann: Oxford, UK, 1996; Volume 1. [Google Scholar]
| Polymer | E (MPa) | (MPa) | |
|---|---|---|---|
| Silicone elastomers | 5–20 | 2.4–5.5 | 0.28–0.48 |
| Ethylene-vinyl acetate | 10–40 | 12–18 | 0.5–1.2 |
| Butyl rubber | 1–2 | 2–3 | 1.5–2 |
| Neoprene | 0.7–2 | 3.4–24 | 4.9–12 |
| Natural rubber | 1.5–2.5 | 20–30 | 12–13.3 |
| Isoprene | 1.4–4 | 20–25 | 6.3–14.3 |
| Polyurethane elastomers | 2–3 | 25–51 | 12.5–17 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rukhlenko, I.D.; Farajikhah, S.; Lilley, C.; Georgis, A.; Large, M.; Fleming, S. Performance Optimization of Polymer Fibre Actuators for Soft Robotics. Polymers 2020, 12, 454. https://doi.org/10.3390/polym12020454
Rukhlenko ID, Farajikhah S, Lilley C, Georgis A, Large M, Fleming S. Performance Optimization of Polymer Fibre Actuators for Soft Robotics. Polymers. 2020; 12(2):454. https://doi.org/10.3390/polym12020454
Chicago/Turabian StyleRukhlenko, Ivan D., Syamak Farajikhah, Charles Lilley, Andre Georgis, Maryanne Large, and Simon Fleming. 2020. "Performance Optimization of Polymer Fibre Actuators for Soft Robotics" Polymers 12, no. 2: 454. https://doi.org/10.3390/polym12020454
APA StyleRukhlenko, I. D., Farajikhah, S., Lilley, C., Georgis, A., Large, M., & Fleming, S. (2020). Performance Optimization of Polymer Fibre Actuators for Soft Robotics. Polymers, 12(2), 454. https://doi.org/10.3390/polym12020454






