Performance of Coarse Graining in Estimating Polymer Properties: Comparison with the Atomistic Model
Abstract
1. Introduction
2. Methodology
2.1. Bead–Spring KG Model
2.2. DPD with the Slip-Spring Model
2.3. Atomistic Model of PE
2.4. Rescaling of the CG Models
3. Results and Discussion
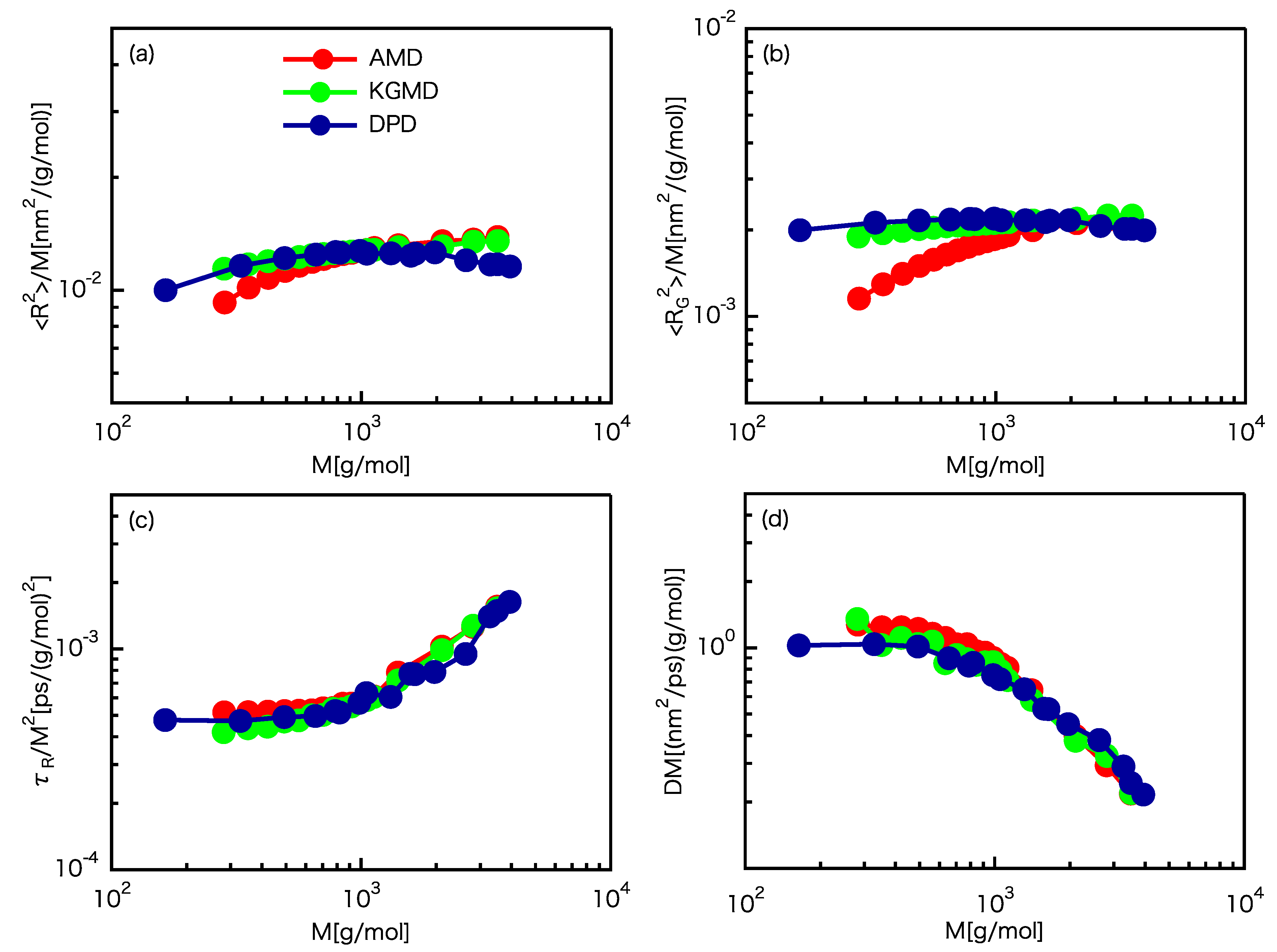
3.1. Scaling Laws
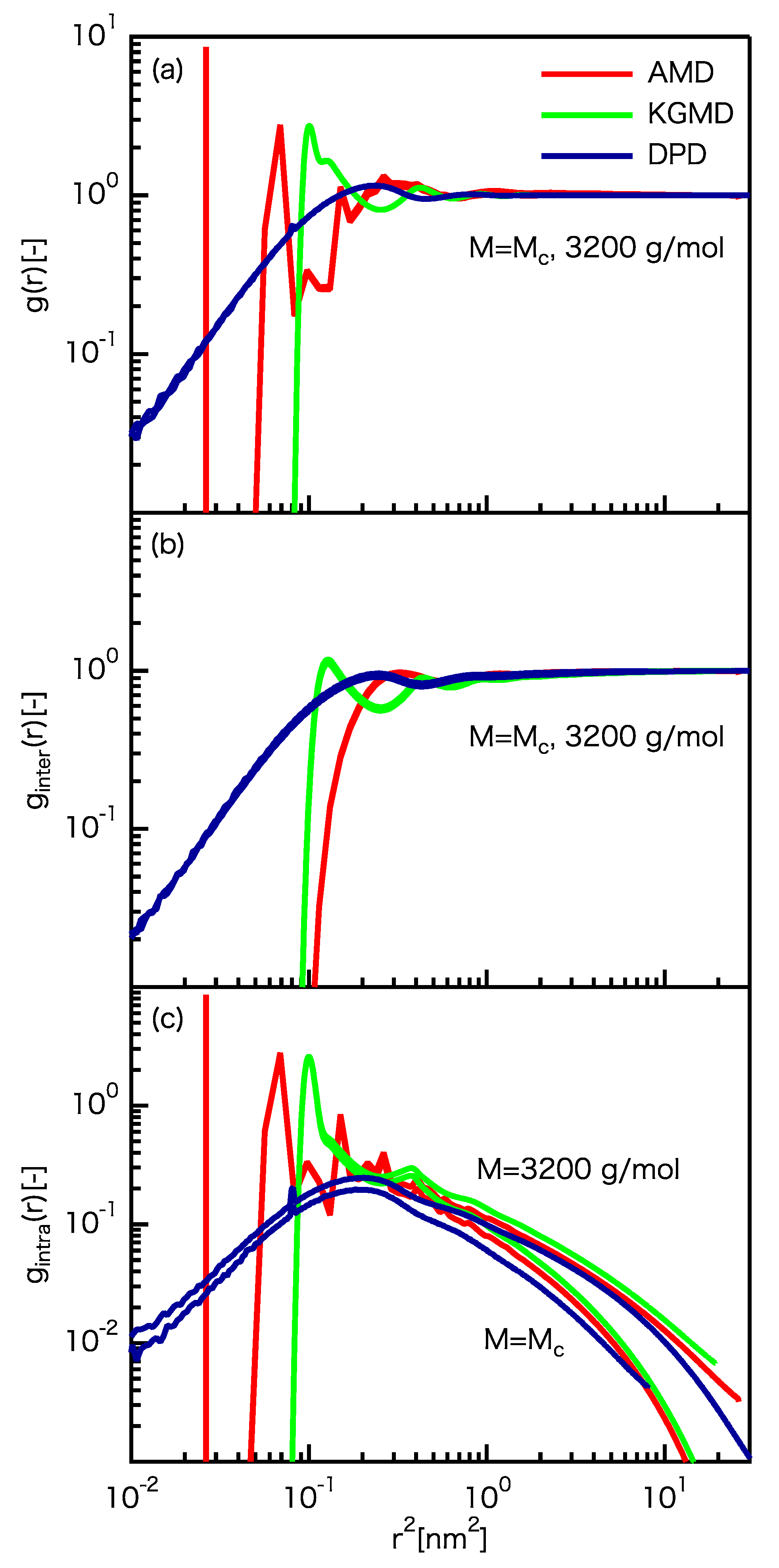
3.2. Static Properties
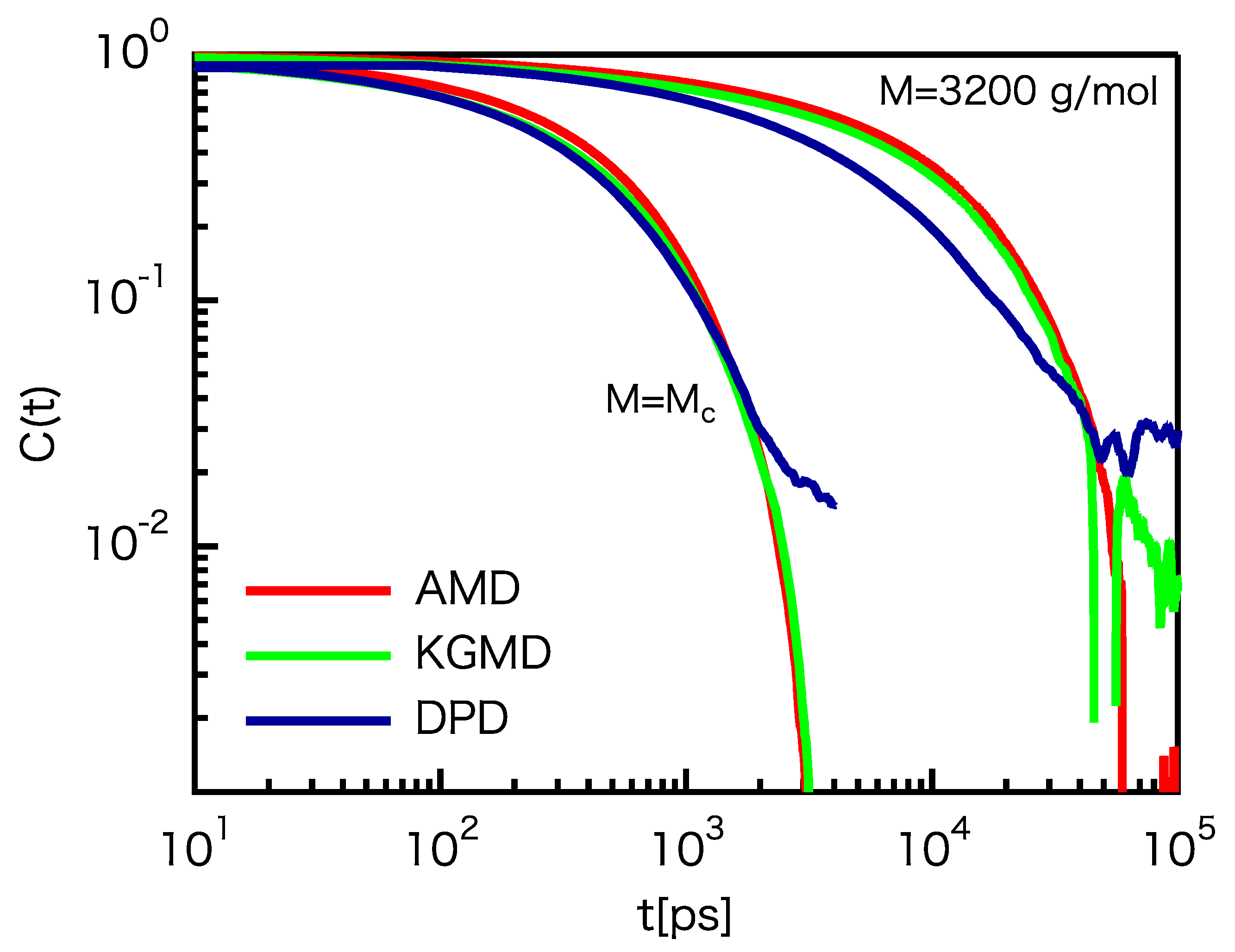
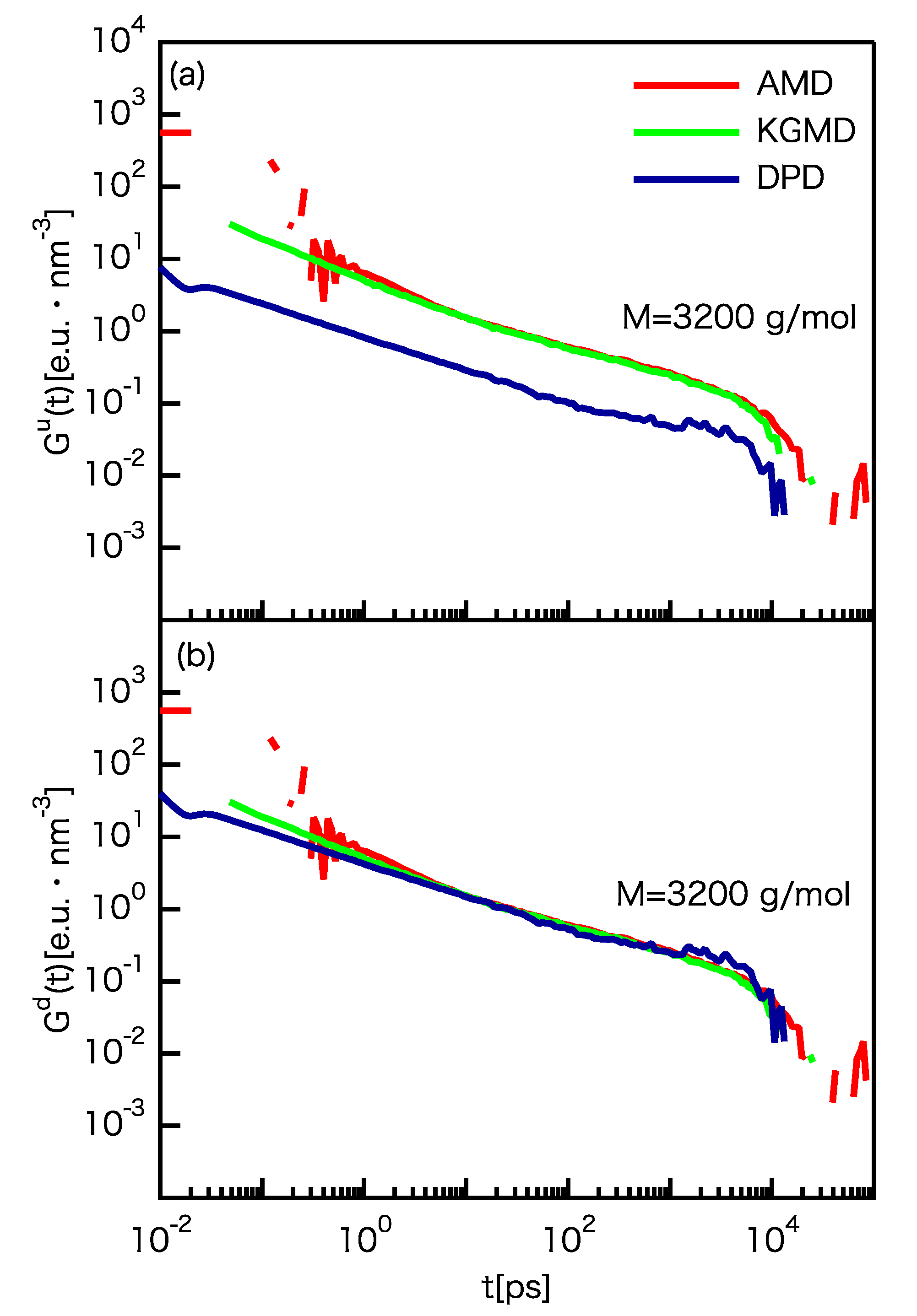
3.3. Dynamic Properties
3.4. Computational Efficiency
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: Oxford, UK, 1988; Volume 73. [Google Scholar]
- Ferry, J.D. Viscoelastic Properties of Polymers; John Wiley & Sons: Hoboken, NJ, USA, 1980. [Google Scholar]
- Masubuchi, Y. Simulating the flow of entangled polymers. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 11–33. [Google Scholar] [CrossRef] [PubMed]
- Brini, E.; Algaer, E.A.; Ganguly, P.; Li, C.; Rodríguez-Ropero, F.; van der Vegt, N.F. Systematic coarse-graining methods for soft matter simulations—A review. Soft Matter 2013, 9, 2108–2119. [Google Scholar] [CrossRef]
- Everaers, R.; Sukumaran, S.K.; Grest, G.S.; Svaneborg, C.; Sivasubramanian, A.; Kremer, K. Rheology and microscopic topology of entangled polymeric liquids. Science 2004, 303, 823–826. [Google Scholar] [CrossRef] [PubMed]
- Groot, R.D.; Warren, P.B. Dissipative particle dynamics: Bridging the gap between atomistic and mesoscopic simulation. J. Chem. Phys. 1997, 107, 4423. [Google Scholar] [CrossRef]
- Jury, S.; Bladon, P.; Cates, M.; Krishna, S.; Hagen, M.; Ruddock, N.; Warren, P. Simulation of amphiphilic mesophases using dissipative particle dynamics. Phys. Chem. Chem. Phys. 1999, 1, 2051–2056. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- McCarty, J.; Clark, A.; Copperman, J.; Guenza, M. An analytical coarse-graining method which preserves the free energy, structural correlations, and thermodynamic state of polymer melts from the atomistic to the mesoscale. J. Chem. Phys. 2014, 140, 204913. [Google Scholar] [CrossRef]
- Clark, A.; Guenza, M. Mapping of polymer melts onto liquids of soft-colloidal chains. J. Chem. Phys. 2010, 132, 044902. [Google Scholar] [CrossRef]
- Fritz, D.; Koschke, K.; Harmandaris, V.A.; van der Vegt, N.F.; Kremer, K. Multiscale modeling of soft matter: Scaling of dynamics. Phys. Chem. Chem. Phys. 2011, 13, 10412–10420. [Google Scholar] [CrossRef]
- Lyubimov, I.; McCarty, J.; Clark, A.; Guenza, M. Analytical rescaling of polymer dynamics from mesoscale simulations. J. Chem. Phys. 2010, 132, 224903. [Google Scholar] [CrossRef]
- Lyubimov, I.; Guenza, M. First-principle approach to rescale the dynamics of simulated coarse-grained macromolecular liquids. Phys. Rev. E 2011, 84, 031801. [Google Scholar] [CrossRef] [PubMed]
- Padding, J.; Briels, W. Systematic coarse-graining of the dynamics of entangled polymer melts: The road from chemistry to rheology. J. Phys. Condens. Matter 2011, 23, 233101. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Aparicio, R.; Colmenero, J.; Alvarez, F.; Padding, J.; Briels, W. Chain dynamics of poly (ethylene-alt-propylene) melts by means of coarse-grained simulations based on atomistic molecular dynamics. J. Chem. Phys. 2010, 132, 024904. [Google Scholar] [CrossRef] [PubMed]
- Peter, C.; Kremer, K. Multiscale simulation of soft matter systems–from the atomistic to the coarse-grained level and back. Soft Matter 2009, 5, 4357–4366. [Google Scholar] [CrossRef]
- Peter, C.; Kremer, K. Multiscale simulation of soft matter systems. Faraday Discuss. 2010, 144, 9–24. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Kremer, K. Dynamics of polystyrene melts through hierarchical multiscale simulations. Macromolecules 2009, 42, 791–802. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Uneyama, T. Comparison among multi-chain models for entangled polymer dynamics. Soft Matter 2018, 14, 5986–5994. [Google Scholar] [CrossRef]
- Takahashi, K.Z.; Nishimura, R.; Yamato, N.; Yasuoka, K.; Masubuchi, Y. Onset of static and dynamic universality among molecular models of polymers. Sci. Rep. 2017, 7, 12379. [Google Scholar] [CrossRef]
- Langeloth, M.; Masubuchi, Y.; Böhm, M.C.; Müller-Plathe, F. Recovering the reptation dynamics of polymer melts in dissipative particle dynamics simulations via slip-springs. J. Chem. Phys. 2013, 138, 104907. [Google Scholar] [CrossRef]
- Swope, W.C.; Andersen, H.C.; Berens, P.H.; Wilson, K.R. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters. J. Chem. Phys. 1982, 76, 637–649. [Google Scholar] [CrossRef]
- Hoogerbrugge, P.; Koelman, J. Simulating Microscopic Hydrodynamic Phenomena with Dissipative Particle Dynamics. Europhys. Lett. 1992, 19, 155–160. [Google Scholar] [CrossRef]
- Espanõl, P.; Warren, P. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef]
- Yu, C.Y.; Ma, L.; Li, K.; Li, S.L.; Liu, Y.N.; Liu, L.F.; Zhou, Y.F.; Yan, D.Y. Computer Simulation Studies on the pH-Responsive Self-Assembly of Amphiphilic Carboxy-Terminated Polyester Dendrimers in Aqueous Solution. Langmuir 2017, 33, 388–399. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Fan, Y.; Zhang, Y.Y.; Yu, C.; Li, H.; Chen, Y.; Hamley, I.W.; Jiang, S.C. Self-Assembly Kinetics of Amphiphilic Dendritic Copolymers. Macromolecules 2017, 50, 1657–1665. [Google Scholar] [CrossRef]
- Zhang, C.Y.; Zhou, H.P.; Li, Y.X.; Zhang, Y.Y.; Yu, C.; Li, H.F.; Chen, Y.; Hamley, I.W.; Jiang, S.C. Investigations on the micellization of amphiphilic dendritic copolymers: From unimers to micelles. J. Colloid Interface Sci. 2018, 514, 609–614. [Google Scholar] [CrossRef]
- Arai, N.; Yasuoka, K.; Zeng, X. Self-Assembly of Janus Oligomers into Onion-like Vesicles with Layer-by-Layer Water Discharging Capability: A Minimalist Model. ACS Nano 2016, 10, 8026–8037. [Google Scholar] [CrossRef]
- Parent, L.R.; Bakalis, E.; Ramirez-Hernandez, A.; Kammeyer, J.K.; Park, C.; de Pablo, J.; Zerbetto, F.; Patterson, J.P.; Gianneschi, N.C. Directly Observing Micelle Fusion and Growth in Solution by Liquid-Cell Transmission Electron Microscopy. J. Am. Chem. Soc. 2017, 139, 17140–17151. [Google Scholar] [CrossRef]
- Arai, N.; Yasuoka, K.; Zeng, X. Self-Assembly of Triblock Janus Nanoparticle in Nanotube. J. Chem. Theory Comput. 2013, 9, 179–187. [Google Scholar] [CrossRef]
- Kobayashi, Y.; Arai, N. Self-Assembly and Viscosity Behavior of Janus Nanoparticles in Nanotube Flow. Langmuir 2017, 33, 736–743. [Google Scholar] [CrossRef]
- Cudjoe, E.; Khani, S.; Way, A.E.; Hore, M.J.A.; Maia, J.; Rowan, S.J. Biomimetic Reversible Heat-Stiffening Polymer Nanocomposites. ACS Cent. Sci. 2017, 3, 886–894. [Google Scholar] [CrossRef]
- Burgos-Mármol, J.J.; Álvarez-Machancoses, O.; Patti, A. Modeling the Effect of Polymer Chain Stiffness on the Behavior of Polymer Nanocomposites. J. Phys. Chem. B 2017, 121, 6245–6256. [Google Scholar] [CrossRef]
- Spenley, N.A. Scaling laws for polymers in dissipative particle dynamics. Europhys. Lett. 2000, 49, 534. [Google Scholar] [CrossRef]
- Likhtman, A.E. Single-Chain Slip-Link Model of Entangled Polymers: Simultaneous Description of Neutron Spin-Echo, Rheology, and Diffusion. Macromolecules 2005, 38, 6128–6139. [Google Scholar] [CrossRef]
- Masubuchi, Y.; Langeloth, M.; Böhm, M.C.; Inoue, T.; Müller-Plathe, F. A Multichain Slip-Spring Dissipative Particle Dynamics Simulation Method for Entangled Polymer Solutions. Macromolecules 2016, 49, 9186–9191. [Google Scholar] [CrossRef]
- Pant, P.K.; Han, J.; Smith, G.D.; Boyd, R.H. A molecular dynamics simulation of polyethylene. J. Chem. Phys. 1993, 99, 597–604. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Madura, J.D.; Swenson, C.J. Optimized intermolecular potential functions for liquid hydrocarbons. J. Am. Chem. Soc. 1984, 106, 6638–6646. [Google Scholar] [CrossRef]
- Martin, M.G.; Siepmann, J.I. Transferable potentials for phase equilibria. 1. United-atom description of n-alkanes. J. Phys. Chem. B 1998, 102, 2569–2577. [Google Scholar] [CrossRef]
- Boyd, R.H.; Gee, R.H.; Han, J.; Jin, Y. Conformational dynamics in bulk polyethylene: A molecular dynamics simulation study. J. Chem. Phys. 1994, 101, 788–797. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Mavrantzas, V.G.; Theodorou, D.N. Atomistic molecular dynamics simulation of polydisperse linear polyethylene melts. Macromolecules 1998, 31, 7934–7943. [Google Scholar] [CrossRef]
- Jin, Y.; Boyd, R.H. Subglass chain dynamics and relaxation in polyethylene: A molecular dynamics simulation study. J. Chem. Phys. 1998, 108, 9912–9923. [Google Scholar] [CrossRef]
- Kavassalis, T.; Sundararajan, P. A molecular-dynamics study of polyethylene crystallization. Macromolecules 1993, 26, 4144–4150. [Google Scholar] [CrossRef]
- Moore, J.; Cui, S.; Cochran, H.; Cummings, P. A molecular dynamics study of a short-chain polyethylene melt.: I. steady-state shear. J. Non-Newton. Fluid Mech. 2000, 93, 83–99. [Google Scholar] [CrossRef]
- Paul, W.; Smith, G.; Yoon, D.Y.; Farago, B.; Rathgeber, S.; Zirkel, A.; Willner, L.; Richter, D. Chain motion in an unentangled polyethylene melt: A critical test of the rouse model by molecular dynamics simulations and neutron spin echo spectroscopy. Phys. Rev. Lett. 1998, 80, 2346. [Google Scholar] [CrossRef]
- Ramos, J.; Vega, J.F.; Theodorou, D.N.; Martinez-Salazar, J. Entanglement relaxation time in polyethylene: Simulation versus experimental data. Macromolecules 2008, 41, 2959–2962. [Google Scholar] [CrossRef]
- Rissanou, A.N.; Power, A.J.; Harmandaris, V. Structural and dynamical properties of polyethylene/graphene nanocomposites through molecular dynamics simulations. Polymers 2015, 7, 390–417. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhuang, X.; Muthu, J.; Mabrouki, T.; Fontaine, M.; Gong, Y.; Rabczuk, T. Load transfer of graphene/carbon nanotube/polyethylene hybrid nanocomposite by molecular dynamics simulation. Compos. Part B Eng. 2014, 63, 27–33. [Google Scholar] [CrossRef]
- Harmandaris, V.A.; Daoulas, K.C.; Mavrantzas, V.G. Molecular dynamics simulation of a polymer melt/solid interface: local dynamics and chain mobility in a thin film of polyethylene melt adsorbed on graphite. Macromolecules 2005, 38, 5796–5809. [Google Scholar] [CrossRef]
- Hu, M.; Keblinski, P.; Schelling, P.K. Kapitza conductance of silicon–amorphous polyethylene interfaces by molecular dynamics simulations. Phys. Rev. B 2009, 79, 104305. [Google Scholar] [CrossRef]
- Taylor, D.; Strawhecker, K.; Shanholtz, E.; Sorescu, D.; Sausa, R. Investigations of the intermolecular forces between RDX and polyethylene by force–distance spectroscopy and molecular dynamics simulations. J. Phys. Chem. A 2014, 118, 5083–5097. [Google Scholar] [CrossRef]
- Hur, K.; Winkler, R.G.; Yoon, D.Y. Comparison of ring and linear polyethylene from molecular dynamics simulations. Macromolecules 2006, 39, 3975–3977. [Google Scholar] [CrossRef]
- Yi, P.; Locker, C.R.; Rutledge, G.C. Molecular dynamics simulation of homogeneous crystal nucleation in polyethylene. Macromolecules 2013, 46, 4723–4733. [Google Scholar] [CrossRef]
- Henry, A.; Chen, G. High thermal conductivity of single polyethylene chains using molecular dynamics simulations. Phys. Rev. Lett. 2008, 101, 235502. [Google Scholar] [CrossRef]
- Henry, A.; Chen, G. Anomalous heat conduction in polyethylene chains: Theory and molecular dynamics simulations. Phys. Rev. B 2009, 79, 144305. [Google Scholar] [CrossRef]
- Hossain, D.; Tschopp, M.; Ward, D.; Bouvard, J.; Wang, P.; Horstemeyer, M. Molecular dynamics simulations of deformation mechanisms of amorphous polyethylene. Polymer 2010, 51, 6071–6083. [Google Scholar] [CrossRef]
- Kim, J.M.; Locker, R.; Rutledge, G.C. Plastic deformation of semicrystalline polyethylene under extension, compression, and shear using molecular dynamics simulation. Macromolecules 2014, 47, 2515–2528. [Google Scholar] [CrossRef]
- Lavine, M.S.; Waheed, N.; Rutledge, G.C. Molecular dynamics simulation of orientation and crystallization of polyethylene during uniaxial extension. Polymer 2003, 44, 1771–1779. [Google Scholar] [CrossRef]
- Yeh, I.C.; Andzelm, J.W.; Rutledge, G.C. Mechanical and structural characterization of semicrystalline polyethylene under tensile deformation by molecular dynamics simulations. Macromolecules 2015, 48, 4228–4239. [Google Scholar] [CrossRef]
- Vu-Bac, N.; Lahmer, T.; Keitel, H.; Zhao, J.; Zhuang, X.; Rabczuk, T. Stochastic predictions of bulk properties of amorphous polyethylene based on molecular dynamics simulations. Mech. Mater. 2014, 68, 70–84. [Google Scholar] [CrossRef]
- Hess, B.; Bekker, H.; Berendsen, H.J.; Fraaije, J.G. LINCS: A linear constraint solver for molecular simulations. J. Comput. Chem. 1997, 18, 1463–1472. [Google Scholar] [CrossRef]
- Pronk, S.; Páll, S.; Schulz, R.; Larsson, P.; Bjelkmar, P.; Apostolov, R.; Shirts, M.R.; Smith, J.C.; Kasson, P.M.; van der Spoel, D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. [Google Scholar] [CrossRef]
- Hoover, W.G. Canonical dynamics: Equilibrium phase-space distributions. Phys. Rev. A 1985, 31, 1695–1697. [Google Scholar] [CrossRef]
- Nosé, S. A unified formulation of the constant temperature molecular dynamics methods. J. Chem. Phys. 1984, 81, 511–519. [Google Scholar] [CrossRef]
- Hockney, R.W. The potential calculation and some applications. Methods Comput. Phys. 1970, 9, 135–211. [Google Scholar]
- Rouse, P.E., Jr. A theory of the linear viscoelastic properties of dilute solutions of coiling polymers. J. Chem. Phys. 1953, 21, 1272–1280. [Google Scholar] [CrossRef]
- Takahashi, K.Z.; Nishimura, R.; Yasuoka, K.; Masubuchi, Y. Molecular Dynamics Simulations for Resolving Scaling Laws of Polyethylene Melts. Polymers 2017, 9, 24. [Google Scholar] [CrossRef]
- Takahashi, K.Z.; Yamato, N.; Yasuoka, K.; Masubuchi, Y. Critical test of bead–spring model to resolve the scaling laws of polymer melts: A molecular dynamics study. Mol. Simul. 2017, 43, 1196–1201. [Google Scholar] [CrossRef]
- Salerno, K.M.; Agrawal, A.; Perahia, D.; Grest, G.S. Resolving Dynamic Properties of Polymers through Coarse-Grained Computational Studies. Phys. Rev. Lett. 2016, 116, 058302. [Google Scholar] [CrossRef]
- Hoy, R.S.; Foteinopoulou, K.; Kröger, M. Topological analysis of polymeric melts: Chain-length effects and fast-converging estimators for entanglement length. Phys. Rev. E 2009, 80, 031803. [Google Scholar] [CrossRef]
- Kröger, M. Shortest multiple disconnected path for the analysis of entanglements in two-and three-dimensional polymeric systems. Comput. Phys. Commun. 2005, 168, 209–232. [Google Scholar] [CrossRef]
- Shanbhag, S.; Kröger, M. Primitive path networks generated by annealing and geometrical methods: Insights into differences. Macromolecules 2007, 40, 2897–2903. [Google Scholar] [CrossRef]
- Flory, P.J. The configuration of real polymer chains. J. Chem. Phys. 1949, 17, 303–310. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628. [Google Scholar] [CrossRef] [PubMed]


| Property | Dimension | Symbol for | UA | (Unit) | KG | (Unit) | DPD | (Unit) |
|---|---|---|---|---|---|---|---|---|
| Scaling Factor | ||||||||
| — | Length | 1 | nm/nm | 0.33 | nm/ | 0.57 | nm/ | |
| — | Time | 1 | ps/ps | 0.080 | ps/ | 0.028 | ps/ | |
| — | Mass | 1 | g/mol/(g/mol) | 14 | g/mol/ | 32 | g/mol/ | |
| — | Energy | — | 1 | J/J | 6.9 | J/ | 6.9 | J/ |
| — | (Carbon num.) | 1 | (carbons/carbons) | 1.0 | (carbons/KG segs.) | 2.3 | (carbons/DPD segs.) | |
| Energy | 1 | e.u./e.u. | 1.0 | e.u./e.u. | 1.0 | e.u./e.u. | ||
| Segment density | (Carbon num.)/Length | 1 | 0.85 | 1.3 | ||||
| Critical segment number | (Carbon num.) | 1 | (carbons/carbons) | 1.0 | (carbons/carbons) | 1.0 | (carbons/carbons) | |
| Strand density | Length | 1 | nm/nm | 0.85 | nm/nm | 1.3 | nm/nm | |
| Energy/Length | (See Equation (22)) | 1 | 0.036 | 0.036 | ||||
| Energy/Length | 1 | 1.0 | 0.19 | |||||
| A | — | 1 | —/— | 1.2 | —/— | 0.14 | —/— |
| UA | KG | DPD | ||
|---|---|---|---|---|
| Static properties | A | B | C | |
| A | C | C | ||
| A | B | B | ||
| A | B | B | ||
| Dynamic properties | D | A | A | A |
| A | A | B | ||
| A | B | B | ||
| A | B | C | ||
| A | A | A | ||
| Computational cost | C | D | B |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miwatani, R.; Takahashi, K.Z.; Arai, N. Performance of Coarse Graining in Estimating Polymer Properties: Comparison with the Atomistic Model. Polymers 2020, 12, 382. https://doi.org/10.3390/polym12020382
Miwatani R, Takahashi KZ, Arai N. Performance of Coarse Graining in Estimating Polymer Properties: Comparison with the Atomistic Model. Polymers. 2020; 12(2):382. https://doi.org/10.3390/polym12020382
Chicago/Turabian StyleMiwatani, Ryota, Kazuaki Z. Takahashi, and Noriyoshi Arai. 2020. "Performance of Coarse Graining in Estimating Polymer Properties: Comparison with the Atomistic Model" Polymers 12, no. 2: 382. https://doi.org/10.3390/polym12020382
APA StyleMiwatani, R., Takahashi, K. Z., & Arai, N. (2020). Performance of Coarse Graining in Estimating Polymer Properties: Comparison with the Atomistic Model. Polymers, 12(2), 382. https://doi.org/10.3390/polym12020382





