Numerical and Experimental Investigation of Oil Palm Shell Reinforced Rubber Composites
Abstract
1. Introduction
2. Experimental Procedure
3. Numerical Studies
4. Results and Discussion
4.1. Evaluation of the Material Coefficients
4.2. ROPS Model Simulations
4.3. Effect of Shape on the Stress–Strain Response of ROPS Specimens
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Shinoj, S.; Visvanathan, R.; Panigrahi, S. Towards industrial utilization of oil palm fibre: Physical and dielectric characterization of linear low density polyethylene composites and comparison with other fibre sources. Biosyst. Eng. 2010, 106, 378–388. [Google Scholar] [CrossRef]
- Al-Oqla, F.M.; Sapuan, S.; Sapuan, M.S. Natural fiber reinforced polymer composites in industrial applications: Feasibility of date palm fibers for sustainable automotive industry. J. Clean. Prod. 2014, 66, 347–354. [Google Scholar] [CrossRef]
- Uddin, N.; Abro, A.M.; Purdue, J.D.; Vaidya, U. Developments in Fiber-Reinforced Polymer (FRP) Composites for Civil Engineering: 13. Thermoplastic Composites for Bridge Structures; Elsevier Inc.: Birmingham, AL, USA, 2003. [Google Scholar]
- Namvar, F.; Jawaid, M.; Tanir, P.M.; Mohamad, R.; Azizi, S.; Khodavandi, A.; Rahman, H.S.; Nayeri, M.D. Potential use of plant fibres and their composites for biomedical applications. BioResources 2014, 9, 5688–5706. [Google Scholar] [CrossRef]
- Shalwan, A.; Yousif, B. In State of Art: Mechanical and tribological behaviour of polymeric composites based on natural fibres. Mater. Des. 2013, 48, 14–24. [Google Scholar] [CrossRef]
- Ticoalu, A.; Aravinthan, T.; Cardona, F. A review of current development in natural fiber composites for structural and infrastructure applications. In Proceedings of the Southern Region Engineering Conference (SREC 2010), Toowoomba, Australia, 11–12 November 2010. [Google Scholar]
- Geethamma, V.; Mathew, K.T.; Lakshminarayanan, R.; Thomas, S. Composite of short coir fibres and natural rubber: Effect of chemical modification, loading and orientation of fibre. Polymer 1998, 39, 1483–1491. [Google Scholar] [CrossRef]
- Zuhri, M.; Sapuan, S.; Ismail, N. Oil palm fibre reinforced polymer composites: A review. Prog. Rubber Plast. Recycl. Technol. 2009, 25, 233–246. [Google Scholar] [CrossRef]
- Vijayan, R.; Krishnamoorthy, A. Review on natural fiber reinforced composites. Mater. Today Proc. 2019, 16, 897–906. [Google Scholar] [CrossRef]
- Alengaram, U.J.; Al Muhit, B.A.; Bin Jumaat, M.Z.; Jing, M.L.Y. A comparison of the thermal conductivity of oil palm shell foamed concrete with conventional materials. Mater. Des. 2013, 51, 522–529. [Google Scholar] [CrossRef]
- Basri, H.; Mannan, M.; Zain, M. Concrete using waste oil palm shells as aggregate. Cem. Concr. Res. 1999, 29, 619–622. [Google Scholar] [CrossRef]
- Teo, D.C.L.; Mannan, A.; Kurian, J.V. Flexural behaviour of reinforced lightweight concrete beams made with oil palm shell (OPS). J. Adv. Concr. Technol. 2006, 4, 459–468. [Google Scholar] [CrossRef]
- Alnashwan, W.; Aloumi, B.; Malasri, S.; Kist, M.; Othmani, A.; Fotso, R.; Johnson, M.; Polania, S.; Sanchez-Luna, Y. Shock absorption of crumb rubber and coconut fiber. Int. J. Adv. Packag. Technol. 2014, 2, 119–128. [Google Scholar] [CrossRef]
- Okpala, D. Palm kernel shell as a lightweight aggregate in concrete. Build. Environ. 1990, 25, 291–296. [Google Scholar] [CrossRef]
- Sahari, J.; Maleque, M.A. Mechanical properties of oil palm shell composites. Int. J. Polym. Sci. 2016, 2016, 1–7. [Google Scholar]
- Eng, C.C.; Ibrahim, N.A.; Zainuddin, N.; Ariffin, H.; Yunus, W.M.Z.W. Impact strength and flexural properties enhancement of methacrylate silane treated oil palm mesocarp fiber reinforced biodegradable hybrid composites. Sci. World J. 2014, 2014, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Charlton, D.J.; Yang, J.; Teh, K.K. A review of methods to characterize rubber elastic behavior for use in finite element analysis. Rubber Chem. Technol. 1994, 67, 481–503. [Google Scholar] [CrossRef]
- Crocker, L.; Duncans, B.C.; Hughes, R.G. Hyperelastic Modelling of Flexible Adhesives. NPL Report No. CMMT(A)183. Teddington, UK. 1999. Available online: http://eprintspublications.npl.co.uk/1158/1/CMMT183.pdf (accessed on 1 May 1999).
- Lindley, P.B. Engineering Design with Natural Rubber; The Natural Rubber Producer’s Research Association Technical Bulletin. The Malaysian Rubber Producers Research Association: Brickendonbury, Bertford, 1964; Available online: https://b-ok.cc/book/4990072/604327 (accessed on 31 January 2020).
- Mooney, M. A Theory of large elastic deformation. J. Appl. Phys. 1940, 11, 582. [Google Scholar] [CrossRef]
- Ogden, R.W. Large deformation isotropic elasticity—On the correlation of theory and experiment for incompressible rubberlike solids. Rubber Chem. Technol. 1973, 46, 398–416. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Ihueze, C.; Mgbemena, C. Modeling hyperelastic behavior of natural rubber/organomodified kaolin composites oleochemically derived from tea seed oils (Camellia Sinensis) for Automobile Tire Side Walls Application. J. Sci. Res. Rep. 2014, 3, 2528–2542. [Google Scholar] [CrossRef]
- Bahrain, S.H.K.; Mahmud, J. Arenga Pinnata—Silicone biocomposite: Quantifying its tensile properties using Neo-Hookean model. Intl. J. Recent Technol. Eng. 2019, 8, 3186–3190. [Google Scholar]
- Hanipah, S.H.; Mohammed, M.A.P.; Baharuddin, A.S. Non-linear mechanical behaviour and bio-composite modelling of oil palm mesocarp fibres. Compos. Interfaces 2016, 23, 37–49. [Google Scholar] [CrossRef]
- Cole, D.; Forrester, S.; Fleming, P. Mechanical characterization and numerical modelling of rubber shockpads in 3G artificial turf. In Proceedings of the 12th Conference of International Sports Engineering Association, Brisbane, Australia, 26–29 March 2018; Volume 2, p. 283. [Google Scholar]
- Mehravar, M.; Fleming, P.; Cole, D.; Forrester, S. Mechanical characterisation and strain rate sensitivity of rubber shockpad in 3G artificial turf. In Proceedings of the 24th UK Conaference of the Association for Computational Mechanics in Engineering, Cardiff, UK, 31 March–1 April 2016; pp. 406–409. [Google Scholar]
- Baranowski, P.; Gieleta, R. Rubber structure under dynamic loading–computational studies. Eng. Trans. 2013, 61, 33–46. [Google Scholar]
- Dassault Systemes, ABAQUS/CAE User’s Manual, Version 6.14. Simulia. 2014. Available online: http://130.149.89.49:2080/v6.14/pdf_books/CAE.pdf (accessed on 9 December 2019).
- Rivlin, R.S. Large elastic deformations of isotropic materials. I. Fundamental concepts. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 1948, 240, 459–508. [Google Scholar] [CrossRef]
- Peeters, F.; Kussner, M. Material law selection in the finite element simulation of rubber—Like materials & its practical application in the industrial design process. In Constitutive Models for Rubber; 1999; Volume 1, pp. 29–36. ISBN 90 58091139. Available online: https://www.crcpress.com/Constitutive-Models-for-Rubber/Dorfmann-Muhr/p/book/9789058091130 (accessed on 30 January 2020).
- Shahzad, M.; Kamran, A.; Siddiqui, M.Z.; Farhan, M. Mechanical characterization and FE modelling of a hyperelastic material. Mater. Res. 2015, 18, 918–924. [Google Scholar] [CrossRef]
- Arruda, E.M.; Boyce, M.C. A three-dimensional constitutive model for the large stretch behavior of rubber elastic materials. J. Mech. Phys. Solids 1993, 41, 389–412. [Google Scholar] [CrossRef]
- Imbimbo, M.; De Luca, A.F.E. stress analysis of rubber bearings under axial loads. Comput. Struct. 1998, 68, 31–39. [Google Scholar] [CrossRef]
- Sujendra, H.M.; Jayaram, A.S.; Chandan, R.; Hattaraki, G. Finite element modelling and simulation of rubber component in predicting hyperelastic material model. Int. J Eng. Technol. 2018, 5, 751–754. [Google Scholar]
- Bäker, M. How to get meaningful and correct results from your finite element model. arXiv 2018, arXiv:1811.05753. Available online: https://arxiv.org/pdf/1811.05753.pdf (accessed on 9 December 2019).
- Milani, G.; Milani, F. Stretch–stress behavior of elastomeric seismic isolators with different rubber materials: Numerical insight. J. Eng. Mech. 2012, 138, 416–429. [Google Scholar] [CrossRef]
- Sayed, A.M. Numerical analysis of the perforated steel sheets under uni-axial tensile force. Metals 2019, 9, 632. [Google Scholar] [CrossRef]
- Ismail, H.; Rosnah, N.; Ishiaku, U.S. Oil palm fibre-reinforced rubber composite: Effects of concentration and modification of fibre surface. Polym. Int. 1997, 43, 223–230. [Google Scholar] [CrossRef]
- Jacob, M.; Thomas, S.; Varughese, K.T. Natural rubber composites reinforced with sisal/oil palm hybrid fibers: Tensile and cure characteristics. J. Appl. Polym. Sci. 2004, 93, 2305–2312. [Google Scholar] [CrossRef]
- Joseph, S.; Joseph, K.; Thomas, S. Green composites from natural rubber and oil palm fiber: Physical and mechanical properties. Int. J. Polym. Mater. 2006, 55, 925–945. [Google Scholar] [CrossRef]
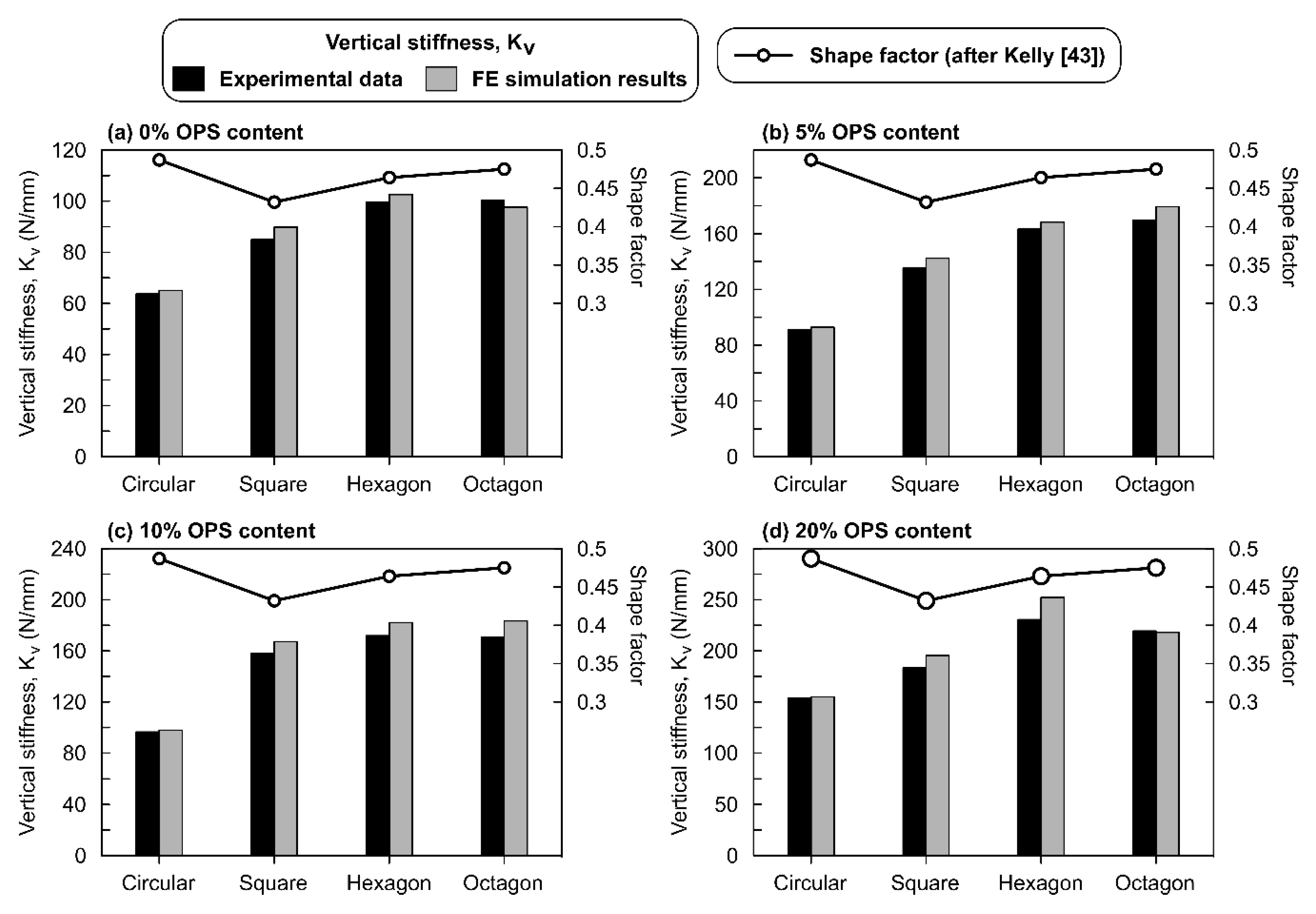
- Farhan, M.M.; Moosa, A.S. The effect of shape factor on the operation periods of anti-vibration rubber. Ind. Eng. Lett. 2017, 7, 31–38. [Google Scholar]
- Kelly, J.M. Analysis of fiber-reinforced elastomeric isolators. J. Seismol. Earthq. Eng. 1999, 2, 19–34. [Google Scholar]
- Soleimanlo, H.S.; Barkhordar, M.A. Effect of shape factor and rubber stiffness of fiber-reinforced elastomeric bearings on the vertical stiffness of isolators. Trends Appl. Sci. Res. 2013, 8, 14–25. [Google Scholar] [CrossRef]

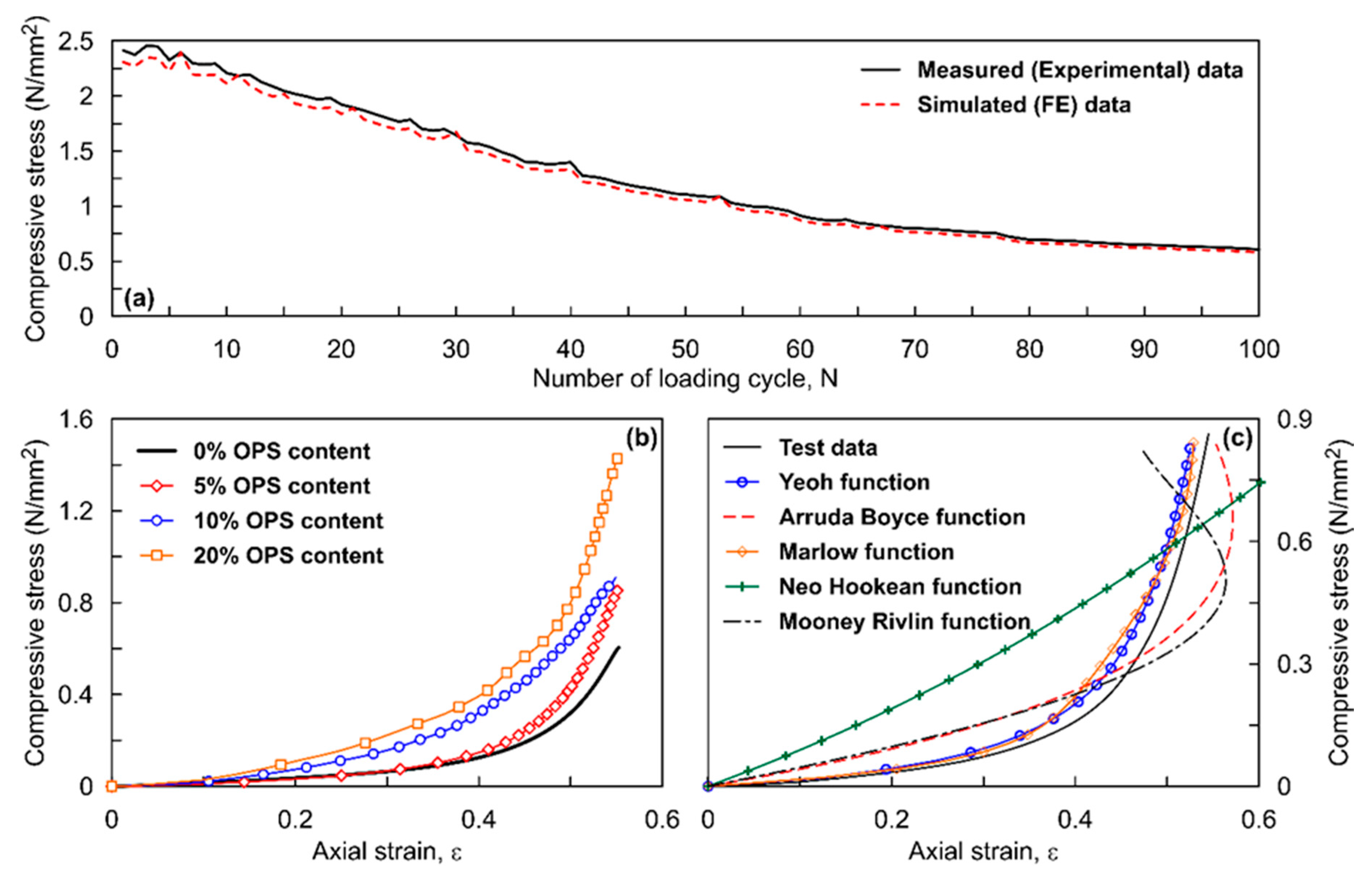

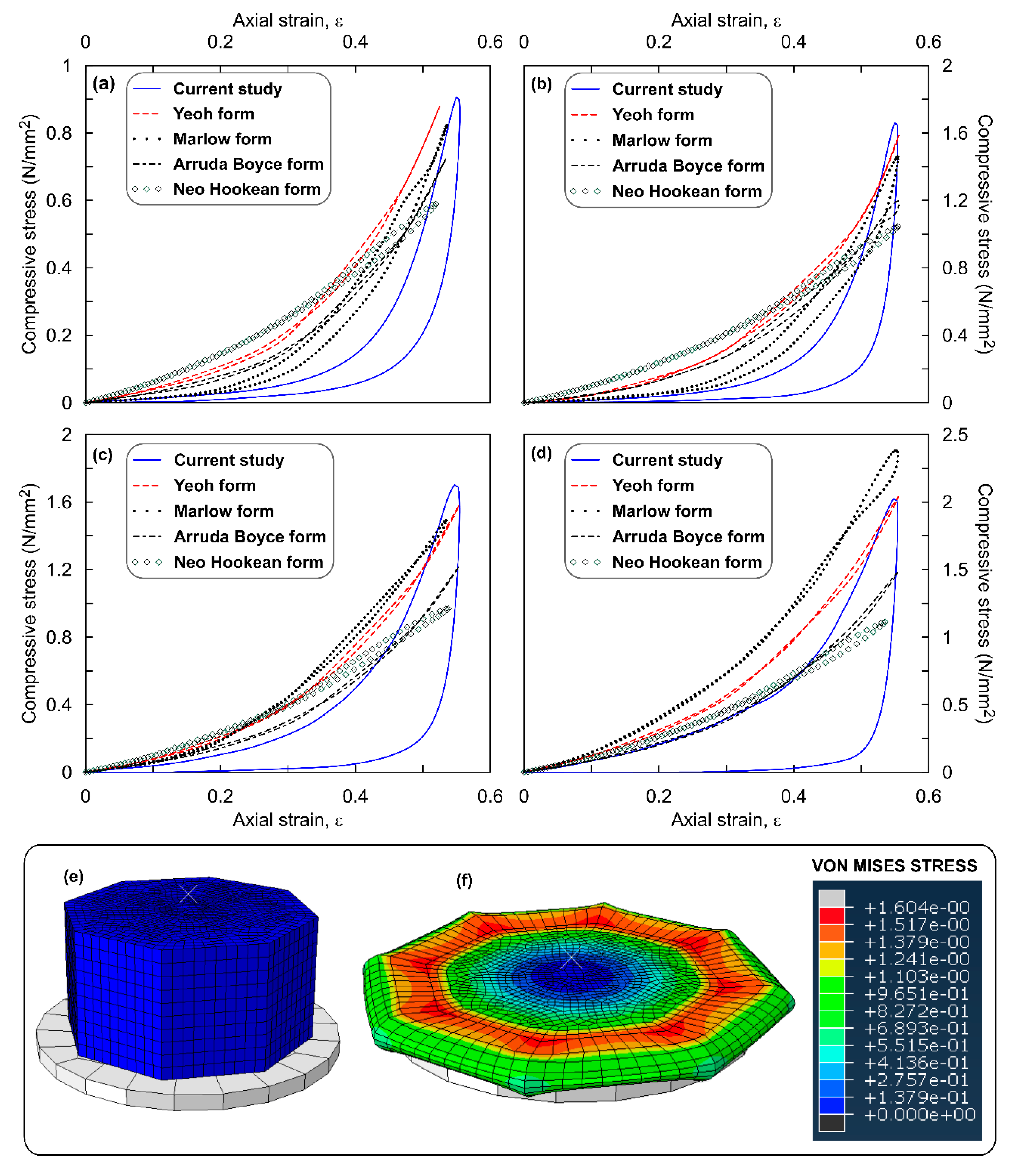
| The Mooney Rivlin function is obtained by setting N = 1 in Equation (1). This function is moderately suitable for large strains in uniaxial tension and shear distortion [20,30]. The mathematical form of this function is Unlike other polynomial functions, the Mooney Rivlin function is predominantly dependent on the first strain invariant ), thereby predicting complex material behaviour even with limited test data and strains less than 100% [31]. |
| The Neo Hookean function is a first order reduced polynomial form obtained by equating to zero in Mooney Rivlin function. The function has the form Neo-Hookean functions are mostly suitable for small strain applications [32]. |
| The Yeoh function is a third order reduced polynomial function by Yeoh [22]. Unlike above 2 functions, Yeoh model is suitable for wider range of strains and simulate different deformation modes even with limited test data. This function is expressed as |
| The Arruda Boyce function [33] is expressed as is a hyperelastic material law. Where, . Arruda Boyce depend on first invariant (; suitable for wide strain range and limited material data |
| The Marlow form is expressed as , where is the first strain invariant, is the elastic volume ratio and represent deviatoric and volumetric part of strain energy, respectively. The Marlow form simulates reasonable behaviour even in cases having single test data. |
| OPS (%) | Mooney Rivlin | Neo Hookean | Yeoh | Arruda Boyce | ||||
|---|---|---|---|---|---|---|---|---|
| C10 | C01 | C10 | C10 | C20 | C30 | µ | λm | |
| 0 | −0.0255 | 0.0412 | 0.0419 | 0.0295 | −0.0042 | 0.0088 | 0.0498 | 2.2196 |
| 5 | 0.0270 | 0.0006 | 0.0807 | 0.0293 | −0.0030 | 1.3414 | 0.0548 | 3.0235 |
| 10 | 0.0293 | 0.0672 | 0.1281 | 0.0705 | 0.0406 | −0.0073 | 0.1226 | 1.0911 |
| 20 | 0.0513 | 0.1439 | 0.1516 | 0.0894 | 0.1350 | −0.0457 | 0.2397 | 1.1606 |
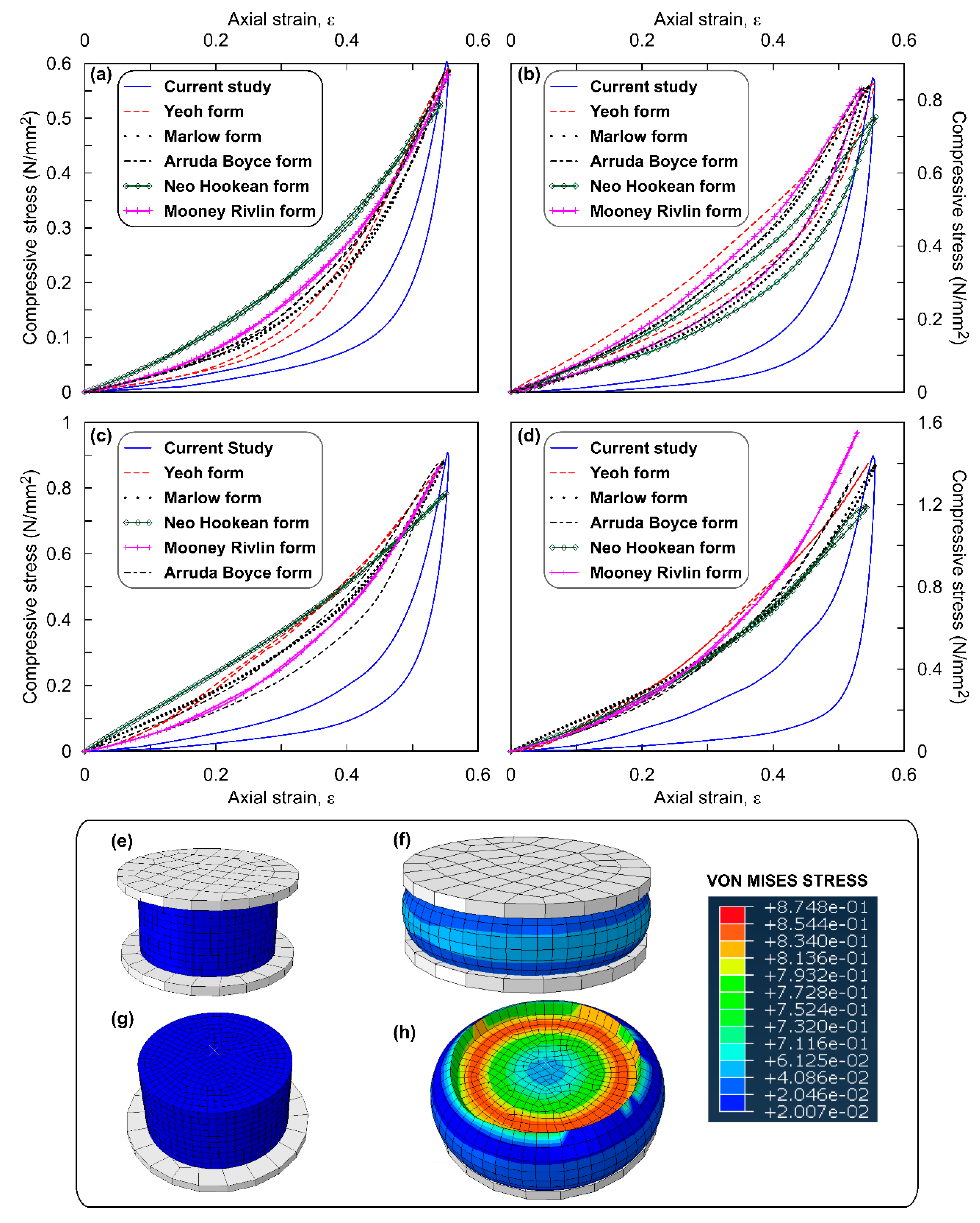
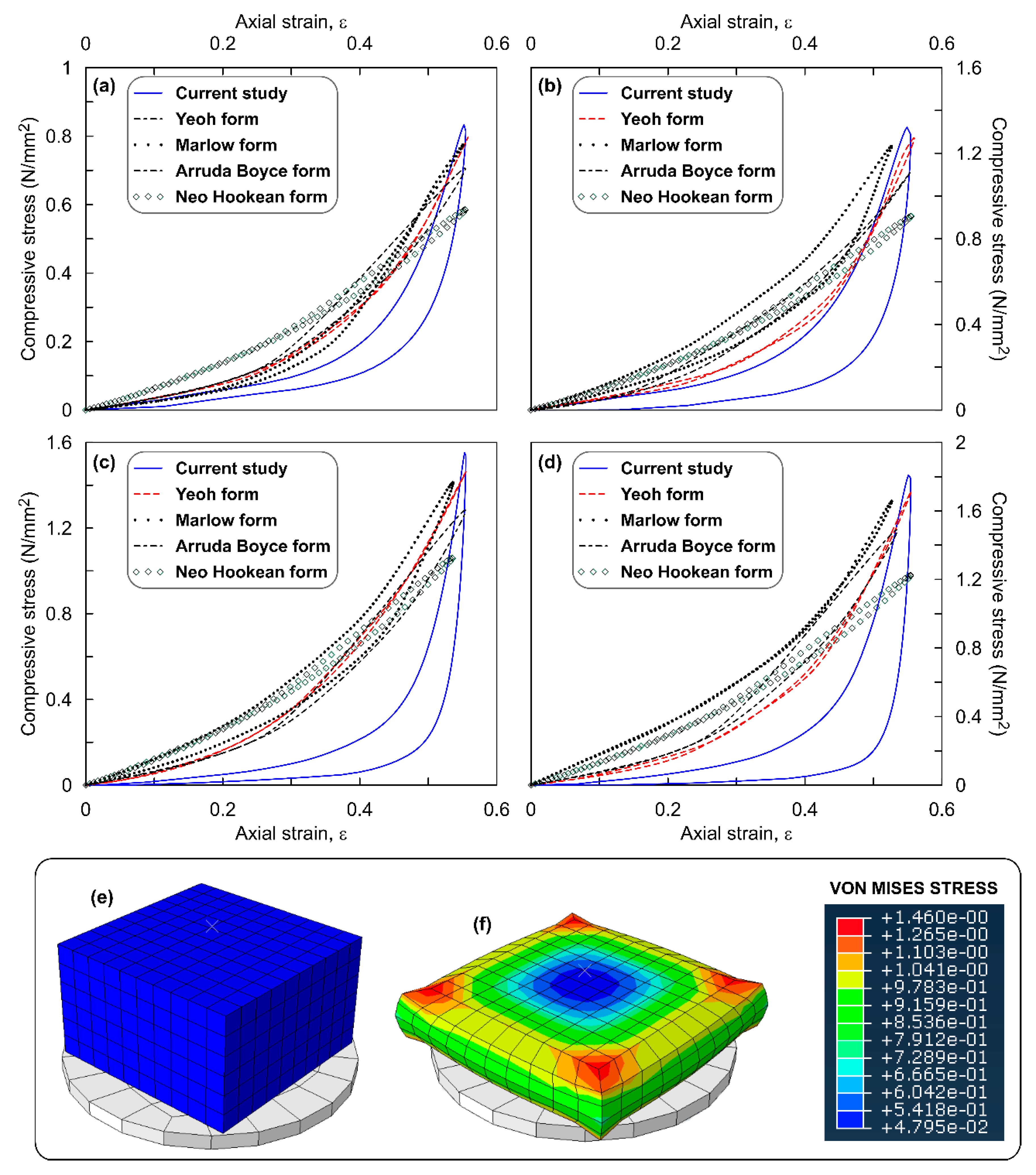
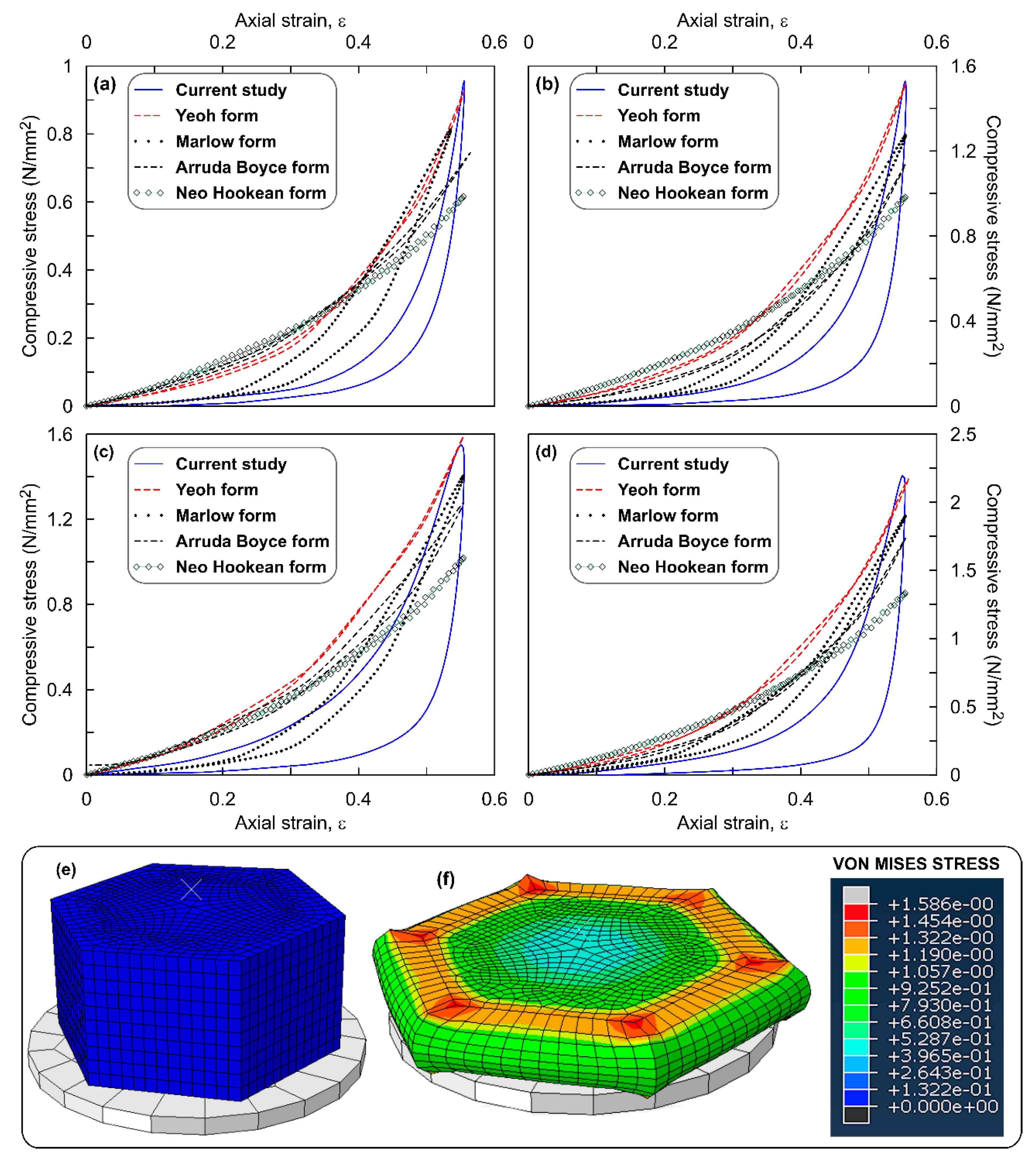
| OPS Content | SEF Type | σmax—Simulation | σmax—Experimental | Error (%) |
|---|---|---|---|---|
| 0% | Yeoh | 581.35 | 604 | −2 |
| Marlow | 591.92 | −3.8 | ||
| Arruda Boyce | 585.88 | −3 | ||
| Mooney Rivlin | 579.84 | −4 | ||
| Neo Hooke | 525.48 | −13 | ||
| 5% | Yeoh | 828.72 | 862 | −2.2 |
| Marlow | 843.173 | −3.9 | ||
| Arruda Boyce | 837.174 | −2.9 | ||
| Mooney Rivlin | 824.41 | −4.4 | ||
| Neo Hooke | 745.199 | −13.6 | ||
| 10% | Yeoh | 867.82 | 909 | −2.5 |
| Marlow | 885.911 | −4.5 | ||
| Arruda Boyce | 874.0035 | −3.9 | ||
| Mooney Rivlin | 852.18 | −6.3 | ||
| Neo Hooke | 775.9224 | −14.6 | ||
| 20% | Yeoh | 1370.989 | 1438 | −2.7 |
| Marlow | 1399.6054 | −4.7 | ||
| Arruda Boyce | 1369.83 | −4.7 | ||
| Mooney Rivlin | 1538.66 | 7 | ||
| Neo Hooke | 1185.631 | −17.6 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anandan, S.; Lim, C.Y.; Tan, B.T.; Anggraini, V.; Raghunandan, M.E. Numerical and Experimental Investigation of Oil Palm Shell Reinforced Rubber Composites. Polymers 2020, 12, 314. https://doi.org/10.3390/polym12020314
Anandan S, Lim CY, Tan BT, Anggraini V, Raghunandan ME. Numerical and Experimental Investigation of Oil Palm Shell Reinforced Rubber Composites. Polymers. 2020; 12(2):314. https://doi.org/10.3390/polym12020314
Chicago/Turabian StyleAnandan, Subhashini, Cuin Yang Lim, Boon Thong Tan, Vivi Anggraini, and Mavinakere Eshwaraiah Raghunandan. 2020. "Numerical and Experimental Investigation of Oil Palm Shell Reinforced Rubber Composites" Polymers 12, no. 2: 314. https://doi.org/10.3390/polym12020314
APA StyleAnandan, S., Lim, C. Y., Tan, B. T., Anggraini, V., & Raghunandan, M. E. (2020). Numerical and Experimental Investigation of Oil Palm Shell Reinforced Rubber Composites. Polymers, 12(2), 314. https://doi.org/10.3390/polym12020314







