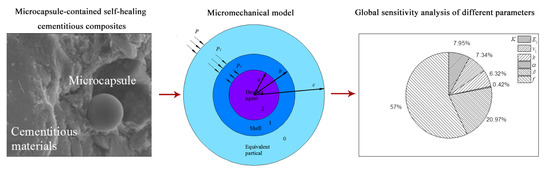
Global Sensitivity Analysis for the Polymeric Microcapsules in Self-Healing Cementitious Composites
Abstract
:1. Introduction
2. A Micromechanical Model for the Microcapsule-Contained Cementitious Composite
2.1. Multilevel Homogenization Scheme for Predicting the Effective Properties
2.2. The First-Level Homogenization
2.3. The Second-Level Homogenization
3. Global Sensitivity Analysis Method
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Baron, R.I.; Bercea, M.; Avadanei, M.; Lisa, G.; Biliuta, G.; Coseri, S. Green route for the fabrication of self-healable hydrogels based on tricarboxy cellulose and poly(vinyl alcohol). Int. J. Biol. Macromol. 2019, 123, 744–751. [Google Scholar] [CrossRef]
- Bercea, M.; Biliuta, G.; Avadanei, M.; Baron, R.I.; Butnaru, M.; Coseri, S. Self-healing hydrogels of oxidized pullulan and poly(vinyl alcohol). Carbohyd. Polym. 2019, 206, 210–219. [Google Scholar] [CrossRef]
- Morariu, S.; Bercea, M.; Gradinaru, L.M.; Rosca, I.; Avadanei, M. Versatile poly (vinyl alcohol)/clay physical hydrogels with tailorable structure as potential candidates for wound healing applications. Mat. Sci. Eng. C 2020, 109, 110395. [Google Scholar] [CrossRef]
- Nita, L.E.; Chiriac, A.; Rusu, A.G.; Bercea, M.; Ghilan, A.; Dumitriu, R.; Mititelu-Tartau, L. New self-healing hydrogels based on reversible physical interactions and their potential applications. Eur. Polym. J. 2019, 118, 176–185. [Google Scholar] [CrossRef]
- Rusu, A.; Nita, L.E.; Bercea, M.; Tudorachi, N.; Diaconu, A.; Pamfil, D.; Rusu, D.; Ivan, F.E.; Chiriac, A. Interpenetrated polymer network with modified chitosan in composition and self-healing properties. Int. J. Biol. Macromol. 2019, 132, 374–384. [Google Scholar] [CrossRef] [PubMed]
- White, S.R.; Sottos, N.; Geubelle, P.; Moore, J.; Kessler, M.R.; Sriram, S.; Brown, E.; Viswanathan, S. Autonomic healing of polymer composites. Nature 2001, 409, 794–797. [Google Scholar] [CrossRef] [PubMed]
- Shahabudin, N.; Yahya, R.; Gan, S.N. Microcapsules filled with a palm oil-based alkyd as healing agent for epoxy matrix. Polymers 2016, 8, 125. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lee, J.; Park, S.J.; Park, C.S.; Kwon, O.S.; Chung, S.Y.; Shim, J.; Lee, C.S.; Bae, J. Effect of a surfactant in microcapsule synthesis on self-healing behavior of capsule embedded polymeric films. Polymers 2018, 10, 675. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, H.J.; Mo, Q.F.; Li, W.Z.; Gu, F.M. Preparation and properties of self-healing and self-lubricating epoxy coatings with polyurethane microcapsules containing bifunctional linseed oil. Polymers 2019, 11, 1578. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zheng, N.; Liu, J.; Li, W. TO/TMMP-TMTGE double-healing composite containing a transesterification reversible matrix and tung oil-loaded microcapsules for active self-healing. Polymers 2019, 11, 1127. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Kim, B.H.; Oh, M.; Park, D.H.; Lee, S. Repeatable crack self-healing by photochemical [2+2] cycloaddition of TCE-co-DCE monomers enclosed in homopolymer microcapsules. Polymers 2019, 11, 104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jeoung, H.J.; Kim, K.W.; Chang, Y.J.; Jung, Y.C.; Ku, H.; Oh, K.W.; Choi, H.M.; Chung, J.W. Self-healing EPDM rubbers with highly stable and mechanically-enhanced urea-formaldehyde (UF) microcapsules prepared by multi-step in situ polymerization. Polymers 2020, 12, 1918. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.X.; Hollar, J.; He, X.D.; Shi, X.M. A self-healing cementitious composite using oil core/silica gel shell microcapsules. Cem. Concr. Comp. 2011, 33, 506–512. [Google Scholar] [CrossRef]
- Zhuang, X.; Zhou, S. The prediction of self-healing capacity of bacteria-based concrete using machine learning approaches. CMC-Comput. Mater. Con. 2019, 1, 57–77. [Google Scholar] [CrossRef] [Green Version]
- Zhuang, X.; Zhou, S. Molecular dynamics study of an amorphous polyethylene/silica interface with shear tests. Materials 2018, 11, 929. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Vu-Bac, N.; Arash, B.; Zhu, H.; Zhuang, X. Interface characterization between polyethylene/ silica in engineered cementitious composites by molecular dynamics simulation. Molecules 2019, 24, 1497. [Google Scholar] [CrossRef] [Green Version]
- Zhou, S.; Xie, L.; Jia, Y.; Wang, C. Review of cementitious composites containing polyethylene fibers as repairing materials. Polymers 2020, 12, 2624. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X. Characterization of loading rate effects on the interactions between crack growth and inclusions in cementitious material. CMC-Comput. Mater. Contin. 2018, 57, 417–466. [Google Scholar] [CrossRef]
- Zhou, S.; Zhuang, X. Micromechanical study of loading rate effects between a hole and a crack. Undergr. Space 2019, 4, 22–30. [Google Scholar] [CrossRef]
- Zhou, S.; Zhu, H.; Ju, J.; Yan, Z.; Chen, Q. Modeling microcapsule-enabled self-healing cementitious composite materials using discrete element method. Int. J. Damage Mech. 2017, 26, 340–357. [Google Scholar] [CrossRef]
- Zhou, S.; Zhu, H.; Yan, Z.; Ju, J.; Zhang, L. A micromechanical study of the breakage mechanism of microcapsules in concrete using PFC2D. Constr. Build. Mater. 2016, 115, 452–463. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, S.; Yan, Z.; Ju, J.W.; Chen, Q. A two-dimensional micromechanical damage-healing model on microcrack-induced damage for microcapsule-enabled self-healing cementitious composites under compressive loading. Int. J. Damage Mech. 2016, 25, 727–749. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, S.; Yan, Z.; Ju, J.W.; Chen, Q. A two-dimensional micromechanical damage-healing model for microcapsule-enabled self-healing cementitious composites under tensile loading. Int. J. Damage Mech. 2015, 24, 95–115. [Google Scholar] [CrossRef]
- Zhu, H.; Zhou, S.; Yan, Z.; Ju, J.W.; Chen, Q. A 3D analytical model for the probabilistic characteristics of self-healing model for concrete using spherical microcapsule. Comput. Concr. 2015, 15, 37–54. [Google Scholar] [CrossRef]
- Yuan, K.Y.; Ju, J.W.; Yuan, W.; Yang, J.M. Numerical predictions of mechanical behavior of innovative pothole patching materials featuring high toughness, low-viscosity nano-molecular resins. Acta Mech. 2014, 225, 1141–1151. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, Q.; Yan, Z.; Ju, J.W.; Zhou, S. Micromechanical models for saturated concrete repaired by the electrochemical deposition method. Mater. Struct. 2014, 47, 1067–1082. [Google Scholar] [CrossRef]
- Yanase, K.; Ju, J.W. Effective elastic moduli of spherical particle reinforced composites containing imperfect interfaces. Int. J. Damage Mech. 2012, 21, 97–127. [Google Scholar] [CrossRef]
- Li, C.; Wang, J.; Dou, F. An estimation approach for the effective elastic modulus of lightweight bulk filling material with compressible inclusions and imperfect interfaces. Materials 2020, 13, 3563. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, H.H.; Ju, J.W.; Yan, Z.G.; Jiang, Z.W.; Chen, B.; Wang, Y.Q.; Fan, Z.H. Stochastic micromechanical predictions for the probabilistic behavior of saturated concrete repaired by the electrochemical deposition method. Int. J. Damage Mech. 2020, 29, 435–453. [Google Scholar] [CrossRef]
- Chen, X.; Li, R.; Sun, L.Z. Dynamic magneto-viscoelastic model for magnetorheological nanocomposites with imperfect interface. Int. J. Damage Mech. 2019, 28, 1248–1260. [Google Scholar] [CrossRef]
- Zhang, Y.; Ju, J.W.; Zhu, H.H.; Yan, Z.G. A novel multi-scale model for predicting the thermal damage of hybrid fiber-reinforced concrete. Int. J. Damage Mech. 2020, 29, 19–44. [Google Scholar] [CrossRef]
- Chen, Q.; Zhu, H.H.; Ju, J.W.; Li, H.X.; Jiang, Z.W.; Yan, Z.G. Stochastic micromechanics-based investigations for the damage healing of unsaturated concrete using electrochemical deposition method. Int. J. Damage Mech. 2020, 29, 1361–1378. [Google Scholar] [CrossRef]
- Shodja, H.M.; Hashemian, B. Variational bounds and overall shear modulus of nano-composites with interfacial damage in anti-plane couple stress elasticity. Int. J. Damage Mech. 2020, 29, 246–271. [Google Scholar] [CrossRef]
- Hong, S.X.; Qin, S.F.; Dong, B.Q.; Xing, F. Corrosion features of the reinforcing bar in concrete with intelligent OH- regulation of microcapsules. Materials 2019, 12, 3966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zuo, J.D.; Li, H.B.; Zhan, J.; Dong, B.Q.; Wang, L.; Chen, D.Z. Preparation and properties of cement mortar/metal hydroxide microcapsules composites. Cem. Concr. Comp. 2020, 105, 103438. [Google Scholar] [CrossRef]
- Confalonieri, R. Monte Carlo based sensitivity analysis of two crop simulators and considerations on model balance. Eur. J. Agron. 2010, 33, 89–93. [Google Scholar] [CrossRef]
- Marino, S.; Hogue, I.B.; Ray, C.J.; Kirschner, D.E. A methodology for performing global uncertainty and sensitivity analysis in systems biology. J. Theor. Biol. 2008, 254, 178–196. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Donckels, B.M.R.; Kroll, S.; Van Dorpe, M.; Weemaes, M. Global sensitivity analysis of an in-sewer process model for the study of sulfide-induced corrosion of concrete. Water Sci. Technol. 2014, 69, 647–655. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Tiede, C. Using a variance-based sensitivity analysis for analyzing the relation between measurements and unknown parameters of a physical model. Nonlinear Proc. Geoph. 2011, 18, 269–276. [Google Scholar] [CrossRef] [Green Version]
- Saltelli, A.; Marivoet, J. Non-parametric statistics in sensitivity analysis for model output: A comparison of selected techniques. Reliab. Eng. Syst. Safe. 1990, 28, 229–253. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Goodier, J.N.; Abramson, H.N. Theory of elasticity. J. Appl. Mech. 1970, 37, 888. [Google Scholar] [CrossRef]
- Ahmed, S.; Jones, F. A review of particulate reinforcement theories for polymer composites. J. Mater. Sci. 1990, 25, 4933–4942. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Chan, K.S. A quantitative model-independent method for global sensitivity analysis of model output. Technometrics 1999, 41, 39–56. [Google Scholar] [CrossRef]
- Saltelli, A. Sensitivity analysis for importance assessment. Risk Anal. 2002, 22, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Shin, M.J.; Guillaume, J.H.; Croke, B.F.; Jakeman, A.J. Addressing ten questions about conceptual rainfall–runoff models with global sensitivity analyses in R. J. Hydrol. 2013, 503, 135–152. [Google Scholar] [CrossRef]











| Parameter | Description | Unit | Scope |
|---|---|---|---|
| E1 | Elastic modulus of the shell | GPa | (1, 10) |
| v1 | Poisson’s ratio of the shell | - | (0.001, 0.499) |
| k | The core-shell ratio | - | (0.1, 0.9) |
| ɑ | The interfacial sliding compliance | 1/MPa | (0.001, 0.01) |
| β | The interfacial separation compliance | 1/MPa | (0.001, 0.01) |
| f | The volume fraction of microcapsules | - | (1%, 10%) |
| Type | Elastic Modulus | Poisson’s Ratio |
|---|---|---|
| C30 | 30 GPa | 0.2 |
| C40 | 32.5 GPa | 0.2 |
| C50 | 34.5 GPa | 0.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Jia, Y.; Wang, C. Global Sensitivity Analysis for the Polymeric Microcapsules in Self-Healing Cementitious Composites. Polymers 2020, 12, 2990. https://doi.org/10.3390/polym12122990
Zhou S, Jia Y, Wang C. Global Sensitivity Analysis for the Polymeric Microcapsules in Self-Healing Cementitious Composites. Polymers. 2020; 12(12):2990. https://doi.org/10.3390/polym12122990
Chicago/Turabian StyleZhou, Shuai, Yue Jia, and Chong Wang. 2020. "Global Sensitivity Analysis for the Polymeric Microcapsules in Self-Healing Cementitious Composites" Polymers 12, no. 12: 2990. https://doi.org/10.3390/polym12122990
APA StyleZhou, S., Jia, Y., & Wang, C. (2020). Global Sensitivity Analysis for the Polymeric Microcapsules in Self-Healing Cementitious Composites. Polymers, 12(12), 2990. https://doi.org/10.3390/polym12122990