The Use of Scattering Data in the Study of the Molecular Organisation of Polymers in the Non-Crystalline State
Abstract
1. Introduction
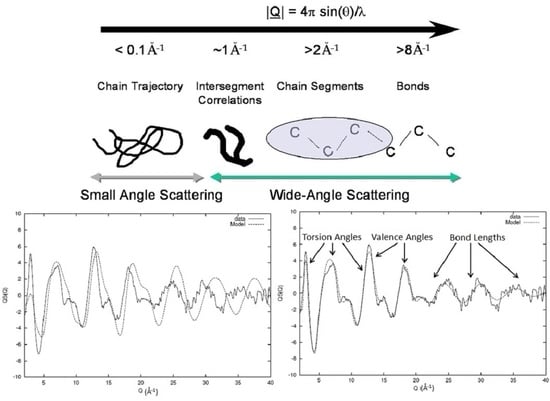
2. Diffraction and Experimental Requirements
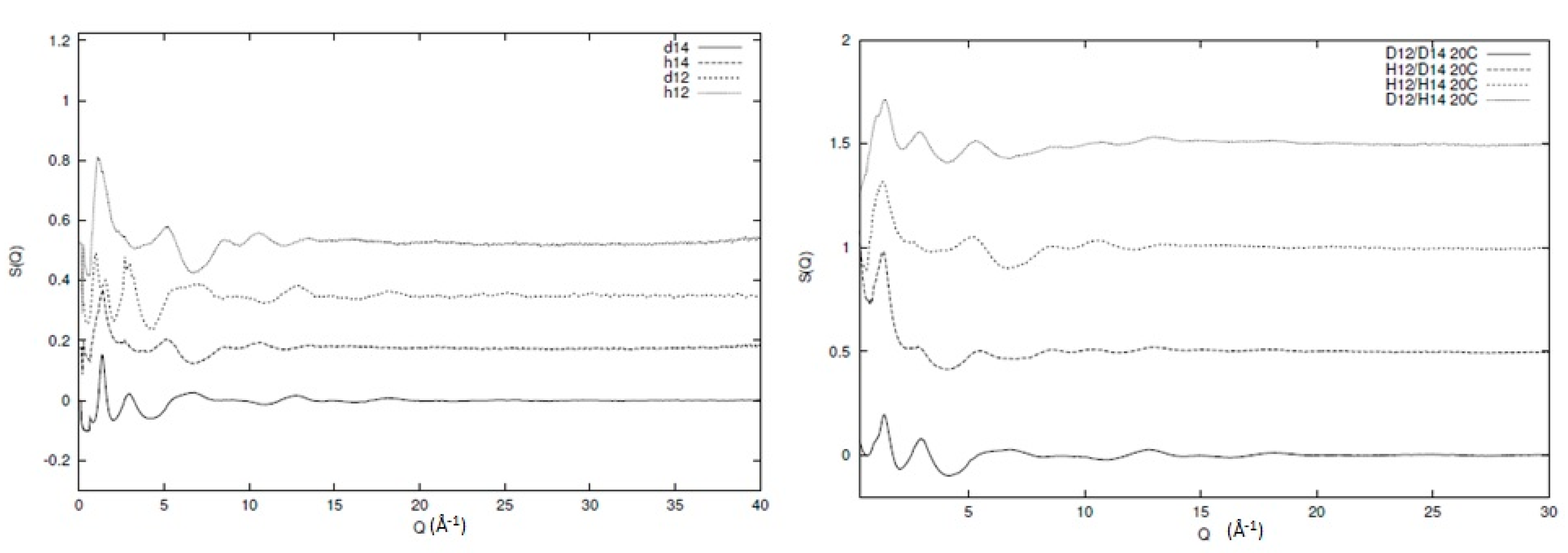
3. Use of Partial Structure Factors
4. Local Mixing in Polymer Blends
5. Coupling Diffraction with Modelling
6. Real vs. Reciprocal Space Functions—The Reverse Monte Carlo Method
The RMC Method
RMC Variations
7. The Role of the Scattering Data
7.1. Intrachain Correlations
7.2. The Case of Selenium
7.2.1. First-Order Probabilities
7.2.2. Conditional Probabilities
7.2.3. Predicted Models
7.2.4. Chain Length
7.2.5. Rings
8. Time-Resolved Crystallisation
9. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Flory, P.J. Statistical Mechanics of Chain Molecules; Wiley-Interscience: New York, NY, USA, 1969. [Google Scholar]
- Mitchell, G.; Rosi-Schwartz, B.; Ward, D. Local order in polymer glasses and melts. Philos. Trans. R. Soc. Lond. Ser. A Phys. Eng. Sci. 1994, 348, 97–115. [Google Scholar] [CrossRef]
- Lovesey, S. Theory of Neutron Scattering from Condensed Matter; Clarendon Press: Oxford, UK, 1984. [Google Scholar]
- Squires, G. Introduction to the Theory of Thermal Neutron Scattering; Dover Publications Inc.: London, UK, 1996. [Google Scholar]
- Mitchell, G.R.; Imae, T. Essentials of Neutron Techniques in Soft Matter; Imae, T., Kanaya, T., Furusaka, T., Eds.; Willey: Hoboken, NJ, USA, 2010. [Google Scholar]
- Gkourmpis, T.; Mitchell, G. Three Dimensional Picture of the Local Structure of 1,4-Polybutadiene from a Complete Atomistic Model and Neutron Scattering Data. Macromolecules 2011, 44, 3140–3148. [Google Scholar] [CrossRef]
- Richter, D. Neutron scattering in polymer physics. Phys. B Condens. Matter 2000, 276, 22–29. [Google Scholar] [CrossRef]
- Frick, B.; Richter, D. The Microscopic Basis of the Glass Transition in Polymers from Neutron Scattering Studies. Science 1995, 267, 1939–1945. [Google Scholar] [CrossRef] [PubMed]
- Mitchell, G.R. Comprehensive Polymer Science; Allen, G., Bevington, J.C., Booth, C., Price, C., Eds.; Pergamon: Oxford, UK, 1989. [Google Scholar]
- Rutledge, G.C.; Theodorou, D.N. Molecular Modeling of Polymers; John Wiley & Sons: New York, NY, USA, 1998. [Google Scholar]
- Theodorou, D.N. Hierarchical modelling of polymeric Materials. Chem. Eng. Sci. 2007, 62, 5697–5714. [Google Scholar] [CrossRef]
- McGreevy, R.L.; Pusztai, L. Reverse Monte Carlo Simulation: A New Technique for the Determination of Disordered Structures. Mol. Simul. 1988, 1, 359–367. [Google Scholar] [CrossRef]
- McGreevy, R.L. Reverse Monte Carlo modelling. J. Phys. Condens. Matter 2001, 13, 877–913. [Google Scholar] [CrossRef]
- Sánchez-Gil, V.; Noya, E.G.; Temleitner, L.; Pusztai, L. Reverse Monte Carlo modeling: The two distinct routes of calculating the experimental structure factor. J. Mol. Liq. 2015, 207, 211–215. [Google Scholar] [CrossRef][Green Version]
- Rosi-Schwartz, B.; Mitchell, G.; Soper, A. Neutron scattering from hydrogenous polymers. Phys. B Condens. Matter 1992, 180, 561–563. [Google Scholar] [CrossRef]
- Rosi-Schwartz, B.; Mitchell, G.; Soper, A. A new approach to neutron scattering for non-crystalline hydrogenous polymers. Polymer 1992, 33, 3744–3747. [Google Scholar] [CrossRef]
- Soper, A. First results from Sandals—The small angle neutron diffractometer for amorphous and liquid samples at ISIS. In Proceedings of the 11th Meeting of the International Collaboration on Advanced Neutron Sources, KEK, Tsukuba, Japan, 22–26 October 1990. [Google Scholar]
- Benmore, C.; Soper, A. The SANDALS Manual. A Guide to Performing Experiments on the Small Angle Neutron Diffractometer for Amorphous and Liquid Samples at ISIS, Council for the Central Lab. of the Research Councils (CLRC): UK, 1998.
- Bowron, D.T.; Soper, A.K.; Jones, K.; Ansell, S.; Birch, S.; Norris, J.; Perrott, L.; Riedel, D.; Rhodes, N.J.; Wakefield, S.R.; et al. NIMROD: The Near and InterMediate Range Order Diffractometer of the ISIS second target station. Rev. Sci. Instrum. 2010, 81, 033905. [Google Scholar] [CrossRef] [PubMed]
- Grazzi, F.; Scherillo, A.; Zoppi, M. A neutron imaging device for sample alignment in a pulsed neutron scattering instrument. Rev. Sci. Instrum. 2009, 80, 93704. [Google Scholar] [CrossRef] [PubMed]
- Warren, B.E.; Mavel, G. Elimination of the Compton Component in Amorphous Scattering. Rev. Sci. Instrum. 1965, 36, 196–197. [Google Scholar] [CrossRef]
- Warren, B.E. X-ray Diffraction; Courier Corporation: Chelmsford, UK, 1990. [Google Scholar]
- Mitchell, G.R.; Windle, A.H. Experimental separation of the coherent component of X-ray scattering prior to RDF analysis of non-crystalline polymers. J. Appl. Crystallogr. 1980, 13, 135–140. [Google Scholar] [CrossRef]
- Genix, A.-C.; Arbe, A.; Alvarez, F.; Colmenero, J.; Schweika, W.; Richter, D. Local Structure of Syndiotactic Poly(methyl methacrylate). A Combined Study by Neutron Diffraction with Polarization Analysis and Atomistic Molecular Dynamics Simulations. Macromolecules 2006, 39, 3947–3958. [Google Scholar] [CrossRef]
- Gerstl, C.; Brodeck, M.; Schneider, G.J.; Su, Y.; Allgaier, J.; Arbe, A.; Colmenero, J.; Richter, D. Short and Intermediate Range Order in Poly (alkylene oxide)s. A Neutron Diffraction and Molecular Dynamics Simulation Study. Macromolecules 2012, 45, 7293–7303. [Google Scholar] [CrossRef]
- Rosi-Schwartz, B.; Mitchell, G. A complete atomistic model of molten polyethylene from neutron scattering data: A new methodology for polymer structure. Polymer 1994, 35, 5398–5407. [Google Scholar] [CrossRef]
- Rosi-Schwartz, B.; Mitchell, G. A detailed single chain model for molten poly(tetrafluoroethylene) from a novel structure refinement technique on neutron scattering data. Polymer 1994, 35, 3139–3148. [Google Scholar] [CrossRef]
- Mitchell, G.; Windle, A. Structure of polystyrene glasses. Polymer 1984, 25, 906–920. [Google Scholar] [CrossRef]
- Lohse, D.J. The application of neutron scattering to the relation between chain dimensions and miscibility for polyolefins. Polym. J. 2012, 45, 20–25. [Google Scholar] [CrossRef]
- Krishnamoorti, R.; Graessley, W.W.; Fetters, L.J.; Garner, R.T.; Lohse, D.J. Thermodynamic Interactions in Polybutadiene Blends. Macromolecules 1998, 31, 2312–2316. [Google Scholar] [CrossRef]
- Gkourmpis, T.; Mitchell, G.R. Experimentally driven atomistic model of 1,2 polybutadiene. J. Appl. Phys. 2014, 115, 053505. [Google Scholar] [CrossRef]
- De Gennes, P.-G. Scaling Concepts in Polymer Physics; Cornell University Press: Ithaca, NY, USA, 1979. [Google Scholar]
- Vaughan, A.; Stevens, G. On crystallization, morphology and radiation effects in poly (ether ether ketone). Polymer 1995, 36, 1531–1540. [Google Scholar] [CrossRef]
- Keller, A. Developments in Crystalline Polymers-1; Applied Science: London, UK, 1982; p. 54. [Google Scholar]
- Mitchell, G.R.; Lovell, R.; Windle, A.H. The local structure of molten polyethylene. Polymer 1982, 23, 1273–1285. [Google Scholar] [CrossRef]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Howe, M.A.; McGreevy, R.L.; Pusztai, L.; Borzsák, I. Determination of Three Body Correlations in Simple Liquids by RMC Modelling of Diffraction Data. II. Elemental Liquids. Phys. Chem. Liq. 1993, 25, 205–241. [Google Scholar] [CrossRef]
- McGreevy, R.L.; Pusztai, L. The structure of molten salts. Proc. R. Soc. Lond. Ser. A: Math. Phys. Sci. 1990, 430, 241–261. [Google Scholar] [CrossRef]
- Jóvári, P.; Kaban, I.; Steiner, J.; Beuneu, B. Local order in amorphous Ge 2 Sb 2 Te 5 and Ge Sb 2 Te 4. Phys. Rev. B 2008, 77, 035202. [Google Scholar] [CrossRef]
- Rosi-Schwartz, B.; Mitchell, G. Extracting quantitative structural parameters for disordered polymers from neutron scattering data. Nucl. Instrum. Methods Phys. Res. Sect. A 1995, 354, 17–29. [Google Scholar] [CrossRef]
- Soper, A.K.; Page, K.; Llobet, A. Empirical potential structure refinement of semi-crystalline polymer systems: Polytetrafluoroethylene and polychlorotrifluoroethylene. J. Phys. Condens. Matter 2013, 25, 454219. [Google Scholar] [CrossRef][Green Version]
- Gkourmpis, T.; Lopez, D.; Mitchell, G. Multiscale modeling of polymers closely coupled to Broad Q neutron scattering from NIMROD. In MRS Online Proceeding Library Archive; Cambridge University Press (CUP): Cambridge, UK, 2013; Volume 1524, p. 1524. [Google Scholar]
- Mitchell, G.R.; Tojeira, A.; Gkourmpis, T.; Holt, J.J.; Harris, P.; Pezzuto, M. Controlling and evaluating the structure and morphology of polymers on multiple scales. J. Mater. Sci. Chem. Eng. 2015, 3, 48. [Google Scholar] [CrossRef][Green Version]
- Mitchell, G.R.; Mateus, A.; Bowron, D.; Bartolo, P. SANS/WANS time-resolving neutron scattering studies of polymer phase transitions using NIMROD. In Proceedings of the MRS Fall Meeting, Boston, MA, USA, 25–30 November 2012. [Google Scholar]
- Mitchell, G.R.; Maetus, A.; Davis, F.; Mohan, S.; Gkourmpis, T.; Youngs, T. New Tools for Understanding Complex Polymer Behaviour. Procedia Manuf. 2017, 12, 280–290. [Google Scholar] [CrossRef]
- Wright, A. Experimental Techniques of Glass Science; American Ceramic Society: Westerville, OH, USA, 1993; p. 205. [Google Scholar]
- Wright, A.C.; Guy, C.A.; Hulme, A.R.; Martin, S.W.; Sinclair, R.N. Diffraction Studies of Some Single-Component Network Glasses Revisited. In Proceedings of the 14th Conference on Glass and Ceramics, USA, 2005. [Google Scholar]
- Edeling, M.; Freyland, W. Molecular Structure of Expanded Liquid Selenium up to 1400 °C. Berichte der Bunsengesellschaft für Physikalische Chemie 1981, 85, 1049–1054. [Google Scholar] [CrossRef]
- Tamura, K.; Hosokawa, S. X-Ray Diffraction Measurements for Expanded Fluid Selenium up to the Supercritical Region. Berichte der Bunsengesellschaft für physikalische Chemie 1992, 96, 681–688. [Google Scholar] [CrossRef]
- Kirchhoff, F.; Kresse, G.; Gillan, M.J. Structure and dynamics of liquid selenium. Phys. Rev. B 1998, 57, 10482–10495. [Google Scholar] [CrossRef]
- Almarza, N.G.; Enciso, E.; Bermejo, F.J. Structure and dynamics of selenium chain melts: A molecular dynamics study. J. Chem. Phys. 1993, 99, 6876–6889. [Google Scholar] [CrossRef]
- Richter, H. Different forms of amorphous selenium. J. Non-Cryst. Solids 1972, 8, 388–394. [Google Scholar] [CrossRef]
- Henninger, E.H.; Buschert, R.C.; Heaton, L. Atomic Radial Distribution in Amorphous Selenium by X?Ray and Neutron Diffraction. J. Chem. Phys. 1967, 46, 586. [Google Scholar] [CrossRef]
- Kaplow, R.; Rowe, T.A.; Averbach, B.L. Atomic Arrangement in Vitreous Selenium. Phys. Rev. 1968, 168, 1068–1079. [Google Scholar] [CrossRef]
- Hansen, F.Y. Structure of amorphous selenium studied by neutron diffraction. J. Chem. Phys. 1975, 62, 1556–1565. [Google Scholar] [CrossRef][Green Version]
- Bichara, C.; Pellegatti, A.; Gaspard, J.-P. Chain structure of liquid selenium investigated by a tight-binding Monte Carlo simulation. Phys. Rev. B 1994, 49, 6581–6586. [Google Scholar] [CrossRef] [PubMed]
- Bellissent, R. Short range order in the disordered states of selenium-tellurium mixtures. Nucl. Instrum. Methods Phys. Res. 1982, 199, 289–294. [Google Scholar] [CrossRef]
- Hohl, D.; Jones, R.O. First principles MD simulation of liquid and amorphous selenium. J. Non-Cryst. Solids 1990, 117–118, 992. [Google Scholar] [CrossRef]
- Unger, P.; Cherin, P. The Physics of Selenium and Tellurium; Cooper, W.C., Ed.; Pergamon Press: Oxford, UK, 1969; p. 223. [Google Scholar]
- Corb, B.; Wei, W.; Averbach, B. Atomic models of amorphous selenium. J. Non-Crystalline Solids 1982, 53, 29–42. [Google Scholar] [CrossRef]
- Lucovsky, G. The Physics of Selenium and Tellurium; Gerlach, E., Grosse, P., Eds.; Springer: New York, NY, USA, 1979. [Google Scholar]













Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gkourmpis, T.; Mitchell, G.R. The Use of Scattering Data in the Study of the Molecular Organisation of Polymers in the Non-Crystalline State. Polymers 2020, 12, 2917. https://doi.org/10.3390/polym12122917
Gkourmpis T, Mitchell GR. The Use of Scattering Data in the Study of the Molecular Organisation of Polymers in the Non-Crystalline State. Polymers. 2020; 12(12):2917. https://doi.org/10.3390/polym12122917
Chicago/Turabian StyleGkourmpis, Thomas, and Geoffrey R. Mitchell. 2020. "The Use of Scattering Data in the Study of the Molecular Organisation of Polymers in the Non-Crystalline State" Polymers 12, no. 12: 2917. https://doi.org/10.3390/polym12122917
APA StyleGkourmpis, T., & Mitchell, G. R. (2020). The Use of Scattering Data in the Study of the Molecular Organisation of Polymers in the Non-Crystalline State. Polymers, 12(12), 2917. https://doi.org/10.3390/polym12122917