Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers
Abstract
1. Introduction
2. Simulation Model and Method
2.1. Model
2.2. Molecule Dynamics Simulation
2.3. KMT Algorithm
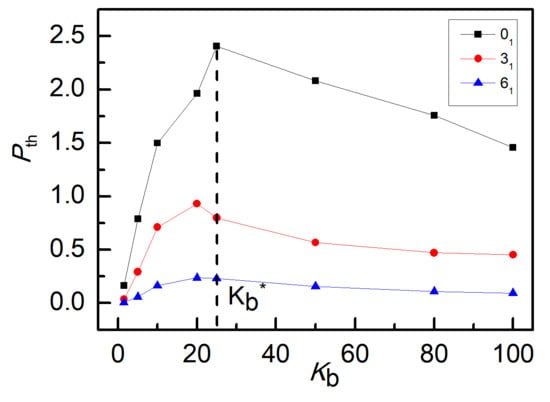
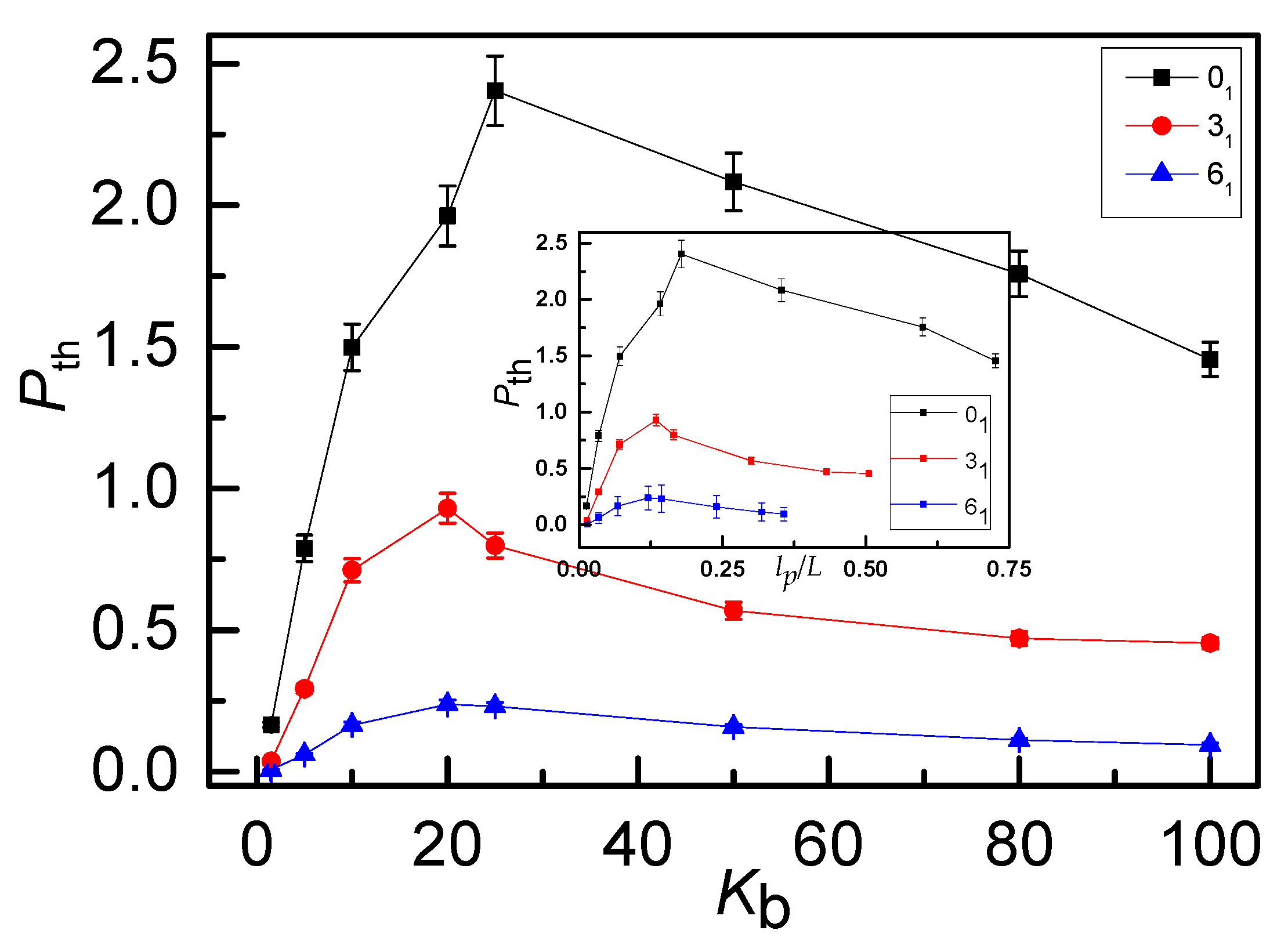
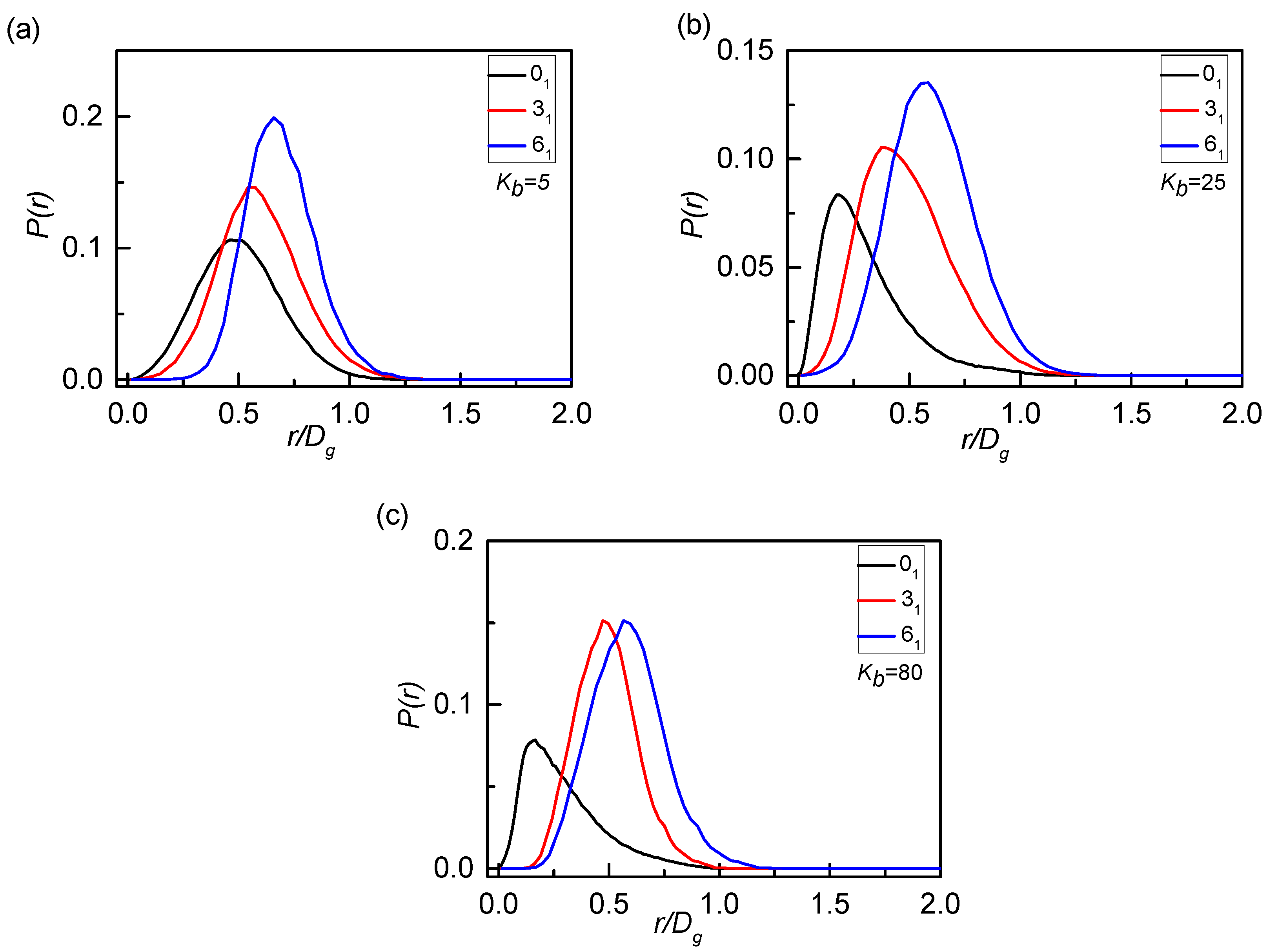
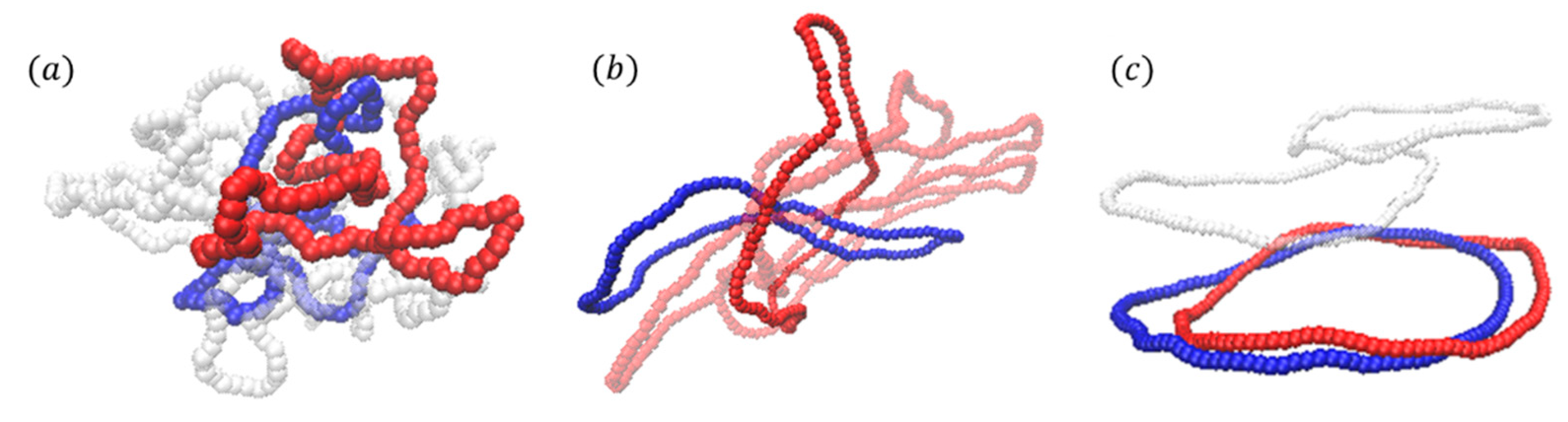
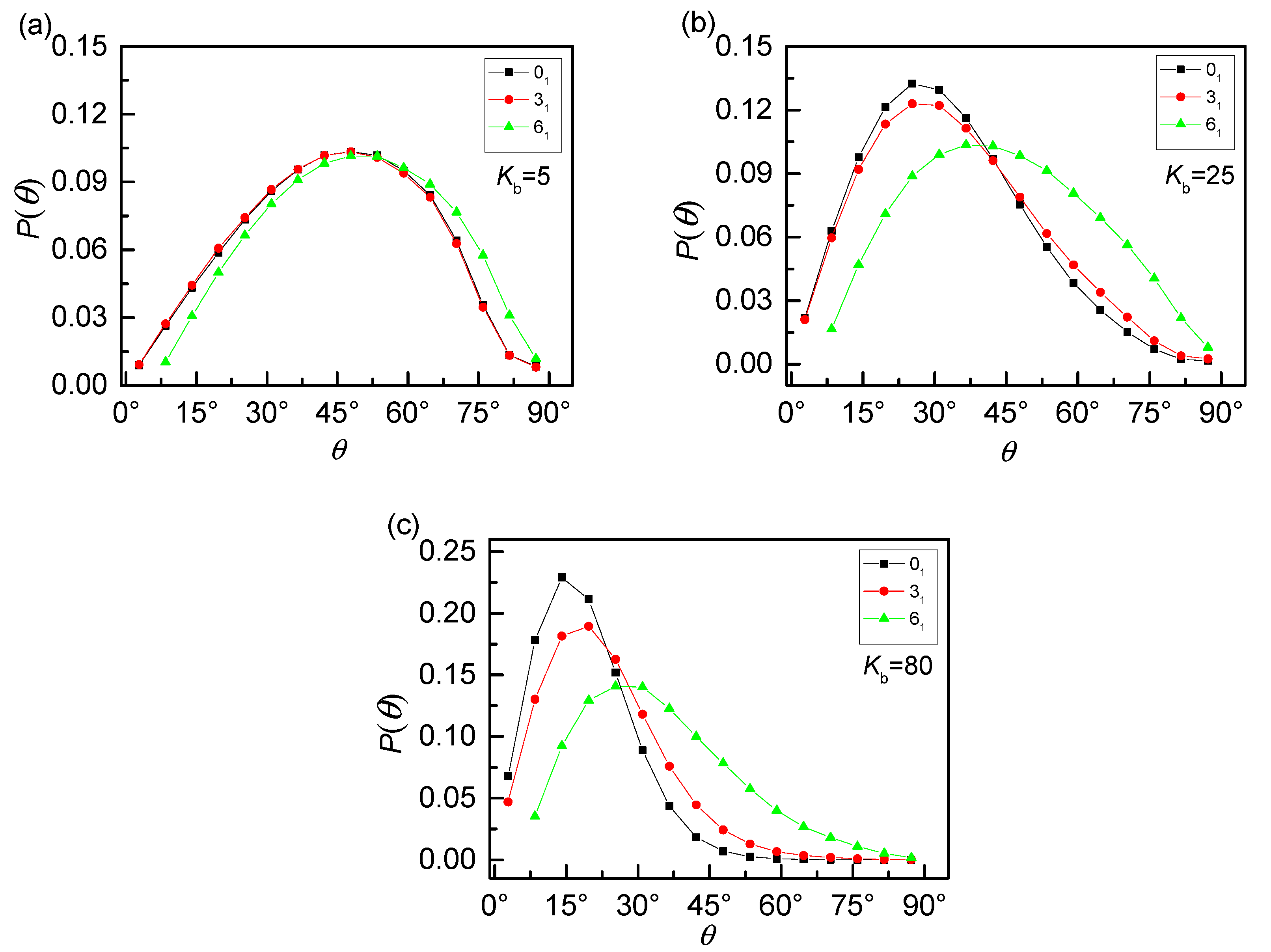
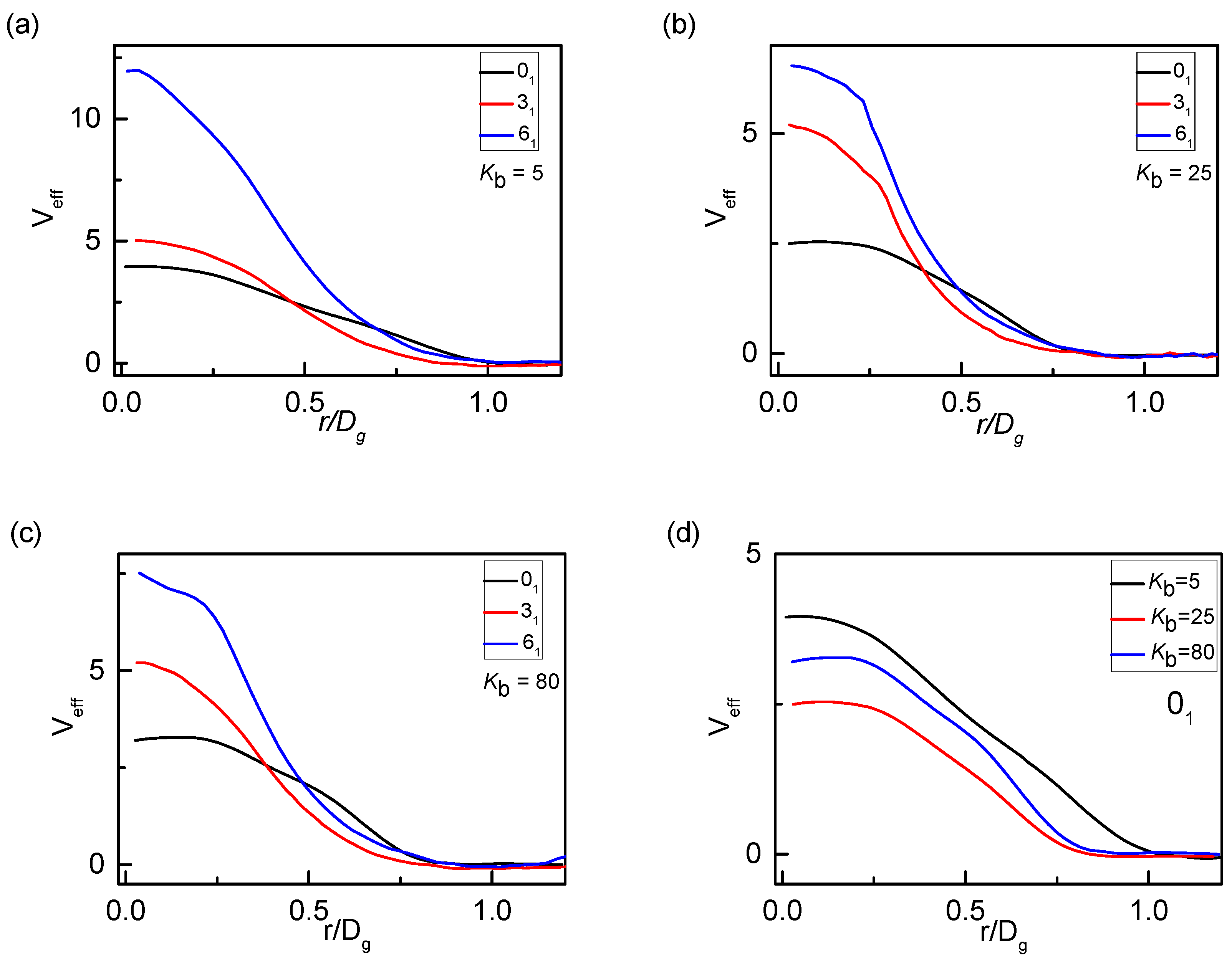
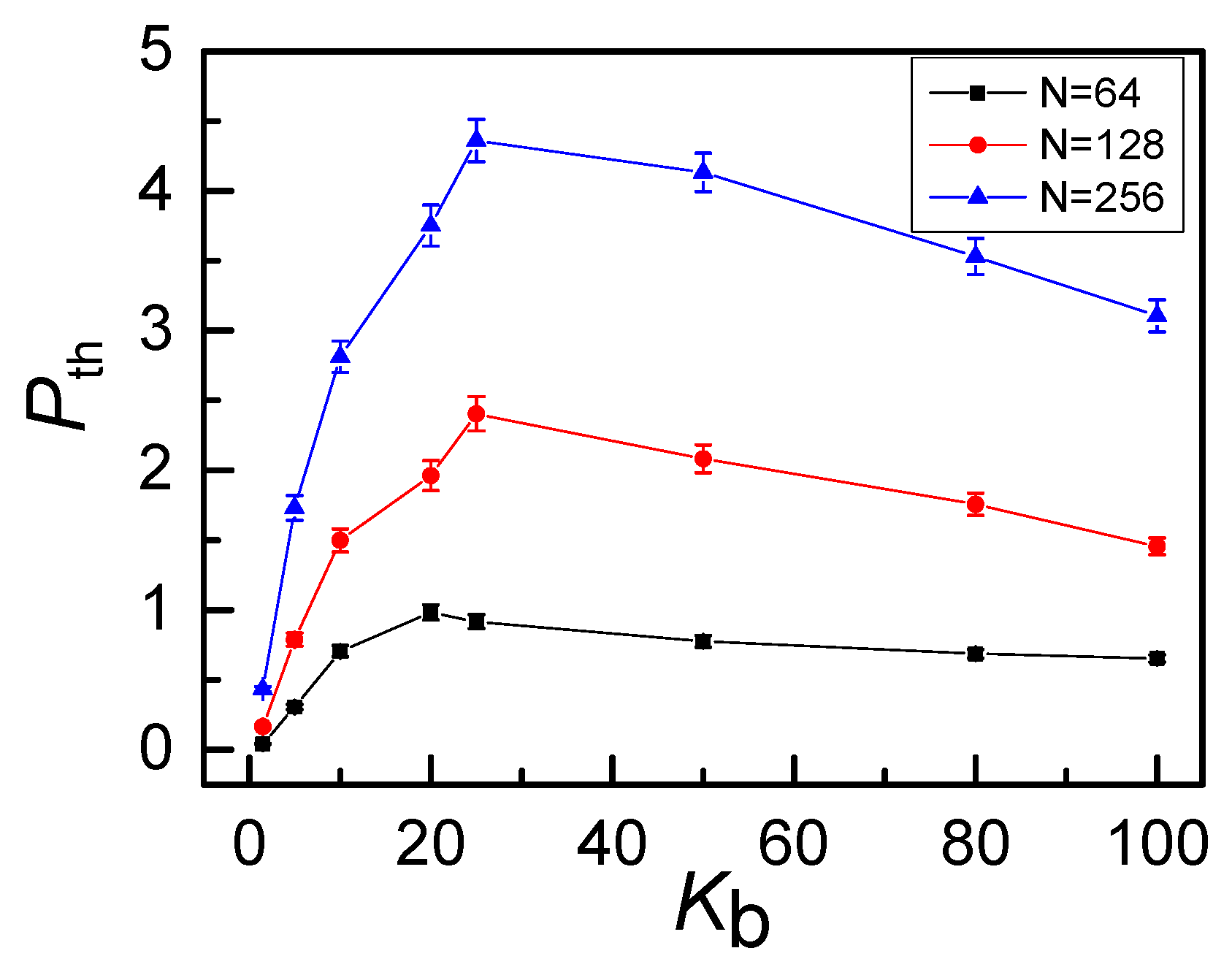
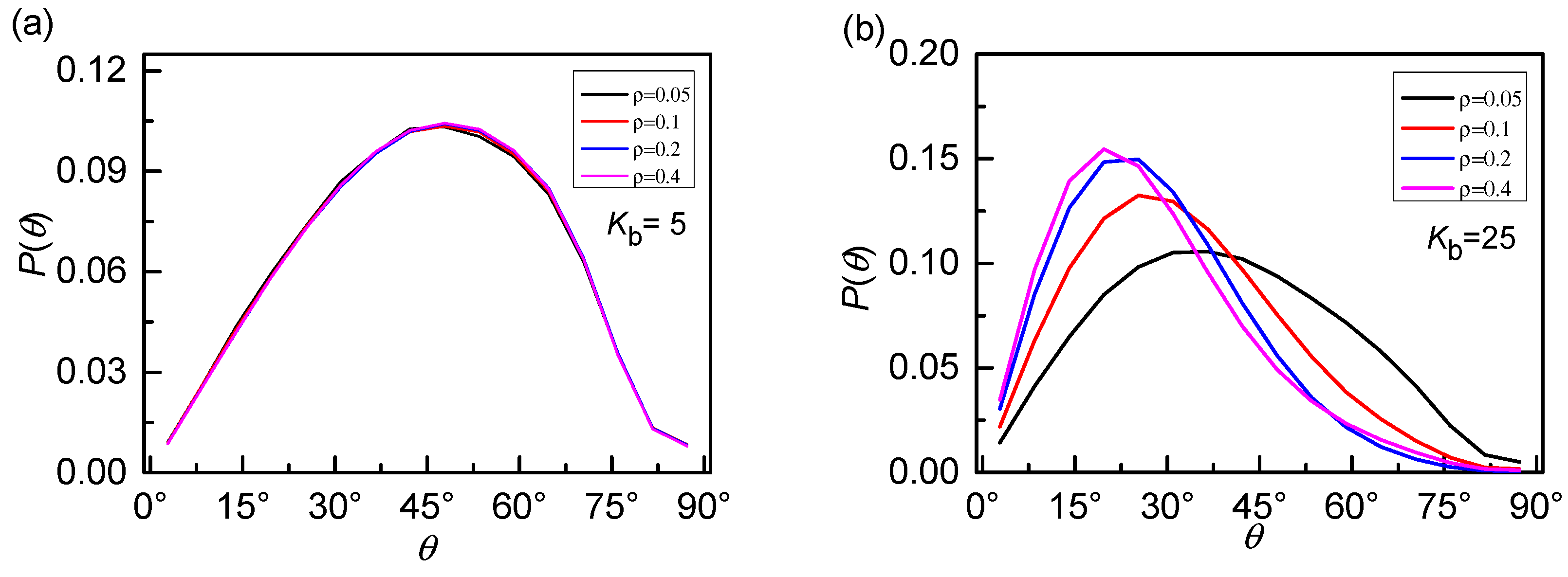
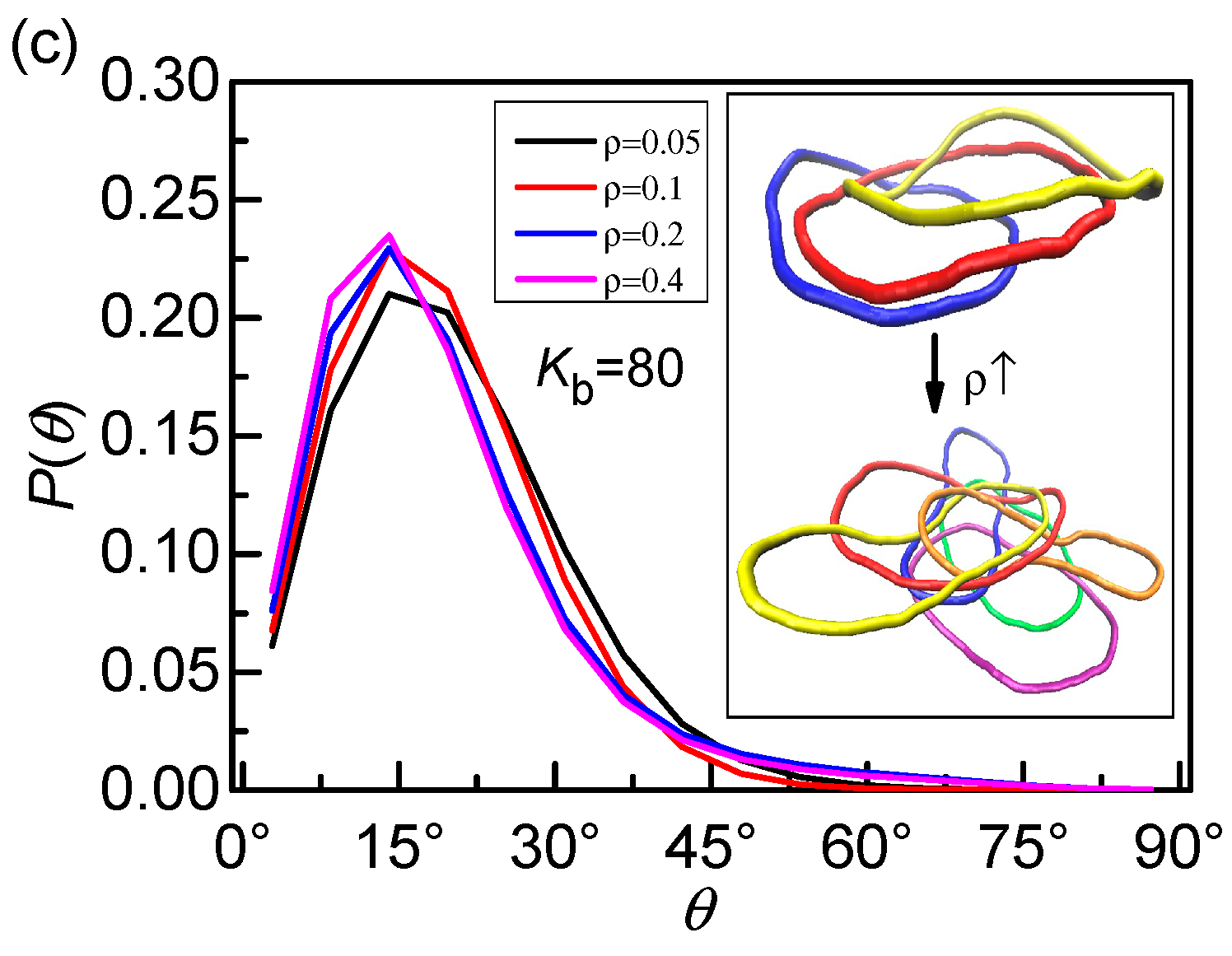
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Guo, H.; Mao, R.; Block, T.M.; Guo, J.T. Production and function of the cytoplasmic deproteinized relaxed circular DNA of hepadnaviruses. J. Virol. 2010, 84, 387–396. [Google Scholar] [CrossRef] [PubMed]
- Conway, J.H. An enumeration of knots and links and some of their related properties. In Computational Problems in Abstract Algebra; Leech, J., Ed.; Pergamon Press: Oxford, UK, 1967; pp. 329–358. [Google Scholar]
- Narros, A.; Moreno, A.J.; Likos, C.N. Influence of topology on effective potentials: Coarse-graining ring polymers. Soft Matter 2010, 6, 2435–2441. [Google Scholar] [CrossRef]
- Daichi, I. Semiflexible ring polymers in dilute solutions. React. Funct. Polym. 2018, 130, 111–117. [Google Scholar]
- Hiroki, A.; Daichi, I. Mean-square radius of gyration and scattering function of semiflexible ring Polymers of the trefoil knot. Polymers 2016, 8, 271. [Google Scholar]
- Moore, N.T.; Grosberg, A.Y. Limits of analogy between self-avoidance and topology-driven swelling of polymer loops. Phys. Rev. E 2005, 72, 061803. [Google Scholar] [CrossRef]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904. [Google Scholar] [CrossRef]
- Reigh, S.Y.; Yoon, D.Y. Concentration dependence of ring polymer conformations from Monte Carlo simulations. ACS Macro. Lett. 2013, 2, 296–300. [Google Scholar] [CrossRef]
- Zhou, X.L.; Jiang, Y.W.; Deng, Z.Y.; Zhang, L.X. Glassy dynamics of nanoparticles in semiflexible ring polymer nanocomposite melts. Sci. Rep. 2017, 7, 44325. [Google Scholar] [CrossRef]
- Zhou, X.L.; Jiang, Y.W.; Chen, J.M.; He, L.L.; Zhang, L.X. Size-dependent nanoparticle dynamics in semiflexible ring polymer nanocomposites. Polymer 2017, 131, 243–251. [Google Scholar] [CrossRef]
- Doi, Y.; Matsubara, K.; Ohta, Y.; Nakano, T.; Kawaguchi, D.; Takahashi, Y.; Takano, A.; Matsushita, Y. Melt rheology of ring polystyrenes with ultrahigh purity. Macromolecules 2015, 48, 3140–3147. [Google Scholar] [CrossRef]
- Yan, Z.C.; Costanzo, S.; Jeong, Y.; Chang, T.; Vlassopoulos, D. Linear and nonlinear shear rheology of a marginally entangled ring polymer. Macromolecules 2016, 49, 1444–1453. [Google Scholar] [CrossRef]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Oxford University Press: New York, NY, USA, 1986. [Google Scholar]
- Kapnistos, M.; Lang, M.; Vlassopoulos, D.; Pyckhout-Hintzen, W.; Richter, D.; Cho, D.; Chang, T.; Rubinstein, M. Unexpected power-law stress relaxation of entangled ring polymers. Nat. Mater. 2008, 7, 997–1002. [Google Scholar] [CrossRef] [PubMed]
- Narros, A.; Moreno, A.J.; Likos, C.N. Effects of knots on ring polymers in solvents of varying quality. Macromolecules 2013, 46, 9437–9445. [Google Scholar] [CrossRef]
- Narros, A.; Moreno, A.J.; Likos, C.N. Effective Interactions of knotted ring polymers. Biochem. Soc. Trans. 2013, 41, 630–634. [Google Scholar] [CrossRef]
- Zhou, X.L.; Guo, F.C.; Li, K.; He, L.L.; Zhang, L.X. Entropy-induced separation of binary semiflexible ring polymer mixture in spherical confinement. Polymers 2019, 11, 1992. [Google Scholar] [CrossRef] [PubMed]
- Khokhlov, A.R.; Nechaev, S.K. Polymer chain in an array of obstacles. Phys. Lett. A 1985, 112, 156–160. [Google Scholar] [CrossRef]
- Obukhov, S.P.; Rubinstein, M.; Duke, T. Dynamics of a ring polymer in a gel. Phys. Rev. Lett. 1994, 73, 1263–1266. [Google Scholar] [CrossRef]
- Grosberg, A.Y. Annealed lattice animal model and Flory theory for the melt of non-concatenated rings: Towards the physics of crumpling. Soft Matter 2014, 10, 560–565. [Google Scholar] [CrossRef]
- Smrek, J.; Grosberg, A.Y. Understanding the dynamics of rings in the melt in terms of the annealed tree model. J. Phys. Condens. Matter 2015, 27, 064117. [Google Scholar] [CrossRef]
- Michieletto, D.; Marenduzzo, D.; Orlandini, E.; Alexander, G.P.; Turner, M.S. Threading dynamics of ring polymers in a gel. ACS Macro. Lett. 2014, 3, 255–259. [Google Scholar] [CrossRef]
- Michieletto, D.; Nahali, N.; Rosa, A. Glassiness and heterogeneous dynamics in dense solutions of ring polymers. Phys. Rev. Lett. 2017, 119, 197801. [Google Scholar] [CrossRef] [PubMed]
- Lee, E.; Kim, S.; Jung, Y. Slowing down of ring polymer diffusion caused by inter-ring threading. Macromol. Rapid Commun. 2015, 36, 1115–1121. [Google Scholar] [CrossRef] [PubMed]
- Smrek, J.; Grosberg, A.Y. Minimal surfaces on unconcatenated polymer rings in melt. ACS Macro. Lett. 2016, 5, 750–754. [Google Scholar] [CrossRef]
- Halverson, J.D.; Smrek, J.; Kremer, K.; Grosberg, A.Y. From a melt of rings to chromosome territories: The role of topological constraints in genome folding. Rep. Prog. Phys. 2014, 77, 022601. [Google Scholar] [CrossRef] [PubMed]
- Marenduzzo, D.; Micheletti, C.; Orlandini, E. Biopolymer organization upon confinement. J. Phys. Condens. Matter 2010, 22, 283102. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Grest, G.S.; Kremer, K. Molecular dynamics simulation for polymers in the presence of a heat bath. Phys. Rev. A 1986, 33, 3628. [Google Scholar] [CrossRef]
- Plimpton, S.J. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Torrie, G.M.; Valleau, J.P. Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling. J. Comput. Phys. 1977, 23, 187–199. [Google Scholar] [CrossRef]
- Jiang, Y.W.; Zhang, D.; He, L.L.; Zhang, L.X. Entropic interactions in semiflexible polymer nanocomposite melts. J. Phys. Chem. B 2016, 120, 572–582. [Google Scholar] [CrossRef]
- Souaille, M.; Roux, B. Extension to the weighted histogram analysis method: Combining umbrella sampling with free energy calculations. Comput. Phys. Commun. 2001, 135, 40–57. [Google Scholar] [CrossRef]
- Deng, Z.Y.; Jiang, Y.W.; He, L.L.; Zhang, L.X. Aggregation–dispersion transition for nanoparticles in semiflexible ring polymer nanocomposite melts. J. Phys. Chem. B 2016, 120, 11574–11581. [Google Scholar] [CrossRef] [PubMed]
- Chandler, D. Introduction to Modern Statistical Mechanics; Oxford University Press: Oxford, UK, 1987. [Google Scholar]
- Frenkel, D.; Smit, B. Understanding Molecular Simulation; Academic Press: San Diego, CA, USA, 1996. [Google Scholar]
- Ferrenberg, A.M.; Swendsen, R.H. Optimized Monte Carlo data analysis. Phys. Rev. Lett. 1989, 63, 1195. [Google Scholar] [CrossRef] [PubMed]
- Koniaris, K.; Muthukumar, M. Knottedness in ring polymers. Phys. Rev. Lett. 1991, 66, 2211–2214. [Google Scholar] [CrossRef] [PubMed]
- Taylor, W.R. A deeply knotted protein structure and how it might fold. Nature 2000, 406, 916–919. [Google Scholar] [CrossRef]
- Virnau, P.; Kantor, Y.; Kardar, M. Knots in globule and coil phases of a model polyethylene. J. Am. Chem. Soc. 2005, 127, 15102–15106. [Google Scholar] [CrossRef]
- Gómez, L.R.; García, N.A.; Pöschel, T. Packing structure of semiflexible rings. Proc. Natl. Acad. Sci. USA 2020, 117, 3382–3387. [Google Scholar] [CrossRef]
- Bernabei, M.; Bacova, P.; Moreno, A.J.; Narros, A.; Likos, C.N. Fluids of semiflexible ring polymers: Effective potentials and clustering. Soft Matter 2013, 9, 1287–1300. [Google Scholar] [CrossRef]
- Poier, P.; Likos, C.N.; Moreno, A.J.; Blaak, R. An Anisotropic effective model for the simulation of semiflexible ring polymers. Macromolecules 2015, 9, 4983–4997. [Google Scholar] [CrossRef]
- Heermann, B. Topological interactions between ring polymers: Implications for chromatin loops. J. Chem. Phys. 2010, 132, 044904. [Google Scholar]
- Mladek, P.B.M.; Kahl, G.; Likos, C.N. Computer assembly of cluster-forming amphiphilic dendrimers. Phys. Rev. Lett. 2008, 100, 028301. [Google Scholar] [CrossRef] [PubMed]
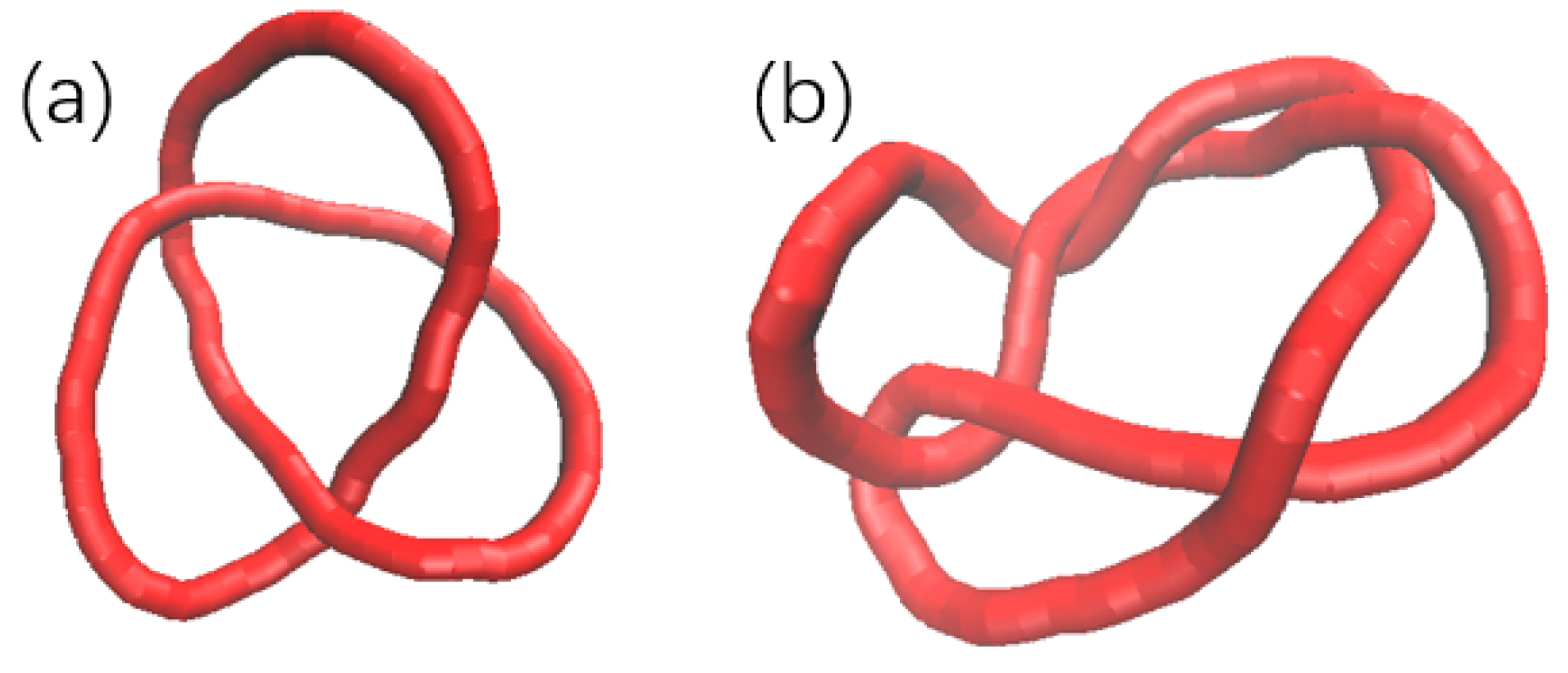





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, F.; Li, K.; Wu, J.; He, L.; Zhang, L. Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers. Polymers 2020, 12, 2659. https://doi.org/10.3390/polym12112659
Guo F, Li K, Wu J, He L, Zhang L. Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers. Polymers. 2020; 12(11):2659. https://doi.org/10.3390/polym12112659
Chicago/Turabian StyleGuo, Fuchen, Ke Li, Jiaxin Wu, Linli He, and Linxi Zhang. 2020. "Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers" Polymers 12, no. 11: 2659. https://doi.org/10.3390/polym12112659
APA StyleGuo, F., Li, K., Wu, J., He, L., & Zhang, L. (2020). Effects of Topological Constraints on Penetration Structures of Semi-Flexible Ring Polymers. Polymers, 12(11), 2659. https://doi.org/10.3390/polym12112659