Abstract
This article presents a mathematical model and theoretical analysis of coating of a thin film of non-Newtonian polymers as they travel through a small space between two reverse-rotating rolls. The dimensionless forms of the governing equations are simplified with the help of the lubrication approximation theory (LAT). By using the perturbation technique, the analytical solutions for velocity, flow rate and pressure gradient were obtained. From an engineering point of view, some significant results such as thickness of the coated web, pressure distribution, separation points, separation force and power input were computed numerically. The effect of velocities ratio and Weissenberg number on these physical quantities is presented graphically; others are shown in tabular form. It is noted that the involved material parameters provide a mechanism to control the flow rate, pressure distribution, the thickness of coating, separation force and power input. Moreover, the separation point is shifted toward the nip region by increasing velocities ratio .
1. Introduction
Roll coating is an engineering procedure in which a uniform thin liquid film is deposited onto a substrate. The phenomenon of roll coating has gained a solid reputation in recent times due to its wide applications in coating industries. In many industrial processes, thin uniform liquid coatings are produced on surfaces with coating materials. Such procedures involve wrapping, wallpaper and adhesive tapes, beautification, books and magazine, plastic films, protection of fabrics or metals, X-ray films, photographic films, coated items, foils and coated paper and magnetic records, etc. These activities rely on a wide range of apparatuses, among which roll coaters are popular. In the roll-coating process, in which the radii of the rolls are much greater than nip distance between the two rotating rolls, when a fluid flows through such a small gap, it comes out as a thin liquid film that can be used to coat a surface. The flow of fluid in a small space between a pair of rotating rollers is the key factor controlling the thickness and uniformity of the coated film. The coating thickness depends primarily on the gap between the adjacent rollers and their relative speeds. According to the direction of the rolls, roll coating is classified as reverse roll-coating , metering roll-coating and forward roll-coating [1,2,3,4]. In the case of forward roll-coating, the two rolls at the nip go in the same direction. The coating fluid forms a bath on the upstream side of the nip and, after leaving the nip, divides into two liquid films that are transferred onto both sides of the roller—one of them is applied for industrial purposes to a web. In reverse roll-coating, the rollers move in the opposite direction and the metering coating on the nip [5,6,7].
A pioneering work including experimental, analytical and computational analysis related to the roll-coating process, can be found in [5,8,9]. In an earlier work, Coyle et al. [10] used a finite element approach backed by experimental outcomes to explain the essential fluid dynamic characteristics of the reverse roll-coating. They also clarified the existence of flow instabilities, including ribbing and cascading. Taylor and Zettlemoyer et al. [11] used the lubrication theory to perceive ink flow behavior in the process of printing press. They obtained the influences of pressure distribution and force. The water flow between two rolls was discussed by Hinter Maier and White et al. [12]. They used the principle of lubrication and verified the findings which were compatible with their experimental results. Greener and Middleman et al. [13] and Ho and Holland et al. [14] developed mathematical models based on the lubrication theory to examine reverse roll-coating systems; however, they ignored the influences of surface tension, existence of free surfaces and dynamics of contact lines. Jang et al. [6] used the finite-volume method and volume of fluid (VoF)-free surface technique to 3D model of non-Newtonian flow in reverse roll-coating. This related work was carried out on inelastic non-Newtonian fluids. The power-law exponent was considered in the range of 0.95 to 1.05. Mainly concentration was paid on the resulting thickness of the coating and the effect of roll-speed on ribbing instabilities. The results show that with the increase of the power-law index, the thickness of the coating film increases. Furthermore, considering dynamic of wetting lines, Shiode et al. [15] used VoF to analyze reverse roll-coating numerically. Their results reveal that the wetting line approaches the nip as the speed ratio increases. Recently, Zahid et al. [16] gave numerical results for second-grade materials by utilizing the lubrication approximation theory. Engineering parameters such as the thickness of the coating, pressure distribution, split location, strength, roll power consumption, stresses and adiabatic temperature rise was achieved among coating roll and coated web. Zahid et al. [17] discussed the Rabinowitz fluid numerically. They presented physical parameters of engineering interest such as stresses, force, separation position, pressure distribution, power input, temperature to rolls and thickness of the coating of the web.
Today, the occurrence of non-Newtonian fluids in mechanical, aeronautical and industrial engineering is more important than Newtonian materials. Because of this reason many non-Newtonian fluid models with different constitutive equations have been proposed [18,19,20,21,22]. The analysis of pseudoplastic fluids has gained importance due to its main uses in the industry [23]. Numerous non-Newtonian polymers are pseudoplastic and are being extensively studied. Pseudoplastic liquids can be established in essential applications such as extruded polymer films, emulsion-coated films such as polymer solutions, photographic films with a high molecular weight and melts. However, less consideration has been paid to the Williamson fluid model, which describes the properties of pseudoplastic fluids [24,25]. Nadeem et al. have debated the peristaltic flow of a Williamson fluid [26]. Cramer et al. [27] demonstrated with experimental evidence that this model is better suited to polymer solutions and particle suspensions than other models.
In this article, we provide a theoretical analysis for the reverse roll-coating process of Williamson fluid films, which is drawn through a small gap between two rolls rotating in opposite directions. With the help of the lubrication approximation theory, the governing equations are simplified. The analytical solutions for flow rate, velocity and pressure gradient are provided by using the perturbation technique. From an engineering point of view, some significant results like pressure distribution, thickness of coated web, separation points, separation force and power input are presented. It was found that the involved material parameters provide a device to control the flow rate, the coating thickness separation points, separation force and power input. Our results are presented both graphically and in tabular form. The following sections describe the mathematical formulation and analytical solution of the problem. At the end, results and discussion and conclusions are presented.
2. Mathematical Formulation
We considered two dimensional steady, laminar flow of an incompressible Williamson fluid between two rolls rotating in the opposite direction with velocities , where is the radius of each roll and subscripts and stand for forward and reverse rotating rolls, respectively. The velocities ratio of both rolls is uniform, and the gap between rolls is . Moreover, the and are taken along and transversal to the flow direction, respectively, as represented in Figure 1.
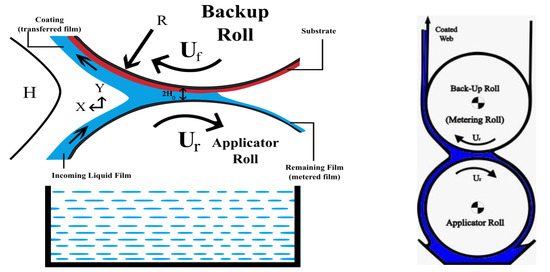
Figure 1.
Geometry of reverse roll-coating (RRC).
The governing equations for the Williamson fluid are:
where denotes the material derivative, presents the density, is the pressure, is the velocity and the extra stress tensor for a Williamson fluid [28] is defined as:
Here and denote the infinite and zero shear rate viscosities, respectively, denotes the first Rivlin–Erickson tensor, and the time constant is denoted by . The shear rate [26] is defined as:
where represents the second tensor of invariant strain. When and , then Equation (3) can be written as:
The above model reduces to Newtonian for . The two-dimensional velocity profile is taken as:
In view of the Equation (6), the component forms of the governing Equations (1) and (2) can be written as:
where and are the stress components.
3. The Dimensionless Form
Introducing the non-dimensional variables:
and dropping the steric for convenience, the dimensionless forms of the Equations (7)–(9) become:
The stresses components involved in Equations (12) and (13) are given by:
where , and
Since is a square root of the ratio of to and is very small, therefore ignoring the term having to get:
It is obvious from Equation (17) that is not a function of , so it is the function of only, i.e., . Thus, the Equation (16) becomes:
The dimensionless boundary conditions subjected to the Equation (18) are given by:
where .
4. Solution of the Problem
The Equation (18) is a nonlinear differential equation; we will employ a regular perturbation technique for to obtain its analytic solution. Therefore:
where , and are the zeroth-order solutions, which represent the Newtonian case [13], while , , , , and are the corrections up to first-order and second-order terms, respectively and have the contribution of non-Newtonian effects. By substituting Equations (20) and (21) into Equation (18) and comparing the same power of , we obtain a system of differential equations as follows:
For :
with boundary conditions:
For :
with boundary condition:
4.1. Zeroth-Order Solution
The solution of zeroth-order boundary value problem (23) and (24) is given by
Now, the zeroth-order dimensionless flow rate is defined as
In addition, from Equations (27) and (28), we get
The integration of Equation (29) with the condition as yields the zeroth-order pressure given by:
To determine the thickness of the coating and the pressure distribution, we need to find the value of . To meet this situation, the Swift–Stieber boundary condition on pressure is applied. It is claimed that at the transition point where a lubrication-type flow gives way to a transverse flow, both the pressure gradient and the pressure disappear. Upon setting in the Equation (29), we get:
Similarly, because of the Swift–Stieber boundary condition on pressure, replacing with in Equation (30), finding value of in terms of from the Equation (31) and substituting this value into the resulting equation from Equation (30), the transcendental equation in is obtained. To handle the complexity of this equation for finding the valve of , we use the numeric technique, namely a regular false position method with a predefined accuracy of and setting different valves of .
4.2. First-Order Solution
The first-order solution procedure resembles to the zeroth-order solution. Using the Equation (23) into Equation (27) and employing boundary conditions (26) to obtain:
The first-order dimensionless flow rate is defined as:
From Equations (30) and (31), we have:
The first-order pressure is obtained by integrating Equation (34) with the condition as we get:
To obtain the value for , the Swift–Stieber boundary condition on pressure will also be applied. It is claimed that the transition point where a lubrication-type flow provides a way to a transverse flow, both the pressure gradient and the pressure disappears. Upon setting in Equation (34), we get:
Similarly, because of the Swift–Stieber boundary condition on pressure, replacing with in Equation (35), finding the value of in terms of from the Equation (36) and substituting this value into the resulting equation from Equation (35), transcendental equation in is obtained. To handle the complexity of this equation for finding the valve of , we use numeric technique, namely a regular false position method with a predefined accuracy of for different valves of . These results are shown in Table 1 and Table 2.

Table 1.
Influence of on flow rate , separation points and thickness of coating , separation force and power input .

Table 2.
Influence of on flow rate , separation points and thickness of coating , separation force and power input .
Second simple material balance relation for can be written as:
which may lead to the form:
where is the thickness of the coating, and are the thickness of fluid films on the reverse roll and forward roll, respectively. The ratio denotes half of the nip region to incoming fluid film from the reverse roll. Thus, we see that to find the thickness of the coating, it is necessary to know .
Thus, the perturbation solution up to first order is given by:
where are given in Equations (27), (29), (32) and (34), respectively.
5. Operating Variables
When pressure distribution, velocity profile and pressure gradient are achieved, it is simple to find the operating variables such as separating force, power input, etc.
5.1. Separating Force
The separating force F in dimensionless form is given by:
where is the non-dimensional separating force per unit width .
5.2. Power Input
The power transferred by the roll to the fluid is obtained by the integral:
where denotes the non-dimensional power. The non-dimensional shear stress is
6. Results and Discussion
This study examined the reverse roll-coating of an incompressible pseudoplastic material (Williamson fluid). The lubrication approximation theory was applied to simplify the governing equations of flow. The numeric results for flow rate , separation points , thickness of the coating , separation force and power input transmitted to the roll are presented in Table 1 and Table 2 for several values of velocities ratio (the ratio of the velocity of the reverse roll to forward roll) and Weissenberg number . Figure 2, Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 present the non-dimensionless velocities outcomes at different positions in the reverse roll-coating process for the different values of involved material parameters and . The velocity in Figure 2 is sketched at the nip against the increasing value of from to . It was observed that the velocity profile decreases by increasing velocities ratio . The maximum speed was found at the roll surface of the reverse roll. Then it starts decreasing while moving towards the forward roll and becomes zero when , beyond this domain—depending upon the valve of —one can see the reverse flow in the direction of the coating web. From Figure 3 and Figure 4, it is clear that, while moving toward the separation points at the different position of the reverse roll-coating process, the domain for , where the velocity becomes zero is increasing. Beyond this domain, depending upon the ratio of velocities while moving towards the upper roll, the magnitude of the velocity increases and attain its maximum speed at the surface of the roll. It is interesting to note that compatibility with the predictions of the model is quite suitable for small , of course, deviations increases as becomes large compared to unity. It is worth mentioning that the data for elastic polymer solutions agree well with the Newtonian theory [13] under the identical physical conditions. Figure 5, Figure 6 and Figure 7 indicate the velocity representations for the different values of at various positions in the roll-coating process. These figures show that the velocity of the fluid increases by increasing . Physically it means that the viscous forces are dominant over the elastic forces (because Weissenberg number is the ratio of viscous forces to elastic forces). It is interesting to remark here that as fluid moves to the separation points of reverse roll-coating, the viscosity of the fluid increases and the coating of the web is done after this position.

Figure 2.
Influence on velocity profile at .
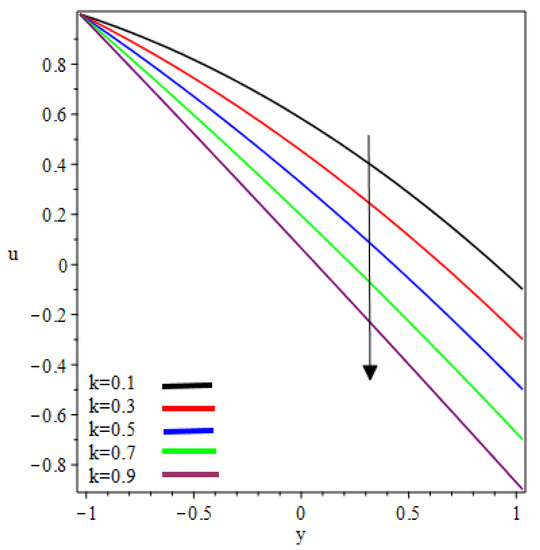
Figure 3.
Influence on velocity profile at .

Figure 4.
Influence on velocity profile at .
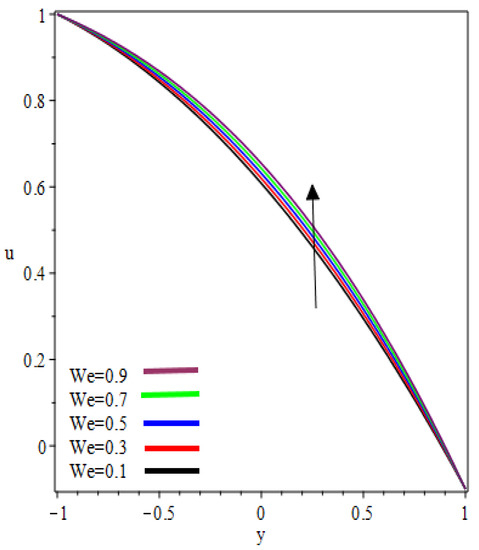
Figure 5.
Influence on velocity profile at .
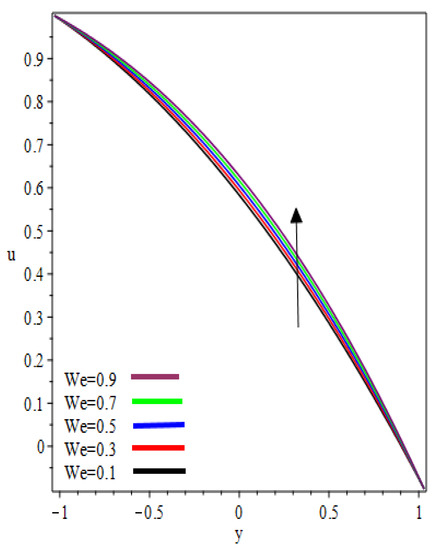
Figure 6.
Influence on velocity profile at .

Figure 7.
Influence on velocity profile at .
The graphic results for pressure gradient against the axial coordinate for the several involved parameters are presented in Figure 8 and Figure 9. From Figure 8 and Figure 9, it was observed that the symmetric profiles about the nip region are found. At nip region, the pressure gradient is negative and increases symmetrically, reaches the maximum value, then decreases exponentially and reaches zero at separation points. One can observe that for a particular value of and , the pressure gradient distribution increases. In addition, these material parameters have a significant effect on the pressure gradient at the nip region because the absolute value of the pressure gradient is maximum at this point. In Figure 8 and Figure 9 Newtonian results [13] are obtained as .

Figure 8.
Influence on pressure gradient.
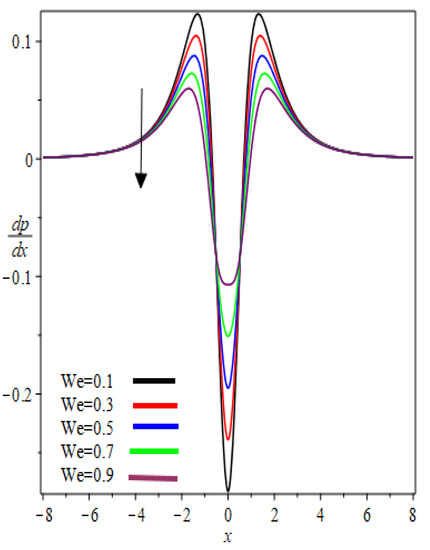
Figure 9.
Influence on pressure gradient.
The graphic representation of pressure distribution for the increasing values of and is sketched in Figure 10 and Figure 11, respectively. From Figure 10, it is observed that when one starts moving toward the negative , the value of pressure increases and the maximum pressure occurs at the critical point ; then the pressure starts decreasing. The concavity changes in the interval and (not shown in the graph). Similar behaviors can be found in Figure 11.

Figure 10.
Influence on the pressure distribution.

Figure 11.
Influence on the pressure distribution.
The numeric results for flow rate, separation points, the thickness of the coating, separating force and power input are presented in Table 1 and Table 2 for the different valves of and . From Table 1, it is observed that the maximum thickness of the coating is 2.3216 for . The coating thickness decreases with an increase in . The minimum thickness of coating 1.1476 was found at . The flow rate, separation points and thickness of coating are decreasing functions of . The roll-separation force decreases, whereas the magnitude of power input increases with an increase in . It can be seen from Table 2 that the thickness of the coating to the maximum can be as high as 3.2452 against the separation point 1.1436. The minimum thickness of the coating was observed as 2.3216. The flow rate, separation points and thickness of coating are increasing functions of . It can be seen that the magnitude of roll-separation force and power input decreases by increasing the value . We found that when all the results of Middleman [13] are retrieved. The graphic relation between the thickness of the coating and the ratio of half of the nip region to incoming fluid film against various values of velocities ratio is presented in Figure 12. It can be seen that thickness of the coating is decreasing function of velocities ratio.

Figure 12.
Thickness of coating versus for different valve of .
7. Conclusions
In this paper, we present the theoretical assessment of reverse roll-coating with the principle of lubrication approximation theory for an incompressible Williamson fluid. The analytical solutions for velocity profiles, pressure gradients and flow rates are obtained by using regular perturbation techniques. The separation points, thickness of the coating, separation force and power input are tabulated in numeric form. The key deductions of the present study are as follows:
- ➢
- Flow velocity increases as increases.
- ➢
- Maximum velocity occurs at the roll surface of the reverse roll.
- ➢
- Absolute pressure gradient is maximum at the nip point.
- ➢
- Viscous forces are dominant over the elastic forces.
- ➢
- Concavity of the pressure distribution changes in the interval .
- ➢
- The velocity ratio parameters and Weissenberg number play important roles in controlling the pressure gradient and pressure distribution.
- ➢
- The Weissenberg number provides an economical mechanism to control the magnitude of separation force and power input.
- ➢
- The Weissenberg number also plays fundamental role to have flow rate, separation points and coating thickness as per desirous.
- ➢
- Pressure distribution, power input and the viscous forces play a significant role in coating thickness.
- ➢
- As a fluid moves to the separation point of reverse roll-coating, the viscosity of the fluid increases and the coating of the web is done after this position.
- ➢
- If , the results of [13] are recovered.
8. Future Work
The effects of heat and the porous medium were not considered in this study. In the future, the effect of heat and porous media will be explored for more complicated rheological non-Newtonian models.
Author Contributions
M.Z. generated the idea, F.A. embedded idea to mathematical model; F.A. and M.Z. solved the problem; F.A. wrote the manuscript; F.A., M.Z. and M.A.R. contributed to the discussion of the problem and analyzed effects of physical parameters on the physical quantities by highlighting physics behind it; Y.H. supervised and funding acquisition; Y.H. and M.A.R. reviewed, edited and contributed to the English corrections. All authors have read and agreed to the published version of the manuscript.
Funding
This research article is funded by the Natural Science Foundation of China, Grant Number 11971378.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| Peripheral velocity of the reverse roll | |
| Peripheral velocity of forwarding roll | |
| Radius of the roll | |
| Velocities ratio | |
| Extra stress tensor | |
| Density | |
| Share rate | |
| Second invariant strain tensor | |
| Weissenberg number | |
| Half the nip separation | |
| Thickness of the coating on reverse roll | |
| Thickness of the coating on the forwarding roll | |
| Coating Thickness | |
| Ratio of the half of the nip region to the coating thickness on the reverse roll | |
| Dimensionless flow rate |
References
- Balzarotti, F.; Rosen, M. Systematic study of coating systems with two rotating rolls. Lat. Am. Appl. Res. 2009, 39, 99–104. [Google Scholar]
- Belblidia, F.; Tamaddon-Jahromi, H.R.; Echendu, S.O.S.; Webster, M.F. Reverse roll-coating flow: A computational investigation towards high-speed defect free coating. Mech. Time Depend. Mater. 2013, 17, 557–579. [Google Scholar] [CrossRef]
- Zafar, M.; Rana, M.A.; Zahid, M.; Malik, M.A.; Lodhi, M.S. Mathematical Analysis of Roll Coating Process by Using Couple Stress Fluid. J. Nanofluids 2019, 8, 1683–1691. [Google Scholar] [CrossRef]
- Zheng, G.; Wachter, F.; Al-Zoubi, A.; Durst, F.; Taemmerich, R.; Stietenroth, M.; Pircher, P. Computations of coating windows for reverse roll coating of liquid films. J. Coat. Technol. Res. 2020. [Google Scholar] [CrossRef]
- Benkreira, H.; Edwards, M.F.; Wilkinson, W.L. A semi-empirical model of the forward roll coating flow of newtonian fluids. Chem. Eng. Sci. 1981, 36, 423–427. [Google Scholar] [CrossRef]
- Jang, J.Y.; Chen, P.Y. Reverse roll coating flow with non-Newtonian Fluids. Commun. Comput. Phys. 2009, 6, 536–552. [Google Scholar]
- Hao, Y.; Haber, S. Reverse roll coating flow. Int. J. Numer. Methods Fluids 1999, 30, 635–652. [Google Scholar] [CrossRef]
- Benkreira, H.; Edwards, M.F.; Wilkinson, W.L. Roll coating of purely viscous liquids. Chem. Eng. Sci. 1981, 36, 429–434. [Google Scholar] [CrossRef]
- Greener, J.; Middleman, S. Theoretical and experimental studies of the fluid dynamics of a two-roll coater. Ind. Eng. Chem. Fundam. 1979, 18, 35–41. [Google Scholar] [CrossRef]
- Coyle, D.J.; Macosko, C.W.; Scriven, L.E. The fluid dynamics of reverse roll coating. Aiche J. 1990, 36, 161–174. [Google Scholar] [CrossRef]
- Taylor, J.; Zettlemoyer, A. Hypothesis on the mechanism of ink splitting during printing. Tappi J. 1958, 12, 749–757. [Google Scholar]
- Hintermaier, J.; White, R. The splitting of a water film between rotating rolls. Tappi J. 1965, 48, 617–625. [Google Scholar]
- Greener, J.; Middleman, S. Reverse roll coating of viscous and viscoelastic liquids. Ind. Eng. Chem. Fundam. 1981, 20, 63–66. [Google Scholar] [CrossRef]
- Ho, W.S.; Holland, F.A. Between-rolls metering coating technique. Tappi J. 1978, 61, 53–56. [Google Scholar]
- Shiode, H.; Tamai, H.; Isaki, T. Flow Simulations of Dynamic Wetting Line at a Reverse-roll Coater Using the VOF Method. Nihon Reoroji Gakkaishi 2009, 37, 59–64. [Google Scholar] [CrossRef]
- Zahid, M.; Rana, M.A.; Siddiqui, A.M. Roll coating analysis of a second-grade material. J. Plast. Film Sheeting 2017, 34, 232–255. [Google Scholar] [CrossRef]
- M, Z.; Zafar, M.; Rana, M.A.; Rana, M.; Lodhi, M.S. Numerical analysis of the forward roll coating of a rabinowitsch fluid. J. Plast. Film Sheeting 2019, 36, 191–208. [Google Scholar] [CrossRef]
- Khandavalli, S.; Rothstein, J.P. Ink transfer of non-Newtonian fluids from an idealized gravure cell: The effect of shear and extensional deformation. J. Non Newton. Fluid Mech. 2017, 243, 16–26. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A.; Ali, Z. Fully developed second order velocity slip Darcy-Forchheimer flow by a variable thicked surface of disk with entropy generation. Int. Commun. Heat Mass Transf. 2020, 117, 104778. [Google Scholar] [CrossRef]
- Wang, J.; Muhammad, R.; Khan, M.I.; Khan, W.A.; Abbas, S.Z. Entropy optimized MHD nanomaterial flow subject to variable thicked surface. Comput. Methods Programs Biomed. 2020, 189, 105311. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A. Heat transport and nonlinear mixed convective nanomaterial slip flow of Walter-B fluid containing gyrotactic microorganisms. Alex. Eng. J. 2020. [Google Scholar] [CrossRef]
- Wang, J.; Khan, M.I.; Khan, W.; Abbas, S.Z.; Khan, M.I. Transportation of heat generation/absorption and radiative heat flux in homogeneous—Heterogeneous catalytic reactions of non-Newtonian fluid (Oldroyd-B model). Comput. Methods Programs Biomed. 2020, 189, 105310. [Google Scholar] [CrossRef] [PubMed]
- Zafar, M.; Rana, M.A.; Zahid, M.; Ahmad, B. Mathematical Analysis of the Coating Process over a Porous Web Lubricated with Upper-Convected Maxwell Fluid. Coatings 2019, 9, 458. [Google Scholar] [CrossRef]
- Lyubimov, D.V.; Perminov, A.V. Motion of a thin oblique layer of a pseudoplastic fluid. J. Eng. Phys. Thermophys. 2002, 75, 920–924. [Google Scholar] [CrossRef]
- Williamson, R.V. The flow of pseudoplastic materials. Ind. Eng. Chem. 1929, 21, 1108–1111. [Google Scholar] [CrossRef]
- Nadeem, S.; Akbar, N.S. Numerical solutions of peristaltic flow of williamson fluid with radially varying mhd in an endoscope. Int. J. Numer. Methods Fluids 2011, 66, 212–220. [Google Scholar] [CrossRef]
- Cramer, S.D.; Marchello, J.M. Numerical evaluation of models describing non-Newtonian behavior. Aiche J. 1968, 14, 980–983. [Google Scholar] [CrossRef]
- Dapra, I.; Scarpi, G. Perturbation solution for pulsatile flow of a non-Newtonian Williamson fluid in a rock fracture. Int. J. Rock Mech. Min. Sci. 2007, 44, 271–278. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).