Investigation on the Coupling Effects between Flow and Fibers on Fiber-Reinforced Plastic (FRP) Injection Parts
Abstract
1. Introduction
2. Theoretical Background
2.1. Models for Polymer Fluid Mechanics
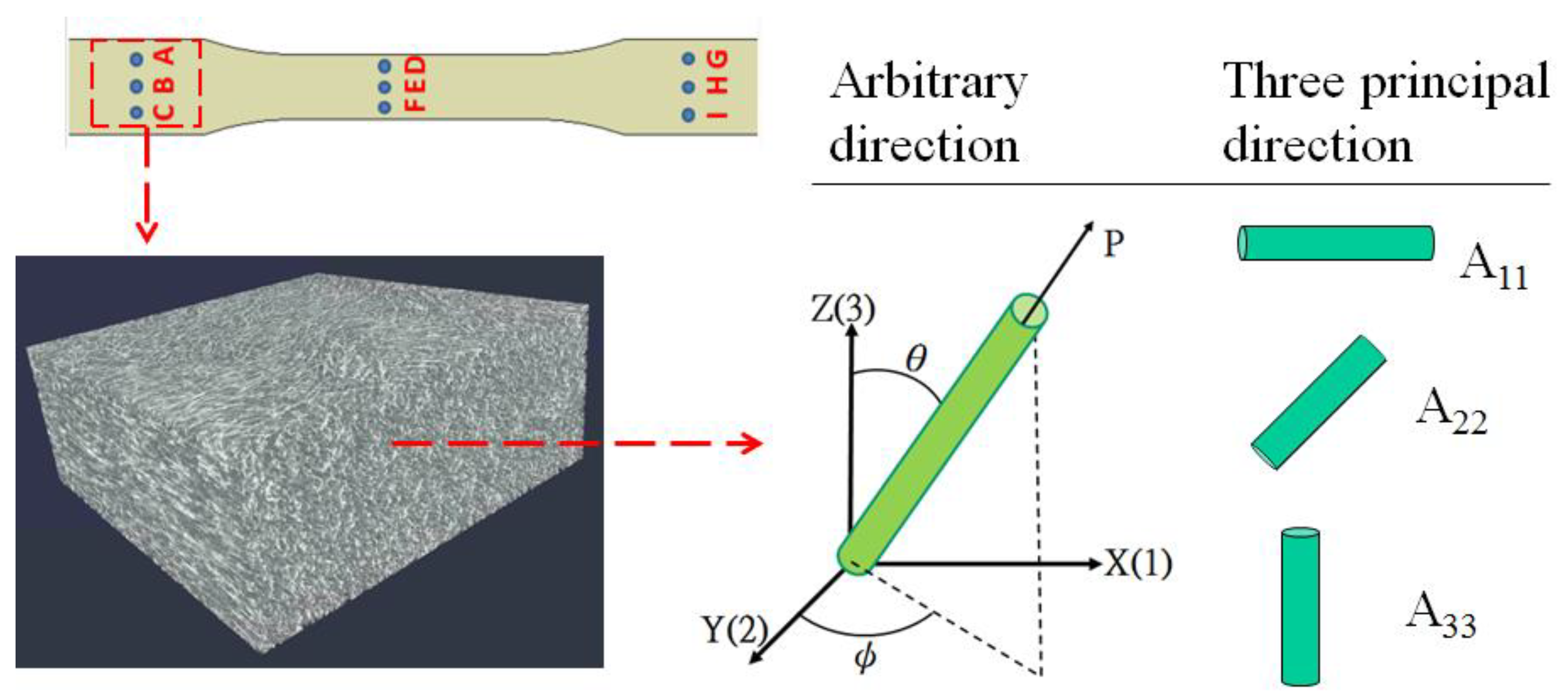
2.2. Models for Fiber Orientation Kinetics
2.3. Models for Evolution of Viscosity by Flow–Fiber Coupling
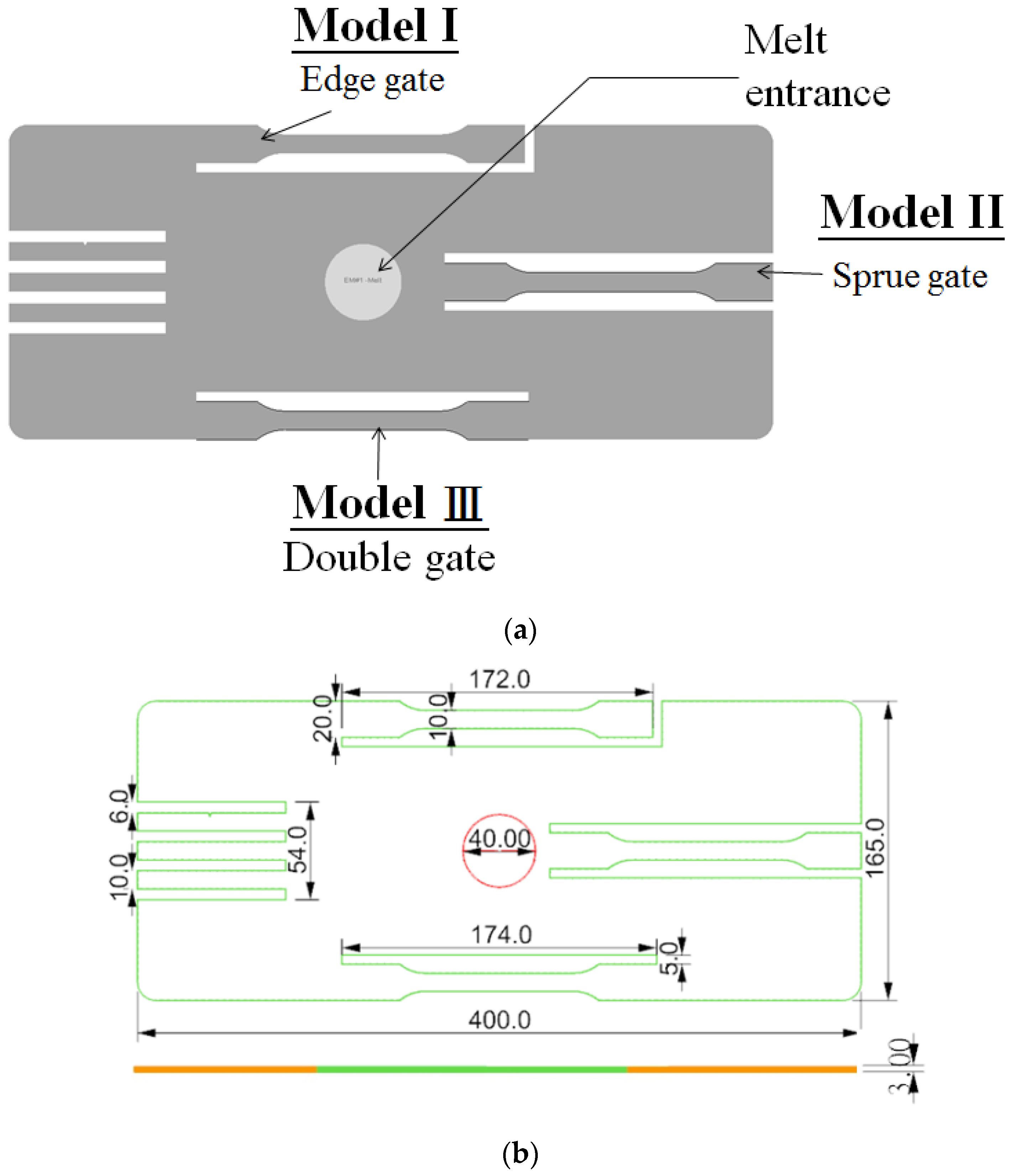
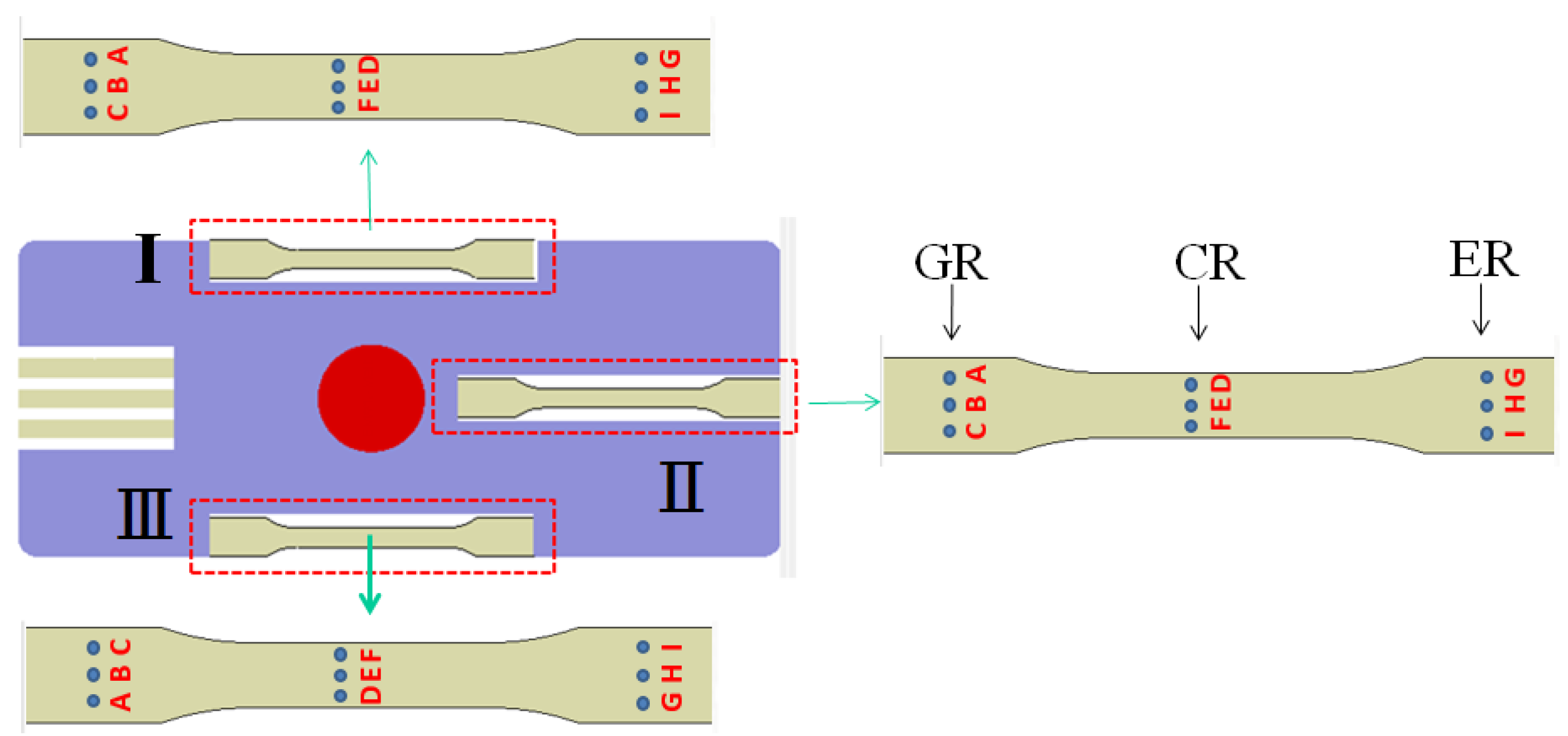
3. Injection Molding System and Related Information
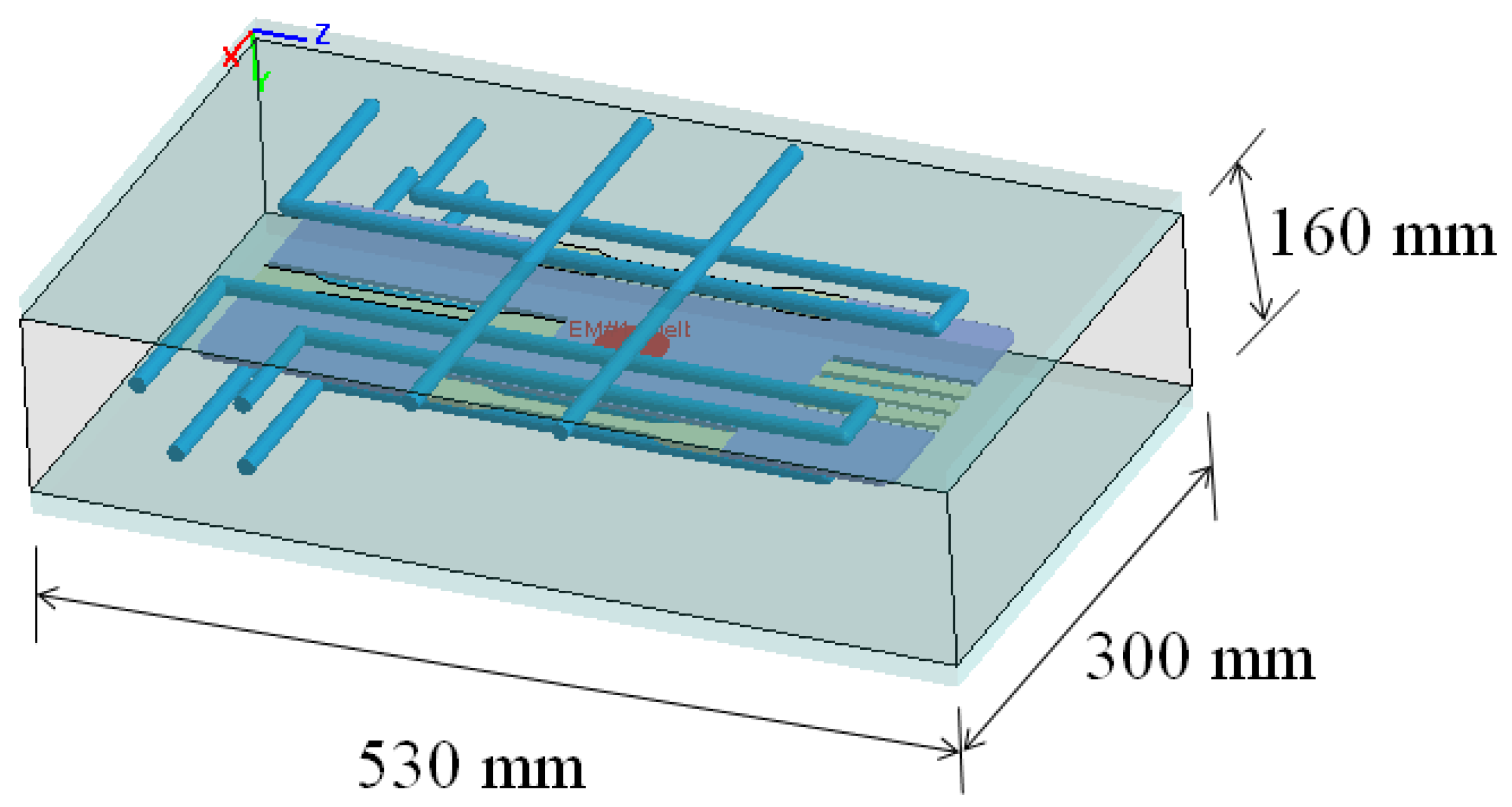
3.1. Simulation Model and Related Information
3.2. Experimental Equipment and Related Information
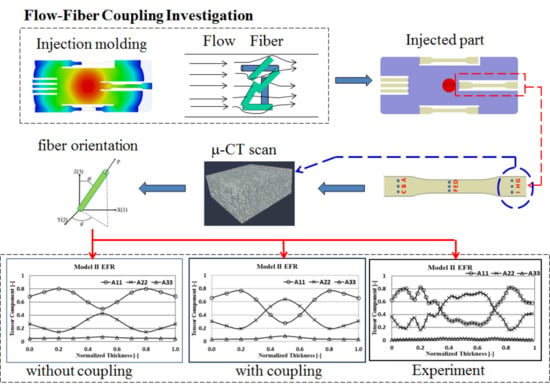
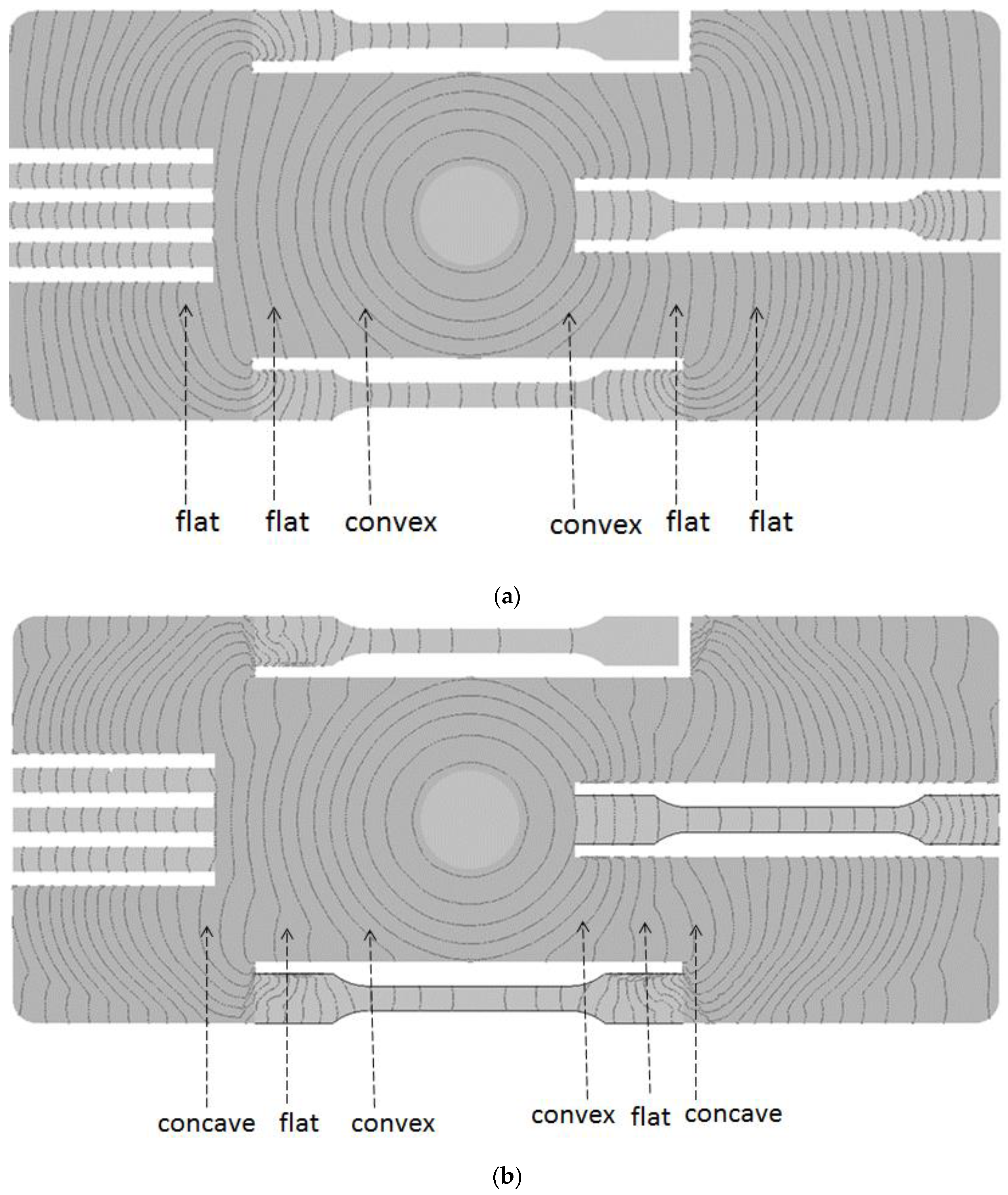
4. Results and Discussion
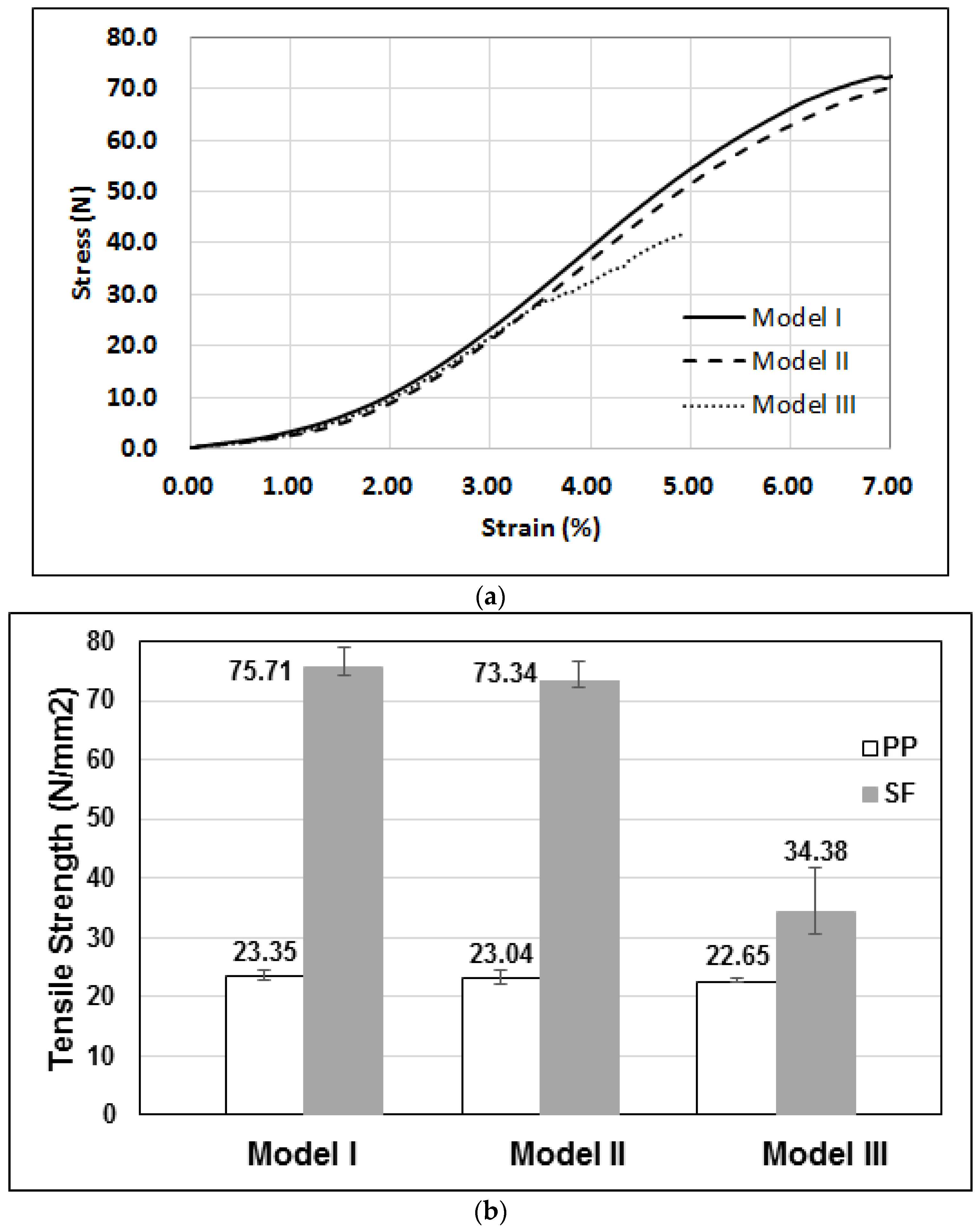
4.1. Mechanical Property Test
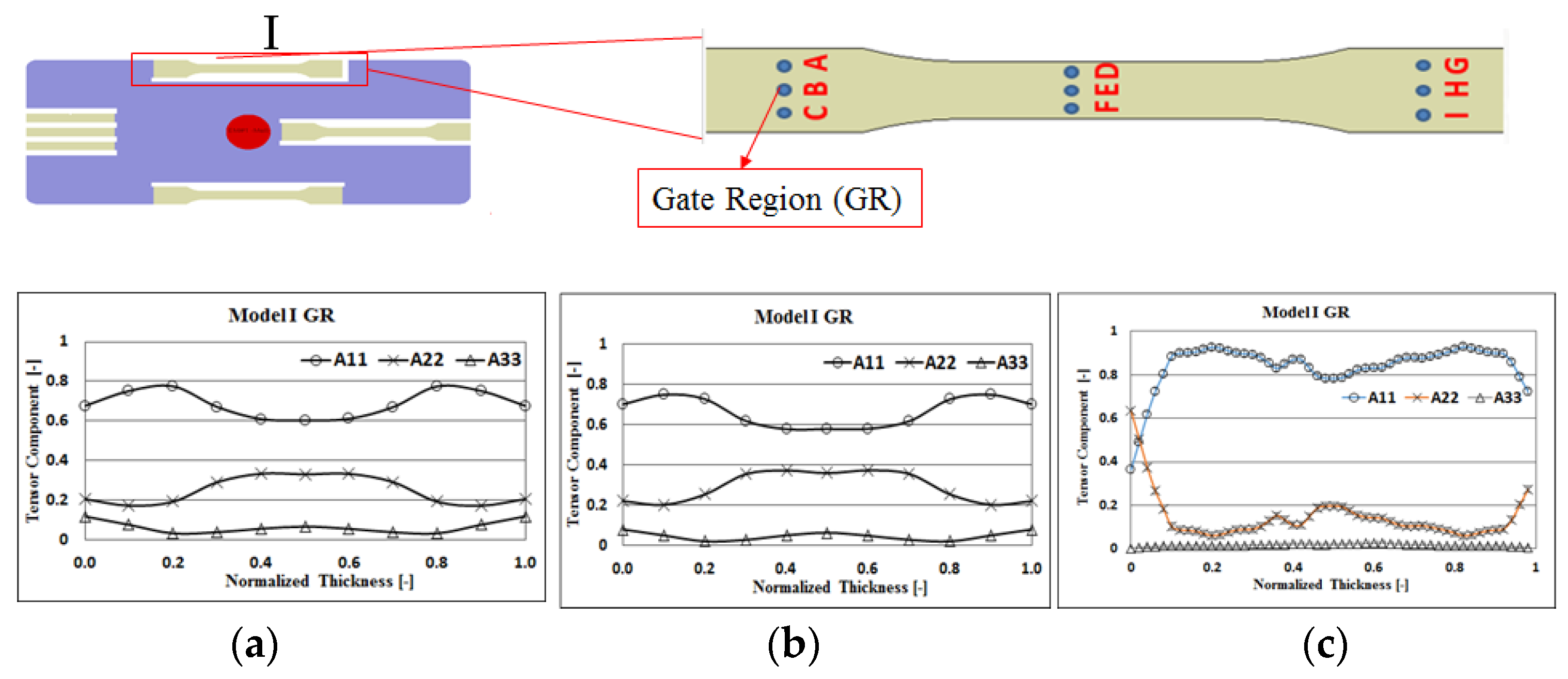
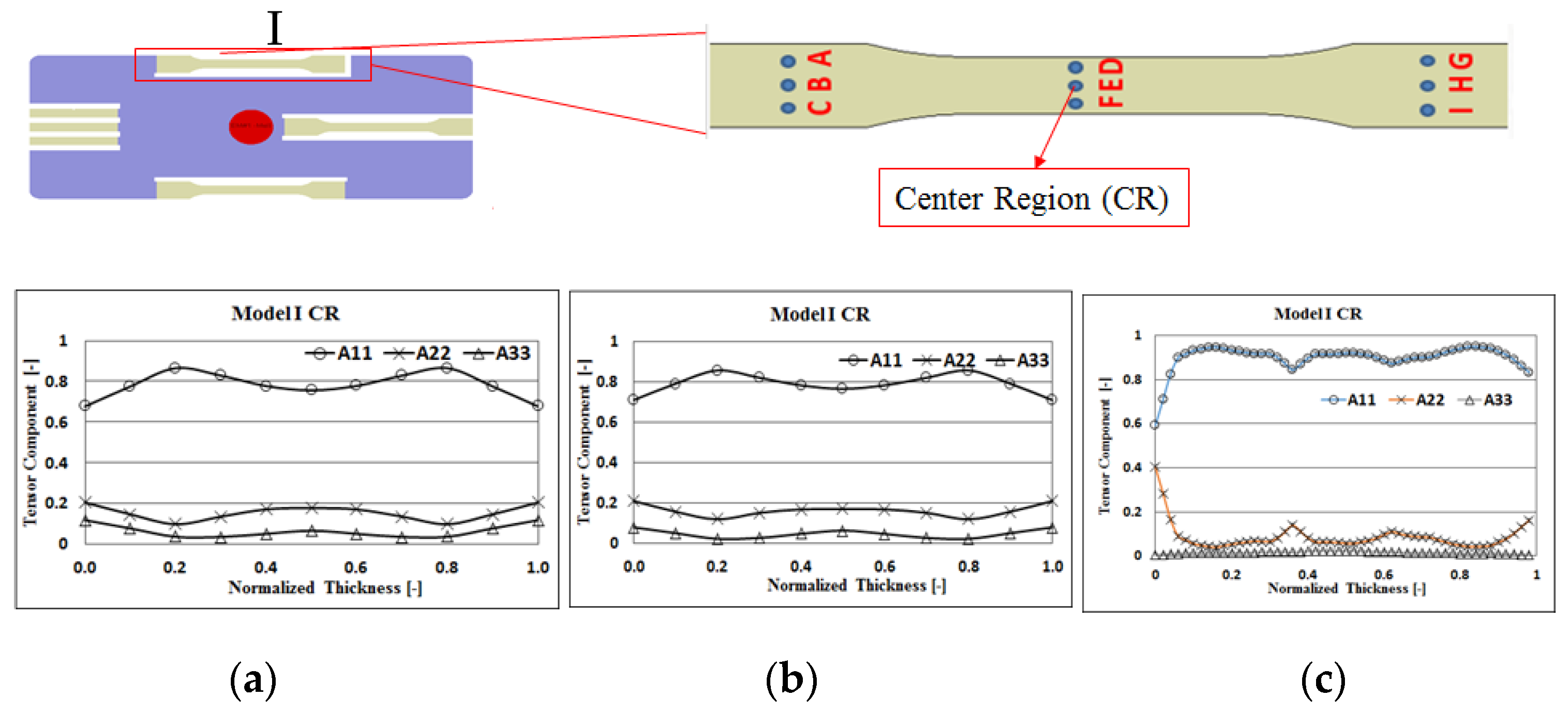
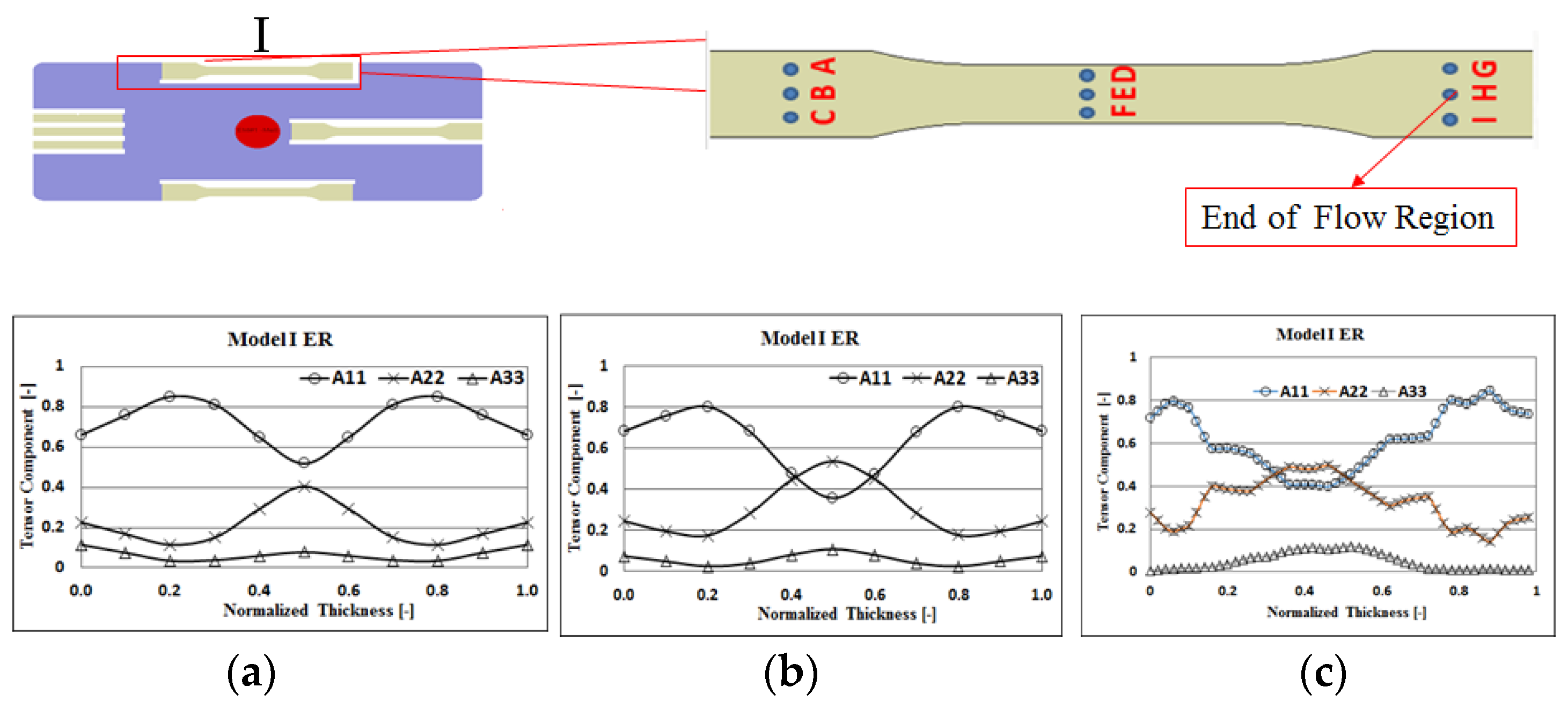
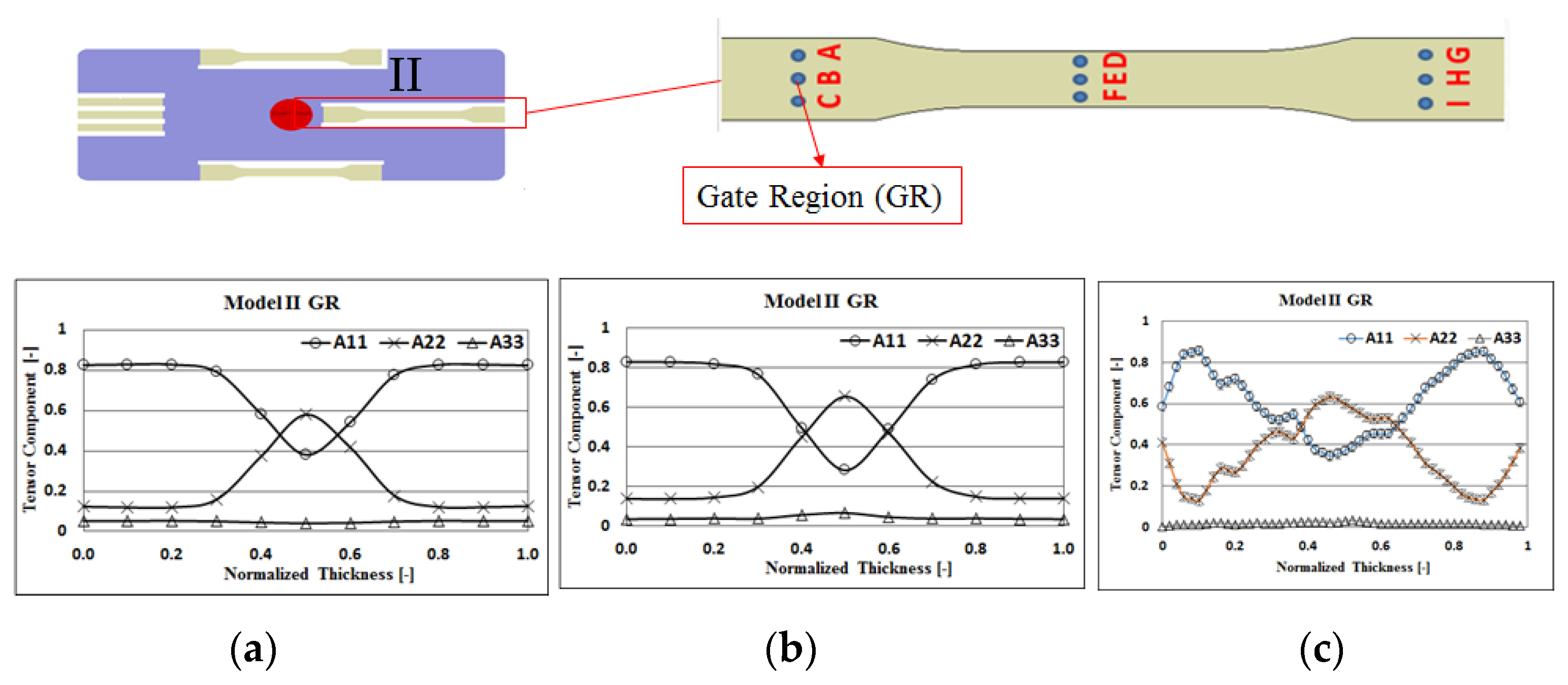
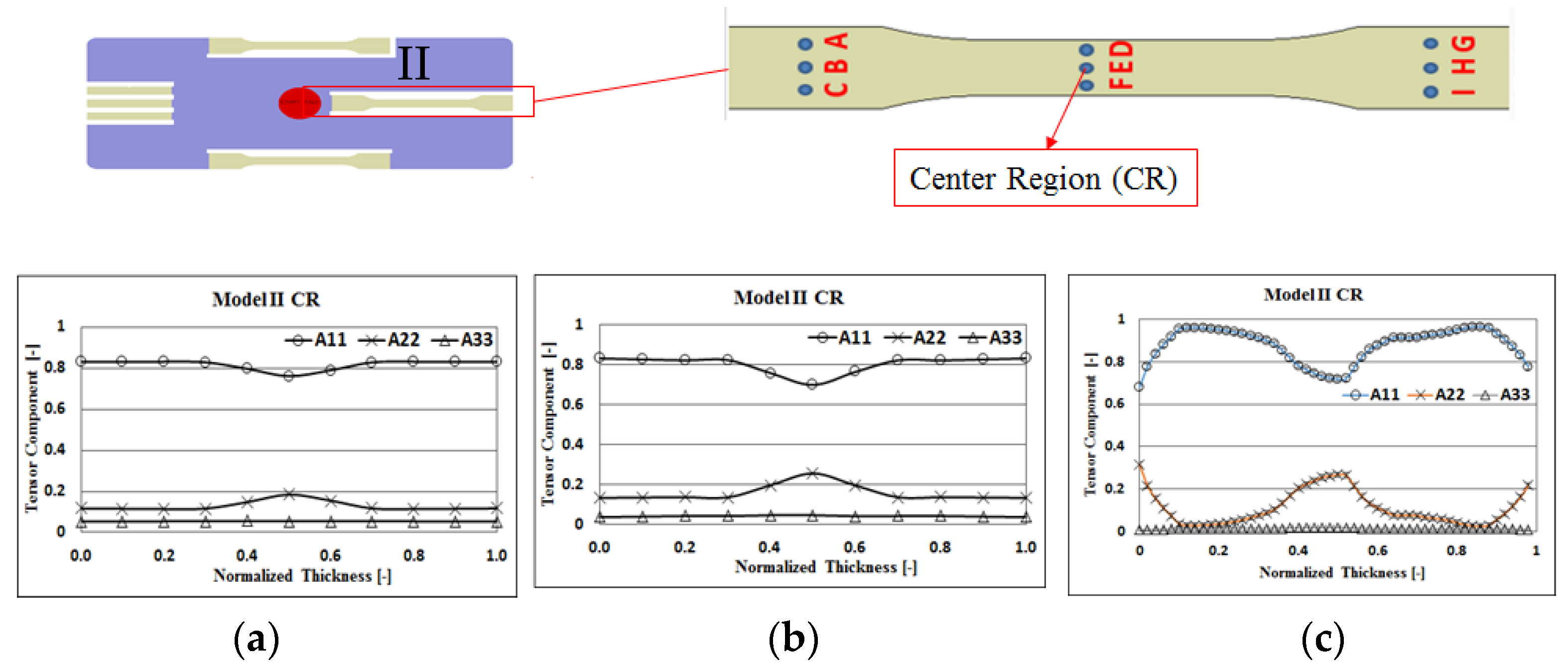
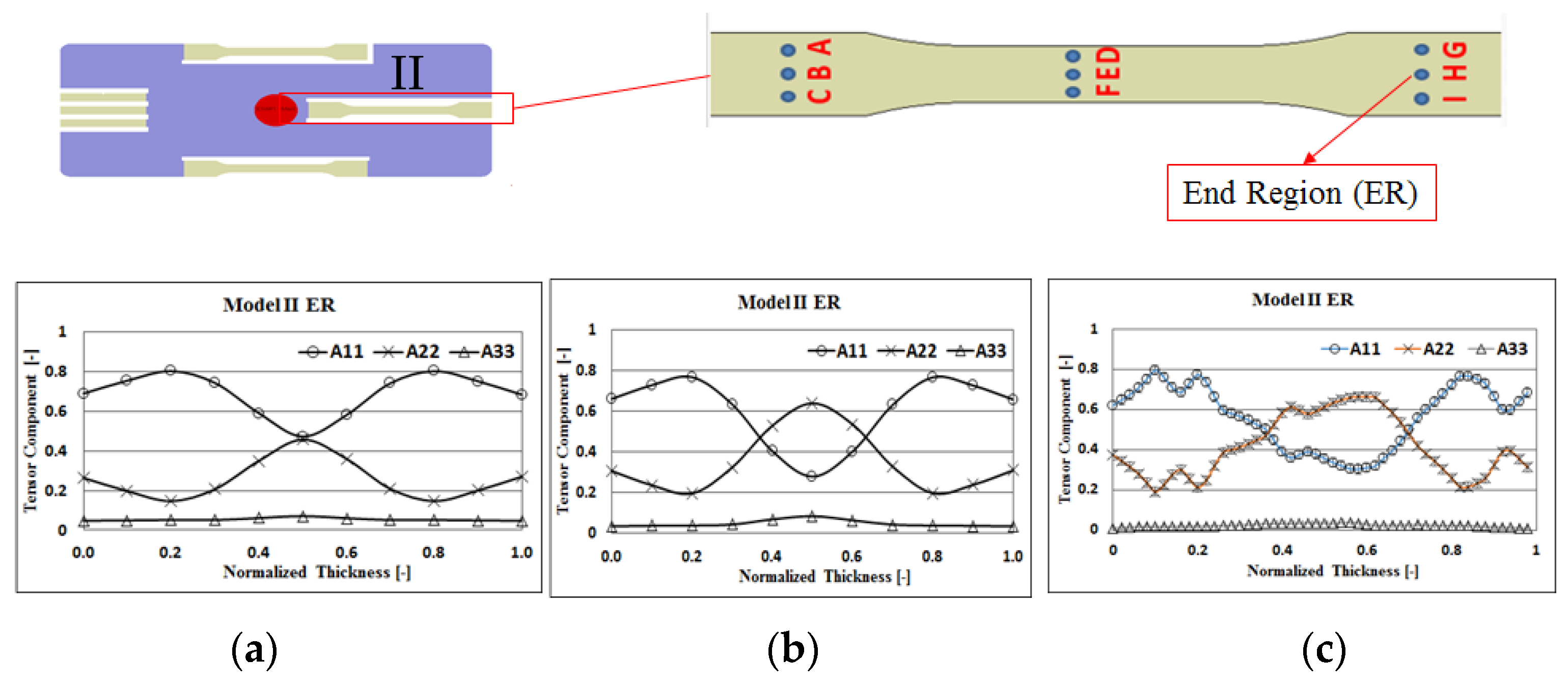
4.2. Fiber Orientation Effects With and Without Flow–Fiber Coupling
4.3. Correlation between Mechanical Property and Fiber Micro-Feature
4.4. Melt Flow Behavior under the Influence of Flow–Fiber Coupling
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Roser, M. Two Centuries of Rapid Global Population Growth Will Come to an End. Available online: https://ourworldindata.org/world-population-growth-past-future (accessed on 18 June 2020).
- Schmidt, C.; Li, W.; Thiede, S.; Kara, S.; Herrmann, C. A methodology for customized prediction of energy consumption in manufacturing Industries. Int. J. Precis. Eng. Manuf.-Green Technol. 2015, 2, 163–172. [Google Scholar] [CrossRef]
- Ritchie, H.; Roser, M. CO2 and Greenhouse Gas Emissions. Available online: https://ourworldindata.org/co2-and-other-greenhouse-gas-emissions (accessed on 18 June 2020).
- EPA of USA. Sources of Greenhouse Gas Emissions. Available online: https://www.epa.gov/ghgemissions/sources-greenhouse-gas-emissions (accessed on 18 June 2020).
- U. S. Department of Energy Report, Lightweight Materials R & D Program; Vehicle Technologies Office: Washington, DC, USA, 2013.
- Othman, R.; Ismail, N.I.; Pahmi, M.A.A.H.; Basri, M.H.M.; Sharudin, H.; Hemdi, A.R. Application of Carbon fiber reinforced plastics in automotive industry: A review. J. Mech. Manuf. 2018, 1, 144–154. [Google Scholar]
- CompositesWorld Report. The Markets: Automotive. Available online: https://www.compositesworld.com/articles/the-markets-automotive (accessed on 19 August 2020).
- Thomason, J.L.; Vlug, M.A. Influence of fiber length and concentration on the properties of glass fiber-reinforced polypropylene: Part 1-Tensile and flexural modulus. Compos. Part A 1996, 27, 477–484. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length and concentration on the properties of glass fibre reinforced polypropylene: Interface strength and fibre strain in injection moulded long fibre PP at high fibre content. Compos. Part A 2007, 38, 210–216. [Google Scholar] [CrossRef]
- Wang, C.; Yang, S. Thermal, Tensile and Dynamic Mechanical Properties of Short Carbon Fibre Reinforced Polypropylene Composites. Polym. Polym. Compos. 2013, 21, 65–71. [Google Scholar] [CrossRef]
- Cilleruelo, L.; Lafranche, E.; Krawczak, P.; Pardo, P.; Lucas, P. Injection moulding of long glass fibre reinforced poly(ethylene terephtalate): Influence of carbon black and nucleating agents on impact properties. Express Polym. Lett. 2012, 6, 706–718. [Google Scholar] [CrossRef]
- Folgar, F.; Tucker, C.L. Orientation Behavior of Fibers in Concentrated Suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Advani, S.G. Flow and Rheology in Polymer Composites Manufacturing; Elsevier: New York, NY, USA, 1994. [Google Scholar]
- Han, K.H.; Im, Y.T. Numerical simulation of three-dimensional fiber orientation in injection molding including fountain flow effect. Polym. Compos. 2002, 23, 222–238. [Google Scholar] [CrossRef]
- Vincent, M.; Giroud, T.; Clarke, A.; Eberhardt, C. Description and modeling of fiber orientation in injection molding of fiber reinforced thermoplastics. Polymer 2005, 46, 6719–6725. [Google Scholar] [CrossRef]
- Ortman, K.; Baird, D.; Wapperom, P.; Aning, A. Prediction of Fiber Orientation in the Injection Molding of Long Fiber Suspensions. Polym. Compos. 2012, 33, 1360–1367. [Google Scholar] [CrossRef]
- Phelps, J.H.; Tucker, C.L., III. An anisotropic rotary diffusion model for fiber orientation in short- and long-fiber thermoplastics. J. Non-Newton. Fluid Mech. 2009, 56, 165–176. [Google Scholar] [CrossRef]
- Wang, J.; O’Gara, J.F.; Tucker, C.L., III. An objective model for slow orientation kinetics in concentrated fiber suspensions: Theory and rheological evidence. J. Rheol. 2008, 52, 1179–1200. [Google Scholar] [CrossRef]
- Wang, J.; Jin, X. Comparison of recent fiber orientation models in autodesk moldflow insight simulations with measured fiber orientation data. In Proceedings of the International Conference of Polymer Processing Society (PPS), Banff, AB, Canada, 4–8 July 2010. [Google Scholar]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Phenomenological improvements to predictive models of fiber orientation in concentrated suspensions. J. Rheol. 2013, 57, 1597–1631. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Method and Computer Readable Media for Determining Orientation of Fibers in a Fluid. U.S. Patent 8,571,828, 29 October 2013. [Google Scholar]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. An objective tensor to predict anisotropic fiber orientation in concentrated suspensions. J. Rheol. 2016, 60, 215–224. [Google Scholar] [CrossRef]
- Tseng, H.C.; Chang, R.Y.; Hsu, C.H. Computer-Implemented Simulation Method and non-Transitory Computer Medium Capable of Predicting Fiber Orientation for Use in a Molding Process. U.S. Patent 9,283,695, 15 March 2016. [Google Scholar]
- Libscomb, G.G.; Denn, M.M.; Hur, D.U.; Boger, D.V. The Flow of Fiber Suspensions in Complex Geometries. J. Non-Newton. Fluid Mech. 1998, 26, 297–325. [Google Scholar] [CrossRef]
- VerWeyst, B.E.; Tucker, C.L., III. Fiber Suspensions in Complex Geometries: Flow/Orientation Coupling. Can. J. Chem. Eng. 2002, 80, 1093–1106. [Google Scholar] [CrossRef]
- Tseng, H.C.; Su, T.H. Coupled flow and fiber orientation analysis for 3D injection molding simulations of fiber composites. Proceedings of PPS-34. AIP Conf. Proc. 2019, 2065. [Google Scholar] [CrossRef]
- Favaloro, A.J.; Tseng, H.C.; Pipes, R.B. A new anisotropic viscous constitutive model or composite molding simulation. Compos. Part A 2018, 115, 112–122. [Google Scholar] [CrossRef]
- Tseng, H.C.; Favaloro, A.J. The use of informed isotropic constitutive equation to simulate anisotropic rheological behaviors in fiber suspensions. J. Rheol. 2019, 63, 263–274. [Google Scholar] [CrossRef]
- Huang, C.T.; Chu, J.H.; Fu, W.W.; Hsu, C.; Hwang, S.J. Flow-induced Orientations of Fibers and Their Influences on Warpage and Mechanical Property in Injection Fiber Reinforced Plastic (FRP) Parts. Int. J. Precis. Eng. Manuf.-Green Technol. 2020, 1–8. [Google Scholar] [CrossRef]
- Grellmann, W.; Seidler, S.; Anderson, P. Polymer Testing, 2nd ed.; Carl Hanser Verlag: Munich, Germany, 2013. [Google Scholar]

| Item | Process Condition |
|---|---|
| Filling time (s) | 1.49 |
| Packing time (s) | 5 |
| Packing pressure (MPa) | 69.1 |
| Cooling time (s) | 15 |
| Melt temperature (°C) | 260 |
| Mold temperature (°C) | 25 |
| Parameters | Values |
|---|---|
| CI | 0.005 |
| CM | 0.5 |
| α | 0.7 |
| Parameters | Values |
|---|---|
| 2000 | |
| 10 |
| Experiment | Model I | Model II | Model III |
|---|---|---|---|
| 1 | 78.95 | 76.71 | 41.69 |
| 2 | 75.93 | 72.13 | 32.70 |
| 3 | 74.67 | 72.47 | 30.63 |
| 4 | 74.17 | 72.40 | 32.07 |
| 5 | 74.83 | 73.00 | 34.8 |
| Average | 75.71 | 73.34 | 34.38 |
| Maximum | 78.95 | 76.71 | 41.69 |
| Minimum | 74.17 | 72.13 | 30.63 |
| Upper Error | 3.24 | 3.37 | 7.31 |
| Lower Error | 1.54 | 1.21 | 3.74 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, C.-T.; Lai, C.-H. Investigation on the Coupling Effects between Flow and Fibers on Fiber-Reinforced Plastic (FRP) Injection Parts. Polymers 2020, 12, 2274. https://doi.org/10.3390/polym12102274
Huang C-T, Lai C-H. Investigation on the Coupling Effects between Flow and Fibers on Fiber-Reinforced Plastic (FRP) Injection Parts. Polymers. 2020; 12(10):2274. https://doi.org/10.3390/polym12102274
Chicago/Turabian StyleHuang, Chao-Tsai, and Cheng-Hong Lai. 2020. "Investigation on the Coupling Effects between Flow and Fibers on Fiber-Reinforced Plastic (FRP) Injection Parts" Polymers 12, no. 10: 2274. https://doi.org/10.3390/polym12102274
APA StyleHuang, C.-T., & Lai, C.-H. (2020). Investigation on the Coupling Effects between Flow and Fibers on Fiber-Reinforced Plastic (FRP) Injection Parts. Polymers, 12(10), 2274. https://doi.org/10.3390/polym12102274