Experimental and Prediction Study of Displacement-Rate Effects on Flexural Behaviour in Nano and Micro TiO2 Particles-Epoxy Resin Composites
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Micro-Particulate Specimens Manufacturing
2.3. Nano-Particulate Specimens Manufacturing
2.4. Experimental Characterization
2.5. Theoretical Backgraound
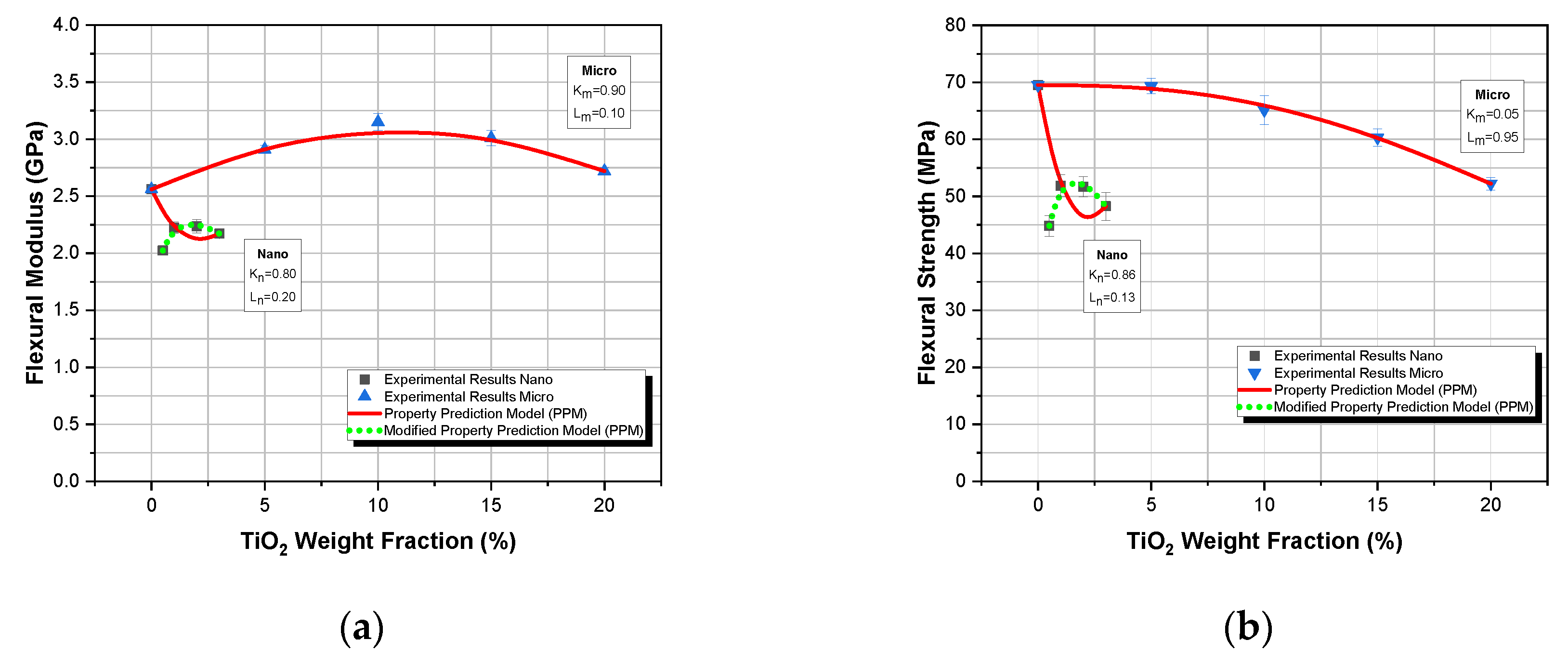
Property Prediction Model (PPM)
3. Results and Discussion
3.1. Scanning Electron Microscopy (SEM)
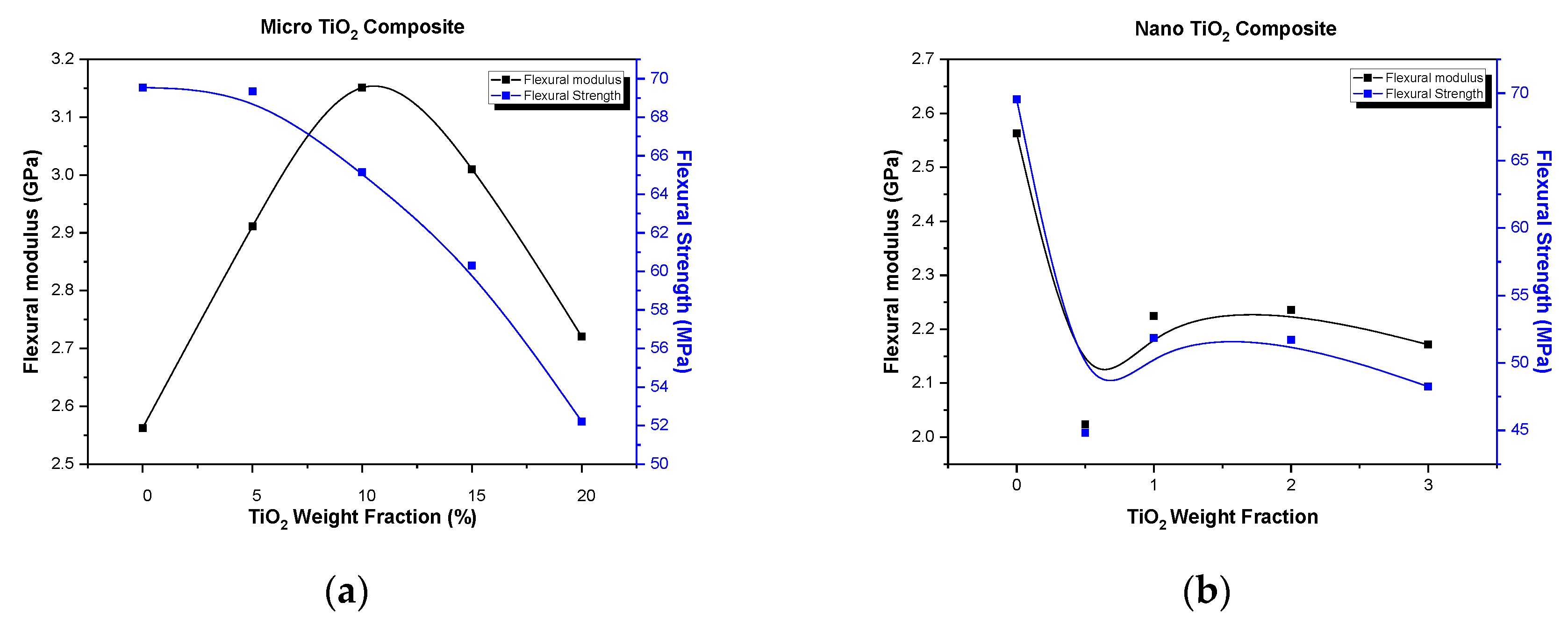
3.2. Flexural Characterization
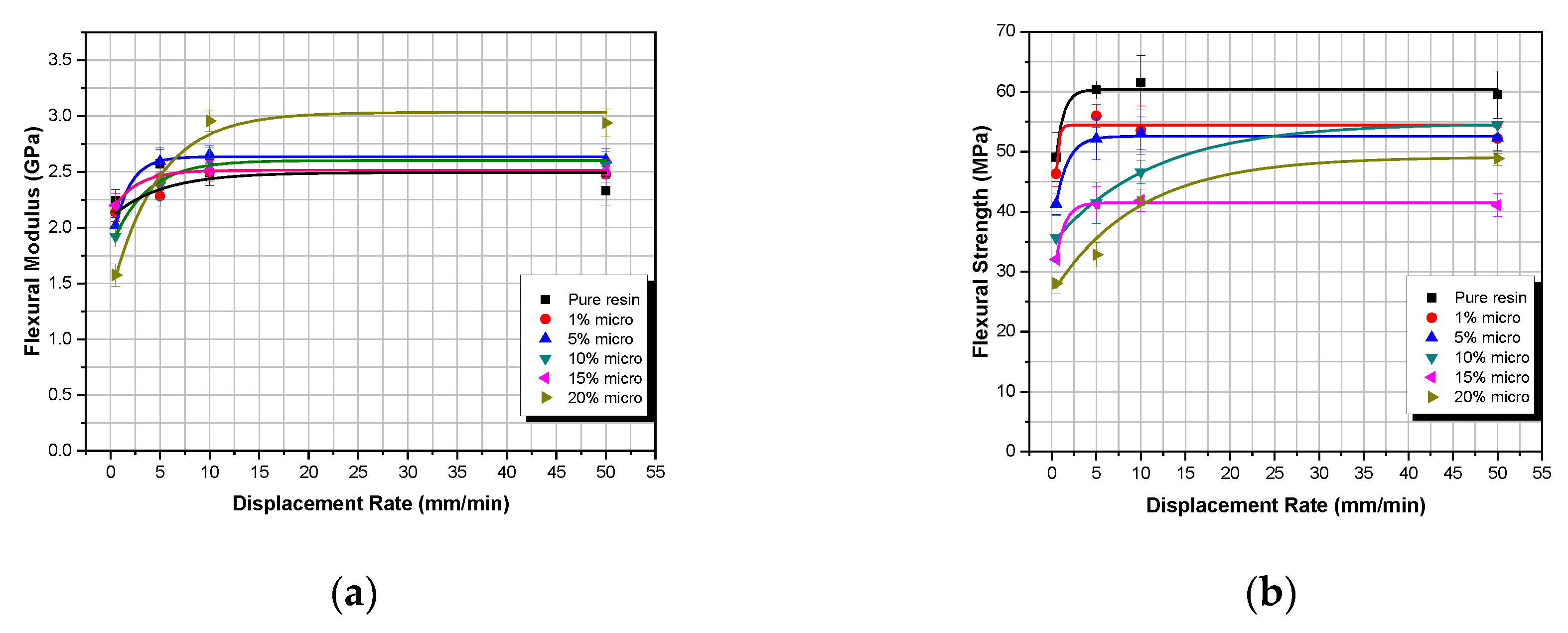
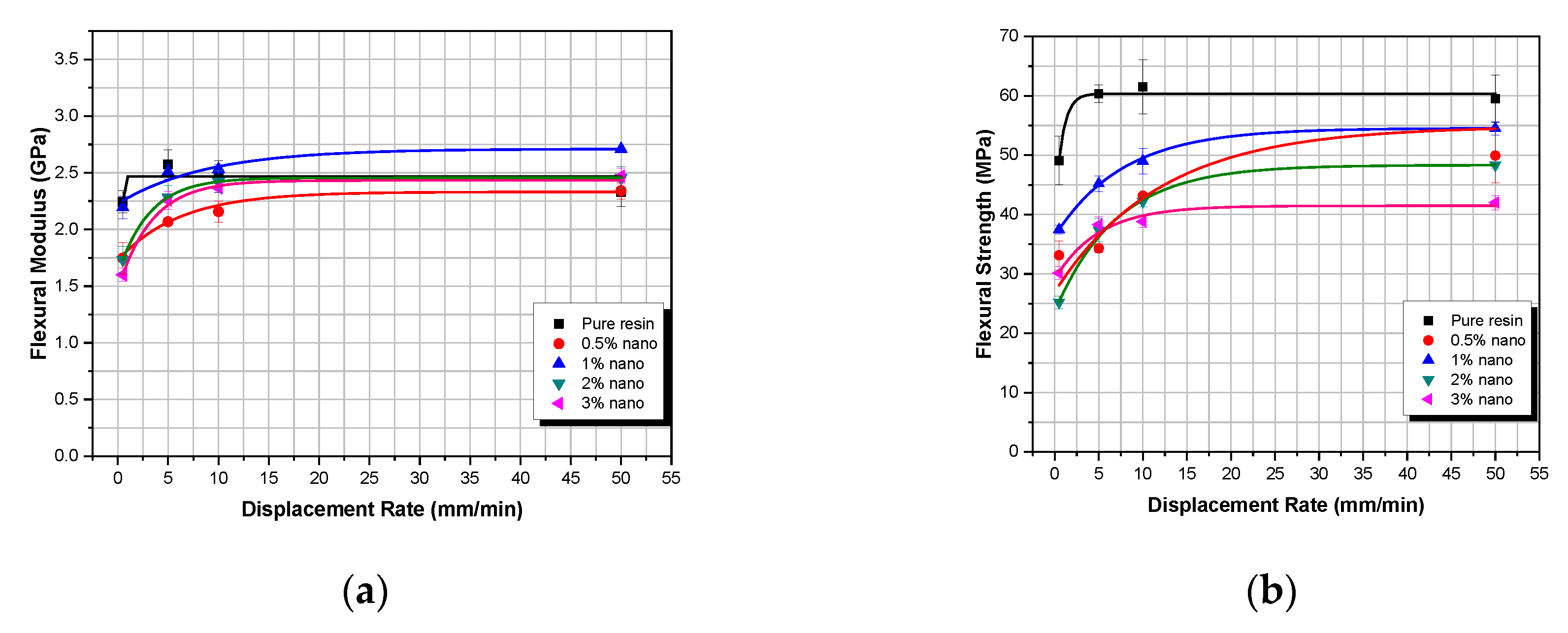
3.3. Displacement-Rate Results
4. Conclusions
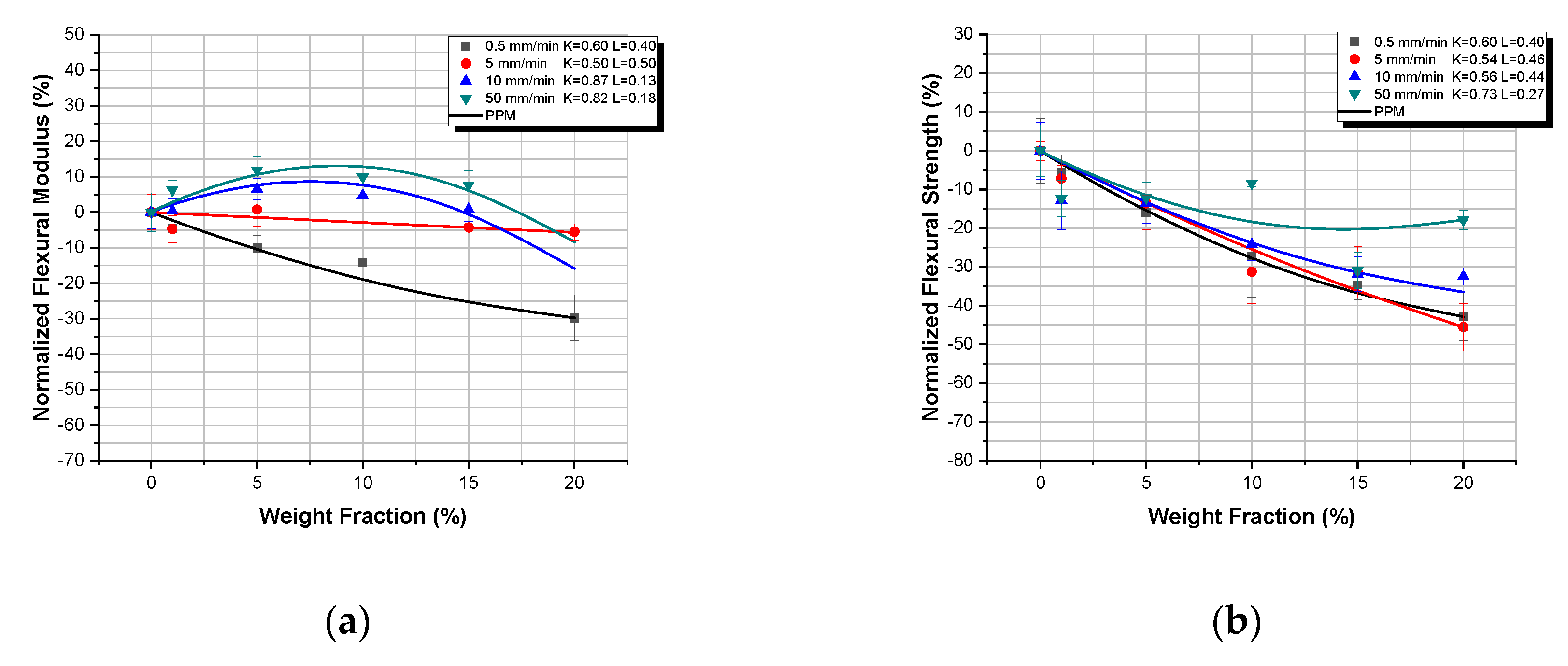
- For the micro TiO2 composites, the flexural strength decreases with the increase of filler weight fraction at all strain rates applied, this behavior being in accordance with similar data found in literature. The decrease in flexural strength can be attributed to the imperfections and the voids introduced into the matrix with the addition of micro-particles.
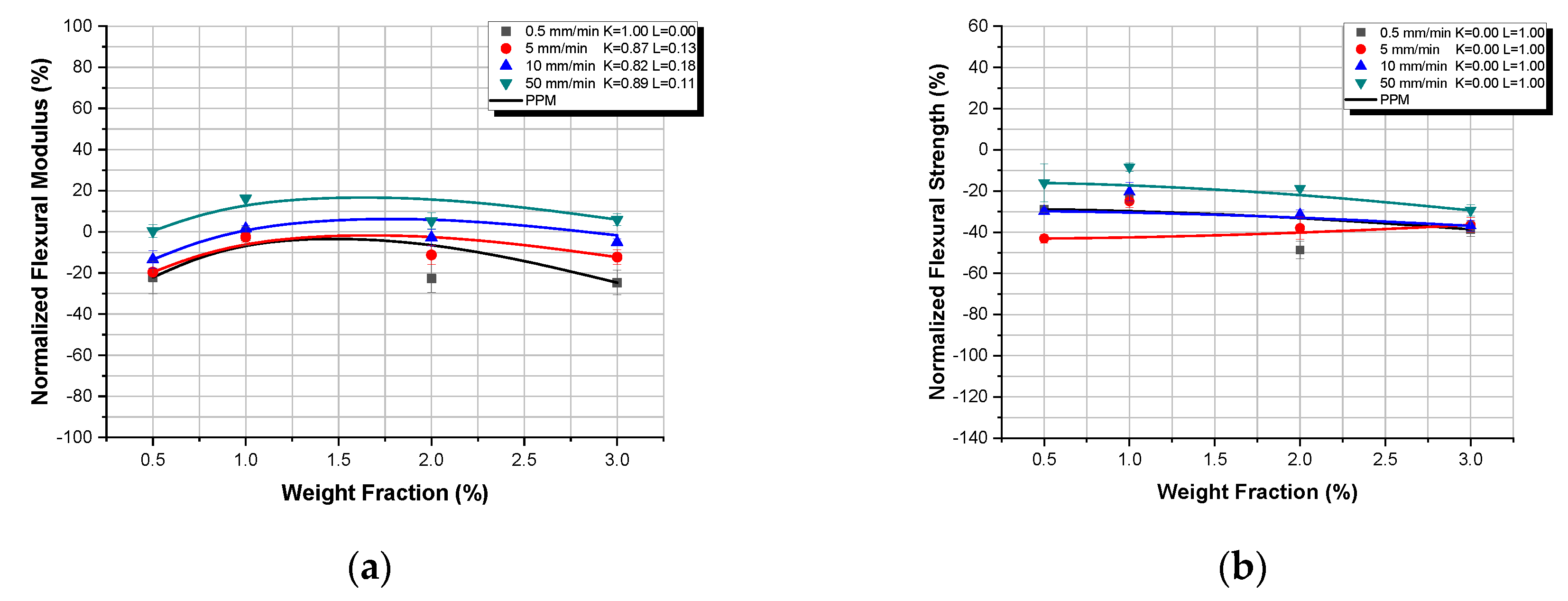
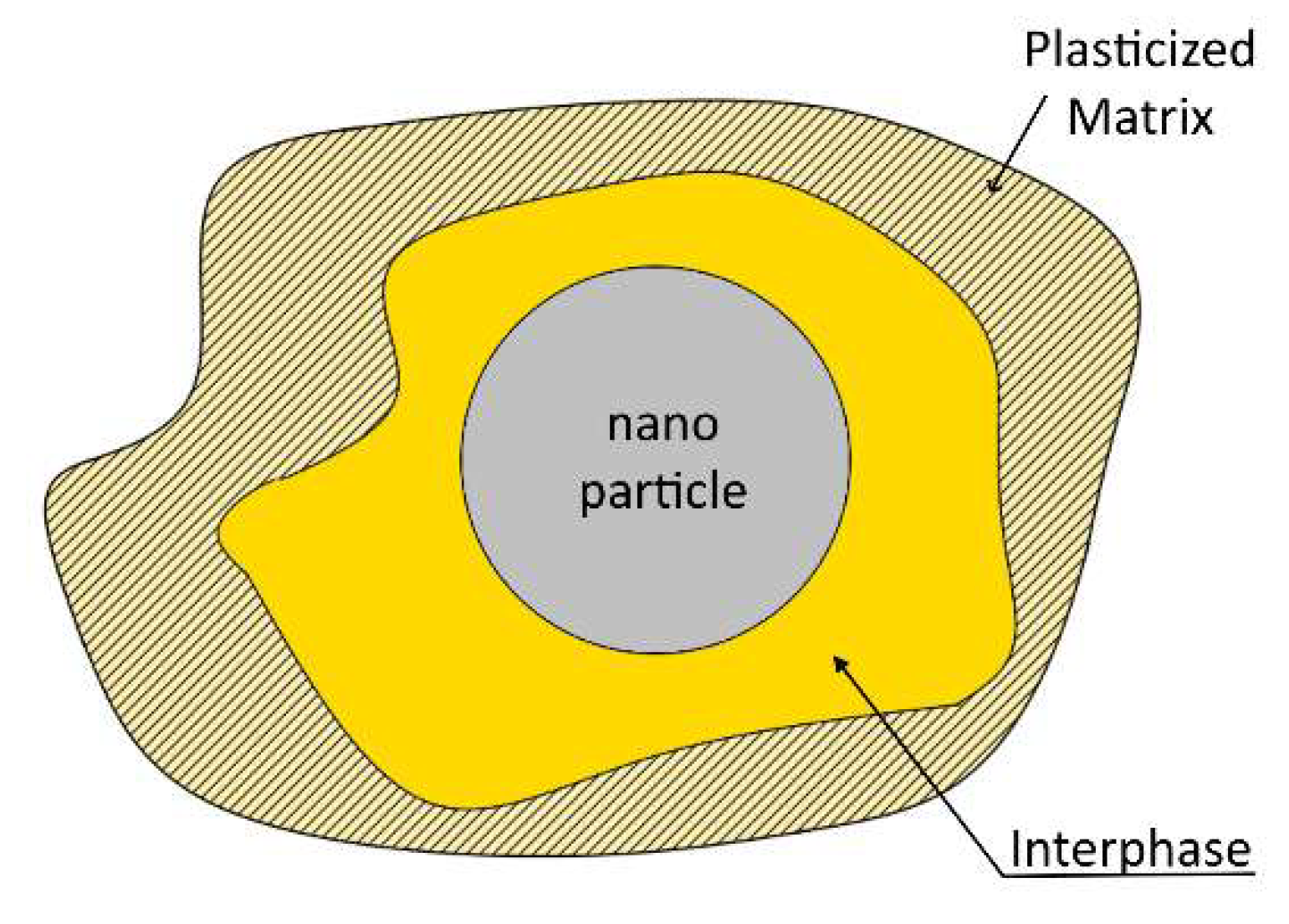
- Adding nano TiO2 in the epoxy matrix led to a decrease in the flexural modulus of all nanocomposites tested under all strain rates applied, except of the highest strain rate. Such a behavior can be attributed to the fact that as the size of nanoparticles approaches the molecular size of polymeric chains, instead of reinforcing the matrix they interfere with polymer macromolecules and thus delaying the crosslinking mechanism between polymer chains to take place. In addition, the creation of a filler–matrix interphase with intermediate properties affects the matrix as well as the overall nanocomposite properties.
- The flexural strength decreases with the increase of filler weight fraction at all strain rates, for the TiO2 nanocomposites. The decrease in flexural strength can be attributed to the imperfections and the voids introduced when the nanoparticles are added.
- The nano TiO2 seems to deteriorate the flexural properties of the epoxy resin. The material seems to have a rubber-like behavior, which means that it tends to develop larger deformations at lower stresses.
- The Property Prediction Model predicted extremely well the mechanical response of both micro- and nanocomposites for all values of TiO2 weight fractions and all displacement rates applied with a minimum deviation from experimental findings.
- Finally, through the application of the Property Prediction Model (PPM) and for any mechanical property, it is possible to accurately calculate the percentage contribution of the filler–matrix adhesion (degree of adhesion K) as well as of the filler dispersion into the matrix material (degree of dispersion, L). K and L values along with the interphasial considerations can give a better insight into understanding the overall mechanical and viscoelastic (displacement rate effects) of both micro- and nanocomposites.
Author Contributions
Funding
Conflicts of Interest
References
- Al-Ajaj, I.A.; Abd, M.M.; Jaffer, H.I. Mechanical Properties of Micro and Nano TiO2/Epoxy Composites. Int. J. Min. Met. Mech. Eng. 2013, 1, 2320. [Google Scholar]
- Al-Turaif, H.A. Effect of nano TiO2 particle size on mechanical properties of cured epoxy resin. Prog. Org. Coat. 2010, 6, 241–246. [Google Scholar] [CrossRef]
- Chatterjee, A.; Islam, M.S. Fabrication and characterization of TiO2–epoxy nanocomposite. Mater. Sci. Eng. A 2008, 487, 574–585. [Google Scholar] [CrossRef]
- Ng, C.B.; Schadler, L.S.; Siegel, R.W. Synthesis and mechanical properties of TiO2-epoxy nanocomposites. Nanostruct. Mater. 1999, 12, 507–510. [Google Scholar] [CrossRef]
- Wetzel, B.; Rosso, P.; Haupert, F.; Friedrich, K. Epoxy Nanocomposites—Fracture and Toughening Mechanisms, Eng. Fract. Mech. 2006, 73, 2375–2398. [Google Scholar] [CrossRef]
- Ahmad, F.N.; Jaafar, M.; Palaniandy, S.; Azizli, K.A.M. Effect of particle shape of silica mineral on the properties of epoxy composites. Compos. Sci. Technol. 2008, 68, 346–353. [Google Scholar] [CrossRef]
- Kim, B.C.; Park, S.W.; Lee, D.G. Fracture toughness of the nano-particle reinforced epoxy composite. Compos. Struct. 2008, 86, 69–77. [Google Scholar] [CrossRef]
- Ho, M.W.; Lam, C.K.; Lau, K.T.; Ng, D.H.; Hui, D. Mechanical properties of epoxy-based composites using nanoclays. Compos. Struct. 2006, 75, 415–421. [Google Scholar] [CrossRef]
- Zhao, R.; Luo, W. Fracture surface analysis on nano-SiO2/epoxy composite. Mater. Sci. Eng. A 2008, 483, 313–315. [Google Scholar] [CrossRef]
- Kurdi, A.; Wang, H.; Chang, L. Effect of nano-sized TiO2 addition on tribological behaviour of poly ether ether ketone composite. Tribol. Int. 2017, 117, 225–235. [Google Scholar] [CrossRef]
- Guo, X.; Guo, Q.; Nie, J.; Liu, Z.; Li, Z.; Fan, G.; Xiong, D.; Su, Y.; Fan, J.; Zhang, D. Particle size effect on the interfacial properties of SiC particle-reinforced Al-Cu-Mg composites. Mater. Sci. Eng. A 2018, 711, 643–649. [Google Scholar] [CrossRef]
- Zhou, Y.; Mallick, P.K. Effects of temperature and strain rate on the tensile behavior of unfilled and talc-filled polypropylene. Part I: Experiments. Polym. Eng. Sci. 2002, 42, 2449–2460. [Google Scholar] [CrossRef] [Green Version]
- Zabihzadeh, S.M. Flexural properties and orthotropic swelling behaviour of bagasse/thermoplastic composites. Bioresources 2010, 5, 650–660. [Google Scholar]
- Delhaye, V.; Clausen, A.H.; Moussy, F.; Othman, R.; Hopperstad, O.S. Influence of stress state and strain rate on the behaviour of a rubber-particle reinforced polypropylene. Int. J. Impact. Eng. 2011, 38, 208–218. [Google Scholar] [CrossRef] [Green Version]
- Reis, P.N.B.; Gorbatikh, L.; Ivens, J.; Lomov, S.V. Strain-rate sensitivity and stress relaxation of hybrid self-reinforced polypropylene composites under bending loads. Compos. Struct. 2019, 209, 802–810. [Google Scholar] [CrossRef]
- Zaiemyekeh, Z.; Liaghat, G.H.; Ahmadi, H.; Khan, M.K.; Razmkhah, O. Effect of strain rate on deformation behavior of aluminum matrix composites with Al2O3 nanoparticles. Mater. Sci. Eng. A 2019, 753, 276–284. [Google Scholar] [CrossRef] [Green Version]
- Prakash, C.; Emre Gunduz, I.; Oskay, C.; Tomar, V. Effect of interface chemistry and strain rate on particle-matrix delamination in An Energetic Material. Eng. Fract. Mech. 2018, 191, 46–64. [Google Scholar] [CrossRef]
- Cano, L.; Di Mauro, A.E.; Striccoli, M.; Curri, M.L.; Tercjak, A. Optical and Conductive Properties of As-Synthesized Organic-Capped TiO2 Nanorods Highly Dispersible in Polystyrene-block-poly (methyl methacrylate) Diblock Copolymer. ACS Appl. Mater. Interfaces 2014, 6, 11805–11814. [Google Scholar] [CrossRef]
- Li, Y.; Luo, J.; Hu, X.; Wang, X.; Liang, J.; Yu, K. Fabrication of TiO2 hollow nanostructures and their application in Lithium ion batteries. J. Alloy. Compd. 2015, 651, 685–689. [Google Scholar] [CrossRef]
- Kociubczyk, A.I.; Vera, M.L.; Schvezov, C.E.; Heredia, E.; Ares, A.E. TiO2 Coatings in Alkaline Electrolytes Using Anodic Oxidation Technique. Procedia Mater. Sci. 2015, 8, 65–72. [Google Scholar] [CrossRef] [Green Version]
- Madhusoodana, C.D.; Manjunath, S.P.; Das, R.N. Preparation of TiO2 membranes on silicon carbide supports for water filtration applications. Procedia Eng. 2012, 44, 939–941. [Google Scholar] [CrossRef] [Green Version]
- Plecenik, T.; Moško, M.; Haidry, A.A.; Ďurina, P.; Truchlý, M.; Grančič, B.; Gregor, M.; Roch, T.; Satrapinskyy, L.; Moskova, A.; et al. Fast highly-sensitive roomtemperature semiconductor gas sensor based on the nanoscale Pt–TiO2–Pt sandwich. Sens. Actuators B Chem. 2015, 207, 351–361. [Google Scholar] [CrossRef] [Green Version]
- Choi, K.I.; Lee, W.; Lee, S.H.; Lim, C. Synthesis of hierarchical hollow electrospun TiO2 nanofibers. Mater. Lett 2015, 158, 36–39. [Google Scholar] [CrossRef]
- Binu, K.G.; Shenoy, B.S.; Rao, D.S.; Pai, R. A variable viscosity approach for the evaluation of load carrying capacity of oil lubricated journal bearing with TiO2 nanoparticles as lubricant additives. Procedia Mater. Sci. 2014, 6, 1051–1067. [Google Scholar] [CrossRef] [Green Version]
- Purniawan, A.; French, P.J.; Pandraud, G.; Sarro, P.M. TiO2 Ald Nanolayer as Evanescent Waveguide for Biomedical Sensor Applications. Procedia Eng. 2010, 5, 1131–1135. [Google Scholar] [CrossRef] [Green Version]
- Kosmulski, M. Surface Charging and Points of Zero Charge; CRC Press: Boca Raton, FL, USA, 2009; ISBN 9781420051889. [Google Scholar]
- Papanicolaou, G.C.; Koutsomitopoulou, A.F.; Sfakianakis, A. Effect of thermal fatigue on the mechanical properties of epoxy matrix composites reinforced with olive pits powder. J. Appl. Polym. Sci. 2011, 124, 67–76. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Kontaxis, L.C.; Koutsomitopoulou, A.F.; Zaoutsos, S.P. Stress relaxation behavior of starch powder-epoxy resin composites. J. Appl. Polym. Sci. 2015, 132, 41697. [Google Scholar] [CrossRef]
- Rabbi, F. Ph.D. Thesis. Available online: http://scholarcommons.sc.edu/etd/2868 (accessed on 11 November 2019).
- Papanicolaou, G.C.; Kostopoulos, V.; Kontaxis, L.C.; Kollia, E.; Kotrotsos, A. A comparative study between epoxy/Titania micro-and nanoparticulate composites thermal and mechanical behavior by means of particle–matrix interphase considerations. Polym. Eng. Sci. 2018, 58, 1146–1154. [Google Scholar] [CrossRef]
- Carponcin, D.; Dantras, E.; Dandurand, J.; Aridon, G.; Levallois, F.; Cadiergues, L.; Lacabanne, C. Discontinuity of physical properties of carbon nanotube/polymer composites at the percolation threshold. J. Non-Cryst. Solids 2014, 392, 19–25. [Google Scholar] [CrossRef] [Green Version]
- Fu, Y.F.; Li, J.; Zhang, F.Q.; Xu, K. The preparation and the friction and wear behaviours of TiO2/CNT/PI composite film. J. Exp. Nanosci. 2016, 11, 459–469. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, H.; Antunes, M.; Velasco, J. Effects of Carbon Nanotubes/Graphene Nanoplatelets Hybrid Systems on the Structure and Properties of Polyetherimide-Based Foams. Polymers 2018, 10, 348. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jacob, G.C.; Starbuck, J.M.; Fellers, J.F.; Simunovic, S.; Boeman, R.G. Strain rate effects on the mechanical properties of polymer composite materials. J. Appl. Polym. Sci. 2004, 94, 296–301. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Michalopoulou, M.V.; Anifantis, N.K. Thermal stresses in fibrous composites incorporating hybrid interphase regions. Compos. Sci. Technol. 2002, 62, 1881–1894. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Anifantis, N.K.; Keppas, L.K.; Kosmidou, T.V. Stress analysis of short fiber-reinforced polymers incorporating a hybrid interphase region. Compos. Interfaces 2007, 14, 131–152. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Keppas, L.K.; Anifantis, N.K. Finite element prediction of debonding onset in short fiber reinforced polymers incorporating a hybrid interphase region. Compos. Interfaces 2008, 15, 477–493. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Bouboulas, A.S.; Anifantis, N.K. Thermal expansivities in fibrous composites incorporating hybrid interphase region. Compos. Struct. 2009, 88, 542–547. [Google Scholar] [CrossRef]
- Portan, D.V.; Papanicolaou, G.C. Properties predictive modeling through the concept of a hybrid interphase existing between phases in contact. AIP Conf. Proc. 2018, 1932, 030033. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Baxevanakis, C. Viscoelastic Modelling and Strain-Rate Behaviour of Plasticized Poly (Vinyl Chloride). J. Mater. Sci. 1991, 26, 4323–4330. [Google Scholar] [CrossRef]
- Theocaris, P.S.; Papanicolaou, G.C.; Kontou, E.A. The Effect of Filler-Volume Fraction and Strain Rate on Tensile Properties of Iron-Epoxy Particulate Composites. J. Reinf. Plast. Compos. 1982, 1, 206–224. [Google Scholar] [CrossRef]
- Papanicolaou, G.C.; Kontaxis, L.C.; Manara, A.E. behaviour and modelling of nano and micro TiO2 powder- epoxy resin composite. Cienc. Tecnol. Mater. 2016, 28, 138–146. [Google Scholar] [CrossRef]

| Property | TiO2 Nanoparticles | TiO2 Microparticles |
|---|---|---|
| Particle size | 21 nm | 0.2 μm |
| Molar Mass | 79.86 g/mol | 79.86 g/mol |
| Specific Surface Area | 35–65 m2/g (BET) | 12 m2/g (BET) |
| Density | 4.26 g/cm3 | 4.1 g/cm3 |
| Melting point | 1843 °C | 1843 °C |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papanicolaou, G.C.; Manara, A.E.; Kontaxis, L.C. Experimental and Prediction Study of Displacement-Rate Effects on Flexural Behaviour in Nano and Micro TiO2 Particles-Epoxy Resin Composites. Polymers 2020, 12, 22. https://doi.org/10.3390/polym12010022
Papanicolaou GC, Manara AE, Kontaxis LC. Experimental and Prediction Study of Displacement-Rate Effects on Flexural Behaviour in Nano and Micro TiO2 Particles-Epoxy Resin Composites. Polymers. 2020; 12(1):22. https://doi.org/10.3390/polym12010022
Chicago/Turabian StylePapanicolaou, George C., Aikaterini E. Manara, and Lykourgos C. Kontaxis. 2020. "Experimental and Prediction Study of Displacement-Rate Effects on Flexural Behaviour in Nano and Micro TiO2 Particles-Epoxy Resin Composites" Polymers 12, no. 1: 22. https://doi.org/10.3390/polym12010022
APA StylePapanicolaou, G. C., Manara, A. E., & Kontaxis, L. C. (2020). Experimental and Prediction Study of Displacement-Rate Effects on Flexural Behaviour in Nano and Micro TiO2 Particles-Epoxy Resin Composites. Polymers, 12(1), 22. https://doi.org/10.3390/polym12010022








