Adsorption of a Helical Filament Subject to Thermal Fluctuations
Abstract
1. Introduction
2. Simulations
2.1. Model
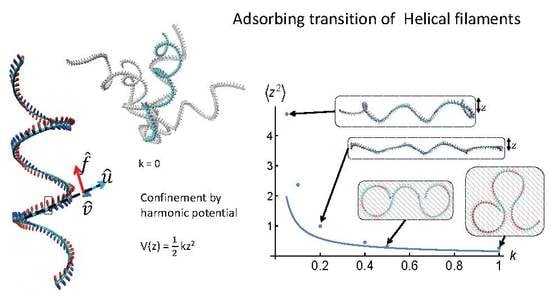
2.2. Simulation Results: H-Filaments Confined by a Harmonic Potential
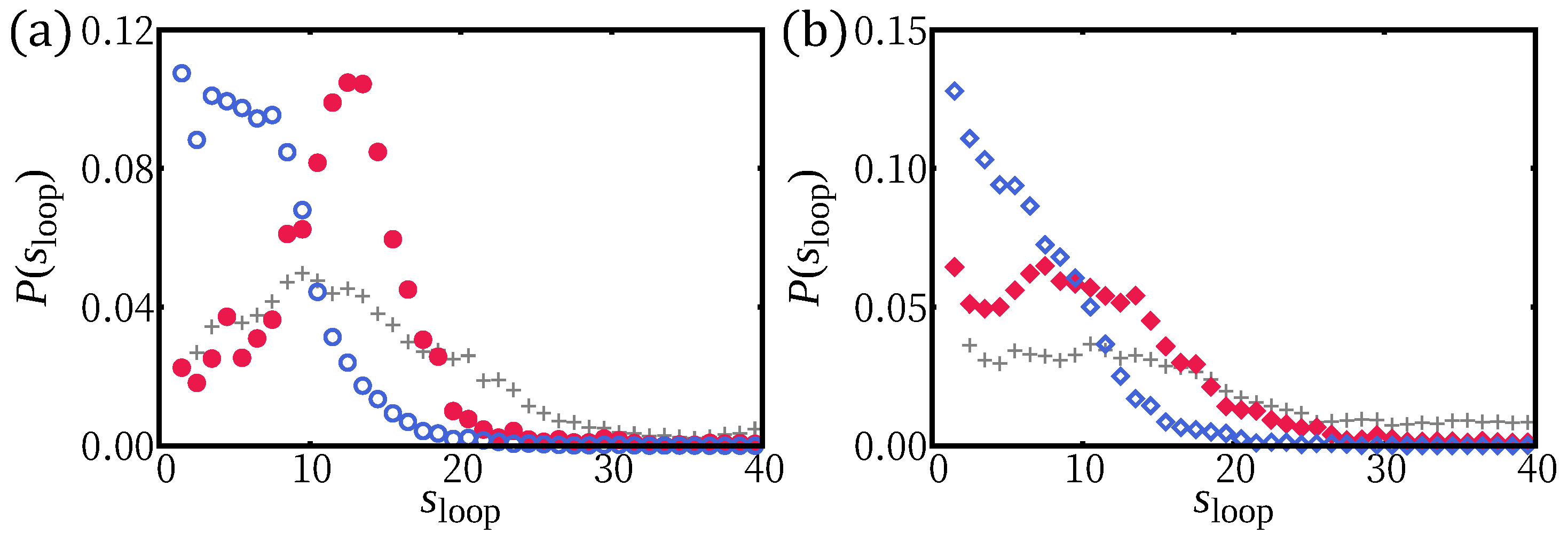
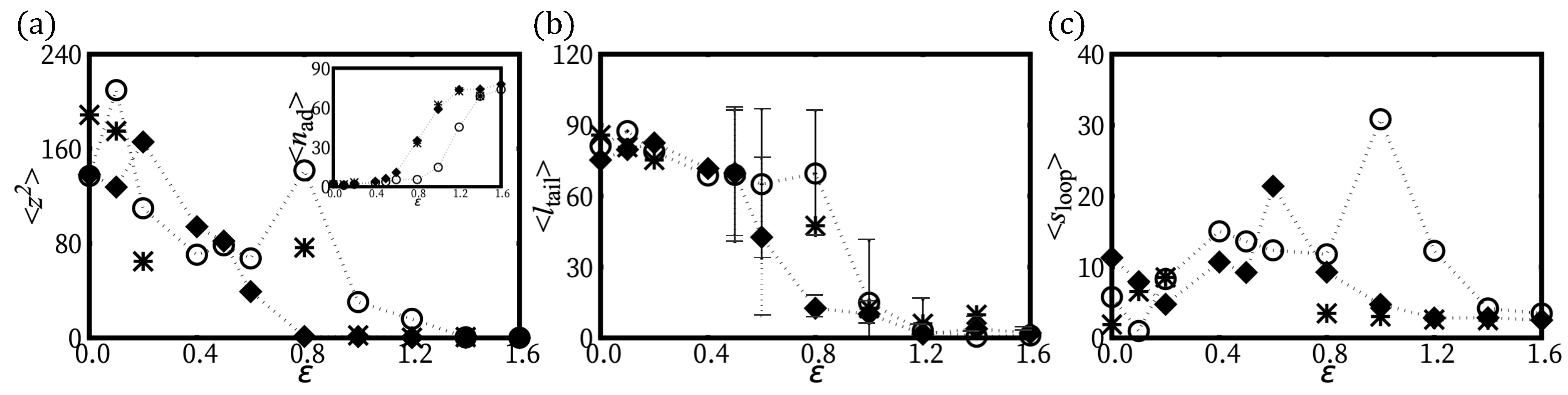
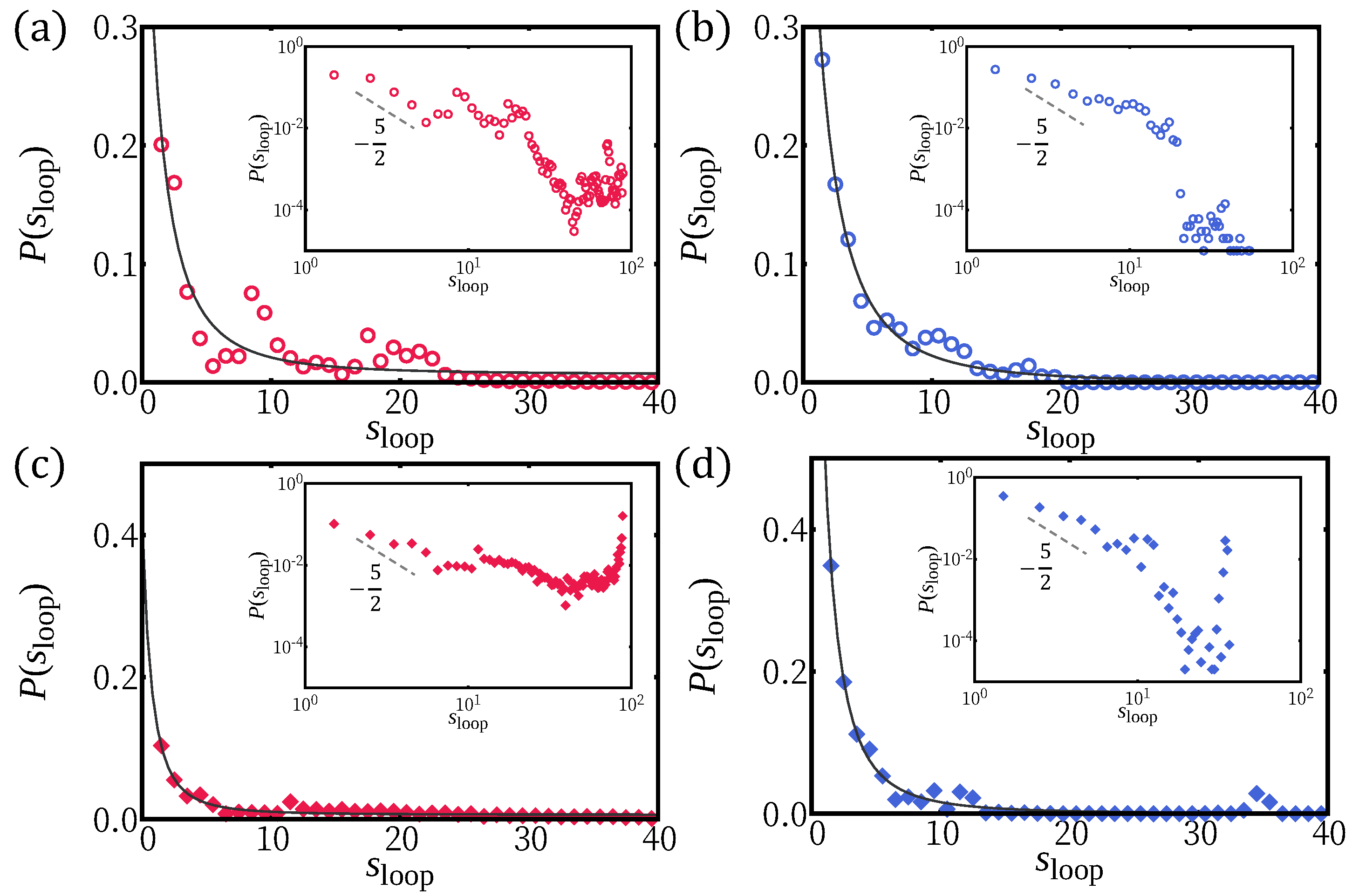
2.3. Simulation Results: H-Filaments Adsorbed in a Localized Surface Potential
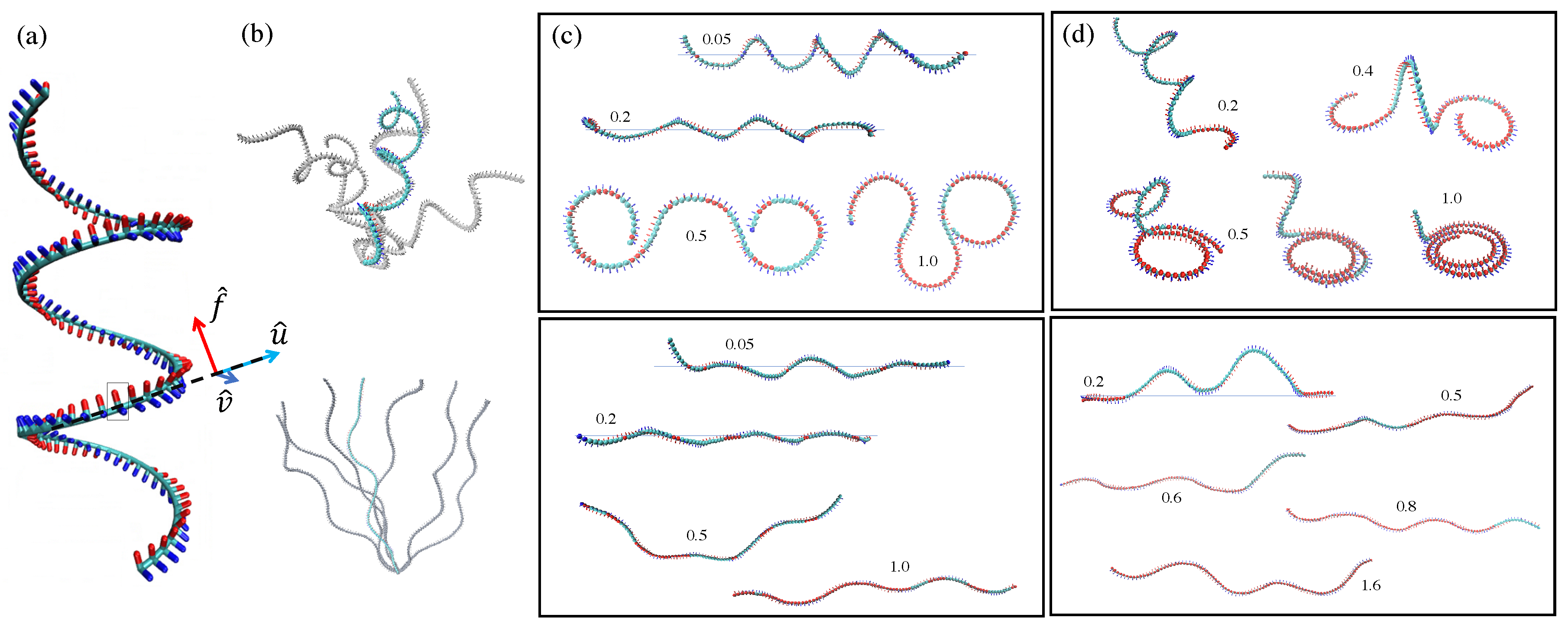
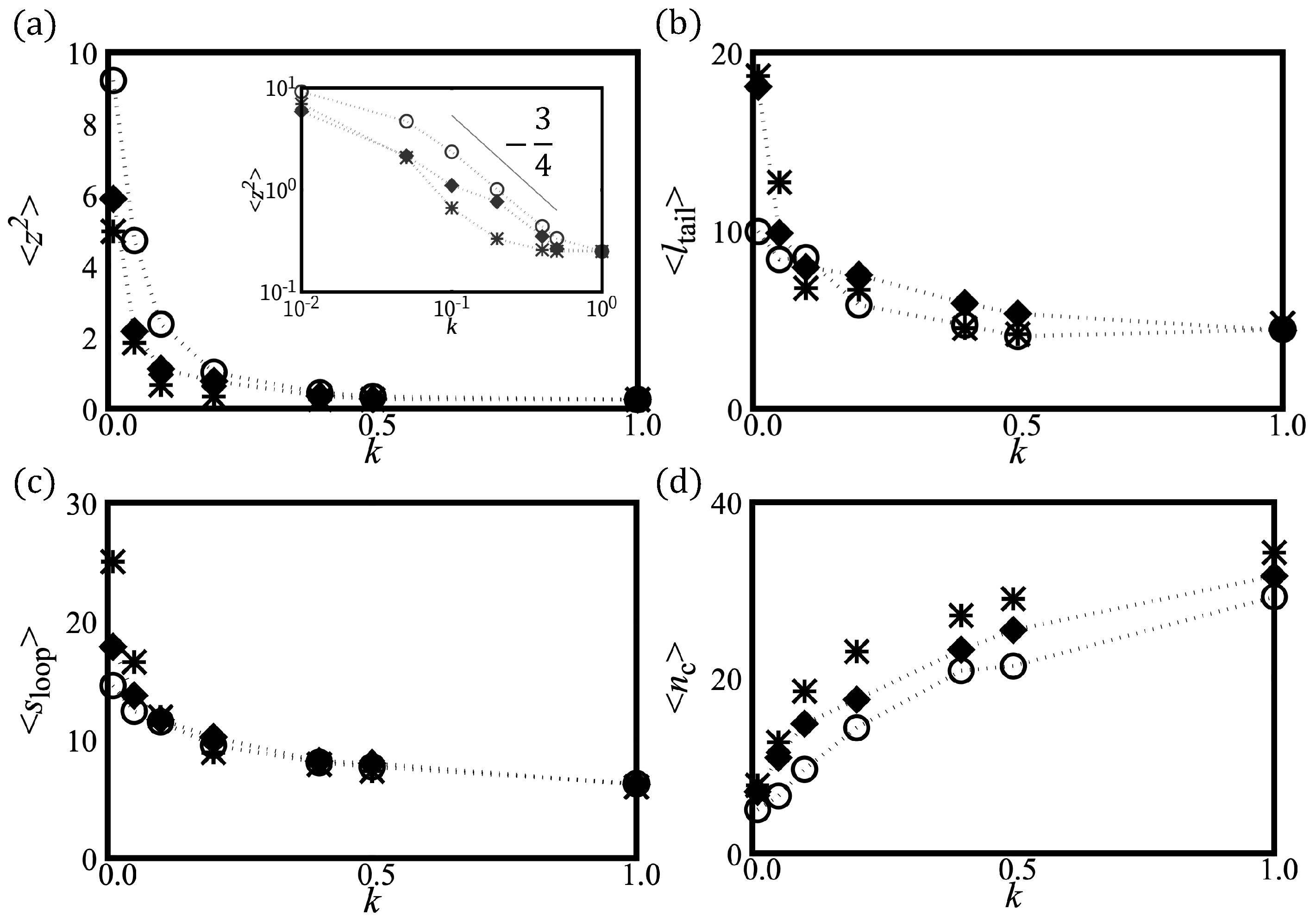
2.3.1. Adsorption of H-Filaments,
2.3.2. Adsorption of H-Filaments,
3. Theory
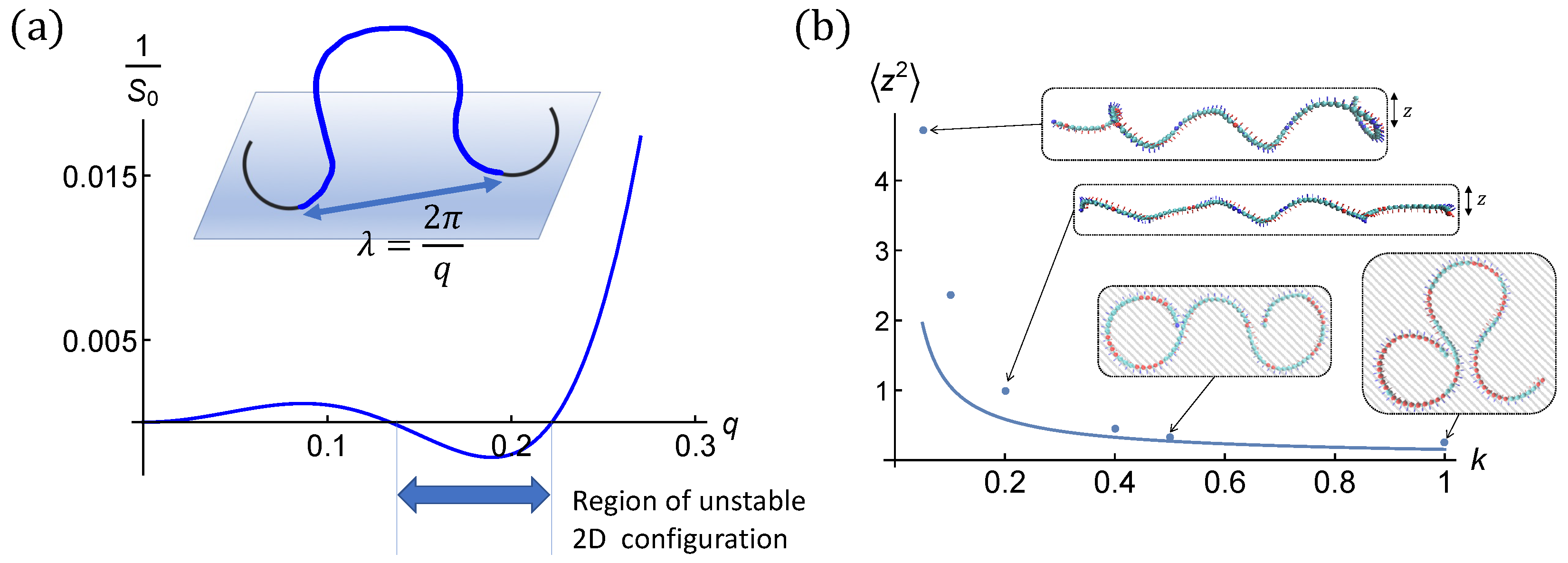
3.1. Instability of the 2D Configuration
- -
- For , only the largest root is positive. All long wavelength are unstable. This corresponds to the case where wavy shapes are favored over circular ones in 2D.
- -
- For , the two roots are positive. The low q-modes are stable. Intermediate wavelength are unstable. This suggests (it is only a linear stability study) that, when the helical chain goes on the surface, it does so by forming loops of intermediate length. This corresponds to the case where circular shapes are favored over wavy ones in 2D.
3.2. H-Filaments Maintained by a Harmonic Surface Potential
3.3. Stability of a Finite Helical Strand
3.4. H-Filaments Adsorbed in a Localized Surface Potential
4. Conclusions
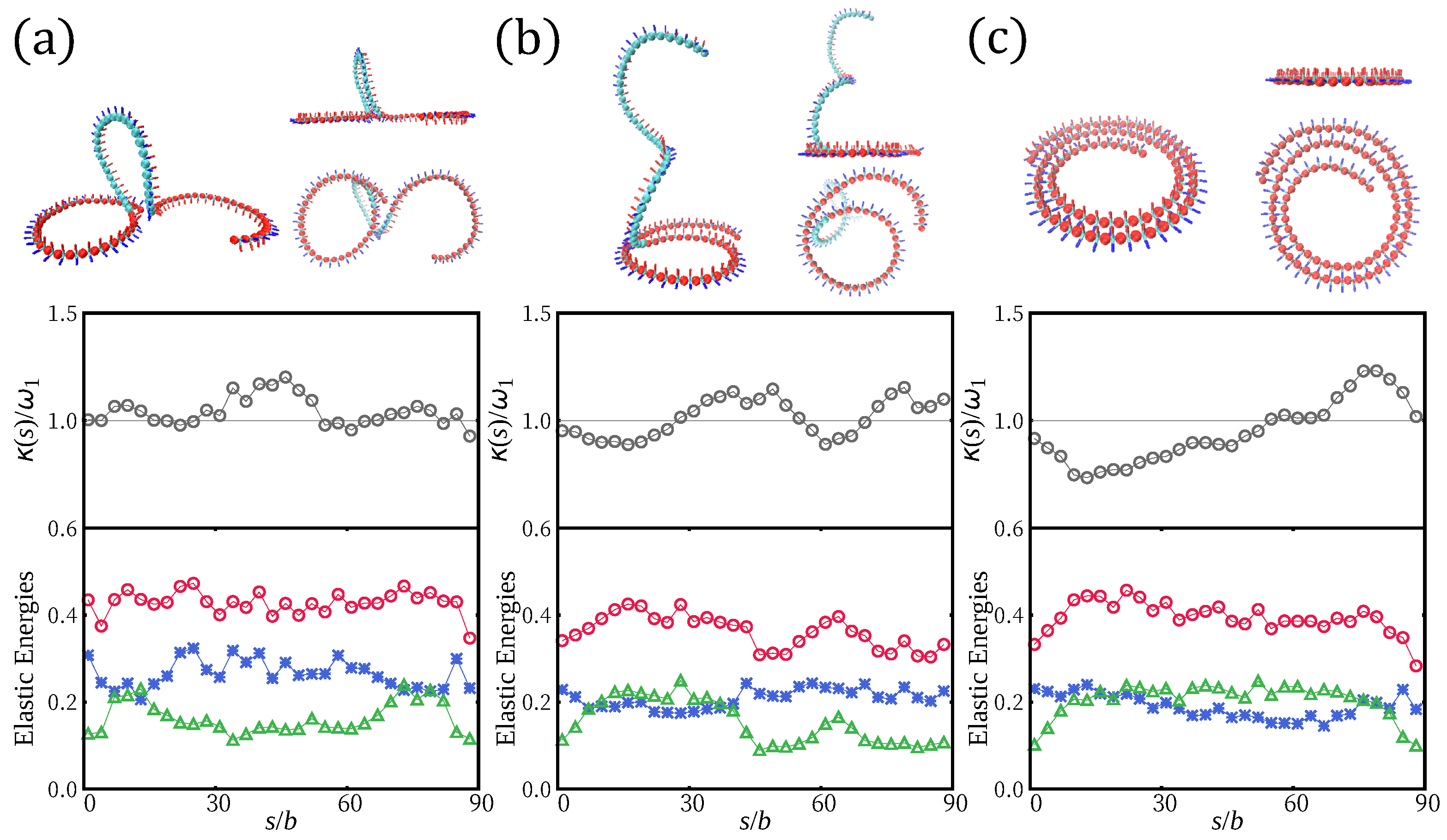
- (a)
- Wavy shapes or 3D loops which avoid self-crossing of the chain, where the frustration of the configuration is mainly localized at some spots along the chain.
- (b)
- Spiral shapes, where the frustration is smeared out and terminal sections escape into 3D tails.
Author Contributions
Funding
Conflicts of Interest
Appendix A. Simulation Method

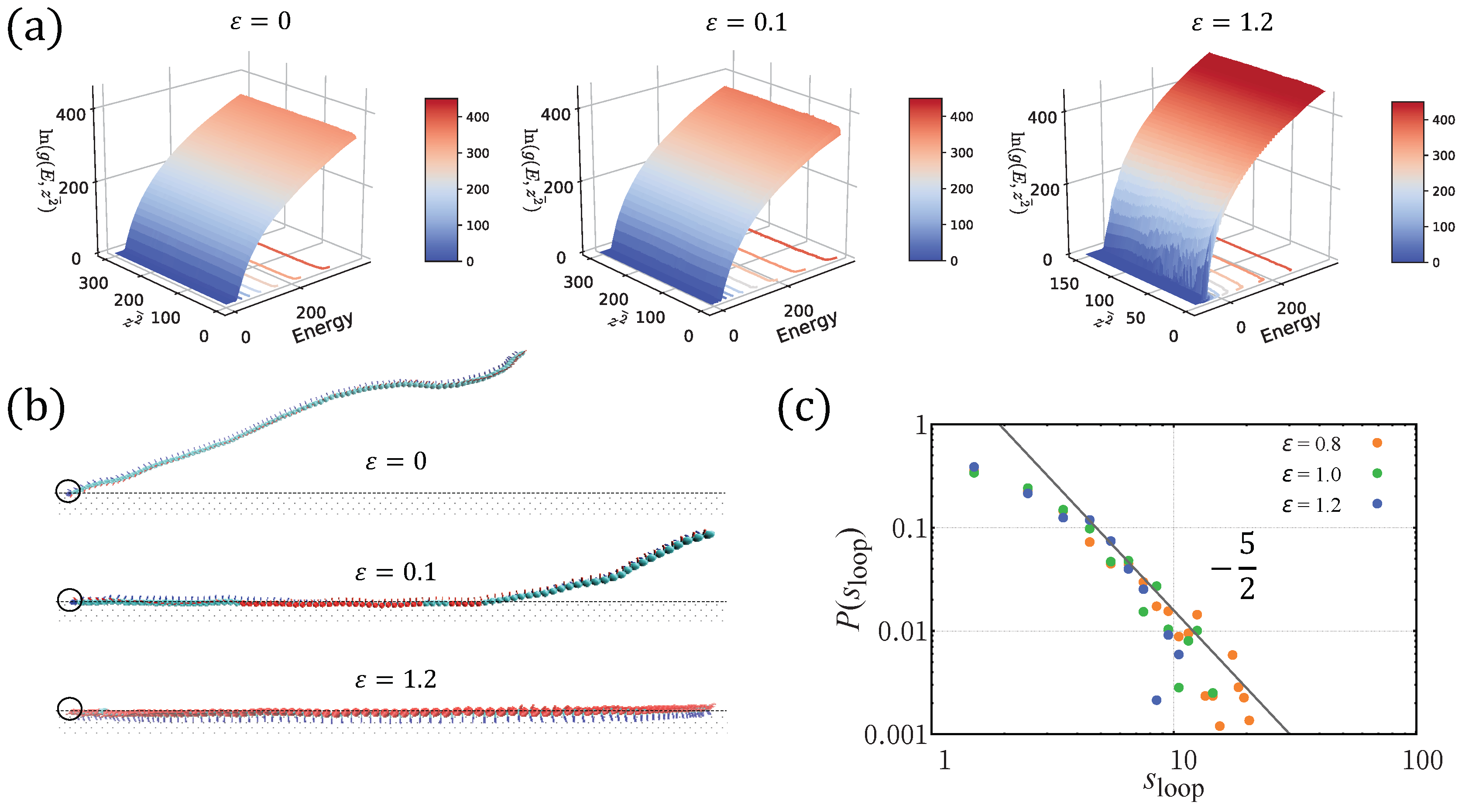
Appendix B. Derivation of Partition Sum
References and Notes
- Fleer, G.; Stuart, M.C.; Scheutjens, J.; Cosgrove, T.; Vincent, B. Polymers at Interfaces; Springer: London, UK, 1993. [Google Scholar]
- Granick, S. Perspective: Kinetic and mechanical properties of adsorbed polymer layers. Eur. Phys. J. E 2002, 64, 421–424. [Google Scholar] [CrossRef] [PubMed]
- Torchilin, V.P.; Trubetskoy, V.S.; Whiteman, K.R.; Ferruti, P.; Veronese, F.M.; Celiceti, P. New Synthetic Amphiphilic Polymers for Steric protection of Liposomes In Vivo. J. Pharm. Sci. 1995, 84, 1049–1053. [Google Scholar] [CrossRef] [PubMed]
- Torchilin, V.P.; Trubetskoy, V.S. Which Polymer can Make nanoparticulate drug delivery carriers long-circulating. Adv. Drug Deliv. Rev. 1995, 16, 141–155. [Google Scholar] [CrossRef]
- Andreeva, D.V.; Fix, J.; Möhwald, H.; Shchukin, D.G. Self-Healing Anticorrosion Coatings Based on pH-Sensitive Polyelectrolyte/Inhibitor Sandwichlike Nanostructures. Adv. Mater. 2008, 20, 2789–2794. [Google Scholar] [CrossRef] [PubMed]
- Sinden, R.R. DNA Structure and Function; Elsevier: San Diego, CA, USA, 1994. [Google Scholar]
- Holmes, K.C.; Popp, D.; Gebhard, W.; Kabsch, W. Atomic model of the actin filament. Nature 1990, 347, 37–44. [Google Scholar] [CrossRef] [PubMed]
- Venier, P.; Maggs, A.C.; Carlier, M.F.; Pantaloni, D. Analysis of microtubule rigidity using hydrodynamic flow and thermal fluctuations. J. Biol. Chem. 1994, 269, 13353. [Google Scholar]
- Volodin, A.; Ahlskog, M.; Seynaeve, E.; Van Haesendonck, C. Imaging the Elastic Properties of Coiled Carbon Nanotubes with Atomic Force Microscopy. Phys. Rev. Lett. 2000, 84, 3342. [Google Scholar] [CrossRef]
- Bassen, D.M.; Hou, Y.; Bowser, S.S.; Banavali, N.K. Maintenance of electrostatic stabilization in altered tubulin lateral contacts may facilitate formation of helical filaments in foraminifera. Sci. Rep. 2016, 6, 31723. [Google Scholar] [CrossRef]
- Li, X.; Holmes, C.K.; Lehman, W.; Jung, H.; Fischer, S. The Shape and Flexibility of Tropomyosin Coiled Coils: Implications for Actin Filament Assembly and Regulation. J. Mol. Biol. 2010, 395, 327. [Google Scholar] [CrossRef]
- Yogurtcu, O.; Wolgemuth, C.; Sun, S. Mechanical Response and Conformational Amplification in a-Helical Coiled Coils. Biophys. J. 2010, 99, 3895–3904. [Google Scholar] [CrossRef]
- Wada, H.; Netz, R. Hydrodynamics of helical-shaped bacterial motility. Phys. Rev. E 2009, 80, 021921. [Google Scholar] [CrossRef] [PubMed]
- Kühn, M.; Schmidt, F.; Eckhardt, B.; Thormann, K.M. Bacteria exploit a polymorphic instability of the flagellar filament to escape from traps. Proc. Natl. Acad. Sci. USA. 2017, 114, 6340–6345. [Google Scholar] [CrossRef] [PubMed]
- Wolgemuth, C.W.; Inclan, Y.; Quan, J.; Mukherjee, S.; Oster, G.; Koehl, M.A.R. How to make a spiral bacterium. Phys. Biol. 2005, 2, 189. [Google Scholar] [CrossRef] [PubMed]
- Taute, K.M.; Pampaloni, F.; Frey, E.; Florin, E.L. Microtubule Dynamics Depart from the Wormlike Chain Model. Phys. Rev. Lett. 2008, 100, 028102. [Google Scholar] [CrossRef] [PubMed]
- Mohrbach, H.; Johner, A.; Kulić, I. Cooperative lattice dynamics and anomalous fluctuations of microtubules. Eur. Biophys. J. 2012, 41, 217. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Khokhlov, A. Statistical Physics of Macromolecules; AIP: New York, NY, USA, 1994. [Google Scholar]
- Köster, S.; Pfohl, T. An in vitro model system for cytoskeletal confinement. Cell. Motil. Cycloskeleton 2009, 66, 771. [Google Scholar] [CrossRef]
- Nödig, B.; Köster, S. Intermediate Filaments in Small Configuration Spaces. Phys. Rev. Lett. 2012, 108, 088101. [Google Scholar] [CrossRef]
- Bouzar, L.; Mueller, M.M.; Messina, R.; Noeding, B.; Koester, S.; Mohrbach, H.; Kulic, I.M. Helical Superstructure of Intermediate Filaments. Phys. Rev. Lett. 2019, 122, 098101. [Google Scholar] [CrossRef]
- Sanchez, T.; Kulić, I.M.; Dogic, Z. Circularization, photomechanical switching, and a supercoiling transition of actin filaments. Phys. Rev. Lett. 2010, 104, 098103. [Google Scholar] [CrossRef]
- Riveline, D. Études du FIlament D’actine et du Moteur Actine-Myosine Sous L’action de Forces Extérieures. Ph.D. Thesis, Paris, France, 1997. Available online: https://www.theses.fr/1997PA066758 (accessed on 9 January 2020).
- Nam, G.; Lee, N.-K.; Mohrbach, H.; Johner, A.; Kulić, I.M. Helices at interfaces. EPL 2012, 100, 28001. [Google Scholar] [CrossRef]
- Chae, M.-K.; Kim, Y.; Johner, A.; Lee, N.-K. Super-helical filaments at surfaces: Dynamics and elastic responses. Soft Matter 2018, 48, 2346–2356. [Google Scholar] [CrossRef] [PubMed]
- De Gennes, P.G. Polymers at an interface; a simplified view. Adv. Colloid Interface Sci. 1987, 27, 189. [Google Scholar] [CrossRef]
- Semenov, A.N.; Bonet-Avalos, J.; Johner, A.; Joanny, J.F. Adsorption of Polymer Solutions onto a Flat Surface. Macromolecules 1996, 29, 2179. [Google Scholar] [CrossRef]
- Lee, N.-K.; Johner, A. Defects on Semiflexible Filaments: Kinks and Twist-kinks. J. Korean Phys. Soc. 2016, 68, 923–928. [Google Scholar] [CrossRef]
- Fierling, J.; Johner, A.; Kulić, I.M.; Mohrbach, H.; Müller, M.M. How bio-filaments twist membranes. Soft Matter 2016, 12, 5747. [Google Scholar] [CrossRef]
- Quint, D.A.; Gopinathan, A.; Grason, G.M. Conformational collapse of surface-bound helical filaments. Soft Matter 2012, 8, 9460. [Google Scholar] [CrossRef]
- Aggeli, A.; Nyrkova, I.; Bell, M.; Harding, R.; Carrick, L.; McLeish, T.; Semenov, A.; Boden, N. Hierarchical self-assembly of chiral rod-like molecules as a model for peptide beta-sheet tapes, ribbons, fibrils, and fibers. Proc. Natl. Acad. Sci. USA 2001, 98, 11857–11862. [Google Scholar] [CrossRef]
- Friedhoff, P.; von Bergen, M.; Mandelkow, E.M.; Mandelkow, E. Structure of tau protein and assembly into paired helical filaments. Biochim. Biophys. Acta (BBA) Mol. Basis Dis. 2000, 1502, 122–132. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Efficient, Multiple-Range RandomWalk Algorithm to Calculate the Density of States. Phys. Rev. Lett. 2001, 86, 2050–2053. [Google Scholar] [CrossRef]
- Wang, F.; Landau, D.P. Determining the density of states for classical statistical models: A random walk algorithm to produce a flat histogram. Phys. Rev. E 2001, 64, 056101. [Google Scholar] [CrossRef]
- Yan, Q.; Faller, R.; de Pablo, J.J. Density-of-states Monte Carlo method for simulation of fluids. J. Chem. Phys. 2002, 116, 8745–8749. [Google Scholar] [CrossRef]
- Rathore, N.; de Pablo, J.J. Monte Carlo simulation of proteins through a random walk in energy space. J. Chem. Phys. 2002, 116, 7225–7230. [Google Scholar] [CrossRef]
- Chirico, G.; Langowski, J. Kinetics of DNA supercoiling studied by Brownian dynamics simulation. Biopolymers 1994, 34, 415. [Google Scholar] [CrossRef]
- Here we reproduce relations expressing the radius and pitch of a helix as a function of its curvature and torsion. One possible representation of the helix in terms of the Euler angles defined below is: ψ = π/2, tanθ = ω1/ω3, ϕ′ = ω3/cosθ.
- Bouzar, L.; Muller, M.M.; Gosselin, P.; Kulic, I.M.; Mohrbach, H. Squeezed helical elastica. Eur. Phys. J. E 2016, 39, 114. [Google Scholar] [CrossRef] [PubMed]
- Kim, Y.; Chae, M.-K.; Lee, N.-K.; Jung, Y.; Johner, A. Irreversible Adsorption of Wormlike Chains: Alignment Effects. Macromolecules 2017, 50, 6285–6292. [Google Scholar] [CrossRef]
- Eslami, H.; Müller-Plathe, F. How thick is the interphase in an ultrathin polymer film Coarse-grained molecular dynamics simulations of polyamide-6, 6 on graphene. J. Phys. Chem. C 2013, 117, 5249–5257. [Google Scholar] [CrossRef]
- Baschnagel, J.; Meyer, H.; Wittmer, J.; Kulić, I.M.; Mohrbach, H.; Ziebert, F.; Nam, G.; Lee, N.-K.; Johner, A. Semiflexible Chains at Surfaces: Worm-Like Chains and beyond. Polymers 2016, 8, 286. [Google Scholar] [CrossRef]
- Lee, N.-K.; Jung, Y.; Johner, A. Irreversible Adsorption of Worm-Like Chains. Macromolecules 2015, 48, 7681–7688. [Google Scholar] [CrossRef]
- Zhou, C.; Schulthess, T.C.; Torbrügge, S.; Landau, D.P. Wang-Landau Algorithm for Continuous Models and Joint Density of States. Phys. Rev. Lett. 2006, 96, 120201. [Google Scholar] [CrossRef]
- We may for example impose the constraint that the square of the sums vanish by a common “Lagrange multiplier” λ, but unlike the usual technique let λ go to infinity. It is then enough to keep the leading quadratic term in lambda, which sets the determinant apart from an unimportant numerical prefactor.
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chae, M.-K.; Kim, Y.; Johner, A.; Lee, N.-K. Adsorption of a Helical Filament Subject to Thermal Fluctuations. Polymers 2020, 12, 192. https://doi.org/10.3390/polym12010192
Chae M-K, Kim Y, Johner A, Lee N-K. Adsorption of a Helical Filament Subject to Thermal Fluctuations. Polymers. 2020; 12(1):192. https://doi.org/10.3390/polym12010192
Chicago/Turabian StyleChae, M.-K., Y. Kim, A. Johner, and N.-K. Lee. 2020. "Adsorption of a Helical Filament Subject to Thermal Fluctuations" Polymers 12, no. 1: 192. https://doi.org/10.3390/polym12010192
APA StyleChae, M.-K., Kim, Y., Johner, A., & Lee, N.-K. (2020). Adsorption of a Helical Filament Subject to Thermal Fluctuations. Polymers, 12(1), 192. https://doi.org/10.3390/polym12010192